Energy and Power Engineering, 2010, 2, 122-126
doi:10.4236/epe.2010.22017 Published Online May 2010 (http://www. SciRP.org/journal/epe)
Anisotropic Scattering for a Magnetized Cold
Plasma Sphere
Yingle Li1, Mingjun Wang1, Qunfeng Dong2, Gaofeng Tang1
1Institute of Radio Wave Propagation & Scattering, Xianyang Normal University, Xian Yang, China
2Northwestern Polytechnical University, Xi'an, China
Received December 10, 2009; revised February 6, 2010; accepted March 9, 2010
Abstract
The transformation of parameter tensors for anisotropic medium in different coordinate systems is derived.
The electric field for a magnetized cold plasma sphere and the general expression of scattering field from
anisotropic target are obtained. The functional relations of differential scattering cross section and the RCS
for the magnetized plasma sphere are presented. Simulation results are in agree with that in the literatures,
which shows the method used and results obtained are correct and the results provide a theoretical base for
anisotropic target identification etc.
Keywords: Anisotropy, Scattering, Plasma
1. Introduction
Plasma is an anisotropic medium in the outside magnetic
field. It has widely applied fields such as modern Radar
system, antenna system and target concealing and thus
has been of increasing interest [1-4]. In [5], the E.M.
scattering features for a conductor sphere coated with
plasma are researched by expanding the electromagnetic
field into a series of vector spherical functions. The
propagation and absorbability of a circular polarizing
E.M. wave in asymmetric plasma are also studied [6,7],
some results are tested with experiments. The interaction
of an E.M. wave and an inhomogeneous plasma slab
with electron distribution in the form of partially linear
and sinusoidal profiles [8] is researched in which it has
been found that inhomogeneous plasma slab can be used
as a broad band radar absorbing layer. The scattering
characteristics of target coated with plasma are re-
searched [9] by using physical optical and input imped-
ance methods. Other targets coated with plasma are
studied [10] based on the medium laminar modeling and
the effect induced by the plasma parameters on scattering
features is analyzed. In recent years, the interaction of
anisotropic targets with light, electromagnetic wave also
has been of great interest [11,12]. The research tech-
niques of scattering wave from anisotropic medium and
plasma can be divided into three, namely, analytical
method, approximation method and numeration. The
later two are based on the first. In some literatures, the
changes of elements of dielectric tensor and permeability
tensor with coordinate systems are ignored, the or-
thonormalities of spherical vector wave functions based
on the Helmholtz equation derived in the isotropic me-
dium are also ignored and being directly used them to the
anisotropic medium. So some errors are inevitable in
those obtained results. On the other hand the expression
of scattering field from a magnetized cold plasma target
is not much published. In the present paper, the expres-
sion of the electric field inside & outside a magnetized
cold plasma spherical target is presented in detail based
on the scale transformation theory of the electromagnetic
field by transforming the dielectric tensor in the right
angle coordinate system into the spherical system. A
formula of computing the scattering field from a general
anisotropic target is then developed. Based on the for-
mulae, the Rayleigh scattering features of a magnetized
plasma sphere are researched. The effects induced on the
feature by the factors of electric density, incident angle
and outside magnetic field etc. are demonstrated. The
time-harmonic factor
j
t
e

is used in this paper.
2. Research of Rayleigh Scattering from a
Magnetized Plasma Sphere
2.1. Expressions of Electric Fields inside and
outside a Magnetized Cold Plasma Sphere
Assume a magnetized cold plasma sphere to have radius
R0 and its centre to be located at the origin of the primary

Y. L. LI ET AL.123
coordinate system Σ. The outside magnetic field is
in z-axis. The dielectric constant tensor of this plasma
sphere is given as [5]
0
B
00
1
0
ε0
00
p
rp
j
εj

 










(1)
By utilizing the relation between D and E and the rela-
tion between the vectors in right angle system and
spherical system, we can obtain the expression of the
dielectric constant tensor in spherical coordinate system
as
11 1213
021 2223
31 3233











ε

(2)
where



2
11 1
12 1
13
2
22 11
23 33
1221 13313223
cos
cos sin
sin
cos
cos ,
,,
p
p
j
j
 


 


 
 
 

 
 

3
0
23
0
22
0
22
1
p
ne B
m
eB
m






,
2
12
0
1ne
m



 ,
2
2
0
22
0
22
1
1
ne
m
eB
m






n, m are the electron density and electron mass respec-
tively,

the angle frequency of incident wave. Expres-
sion (2) indicates that the dielectric tensor is relative to
the observing point. When the frequency is low, the con-
dition 0
R

 is satisfied, it is so approximately con-
sidered that the magnetized cold plasma sphere locates in
the electrostatic field [13,14]. The plasma has not electric
charge in whole, according to the formulae 0,

D
and considering that the differential of poten-
tial u is not relative to the order for x and y, the differen-
tial equation of u is obtained as in the primary coordinate
system
uE
22 2
1
22 2
0
uu u
xy z

 
 
  (3)
Now, a scale coordinate system Σ ’ is introduced as a
new coordinate system. The coordinates of this system
are indicated with x’, y’ and z’. The relation of coordi-
nates between the two systems is written as
1
',','
x
yz
xyz



The differential equation of the potential in the
scale coordinate system is derived by substituting the
above expressions into Equation (3) and using the
condition u =u’ [14] at any spatial point, and it is ex-
pressed as
222
222
'''
0
'''
uuu
xyz



 (4)
The condition u = u’ is understandable, for the poten-
tial is defined as the work done by the electric field to
move a unit charge from one point to the reference point,
namely W/q, so both the numerator and the denominator
are scale invariants. Equation (4) shows that a mag-
netized cold plasma sphere in the primary coordinate
system is transformed into an isotropic sphere in the
scale coordinate system from the view point electric
potential equation. This manipulation can greatly sim-
plify the electromagnetic scattering problems. It is
well known that the solution of Equation (4) can be
obtained by using the method of separation of vari-
ables as follows:



,
,
,
,
'',','' cos'cos
'cos'sin'
nm
mn n
mn
nm
mn n
mn
uRa RPm
cRP m
'







 (5)
Expression (5) is a general solution in the scale coor-
dinate system. The parameters in the two coordinate sys-
tems can be found in literature [10]. The electric potential
outside the sphere is expressed as
 

,
1,
1
,
,
,1
,
,,cos cos
cos sin
mn nm
mn n
n
mn
mn
nm
mn n
n
mn
f
uRe RPm
R
h
g
RP
Rm
















(6)
On the surface of the sphere, the electric potential in-
side the sphere is equal to that outside the sphere and the
electric displacement D is continuous in the normal di-
rection, namely
00
0
0
1
1
011 12130
11
sin
RR RR
R
R
RR
uu
u uu u
RR RR
 





   
 



(7)
Inserting Expressions (5), (6) and (7) into the above
conditions yields the solution of electric potential inside
and outside a magnetized cold plasma sphere as



22
1
22
32
3
,, coscossin
244
32 sin sin
44
p
p
p
p
BB jC
A
uR RR
CCjBR




 







(8)

Y. L. LI ET AL. 124



1
3
01
2
1
32 2
0
22
32 2
0
22
,, cos
sin cos
sin sin
1cos
2
23
sin cos
44
23
sin sin
44
pp
p
pp
p
uR AR
BR
CR
AR
R
RB BBBjC
RC CCCjB
 




 


 










 

(9)
where
00 000 00
cos ,sincos ,sinsinAE BECE0





 .
From Expression (8), the electric field is obtained as




22 22
1
32 32
ˆˆ
44 44
3ˆ
2
ˆˆˆ
pp
pp
xyz
CC jBBB jC
y
x
Az
Ex Ey Ez
 
 

 
 
 


E
(10)
The above result is obviously in agree with those in
the reference [10] when the dielectric tensor is a uniform
medium, which tests the correctness of Expression (10).
2.2. The Scattering Feature of a Magnetized
Cold Plasma Sphere
The scattering field from an anisotropic target is derived
as following by using the researching method in the lit-
erature [13]

sˆˆ
,
j
kr
e
Efir
r
 (11)
where



2
ˆ
'
ˆˆˆˆ
,'
4
jr
v
k
f
irr redv



 kr
DE (12)
is the amplitude of scattering field and E D are respec-
tively electric field & the ‘electric displacement’ inside
the plasma sphere, in which r


D
E, has the same
unit with E. Expression of D-E written as










1
ˆˆ ˆ 111
x
pyy pxz
EjExEjEy Ez   DE
Inserting the above into Expression (12) and consid-
ering that 2 ''kr r




   

 



2
1
1
ˆˆ 11
V
ˆˆˆ
,1
4
1
ˆ
11
xpy ypx
z
xpyx
ypxyzz
EjExEjEy
k
fir Ez
EjEr
r
EjEr Er










 


















 



(13)
The symbol V is the sphere’s volume and vectors
are respectively the vectors in scattering direction and
incident direction.
ˆ
ˆ,ri
ˆˆˆ ˆˆ ˆˆ sincossin sincos
x
yz
rxyzrxryrz



 . In our
knowledge, Expression (13) is a novel one. The projec-
tions of amplitude in the right coordinate system are




 

  
2
2xpy
x
1
ε1E jεE1
kV
ˆˆ
fi,r 4π11
x
py x
ypxxy zxz
EjEr
EjErrErr

 


 





 






 




2
2p
1
ε1E jεE1
kV
ˆˆ
fi,r 4π11
yx ypxy
y
xpyxyzyz
EjEr
EjErr Err

 


 





 









   
2
211
11
kV
ˆˆ
fi,r4π11
zzz
z
y
px zyxpy xz
EEr
EjErr EjErr

 








 


The differential scattering cross section is presented as


2
dxxyy
ˆˆ
f,ff ff ffir 


zz

(14)
Since the inner electric field is dependent on the direc-
tion of the incident wave. So it can be seen from (13) that
there are two parts in the differential scattering cross
section, the first part is relative to the incident direction,
the second is relative to both incident direction and the
observing azimuth angle. After considering the or-
thonormalities of trigonometric functions, the scattering
cross section is obtained
 

22
42 xpy ypx
2
1z
ε1E jεEε1EjεE
6k V
5πε1E



 








(15)
Expression (14) is an analytical one and a novel result
in our knowledge.
2.3. Discussion
In order to test the rightness of expression (14), we as-
sume that the incident electric field E0 is in the
x-direction and now obtain B = C = 0，A = –E0. If the
medium is an isotropic one and now assume
1p
,
1 , the amplitude is derived as
following 0



 is reasonable.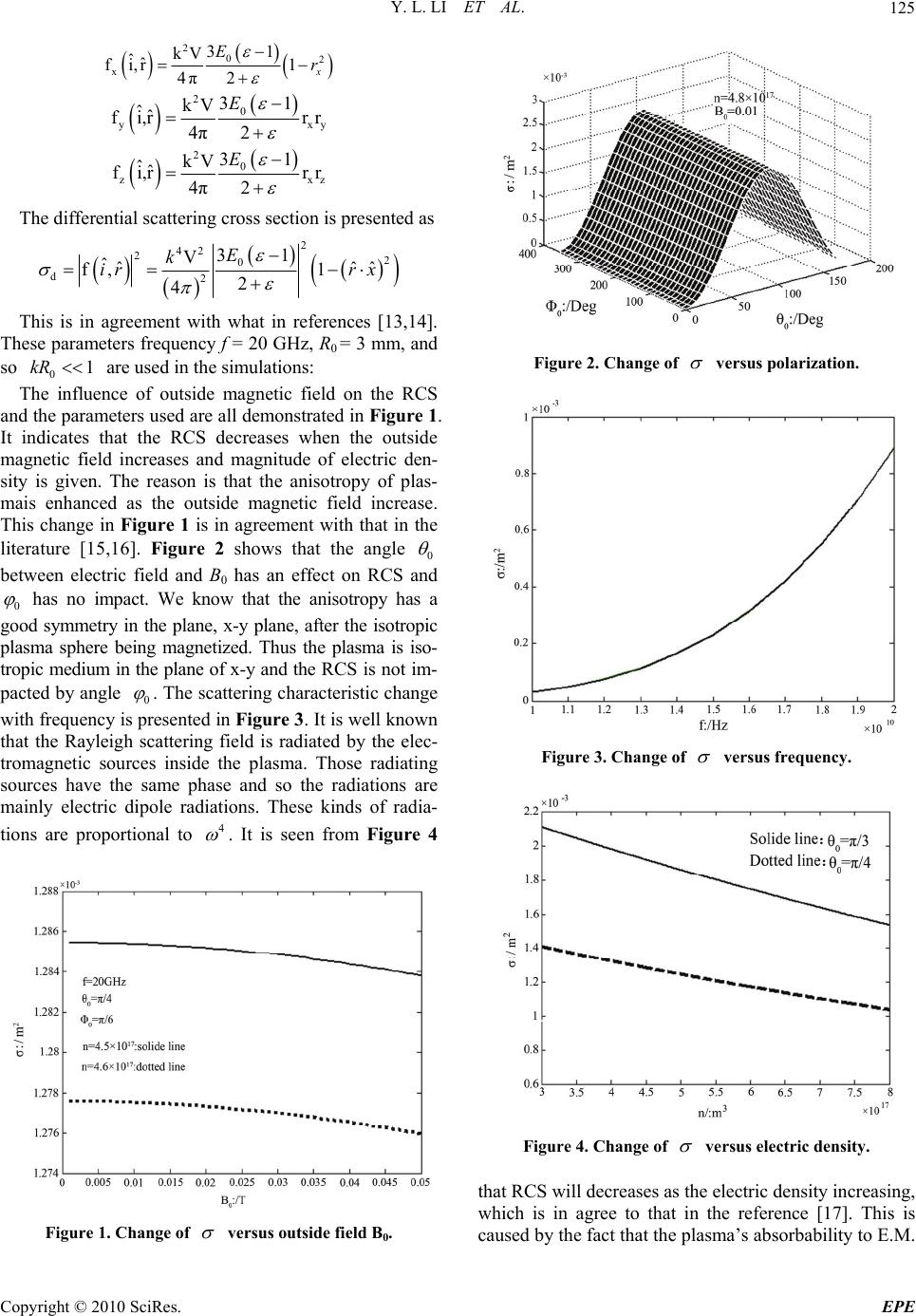

Y. L. LI ET AL.125




2
02
x
31
kV
ˆˆ
fi,r 1
4π2
x
Er 






2
0
yx
31
kV
ˆˆ
fi,r rr
4π2
E 




y

2
0
zx
31
kV
ˆˆ
fi,r rr
4π2
E 


z
The differential scattering cross section is presented as


 

2
42
22
0
d2
31
V
ˆˆˆˆ
f, 1
2
4
E
k
ir rx




 

This is in agreement with what in references [13,14].
These parameters frequency f = 20 GHz, R0 = 3 mm, and
so are used in the simulations:
01kR
The influence of outside magnetic field on the RCS
and the parameters used are all demonstrated in Figure 1.
It indicates that the RCS decreases when the outside
magnetic field increases and magnitude of electric den-
sity is given. The reason is that the anisotropy of plas-
mais enhanced as the outside magnetic field increase.
This change in Figure 1 is in agreement with that in the
literature [15,16]. Figure 2 shows that the angle 0

between electric field and B0 has an effect on RCS and
0

has no impact. We know that the anisotropy has a
good symmetry in the plane, x-y plane, after the isotropic
plasma sphere being magnetized. Thus the plasma is iso-
tropic medium in the plane of x-y and the RCS is not im-
pacted by angle 0

. The scattering characteristic change
with frequency is presented in Figure 3. It is well known
that the Rayleigh scattering field is radiated by the elec-
tromagnetic sources inside the plasma. Those radiating
sources have the same phase and so the radiations are
mainly electric dipole radiations. These kinds of radia-
tions are proportional to 4

. It is seen from Figure 4
Figure 1. Change of

versus outside field B0.
Figure 2. Change of

versus polarization.
Figure 3. Change of

versus frequency.
Figure 4. Change of

versus electric density.
that RCS will decreases as the electric density increasing,
which is in agree to that in the reference [17]. This is
caused by the fact that the plasma’s absorbability to E.M.

Y. L. LI ET AL. 126
wave is enhanced as the electric density being increased.
3. Conclusions
In this paper, the electric fields inside and outside a
magnetized cold plasma sphere are investigated. We use
the scale transformation theory of the electromagnetic
field to reconstruct the Laplace equation and then obtain
two analytical expressions of the electric potentials in-
side and outside the magnetized cold plasma sphere in
detail. Its correctness is tested with literature. The dielec-
tric tensor in different coordinate systems and a general
formula to compute the scattering field from anisotropic
target are presented. We take the magnetized cold plasma
sphere as an example, its analytical RCS is obtained first
in detail and simulations are presented which indicates
the characteristic of electric dipole radiation. How to use
the scale transformation theory to study the analytical
scattering feature for a multilayer magnetized cold
plasma target is our next research subject.
4. Acknowledgements
This project was supported by the National Natural Sci-
ence Foundation of China (Grant No. 60971079,
60801047), the Natural Science Foundation of Shaanxi
Province (Grant No. 2009JM8020) and Natural Science
Foundation of Shaanxi Educational Office (Grant No.
09JK800).
5
. References
[1] E. A. Soliman, A. Helaly and A. A. Megahed, “Propaga-
tion of Electromagnetic Waves in Planar Bounded Plasma
Region,” Progress in Electromagnetics Research, Vol. 67,
2007, pp. 25-37.
[2] H. Huang, Y. Fan, B. Wu, F. Kong and J. A. Kong, “Sur-
face Modes at the Interfaces between Isotropic Media and
Uniaxial Plasma,” Progress in Electromagnetics Re-
search, Vol. 76, 2007, pp. 1-14.
[3] L. Qi and Z. Yang, “Modified Plane Wave Method Ana-
lysis of Dielectric Plasma Photonic Crystal,” Progress in
Electromagnetics Research, Vol. 91, 2009, pp. 319-332.
[4] V. Kumar, K. S. Singh and S. P. Ojha, “Band Structure,
Reflection Properties and Abnormal Behaviour of One-
Dimensional Plasma Photonic Crystal,” Progress in Elec-
tromagnetics Research M, Vol. 9, 2009, pp. 227-247.
[5] W. Ren and L. Q. Xiao, “Analysis of Electromagnetic
Scattering by a Plasmas-Coated Conducting Sphere Us-
ing Simplified Wave Functions,” Journal of Hangzhou
Dianzi University, in Chinese, Vol. 28, 2008, pp. 1-6.
[6] S. B. Liu, J. J. Mo and N. C. Yuan, “Research on the Ab-
sorption of EM-Wave by Inhomogeneous Magnetized
Plasmas,” Acta Electronica Sinica, in Chinese, Vol. 31,
2003, p. 372.
[7] D. J. Gregolre, J. Santoru and R. W. Schumacher, “Elec-
tromagnetic Wave Propagation in Unmagnetized Plas-
mas,” AD-A250 710, 1992.
[8] Y. Chang, W. F. Chen and N. Luo, “Analysis of the Spa-
tial Scattering Characteristic for the Reentry Target
Cloaked by Plasma Based on the Physical Optics
Method,” Journal of Microwave, in Chinese, Vol. 24,
2008, pp. 2-6.
[9] C. S. Gürel and E. Oncü, “Interaction of Electromagnetic
Wave and Plasma Slab with Partially Linear and Sinu-
soidal Electron Density Profile,” Progress in Electro-
magnetics Research Letters, Vol. 12, 2009, pp. 171-181.
[10] D. Klement and V. Stein, “Special Problems in Applying
the Physical Optics Method for Backscatter Computa-
tions of Complicated Objects,” IEEE Transactions in An-
tennas and Propagation, Vol. 36, No. 2, 1988, pp. 228-
237.
[11] H. T. Chen, G.-Q. Zhu and S.-Y. He, “Using Genetic
Algorithm to Reduce the Radar cross Section of Three-
Dimensional Anisotropic Impedance Object,” Progress in
Electromagnetics Research B, Vol. 9, 2008, pp. 231-248.
[12] V. G. Gavrilenko, G. V. Jandieri, A. Ishimaru and V. G.
Jandieri, “Peculiarities of Spatial Spectrum of Scattered
Electromagnetic Waves in Anisotropic Inhomogeneous
Medium,” Progress in Electromagnetics Research B, Vol.
7, 2008, pp. 191-208.
[13] A. Ishimaru, “Wave Propagation and Scattering in Ran-
dom Medium,” Academic Press, New York, 1978, Part I,
pp. 27-30.
[14] Y. L. Li and J. Y. Huang, “The Scale-Transformation of
Electromagnetic Theory and its Applications,” Chinese
Physics, in Chinese, Vol. 14, 2005, pp. 646-656.
[15] Y. Li, L. J. Xu and N. C. Yuan, “The Parallel JEC-FDTD
Algorithm for Magnetized Plasmas and its Application,”
Acta Electronica Sinica, in Chinese, Vol. 36, 2008, pp.
1119-1124.
[16] S. B. Liu, G. F. Zhang and N. C. Yuan, “Finite-Difference
Time-Domain Analysis on Radar cross Section of Con-
ducting Cube Scatter Covered with Plasmas,” Acta
Physica Sinica, in Chinese, Vol. 53, 2004, pp. 2633-2638.
[17] J. J. Mo, S. B. Liu and N. C. Yuan, “Analysis of Wide
Band Scattering for Perfectly Conducting Cylinder
Coated with Non-Uniform Plasma,” Journal of Micro-
wave, in Chinese, Vol. 19, 2003, pp. 20-25.