Energy and Power Engineering, 2010, 2, 111-121
doi:10.4236/epe.2010.22016 Published Online May 2010 (http://www. SciRP.org/journal/epe)
111
Sequential Approach with Matrix Framework for Various Types
of Economic Thermal Power Dispatch Problems
Subramanian Srikrishna, Ganesan Sivarajan
Department of Electrical Engineering, FEAT, Annamalai University, Annamalainagar, India
Received January 22, 2010; revised February 25, 2010; accepted March 24, 2010
Abstract
This paper presents a sequential approach with matrix framework for solving various kinds of economic dis-
patch problems. The objective of the economic dispatch problems of electrical power generation is to sched-
ule the committed generating units output so as to meet the required load demand while satisfying the system
equality and inequality constraints. This is a maiden approach developed to obtain the optimal dispatches of
generating units for all possible load demands of power system in a single execution. The feasibility of the
proposed method is demonstrated by solving economic load dispatch problem, combined economic and
emission dispatch problem, multiarea economic dispatch problem and economic dispatch problem with mul-
tiple fuel options. The proposed methodology is tested with different scale of power systems. The generating
unit operational constraints are also considered. The simulation results obtained by proposed methodology
for various economic dispatch problems are compared with previous literatures in terms of solution quality.
Numerical simulation results indicate an improvement in total cost saving and hence the superiority of the
proposed method is also revealed for economic dispatch problems.
Keywords: Combined Economic and Emission Dispatch, Composite Cost Function, Economic Dispatch, Multiarea
Economic Dispatch, Multiple Fuel Options, Prohibited Operating Zone, Ramp Rate Limits, Sequential
Approach, Transmission Loss
1. Introduction
The primary objective of the economic dispatch problem
is to schedule the generations of thermal units so as to
meet the required load demand at minimum operating
cost while satisfying the individual and system operating
constraints. Traditionally, the cost function for generat-
ing units has been approximated as a quadratic function.
A variety of optimization techniques has been used for
solving economic dispatch problems. The conventional
methods include traditional lambda-iteration method, the
base point and participation factors method, and the gra-
dient methods are suggested to solve economic dispatch
problems [1,2]. The applications of classical methods,
such as linear or quadratic programming are also applied
for solving economic dispatch problems [3,4].
The methods based on operational research and artifi-
cial intelligence concepts such as genetic algorithm,
evolutionary algorithms, fuzzy and artificial neural net-
works have been given attention for solving economic
dispatch problems because of their ability to find the
solution near global optimal. Simulated Annealing tech-
nique (SA) and Genetic Algorithm (GA) have been ap-
plied to determine the optimal generation schedule for
economic dispatch problem in a power system [5,6]. Ar-
tificial neural network based models are developed for
the solution of economic power dispatch problem [7,8].
Particle Swarm Optimization method (PSO) has been
applied for solving economic dispatch problems with
various operating constraints like prohibited operating
zones and ramp rate limits [9,10]. Evolutionary strategy
based algorithm is suggested for solving economic dis-
patch problem [11]. A partition approach based solution
for economic dispatch problems considering the physical
limitations of the system is presented [12]. An enhanced
Hopfield neural network model is developed to solve
economic dispatch problems [13]. The heuristic search
techniques such as Differential Evolution (DE), Chaotic
and ant swarm optimization algorithm and Direct Search
GA (DSGA) have been applied to solve economic dis-
patch problems [14-17]. Hybrid approaches including
SA-PSO and Bacterial foraging-Nelder Mead method
have also been developed to obtain the dispatches of
generating units [18,19].

S. SUBRAMANIAN ET AL. 112
i
L
00
Due to environmental concerns, Combined Economic
and Emission Dispatch (CEED) problem has been for-
mulated to determine the optimal amount of generated
power for the generating units in the system by mini-
mizing the fuel cost and emission level simultaneously
subject to various system constraints. The passage of
clean air act amendments in 1990 has forced utilities to
reduce their SO2 and NOx emissions since both are the
primary power plant emissions [20]. A general formula-
tion based on the Lagrange relaxation method is pre-
sented for solving environmental constrained economic
dispatch problem [21]. Lamount and Qbesses detailed
various emission dispatching strategies and solution
procedure based on emission shadow prices [22]. Srik-
rishna and Palanichamy suggested price penalty factor to
convert bi objective function into a single objective func-
tion [23]. Fuzzy logic and neural network models are
developed for solving this multiobjective optimization
problem [24-28]. The heuristic search methods are ap-
plied to solve this problem [29,30]. Quadratic Program-
ming (QP) method based solution for this multi objective
problem is presented [31].
Dynamic programming recursive approach is devel-
oped for solving emission constrained economic dispatch
problem [32]. L. Wang and C. Singh investigated to
solve this problem by applying a fuzzified multi objec-
tive particle swarm optimization algorithm [33]. An ap-
proach based on constrained pattern search method is
presented to solve this problem [34]. Simplified recur-
sive approach is presented for the solution of this mul-
tiobjective optimization problem [35]. The authors de-
veloped a generalized equation to find the optimal gen-
erations of units. Palanichamy and Sundar Babu devel-
oped direct method for solving this type of problems
based on mathematical modeling [36]. Artificial neural
network (ANN), Fuzzy logic based models and heuristic
search techniques are used for solving this multiobjective
problem [37-40].
The economic dispatch problem of a power system is
extended to take into consideration of additional neces-
sary constraints such as transmission capacity limits to
ensure security of the system. Direct Search Method
(DSM) and ANN models have been suggested for solv-
ing the multi area economic dispatch problem [41,42].
In certain fossil fired generating units use different fu-
els hence the cost function are represented as a seg-
mented piecewise quadratic function. This problem faces
with the problem of identification of the most economi-
cal fuel of each unit. Lin and Viviani reported Hierar-
chical Method [HM] to solve the economic dispatch
problem with piecewise quadratic functions [43]. Artifi-
cial neural network models and heuristic search tech-
niques are used for solve this problem [44-48].
In this article, simplified methodology is presented for
solving economic dispatch problems namely, large scale
economic dispatch, economic dispatch with operational
constraints, combined economic and emission dispatch,
multi area economic dispatch and economic dispatch
with multiple fuel options. The proposed approach is
demonstrated with suitable test systems.
2. Problem Formulation
The problem formulation for economic dispatch, com-
bined economic and emission dispatch, multiarea eco-
nomic dispatch and economic dispatch with multiple fuel
options are described as follows.
2.1. Economic Dispatch (ED) Problem with
Generator Operating Constraints
The objective of economic dispatch is to simultaneously
minimize the generation cost rate and to meet the load
demand of a power system over some appropriate period
while satisfying various operating constraints. The ob-
jective function of an economic dispatch problem can be
formulated as,
11
nn
2
Tii iiii
i= i=
minF=F(P)=aP+bP+ c
 (1)
Constraints
1) Power balance constraint
1
n
iGD
i=
P=P=P +P
 (2)
The transmission loss can be expressed as,
0
11 1
nn n
Liijjii
i= j=i=
P=PB P+BP+B
  (3)
or approximately
11
nn
L
iijj
i= j=
P=PB P
 (4)
2) Generator operational constraints
a. Generator capacity constraint
i,mini i,max
PPP (5)
b. Ramp rate limits
The inequality constraints due to ramp rate limits for
unit generation changes are given
1) as generation increases
0
ii
PP URi
i
(6)
2) as generation decreases
0
ii
PP DR (7)
The generator operation constraint after including
ramp rate limit of generators can be described as,
00
i
()
i,miniii,max ii
maxP,PDRPmin(P,P+UR ) (8)

S. SUBRAMANIAN ET AL.113
)
i
i
)
i
c. Prohibited operating zone constraint
The feasible operating zones of unit i can be described
as follows,
l
i,minii ,1
PPP
1,23
ul
i,j-i i,ji
PPPj =,,....,n (9)
i
u
i,nii ,max
PPP
2.2. Combined Economic and Emission
Dispatch (CEED) Problem
This problem is formulated by including the reduction of
emission as an objective. Like the fuel cost function
given in (1), the total emission of generation ET (kg/h)
can be expressed by a quadratic function of generation
as,
2
1
(
n
Tiiii
i=
E= dP+eP+f
 (10)
A multi-objective optimization problem is converted
in to a single objective optimization problem by intro-
ducing price penalty factor h as follows,
n22
ii
i1
()(
Tiiiiiii
F
aPb PchdPe Pf


 (11)
and this objective function has to satisfy the power bal-
ance constraint and the generation capacity constraints.
The price penalty factor that coordinates the emission
with the normal fuel cost.
2.3. Multi Area Economic Dispatch (MAED)
Problem
The objective of multi area economic dispatch is to de-
termine the generation levels and the interchange power
between areas that minimize the system operation cost
while satisfying a set of constraints as,
2)
m
N
MM
mmnmn mnmn mn
m=1m=1 n=1
minF= min(aPbPc
 (12)
Subject to
1) Area power balance constraint
m
mm
N
mnkjjk DM
m=1j βjβ
P+t-t-P =0

 (13)
2) Generation limits constraint
mn,min mn mn,max
PPP (14)
3) Tie line limits constraint
j
k,min jkjk,max
ttt (15)
2.4. Economic Dispatch Problem with
Multiple Fuel Options (EDMFO)
In economic dispatch problem, the fuel cost of each gen-
erator is represented by a single quadratic cost function.
Owing to multiple fuel options, the cost function may
become piecewise quadratic. Hence, the economic dis-
patch problem with piecewise quadratic function is de-
fined as,
1
N
j
j
j=
minF (P )
 (16)
where,
111 1
222 2
1
1
2
2
jjjj jj,min jj
2
jjjj jj1 jj
jj
2
j
m jjm jjmj,m-jj,max
aP+bP+c,fuel,PP P
aP+bP+c,fuel,PP P
F(P)=
.
aP+bP+c, fuelm,PPP







(17)
This objective function is minimized subject to power
balance constraint.
3. Solution Methodology
3.1. Demonstration of Sequential Approach with
Matrix Framework
Sequential approach with matrix framework is proposed
for solving economic dispatch problems. This is the first
method developed to obtain the optimal dispatches for all
possible load demands in a system. The demonstration of
the solution methodology is presented in this section.
The electric power production in a power plant is al-
lowed to vary from minimum technical limit (Pmin) to
maximum technical limit (Pmax). Initially the Pi,min of all
generating units in a power plant are considered as initial
state input values and is represented by a single dimen-
sional matrix as,
[]
1,min 2,min3,minn,min
s=PPP,......,P (18)
Based on the above single dimensional matrix, a
square matrix (I) is developed to identify the economic
schedule of generation. The formation of the square ma-
trix is as follows. The process starts with a step incre-
ment in generation by Δ MW in P1,min by keeping the
remaining units at its input value. This will form first
row of the square matrix.
[Δ]
11,min2,min 3,minn,min
IP+PP,......,P

(19)
The increment in generation is made in the second
element by keeping the other elements at its input value
that leads to the development of second row of the
square matrix.

S. SUBRAMANIAN ET AL. 114
[Δ]
21,min 2,min3,minn,min
I=PP+P,......, P (20) Δ
n
i,iLi, j
j=1
ji
P=(pd+)+ P-Pi=1,2,...,n

 (23)
In the same logic, an increment is made for remaining
units one at a time and a square matrix with a dimension
equal to the number of units has been developed. For
every step increment in the operating range of the plant
the unit one at a time is allowed to experience the change
in generation thus leads to the formation of the square
matrix.
The detailed computational flow of the proposed
method is presented in Figure 1. The proposed method-
ology in the form of matrix framework to support the
demonstration is as follows.
Δ
Δ
Δ
1,min 2,minn,min 1
1,min 2,minn,min 2
1,min 2,minn,min n
P+P... P I
PP+...P
I
I....
.
PP...P+
I
 



 


(21)




Δ
Δ
Δ
Δ
Δ
1,min 2,minn,min
1,min 2,minn,min
1,min 2,minn,min
1,max 2,maxn,max
1,max 2,maxn,max
1,max 2,maxn,
I
nitial Stage
fit1
P+P. P
Choose PP+.P fit 2
.... min fit
PP.P+
fit n
Final Stage
P- P.P
PP-.P
. ...
PP.P






















Δ
max
fit1
Choose
fit 2
min fit
-fit n

 













Each element in the square matrix represents the gen-
eration of a unit corresponding to the column that should
satisfy the unit capacity constraints. In addition, the op-
erational constraints such as ramp rate limits and prohib-
ited operating zones are also enforced. The operating
regions of the unit after including ramp rate limits are
identified as mentioned in Equation (8). The operating
regions of the units having prohibited operating zones
are separated into isolated sub regions and it is identified
using Equation (9). The operating regions of the units
having prohibited operating zones and ramp rate con-
straints are obtained as mentioned earlier. The units are
allowed to operate in the one of the operating zones. If
the generation of a unit falls in a prohibited operating
zone, the feasible optimal level would most likely to be
located in any one of the adjacent feasible operating re-
gions, that is, the operating region above or below the
prohibited operating zone.
4. Simulations Results and Discussions
A simplified methodology based on sequential approach
with matrix framework is developed for solving different
kinds of economic dispatch problems. The effectiveness
of this approach is tested for solving various kinds of
economic dispatch problems including combined eco-
nomic and emission dispatch problem, multi area eco-
nomic dispatch problem and economic dispatch with
multiple fuel options.
In the square matrix the unit generations of each row
that satisfy the constraints are identified and total fuel
cost of generation is evaluated. The desired economic
schedule of generation is identified by analyzing fitness
of each row. The fitness function of each row is calcu-
lated as,
The algorithm for solving the examples were imple-
mented in Matlab 7.0 platform and executed with Pen-
tium IV, 2.8 GHz personal computer. The proposed
methodology provides the optimal schedule of genera-
tions for all possible load demands which is varied from
minimum technical limit by a small increment to maxi-
mum technical limit of the system. The selection of in-
crement is also an important factor. Too large increment
may end up with unfeasible solution and too small in-
crement may take long execution time. Based on experi-
ence, the desired increment is chosen as 1 MW.

Δ
T
F(j)
f
it (j)=j=1,2,...n
pd + (22)
where, pd is the total of input values.
The schedule with the minimum fitness is chosen as
the successive state input values. This process is repeated
till all the generating units reach their maximum genera-
tion capacity. The feasible solutions for every increment
from Pmin to Pmax are obtained and hence the best solution
for any load demand falls in the operating boundary can
be easily sited.
4.1. Case A: Economic Dispatch (ED) Problem
with Generator Operating Constraints
The objective is the minimization of total fuel cost sub-
ject to power balance and generator operational con-
straints. The effectiveness and efficiency of the devel-
oped approach is tested with large scale economic dis-
In practical applications, the total generation must be
equal to the power demand and transmission loss. In
such cases, the power balance constraint is exactly met
by calculating the diagonal unit generation as follows.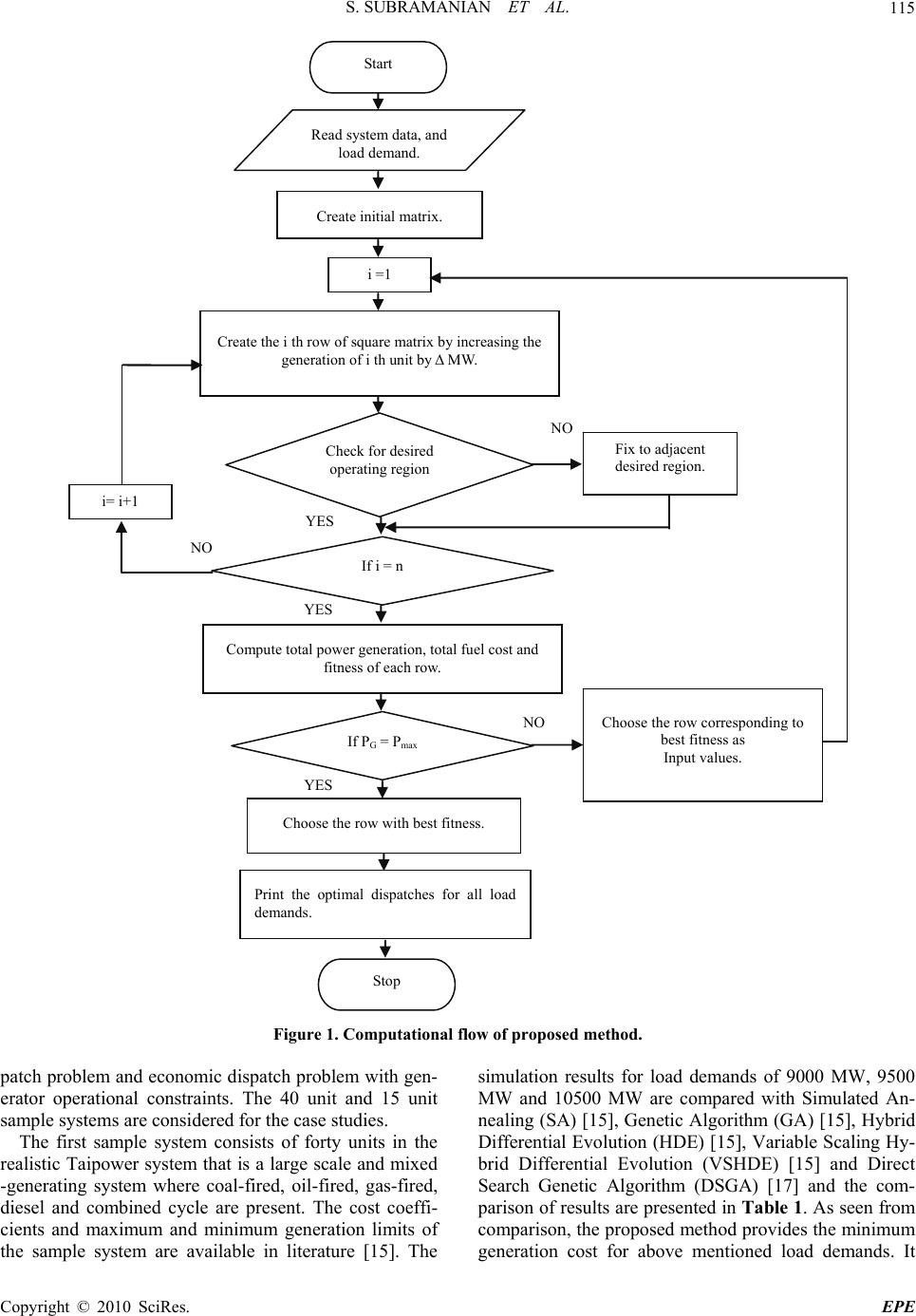

S. SUBRAMANIAN ET AL. 115
i= i+1
Choose the row corresponding to
best fitness as
Input values.
Start
Read system data, and
load demand.
Create initial matrix.
i =1
Create the i th row of square matrix by increasing the
generation of i th unit by Δ MW.
Check for desired
operating region
Fix to adjacent
desired region.
If i = n
Compute total power generation, total fuel cost and
fitness of each row.
Choose the row with best fitness.
If P
G
= P
max
Print the optimal dispatches for all load
demands.
Stop
YES
YES
NO
YES
NO
NO
Figure 1. Computational flow of proposed method.
patch problem and economic dispatch problem with gen-
erator operational constraints. The 40 unit and 15 unit
sample systems are considered for the case studies.
The first sample system consists of forty units in the
realistic Taipower system that is a large scale and mixed
-generating system where coal-fired, oil-fired, gas-fired,
diesel and combined cycle are present. The cost coeffi-
cients and maximum and minimum generation limits of
the sample system are available in literature [15]. The
simulation results for load demands of 9000 MW, 9500
MW and 10500 MW are compared with Simulated An-
nealing (SA) [15], Genetic Algorithm (GA) [15], Hybrid
Differential Evolution (HDE) [15], Variable Scaling Hy-
brid Differential Evolution (VSHDE) [15] and Direct
Search Genetic Algorithm (DSGA) [17] and the com-
parison of results are presented in Table 1. As seen from
comparison, the proposed method provides the minimum
generation cost for above mentioned load demands. It
C
opyright © 2010 SciRes. EPE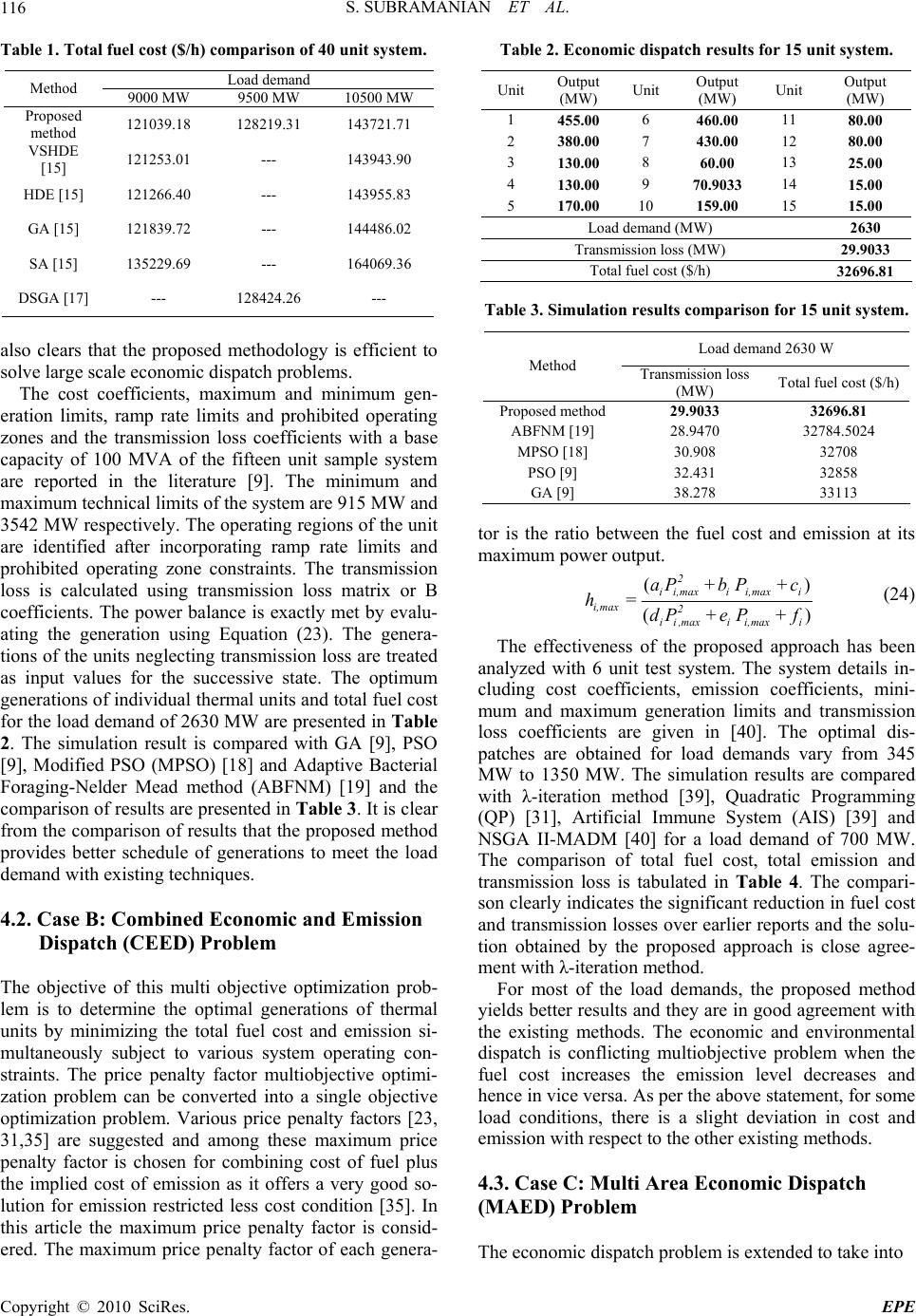

S. SUBRAMANIAN ET AL. 116
Table 1. Total fuel cost ($/h) comparison of 40 unit system.
Load demand
Method 9000 MW 9500 MW 10500 MW
Proposed
method 121039.18 128219.31 143721.71
VSHDE
[15] 121253.01 --- 143943.90
HDE [15] 121266.40 --- 143955.83
GA [15] 121839.72 --- 144486.02
SA [15] 135229.69 --- 164069.36
DSGA [17] --- 128424.26 ---
also clears that the proposed methodology is efficient to
solve large scale economic dispatch problems.
The cost coefficients, maximum and minimum gen-
eration limits, ramp rate limits and prohibited operating
zones and the transmission loss coefficients with a base
capacity of 100 MVA of the fifteen unit sample system
are reported in the literature [9]. The minimum and
maximum technical limits of the system are 915 MW and
3542 MW respectively. The operating regions of the unit
are identified after incorporating ramp rate limits and
prohibited operating zone constraints. The transmission
loss is calculated using transmission loss matrix or B
coefficients. The power balance is exactly met by evalu-
ating the generation using Equation (23). The genera-
tions of the units neglecting transmission loss are treated
as input values for the successive state. The optimum
generations of individual thermal units and total fuel cost
for the load demand of 2630 MW are presented in Table
2. The simulation result is compared with GA [9], PSO
[9], Modified PSO (MPSO) [18] and Adaptive Bacterial
Foraging-Nelder Mead method (ABFNM) [19] and the
comparison of results are presented in Table 3. It is clear
from the comparison of results that the proposed method
provides better schedule of generations to meet the load
demand with existing techniques.
4.2. Case B: Combined Economic and Emission
Dispatch (CEED) Problem
The objective of this multi objective optimization prob-
lem is to determine the optimal generations of thermal
units by minimizing the total fuel cost and emission si-
multaneously subject to various system operating con-
straints. The price penalty factor multiobjective optimi-
zation problem can be converted into a single objective
optimization problem. Various price penalty factors [23,
31,35] are suggested and among these maximum price
penalty factor is chosen for combining cost of fuel plus
the implied cost of emission as it offers a very good so-
lution for emission restricted less cost condition [35]. In
this article the maximum price penalty factor is consid-
ered. The maximum price penalty factor of each genera-
Table 2. Economic dispatch results for 15 unit system.
Unit Output
(MW) Unit Output (MW) Unit Output (MW)
1 455.00 6 460.00 11 80.00
2 380.00 7 430.00 12 80.00
3 130.00 8 60.00 13 25.00
4 130.00 9 70.9033 14 15.00
5 170.00 10 159.00 15 15.00
Load demand (MW) 2630
Transmission loss (MW) 29.9033
Total fuel cost ($/h) 32696.81
Table 3. Simulation results comparison for 15 unit system.
Load demand 2630 W
Method Transmission loss
(MW) Total fuel cost ($/h)
Proposed method 29.9033 32696.81
ABFNM [19] 28.9470 32784.5024
MPSO [18] 30.908 32708
PSO [9] 32.431 32858
GA [9] 38.278 33113
tor is the ratio between the fuel cost and emission at its
maximum power output.
()
()
2
ii,max ii,max i
i,max 2
ii ,maxii,maxi
aP+b P+c
h=
dP+e P+f
(24)
The effectiveness of the proposed approach has been
analyzed with 6 unit test system. The system details in-
cluding cost coefficients, emission coefficients, mini-
mum and maximum generation limits and transmission
loss coefficients are given in [40]. The optimal dis-
patches are obtained for load demands vary from 345
MW to 1350 MW. The simulation results are compared
with λ-iteration method [39], Quadratic Programming
(QP) [31], Artificial Immune System (AIS) [39] and
NSGA II-MADM [40] for a load demand of 700 MW.
The comparison of total fuel cost, total emission and
transmission loss is tabulated in Table 4. The compari-
son clearly indicates the significant reduction in fuel cost
and transmission losses over earlier reports and the solu-
tion obtained by the proposed approach is close agree-
ment with λ-iteration method.
For most of the load demands, the proposed method
yields better results and they are in good agreement with
the existing methods. The economic and environmental
dispatch is conflicting multiobjective problem when the
fuel cost increases the emission level decreases and
hence in vice versa. As per the above statement, for some
load conditions, there is a slight deviation in cost and
emission with respect to the other existing methods.
4.3. Case C: Multi Area Economic Dispatch
(MAED) Problem
The economic dispatch problem is extended to take into

S. SUBRAMANIAN ET AL.117
Table 4. Simulation results comparison of six-generator
system.
Load demand 700 MW
Method
Total fuel
cost ($/h)
Total
emission
(kg/h)
Transmission
loss (MW)
λ-iteration
[39] 37781 442 21.17
QP [31] 37488 439.7 17.054
AIS [39] 37344 438.1 16.91
NSGA
II-MADM
[40]
38331.647 443.138 14.645
Proposed
method 37166.73 453.44 17.64
considerations of transmission capacity limits to ensure
the security of the system. A two area system with four
thermal generating units is considered to illustrate the
effectiveness of the proposed approach. The system data
are available in the literature [41]. The total load demand
in area 1 and area 2 are 70% and 30% of total load de-
mand respectively and these two areas are interconnected
through transmission lines. Each area consists of two
generating units and for the sake of comparison with
earlier reports transmission losses are not considered.
The line flow limits of 90 MW, 120 MW and 200 MW
are considered for the analysis. The optimum generations
of individual units of each area for load demand of 1200
MW including transmission line limits are tabulated in
Table 5.
The total generation of area 2 is greater than the total
generation of area 1 that can export as much economical
excess as power to area 1 to satisfy the requirement in
area 1 without violating transmission line flow limits.
The results obtained by this proposed methodology are
Table 5. Optimal generation results of two area system in-
cluding transmission capacity constraints.
Flow limit (MW)
Load 1120 MW
90 MW 90 MW 90 MW
P1
(MW) 528 506 445
Optimal
generation
in area-1 P2
(MW) 166 158 139
P1
(MW) 159 173 212
Optimal
generation
in area-2 P2
(MW) 267 283 324
Total fuel cost ($/h) 10700.80 10669.09 10604.68
Table 6. Comparison of total fuel cost for MAED.
Total generation cost ($/h)
Load
(MW)
Flow
limit
(MW) EDSM
[43] NN [44] Proposed method
90 7812.2 7812.2 7811.94
120 7791.5 7791.5 7791.25
800
200 7754.8 7754.8 7754.70
90 9874.7 9874.7 9874.20
120 9846.4 9846.4 9846.01
1030
200 9789.7 9789.7 9789.42
90 10701 10701 10700.80
120 10670 10670 10669.09
1120
200 10605 10605 10604.68
compared with Economic Dispatch Direct Search
Method (EDSM) [41] and Neural Network (NN) [42]
and the comparison of results are presented in Table 6.
4.4. Case D: Economic Dispatch Problem
with Multiple Fuel Options (EDMFO)
The economic dispatch problem with multiple fuel op-
tions has been solved in two phases. In first phase, the
most economic fuel of each generating unit is identified.
The economic dispatch of generating units is determined
by a sequential approach with the selected fuels in sec-
ond phase. The implementation procedure of the pro-
posed methodology has been detailed as follows.
The primary search process calculates the composite
cost function of each generating unit and the detailed
derivation of composite cost coefficients are presented in
Appendix. Then sequential approach with matrix frame-
work is performed to identify the most economic fuel of
each unit. The composite function and capacity of the
units are using for the above process. This phase pro-
vides the generation dispatches and the fuel correspond-
ing to the dispatches is known as the most economic fuel.
The generation limits corresponding to the selected fuel
is the desired operating region of the unit. At the end of
first phase, the most economic fuel and the desired oper-
ating region of each unit are obtained. In second phase,
the generation dispatches of the units are refined within
the desired operating regions. The cost functions of the
selected fuels are considered and sequential approach
with matrix framework is performed again to obtain the
optimal dispatches of generating units.
The effectiveness of this proposed approach for solv-
ing this problem is tested with a sample system consists
of ten generating units, each unit with two or three fuel
options. The details of fuel options, cost coefficients and
maximum and minimum generations of each fuel in each
generating unit are available in the literature [43]. The
simulation result for load demand of 2700 MW is de-

S. SUBRAMANIAN ET AL. 118
tailed in Table 7. The total fuel cost for load demands of
2500 MW, 2600 MW and 2700 MW obtained by this
methodology, Hierarchical Method (HM) [43], Hopfield
Neural Network (HNN) [44], Adaptive Hopfield Neural
Network (AHNN) [45], Hybrid Genetic Algorithm
(HGA) [46], Classical Evolutionary Programming (CEP)
[47], Fast Evolutionary Programming (FEP) [47], Im-
proved Fast Evolutionary Programming (IFEP) [47] and
Particle Swarm Optimization [48] are compared and the
comparison of results are detailed in Table 8. From the
comparison of results, it is clear that the proposed ap-
proach provides comparable result for economic dispatch
problem with piecewise quadratic function.
The computational time for the above case studies by
the proposed approach is presented in Table 9.
The proposed methodology has following merits.
Table 7. Economic dispatch results of 10 unit system with
multiple fuel options (Load=2700 MW).
Unit Fuel
type
Generation
(MW) Unit Fuel type
Generation
(MW)
1 2 218 6 3 240
2 1 212 7 1 288
3 1 281 8 3 240
4 3 240 9 3 428
5 1 278 10 1 275
Total cost ($/h) 623.81
Table 8. Comparison of total fuel cost for 10 unit system
with multiple fuel options.
Total fuel cost ($/h)
Method 2500 MW 2600 MW 2700 MW
HM [43] 526.70 574.03 625.18
HNN [44] 526.13 574.26 626.12
AHNN [45] 526.23 574.37 626.24
HGA [46] 526.24 574.38 623.81
IFEP [47] 526.25 --- ---
FEP [47] 526.26 --- ---
CEP [47] 526.25 --- ---
PSO [48] --- --- 623.88
Proposed
method 526.24 574.38 623.81
Table 9. Total execution time for various case studies.
Case study Test system Execution time (s)
40 Unit 1.5337
ED 15 Unit 0.6642
CEED 6 Unit 0.2613
MAED Two area system 0.2534
EDMFO 10 Unit 0.2700
 From these studies, this approach has the compe-
tence to solve various types of economic dispatch prob-
lem.
 It is a first method that provides the optimal solu-
tion for all possible load demands of system in a single
run.
 It provides the schedule with minimum total cost in
all cases hence global optimal solution.
 The performance of the proposed approach is inde-
pendent of the number of generating units in the system
and hence it is suitable for system of any size.
 The computational procedure is minimal.
 It offers the solution for all load demands of a sys-
tem hence it takes a reasonable execution time.
5. Conclusions
This article presents sequential approach with matrix
framework for solving various kinds of economic dis-
patch problems. The proposed methodology is validated
by solving the different economic load dispatch problem
such as large scale economic dispatch, economic dis-
patch with generator operating constraints, combined
economic and emission dispatch, multiarea economic
dispatch and economic dispatch with multiple fuel op-
tions. The different scale of power systems are consid-
ered in each case. The practical operational constraints of
generators like ramp rate limits and prohibited operating
zones are also taken into account for the solution of eco-
nomic dispatch problems. The price penalty factor ap-
proach is used to convert the multi objective optimiza-
tion problem into single objective optimization problem
and maximum price penalty factor is considered as it
offers very good solution for emission constrained less
cost condition. The proposed approach is extended for
solving economic dispatch problems with line flow con-
straints. Further, simple methodology for solving eco-
nomic dispatch problem with multiple fuel options is
presented. The most economic fuel of generating unit is
identified by using the composite cost function and se-
quential approach with matrix frame work. These decen-
tralized approaches provide simple solution methodology
for economic dispatch problem with multiple fuel op-
tions. The simulation results of different case studies are
compared with recent reports. The comparison of results
concludes that the proposed methodology provides the
minimum total fuel cost hence global optimal solution
for various types of economic dispatch problems.
6. Acknowledgements
The authors gratefully acknowledge the management the
support and facilities provided by the authorities of An-
namalai University, Annamalainagar, India to carry out
this research work.

S. SUBRAMANIAN ET AL.119
7
. References
[1] A. J. Woods and B. F. Wollenberg, “Power Generation,
Operation and Control,” John Wiley & Sons, New York,
1996.
[2] O. I. Elgerd, “Electric Energy Systems Theory, An intro-
duction,” 2nd Edition, McGraw Hill Book Company,
New York, 1982.
[3] R. B. Adler and R. Fischal, “Security Constrained Eco-
nomic Dispatch with Participation Factors Based on
Worst Case Bus Load Violations,” IEEE Transactions on
Power Apparatus and Systems, Vol. 96, 1977, pp. 347-
356.
[4] R. T. Bui and S. Ghaderpanah, “Real Rescheduling and
Security Assessment,” IEEE Transactions on Power Ap-
paratus and Systems, Vol. PAS-101, No. 8, 1982, pp.
2906-2915.
[5] K. P. Wong and C. C. Wang, “Simulated Annealing
Based Economic Dispatch Algorithm,” IEE Proceedings
in Generation, Transmission and Distribution, Vol. 140,
No. 6, 1993, pp. 509-515.
[6] S. O. Orero and M. R. Erving, “Economic Dispatch of
Generators with Prohibited Operating Zones: A Genetic
Algorithm Approach,” IEE Proceedings in Generation,
Transmission and Distribution, Vol. 143, No. 6, 1996, pp.
529-534.
[7] M. Djukanovic, M. Calovic, B. Milosevic and D. J.
Sobejic, “Neural-Net Based Real Time Economic Dis-
patch for Thermal Power Plants,” IEEE Transactions on
Energy Conversion, Vol. 11, No. 4, 1996, pp. 755-761.
[8] R. Naresh, J. Dubey and J. Sharma, “Two-Phase Neural
Network Based Modelling Framework of Constrained
Economic Load Dispatch,” IEE Proceedings in Genera-
tion, Transmission and Distribution, Vol. 151, No. 3,
2004, pp. 373-378.
[9] Z. L. Gaing, “Particle Swarm Optimization to Solving the
Economic Dispatch Considering the Generator Constr-
aints,” IEEE Transactions on Power Systems, Vol. 18, No.
3, 2003, pp. 1187-1195.
[10] J.-B. Park, K.-S. Lee, J.-R. Shin and K. Y. Lee, “A Parti-
cle Swarm Optimization for Economic Dispatch with
Non-Smooth Cost Function,” IEEE Transactions on
Power Systems, Vol. 20, No. 1, 2005, pp. 34-42.
[11] A. P. Neto, C. Unsihuay and O. R. Saveedra, “Efficient
Evolutionary Strategy Optimization Procedure to Solve
the Non-Convex Economic Dispatch Problem with Gen-
erator Constraints,” IEE Proceedings on Generation
Transmission and Distribution, Vol. 152, No. 5, 2005, pp.
653-660.
[12] W.-M. Lin, H.-J. Gow and M.-T. Tsay, “A Partition Ap-
proach Algorithm for Non-Convex Economic Dispatch,”
Electric Power and Energy Systems, Vol. 29, No. 5, 2007,
pp. 432-438.
[13] A. Y. Abdelaziz, S. F. Mekhamer, M. A. L. Badr and M.
Z. Kamz, “Economic Dispatch Using an Enhanced Hop-
field Neural Network,” Electric Power Components and
Systems, Vol. 36, No. 7, 2008, pp. 719-732.
[14] N. Noman and H. Iba, “Differential Evolution for Eco-
nomic Dispatch Problems,” Electric Power Systems Re-
search, Vol. 78, No. 8, 2008, pp. 1322-1331.
[15] J.-P. Chiou, “Variable Scaling Hybrid Differential Evolu-
tion for Large Scale Economic Dispatch Problems,” Elec-
tric Power Systems Research, Vol. 77, No. 3-4, 2007, pp.
212-218.
[16] J. Cai, X. Ma, L. Li, Y. Yang, H. Peng and X. Wang,
“Chaotic Ant Swarm Optimization to Economic Dis-
patch,” Electric Power Systems Research, Vol. 77, No. 10,
2007, pp. 1373-1380.
[17] A. Theerthamalai and S. Maheswarapu, “Directional
Search Genetic Algorithm Applications to Economic Dis-
patch of Thermal Units,” International Journal of Com-
putational Methods in Engineering Science and Mechan-
ics, Vol. 9, No. 4, 2008, pp. 211-216.
[18] C. C. Kuo, “A Novel Coding Scheme for Practical Eco-
nomic Dispatch by Modified Particle Swarm Approach,”
IEEE Transactions on Power Systems, Vol. 23, No. 4,
2008, pp. 1825-1835.
[19] B. K. Panigrahi and V. R. Pandi, “Bacterial Foraging
Optimization: Nelder-Mead Hybrid Algorithm for Eco-
nomic Load Dispatch,” IET Generation, Transmission
and Distribution, Vol. 2, No. 4, 2008, pp. 556-565.
[20] “Potential Impacts of Clean Air Regulations on System
Operations,” IEEE Current Operating Problems Working
Group, Vol. 10, 1998, pp. 647-653.
[21] A. A. El-keib, H. Ma and J. L. Hart, “Environmentally
Constrained Economic Dispatch Using a Lagrangian Re-
laxation Method,” IEEE Transactions on Power Systems,
Vol. 9, No. 4, 1994, pp. 1723-1729.
[22] M. W. Lamont and E. V. Qbessis, “Emission Dispatch
Models and Algorithms for the 1990’s,” IEEE Transac-
tions on Power Systems, Vol. 10, No. 2, 1995, pp. 941-
947.
[23] K. Srikrishna and C. Palanichamy, “Economic Thermal
Power Dispatch with Emission Constraint,” Journal of
Institution of Engineers (India), Vol. 72, 1991, pp. 11-18.
[24] Y. H. Song, G. S. Wang, P. Y. Wang and A. T. Johns,
“Environmental/Economic Dispatch Using Fuzzy Logic
Controlled Genetic Algorithms,” IEE Proceedings on
Generation, Transmission and Distribution, Vol. 144, No.
4, 1997, pp. 377-382.
[25] G. Singh, S. C. Srivastava, P. K. Kalra and D. M. Vinoth
Kumar, “Fast Approach to Artificial Neural Network
Training and its Application to Economic Load Dis-
patch,” Electrical Machines and Power Systems, Vol. 23,
No. 1, 1995, pp. 13-24.
[26] C. T. Su and G. J. Chiou, “A Fast Computation Hopfield
Method to Economic Load Dispatch of Power Systems,”
IEEE Transactions on Power Systems, Vol. 12, No. 4,
1997, pp. 1759-1764.
[27] C. M. Haung, H. T. Yang and C. L. Huang, “Bi-objective
Power Dispatch Using Fuzzy Satisfaction-Maximizing
Decision Approach,” IEEE Transactions on Power Sys-
tems, Vol. 12, No. 4, 1997, pp. 1715-1721.
[28] P. K. Hota, R. Chakrabarti and P. K. Chattopadhyay,

S. SUBRAMANIAN ET AL. 120
“Economic Emission Load Dispatch through an Interac-
tive Fuzzy Satisfying Method,” Electric Power Systems
Research, Vol. 54, No. 3, 2000, pp. 151-157.
[29] K. P. Wong and J. Yuryevich, “Evolutionary Program-
ming Based Algorithm for Environmentally Constrained
Economic Dispatch,” IEEE Transactions on Power Sys-
tems, Vol. 13, No. 2, 1998, pp. 301-309.
[30] P. Venkatesh, R. Gnanadass and N. P. Padhy, “Compari-
son and Application of Evolutionary Programming Tech-
niques to Combined Economic Emission Dispatch with
Line Flow Constraints,” IEEE Transactions on Power
Systems, Vol. 18, No. 2, 2003, pp. 688-697.
[31] R. M. S. Danaraj and F. Gajendran, “Quadratic Program-
ming Solution to Emission and Economic Dispatch Prob-
lems,” Journal of Institution of Engineers (India), Vol. 86,
2005, pp. 129-132.
[32] S. Muralidharan, K. Srikrishna and S. Subramanian, “Emi-
ssion Constrained Economic Dispatch—A New Recur-
sive Approach,” Electric Power Components and Systems,
Vol. 34, No. 3, 2006, pp. 343-353.
[33] L. F. Wang and C. Singh, “Environmental/Economic
Power Dispatch Using a Fuzzified Multi-Objective Parti-
cle Swarm Optimization Algorithm,” Electric Power
Systems Research, Vol. 77, No. 12, 2007, pp. 1654-1664.
[34] J. S. AL-Sumait, J. K. Sykulski and A. K. L-Othman,
“Solution of Different Types of Economic Dispatch Prob-
lems Using Pattern Search Method,” Electric Power
Components and Systems, Vol. 36, No. 3, 2008, pp. 250-
265.
[35] R. Balamurugan and S. Subramanian, “A Simplified Re-
cursive Approach to Combined Economic Emission Dis-
patch,” Electric Power Components and Systems, Vol. 36,
No. 1, 2008, pp. 17-27.
[36] C. Palanichamy and N. S. Babu, “Analytical Solution for
Combined Economic and Emissions Dispatch,” Electric
Power Systems Research, Vol. 78, No. 7, 2008, pp. 1129-
1137.
[37] K. T. Chaturvedi, M. Pandit and L. Srivstava, “Modified
Neo-Fuzzy Neuron Based Approach for Economic and
Environmental Optimal Power Dispatch,” Applied Soft
Computing, Vol. 8, No. 4, 2008, pp. 1428-1438.
[38] S. Agrawal, B. K. Panigrahi and M. K. Tiwari, “Multi-
Objective Particle Swarm Algorithm with Fuzzy Cluster-
ing for Electrical Power Dispatch,” IEEE Transactions on
Evolutionary Computation, Vol. 12, No. 15, 2008, pp.
529-541.
[39] R. Geetha, R. Bhuvaneswari and S. Subramanian, “Artifi-
cial Immune System Based Combined Economic and
Emission Dispatch,” Proceedings of IEEE TENCON,
IEEE Region 10 conference, Hyderabad, 2008.
[40] X. B. Li, “Study of Multi-Objective Optimization and
Multi-Attribute Decision-Making for Economic and En-
vironmental Power Dispatch,” Electric Power Systems
Research, Vol. 79, No. 5, 2009, pp. 789-795.
[41] C. L. Chen and N. Chen, “Direct Search Method for Solv-
ing Economic Dispatch Problem Considering Transmis-
sion Capacity Constraints,” IEEE Transactions on Power
Systems, Vol. 16, No. 4, 2001, pp. 764-769.
[42] T. Yalcinoz and M. J. Short, “Neural Networks Approach
for Solving Economic Dispatch Problem with Transmis-
sion Capacity Constraints,” IEEE Transactions on Power
Systems, Vol. 13, No. 2, 1998, pp. 307-313.
[43] C. E. Lin and G. L. Viviani, “Hierarchical Economic Dis-
patch for Piecewise Quadratic Cost Functions,” IEEE
Transactions on Power Apparatus and Systems, Vol. PAS
-103, No. 6, 1984, pp. 1170-1175.
[44] J. H. Park, Y. S. Kim, I. K. Eom and K. Y. Lee, “Eco-
nomic Load Dispatch for Piecewise Quadratic Cost Func-
tion using Hopfield Neural Network,” IEEE Transactions
on Power Systems, Vol. 8, No. 3, 1993, pp. 1030-1038.
[45] K. Y. Lee, A. S. Yome and J. H. Park, “Adaptive Hop-
field Neural Networks for Economic Load Dispatch,”
IEEE Transactions on Power Systems, Vol. 13, No. 2,
1998, pp. 519-526.
[46] S. Baskar, P. Subbaraj and M. V. C. Rao, “Hybrid Ge-
netic Algorithm Solution to Economic Dispatch Problem
with Multiple Fuel Options,” Journal of Institution of
Engineers (India), Vol. 82, 2001, pp. 177-183.
[47] T. Jayabarathi, K. Jayaprakash, D. N. Jayakumar and T.
Raghunathan, “Evolutionary Programming Techniques
for Different Kinds of Economic Dispatch Problems,”
Electric Power Systems Research, Vol. 73, No. 2, 2005,
pp. 169-176.
[48] D. N. Jeyakumar, T. Jayabharathi and T. Raghunathan,
“Particle Swarm Optimization for Various Types of Eco-
nomic Dispatch Problems,” Electric Power and Energy
Systems, Vol. 28, No. 1, 2006, pp. 36-42.

S. SUBRAMANIAN ET AL.121
Nomenclature
ai, bi, ci Cost coefficients of generating unit i
di, ei, fi Emission coefficients of generating unit i
Bij, B0i, B00 Transmission loss coefficients or B coef-
ficients
ET Total emission of generators in (kg/h)
FT Total operating cost or total fuel cost of
generation in ($/h)
n Number of generating units
ni Number of prohibited operating zones
Pi Real power generation of generating unit
i in MW
Pi,min Minimum value of real power allowed at
generator i in MW
Pi,max Maximum value of real power allowed at gen-
erator i in MW
PD Total load demand of the system in MW
PL Total transmission losses in MW
Pi
0 Output power of generator i before dis-
patched hour in MW
Pi,j
l Lower bound of generation of unit i in
prohibited operating zone j in MW
Pi,j
u Upper bound of generation of unit i in
prohibited operating zone j in MW
URi Up ramp limit of i th generator in
(MW/h)
DRi Down ramp limit of i th generator in
(MW/h)
h Price penalty factor in ($/kg)
hi, max Maximum price penalty factor of unit i in
($/kg)
M Number of areas in an interconnected
system
Nm Number of on-line units for the area m in
an M area system
amn, bmn, cmn Cost coefficients of generating unit n in
area m
Pmn Power output of generator n in area m in
MW
PDm Load demand for area m in MW
tjk Economic tie transfer from area j to k in
MW
tjk, min, tjk, max Tie line minimum and maximum capac-
ity limits in MW
βm Set of tie lines in area m
s One dimensional matrix consists of input
values
I Square matrix consists of real power
generations of units
fit Fitness of the solution in ($/MWh)
Pmin Minimum technical limit in MW
Pmax Maximum technical limit in MW
Appendix
The incremental production cost of a plant is a prior re-
quirement for coordination among plants. The incre-
mental production cost of the plant can be derived by a
simple realignment of the fuel cost coefficients of the
units. Consider an “n” unit system and the cost equation
of n th unit is,
2
F
=aP+bP+c
nnnnnn
(A.1)
and the composite cost function of the plant can be writ-
ten as,
2
F
=AP +BP +C
TGG
(A.2)
The composite cost coefficients are derived as follows.
The total fuel cost ($/h) of the “n” unit system can be
written as,
F
=F +F+F+.....+F
n
T123 (A.3)
For most economical generation,



;
.
;
;
11 1111
nn nnnn
GG
2aP +bP=λ-b/ 2a
2aP+bP =λ-b/2a
2AP+ BP=λ-B/ 2A








(A.4)
where, λ is the incremental production cost of the plant in
MW.
The total generation of the plant can be written as,
G123
P= P+P+ P+....+ P
n




 
G123n
112233nn
P= λ/21/ a+1/ a+1/ a+...+1/ a
-1/2 b/a+b/a+b/a+...+b/a










123 n
112233 nn
123 n
λ=21/1/a+1/ a+1/ a+...+1/aP
+b/ a+b/a+b/a+...+b/ a
1 /1/a+1 /a+1 /a+...+1 /a
G








(A.5)
By comparing (A.4) and (A.5),


123 n
A
=1 /1/a+1 /a+1 /a+....+1 /a (A.6)


112233 nn
B=b/ a+b/ a+b/ a+....+b/ aA (A.7)
The fuel cost can be rewritten as,
;
;
22
nnnn
22
T
F=λ/4a-b/4a +c
F=λ/4A-B /4A+C
n
(A.8)
From (A.8),



123 n
222 2
112233 nn
2
C =c+c+c+...+c
b/ 4a+b/ 4a+b/ 4a+...+b/ 4a
+B/ 4A
(A.9)