Paper Menu >>
Journal Menu >>
 Open Journal of Safety Science and Technology, 2012, 2, 8-15 http://dx.doi.org/10.4236/ojsst.2012.21002 Published Online March 2012 (http://www.SciRP.org/journal/ojsst) An Investigation on the Dynamic Stability of Scissor Lift Ren G. Dong1*, Christopher S. Pan1, Jared J. Hartsell1, Daniel E. Welcome1, Tim Lutz1, Anne Brumfield1, James R. Harris1, John Z. Wu1, Bryan Wimer1, Victor Mucino2, Kenneth Means2 1National Institute for Occupational Safety and Health, Morgantown, USA 2Department of Mechanical and Aerospace Engineering, West Virginia University, Morgantown, USA Email: *RDong@cdc.gov Received November 30, 2011; revised January 4, 2012; accepted January 16, 2012 ABSTRACT The tip-over of scissor lifts in operation has frequently resulted in the death and/or severe injuries of workers. The ob- jective of this study is to enhance the und erstanding of its major mechanisms and factors influencing scissor lift stabilit y. Both experimental and modeling approaches were used in this study. Two series of experiments were performed under possible tip-over scenarios: curb impact and pothole depression. Based on the dynamic characteristics identified from the experimental results, a lumped-parameter model of the scissor lift was developed. It was applied to investigate the effect of scissor structure flexibility on the tip-over potential of the lift, to understand tip-over mechanisms, and to ex- plore preventive strategies. This study found that the fundamental natural frequencies of the lift were generally in a range of 0.30 - 2.08 Hz, which are likely related to the tip-over. Increasing flexibility of the lift structure generally in- creased the tip-over poten tial. The tip-over threshold was also a function of bo th ground slope and tilt speed of the lift. The results suggest that the lift should not be elevated on largely deformable and/or uneven surfaces such as bridged wood board or a soft soil base. The worker on the lift platform should avoid any large continuous periodic movement or forceful action in the horizontal p lane, especially when the lift is fully elevated. Besides the tilt angle of the lift, the tilt speed should be monito red to help prevent the tip-ov er. Keywords: Scissor Lift; Mobile Elevating Work Platform; Tip-Over of Scissor Lift; Stability of Scissor Lift 1. Introduction Scissor lifts are typical mobile elevating work platforms (MEWPs). Their primary function is to elevate workers, tools, and materials to a desired working height, while allowing the operator to control the movement and posi- tion of the lift. Compared with a ladder, a MEWP greatly reduces the psychological stress and physical demands on a worker at elevated height. Therefore, if a scissor lift is properly d esigned, manufa ctured, maintain ed, and app r o- priately used, it can increase not only the workers’ pro- ductivity but also their safety. For these reasons, scissor lifts with different capacities and elevating heights are in- creasingly used at many workplaces [1,2]. Unfortunately, fatal and non-fatal incidents have also happened during scissor lift operations [3,4 ]. Many of these incidents were associated with lift tip -over and/or workers fallin g within or from the platform. Many of them can be prevented by enhancing safety education, training programs, manage- ment controls, and equipment maintenance. However, fur- ther studies are required to enhance the understanding of the mechanisms of the tip-over events and to develop more effective engineering and operational interventions to prevent them. As reflected in the current standards on the MEWPs [5,6], the basic mechanisms of the MEWP instability have been generally understood. Its major factors include travel speed, ground slope, elevated height, load weight and its position on the lift platform, wind effect, etc. The stan- dardized certification tests are u sually conducted using new MEWPs. The joints in the lift structures could wear out after the scissor lifts are used for a certain period of time; the stiffness of the lift could thus be reduced. It is unclear whether the increased flexibility due to wear increases tip- over potential. While the standardized analyses are gen- erally based on static loads, it is also unclear how the workers’ activities on the platform affect the stability of the scissor lift. While the tilt angle of the lift is usually monitored, it is unclear whether the control of the tilt angle alone is sufficient to prevent the tip-over. It is also un- clear how to determine the lift stability when the plat- form accidently hits a structure. A dynamic model of the scissor lift is required to study these issues. Because the actual tip-over is likely to occur as a result of combined internal and external factors, such a model is also required to examine the combined effects. For example, the model can be used to simulate the in- *Corresponding a uthor. C opyright © 2012 SciRes. OJSST 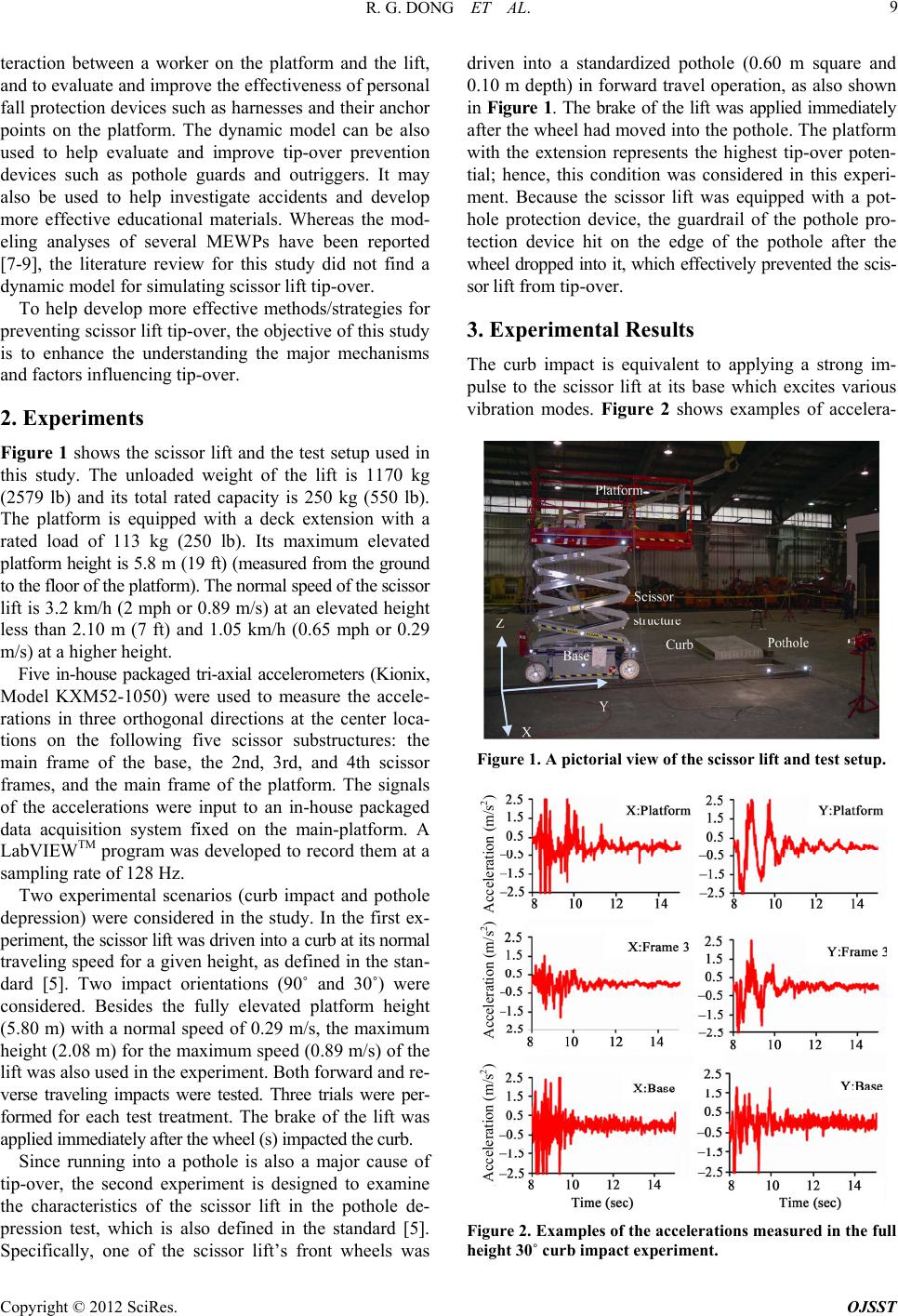 R. G. DONG ET AL. 9 teraction between a worker on the platform and the lift, and to evaluate and improve the effectiveness of personal fall protection devices such as harnesses and their anchor points on the platform. The dynamic model can be also used to help evaluate and improve tip-over prevention devices such as pothole guards and outriggers. It may also be used to help investigate accidents and develop more effective educational materials. Whereas the mod- eling analyses of several MEWPs have been reported [7-9], the literature review for this study did not find a dynamic model for simulating scissor lift tip-over. To help develop more effective methods/strategies for preventin g scissor lift tip-over, the objectiv e of this study is to enhance the understanding the major mechanisms and factors influe ncing tip-over. 2. Experiments Figure 1 shows the scissor lift and the test setup used in this study. The unloaded weight of the lift is 1170 kg (2579 lb) and its total rated capacity is 250 kg (550 lb). The platform is equipped with a deck extension with a rated load of 113 kg (250 lb). Its maximum elevated platform height is 5.8 m (19 ft) (measured from the ground to the floor of the platform). The normal speed of the scissor lift is 3.2 km/h (2 mph or 0.89 m/s) at an elevated height less than 2.10 m (7 ft) and 1.05 km/h (0.65 mph or 0.29 m/s) at a higher height. Five in-house packaged tri-axial accelerometers (Kionix, Model KXM52-1050) were used to measure the accele- rations in three orthogonal directions at the center loca- tions on the following five scissor substructures: the main frame of the base, the 2nd, 3rd, and 4th scissor frames, and the main frame of the platform. The signals of the accelerations were input to an in-house packaged data acquisition system fixed on the main-platform. A LabVIEWTM program was developed to record them at a sampling rate of 128 Hz. Two experimental scenarios (curb impact and pothole depression) were considered in the study. In the first ex- periment, the scissor lift was driven into a curb at its normal traveling speed for a given height, as defined in the stan- dard [5]. Two impact orientations (90˚ and 30˚) were considered. Besides the fully elevated platform height (5.80 m) with a normal speed of 0.29 m/s, the maximum height (2.08 m) for the maximum speed (0.89 m/s) of the lift was also used in the experiment. Both forward and re- verse traveling impacts were tested. Three trials were per- formed for each test treatment. The brake of the lift was applied immediately after the wheel (s) impacted the curb. Since running into a pothole is also a major cause of tip-over, the second experiment is designed to examine the characteristics of the scissor lift in the pothole de- pression test, which is also defined in the standard [5]. Specifically, one of the scissor lift’s front wheels was driven into a standardized pothole (0.60 m square and 0.10 m depth) in forward travel operation, as also shown in Figure 1. The brake of the lift was applied immediately after the wheel had moved into the pothole. The platform with the extension represents the highest tip-over poten- tial; hence, this condition was considered in this experi- ment. Because the scissor lift was equipped with a pot- hole protection device, the guardrail of the pothole pro- tection device hit on the edge of the pothole after the wheel dropped in to it, which effectively preven ted the scis- sor lift from tip-over. 3. Experimental Results The curb impact is equivalent to applying a strong im- pulse to the scissor lift at its base which excites various vibration modes. Figure 2 shows examples of accelera- Figure 1. A pictorial view of the scissor lift and test setup. Acceleration (m/s 2 ) Acceleration (m/s 2 ) Acceleration (m/s 2 ) Figure 2. Examples of the accelerations measured in the full height 30˚ curb impact experiment. Copyright © 2012 SciRes. OJSST  R. G. DONG ET AL. 10 tions measured on the base, third scissor frame, and plat- form in the X and Y directions in a 30˚ curb impact when the lift was fully elevated. There were many high sharp peaks during the impact, as shown in Figure 2. The vi- bration displacement history in each direction was esti- mated by integrating the acceleration history. The results indicate that the high frequency components played little role in determining the displacement. Hence, the high fre- quency components are not important where tip-over is of concern. The response in the vertical direction (Z) pri- marily includes random high frequency vibrations; hence, the response in this direction is not important for the purpose of this study. As also shown in Figure 2, the ac- celerations measured on the base quickly decayed to its noise level after the impact, which suggests the base is very rigid. The accelerations measured on the scissor structure and the platform in the longitudinal (Y) and lateral (X) directions generally show a consistent low frequency waveform. Unlike the sharp peaks, the magnitude of this waveform generally increases with the increase in the measurement height. Moreover, the waveforms measured at different locations on the scissor structure are approxi- mately in phas e. These observations sugges t that the d omi - nant displacements of the platform result from the pitch and rolling motions of the lift. Such motions could signifi- cantly affect the CG position of the scissor lift and its stability. A frequency spectrum analysis was further per- formed to identify the dominant vibration frequency in each direction. Table 1 lists the resonant frequencies for the fully-elevated height of the lift. Mainly because the speed in the low-height tests is about three times that of the full-height tests, the impact peaks observed in such tests were much higher than those shown in Figure 2. However, the accelerations quickly decayed within one second after the impact. It was very difficult to identify the dominant pitch and roll wave- forms and frequencies. This observation suggests the scissor lift at the low-elevated height is much more rigid than when it is fully elevated. The rigid model used in the standards may be sufficient for the stability analysis of the scissor lift at the low-elevated height. Therefore, the modeling study focused on the tip-over at the fully- elevated height. The acceleration responses measured in the pothole depression test were similar to those shown in Figure 2, except that these resonant frequencies were largely dif- ferent in the rolling axis (around the Y axis), which are also listed in Table 1. This is largely because when a wheel dropped into the depression, at least one of the other three wheels lifted from the ground. This could reduce the ef- fective wheel-ground contact stiffness. These observations further demonstrate that the mass distribution, the lift struc- tural stiffness, and the wheel-ground contact conditions could play roles in the determination of the dynamic re- sponses of the scissor lift. The results listed in Tab le 1 suggest that the most im- portant resonant frequencies of the scissor lift are gener- ally in the range of 0.3 - 2.08 Hz. The major frequencies of the human movements and actions are likely to be in this frequency range. Therefore, a resonance of the lift could be excited if a worker on the lift platform made a con- tinuous periodical movement or regularly applied a large force in the horizontal plane. This may be one of the me- chanisms or contributing factors for lift tip-over. 4. Scissor Lift Model As above-mentioned, high frequency dynamic responses to curb impact and pothole depression could be substan- tial. However, such responses did not lead to tip-over of the scissor lift. On the other hand, the low frequency roll and pitch responses could cause significant deformations of the scissor lift substructures, as reflected from the mea- surements of the accelerations at several different loca- tions. The deformations could significantly affect the CG of the lift, which is directly associated with the stability of the lift [5,6]. Therefore, the rigid body modes and fun- damental bending vibration modes of the scissor lift are important to the tip-ov er event. This further suggests that a lumped-parameter model can be sufficient for simulat- ing the basic tip-over behaviors. Because the wheel im- pacts and the lifting of the wheels from the ground are non-linear events, it is also necessary to consider them in the simulation. The software ADAMS/View allowed us to efficiently create a model that simulated the non-linear tip-over event [10]; hence, the model of the scissor lift Table 1. The dominant vibration frequencies in the curb impact and pothole depression experiments with the lift fully elevated (at 5.80 m). Test treatment Impact angle Bounce (Hz) Pitch (Hz) Rolling (Hz) 30˚ 6.75 1.00 0.67 Curb impact: no e x te n s i o n, forward travel 90˚ 5.83 1.25 0.75 30˚ 6.75 1.00 0.58 Curb impact: no e x te n s i o n, reverse travel 90˚ 6.33 1.17 0.50 30˚ 6.17 1.17 0.83 Curb impact: with extension, forward travel 90˚ 5.08 1.25 0.67 30˚ 5.42 1.08 0.75 Curb impact: with extension, reverse travel 90˚ 5.33 1.25 0.75 Pothole depression: right wheel drop 1.17 0.30 Pothole depression: left wheel drop 1.00 0.43 Copyright © 2012 SciRes. OJSST  R. G. DONG ET AL. Copyright © 2012 SciRes. OJSST 11 was created using this program. Figure 3 shows the pro- posed scissor lift model. To determine the nominal wheels’ contact stiffness, the deformations of the wheels were measured while the fully loaded scissor lift was standing on level concrete pavement. The nominal stiffness of each wheel contact element was calculated from the measured average deformation (2.5 mm) of the four wheels and the full weight (13,925 N) loaded on the wheels. The dimensions, connection points, mass properties, and center of mass (CM) of each part of the scissor lift were derived from its corresponding components or assemblies in the technical drawings. The parameters of the constraints/ connections of the model are listed in Table 2. Figure 3. An ADAMS model of the scissor lift. Table 2. Major flexible connections and their major parameters of the model (K: stiffness. C: damping. ID refers to the con- straint number in Figure 3). Constraint ADAMS Solid to solid contact ID Location K (106 N/m) C (103 N-s/m) Force Exponent Penetration Depth (mm) 12a wheel to road 1.39 10.0 1.5 2.5 12b whee l to c urb 1.39 10.0 1.5 2.5 13 pothole protection device to road 10.00 200.0 2.2 0.1 14 outer scissor frame 1 roller to base 1.18 8.0 1.2 0.1 15 outer sciss or frame 4 r o lle r to platform 1.00 5.0 2.2 0.1 Translational Rotational ADAMS bushing or spring-damper K (106 N/m) C (103 N-s/m) Kr (N-m/deg) Cr (N-m-s/deg) Y 4.00 100.0 0.05 0.0005 Z 1.18 8.0 0.10 0.0010 16 outer scisso r frame 1 to base X 0.40 20.0 0.05 0.0005 17 actuator axis 90.00 40.0  R. G. DONG ET AL. 12 The contact stiffness between the pothole edge and the pothole guardrail (Connection #15) depends on their com- bined stiffness. To understand the basic pothole response, the simulated pothole was assumed to be identical to that used in the experiment (Figure 1), which was a square hole on a steel plate. While the steel edge is very rigid, the contact stiffness primarily depends on the guardrail bending stiffness. A beam model simply supported on two points at the actual guardrail support locations on the base was used to estimate the stiffness. Obviously, the stiff- ness is a function of the contact point when the wheel moves into the pothole. The estimated minimum stiffness is 5500 kN/m when the contact is at the middle point of the guardrail. At the contact range (about 1/4 distance of the guardrail from the center) observed in the majority of testing trials, the stiffness was approximately 10,000 kN/m and it wa s us ed in th e si mu la tio n . Th e av e r ag e co e ff ic ie n t of friction (0.3 to 0.35) for a steel-to-steel contact was also used for this contact element [11]. The equivalent stiffness values for the connections be- tween the scissor structure and the base were determined based on the mean roll and pitch frequencies for the plat- form with the extension, which are presented in the next section. The damping values for these connections were also determined based on the mean decay rates of the fundamental pitch and rolling responses measured in the curb impact. Similarly, the stiffness and damping of the actuator spring and damper were also estimated from the bouncing responses measured in the curb-impact tests. 5. Model Evaluations The validation of the model for the critical rigid body motion largely depends on the system’s center of mass (CM) position. To verify the CM of the model, an ex- periment was also performed to measure the CG of the scissor lift using a tilt table method. A sufficiently large tilt angle is required to reliab ly measure the CG; howev er, because of our limited lab space and the safety concern, only four elevated heights (measured from the ground to the floor of the main platform) were considered, as listed in Table 3. In the measurement, the platform and exten- sion were not loaded. The CGs for the fully extended plat- form and non-extended platform were measured. The CG positions were also calculated from the model (without the load weights). The percent differences between the modeling results and the experimental data are listed in Table 3. The small differences suggest that they agreed with each other excellently. This suggests that the basic mass distribution in the model is very reasonable. For the purpose of this study, the pavement was con- sidered perfect in the modeling. Figure 4 shows the pre- dicted responses in the 30˚ forward curb impact with the full height platform and extension. Compared with those shown in Figure 2, the model peak magnitudes are not exactly the same as those observed in the experimental data but their basic response trends and the acceleration distributions on the scissor lift are very similar. In the 90˚ curb impact, the excited major motions are in the traveling direction (Y). Figure 5 shows the com- parison of the modeling (right column) and experimental (left column) responses of the scissor lift without pulling out the extension. Their basic dynamic features are very similar. Figure 6 shows the comparisons of the predicted and Table 3. Percent differences between the measured and mod- eled centers of gravity (CG) of the scissor lift. Percent difference (%) Without platform extension With platform extension Elevated height (m) X Y Z X Y Z 0.997 0.2 0.0 4.3 0.0 0.2 3.0 1.524 0.1 0.0 1.9 0.2 0.1 1.4 2.155 0.2 0.2 2.0 0.4 0.2 0.7 3.052 0.2 0.2 0.7 0.7 0.2 0.7 Figure 4. Examples of the accelerations predicted in the mo- deling for simulating the full height 30˚ curb impact. Copyright © 2012 SciRes. OJSST 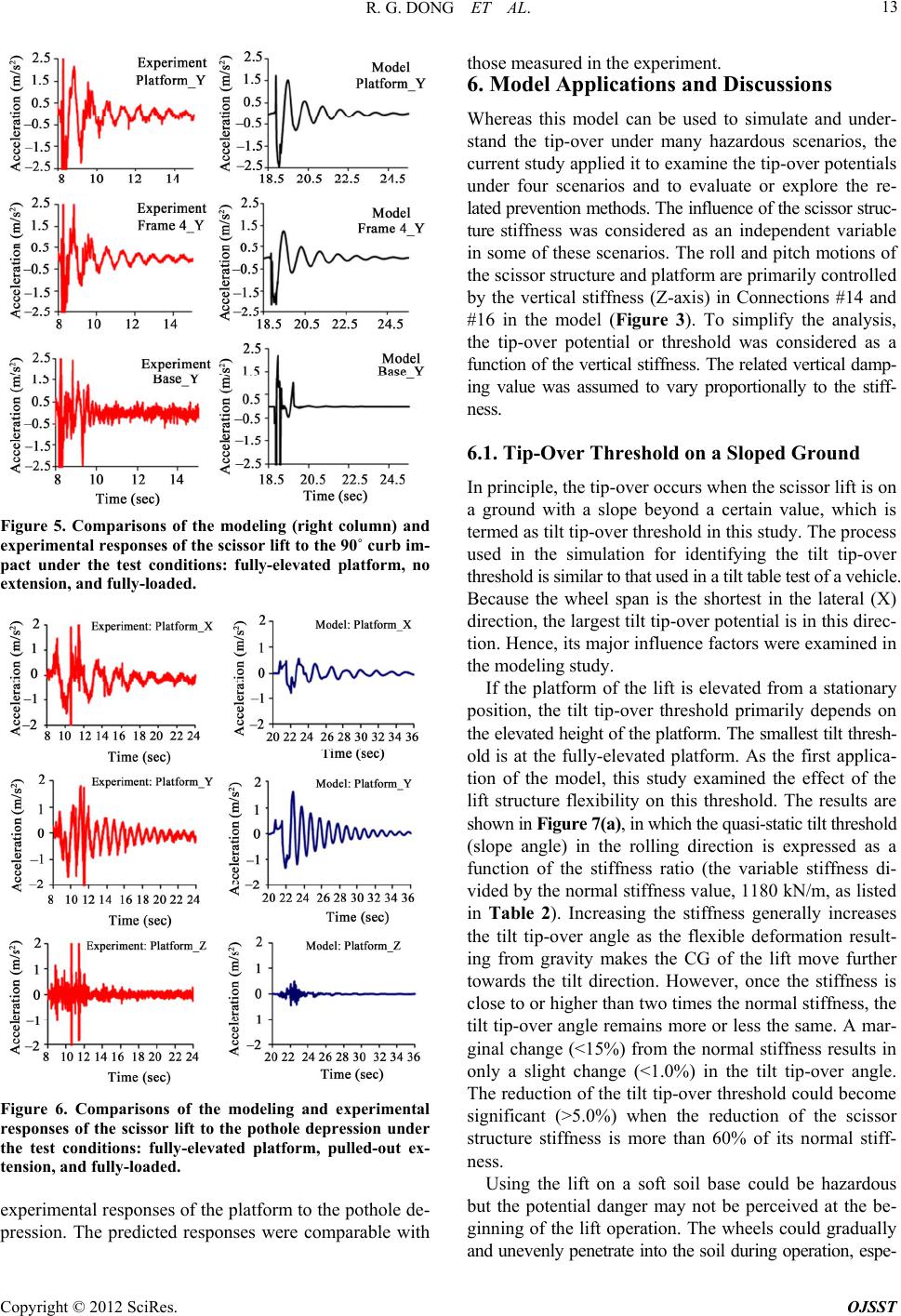 R. G. DONG ET AL. 13 Figure 5. Comparisons of the modeling (right column) and experimental responses of the scissor lift to the 90˚ curb im- pact under the test conditions: fully-elevated platform, no extension, and fully-loaded. Figure 6. Comparisons of the modeling and experimental responses of the scissor lift to the pothole depression under the test conditions: fully-elevated platform, pulled-out ex- tension, and fully-loaded. experimental responses of the platform to the pothole de- pression. The predicted responses were comparable with those measured in the experiment. 6. Model Applications and Discussions Whereas this model can be used to simulate and under- stand the tip-over under many hazardous scenarios, the current study applied it to examine th e tip-over potentials under four scenarios and to evaluate or explore the re- lated prevention methods. Th e influence of the scissor struc- ture stiffness was considered as an independent variable in some of these scenarios. The roll and pitch motions of the scissor structure and platform are primarily controlled by the vertical stiffness (Z-axis) in Connections #14 and #16 in the model (Figure 3). To simplify the analysis, the tip-over potential or threshold was considered as a function of the vertical stiffness. The related vertical damp- ing value was assumed to vary proportionally to the stiff- ness. 6.1. Tip-Over Threshold on a Sloped Ground In principle, the tip-over occurs when the scissor lift is on a ground with a slope beyond a certain value, which is termed as tilt tip-over threshold in this stud y. Th e process used in the simulation for identifying the tilt tip-over threshold is similar to that used in a tilt ta ble test of a vehicle. Because the wheel span is the shortest in the lateral (X) direction, the largest tilt tip-over potential is in this direc- tion. Hence, its major influence factors were examined in the modeling study. If the platform of the lift is elevated from a stationary position, the tilt tip-over threshold primarily depends on the elevated height of the platform. The smallest tilt thresh- old is at the fully-elevated platform. As the first applica- tion of the model, this study examined the effect of the lift structure flexibility on this threshold. The results are shown in Figure 7(a), in which the quasi -static tilt t hreshol d (slope angle) in the rolling direction is expressed as a function of the stiffness ratio (the variable stiffness di- vided by the normal stiffness value, 1180 kN/m, as listed in Table 2). Increasing the stiffness generally increases the tilt tip-over angle as the flexible deformation result- ing from gravity makes the CG of the lift move further towards the tilt direction. However, once the stiffness is close to or higher than two times the normal stiffness, the tilt tip-over angle remains more or less the same. A mar- ginal change (<15%) from the normal stiffness results in only a slight change (<1.0%) in the tilt tip-over angle. The reduction of the tilt tip-ov er threshold could become significant (>5.0%) when the reduction of the scissor structure stiffness is more than 60% of its normal stiff- ness. Using the lift on a soft soil base could be hazardous but the potential danger may not be perceived at the be- ginning of the lift operation. The wheels could gradually and unevenly penetrate into the soil during operation, espe- Copyright © 2012 SciRes. OJSST  R. G. DONG ET AL. Copyright © 2012 SciRes. OJSST 14 cially when there is some water in the working area. The (a) (deg/s) (deg) (b) (c) (d) Figure 7. The tip-over thresholds under four hazardous co n d i - tions. (a) The effect of the structure stiffness of scissor lift on the quasi-static t ip-ov er thresh old (tilt an gle) . (b) The effect of tilt speed on the tip-over threshold (tilt angle). (c) The effect of curb impact speed on the tip-over. (d) The effect of scissor structure stiffness on the requirement of the guard- rail height in the pothole depression. wheel penetrations could in effect form a sloped uneven support. Then, the activities of the workers on the plat- form could cause some rocking motions of the lift, which could further accelerate the formation of uneven support. Rocking motions could also happen when the lift is on other deformable surfaces such as bridged wood boards or metal sheets. If the motion of a worker on the platform is periodic and its frequency is close to the resonant fre- quency of the lift, the rocking motion could be signify- cantly amplified and eventually result in a tip-over inci- dent. This may be one of the mechanisms of tip-over at some construction sites. While it is beyond the scope of this study to simulate these hazardous conditions and the related tip-over events, the effect of the rock/til t speed on the tilt threshold was examined, as plotted in Figure 7(b). As expected, if the tilt speed is low, the threshold is close to the quasi-static threshold. However, the tilt threshold is substantially reduced when the tilt speed is greater than 2.5˚/second. This is because the dynamic energy could increase the tip-over potential. This observation suggests that moni- toring the tilt angle alone may no t be sufficient to prev en t tip-over. Both the tilt angle and tilt speed should be con- sidered in the design of a preventive device such as a tip- over monitoring and warning system. This study also used the model to explore a hypothe- sized intervention approach. Theoretically reducing the platform height can lower the CG of the lift and increase the tip-over threshold. The height reduction may be auto- matically actuated when the tilt ang le and speed of th e lift reach certain values. As a preliminary exploration, the high- est possible downward acceleration (1 g) of the platform was used in the simulation. The results indicate that this approach would not work if the action takes place when the lift goes beyond the threshold shown in Figure 7(a), because it takes too much time for the platform to be actuated and lowered to a required safe height. To make this approach work, the descending action must be actu- ated before the lift reaches the threshold and the specific action time depends on the tilt speed. 6.2. Tip-Over Threshold of Curb Impact Speed The impact speed determines the kinetic energy of the scissor lift. The kinetic energy is partially consumed due to the system damping and partially transferred into po- tential energy. The potential energy includes the gravita- tional potential en ergy resulting from the lift’s CG elev a- tion and the elastic potential energy of the lift structures. In the standardized analysis, only the gravitational poten- tial energy is considered in the calculation of the tip-ov er speed thresho ld [5]. Th eref ore, the rigid body assu mption used in the analysis would be on the conservative side if  R. G. DONG ET AL. 15 th e CG change due to the flexibility of the structures could be ignored. In reality, both damping and flexibility play some roles in the impact event. While the damping and elasticity of the scissor lift structures tend to absorb part of the impact energy, the CG change due to the flexibility of the structures tends to increase the tilt effect du ring the impact. As a result, the flexibility did not substantially affect the tip-over threshold of the impact speed, as shown in Figure 7(c). However, the results suggest that to reduce the tip-over potential, it is better to keep the scissor structures as stiff as possible. 6.3. Tip-Over Threshold of Pothole Guardrail Height Figure 7(d) shows the effect of the structure stiffness on the pothole guardrail height design. Again, because the flexibility of the structure mak es the CG of the lift move further toward the tilt direction, a reduction in the stiff- ness of the lift requires reducing the pothole guardrail height from the ground so that the tilt angle can be con- trolled within the stable limit. The results also indicate that pothole guardrails should be designed to be as low as possible, providing that this will not affect the movement of the scissor lift when its pothole guardrails are not de- ployed. 7. Conclusion The results of this study confirmed that increasing the flexibility of the scissor lift structure generally increases the tip-over potential. The tip-over threshold is a function of both ground slope and tilt sp eed of the lift. The curren t results also suggest that when the scissor lift system be- comes slack due to severe wear of structural joints and/or any structural damage, the scissor lift should not be used before fixing the problem. The lift should not be elevated on soft ground and/or uneven surfaces. The worker on the lift platform should avoid any large continuous periodic movement or forceful action in the horizontal plane, es- pecially when the lift is fully elevated. Besides the tilt angle, the tilt speed of the lift can be measured and used to help prev ent the tip-over. 8. Disclaimer The content of this publication does not necessarily re- flect the views or policies of the National Institute for Occupational Safety and Health (NIOSH), nor do es men- tion of trade names, commercial products, or organiza- tions imply endorsement by the U.S. Government. REFERENCES [1] M. J. Burkart, M. McCann and D. M. Paine, “Aerial Work Platforms, in Elevated Work Platforms and Scaf- folding,” McGraw-Hill, New York, 2004. [2] S. Mohan and W. C. Zech, “Characteristics of Worker Accidents on NYSDOT Construction Projects,” Journal of Safety Research, Vol. 36, No. 4, 2005, pp. 353-360. doi:10.1016/j.jsr.2005.06.012 [3] M. McCann, “Death in Construction Related to Personnel Lifts, 1992-1999,” Journal of Safety Research, Vol. 34, No. 5, 2003, pp. 507-514. doi:10.1016/j.jsr.2003.07.001 [4] C. S. Pan, A. Hoskin, M. McCann, D. Castillo, M. Lin and K. Fern, “Aerial Lift Fall Injuries: A surveillance and Evaluation Approach for Targeting Prevention Activities,” Journal of Safety Research, Vol. 38, No. 6, 2007, pp. 617-625. doi:10.1016/j.jsr.2007.08.002 [5] ISO 16653, “Mobile Elevating Work Platforms—Design Calculations, Safety Requirements and Test Methods,” International Organization for Standardization, Geneva, 2003. [6] ANSI A92.6, “Self-Propelled Elevating Aerial Work plat- forms,” American National Standards Institute, New York, 1999. [7] R. F. Abo-Shanab and N. Sepehri, “Tip-Over Stability of Manipulator-Like Mobile Hydraulic Machines,” Journal of Dynamic Systems Measurement and Control, Vol. 127, No. 2, 2005, pp. 295-301. doi:10.1115/1.1898239 [8] A. Ghasempoor and N. Sepehri, “A Measure of Stability for Mobile Manipulators with Application to Heavy-Duty Hydraulic Machines,” Journal of Dynamic Systems, Meas- urement, and Control, Vol. 120, No. 3, 1998, pp. 360-370. doi:10.1115/1.2805410 [9] S. Tamate, N. Suemasa and T. Katada, “Analyses of In- stability in Mobile Cranes Due to Ground Penetration by Outriggers,” Journal of Construction Engineering and Management, Vol. 131, No. 6, 2005, pp. 698-704. doi:10.1061/(ASCE)0733-9364(2005)131:6(689) [10] “ADAMS Guide,” 2007 Version, MSC Software Incor- porated, Ann Arbor, USA. Copyright © 2012 SciRes. OJSST |

