Open Journal of Fluid Dynamics, 2012, 2, 14-27
http://dx.doi.org/10.4236/ojfd.2012.21002 Published Online March 2012 (http://www.SciRP.org/journal/ojfd)
Radiation Effects on Free Convection MHD Couette Flow
Started Exponentially with Variable Wall Temperature in
Presence of Heat Generation
Sanatan Das, Bhaskar Chandra Sarkar, Rabindra Nath Jana
Department of Applied Mathematics, Vidyasagar University, Midnapore, India
Received December 29, 2011; revised January 29, 2012; accepted February 5, 2012
ABSTRACT
Radiation effects on free convection MHD Couette flow started exponentially with variable wall temperature in the
presence of heat generation have been studied. The governing equations are solved analytically using the Laplace
transform technique. The variations of velocity and fluid temperature are presented graphically. It is observed that the
velocity decreases with an increase in either magnetic parameter or radiation parameter or Prandtl number. It is also
observed that the velocity increases with an increase in either heat generation parameter or Grashof number or acceler-
ated parameter or time. An increase in either radiation parameter or Prandtl number leads to fall in the fluid temperature.
It is seen that the fluid temperature increases with an increase in either heat generation parameter or time. Further, it is
seen that the shear stress at the moving plate decreases with an increase in either magnetic parameter or radiation pa-
rameter while it increases with an increase in either heat generation parameter or Prandtl number. The rate of heat
transfer increases with an increase in either Prandtl number or time whereas it decreases with an increase in heat gen-
eration parameter.
Keywords: MHD Couette Flow; Free Convection; Magnetic Parameter; Radiation; Heat Generation; Prandtl Number;
Grashof Number and Accelerated Parameter
1. Introduction
Couette flow is one of the basic flow in fluid dynamics
that refers to the laminar flow of a viscous fluid in the
space between two parallel plates, one of which is mov-
ing relative to the other. The flow is driven by virtue of
viscous drag force acting on the fluid and the applied
pressure gradient parallel to the plates. Couette flow is
frequently used in physics and engineering to illustrate
shear-driven fluid motion. Some important application
areas of Couette motion are MHD power generators and
pumps, aerodynamics heating, electrostatic precipitation,
polymer technology, petroleum industry, purification of
crude oil etc. In space technology applications and at
higher operating temperatures, radiation effects can be
quite significant. Radiative free convection MHD Cou-
ette flows are frequently encountered in many scientific
and environmental processes, such as astrophysical flows,
heating and cooling of chambers and solar power tech-
nology. Heat transfer by simultaneous radiation and con-
vection has applications in numerous technological prob-
lems including combustion, furnace design, the design of
high temperature gas cooled nuclear reactors, nuclear
reactor safety, fluidized bed heat exchanger, fire spreads,
solar fans, solar collectors natural convection in cavities,
turbid water bodies, photo chemical reactors and many
others. Free convection in channels formed by vertical
plates has received attention among the researchers in
last few decades due to it’s widespread importance in
engineering applications like cooling of electronic equip-
ments, design of passive solar systems for energy con-
version, design of heat exchangers, human comfort in
buildings, thermal regulation processes and many more.
Researchers in this field such as Singh [1], Singh et al.
[2], Jha et al. [3], Joshi [4], Miyatake et al. [5], Tanaka et
al. [6], Mohanty [7]. Jha [8] have studied the natural
Convection in unsteady MHD Couette flow. The radia-
tive heat transfer to magnetohydrodynamic Couette flow
with variable wall temperature have been investigated by
Ogulu and Motsa [9]. Chaudhary and Jain [10] have
analyzed the exact solutions of incompressible Couette
flow with constant temperature and constant heat flux on
walls in the presence of radiation. The radiation effects
on MHD Couette flow with heat transfer between two
parallel plates have been examined by Mebine [11]. Jha
and Ajibade [12] have discussed the free convective flow
C
opyright © 2012 SciRes. OJFD

S. DAS ET AL. 15
of heat generating fluid between vertical porous plates
with periodic heat input. Jha and Ajibade [13] have stud-
ied the unsteady free convective Couette flow of heat
generating/absorbing fluid. MHD oscillatory Couette flow
of a radiating viscous fluid in a porous medium with pe-
riodic wall temperature have been investigated by Israel-
Cookey et al. [14]. The effects of thermal radiation and
free convection currents on the unsteady Couette flow
between two vertical parallel plates with constant heat
flux at one boundary have been studied by Narahari [15].
Unsteady free convective Couette flow of heat generat-
ing/absorbing fluid in porous medium has been investi-
gated by Deka and Bhattacharya [16]. Kumar and Varma
[17] have studied the radiation effects on MHD flow past
an impulsively started exponentially accelerated vertical
plate with variable temperature in the presence of heat
generation.
In this present paper, we have investigated the radia-
tion effects on free convection MHD Couette flow of a
viscous incompressible heat generating fluid in the pres-
ence of variable temperature. It is observed that the ve-
locity 1 decreases with an increase in either magnetic
parameter
u
2
M
or radiation parameter or Prandtl
number . It is also observed that the velocity 1
u
increases with an increase in either heat generation pa-
rameter or Grashof number or accelerated parame-
ter or time
R
Pr
Gr
a

. An increase in either radiation pa-
rameter or Prandtl number leads to fall in the
fluid temperature
RPr

. It is seen that the fluid temperature

increases with an increase in either heat generation
parameter

or time

. Further, it is seen that the
shear stress at the moving plate
x

decreases with an
increase in either magnetic parameter or radiation pa-
rameter while it increases with an increase in either heat
generation parameter or Prandtl number. The rate of heat
transfer increases with an increase in either
Prandtl number Pr or time

0 




whereas it decreases with
an increase in heat generation parameter

.
2. Formulation of the Problem and Its
Solutions
Consider the unsteady free convection MHD Couette
flow of a viscous incompressible radiative heat generat-
ing fluid between two infinite vertical parallel walls
separated by a distance . The flow is set up by the
buoyancy force arising from the temperature gradient
occurring as a result of asymmetric heating of the parallel
plates as well as constant motion of one of the plates.
Choose a cartesian co-ordinates system with the x-axis
along one of the plates in the vertically upward direction
and the y-axis normal to the plates (See Figure 1). Ini-
tially, at time , both the plates and the fluid are
assumed to be at the same temperature and station-
h
0t
h
T
Figure 1. Geometry of the problem
ary. At time , the plate at starts moving in
its own plane with a velocity and is heated with
>0t=0y
0
at
ue
temperature

0
0
hh
t
TTT
t
 whereas the plate at
=yh
t
is stationary and maintained at a constant tem-
perature h, where 0 and are constants. A uni-
form magnetic field of strength 0 is imposed perpen-
dicular to the plates. It is also assumed that the radiative
heat flux in the x-direction is negligible as compared to
that in the y-direction. As the plates are infinitely long,
the velocity and temperature fields are functions of
and only.
Tu a
B
y
The Boussinesq approximation is assumed to hold and
for the evaluation of the gravitational body force, the
density is assumed to depend on the temperature accor-
ding to the equation of state

00
=1 h TT  





, (1)
where is the fluid temperature,
T

the fluid density,

the coefficient of thermal expansion and 0

the
density at the entrance of the channel.
For the fully developed flow, the governing equations are

2 2
0
2
1
=h
B
up u
g
TT u
tx y



 
 
 , (2)

2
0
2
=r

p
h
q TT
ck QTT
ty y

 
 
 , (3)
where is the velocity in the u
x
-direction,
g
the
acceleration due to gravity,

the kinematic coefficient
of viscosity, the thermal conductivity,
k
p
c the
specific heat at constant pressure, the radiative heat
flux and a constant.
r
q
0
The initial and the boundary conditions for velocity
and temperature distribution are as follows:
Q

00
0
0, for 0 and 0,
, at 0 for > 0,
0, at for > 0.
h
at hh
h
uTTyht
t
uueTT TTyt
t
uTTyht




(4)
It has been shown by Cogley et al. [13] that in the

S. DAS ET AL.
16
optically thin limit for a non-gray gas near equilibrium,
the following relation holds

0
4d
p
rhhh
e
qTT K
yT





 


, (5)
where
K

is the absorption coefficient,

is the wave
length,
p
e

is the Plank's function and subscript ‘’
indicates that all quantities have been evaluated at the
temperature h which is the temperature of the plate at
time . Thus our study is limited to small difference
of plate temperature to the fluid temperature.
h
T
0t
On the use of the Equation (5), Equation (3) becomes
 
2
0
24

p
hh
TT
c kTTIQTT
ty



, (6)
where
0
p
hh
e
I
K
T


d






. (7)
Greif et al. [18] showed that, for an optically thin limit,
the fluid does not absorb its own emitted radiation, this
means that there is no self-absorption, but the fluid does
absorb radiation emitted by the boundaries.
Using condition at , Equation (2) yields yh
1=0 p
x 

. (8)
On the use of (8), Equation (2) becomes

2
2
0
2
h
B uu
g
TT u
ty





. (9)
Introducing non-dimensional variables
y
h
 , 2
t
h

 , 1
0
u
uu ,
0
h
h
TT
TT


, (10)
Equations (9) and (6) become
2
2 11
1
2
uu
GrM u 



, (11)
2
2
Pr R






, (12)
where
22
20
Bh
M



 is the magnetic parameter,
2
4
I
h
Rk  the radiation parameter,
2
0
Qh
k
  the heat
generation parameter,
2
0
0
()
h
g
TTh
Gr u



 the Grashof
number and
p
c
Pr k


 the Prandtl number.
The corresponding initial and boundary conditions for
and
1
u

are
1
1
1
0,0 for 01 and 0,
, at 0 for > 0,
0, 0at1for> 0,
a
u
ue
u



 
 

 


(13)
where
2
ah
a


 is the accelerated parameter.
Taking Laplace transformation, the Equations (11) and
(12) become
2
2
1
11
2
d
d
u
s
uGrM 

u (14)
2
2
d
d
Prs R







(15)
where
 
 
11
0
0
,,d
and ,,d.
s
s
ususe
sse












(16)
The corresponding boundary conditions for 1
u and

are
 
 
12
1
11
0,, 0,,
1,0, 1,0.
us s
sa
s
us s






(17)
The solutions of the Equations (15) and (14) subject to
the boundary conditions (17) are easily obtained and are
given by
 

2
sinh 1
1
,
sinh
Pr s
ssPr s


 


, (18)




 

2
12
2
2
2
sinh 1
1
,
sinh
1
sinh 1
sinh 1
sinh
sinh
sM
ussa sM
Gr
Prsbs
Pr s
sM
Pr s
sM






















(19)
where =R
Pr



and
2
=1
Pr M
bPr
 

The inverse transforms of (18) and (19) give the
temperature and the velocity field distributions as


11
=0
,,
n
FcPr FdPr

,

 






, (20)
  

 
 
122
=0
33 44
,,,
1
,, ,,
n
Gr
uFcFd
Pr
FcFdFcPrFdPr
 
 






 



(21)

S. DAS ET AL.
17
where 2, 22cn dn

  


 

22
1
22
2
3
,erfcerfc ,
22
424 2
1
, erfcerfc,
222
1
, erfcerf
24 24
2
zz
azMa zMa
Mz Mz
zzz z
Fz ee
zz
FzeeM aeM a
zz z
Fze Me
bM M













 
 
 
 








 
 
  
 







 

22
2
22
2
4
c2
1
erfcerfc
222
erfcerfc,
222
1
,erfc
242
Mz Mz
bzM bzM b
z
zM
zz
eMeM
b
ez z
eMbe M
b
zz
Fz e
b























 





 



 


b




2
2
erfc
242
1
erfcerfc
222
erfc()erfc()
222
z
zz
bzb zb
zz
e
zz
ee
b
ez z
ebeb
b





 

 






 
 



 






 





 


(22)
and erfc is the complementary error function.
 

  
122 2
=0
55 11
(,), ,
,,,,
n
Gr
uFcFd
M
Fc FdFcFd
 












. (26)
2.1. Solution for Prandtl number Pr = 1
As the Prandtl number is a measure of the relative
importance of the viscosity and thermal conductivity of
the fluid, the case corresponds to those fluids
whose momentum and thermal boundary layer thick-
nesses are of the same order of magnitude. Thus, the
solution for the velocity field has to be re-derived when
Prandtl number . The solution of the Equations
(15) and (14) subject to the boundary conditions (17) are
easily obtained and are given by
1Pr
1 Pr
where

5,erfc
24 2
erfc
24 2
Mz
Mz
zz
Fze M
M
zz
eM
M









 






 



(27)
and


1,
F
z

and


2,
F
z

are given by (22).
 
2
sinh 1
1
,sinh
s
sss


 

, (23)
3. Results and Discussion
 
 
2
12
2
22 2
sinh 1
1
,
sinh
sinh1 sinh1
.
() sinh
sinh
sM
us
sa sM
sM s
Gr
sM s
sM







 






,
We have presented the non-dimensional velocity and
temperature for several values of magnetic parameter
2
M
, radiation parameter , heat generation parameter R

, Prandtl number , Grashof number , accele-
rated parameter and time
Pr Gr
a

in Figures 2-12. Fig-
ures 2-8 represent the velocity 1 u against

for
several values of 2
M
, R,

, PrGr aand , , ,

.t
is seen from Figure 2 that the velocity 1 u decreases
with an increase in magnetic parameter
(24)
The inverse transforms of (23) and (24) give the
temperature and velocity distributions as
 
11
=0
,,
n
Fc Fd

 

 



, (25)
I
2
M
. The
application of the transverse magnetic field plays the role
of a resistive type force (Lorentz force) similar to drag
orce (that acts in the opposite direction of the fluid f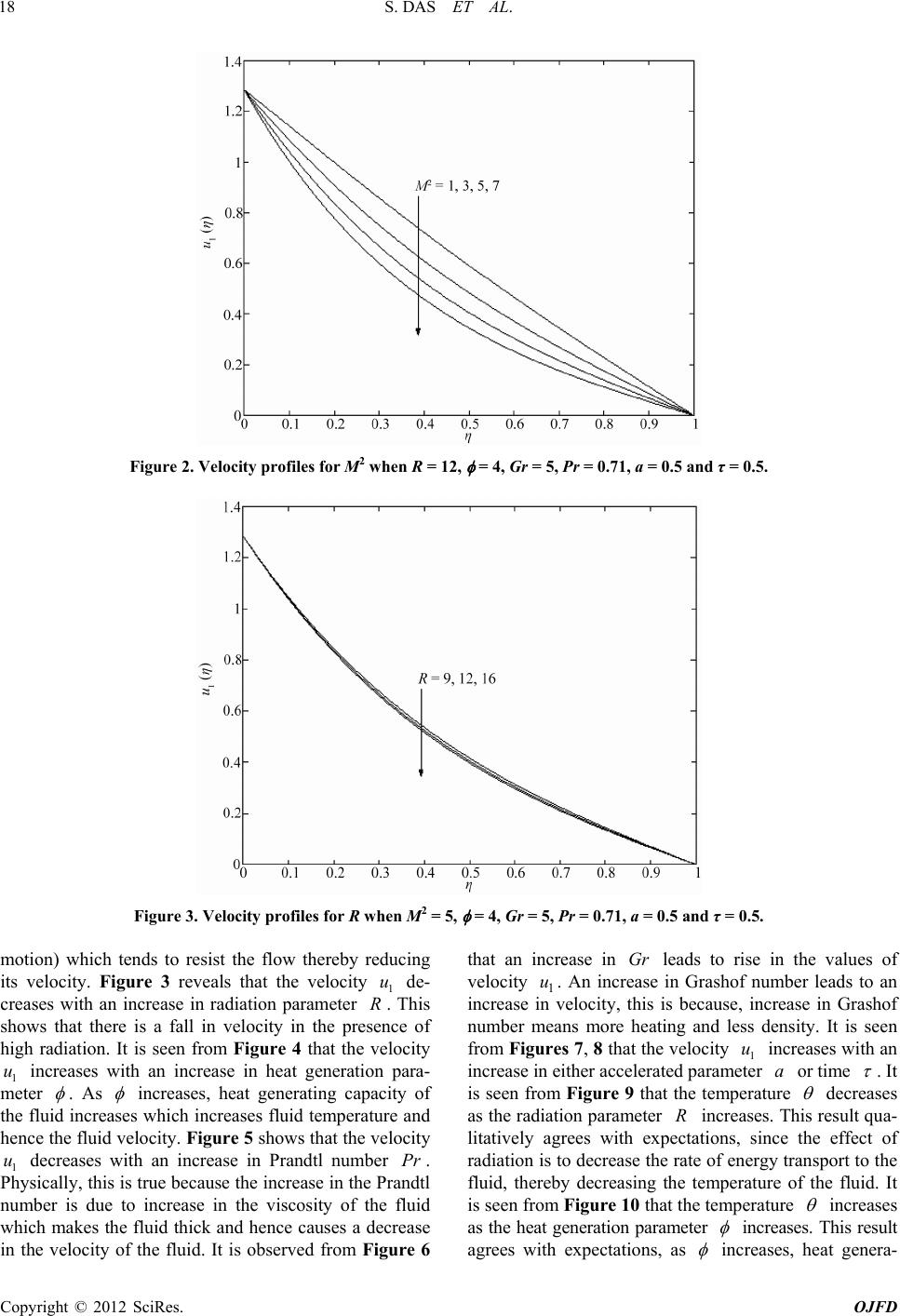

S. DAS ET AL.
18
Figure 2. Velocity profiles for M2 when R = 12,  = 4, Gr = 5, Pr = 0.71, a = 0.5 and τ = 0.5.
Figure 3. Velocity profiles for R when M2 = 5,  = 4, Gr = 5, Pr = 0.71, a = 0.5 and τ = 0.5.
motion) which tends to resist the flow thereby reducing
its velocity. Figure 3 reveals that the velocity de-
creases with an increase in radiation parameter . This
shows that there is a fall in velocity in the presence of
high radiation. It is seen from Figure 4 that the velocity
increases with an increase in heat generation para-
meter
1
u
R
1
u

. As

increases, heat generating capacity of
the fluid increases which increases fluid temperature and
hence the fluid velocity. Figure 5 shows that the velocity
decreases with an increase in Prandtl number .
Physically, this is true because the increase in the Prandtl
number is due to increase in the viscosity of the fluid
which makes the fluid thick and hence causes a decrease
in the velocity of the fluid. It is observed from Figure 6
that an increase in leads to rise in the values of
velocity . An increase in Grashof number leads to an
increase in velocity, this is because, increase in Grashof
number means more heating and less density. It is seen
from Figures 7, 8 that the velocity increases with an
increase in either accelerated parameter aor time
1
uPr
Gr
1
u
1
u

.t
is seen from Figure 9 that the temperature
I

decreas
as the radiation parameter R increase. This result qua-
litatively agrees with expectations, since the effect of
radiation is to decrease the rate of energy transport to the
fluid, thereby decreasing the temperature of the fluid. It
is seen from Figure 10 that the temperature
es
s

increases
as the heat generation parameter

increases. This result
agrees with pectations, as ex

increases, heat genera-

S. DAS ET AL. 19
Figure 4. Velocity profiles for  when M2 = 5, R = 12, Gr = 5, Pr = 0.71, a = 0.5τ = 0.5. and
Figure 5. Velocity profiles for Pr when M2 = 5, R = 12, Gr = 5,  = 4, a = 0.5 and τ = 0.5.
ting capacity of the fluid increases and hence the fluid
temperature increases. It is observed from Figure 11 that
the temperature

decreases with an increase in Prandtl
number Pr . Th implies that an increase in Prandtl
number ls to fall the thermal boundary layer flow.
This is because fluids with large Pr have low thermal
diffusivity which causes low heat ptration resulting in
reduced thermal boundary layer. Figure 12 reveals that
the temperature
is
ead
ene

increases with an increase in time

.
The trend shows that the temperature increases with
increasing time. It is observed from that Figures 9-12
temperature decreases gradually from highest value on
the moving plate to a zero value on the stationary plate.
The rate of heat transfer at the moving plate (0


) is
given by


11
=0
=0
0,
n
Gc PrGdPr


,,








 



,
(28)
2, 22cndn



 where

2
1
4
,erfc erfc
42 2
erfcerfc.
22 π
424 2
zz
z
zz
Pr zz
Gz ee
zzz zPr
Pr eee






 





 










  
 

  
  


(29)

S. DAS ET AL.
20
Figure 6. Velocity profiles for Gr when M2 = 5, R = 12,  = 4, Pr = 0.71, a = 0.5 and τ = 0.5.
Figure 7. Velocity profiles for a when M2 = 5, R = 12, Gr = 5,  = 4, Pr = 0.71 and τ = 0.5.
Numerical results of the rate of heat transfer


0 

 explained by the fact that frictional forces become
dominant with increasing values of and hence yield
greater heat transfer rates. Further,n that for fixed
value of
Pr
it is see

, Pr
at the moving plate (0

)
ented in the
n param
against the r
parameter are presTable 1 fo
values of heat generatioeter
adiation
r various R

, Prandtl
and ti
number
Pr me

.
pa
ases
r
and

, the rate oeat transfer f h


0 


From
dime
increas
the
nsional s
es with an increas
poi
s at t
Table thr the fixe
diationrameter , the rate of he
time
1 shows
Rat fod value at transfer of ra



num
incre
Pr o

0
ber
e iation parameter.
calnt ofi is necessary to
plate. The non-
ear streshe plate (
n radi
ew, itphysi
h
with an increase in either Prandtl

v
know the shear stress at the moving
and it decreases with an in-
crease in heat generation parameter

. This may be
) is obtained 0


as follows:


 


1
22344
=0
0
,,,,,,
(1)
xn
uGr
GcGdGcGGcPr GdPr
Pr





  
 
 

 
. (30)
ere
3d
wh

S. DAS ET AL. 21
Figure 8. Velocity profiles for τ when M2 = 5, R = 12, Gr = 5,  = 4, a = 0.5 and Pr = 0.71.
Figure 9. Temperature profiles for R when Pr = 0.71,  = 4 and τ = 0.5.
Table 1. Rate of heat transfer –10–1θ′(0) at the moving plate η = 0 with a = 0.5.
 Pr τ
R
2 3 4 0.71 2 7 0.3 0.4 0.5
8
10
12
14
1.36959
1.53971
1.69340
1.83453
1.27657
1.45
1.76535
1.17686
1.69340
1.36959
1.83453
1.62291
2.01991
2.40040
2.66810
0.87900
1.14169
12448
1.25683
37716
1.48812
1.36959
1.53971
1.69340
1.83453
702 1.36959 1.53971 1.76369 2.49186 0.97383
1.61833 1.53971 1.69340 1.89559 2.58105 1.06088 1.
1.

S. DAS ET AL.
22
Figure 10. Temperature profiles for  when R = 12, Pr = 0.71 and τ = 0.5.
Figure 11. Temperature profiles for Pr when R = 12,  = 4 and τ = 0.2.
Figure 12. Temperature profiles for τ when Pr = 0.71, R = 12 and  = 4.

S. DAS ET AL.
23

 


22
22
2
4
22 2
32
,
1 2
erfc erfc
222π
11 11
,erfc
424 424 22
zMa
azMa zMa
Mz
Gz
zz
eMaeMa eMae
zM zz
GzMe MM
bM MbM M b











 

 

 


 
 


 


 
 

 

 

 

  
 


 

22
22
22
2
4
2
4
22 2
2
4
2
12
erfc2π
2
erfcerfc,
222π
zM
Mz
z
bMb
zM bzM b
M
b
z
eM e
bb
ez z
MbeMb eMbe
b
Gz










 



 

 













 


 



 


 
 

 
2 2
2
,
11
erfc
22 22
442 44
erfc2
erfcerfc
222
z
z PrzPr
e Pr




 
 
 



z
bzb zb
Prz Pr
Pr
bb bb
z
e
ezz
Prb ebeb
b



 

 






 
 
 
 
 
 
 
 
   

 






 



2
4
2.
π
zPr b
Pre









 


 



 


 
 
(31)
For , the non-dimensional shear stress at the moving plate ( 1Pr0


) is given by
 

   
2255 66
2
=0
,, ,,,,
xn
Gr
Gc GdGcGdGc Gd
M

 


  
 



 (32)
where

22
5
4
1
,424
1
erfc424
2
erfc ,
π
2
Mz
zM
Mz
z
Gz M
MM
zz
eMM
MM
z
eMe


















 



 


 










(33)
and

1,Gz


is given by (29)
2
6
4
,
1erfc
z
zz
e


 
2
44 2
1
erfc
2
44 2
.
π
z
z
Gz
zz
e
e




 



 


 


  


 
 
  
 


and


 


 

2,Gz

,

3,Gz

and

4,Gz

are given by
(31).
Numerical results of the non-dimensional shear stress
x

at the moving plate (0


) are presented in Figures
18 against Grashof for various values of
gnetic parameter
13-
ma
number
2
Gr
M
, radiation parameter , heat
ration paramete
R
gene r

, Prandtl number time Pr and

.
Gras
Figures 13 and at for the fiue of
hof number ss
14
, th
show th
e shear
xed val
Gr stre
x

decreas
2
es with
rease inan inc either magnetic parameter
M
or
crea
2
radia-
on parameter wse in
hof num
ti
Gras
R a
Gr
nd
fo
it increa
r the fi
ses
xed
ith
valu
an in
of ber es
M
and
at the R. These resut with
inccrease iile it
decreases
lts are in agreem
cr
en
eithe
th
n
r
e
Gr
2
fact th
whvelocityreases with an in
eases in with an in
M
or
e
R. It is
seen from at the Figures 15 and 16 th sh ar stress
x

eneration increases
eter
with an increase in either heat g
param

or
hof
the sheas
Pra
Gr
ndtl
.
number
Figures
Pr
an
fo
d
r fixed value of
hat Gras num
r stres
ber 1718 reveal t
x

e
dec
ter a
reases
or
with an increase in either
accelerated paramtime

for fixed value of
Gras
hof number Gr

S. DAS ET AL.
24
12,  = 4, Pr = 0.71, a = 0.5 and τ = 0.5. Figure 13. Shear stress τx for M2 when R =
Figure 14. Shear stress τx for R when M2 = 5,  = 2, Pr = 0.71, a = 0.5 and τ = 0.5.
Figure 15. Shear stress τx for  when M2 = 5, R = 12, Pr = 0.71, a = 0.5 and τ = 0.5.

S. DAS ET AL. 25
Figure 16. Shear stress τx for Pr when M2 = 5, R = 12,  = 4, a = 0.5 and τ = 0.5.
Figure 17. Shear stress τx for a when M2 = 5, R = 12,  = 4, Pr = 0.71 and τ = 0.5.
4. Single Vertical Plate
In the limit, that is, when one of the plates h
(1


is reduce
) is an infinite distance, then the problem
dpast a vertical plate started
exponentially accelerated with variable temperature in
the presence of heat generation. In this case, on taking
limits and
placed at
to the flow
0d, 0nc

, the Equations (20)
and (21) become


1
,,
F
Pr

  , (34)
 



12 34
,,,,
1
Gr
uF FFPr
Pr

 


 


, (35)

S. DAS ET AL.
26
Figure 18. Shear stress τx for τ when M2 = 5, R = 12,  = 4, a = 0.5 and Pr = 0.71.
where


 

22
1
22
2
3
,erfcerfc,
22
424 2
1
,erfc erfc
222
1
, erfcerf
24 24
2
zz
azMa zMa
Mz Mz
zzz z
Fz ee
zz
Fze eMaeMa
zzz
FzeMe
bM M













 

 
 








 

  
 

,






 

22
2
22
2
4
c2
1
erfcerfc
222
erfcerfc,
222
1
,erfc
242
Mz Mz
bzM bzM b
z
zM
zz
eMeM
b
ez z
eMbe M
b
zz
Fze
b






















 













b




 
2
2
erfc
242
1
erfcerfc
222
erfcerfc
222
z
zz
bzbzb
zz
e
zz
ee
b
ez z
ebe b
b




 

 

 






 
 
















(36)
and

0
uy t

01
2
00
0
0
22
2
200
222
000
,,,,,
4
, , ,
h
tu
u TT u
BQ
I
MR
ukuku
 

 


 

 (37)
0
3
0
, .
h
p h
T T
u
t
c
gTT
GrPr k
u





Equations (34) and (35) are identical with the Equa-
ma [17]. For tions (9) and (10) of Kumar and Var1Pr

,
the solutions (25) and (26) for the temperature and
velocity distributield ions y




1
,,F

  , (38)
 

 
,F
12 51
2
,, ,
Gr
uF F
M

 

 


where
 ,
(39)


1,
F
z

,


2,
F
z

and

3,
F
z

are given by
(36) and


5,
F
z

is given by (27).

S. DAS ET AL. 27
5. Conclusion
The radiation effects on free convection MHD Couette
flow started exponentially accelerated with variable tem-
perature in the presence of heat generation have been
studied. The dimensionless governing equations are solved
by the usual Laplace transform technique.It is observed
that the velocity decreases with an increase in either
magnetic param
1 u
eter 2
M
. It is also
with an increase
or radiation parameter or
Prandtl number observed that the velcity
increases in either heat genen
eter
R
o
ratio
Pr
1
u
param

orf number or acc
eter or
G
tim
rasho
e
Gr elerated
param a

.
ndtl n
An increase in either radiation
eter umber leads to
fluid temp
param R
erature
or Pra Pr fall in the

. It is seen that the fluid temperature

param
increase heat genen
eter
eases with an incrin eitherratio

m
or tim
ng
e
plate
. Further, it is seen that the shear
stress at theovi
x

with an incease
in either
decreases r
2
M
o
creases
r r
incr
adiation parameter R while it in-
either heat generation para- with anease in
meter

0 

ber
or Pr
or
aof he
se in either Prandtl
ndtl n
increase
tim
umb
s with a
e
er Pr
n in
. The rate
a
at trans-
fer
num

cre
Pr

ration
whe
pa
r
ram
eas it
eter
decreases with an
increase int hea gene

.
REFERENCES
[1] A. K. Singh, “Natural Convection in Unsteady Couette
Motion,” Defense Science Journal, Vol. 38, No. 1, 1988,
pp. 35-41.
[2] A. K. Singh and T. Paul, “Transient Natural Convection
between Two Vertical Walls Heated/Cooled Asymetri-
cally,” International Journal of Applied Mechanics and
Engineering, Vol. 11, No. 1, 2006, pp. 143-154.
[3] B. K. Jha, A. K. Singh and H. S. Takhar, “Transient Free
Convection Flow in a Vertical Channel due to Symmetric
Heating,” International Journal of Applied Mechanics
and Engineering, Vol. 8, No. 3, 2003, pp. 497-502.
[4] H. M. Joshi, “Transient Effects in Natural Convection
Cooling of Vertical Parallel Plates,” International Com-
munications in Heat and Mass Transfer, Vol. 15, No. 2,
1988, pp. 227-238. doi:10.1016/0735-1933(88)90068-1
[5] O. Miyatake and T. Fujii, “Free Convection Heat Transfer
between Vertical Plates—One Plate Isothermally Heated
Thermally Insulated,” Heat Transfer—Japa-
se Research, Vol. 1, 1972, pp. 30-38.
[6] H. Tanaka, O. Miyatake, T. Fujii and M. Fujii, “Natural
Convection Heat Transfer between Vertical Parallel Pla-
tes—One Plate with a Uniform Heat Flux and the Other
Thermally Insulated,” Heat Transfer—Japanese Resear-
ch, Vol. 2, 1973, pp. 25-33.
[7] H. K. Mohanty, “Transient Free Convection Horizontal
Laminar Flow between Two Parallel Plates,” Acta Me-
chanica, Vol. 15, No. 3-4, 1972, pp. 273-293.
doi:10.1007/BF01304296
[8] B. K. Jha, “Natural Convection in Unsteady MHD Cou-
ette Flow,” Heat and Mass Transfer, Vol. 37, No. 4-5,
2001, pp. 329-331. doi:10.1007/PL00013295
[9] A. Ogulu and S. Motsa, “Radiative Heat Transfer to Mag-
netohydrodynamic Couette Flow with Variable Wall
Temperature,” Physica Scripta, Vol. 71, No. 4, 2005, pp.
336-339. doi:10.1238/Physica.Regular.071a00336
[10] R. C. Chaudhary and P. Jain, “Exact Solutions of Incom-
pressible Couette Flow with Constant Temperature and
Constant Heat Flux on Walls in the Presence of Radia-
tion,” Turkish Journal of Engineering & Environmental
Sciences, Vol. 3, No. 1, 2007, pp. 297-304.
[11] P. Mebine, “Radiation Effects on MHD Couette Flow
With Heat Transfer between Two Parallel Plates,” Global
Journal of Pure and Applied Mathematics, Vol. 3, No. 2,
2007, pp. 1-12.
e Convective Flow of
between Vertical Po-
rous Plates with Periodic Heat Input,” International Com-
munications in Heat and Mass Transfer, Vol. 36, No. 6,
2009, pp. 624-631.
doi:10.1016/j.icheatmasstransfer.2009.03.003
and Other
ne
[12] B. K. Jha and A. O. Ajibade, “Fre
Heat Generating/Absorbing Fluid
[13] B. K. Jha and A. O. Ajibade, “Unsteady Free Convective
Couette Flow of Heat Generating/Absorbing Fluid,” In-
ternational Journal of Energy and Technology, Vol. 2,
No. 12, 2010, pp. 1-9.
[14] C. Israel-Cookey, E. Amos and C. Nwaigwe, “MHD Os-
cillatory Couette Flow of a Radiating Viscous Fluid in a
Porous Medium with Periodic Wall Temperature,” Amer-
ican Journal of Scientific Industrial Research, Vol. 1, No.
2, 2010, pp. 326-331.
[15] M. Narahari, “Effects Of Thermal Radiat
Convection Currents on the Unsteady Couette Flow be-
tween Two Vertical Parallel Plates with Constant Heat
Flux at one Boundary,” WSEAS Transactions on Heat
and Mass Transfer, Vol. 5, No. 1, 2010, pp. 21-30.
[16] R. K. Deka and A. Bhattacharya, “Unsteady Free Con-
vective Couette Flow of Heat Generating/Absorbing Fluid
in Porous Medium,” International Journal of Mathe-
matical Archive, Vol. 2, No. 6, 2011, pp. 853-863.
[17] A. G. V. Kumar and S. V. K. Varma, “Radiation Effects
on MHD Flow Past an Impulsively Started Exponentially
Accelerated Vertical Plate with Variable Temperature in
, No. 4
. C. Lin, “Laminar Convection
of a Radiating Gas in a Vertical
Fluid Mechanics, Vol. 46, 1970, pp
doi:10.1017/S0022112071000673
ion and Free
the Presence of Heat Generation,” International Journal
of Engineering Science and Technology, Vol. 3,
2011, pp. 2897-2909.
[18] R. Grief, I. S. Habib and J
Channel,” Journal of
. 513-520.