Wireless Sensor Network, 2010, 2, 365-372
doi:10.4236/wsn.2010.24048 Published Online May 2010 (http://www.SciRP.org/journal/wsn)
Detection Proposal Schemes for Spectrum Sensing in
Cognitive Radio
Nawaf Hadhal Kamil, Xiuhua Yuan
Wuhan National Laboratory for Optoelectronics, College of Optoelectronics Science and Engineering,
Huazhong University of Science and Technology, Wuhan, China
Received February 4, 2010; revised February 22, 2010; accepted March 11, 2010
Abstract
The most important components of the cognitive radio concept is its ability to measure, sense and learn. One
also should be aware of the parameters related to the radio channel characteristics and the availability of
spectrum and power. In cognitive radio technology, primary users can be defined as the users who have the
highest priority on the usage of a specific part of the spectrum. Secondary users, have lower priority, and
should not cause any interference to the primary users when using the technology. Therefore, the secondary
users need to have certain cognitive radio capabilities, such as sensing the spectrum to check whether it is
being used by primary user or not, and changing the radio parameters to exploit the unused part of the spec-
trum. In this paper we proposed a new approach for spectrum sensing, In the first approach the primary sig-
nal is known so we use the code value with match filter to detect the primary user, on the other hand, when
the primary user signal is unknown we proposed a new strategy for energy detection in both non-cooperation
and cooperation schemes. Then we will prove by simulation results that the new approach is better than the
conventional energy detection.
Keywords: Cognitive Radio, Spectrum Sensing, Spectrum Performance
1. Introduction
Spectrum sensing is an exceptionally important task in a
cognitive radio system. The transmissions of licensed
users have to be reliably detected: Thus, spectrum sens-
ing is the first step towards adaptive transmission in free
spectral bands. Without causing any interference to the
primary user, the secondary system has to be spectrum
aware to exploit the available spectrum efficiently. There
are certainly a number of approaches that can be used to
check whether the primary user signal is present or not,
but the only autonomous and flexible approach is based
on measurements of the actual occupancy in given loca-
tion and time [1]. Spectrum sensing could add robustness
and responsiveness to changes in the environment be-
cause it provides real-time feedback. Therefore, we argue
that spectrum sensing should be considered as an impor-
tant part of any cognitive radios system. Wireless sys-
tems today are characterized by wasteful static spectrum
allocations, fixed radio functions, and limited network
coordination. Some systems in unlicensed bands have
achieved great spectrum efficiency but are faced with an
increasing interference that limits network capacity and
scalability [2]. When the ultimate cognitive radio is con-
sidered, it is a more general term that involves obtaining
the spectrum usage characteristics across multiple di-
mensions such as time, space, frequency, and code.
However, this requires more powerful signal analysis
technique because of the additional computational com-
plexity. Even though there are many kinds of primary
user systems, the cognitive radio’s knowledge of their
characteristics and requirements for interference protec-
tion can be abstracted by a few generally applicable pa-
rameters. Three critical requirements for sensing radio
are the detection time and the detection probability and
the minimum detectable signal level. The required detec-
tion time and probability of detection are set by the pri-
mary user tolerances to QoS degradation. While these are
two conflicting requirements, the cognitive radio system
goal is to minimize detection time in order to increase
the time available to use the channel [3]. In spectrum
sensing many techniques exist to detect the primary user,
two of the most practical techniques being energy detec-
tion and match filter detection. Spectrum sensing is still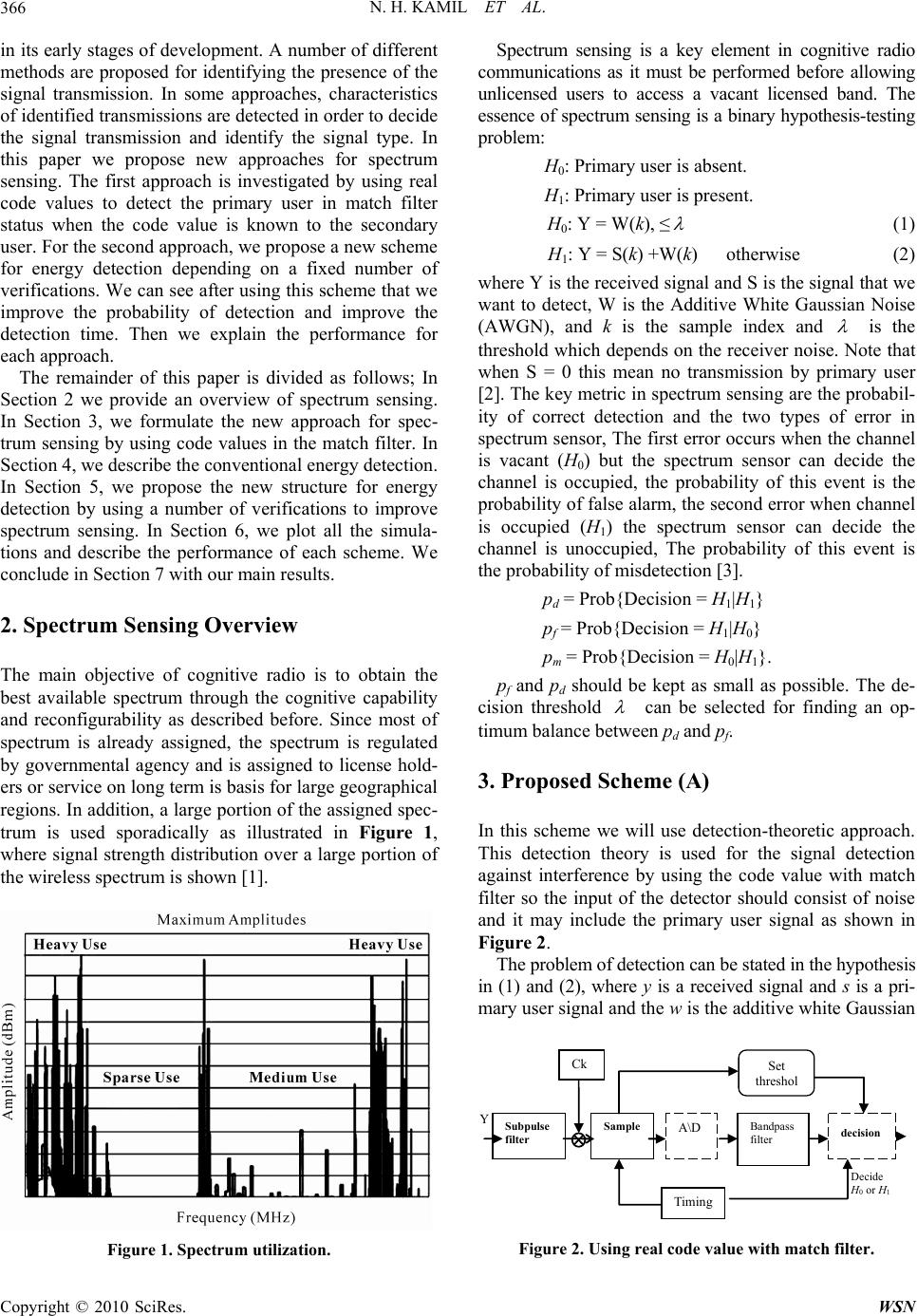

N. H. KAMIL ET AL. 366
in its early stages of development. A number of different
methods are proposed for identifying the presence of the
signal transmission. In some approaches, characteristics
of identified transmissions are detected in order to decide
the signal transmission and identify the signal type. In
this paper we propose new approaches for spectrum
sensing. The first approach is investigated by using real
code values to detect the primary user in match filter
status when the code value is known to the secondary
user. For the second approach, we propose a new scheme
for energy detection depending on a fixed number of
verifications. We can see after using this scheme that we
improve the probability of detection and improve the
detection time. Then we explain the performance for
each approach.
The remainder of this paper is divided as follows; In
Section 2 we provide an overview of spectrum sensing.
In Section 3, we formulate the new approach for spec-
trum sensing by using code values in the match filter. In
Section 4, we describe the conventional energy detection.
In Section 5, we propose the new structure for energy
detection by using a number of verifications to improve
spectrum sensing. In Section 6, we plot all the simula-
tions and describe the performance of each scheme. We
conclude in Section 7 with our main results.
2. Spectrum Sensing Overview
The main objective of cognitive radio is to obtain the
best available spectrum through the cognitive capability
and reconfigurability as described before. Since most of
spectrum is already assigned, the spectrum is regulated
by governmental agency and is assigned to license hold-
ers or service on long term is basis for large geographical
regions. In addition, a large portion of the assigned spec-
trum is used sporadically as illustrated in Figure 1,
where signal strength distribution over a large portion of
the wireless spectrum is shown [1].
Figure 1. Spectrum utilization.
Spectrum sensing is a key element in cognitive radio
communications as it must be performed before allowing
unlicensed users to access a vacant licensed band. The
essence of spectrum sensing is a binary hypothesis-testing
problem:
H0: Primary user is absent.
H1: Primary user is present.
H0: Y = W(k), ≤

(1)
H1: Y = S(k) +W(k) otherwise (2)
where Y is the received signal and S is the signal that we
want to detect, W is the Additive White Gaussian Noise
(AWGN), and k is the sample index and

is the
threshold which depends on the receiver noise. Note that
when S = 0 this mean no transmission by primary user
[2]. The key metric in spectrum sensing are the probabil-
ity of correct detection and the two types of error in
spectrum sensor, The first error occurs when the channel
is vacant (H0) but the spectrum sensor can decide the
channel is occupied, the probability of this event is the
probability of false alarm, the second error when channel
is occupied (H1) the spectrum sensor can decide the
channel is unoccupied, The probability of this event is
the probability of misdetection [3].
pd = Prob{Decision = H1|H1}
pf = Prob{Decision = H1|H0}
pm = Prob{Decision = H0|H1}.
pf and pd should be kept as small as possible. The de-
cision threshold

can be selected for finding an op-
timum balance between pd and pf.
3. Proposed Scheme (A)
In this scheme we will use detection-theoretic approach.
This detection theory is used for the signal detection
against interference by using the code value with match
filter so the input of the detector should consist of noise
and it may include the primary user signal as shown in
Figure 2.
The problem of detection can be stated in the hypothesis
in (1) and (2), where y is a received signal and s is a pri-
mary user signal and the w is the additive white Gaussian
Decide
H
0
or H
1
Ck
Subpulse
filter Sample
A\D
Bandpass
filter decision
Timing
Set
threshol
Y
Figure 2. Using real code value with match filter.

N. H. KAMIL ET AL.367
noise, When using Neyman-Pearson test, we can get that
[4]:
 

1
0
1
0
|
|
H
y
yH
fyH
Ly fyH


 (3)
where L(y) is likelihood ratio (LR) function and (|.)
y
f
y
The conditional probability density function (pdf) of y
and the threshold

which depends on the probability
of false alarm (pf). The conditional LR should average
over these parameters and this detector is called the ALR
(Average Likelihood Ratio) detector [5].
In this problem we assumed that the primary user
transmitter sends a code value with the sample and the
cognitive user should have knowledge about the this
code value, it is assumed that the cognitive user received
pulse consisting of kth sample, the sample of the signal
should have the following form:
, 0, 1,..., -1 jk
kk k
s
vec kN

 (4)
where is the amplitude and
k
vk

is the phase of nth
sample, and is the real code value in this sample, so
we can defined as:
k
C

01 1
...T
N
ssss






k
(5)

01 1
... T
N
wwww

 (6)

01 1
...T
N
cccc

 (7)

01 1
...T
N
yyyy

 (8)
where w is the noise vector and y is the received vector
so: y = s + w.
It is assumed that the noise is a complex Gaussian
noise, with following pdf:
1
0
()( )
k
N
ww
k
f
wfw


 (9)

22
2
1 e
k
k
w
wk
fw



 (10)
If the signal vector, s is completely known to the re-
ceiver the likelihood ratio will be [6]:


22
12
|exp Re
HH
ww
Lyss sy s



 




(11)
A practical case is considered where k

in Equation
(4) is the same for each sample and is modeled as a uni-
formly distributed random variable. In this case, it can be
assumed that:
, 0,1,...-1
k
vvkN (12)
where v is usually assumed to have Rayleigh distribu-
tion with parameter (i.e., a

2va
v
v
fv e
a

) [6] with
this assumption, it is obtained that:
N-1
2
k0
v c
H
k
ss

 2

(13)
By definition of .
H
A
yc, and where
12
0
u
N
k
k
c




and by average v and the Equation (11) becomes:
 
22
2
/
02
0
12
||,
2
w
vv
LyvLyv deIA







 
(14)
This integral is a special variant of the general form of
the Watson integral [7]:
2
2a|A|/(12)
2
w
2
()(1/ 1) ewau
au
Ly



 (15)
The following test can be used:
1
0
H
N-1
H
1k
k0
.y
k
H
Lycc





 (16)
We can say that the above detector is well-known
matched filter that is used in practical receivers.
The most important step is to evaluate the perform-
ance of the derived detector and to find the relation be-
tween (probability of false alarm) and (probability
of detection) .
fa
p
d
p
In case of 0
H
:
k
yw
k

(17)
The distribution of it is similar normal distribution,
so under
k
w
0
H
hypothesis the is equal to
1
L22


and when has Rayleigh distribution [7] with pa-
rameter
1
L
2
u  2 then the probability of false alarm
would be:

22
11 01
|w
u
fa cL
pfLHdLe





 (18)
Under 1
H
hypothesis it can be seen that:
j
e
kk k
y
vc w


 (19)
In the distribution of , when given v and , the
probability of detection by using a code will be:
1
L

 
22
-1 2
L1 1
1
f|d e
w
uau
dc
pLHL




  (20)
After we obtain the probability of false alarm and de-
tection probability, the relation between probability of
false alarm and probability of detection will be:

N. H. KAMIL ET AL. 368
2
2
1/(1 )
au
d-cfa-c
pp


 (21)
By definition the SNR for the received signal is:


2
.2
.
H
H
w
Es sau
SNR N
Ew w


 (22)
So Equation (21) will be:

1/ 1SNR N
d-cfa-c
pp



(23)
=1
m-c d-c
pp (24)
where N is the number of sample. From Equation (23) it
can be seen that the ROC of the detector depends on
SNR and the code parameters would have no effect on
performance. In this way we can investigate the code
value to detect the presence of the primary user.
4. Energy Detection
The energy detector is known as radiometry and it is the
most common method of spectrum sensing because it is
requires low implementation complexities [8,9]. More-
over, the cognitive user’s receivers do not need any
knowledge of the primary users’ signals. The signal is
detected by comparing the output of the energy detector
with a threshold that depends on the noise floor [10].
Some of challenges with energy detector-based sensing
it’s include the selection of the threshold for detecting
primary users, inability to differentiate interference from
primary users and noise, and the poor performance under
low Signal-to-Noise-Ratio (SNR) values [9]. Moreover,
the energy detector does not work efficiently for detect-
ing spread spectrum signals [8]. Energy detection is the
classical method for detecting in unknown signals. At
first the input signal is filtered with a Band Pass Filter
(BPF) to select the bandwidth. Next the filtered signal is
squared and integrated over the observation interval.
Then the output of the integrator is compared to a thre-
shold to decide whether if the primary user is present or
not. When the spectral environment is analyzed at the
digital domain, fast Fourier transform (FFT) based me-
thods are usually used in order to obtain frequency re-
sponse. FFT also is generates the resolution in frequency
domain. A practical energy detection method for cogni-
tive radio is Welch’s periodogram [11] which is ex-
plained in Figure 3.
Figure 3. Energy detection using Welch’s periodogram.
The detection test follows the two hypotheses in (1)
and (2), The noise is assumed to be additive, white and
Gaussian (AWGN) with zero mean and variance 2
w

.
The decision statistic for the energy detector is:
2
([])
N
TYn

(25)
In this architecture, we have 2N degrees of freedom to
improve signal detection. The frequency resolution of the
FFT increases with the number of points K (equivalent to
changing the analog pre-filter), which effectively in-
creases the sensing time. Increasing the number of sam-
ple N also will improves the estimate of the signal energy.
The performance of detection is measured by a resulting
pair of probability of detection and probability of false
alarm (pd, pfa). Each one is associated with the threshold
value

that tests the decision statistic:
T >

decide signal present
T <

decide signal absent
When the signal is not present, the decision statistic
has a central chisquare distribution with N degrees of
freedom. When the signal is present the decision statistic
has a non-central chi-square distribution with the same
number of degrees of freedom. For simplicity we assume
that the time-bandwidth product TW, is integer number
denoted by m. In non-fading environment the pd and pfa
can be evaluated as:


1
|2SNR,
dm
ppTH Q

   (26)



0
,/2
|
fa
m
ppTH m



 
 (27)
where (.) and (.,.)

 are complete and incomplete
gamma function respectively [12], and is the
generalized Marcum Q-function [14] defined as fol-
lows:
(.,.)
m
Q
 
22
2
1
1
,
ya
m
mm
m
b
y
QabeI aydy
a




 (28)
where is the modified Bassel function of
(m-1)th order.
1(.) m
I
And the relation between pd and pfa will be [17]:
 
1
1.
21
dfa
pQQpNSNR
SNR






(29)
The tradeoff between pm = 1 – pd (probability of mis-
detection) and probability of false alarm pf has different
implications in the context of dynamic spectrum sharing.
A high pm would be missing the presence of the primary
user which would increase the interference to the pri-
mary licensee. A high probability of false alarm would

N. H. KAMIL ET AL.369
result in low spectrum utilization which increases the
number of missed opportunities.
From (27) we can see that pf is independent of SNR
which under H0 means there is no primary user present.
The fading environment under Rayleigh fading, (26)
gives the probability of detection conditioned on instan-
taneous SNR, so in this case would be derived by aver-
aging (26) over fading statistic [14],

21
2
2
0
2
2(1 )2
0
11
!2
1
!21
m
m
d
k
k
m
SNR
k
SNR
pe kSNR
SNR
ee
kSNR













 

 
 






 





(30)
5. Proposed Scheme (B)
5.1. For the Non-Cooperation Scheme
In this scheme we propose a new algorithm for use with
the conventional energy detection in spectrum sensing.
We propose new structure where each cognitive radio
has energy detector with multiples verification using
time delay to enhance the spectrum sensing and opportu-
nities. Also, the performance is investigated by simula-
tion and compared to that of the conventional energy
detector. If the detector makes the decision that there is
no primary user but the primary user is actually exists, it
could cause harmful interference to the primary user. On
the other hand, if the detector make own decision about
that there is primary user but there is no primary user, it
could miss the chance to transmit. So, collaborative sens-
ing was proposed to enhance the spectrum sensing [15].
In this scheme we describe a new energy detection struc-
ture where the energy detector engages in multiples veri-
fication by using time delay to enhance the reliability of
sensing, as shown in Figure 4.
Time delay
Energy detection
Collaborative decision
T1 T2 T3
V1 Decide
H0 or H1
V2 Decide
H0 or H1
V3 Decide
H0 or H1
Final decision
H0 or H1
Figure 4. Proposed structure (B).
The received signal from the secondary user’s antenna
is delayed accumulatively and then goes through the en-
ergy detector. Here we have V of verification and each
one makes its own decision H0 or H1 by comparing the
threshold

value then each decision uses collaborative
decision device to make a final decision whether signal is
exist or not. Collaborative decision has many rules, In
AND-rule when k = V “k out of V” where V is an verifi-
cation number and k is the reference number so in this
case if all V decide 1
H
so the final decision will be 1
H
,
In OR-rule, when k = 1 it’s mean that if one of k from V
verification decide 1
H
so the final decision will be 1
H
,
another commonly used rule if 1
2
V
k 


1V
H
which mean when the more than a half V choose so
the final decision will be
1
1
H
[16]. In our scheme, we
assume that if there is equal or more than half verifica-
tion, will be decide, 1
H
so the final decision will be
occupied. For example if we assume that we have three
of verification, so in collaborative decision device finally
decides 1
H
or 0
H
by compare the reference number k


V
fa
1k
d-V
p
where V is the number of verification, it
means if two or three verification decide so the fi-
nal decision will be . So the probability of detection
and false alarm for collaborative decision denoted by
() may be written as follows:
1
H
1
H
and -V p

1
2
11
V
d-V d
pp

  (31)

1
2
11
V
fa-V fa
pp

  (32)
And the probability of misdetection so:
1
md
pp

1
2
1
V
m-Vd
pp

 (33)
And we can say that the detection time will be:

1
2
11
n-v V
d
V
T
P



(34)
In Section 6, we will explain the performance for this
approach by plot curves and we can see that the prob-
ability of detection when we use this approach better
than when we use the conventional energy detection,
when we increase the number of verification we can see
that the probability of detection will increase as well as
the detection time, so to improve the detection time we
use this scheme in cooperation network.
5.2. For Cooperation Scheme
One of the ways to improve the channel sensing reliability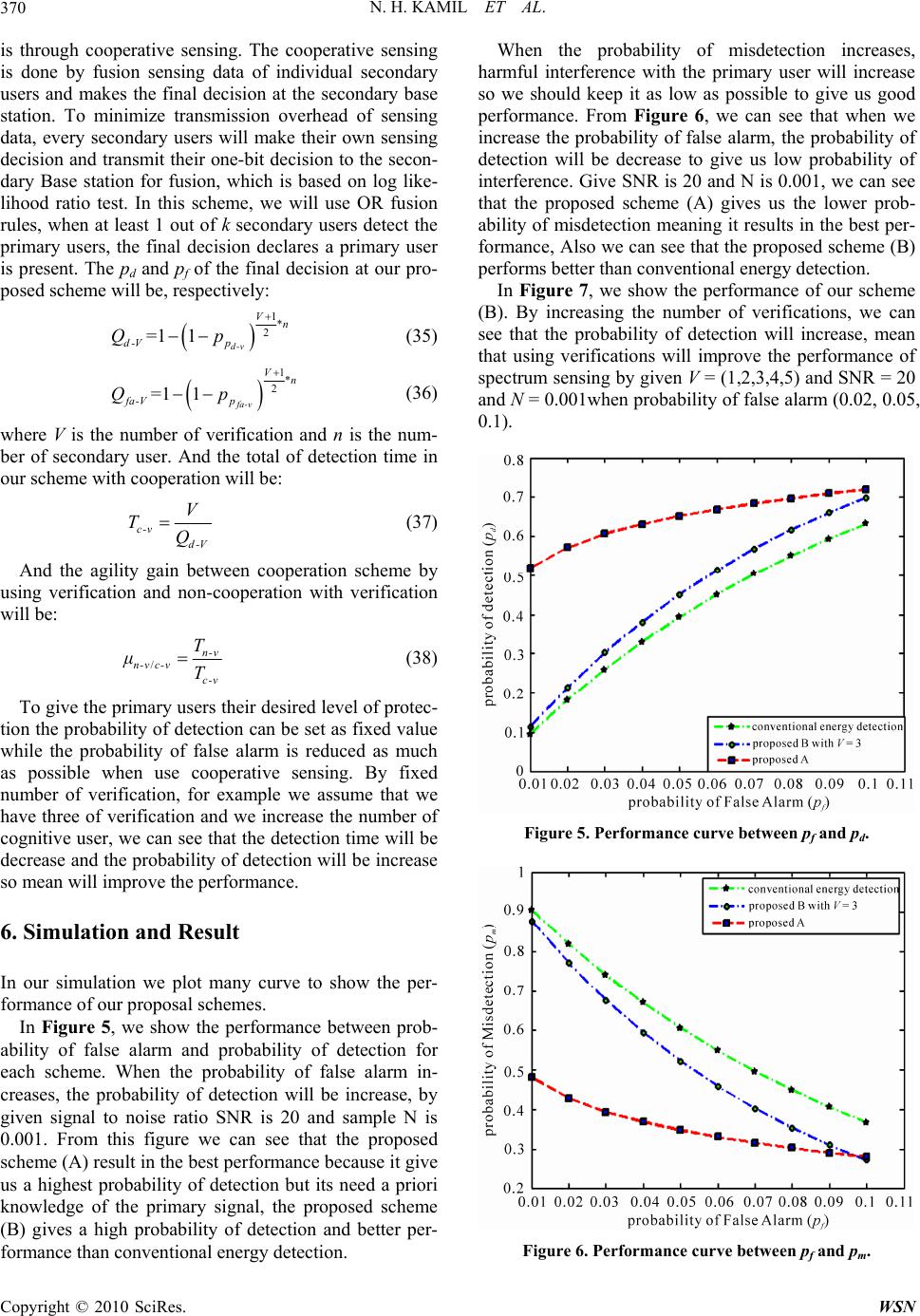

N. H. KAMIL ET AL. 370
is through cooperative sensing. The cooperative sensing
is done by fusion sensing data of individual secondary
users and makes the final decision at the secondary base
station. To minimize transmission overhead of sensing
data, every secondary users will make their own sensing
decision and transmit their one-bit decision to the secon-
dary Base station for fusion, which is based on log like-
lihood ratio test. In this scheme, we will use OR fusion
rules, when at least 1 out of k secondary users detect the
primary users, the final decision declares a primary user
is present. The pd and pf of the final decision at our pro-
posed scheme will be, respectively:

1*
2
=1 1d-v
Vn
d-V p
Qp

 (35)

1*
2
=1 1fa-v
Vn
fa-V p
Qp

 (36)
where V is the number of verification and n is the num-
ber of secondary user. And the total of detection time in
our scheme with cooperation will be:
c-v
d-V
V
TQ  (37)
And the agility gain between cooperation scheme by
using verification and non-cooperation with verification
will be:
/
n-v
n-v c-v
c-v
T
μT  (38)
To give the primary users their desired level of protec-
tion the probability of detection can be set as fixed value
while the probability of false alarm is reduced as much
as possible when use cooperative sensing. By fixed
number of verification, for example we assume that we
have three of verification and we increase the number of
cognitive user, we can see that the detection time will be
decrease and the probability of detection will be increase
so mean will improve the performance.
6. Simulation and Result
In our simulation we plot many curve to show the per-
formance of our proposal schemes.
In Figure 5, we show the performance between prob-
ability of false alarm and probability of detection for
each scheme. When the probability of false alarm in-
creases, the probability of detection will be increase, by
given signal to noise ratio SNR is 20 and sample N is
0.001. From this figure we can see that the proposed
scheme (A) result in the best performance because it give
us a highest probability of detection but its need a priori
knowledge of the primary signal, the proposed scheme
(B) gives a high probability of detection and better per-
formance than conventional energy detection.
When the probability of misdetection increases,
harmful interference with the primary user will increase
so we should keep it as low as possible to give us good
performance. From Figure 6, we can see that when we
increase the probability of false alarm, the probability of
detection will be decrease to give us low probability of
interference. Give SNR is 20 and N is 0.001, we can see
that the proposed scheme (A) gives us the lower prob-
ability of misdetection meaning it results in the best per-
formance, Also we can see that the proposed scheme (B)
performs better than conventional energy detection.
In Figure 7, we show the performance of our scheme
(B). By increasing the number of verifications, we can
see that the probability of detection will increase, mean
that using verifications will improve the performance of
spectrum sensing by given V = (1,2,3,4,5) and SNR = 20
and N = 0.001when probability of false alarm (0.02, 0.05,
0.1).
Figure 5. Performance curve between pf and pd.
Figure 6. Performance curve between pf and pm.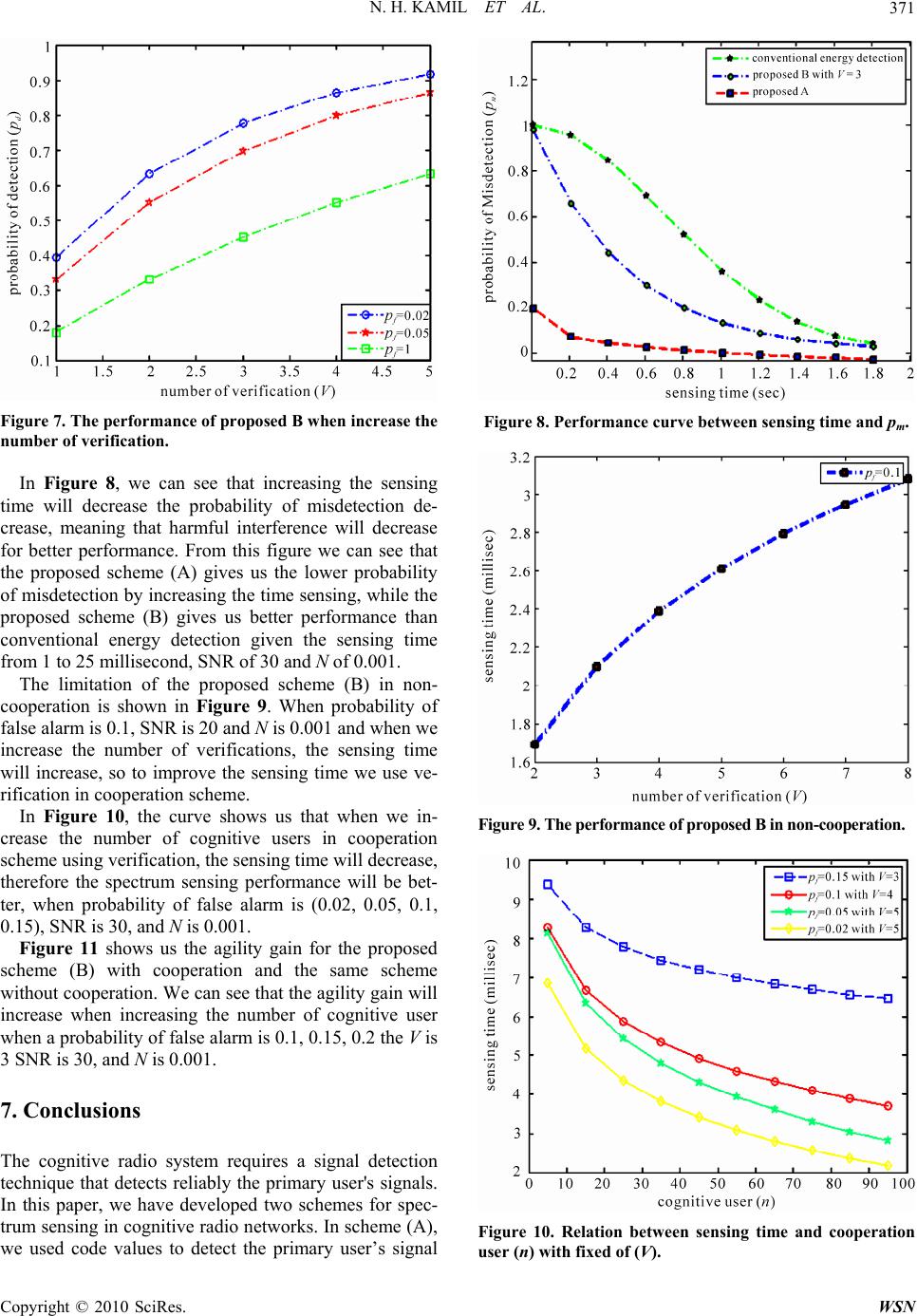

N. H. KAMIL ET AL.371
Figure 7. The performance of proposed B when increase the
number of verification.
In Figure 8, we can see that increasing the sensing
time will decrease the probability of misdetection de-
crease, meaning that harmful interference will decrease
for better performance. From this figure we can see that
the proposed scheme (A) gives us the lower probability
of misdetection by increasing the time sensing, while the
proposed scheme (B) gives us better performance than
conventional energy detection given the sensing time
from 1 to 25 millisecond, SNR of 30 and N of 0.001.
The limitation of the proposed scheme (B) in non-
cooperation is shown in Figure 9. When probability of
false alarm is 0.1, SNR is 20 and N is 0.001 and when we
increase the number of verifications, the sensing time
will increase, so to improve the sensing time we use ve-
rification in cooperation scheme.
In Figure 10, the curve shows us that when we in-
crease the number of cognitive users in cooperation
scheme using verification, the sensing time will decrease,
therefore the spectrum sensing performance will be bet-
ter, when probability of false alarm is (0.02, 0.05, 0.1,
0.15), SNR is 30, and N is 0.001.
Figure 11 shows us the agility gain for the proposed
scheme (B) with cooperation and the same scheme
without cooperation. We can see that the agility gain will
increase when increasing the number of cognitive user
when a probability of false alarm is 0.1, 0.15, 0.2 the V is
3 SNR is 30, and N is 0.001.
7. Conclusions
The cognitive radio system requires a signal detection
technique that detects reliably the primary user's signals.
In this paper, we have developed two schemes for spec-
trum sensing in cognitive radio networks. In scheme (A),
we used code values to detect the primary user’s signal
Figure 8. Performance curve between sensing time and pm.
Figure 9. The performan ce of proposed B in non- coopera tion.
Figure 10. Relation between sensing time and cooperation
user (n) with fixed of (V).

N. H. KAMIL ET AL. 372
by using matched filter when the primary signal’s infor-
mation is known to the secondary users. In proposed
scheme (B), we developed an energy detection method
using number of verifications for non-cooperation and
cooperation schemes. In Section 6, we showed the simu-
lation and results and explained the performance im-
provement resulting from our schemes.
8. References
[1] L. F. Akyildiz, W. Y. Lee, M. C. Vuran and S. Mohanty
“Next Generation/Dynamic Spectrum Access/Cognitive
Radio Wireless Networks: A Survey,” Broadband and
Wireless Networking Laboratory, School of Electrical
and Computer Engineering, Georgia Institute of Tech-
nology, Atlanta, 2006.
[2] H. Tang, “Some Physical Layer Issues of Wide-Band
Cognitive Radio Systems,” Proceedings of IEEE Interna-
tional Symposium on the New Frontiers in Dynamic Spec-
trum Access Networks, Baltimore, 8-11 November 2005,
pp. 151-159.
[3] C. X. Wang, H. H. Chen, X. Hong and M. Guizani, “Cog-
nitive Radio Network Management,” IEEE Vehicular
Technology Magazine, Vol. 3, No. 1, 2008, pp. 28-35.
[4] M. Barkat, “Signal Detection and Estimation,” Artech
House, London, 1991.
[5] H. L. V. Trees, “Detection, Estimation and Modulation
Theory,” Part 1, John Wiley and Sons, Inc., Hoboken,
1968.
[6] H. V. Poor, “An Introduction to Signal Detection and
Estimation,” 2nd Edition, Springer-Verlag, Berlin, 1994.
[7] A. Papoulis, “Probability, Random Variable, and Sto-
chastic Processes,” McGrow-Hill, New York, 1985.
[8] D. Cabric, S. M. Mishra and R. W. Brodersen, “Imple-
mentation Issues in Spectrum Sensing for Cognitive Ra-
dios,” Proceedings of Asilomar Conference on Signals,
Systems and Computers, Pacific Grove, Vol. 1, 7-10 No-
vember 2004, pp. 772-776.
[9] S. Shankar, C. Cordeiro and K. Challapali, “Spectrum
Agile Radios: Utilization and Sensing Architectures,”
Proceedings of IEEE International Symposium on New
Frontiers in the Dynamic Spectrum Access Networks,
Baltimore, 8-11 November 2005, pp.160-169.
[10] H. Urkowitz, “Energy Detection of Unknown Determi-
nistic Signals,” Proceedings of IEEE, Vol. 55, No. 4, April
1967, pp. 523-531.
[11] P. D. Welch, “The Use of Fast Fourier Transform for the
Estimation of Power Spectra: A Method Based on Time
Averaging over Short, Modified Periodograms,” IEEE
Transactions on Audio and Electroacoustics, Vol. 15, No.
6, June 1967, pp. 70-73.
[12] I. S. Gradshteyn and I. M. Ryzhik, “Table of Integral,
Series and Products,” 5th Edition, Academic Press, Cleve-
land, 1994.
[13] A. H. Nuttall, “Some Integrals Involving QM Function”
IEEE Transaction on Information Theory, Vol. 21, No. 1,
January 1975, pp. 95-96.
[14] F. F. Digham, M. S. Alouini and M. K. Simon, “On En-
ergy Detection of Unknown Signal over Fading Channel,”
Proceedings of IEEE International Conference on Com-
munications (ICC03), 11-15 May 2003, pp. 3575-3579.
[15] A. Ghasemi and E. S. Sousa, “Collaborative Spectrum
Sensing for Opportunistic Access in Fading Environ-
ments”, 1st IEEE International Symposium on New Fron-
tiers in Dynamic Spectrum Access Networks, Baltimore,
8-11 November 2005, pp. 131-136.
[16] A. Ghasemi and E. Sousa “Collaborative Sepectrum
Sensing for Opportunistic Access in Fading Environ-
ment,” Proceedings of DySpan’05, Baltimore, 8-11 No-
vember 2005.
[17] C. Y. E. Peh and Y. C. Liang, “Optimization for Coop-
erative Sensing in Cognitive Radio Networks,” IEEE
Wireless Communications and Networking Conference,
Hong Kong, 11-15 March 2007.