ABSTRACT

The quantum mechanical relationships between time-dependent oscillators, Hamilton- Jacobi theory and an invariant operator are clarified by making reference to a system with a generalized oscillator. We introduce a linear transformation in position and momentum, and show that the correspondence between classical and quantum transformations is exactly one-to-one. We found that classical canonical transformations are constructed from quantum unitary transformations as long as we are concerned with linear transformations. We also show the relationship between the invariant operator and a linear transformation.

Keywords:

Quantum Canonical Transformation, Linear Transformation, Generalized Oscillators, Invariant Operator

1. Introduction

Canonical transformations are a highlight in classical mechanics. They give not only solutions to classical mechanical systems, but also an insight into the quantization of them. However, the idea of canonical transformations has so far not been fully utilized in quantum systems. This issue was raised by Dirac [1] [2] [3] just after the birth of quantum mechanics. There, he only discussed the case of a time-independent canonical transformation. Recently, there has been renewed interest coming in this field in the context of Hamilton-Jacobi theory [4] [5] and action-angle variables [6] . While these articles were focused on time-independent transformations, time-dependent ones were also discussed [7] . Moreover, the introduction of an invariant operator to construct solutions for time-dependent Hamiltonian systems has also been proposed [8] [9] [10] . This invariant operator was constructed by means of a time-dependent quantum canonical transformation [11] [12] .

These various methods have been investigated for various purposes. However, there has been no unification of these various methods. The purpose of the present paper is to provide a unified description of these methods in terms of a linear transformation for position and momentum by referring to the system of a generalized oscillator. Since we are concerned with a linear canonical transformation, the classical and quantum correspondence is one-to-one. We also show that the invariant operator can be considered as part of a linear canonical transformation.

The organization of the paper is as follows. In Section 2, we define a linear canonical transformation in position and momentum and apply this to a genelarized oscillator. Moreover, we show two special cases of linear canonical transformations. One is the transformation to a time-dependent oscillator, and the other is to construct a Hamilton- Jacobi theory. In Section 3, we introduce a unitary operator that generates a linear transformation in position and momentum in quantum mechanics. We apply this unitary operator to a genelarized oscillator and obtain the same results as the classical cases mentioned in Section 2. In Section 4, we introduce an invariant operator. We show that this is also derived from a unitary operator that generates a linear transformation. We give two special cases for the coefficients of the linear transformation. The foregoing research is just one special case of a linear canonical transformation. Section 5 is devoted to a summary.

2. Classical Linear Canonical Transformations

A linear canonical transformation is defined by a transformation from old position and momentum variables 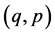to new one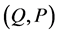s as

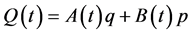, (1a)

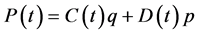, (1b)

where A, B, C and D are real functions of time t. 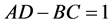is needed in order that 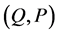are canonical, that is, the Poisson bracket must satisfy

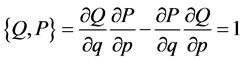. The condition 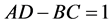is kept throughout this paper. This transformation is generated by the generating function

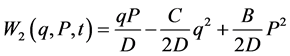, (2)

with

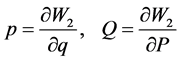, (3)

which is known from classical mechanics [13] .

Now the Hamiltonian which we consider in this paper is

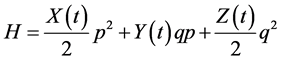, (4)

where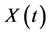, 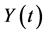and 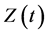are real functions of time t. The equation of motion of this system is given by

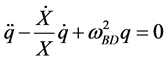, (5)

where

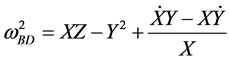. (6)

The dot above the variables denotes the time derivatives of the variables. For later use, we derive the equation of motion for p from the Hamiltonian (4),

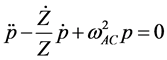, (7)

where

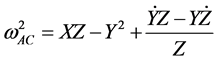. (8)

We will see these equations in later sections.

The transformed Hamiltonian K is derived from the classical mechanics [13]

. (9)

From the linear canonical transformation (1), we obtain

(10)

and

(11)

Collecting these equations together, we obtain the transformed Hamiltonian K as follows

(12)

Up till now, we have placed no constraint on the coefficients A, B, C and D, except. Here we see two cases which are of interest in both classical and quantum mechanics.

2.1. Case 1: Time-Dependent Oscillator

We assign the coefficients of (1) [7] [11] as

. (13)

Substituting these coefficients and their time derivatives

, (14)

(15)

into (12), we obtain the transformed Hamiltonian

(16)

where

(17)

and is defined by (6). This is a time-dependent oscillator which has no cross term such as. This system is investigated in [7] [11] . As we have seen, this is a special case of a linear transformation (1) in position and momentum with the coefficients (13).

2.2. Case 2: Hamilton-Jacobi Theory

Next let us consider another constraint. We impose the additional condition on the coefficients.

(18a)

(18b)

These constraints show that the coefficients are the solution to the equation of motion (5) and (7), that is,

(19a)

(19b)

where and are defined by (6) and (8). The same equations are also satisfied by C and D.

We substitute (18) into the transformed Hamiltonian (12). For the time-derivative parts in (12), we obtain

(20)

(21)

(22)

so that the transformed Hamiltonian becomes zero;

(23)

which means that the new variables are constant. This corresponds to the Hamilton-Jacobi theory for a generalized oscillator.

3. Quantum Linear Canonical Transformations

Since we are concerned with linear canonical transformations, the classical and quantum correspondence is exactly one-to-one [14] . Let us consider the following unitary operator:

(24)

where describes the q-number. and are quantum canonical variables which satisfy. We set for simplicity., and are all real functions of time t.

Next we show a “normal-ordering” of the unitary operator (24). For this we introduce the operators [15]

(25)

which form the SU(1, 1) Lie algebra

(26)

We rewrite the unitary operator (24) in the “normal-ordered” form as

(27a)

(27b)

where

(28)

and. The details of the calculation are given in the Appendix.

Corresponding to the classical linear transformation (1), the new quantum variables and are generated by this unitary operator (27). By repeated usage of (A.17) and the formula [16] ,

(29)

we obtain

(30a)

(30b)

where from (28), is satisfied which implies that the new variables and are canonical variables;. When we choose in order to satisfy (28), then we are able to replace all classical linear transformations (1) with quantum ones (30).

To recognize this statement, let us consider the generalized oscillator. The quantum counterpart of the Hamiltonian (4) is

, (31)

and the quantum counterpart of the transformed Hamiltonian is defined by

(32)

Substituting (27b) and (31) into (32), we obtain

(33)

and using (A.18),

(34)

Collecting these equations together, we obtain the transformed Hamiltonian which is given as

(35)

The time derivative of the condition gives the following equations;

(36)

(37)

(38)

Then we recover the same form of the transformed Hamiltonian

(39)

with (12) in the classical transformed Hamiltonian. It is realized that the linear transformation in position and momentum gives the same transformed Hamiltonian (12) and (39). So, the same constraints (13) and (18) give the same results for the time- dependent oscillator and the Hamilton-Jacobi relations, as mentioned in section 2. As long as we are concerned with linear canonical transformations, the correspondence between the canonical transformation in classical mechanics and the unitary transformation in quantum mechanics is one-to-one. Referring to the generalized oscillator, the quantum unitary transformation is constructed in parallel with the classical canonical transformation.

4. Invariant Operator

An invariant operator for a given Hamiltonian is a constant of motion that obeys the equation

. (40)

This was first investigated for the time-dependent harmonic oscillator [10] . For the generalized oscillator (31), we assume that the form of is

(41)

where x, y and z are real functions of time t. The time derivative of is given by

(42)

In order to satisfy (40), we demand for the coefficients x, y and z, that

(43a)

(43b)

(43c)

On the other hand, the invariant operator was derived from the time- independent harmonic oscillator

, (44)

whose eigenvalues and eigenfunctions are well known in elementary quantum mechanics.

We see that this unitary operator is also a linear canonical transformation [12] . Using (27b) and (44), we obtain from (A.18),

(45)

(46)

To satisfy (41), we assign

(47a)

(47b)

(47c)

for x, y and z. In other words, the coefficients A, B, C and D in the unitary operator which gives rise to the linear transformation should satisfy (43) and (47).

The Hamiltonian (44) can be written down in terms of annihilation and creation operators (and its Hermitian conjugate) as

, (48)

whose eigenvalues and eigenstates are given by [16]

(49)

where is an eigenstate belonging to the eigenvalue.

This implies that we define the time-dependent operators by

(50a)

(50b)

and the invariant operator is written in the form

, (51)

and its eigenstates are

(52)

These are the same eigenvalues as for the time-independent case.

When we choose the squeezing coefficients

(53)

then we construct the same results as in [11] [17] [18] .

The invariant operator is classified according to an auxiliary equation. We will see two cases below.

4.1. Case 1

There are some kinds of invariant function that are classified as auxiliary equations. One example is [7]

(54)

where

(55)

Equation (47a) means

,

and from the derivative of with respect to t and (43a), we obtain

,

which fulfills the condition (47b). Equation (43b) gives

(56)

(57)

where

,

and is defined by (17). From (43c), this M satisfies the differential equation

With the initial condition (at), we obtain

(58)

This is the auxiliary equation [11] [12] . From (57) and (58), z becomes

,

which is identical with (47c).

4.2. Case 2

Another kind of invariant function [19] is

. (59)

From (43a) and (47a), we obtain

,

then,

,

which fulfills the condition (47b). Eq.(43b) gives

(60)

(61)

where

,

and is defined by (6). From (43c), this N satisfies the differential equation

With the initial condition (at), we obtain

(62)

This is the auxiliary equation [19] [20]

(63)

This is an inhomogeneous differential equation of (5). From (61) and (62), z becomes

,

which is identical with (47c).

5. Summary

We investigated a linear transformation in position and momentum by referring to a generalized oscillator. We found that the correspondence between the classical canonical transformation and the quantum unitary transformation is one-to-one, that is, as long as we are concerned with linear transformations, all classical transformations can be constructed as quantum ones. As examples of this, the transformation to a time- dependent oscillator and the construction of Hamilton-Jacobi theory are derived both for the classical and quantum cases. The notion of linear transformations is also applicable to the invariant operator. On choosing the coefficients for the linear transformation, we were able to repeat the results obtained in previous work.

Cite this paper

Ogura, A. (2016) Classical and Quantum Behavior of Generalized Oscillators in Terms of Linear Canonical Transformations. Journal of Modern Physics, 7, 2205-2218. http://dx.doi.org/10.4236/jmp.2016.715191

References

Appendix

In this Appendix, we derive the “normal-ordering” of (27a). To accomplish this program, we apply the idea of Truax [21] straightforwardly. We define a operator

, , (A.1)

where is a real parameter and is the identity operator. We can choose a second representation

, (A.2)

subject to the constraint, that is, ,.’s are to be determined by. Differentiating both sides, we obtain

(A.3)

where primes indicate differentiation with respect to. Multiplying from the right by

(A.4)

we obtain

(A.5)

From the theorem (29) and the commutation relations (26), we obtain

(A.6)

We identify the coefficients of the respective basis elements of the Lie algebra and obtain a system of coupled nonlinear equations [15] ,

(A.7a)

(A.7b)

(A.7c)

with initial conditions. Substituting (A.7a) into (A.7b), we obtain

. (A.8)

Together, Equations ((A.7a), (A.7c), and (A.8)) imply

(A.9)

a Riccati equation for. Substituting, , we transform (A.9) into the second order, ordinary differential equation,

(A.10)

with constant coefficients. Subject to the initial conditions, this equation has the solution

(A.11)

where is a constant of integration and. Therefore, we get for the expression

. (A.12)

Substituting (A.12) into (A.8) for and integrating, we obtain the following expression:

. (A.13)

We can integrate the differential Equation (A.7a) to get the following

. (A.14)

To obtain the final result, choose and we obtain

(A.15)

where A, B, C and D are defined by (28). This is the desired expression for the “normal ordering” of the unitary operator. We decompose this unitary operator in three parts and assign

(A.16a)

(A.16b)

(A.16c)

The following equations

(A.17a)

(A.17b)

and

(A.18a)

(A.18b)

are helpful.