Journal of Modern Physics
Vol.07 No.13(2016), Article ID:71091,16 pages
10.4236/jmp.2016.713163
A Possible Alternative to the Accelerating Universe III
Frank R. Tangherlini
San Diego, CA, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 23, 2016; Accepted: September 27, 2016; Published: September 30, 2016
ABSTRACT
This work extends the author’s two previous works (2015), Journal of Modern Physics, 6, 78-87, and 1360-1370, by obtaining the index of refraction n of the dark energy for additional values of the cosmological density parameters, and for the two methods of obtaining n: least squares fit, and electromagnetic theory. Comparison of the alternative model with the accelerating universe for the new values of the density parameters and n is given in two tables. The new values for n are used to obtain a range of ages for the Einstein de Sitter (EdS) universe. It is shown that the EdS universe must be older than the comparison accelerating universe. This requirement is met for the Planck 2015 value of the Hubble constant, corrected for the speed of light reduction by n. A supporting measurement as well as a disagreeing measurement is also discussed. Possible support from a stellar age determination is also discussed. It is shown that the expression obtained earlier for the increased apparent magnitude of the SNe Ia provides as good a fit for a closed universe with , as it does for the flat EdS universe. Comparison is presented in a third table. An upper bound on
, as it does for the flat EdS universe. Comparison is presented in a third table. An upper bound on 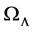 is given for a closed universe that eventually collapses back on itself that is too small for the value needed for the accelerating universe.
is given for a closed universe that eventually collapses back on itself that is too small for the value needed for the accelerating universe.
Keywords:
Dark Energy, Speed of Light, Age of Universe, Closed Universe

1. Introduction
In two previous works by the author [1] [2] , hereafter referred to as I and II, it was shown that it is possible to explain the diminished brightness of the Type Ia supernovae (SNe Ia) found by Perlmutter et al. [3] [4] , Riess et al. [5] , and Schmidt et al. [6] , and the increased distance to the “standard ruler” of the baryon acoustic oscillations (BAO) determined by Anderson et al. [7] [8] , by assuming that the speed of light through the dark energy of intergalactic space has been reduced to c/n, where n is the index of refraction of the dark energy. Thus, in this alternative model, the dark energy no longer has associated with its energy-momentum source tensor a negative pressure that causes the expansion of the universe to accelerate (for a review see, e.g., Wang [9] ), but instead has an index of refraction greater than unity. It was also assumed that the dark energy is another phase of dark matter, and that the phase transformation started to take place at about redshift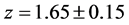 , as discussed in Riess et al. [10] , where there appears to be a supernova not exhibiting acceleration, and in the proposed alternative model, is where the dark energy started to appear as a consequence of the expansion cooling of the dark matter that was present in intergalactic space. Since that expansion cooling did not take place for the dark matter associated with the galaxies, because it is the space between the galaxies that expands, not the galaxies themselves, hence within the galaxies, n remains unity, and the speed of light is c. Since galaxies do not have a sharp boundary, with the dark matter halos extending well beyond the central luminous baryonic regions, there will be a transition region where n changes from unity to its intergalactic value, but for simplicity this is ignored at this stage of the study.
, as discussed in Riess et al. [10] , where there appears to be a supernova not exhibiting acceleration, and in the proposed alternative model, is where the dark energy started to appear as a consequence of the expansion cooling of the dark matter that was present in intergalactic space. Since that expansion cooling did not take place for the dark matter associated with the galaxies, because it is the space between the galaxies that expands, not the galaxies themselves, hence within the galaxies, n remains unity, and the speed of light is c. Since galaxies do not have a sharp boundary, with the dark matter halos extending well beyond the central luminous baryonic regions, there will be a transition region where n changes from unity to its intergalactic value, but for simplicity this is ignored at this stage of the study.
The purpose of this work is to extend the previous work in I and II by making use of additional values of the cosmological density parameters to obtain new values for n, and to use these new values to obtain additional estimates of the age of the universe according to the alternative model.
Also, since the comparisons in I and II have been between the LCDM accelerating universe, and only the flat Einstein de Sitter universe, for completeness, an additional comparison is made here with a closed universe.
In Section 2, the new values of n will be obtained by using both the least squares method that was introduced in I, and the square root method based on electromagnetic theory that was introduced in II. Both methods will be based on the values of the cosmological density parameters from the Planck satellite work of Abe et al. [11] . A comparison with the prediction for the increased distance to the SNe Ia, and the BAO standard ruler for different values of the cosmological density parameters is presented in Table 1 and Table 2. In Section 3, the range of values for n obtained in Section 2 is used to obtain a range of ages for the universe. All of these ages are greater than or equal to 14 Gyr, and hence exceed that for the accelerating universe of 13.8 ± 0.1 Gyr as given in [11] . Significantly, a qualitative argument is presented that shows that the age of the comparison Einstein de Sitter universe has to be greater than that of the accelerating universe, as was already found quantitatively in II. Possible empirical supports, as well as a possible empirical objection to the alternative model, are also discussed. In Section 4, as mentioned above, instead of comparing the accelerating universe with the flat Einstein de Sitter universe, the comparison is made with a closed universe. In I it was briefly noted that the expression that was found there for the increase in the apparent magnitude of the SNe Ia did not require the universe to be flat, and in this section, this is demonstrated for a closed university with a total density parameter,  , which is the one sigma upper bound given in [11] . It is also shown that fothis case, both the least squares value of n, and the age of the closed universe, are the same (to three places) as that for the Einstein-de Sitter universe. In Table 3, a comparison is made between the closed universe and the flat universe for their percentage fit with the accelerating universe. An upper bound on
, which is the one sigma upper bound given in [11] . It is also shown that fothis case, both the least squares value of n, and the age of the closed universe, are the same (to three places) as that for the Einstein-de Sitter universe. In Table 3, a comparison is made between the closed universe and the flat universe for their percentage fit with the accelerating universe. An upper bound on 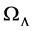 for a closed universe that eventually collapses back on itself is also derived and discussed. In Section 5, there are concluding remarks.
for a closed universe that eventually collapses back on itself is also derived and discussed. In Section 5, there are concluding remarks.
2. Additional Determinations of n
In I, where the cosmological density parameters were given by ,
, 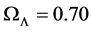 , the least squares value of n was found to be
, the least squares value of n was found to be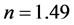 . In II, upon setting
. In II, upon setting  (where the subscript “de” refers to dark energy which in the alternative model has the same energy density as the cosmological term, but, in contrast, has negligible stress), and using the electromagnetic relation,
(where the subscript “de” refers to dark energy which in the alternative model has the same energy density as the cosmological term, but, in contrast, has negligible stress), and using the electromagnetic relation, 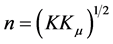 , where K is the dielectric constant, and
, where K is the dielectric constant, and  is the relative permeability of the dark energy, and the assumption that
is the relative permeability of the dark energy, and the assumption that 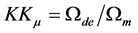 so that one has another method of determining n given by
so that one has another method of determining n given by , it was found for the above density parameters that
, it was found for the above density parameters that . In what follows, it will be convenient to denote the least squares value for n as
. In what follows, it will be convenient to denote the least squares value for n as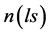 , and to denote the value for n obtained from the square root as
, and to denote the value for n obtained from the square root as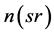 . It was also found in II that
. It was also found in II that 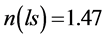 and
and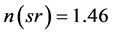 , upon employing the one sigma upper limit of
, upon employing the one sigma upper limit of 
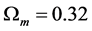





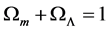


For the reader’s convenience, the analysis leading to 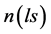




with

where 


so that for the values

As noted in I and II, this integral has to be evaluated numerically. In contrast, for the Einstein de Sitter universe, with


As in I and II, the difference of the logarithmic proportional distances between the accelerating universe and the Einstein de Sitter universe is given by
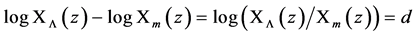
where
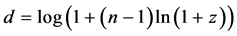
is the prediction of the alternative model under the assumption (for which there is as yet no theoretical foundation) that the light speed has been reduced to c/n when traveling through the dark energy of intergalactic space, as shown in I, Section 4, page 82, and where the increase in apparent magnitude δm is shown to be given by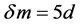

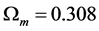



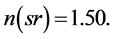



Table 1. Comparison of 




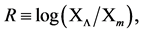



In Table 2, the percentage disagreement results are given for 

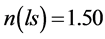



Table 2. Comparison of 
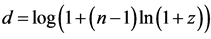


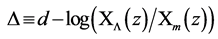


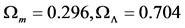
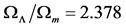
It is clear from the last column in Table 2, in which, particularly at

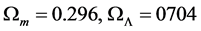

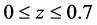
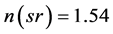


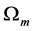


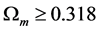
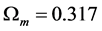


Also, since for
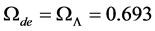



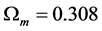



Indeed, for n = 1.49, at z = 0.5, one finds from Table 1 that
It will be noticed from the tables that lower values of n fit better for higher values of z, while higher values of n fit better for lower values of z. Interestingly, the disagreement for the lower values of z, i.e.
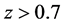

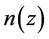

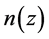
3. Age of the Universe
In II it was found that for

been decelerating, the former’s deceleration would have diminished more rapidly to zero. Call this value of the expansion parameter for the accelerating universe







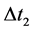

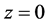
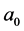
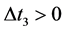


Now, as was discussed in II, because the determination of the Hubble constant involves the first order Doppler effect for the light that has traveled through intergalactic space, and since the distances involved are for z < 0.5 in which, according to the model, the speed of light is c/n, one has to correct the Doppler expression to allow for this, so that it becomes





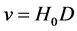




Since the age of the Einstein de Sitter universe, taken to be from the big bang to the present epoch, and denoted by





Since (11) is indifferent to whether one works with


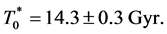
This clearly exceeds the age of the accelerating universe of
With regard to this revision of the Hubble constant, it should be pointed out that since the light from, say, the Cepheid variables that is used in determining H0, passes through the host galaxy as well as our own Galaxy, where in both cases the speed of light is c, this has the consequence that the effective speed of light for the entire path is greater than c/n. However a rough estimate indicates that a correction for this effect would be less than 0.5 percent, and in view of the sizes of the other uncertainties, it can be ignored at this stage of the study.
An interesting hint of possible support for the alternative model comes from the fairly recent study of the star HD 140283 by Bond et al. [12] , who describe it as a subgiant with low metallicity in the solar neighborhood, at approximately 100 lyr from earth. They found that when all uncertainties are included the star’s age is 14.46 ± 0.8 Gyr. They emphasized that this age was not in disagreement with the age of the universe when allowance was made for the uncertainty in the star’s age. At that time, 2013, no other age than that of the accelerating universe (which was then given as 13.77 ± 0.06 Gyr) was available for comparison, but clearly the mean age they found for the star puts its age closer to 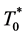
Quite recently there has appeared the latest finding of Riess et al. [13] that yields a 2.4% determination of the local value of the Hubble constant of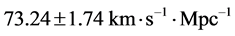


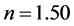

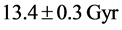



It has undoubtedly been noticed that the value of n is very nearly―if not exactly― the reciprocal of the two-thirds factor relating the age of the Einstein de Sitter universe to the Hubble time. At this writing, there is no explanation for this unexpected relation, and it is left to future studies to find a possible solution.
4. Comparison with a Closed Universe
As mentioned in I, the expression that was derived therein Section 4, p.82, for the increased apparent magnitude of the SNe Ia given by
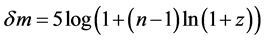
does not just hold for the flat Einstein de Sitter universe, it is applicable to any isotropic universe for which the expansion parameter satisfies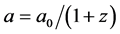

The standard line element for a general, homogeneous, isotropic, time-orthogonal, FLRW universe, in isotropic coordinates, can be written as

with



For the Einstein de Sitter universe k = 0, while in this section k = 1. Hence this equation can be rewritten as

Since 


Hence, at the present epoch, z = 0, with


where


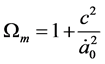
One now proceeds as in I and II. From (17), and the relations leading to (19), one has

Then from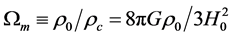


Upon replacing 
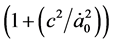

The proportional distance function X(z), as previously mentioned, is defined as

Now 


Upon denoting the ratio 

After combining the factor 

The following cosmological density parameters, 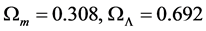


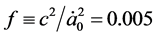

Table 3. Comparison of



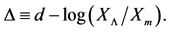


As can be seen from the table, the fit for the closed universe is very nearly the same as for the flat Einstein de Sitter universe. Moreover, as will be shown next, the age of the closed universe is very nearly the same as for the flat universe for this value of 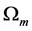
It is convenient to rewrite (15) as

where

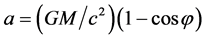
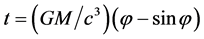
From these two equations one obtains an expression for 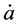
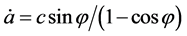
from which, together with (28), one obtains the Hubble parameter 
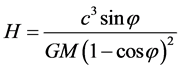
For



which is the same relation that holds for the Einstein de Sitter universe. For the larger value of 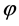

After setting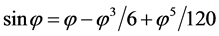

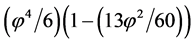

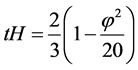
To determine 








After substituting the approximation 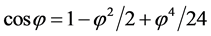

Upon setting 
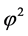

The positive root for 
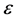


With

Although for the closed universe, from (30), 

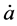
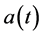
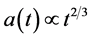







Finally, in I it was pointed out that there is a fundamental difficulty with the cosmological term
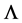




Either from the field equation for stress, or by differentiating the above equation, taking into account that 

Under the assumption that the universe does collapse back on itself after reaching the value of the expansion parameter when it stops increasing and starts to recoil denoted by






After dividing both sides of the inequality by

Thus, under these circumstances, 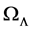

5. Concluding Remarks
It is clear from the work in the preceding sections, as well as that in I and II, that the proposed alternative model, based on the slowing down of light by the dark energy in intergalactic space, can explain the diminished brightness of the SNe Ia, and the increased distance to the “standard ruler” of the BAO, as well as can the accelerating universe, that is based on attributing a negative pressure to the dark energy, such as displayed by the cosmological term. However, the crucial test for the alternative model will be for astronomers to determine through suitable observations, such as the one described in Section 4 of II, whether in fact the speed of light in intergalactic space for, say, z ≤ 0.7 is c/n, with n ≈ 1.50. If eventual astronomical observation should show that this is indeed the case, it will then prove theoretically challenging to obtain a general expression for n as a function of redshift, and to show further that n does not exhibit any evidence of dispersion in the optical range, as found by the SNe Ia studies.
Finally, it follows from the discussion in Section 3 that the alternative model is predicting a greater age for the universe than that predicted by the accelerating universe. As was further discussed there, this has bearing on the maximum age of stars, and the value of the Hubble constant, so that their more accurate determination should provide two other areas to test the model astronomically.
Acknowledgements
I am indebted to Prof. David Weinberg for helpful critical comments concerning the alternative model, and the problems of obtaining astronomical verification. I am also indebted to Prof. Don A. VandenBerg for clarifying the uncertainties in the age of HD 140283, the difficulties in reducing them, and much helpful discussion. I am further indebted to Dr. Gregory B. Malykin for numerous questions, and assistance in obtaining astronomers’ comments on the model.
Cite this paper
Tangherlini, F.R. (2016) A Possible Alternative to the Accelerating Universe III. Journal of Modern Physics, 7, 1829-1844. http://dx.doi.org/10.4236/jmp.2016.713163
References
- 1. Tangherlini, F.R. (2015) Journal of Modern Physics, 6, 78-87.
http://dx.doi.org/10.4236/jmp.2015.61010 - 2. Tangherlini, F.R. (2015) Journal of Modern Physics, 6, 1360-1370.
http://dx.doi.org/10.4236/jmp.2015.69141 - 3. Perlmutter, S., et al. (1998) Nature, 391, 51-5. (Erratum, 392, 311.)
- 4. Perlmutter, S., et al. (1999) Astrophysical Journal, 517, 565-586.
http://dx.doi.org/10.1086/307221 - 5. Riess, A., et al. (1998) Astronomical Journal, 116, 1009-1038.
http://dx.doi.org/10.1086/300499 - 6. Schmidt, B., et al. (1998) Astrophysical Journal, 507, 46-63.
http://dx.doi.org/10.1086/306308 - 7. Anderson, L., et al. (2012) Monthly Notices of the Royal Astronomical Society, 427, 3435-3467.
http://dx.doi.org/10.1111/j.1365-2966.2012.22066.x - 8. Anderson, L., et al. (2014) Monthly Notices of the Royal Astronomical Society, 439, 83-101.
http://dx.doi.org/10.1093/mnras/stt2206 - 9. Wang, Y. (2010) Dark Energy. Wiley-VCH, Verlag GmbH & Co, KGaA, Weinheim, 35-49.
- 10. Riess, A.G, Nugent, P.E., Gilliland, R.L., Schmidt, B.P., Tonry, J., Aguilar, J.A., et al. (2001) Astrophysical Journal, 560, 49-71.
http://dx.doi.org/10.1086/322348 - 11. Abe, P.A.R., et al. (2015) Astronomy and Astrophysics, 584, 1-67.
http://dx.doi.org/10.1051/0004-6361/201526586e - 12. Bond, H.E., Nelan, E.P., VandenBerg, D.A., Schaefer, G.H. and Harmer, D. (2013) Astrophysical Journal Letters, 765, L12.
http://dx.doi.org/10.1088/2041-8205/765/1/L12 - 13. Riess, A. G., et al. (2016) Astroph, arXiv.1604. 0142442
- 14. Riess, A. G., et al. (2011) Astrophysical Journal, 730, Article ID: 119.
http://dx.doi.org/10.1088/0004-637X/730/2/119 - 15. Cheng, C., and Huang, Q. (2015) Science China Physics, Mechanics and Astronomy, 58, 599801.
http://dx.doi.org/10.1007/s11433-015-5684-5 - 16. Tangherlini, F.R. (1984) Annals of the New York Academy of Sciences, 422, 385-389.
http://dx.doi.org/10.1111/j.1749-6632.1984.tb23407.x - 17. Tangherlini, F.R. (1993) Il Nuovo Cimento B, 108, 911-930.
http://dx.doi.org/10.1007/BF02828738 - 18. Guth, A.H. (1981) Physical Review D, 23, 347-356.
http://dx.doi.org/10.1103/PhysRevD.23.347 - 19. Guth, A.H. (1997) The Inflationary Universe. Addison-Wesley, Reading, 167-187.
- 20. Linde, A.D. (1982) Physics Letters B, 108, 389-392.
http://dx.doi.org/10.1016/0370-2693(82)91219-9 - 21. Albrecht, A. and Steinhardt, P.J. (1982) Physical Review Letters, 48, 1220-1223.
http://dx.doi.org/10.1103/PhysRevLett.48.1220 - 22. Tangherlini, F.R. (1993) Il Nuovo Cimento B, 108, 1253-1273.
http://dx.doi.org/10.1007/BF02741278 - 23. Einstein, A. (1923) The Meaning of Relativity. Translation by Adams, E.P., 3rd Edition, Princeton University Press, Princeton, 107.
- 24. Silberstein, L. (1924) The Theory of Relativity. 2nd Edition, Macmillan, London, 479-480.
- 25. Tangherlini, F.R. (1997) General Relativity and Gravitation, 29, 869-880.
http://dx.doi.org/10.1023/A:1018835300818 - 26. Tangherlini, F.R. (1998) Il Nuovo Cimento B, 113, 785-804.
- 27. Weinberg, S. (1987) Physical Review Letters, 59, 2607-2610.
http://dx.doi.org/10.1103/PhysRevLett.59.2607 - 28. Weinberg, S. (1989) Reviews of Modern Physics, 61, 1-23.
http://dx.doi.org/10.1103/RevModPhys.61.1 - 29. Barrow, J.D. and Tipler, F. (1986) The Anthropic Cosmological Principle. Oxford University Press, New York, 15-26.
- 30. Tangherlini, F.R. (1989) Il Nuovo Cimento B, 103, 311-317.
http://dx.doi.org/10.1007/BF02737134 - 31. Tangherlini, F.R. (1991) Il Nuovo Cimento B, 106, 123-145.



