Received 22 July 2016; accepted 28 August 2016; published 31 August 2016

ABSTRACT

For the unification of gravitation with electromagnetism, weak and strong interactions, we use a unique and very simple framework, the Clifford algebra of space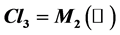. We enlarge our previous wave equation to the general case, including all leptons, quarks and antiparticles of the first generation. The wave equation is a generalization of the Dirac equation with a compulsory non-linear mass term. This equation is form invariant under the group of the invertible elements in the space algebra. The form invariance is fully compatible with the 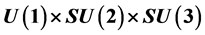gauge invariance of the standard model. The wave equations of the different particles come by Lagrange equations from a Lagrangian density and this Lagrangian density is the sum of the real parts of the wave equations. Both form invariance and gauge invariance are exact symmetries, not only partial or broken symmetries. Inertia is already present in the 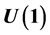part of the gauge group and the inertial chiral potential vector simplifies weak interactions. Relativistic quantum physics is then a naturally yet unified theory, including all interactions.

Keywords:

Electromagnetism, Weak Interactions, Strong Interactions, Gravitation, Clifford Algebra, Dirac Equation, Lagrangian Formalism, Gauge Groups, Relativistic Invariance, Electron, Magnetic Monopole, Quark, Photon, Gauge Boson, Unification

1. Introduction

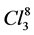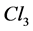The aim of this work is to construct with the same logic and mathematical rigour of General Relativity (GR), a quantum wave of all fermions of one generation in a well-defined framework: the wave is a function of space and time into where is the Clifford algebra of space. We extend the relativistic constraints and replace the 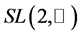group by the greater group 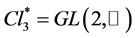and we use only true representations and exact calculations. The Lagrangian density has a double link with the wave equations, both cause and consequence. This is new and gives both the limits and the physical reason of the existence of a Lagrangian formalism. We present here the fermionic part of the wave equations. The wave equations have mass terms, and they are invariant both under 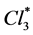and under precisely the 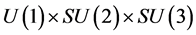gauge group of the Standard Model of Quantum Physics (SM). This gauge symmetry is a local and exact one. Complicated calculations of the second quantization are not used. Spontaneously broken symmetry is useless. Nevertheless we get many results of the SM, with less free parameters, which is better. Mass terms of our wave equations allow us to study inertia and gravitation directly from the wave equations. The inertial part of the gravitation generates eight potential space-time vectors. Only seven of these eight terms are present in the Christoffel symbols used in differential geometry. The eighth, the chiral one, is yet in the 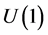gauge and explains the complexity of weak interactions. Using this chiral inertial potential vector, we simplify the electro-weak gauge. We study here the fermionic part of the SM. This SM uses also twelve bosons whose components are built from the tensorial densities available from the spinor wave. They will be detailed in another article.

After Maxwell’s electromagnetism, the discovery of electromagnetic wave and the understanding of the electromagnetic properties of light, electromagnetic laws became relativistic covariant laws [1] . The electromagnetic field became an anti-symmetric tensor and the Maxwell’s laws were invariant under a greater group than the invariance group of mechanics. In 1915, Einstein was able to include the gravitation in the same frame. His theory of gravitation (GR) [2] [3] is extremely precise, and gravitational waves are now experimentally observed. Next Einstein tried to reunite electromagnetism and gravitation into a unique field theory [4] .

From relativistic ideas de Broglie found the wave associated to the movement of any particle [5] . Only a few months after his dissertation, Schrödinger found a non-relativistic wave equation for his wave. This wave equation explained the quantization of energy levels and started quantum mechanics. At the same time, the spin 1/2 of the electron was discovered. Pauli gave a non-relativistic wave equation accounting for the spin 1/2. This equation was the starting point used by Dirac to get his wave equation [6] . The Dirac equation is such a success that now again it is an important item of the SM. Only the Dirac equation actually explained the true number of energy levels, the true energy levels and quantum numbers of the hydrogen atom [7] . Nevertheless if the Dirac equation was, a long time ago, explained in many books from Ref. [8] to [9] , then quantum mechanics even forgot to teach this part of the quantum theory [10] . First the Dirac wave was the wave of only one electron while the Schrödinger equation accounted for systems of electrons. Next the problem of negative energies was not solved by the Dirac equation, the charge conjugation did not account for negative energies in the framework of the first quantization, only the second. With this second quantization the electromagnetic field became a field of operators creating and annihilating photons, with bras and kets in Hilbert linear spaces. This field followed a Hamiltonian dynamics with a Schrödinger equation and its unique time variable [11] . Therefore, even if quantum fields incorporated the electromagnetic field and should be compatible with GR, the methods of the second quantization, with path integrals and Feynman graphs, were not sufficient to incorporate GR. Several problems arose¹, often not well exposed, either presenting the Dirac equation from a Hamiltonian dynamics², either forgetting that the matrices of replacing the Lorentz transformations were not unitary [11] , either with wrong calculations.³ The result was an unsolved problem: the union of GR and SM. Nowadays quantum mechanics is understood as a gauge theory using a gauge group [14] . The electron is a member of the “first generation” of fundamental fermions. This first generation is replicated into a second and a third one with increasing mass. A Lagrangian density gives the wave equations, both for fermions and gauge bosons. Each generation has a separate Lagrangian density [12] . After the great success of the Weinberg-Salam theory [15] unifying electromagnetism and weak interactions with a gauge group [16] , great unified theories [17] tried to extend this unification to include strong interactions. These theories predicted the disintegration of the proton, but none disintegration was observed. Numerous and complicated attempts with quantum groups, strings, branes and many supplementary dimensions, supergravity, loop quantum gravity, were developed. All these attempts were based on the methods of the second quantization and consequently were finally based upon the non-relativistic Schrödinger equation. None of these attempts were able to incorporate GR in a renormalizable way.

We began our work with the Dirac equation of the electron [6] . All calculations are there made with mathematical rigour [7] and with very accurate experimental results. Another reason of this work is the study of the finite representations of the Lorentz proper group [18] : relativistic quantum mechanics uses not the Lorentz group but another one, in a way which is not a consequence of the principles of the theory.

2. Waves and Wave Equations

Since 1928 the relativistic invariance of the Dirac theory used the previous Pauli matrices for the spin of the electron: the space-time variable was replaced by

(2.1)

This is equivalent to say that the three Pauli matrices:

(2.2)

form a orthogonal oriented basis in space. We shall put arrows on vectors in space, so any vector reads

(2.3)

Contrary to the Clifford community [19] - [22] we use the matrix representation generated by the Pauli matrices. First the geometric algebra of space and are isomorphic algebras on the real field, the sum and the product of matrices are familiar in quantum physics. This matrix representation identifies complex numbers and scalar matrices in the Pauli algebra. With this identification we write the x of (2.1) as, we consider as a basis in space-time and we use the Einstein’s convention of summation on up and down indexes, with Latin indexes in space and Greek indexes in space-time. Any element z in the Clifford algebra of space is a sum of a real part x, a vector part, an axial-vector part and a pseudo-scalar part and we need (a detailed course on Clifford Algebra is available in the first chapter of [23] - [26] ).

(2.4)

The application is the main automorphism of. The reverse is also the adjoint (transposed conjugate matrix), so is the reversion. The third conjugation, is the product of the two previous ones and we shall need:

(2.5)

Space-time is then made of the auto-adjoint part of the space algebra. We use:

The main reason to the use of the geometric algebra is the ability to read all relativistic quantum physics in this algebra: The fermion wave is a function of space and time into:

(2.6)

It is made of eight waves, functions of space-time with value in which is a 8-dimensional linear space on the real field. The link between and the complex formalism is simple only if we use the left and right Weyl spinors and by letting:

(2.7)

For we let:

(2.8)

Our non-linear wave equation of the electron, which has the Dirac equation as linear approximation when the Yvon-Takabayasi angle is small or negligible, reads [23] - [35] :

(2.9)

where This equation is invariant under any transformation D defined by an element M of the Lie group (group of invertible elements of):

(2.10)

(2.11)

(2.12)

(2.13)

Relations (2.13) are the reason of the existence and the definition of “left” and “right” waves in quantum physics. Right waves transform with a left multiplication by M while left waves transform by a multiplication by. Therefore and are right waves while and are left waves. Only one M term is present in (2.11) when two M terms are present in (2.10) and (2.12): consequently the wave turns with the angle when the space turns with the angle. The invariant form of the Dirac equation, which is the linear approximation of (2.9) reads:

(2.14)

where is the Yvon-Takabayasi angle. Our wave equation, in the invariant form, appears then as a simplification of the Dirac equation.

Equations (2.10)-(2.13) have no geometric reason to be restricted to. The main change that we propose replaces this condition by the less restrictive condition. We then enlarge to which is also the multiplicative group in the geometric algebra. This is significant because geometry is linked to gravitation in GR. First reason: this change is possible and astonishing! For any invertible M Equations (2.10) - (2.13) are satisfied, so the restriction is unnecessary. Next the representations used in the case of spin 1/2 particles are now correctly used. The quantum theory associated to each Lorentz transformation R an element but there are two M for one R and only for particular R (“bi-valued” representations). Now to any M we associate one and is a true mathematical function. Moreover for the gravitation we shall need below the four kinds of representations of while has only two kinds of representations. Finally this important change is validated by all new results that we get from this hypothesis. Considering all M elements with and noting the set of these elements, we let:

(2.15)

and the R transformation satisfies:

(2.16)

Then and D is a “Lorentz dilation” made of the Lorentz transformation R conserving space orientation and time orientation (this is not a trivial result, relations (2.12) like and are proved in Ref. [23] p. 115-118) and of the homothety with ratio. We explained previously how theses dilations constitute a 7-dimensional Lie group [32] and how all laws of electromagnetism, quantum wave of the electron included, are invariant not only under the group found in 1928 from the Dirac theory, necessary to account for the spin 1/2, but under the group. Since the study of the Lie groups [36] used in quantum physics is based on the properties of the groups, and since is exactly one of them, we conserve the matrix representations of this group, Clebsh-Gordan or Racah coefficients and so on. The first difference is the four kinds of matrix representations that we use now with. This has no incidence on spin representations because. Main difference: we now know from where come the representations of which is a subgroup of. Wave Equations (2.9) and (2.14) are invariant under because:

(2.17)

Then, if we suppose we get:

(2.18)

And we are allowed to say that this equation is “form invariant” since it has exactly the same form in the primed and non-primed basis. We explained how the variation of the mass term is linked to the relation, then to the existence of the Planck constant [26] . This enlarged invariance has another unexpected consequence: if we compute in the basis of the eight numeric equations equivalent to (2.9) or (2.14) the real part (first term of the basis, 1) is, where is the Lagrangian density allowing us to get the wave Equation (2.9) or (2.14) by means of variation calculus. Therefore a double link exists between wave equation and Lagrangian formalism. We prove below that this double link is conserved in the general case. Another one of the eight numeric equations is simple, the equation corresponding to the term which reads:

(2.19)

This J current is the conservative probability current, being the probability density. We shall see in the next section how this is generalized for the whole wave.

3. Weak and Strong Interactions

We studied strong and weak interactions with Clifford algebras having two fictitious supplementary dimensions [25] [37] - [41] of space. Since space-time has one dimension more than space, we passed from three to six dimensions. This induces three doubling of the dimension of the algebra, and we get the same number of variables if we replace by. The general wave that we consider is a function of space and time into with where R is the right part and L is the left part of the wave. The states of color of the quark d that we named are associated to and. The states of color of the quark u that we named are associated to. Similarly we let for the neutrino:. We remark that this conserves the 1 + 3 + 3 + 1 structure of the algebra of space. Moreover we now consider these states of color like complete waves, with a left and a right part. This is then a generalization of our previous works. We use now:

(3.1)

with the Weyl representation:

(3.2)

Consequently the waves, have value in the Clifford algebra of space-time and the global wave has value in the Clifford algebra of an extended space-time, with two more dimensions of space which are fictitious and not present in the dynamics of the wave. Main interest of this writing, this allows an equal treatment of the eight that we need. The part of the wave is the lepton part, made of the wave of the electron and the wave of the neutrino which is also the wave of the Lochak’s magnetic monopole [26] [42] - [44] . The wave equation reads:

(3.3)

The covariant derivative reads:

(3.4)

with

(3.5)

for We use two projectors satisfying

(3.6)

Three operators act on the quark sector like on the lepton sector:

(3.7)

The fourth operator acts differently on the lepton wave and on the quark sector:

(3.8)

The value −1/3 is compulsory [45] [46] and gives the four correct values of the charges of quarks and anti-

quarks [25] [47] . To simplify notations we use now instead. So we have

and

(3.9)

Since the left up term of each matrix is zero, the wave equation splits into a lepton part and a quark part.

3.1. The Lepton Wave

Only the part of the gauge group acts on electron + neutrino. The physical translation is: leptons do not strongly interact; they have only electromagnetic and weak interactions. This is fully satisfied in experiments. Since it is independent on the energy scale, two consequences result: strict conservation of the baryonic number, general failure of great unified theories. The wave equation acts separately in a lepton part and a quark part:

(3.10)

We study first the lepton part of the wave equation. The lepton sector of the standard model, for the first generation, accounts for the electron, the positron, the left neutrino and the right anti-neutrino. We note the wave of the electron and the wave of the neutrino as

(3.11)

Like previously are right waves and are left waves. The SM uses a charge conjugation which, up an electric phase, lets for the positron wave and for the anti-neutrino wave:

(3.12)

where we use the matrix representation of Weyl matrices (3.2) which gives:

(3.13)

We use (2.7), and. The link (3.12) of the SM between the wave of the particle and the wave of its anti-particle simply reads:

(3.14)

The lepton wave reads:

(3.15)

It is a well-defined function of space and time with value into the space-time algebra. Separating

and the Weinberg-Salam model uses projectors, which read with our choice (3.2) of Dirac

matrices:

(3.16)

Then for particles left waves are waves and right waves are waves. This is invariant, consequently relativistic invariant. With space algebra the separation between left and right waves uses:

(3.17)

To get the gauge group of the Weinberg-Salam theory we let (see [26] 6.1):

(3.18)

We explained there how the covariant derivative of the Weinberg-Salam model used:

(3.19)

with for a doublet of left-handed particles and for a singlet of right-handed particle. Y was the

weak hypercharge, for the electron. The transposition into Clifford algebra used four space- time vectors named “potentials”:

(3.20)

which express the covariant derivative in a unique term:

(3.21)

For the calculation of the covariant derivative we use the Socroun’s method incorporating the constants into the potentials [48] . The potentials simplify the calculation of the group by using three subgroups. We let:

(3.22)

A detailed calculation was made in [26] 6.1. We have previously supposed that and have the same behaviour under the dilation R induced by M. We need here another behaviour:. We got, with the replacement of by, the replacement of by and the replacement of D by:

(3.23)

This system is equivalent to:

(3.24)

These derivatives are exactly equivalent to those of the Weinberg-Salam model. Equation (3.10) reads

(3.25)

where is a term (below) depending on. The Weinberg-Salam model does not use and for electro-weak interactions we can cancel this right wave of the neutrino. But when some neutrinos are observed they are able to change into neutrinos of other generations. These changes are studied by using both right and left waves. It is the same if we study the Lochak’s magnetic monopole. If the wave is used we get many relativistic invariants, unknown in the Dirac theory where only was used:

(3.26)

When the wave of quarks is zero we also have:

(3.27)

The lepton wave Equation (3.25) is equivalent to the system:

(3.28)

3.2. Double Link with the Lagrangian Density

For comparing the previous equations with the usual complex matrix formalism, we associate to and the Weyl spinors and and we get:

(3.29)

Equations (3.28) are equivalent to:

(3.30)

Like with the linear Dirac mass term, the covariant derivatives of left spinors are linked by the mass term to right ones and the covariant derivatives of right spinors are linked by the mass term to left ones. But we now have terms which also change with a gauge transformation [26] , compensating exactly the difference between left and right spinors: these equations are both invariant under (therefore relativistic invariant) and gauge invariant under the gauge group generated by the four. The form invariance under is proved in [26] B.4.1 and gauge invariance is proved in B.4.2 to B.4.4.

Now we multiply on the left side the second relation (3.28) by:

(3.31)

With the left and right spinors this equation reads:

(3.32)

We name the real part of:

(3.33)

This gives:

(3.34)

Then (3.32) is equivalent to:

(3.35)

This complex equation is equivalent to the real system:

(3.36)

We remark that we get not four numeric equations but only two for the four variables of the spinor wave. This will be the same for the other spinor waves. We see this first with. We multiply on the left the first equation (3.28) by:

(3.37)

With the left and right spinors this equation reads:

(3.38)

This equation is equivalent to:

(3.39)

This complex equation is equivalent to the real system:

(3.40)

because. Next we multiply on the left the third Equation (3.28) by:

(3.41)

We let:

(3.42)

We get:

(3.43)

With the left and right spinors (3.41) reads:

(3.44)

This equation is equivalent to:

(3.45)

Separating the real and the imaginary part we get the equivalent system:

(3.46)

We multiply on the left the last Equation (3.28) by:

(3.47)

With the left and right spinors (3.47) reads:

(3.48)

This equation is equivalent to:

(3.49)

Separating the real and the imaginary part we get the equivalent system:

(3.50)

Adding and subtracting the second Equations (3.46) and (3.50) we get:

(3.51)

The lepton part of the Lagrangian density is the sum of the real parts in (3.36), (3.40), (3.46), (3.50):

(3.52)

This gives:

(3.53)

Since we get:

(3.54)

Now we derive the wave equations resulting from the Lagrange equations. The Lagrange equation:

(3.55)

gives

(3.56)

which is the first Equation (3.30), equivalent to the first Equation (3.28). Similarly deriving with we get

the third Equation (3.30), equivalent to the third Equation (3.28). Next the Lagrange equation

(3.57)

gives

(3.58)

which is equivalent to the second Equation (3.28). The Lagrange equation gives the

last Equation (3.28). This establishes the double link between wave equations and Lagrangian density. The link from Lagrangian density to wave equations was known from the beginning of quantum mechanics. The link from wave equations to Lagrangian density is the true reason of the existence of a Lagrangian mechanism. This link is much stronger than the first one on the physical point of view, because the old link supposes an integration by parts and a cancellation of terms. The possibility of this cancellation is dubious in the case of propagating waves (like gravitational waves).

3.3. Double Link with the Lagrangian Density (Quark Case)

Noting and we have

(3.59)

We note and. The covariant derivative reads, with:

(3.60)

When is zero the term is a sum of 66 terms (relativistic invariants):

(3.61)

where in and:

(3.62)

And when the wave is complete, with both lepton and quarks terms we have:

(3.63)

This is a sum of 72 terms, all positive.

3.4. The Quark Wave

Like in the lepton case the Lagrangian density is doubly linked to wave equations in the quark case. The Lagrangian density reads:

(3.64)

(3.65)

We can derive from this Lagrangian density the wave equations:

(3.66)

(3.67)

(3.68)

(3.69)

To get the Lagrangian density from these wave equations we multiply (3.66) on the left by and (3.67) by We let:

(3.70)

and we get:

(3.71)

Then (3.66) gives:

(3.72)

Like in the lepton case, the particular form of this wave equation allows us to get an equivalent system with only two numeric equations:

(3.73)

(3.74)

By adding and using we get:

(3.75)

Only the sum of the three currents generated by the three colors of the d quark is a conservative space-time vector. Similarly for the u quark, with colour states we get:

(3.76)

Next the particular form of this wave equation allows us to get an equivalent system with only two numeric equations:

(3.77)

(3.78)

And we also get

(3.79)

For the left waves, we multiply (3.68) on the left by or (3.69) by and we get, with:

(3.80)

(3.81)

Here also this wave equation is equivalent to a system of only two numeric equations:

(3.82)

Finally for the left waves of the u quark we have:

(3.83)

Here also this wave equation is equivalent to a system of only two numeric equations:

(3.84)

For the left waves of quarks only one sum gives a conservative space-time vector, because the weak gauge links the waves of the u and d quarks:

(3.85)

This means that a conservative probability current does not exist for an isolated coloured quark, and this is well known, since it is impossible to observe such isolated states.

The Lagrangian density is the sum on of the sum of Equations (3.73), (3.77), (3.82) and (3.84). All mass terms are gotten twice and the sum of all squares is exactly. The Lagrangian density for all objects of the first generation is the sum. Since is the sum of the lepton part and the quark part, it is sufficient to add the 16 equations, 4 from the lepton case, 12 from the quark case, to get the simplification by in the mass term. This achieves the general proof of the double link between wave equations and Lagrangian density.

3.5. Lessons of This Calculation

The previous calculation proves that the use of and algebras is unnecessary. The algebra is then the unique framework allowing us to describe all interactions of quantum physics, if we use also this framework to describe gravitation. In this framework we are also able to establish the double link between wave equations and Lagrangian density. The existence of a Lagrangian principle is then compulsory; it is not the consequence of a meta-physical prescription but a mere consequence of the physical laws of quantum physics. The necessity of a physical reason for the Lagrangian formalism was explored by L. de Broglie, his idea was the stationary action of the particle as a limit case of the growing entropy in thermodynamics [49] . We may now consider the quantum wave equations themselves as a necessary consequence of the geometry of the space-time: the form of the mass term results from the constraints of the invariance under and from the gauge group which is the greatest possible group compatible with the algebra.

The existence of the double link has other consequences that we shall develop in the second part of this work on the boson part of the SM: only the fermion wave is linked to a Lagrangian density which is made of the wave equations and is then necessary. The dynamics of the boson part must then be a consequence of the dynamics of the fermion wave. The SM considers the dynamics of boson waves as a consequence of the Lagrangian density, but the relations between potentials and fields are not deduced, they are postulated independently of the laws giving the dynamics of the fields.

We previously got this double link, first in the wave of the electron [33] , next for electro-weak and strong interactions [25] [26] , but we did not see the reduction of the number of the numeric equations. The reason was the rebuilding of the wave equation on the Dirac form from the Lagrangian density, the wave of the electron incorporating both left and right waves, while the Lagrangian density separates the left and right parts of the wave. It is very easy, in this rebuilding, to use the main automorphism equivalent to the P transformation of quantum physics. But this transformation is not a symmetry of quantum physics, because it is not a symmetry of weak interactions. All our wave equations have a factor which becomes when we use the main automorphism, losing the possibility of factorization.

Moreover the 16 equations containing and are consequence of the Lagrangian formalism which is a consequence of the 16 other equations. This was first seen by Boudet [50] in the frame of the linear Dirac theory of the electron. Our study proves that it is general: the numeric equations equivalent to the wave equations of the “matter” (spinor waves) may be split into two parts: a dynamical part containing rotational-like terms, and a conservative part containing divergence-like terms, and the conservative part is a consequence of the dynamical equations.

The building of the wave equations from the Lagrangian density uses but this process could also use or. This may be the origin of the existence of three and only three generations of fundamental fermions with same dynamics.

Finally the synthesis of all interactions in a unified frame is the simple question: how these dynamical quantum equations are linked to GR?

4. Inertia and Gravitation

In [26] Ch.9 we considered an element M not restricted to be constant in space-time. In the vicinity of a point x where we use:

(4.1)

where is the chiral potential. We get

(4.2)

The dilation D defined from M in (2.10) gives:

(4.3)

Christoffel’s symbols being defined as

(4.4)

we then get

(4.5)

Since D is a dilation, product in any order of a Lorentz transformation and an homothety, the Christoffel’s symbols have this particular form and we get not 64 but only functions: the four present in (4.1) are not in the geometry, because the kernel of the group homomorphism is the group generated by i [23] [47] . Since the Christoffel’s symbols are not symmetric, a torsion exists, like in any geometry able to account for spin 1/2. Vectors transforming as (4.4) are the contravariant ones. Now for covariant vectors we have

(4.6)

with the same. This is an important difference with all preceding attempts, using always variable. This gives

(4.7)

Therefore we get for covariant vectors the usual transformation:

(4.8)

This relation allows the covariant derivative to be commutative with contractions. It leads the covariant derivative back to partial derivative for scalars. The connection (4.5) is new, because all preceding attempts have used variable, while we use constant. The relativistic transformation of the Dirac wave uses a

matrix and transforms into, the Dirac equation satisfies, if

and we may remark that the ma-

trices are not changed in the frame of. Then why could they change as soon as the theory uses curvilinear coordinates? Actually the first Dirac theory used the transformation (2.10) and constant matrices, as soon as 1928.

A non vanishing torsion was used previously by A. Einstein [4] to unify gravitation and electromagnetism. Since his attempt was studied at the very early times of quantum mechanics he evidently did not start from the Dirac wave, which was invented 3 years later. We next get

(4.9)

with

(4.10)

This introduces 8 space-time vectors that we name “potentials of inertia”:

(4.11)

In space algebra we need also

(4.12)

Now we look at the simple case (negligible gravitation) where all terms are zero, but not. We then get simply:

(4.13)

Without the neutrino and quarks wave, we have and, where is the Yvon- Takabayasi angle. We then get

(4.14)

Using the main automorphism on the first Equation (4.14) we get

(4.15)

The wave equation of the electron alone is then equivalent to the system:

(4.16)

This system reads:

(4.17)

If we have:

(4.18)

using

(4.19)

we get:

(4.20)

which is our wave Equation (2.9) of the electron alone, with the only change of into. The complication of the two parts of the electron wave with different eigenvalues of the weak hypercharge simply comes from the strange fact that the chiral potential is both a gauge potential and a potential of inertia. The introduction of the inertial potential into the Dirac equation gives the weak hypercharge. This means that the Dirac wave is yet a unitary electromagnetic-gravitational wave.

Now we consider the neutrino wave where replaces. This means that, when sees the Clifford algebra of space with the basis as a direct oriented basis, sees the same algebra reversed, or with the same basis as an inverse basis. These waves satisfy:

(4.21)

Without quark and electron waves, we have and, we then get

(4.22)

Using the main automorphism on the first Equation (4.22) we get the system:

(4.23)

This gives:

(4.24)

Adding we get:

(4.25)

which is a Dirac-like wave equation in inverse order. Next if we consider the wave alone we have while if we consider the wave alone we have and we get:

(4.26)

This gives:

(4.27)

And the wave equations become:

(4.28)

which also are Dirac-like wave equations.

Since a mass term is present in the wave equations we are able to study in an unified way quantum behaviour and inertia-gravitation. In a rotating frame [51] the limit speed is not equal to c but varies. The limit speed becomes where T is the period of the rotation of the frame. We also have where is the frequency of rotation of the frame and is the frequency of the wave. Therefore this effect is very small.

The inclusion of inertia necessitates the use of two forms of differential operator, acting on the right or on the left side. This unified behaviour links the complicated operators of the electro-weak gauge to the unique electric gauge. The SM is not only able to incorporate inertia and gravitation. This is already realized since 1928 in the Dirac theory. The gravitation is not a very little force, it has the same strength as electromagnetism, but this is usually not obvious, because the proper masses of quantum physics are very small in comparison with the Planck mass.

5. Conclusions

All waves of the fermion part of the SM may be described as functions of space-time in the Clifford algebra of space. Contrary to the common expectation, the algebra of space is the framework of the unification of all interactions, not the algebra of space-time. The global wave is a function of space-time in a 64-dimensional linear space isomorphic to, or to the space of all linear applications (called operators in the SM) from into. In this space multiplications by the left and multiplication by the right place play the same role. Consequently, 32 parameters concern waves similar to the wave of the electron ruled by a Dirac equation. 32 parameters are those of waves similar to the wave of the neutrino, with a reverse Dirac equation. This global wave is obtained also as eight waves which are functions of space-time into.

The wave equations result from Lagrange equations calculated from a Lagrangian density and this Lagrangian density is exactly the sum of the real part of these wave equations. This gives both the reason and the limit of the Lagrangian physics. This limit comes from the fact that only the fermion part of the SM allows us to get a double link between wave equations and Lagrangian density.

The Lorentz group of the restricted relativity is extended to a greater group of invariance. This group has a geometric origin, since it is the group of the invertible elements of the algebra constructed from the 3-di- mensional space. The invariance under this greater group rules all waves of quantum physics. This group has not only two kinds of non-equivalent representations, but four, all necessary for the waves. We must consider not only waves but also waves. The use of the algebra seems paradoxical for a relativistic unified model. Nevertheless is the best framework since including both the space-time and the group of invariance of the quantum waves. The four kinds of representations of the group are necessary used, and we must distinguish and. Since only two kinds of representations are used in space-time algebra. Then it is very difficult to account there for chirality and to include both weak interactions and gravitation. No- natural differential operator in space-time algebra includes the four and operators. In space-time algebra, the orientation of the global space-time is available, not the separate orientations of time and space needed in quantum physics.

We previously studied several particular cases and we obtained several important results: the gauge invariance is exact in the particular case where only the electron has a non-zero right wave [26] . In a second paper, we will study this gauge invariance in the general case. We explained in [46] how the additivity of the potential terms is equivalent to the Pauli principle. We have less free parameters in comparison with the SM using second quantification, because the study of the electron fixes the value of the Weinberg-Salam angle [45] . Consequently this fixes the values of the charges of quarks and antiquarks [46] . The proper masses are no more the fundamental quantities that the theory must account for. These fundamental quantities are actually the products and there is only one proper mass in each generation.

Old questions may also receive a very different answer: the density of probability is in the non-relativistic quantum theory a fundamental quantity; it is the square of the modulus of the wave. This has survived in the Dirac theory, because the density of probability becomes, the time component of the conservative current, and because. This induces the confusion between and. The generalization of the wave breaks this confusion: J is generalized as the contravariant sum of the 16 currents of the Weyl spinors, while is the sum of 72 relativistic invariant terms. The density of probability always exists (see [26] Chapter 9) and the wave is normalized in the stationary case, but this density has none metaphysical property ruling all physical laws. The normalization of the wave is only a consequence of the principle of equivalence between the inertial mass-energy (sum over the whole space of the density of energy of the wave) and the gravitational mass-energy of the particle (linked to the frequency of the de Broglie’s clock).

Cite this paper

Claude Daviau,Jacques Bertrand,Dominique Girardot, (2016) Towards the Unification of All Interactions (The First Part: The Spinor Wave). Journal of Modern Physics,07,1568-1590. doi: 10.4236/jmp.2016.712143

References