Received 22 December 2015; accepted 24 January 2016; published 28 January 2016

ABSTRACT

Quantum aspects of the Joule-Lenz law for the dissipation energy have been studied. In the first step, in an analysis of the energy-time principle of uncertainty, this gives a lower limit of the time interval and an upper limit of the energy interval which can be admitted in a quantum transition process. Moreover, for the low energy excitations, the transition time between the levels is found to be close to the oscillation time periods characteristic for these levels. A reference obtained among the transition time Dt, transition energy DE and the Planck constant h indicates that Dt should approach approximately the time period of the electromagnetic wave produced in course of the transition.

Keywords:

Joule-Lenz Law, Quanta of Energy, Uncertainty Principle for Energy and Time, Energy Emission Rate

1. Introduction

Certainly any change of a physical system represented by a single physical event is connected with some interval of time Dt. This is a rather trivial statement concerning both the classical and quantum physical theory. However, the approach to Dt offered by each of these two theoretical formalisms is quite different.

In brief one can say that Dt given by the classical physics is usually of a definite character. On the other hand, the quantum theory provides systematically Dt of a probabilistic, or statistical nature.

This kind of discrepancy began to exist already on the level of the old quantum theory [1] - [3] , it became however, more acute in the modern quantum mechanics [4] - [6] . For example, when concerning the spectroscopy phenomena, it is hardly possible to define the time moment in which the transition of the electron particle from one of the quantum levels to another begins, as well as the time moment when this transition ends. Nevertheless the exsistence of a finite interval Dt between these two limiting events seems intuitively to be rather evident.

An approach to Dt connected with a single electron transition of a quantum system becomes easy to effectuate when, for example, the interval DE of the system energy is known together with the time rate of this energy change. Such knowledge is offered, for example, by the Joule-Lenz dissipation law for energy [7] [8] .

The law is of a typical classical nature, nevertheless its inspection done on the basis of quantum parameters, shows a posteriori its formal behaviour much similar to the Heisenberg uncertainty principle specialized for the case of quantum intervals belonging to energy and time.

In the first step we show the quantum aspect of the Joule-Lenz law and its effect on the uncertainty principle. This approach allowed us to obtain a minimal admissible interval of time associated with the electron transition process. In the next step, a maximal limit of the electron transition energy could be calculated. As a final result, due to the existence of a minimal interval of time, a minimal geometrical size of a distance parameter entering small quantum systems could be estimated.

2. Historical Background of the Heisenberg Uncertainty Principle

A complementary character of the intervals of energy and time concerning a given physical phenomenon has found its well-known representation in the Heisenberg principle of uncertainty [4] [9] . Mathematically the principle states that the product of DE and Dt should not provide a number smaller than the Planck constant: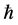

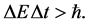(1)

The Formula (1) has been outlined parallelly to the Heisenberg rule of uncertainty concerning a product of the change of a Cartesian coordinate of the particle position and the particle momentum, for example

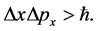(2)

Evidently the Formula (2) can be extended equally to the Cartesian coordinates y and z.

But a mathematical and historical background of (1) and (2) became much different: the Formula (2) found its wide justification in numerous approaches [10] [11] contrary to the rule of (1) which was strongly objected on several occasions [12] - [14] . In effect, in some textbook presentations (see e.g. [15] [16] ), the Formula (1) contrary to (2) did not appear at all.

A characteristic point is that shortly after (1) and (2) have been published, some proposals concerning the limits of the observables entering (1) and (2) were done. These limits concerned in particular and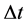. According to [17] - [20] , 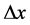should be not smaller than the Compton wave length

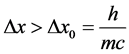(3)

and should satisfy the relation

(4)

3. Modification of the Principle (1) and Its Effect

An essential change of (1) can be attained when the velocity condition of the special theory of relativity, namely

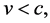(5)

is applied in the motion analysis of the fermion particles [21] - [23] . In this case the transition energy 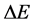done within the time interval 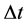should satisfy instead of (1) the formula

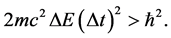(6)

By assuming that

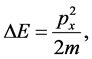(7)

where 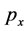is the electron momentum

(8)

because of the Hamilton equation

(9)

we obtain from (8)

(10)

This expression substituted into (6) together with (7) gives the relation

(11)

from which

(12)

By dividing (12) by c, an operation similar to that applied in (4), we obtain

(13)

The limits in (12) and (13) are smaller than, respectively, limits in (3) and (4) solely by the factor of; see [24] . This is an important correction because from (12) assumed as a radius of the circular-like trajectory of a spinning electron leads to a correct driving velocity of that electron. The correctness property is examined by the agreement of the driving velocity provided by a spinning particle with the Bohr orbital velocity of the electron; see [25] [26] and Section 3.1. Moreover the magnetic moment produced by a spinning particle is equal to that experimentally observed [25] [26] .

3.1. Driving Velocity of a Spinning Electron Is Equal to the Velocity on the Bohr Orbit

A spinning electron provides the electric field of the strength

(14)

and the magnetic field due to the same electron is [25] [26]

(15)

The driving velocity of a spinning electron is given by the formula [25] [26]

(16)

The result in (16) is exactly equal to the orbital electron velocity on the Bohr quantum level. This velocity is obtained from the relation

(17)

where

(18)

is the Bohr radius of the first orbit and

(19)

is the corresponding circulation time period, see e.g. [27] .

4. Joule-Lenz law and Its Quantum Aspect

Our aim is now to obtain a minimal with the aid of a more fundamental reasoning than applied in (13). To this purpose the rate of energy produced according to the Joule-Lenz classical law [7] [8] [28]

(20)

is examined for the case of the quantum systems. R is the electric resistance

(21)

V is a voltage of the electron transition, and

(22)

the current intensity. We assume that any considered quantum state is periodic in time, which means that after the time interval the state n is exactly the same as before.

Let the voltage be calculated by assuming that

(23)

where

(24)

is the energy difference between two neighbouring quantum states. In Section 5.1 the Formula (20) modified into

(24a)

has been applied―together with (21)-(24) ―to three quantum systems: the hydrogen atom, electron particle in a one-dimensional potential box and the harmonic oscillator. A posteriori several characteristic features concerning R and the Joule-Lenz law have been obtained.

The first of them is that

(25)

is a constant for all systems and all quantum states taken into account. The constant number (25) is well known from the experiments on the quantum Hall effect [29] . Another feature is that the product of and calculated in all examined cases is formally similar to that represented by the Formula (1):

(26)

In fact the Formula (26) disproves that given in (1) in the sense that now we have

(26a)

instead of (1).

Another result found in the course of calculations is that

(27)

other arguments justifying (26) and (27) are given in [30] .

5. Repercussions of (26) on the Energy-Time Uncertainty Principle

By assuming that in (26) is equal to entering (6) we obtain―after a substitution of (26) into (6)―the relation

(28)

from which

(29)

But the Formula (26) can be applied also in the case when

(30)

Since in this case, this substitution gives the relation

(31)

from which a maximal energy involved in an electron transition is

(32)

Let us note that the energy

(33)

estimated as valid for transition from the Dirac’s antiparticle sea to the electron particles area [31] [32] satisfies the condition imposed by (32):

(33a)

5.1. Quantum Aspect of the Joule-Lenz Law Demonstrated on Three Quantum Systems

This kind of relation involves the Planck constant h. As a beginning the Joule-Lenz Formula (20) for the emission within the time interval is applied in the form:

(34)

Here R is the electric resistance of the circuit having intensity i associated with the emission. The R, i and the potential V of the emission are given in (21)-(23).

For particular systems considered in the present paper this gives

(35)

for the hydrogen atom because the time period in this case is (see e.g. [27] )

(36)

For the electron particle in a one-dimensional potential box

(37)

because the particle energy and its velocity are coupled by the Formula (see e.g. [33] )

(38)

so

(38a)

and the time period of the electron oscillation in the box having length L is

(38b)

In the case of the quantum harmonic oscillator its energy is

(39)

where the last step is valid for large n, and the oscillator frequency is

(39a)

valid for all quantum states n, so the time period of the oscillation

(39b)

is the same for all states n giving

(40)

The needed to obtain V in (23) are (see e.g. [27] )

(41)

for the hydrogen atom on condition a transition between the quantum levels and n is considered.

For a similar pair of levels in a one-dimensional potential box we have

(42)

[see (38)] and for the quantum harmonic oscillator the separation between a pair of the neighbouring quantum levels of energy is the same for all pairs:

(43)

This gives

(44)

for the transition in the hydrogen atom on condition large is considered,

(45)

for a similar transition in a one-dimensional potential box, and

(46)

for a transition done also between the neighbouring levels in the harmonic oscillator.

A characteristic point is that all R are the same [see (44), (45) and (46)] giving the result typical for the electric resistance in the integer quantum Hall effect; see e.g. [29] .

As a result of substitution of the data calculated in (35) and (44) into the Formula (34) we obtain the following quantum emission rate

(47)

for the hydrogen atom; for the electron particle in a one-dimensional potential box (34) gives

(48)

[see (45) and (37)]; finally in the case of the quantum harmonic oscillator the data of (40) and (46) substituted to (34) give the emission rate

(49)

A characteristic point other than equal R values obtained in (44)-(46) is the quantum property which concerns the products of and. The which can be readily obtained from (47), (48) and (49) are:

(50)

for the transition examined in the case of the hydrogen atom,

(51)

for the transition in a one-dimensional potential box,

(52)

for the transition considered in the harmonic oscillator.

The time intervals of (50), (51) and (52) can be multiplied by the intervals which were at the basis of the mentioned results for; see (41), (42) and (43). In effect we obtain

(53)

(54)

and

(55)

respectively in the case of the hydrogen atom, a particle in the potential box and the harmonic oscillator.

Because of the results obtained in (53), (54) and (55) the time rate of the quantum emission of energy takes the form

(56)

in view of the fact that

(57)

is given systematically by equations (53)-(55); see also [30] .

6. Observables Obtained with the Aid of the Time Intervals Dt and Dt_min

Some interesting results seem to be obtained with the aid of the velocity observable

(58)

and the intervals of time combined with it. A simple multiplication applied in (58) should give

(59)

Our first aim is to check whether result (59) is obtained when entering (59) satisfies the relation

(60)

where the last formula is a result of (26).

For the hydrogen atom we have the orbit radius:

(61)

and the electron velocity in state n is

(62)

In the next step the energy interval concerning the neighbouring levels and n is that given in (41) so, because of (60), we have

(63)

see (36). The result for the product of the velocity and time

(64)

represents the whole of the circular length associated with the orbit n; see (61).

For a free particle in the potential box having length L the distance travelled within one period of time is the same for all n namely

(65)

The velocity term in (65) satisfies the formula for the kinetic energy of a free particle; see (38). The second term in (65) should be evidently

(66)

because the energy difference of free electrons is given in (42), so we obtain equal to in (66). This time interval multiplied by entering the Formula (38) gives the product identical with that calculated in (65).

For the low energy excitation of the harmonic oscillator we have

(67)

where is the circular frequency. Therefore

(68)

All formulae (63), (66) and (68) give

(69)

where T is a time period characteristic for a quantum state involved in the energy transition.

Other calculations for the harmonic oscillator are less accurate because the variables applied in them are dependent on time, for that reason only the average quantities are taken into account [34] . The average distance having the same sign occupied by the oscillator is evidently

(70)

where a is the oscillator amplitude.

Since the absolute value of the oscilator velocity is [34]

(71)

where k is oscillator strength and the oscillator frequency, the average oscillator velocity taken over the distance of the amplitude is

(72)

Because of (67) we have

(73)

which is a result times larger than in (70).

In general we found that can reproduce the observables of geometrical distance in small quantum systems with the accuracy to a constant coefficients.

An interesting point is the calculation of the distance observables when the interval is replaced by given in (29). For the hydrogen atom in the state of we obtain

(74)

which is equal to times the radius of a sphere representing the microstructure of the electron particle [8] [35] .

A similar product calculated for a one-dimensional free-electron case gives

(75)

where is taken from (65). Here we require that the equality of (75) with entering should be satisfied, in result an equation for is obtained. Its solution is close to derived in (12).

For the harmonic oscillator a requirement that (72) should hold also in the case of, so

(76)

leads to a maximal frequency which can be admitted by the oscillator:

(77)

This number is not extremely different from a maximal frequency of the oscillator attained in another way [21] .

7. Discussion on Dt and Emission Rate of the System Energy

If we combine the Formulaes (26) and (69) together with

(78)

we obtain

(79)

which is the well-known fundamental Planck formula on condition is considered as the frequency of the electromagnetic wave associated with the energy. Consequently T has to be identified with the time period of that wave. From our derivation of (68) given in Section 6 it can be deduced that T is not much different than the time periods associated with quantum states and n entering the difference; see (63), (66) and (68).

A new result in (78) which seems to be neglected by many authors is that

(80)

This means that performance of the electron transition between quantum states and n occupies solely one oscillation time period of the electromagnetic wave strictly connected with the period of the quantum level involved in the mentioned transition.

In effect of (26) and (69) the emission rate of energy in a quantum system can take a very simple formula

(81)

A maximal time rate of energy which can be attained by a fermion particle of mass m in a single transition is

(81a)

see (29) and (32).

For the hydrogen atom at large n we have [see (41) and (50)]

(82)

This result can be compared with a classical emission rate; see Section 9.

On the other hand for a harmonic oscillator we obtain

(83)

A reference of this formula to the classical emission rate of energy is discussed also in Section 9.

8. Corollary Concerning the Time Rate of Disspation Energy in a Metal

The Joule-Lenz dissipation rate of the electron energy in a metal referred to a single electron transition can be represented by the formula [8] :

(84)

Here l is the electron free path, is the strength of the electric field acting on the metal, is the average electron velocity which is

(85)

where is the Fermi velocity because the electrons located mainly near the Fermi level are submitted to the motion due to the action of, the parameter is the relaxation time. The work done along the length l is connected with by the acceleration formula

(86)

because

(87)

In effect from (86)

(88)

On the other hand, because of (84) and (85)

(89)

where the last step is coming from the present formalism; see (81). From (88) and (89) we obtain the relation

(90)

or

(91)

If we note that relation

(92)

is satisfied for small according to the present formalism, we obtain

(93)

In consequence the rate

(94)

does hold for a single electron transition in the metal. The Formula (94) can be submitted to the experimental verification.

It can be noted that for

(95)

which is the case of the electron transport in superconductors, we obtain in result of (94) that

(96)

9. Application of the Formalism: Classical Emission Rate of Energy Compared with the Quantum Rate

The classical emission rate depends both on the amplitude a of the oscillator and the emitted frequency [36] :

(97)

We assume the transition is going on between two neighbouring quantum levels and n.

For the harmonic oscillator being in state n the amplitude can be deduced from a classical relation between the energy and amplitude. Therefore for the energy

(98)

this gives (see e.g. [34] )

(99)

The frequency is assumed to be that given by the transition energy

(100)

For the classical emission rate of the harmonic oscillator having frequency we obtain with the aid of (98) the formula

(101)

and an interesting result is the ratio of the classical and quantum emission rates of the oscillator. This is given by the formula [see (83)]

(102)

The ratio (102) differs solely by the factor of

(103)

from the damping constant

(104)

of the classical emission see [36] [37] . The T entering (103) is the oscillation time period of the electromagnetic wave having the frequency. The product

(105)

is the number of excitations within the time period T; see [36] .

A similar calculation can be done for the hydrogen atom. In this case the classical emission rate between levels nad n becomes

(106)

here (61) and (62) are taken into account. The quantum rate of emission is

(107)

on the basis of (80) and (81). Therefore the ratio of (106) to (107) becomes

(108)

where

(109)

is the fine-structure atomic constant; see e.g. [4] .

10. Summary

The physical consequencies of a quantum aspect of the Joule-Lenz law for the dissipation rate of energy are examined.

The mentioned aspect seems to influence the uncertainty principle for energy and time. In consequence a lower limit of the time interval and an upper limit of the energy interval admissible in a quantum transition process could be calculated.

The next point concerned the time rate of the low-energy transitions was performed in small quantum systems. On the basis of the Joule-Lenz law the transition time between quantum levels could be calculated in a definite, i.e. non-probabilistic, way. This calculation indicates a similarity existent in the size of the seeked transition time and time periods characterizing the examined quantum levels.

In effect a simple formula coupling the transition time with transition energy could be obtained. The formula makes a reference to the Planck constant h and points out that transition time is in fact equal to the time period T of the electromagnetic wave produced in effect of the transition.

As an application of the theory, the classical and quantum emission rate of energy in two systems (harmonic oscillator and the hydrogen atom) taken as examples have been calculated and compared.

Cite this paper

StanisławOlszewski, (2016) Quantum Aspects of the Joule-Lenz Law. Journal of Modern Physics,07,162-174. doi: 10.4236/jmp.2016.71018

References