Received 7 July 2015; accepted 24 August 2015; published 27 August 2015

ABSTRACT

Assuming the light as composed of longitudinal-extended elastic (and massive) particles emitted during an emission time T at speed c (=u) (with u the escape speed from all the masses, toward the infinity), it is shown that c is invariant (under the Newtonian mechanics laws), for an Observer fixed to the initial emission point E_p (the point where the emission starts), in spite of any motion of the source (of light) with respect to E_p. On the contrary, an Observer, in motion from E_p during the emission, will state (indirectly) a Galilean variation of c which can be proved and evaluated by an appropriate feasible experiment described here.

Keywords:

Escape Speed toward the Infinity, Longitudinal-Extended Elastic Particles

1. Introduction

This paper, in accordance with the Newtonian laws, is based on following assumptions:

I. Gravity fields fixed to their related masses (intending that each field is co-moving with its generating mass).

II. Finite mass of the universe, implying a finite value of U (total gravitational potential) and therefore of u escape speed toward the infinity due to all the masses in space.

III. Light composed of longitudinal-extended elastic particles (as defined in Section 3) moving at speed c = u. This equality is supported by a cosmological reason.

On above bases (including, needless to say, Newton’s absolute time and space) we obtain:

1) The relation u = (−2U)^1/2, where u is total escape speed, from all the masses, toward the infinity and U (total gravitational potential, due to all the masses in space), while the assumption c = u (which implies the massiveness of the light and also c_∞ ® 0), gives to the speed of light a cosmological/anthropic reason to its value, as highlighted in Section 2.

2) The constancy of the speed of light, under the Newtonian laws, for an Observer fixed to the (initial) emission point, E_p, (the point where the emission of light starts), in spite of any motion of the source with respect to E_p.

3) A variation of c (in accordance with the Galileo’s velocities composition law), if the Observer is in motion with respect to the said emission point (taken as reference frame): for instance, on Earth, an Observer in motion from the source (of light) fixed to the ground during the emission. This variation of c (contrary to the 2^nd postulate of Special Relativity) can be proved by a feasible experiment described here.

2. Total Escape Speed, from All the Masses in Space

Here we get the escape speed due to one, two and n masses; then we assume u = c (= −2U)^1/2, with u the total escape speed (from all the masses), and U the total gravitational potential .

As known, considering in space one only mass M (regarded as a point-like), the gravitational potential U acting on a particle having mass, assuming U_¥ = 0, with s the distance M-m, is U = −MG/s (this relation, according to our first assumption (I), is always valid in spite of any reciprocal motion between M and m). The related Conservation of Energy (CoE), E = U + K, where K (= 1/2u²) represents the unitary (for unit of mass) kinetic energy of our particle arriving from the infinity (where u_¥ = 0), for E = 0, gives U = −K, leading to

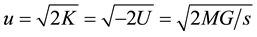(1)

which is a scalar, (called escape speed), representing (in the considered point) the value of the velocity u, any massive particle, under a potential U, needs to reach the infinity; thus u (escape velocity) has to be referred to M; if M is a real mass, u has to be referred to the point of M where 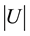has the max value, intending this point as the Centre of potential C_p. Therefore we have to write

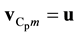(2)

meaning that the escape velocity of our particle m has to be referred to C_p.

Considering now two masses M₁ and M₂, having, at a given time, distances s₁ and s₂ from a considered point, the potential U_1,2 in this point becomes

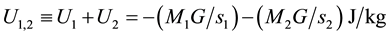. (3)

Without the assumption I, the Equation (3) is still valid, but U_1,2 could have a different value, depending on the assigned values of s₁ and s₂, at the considered time.

Now, the escape speed from two masses can be written

(4)

representing the value, in the considered point, of the (escape) velocity u_1,2 which has to be referred to the Centre of potential C_p, (where 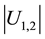has the max value).

Then, as 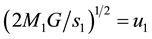and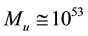, we also get

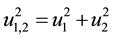(5)

therefore the escape speed due to all the n masses in space becomes

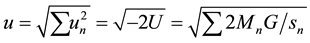(6)

with 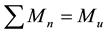the universe mass, 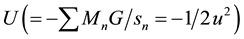the total gravitational potential in the considered point, where u (function of U) can be called total escape speed (toward the infinity), while the escape velocity u is referred to C_p (centre of potential of all the masses).

Now, considering as origin of our Reference frame, the initial position of m, we may call it Emission point E_p, (the point where m will be given the speed u), the following relation

(7)

may be called as relative escape velocity of m from E_p, with.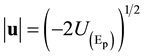

The particle m, at the time of its emission, has, in general, a velocity with respect to E_p, hence, from C_p,

it has a velocity; thus if it turns out that m tends to the infinity:

in particular, if the velocity is provided to a great number of particles all around E_p, more than half of them will surely tend to the infinity.

We assume now the equality c = u, hereafter supported by the estimated mass of the universe and also by this cosmological/anthropic reason: in fact, if c < u, all the masses in space, (having speed lower than u), will tend to a gravitational collapse, whereas for c ≥ u, the mass of light, going toward the infinity in an unlimited time, tends to avoid the said collapse.

Here we also point out that the energy of light (mc²) seems to be not in accordance with the said relation E = U + K = 0, where K = 1/2mu², but, as shown on [1] , the energy of light is given by a kinetic energy K = 1/2mc², complying the said relation (plus an internal energy of the same value).

This following part of Section 2, is only a support to our assumption c = u.

The mass of universe, by some authors, is estimated [2] -[4] to be kg; the same order of magnitude is given throughout the number () of observable stars [5] [6] , and since from Earth the distribution of the masses appears to be homogeneous and isotropic, under our assumption U_¥ = 0, we may assume their density as decreasing, from the Local Group (LG) toward the infinity, like a function ρ = ρ_ce^−as with 9.2 × 10⁻²⁷ kg/m³ the critical density [7] . So the mass of universe can be written

(8)

yielding

. (9)

From the LG, the variation of U, due to an increase of the distance ds, can be written as dU = −dmG/s where dm = ρ4πs²ds with ρ = ρ_ce^−as, hence the potential on Earth becomes

(10)

Now, according to Equation (6), on Earth it is

(11)

Therefore, on Earth, u₀ = c₀, so that and, in general we may argue

(12)

The equality c = u means that, along any free path, the speed of light only depends on the value of the potential along that path.

3. Invariance of the Total Escape Speed u for a Particular Particle, Here Defined

Here it is shown that under the assumption III, should a source of photons, during their emission, move from its initial Emission point (E_p), their length will vary, and since their transit time, (time to cross an Observer), will also vary, their speed becomes constant for any Observer fixed to E_p, in spite of any motion source-E_p.

The Galileo’s velocities composition law, which is related to point-particles, cannot be, apparently, applied to a particle defined as follows:

“longitudinally-extended, elastic non divisible particle emitted at speed u by a source during an emission time T, and moving along rays, (continuous succession of photons)”.

Of course, more photons emitted during an emission time T need an equal number of rays.

Calling front and tail the extremities of a photon, every tail, (along a ray free path), corresponds to the front of the next photon.

Now, on Figure 1, let S be a Source (of light), starting to emit, at t = 0, a photon (with front A) and let the initial Emission point E_p (the point where the emission starts), be the origin of our reference frame; then let S

move, during the emission time T, from E_p to S_T. For instance, E_p may be a generic point on the Earth’s surface, with S coincident to E_p at t = 0.

Now, the relative escape velocity of the front A (being a point-particle), from Equation (7), can be written

(13)

which gives, as hereafter shown, to the (whole) photon, for an Observer in E_p, (or fixed to it), a constant speed (u), in spite of any motion of S from E_p. At this purpose, still referring to Figure 1, let the source S have a velocity with respect to E_p; hence the velocity of the front A, with respect to S, that is, v_SA, from Equation (13), becomes

(14)

Therefore, at t = T, when S has reached the point S_T, we get

(15)

where λ' is the photon AB emitted with the source in motion from E_p, while λ (º uT) should be the photon (AE_p) if S, during the emission, should be fixed to E_p.

Thus, after the emission time T, as for a source receding from the front A, as in Figure 1, the photon length λ', (for any Observer), from Equation (15), turns out to be

(16)

where, where is the path E_p-S_T covered by S during T, with, showing that the length of an emitted photon, for a given source, only depends on.

Now, the speed of a point-particle is defined through two Observers, while the speed u' of a photon, (since its length could vary), does not correspond to the speed of any point of it, hence to define the speed of a photon we must consider its length referred to the time T' (transit time) the photon (front to tail) needs to cross one Observer, leading to

(17)

which is the average speed of the photon along the path λ'.

As for this definition, let us consider a system composed of two balls connected through an elastic thread and let them fall in vertical line: during the fall, each part of the system has different speed, that is why we need the Equation (16) to define the speed of the whole photon.

Still returning to Figure 1, for an Observer fixed in E_p, the transit time T' of the photon AB is given by the time the front A needs to cover the path λ, that is T (= λ/u), plus the time the tail B needs to cover the path S_T-E_P = which, (since the tail B is emitted by S, see Equation (13), at the same velocity u as the other parts of the photon), is, giving

(Observer fixed to E_p). (18)

Thus, see Equation (17), the speed of the photon AB, referred to our Observer fixed to E_p, becomes

(19)

showing that, on our bases, an Observer, fixed to the Emission point E_p (point where the light starts to be emitted), states that the speed of light is invariant (and equal to the total escape speed), in spite of any speed Source-E_p.

Now, what about for an Observer in motion from E_p? Well, the length λ' of an emitted photon does not depend, see Equation (16) on the Observer motion, while the photon transit time T', depends, for an Observer fixed to E_p, see Equation (18), on and it also depends, for an Observer in motion from E_p, on, leading, in short, to, where the sign ± is obviously given by the same/opposite direction Observer-source with respect to the one of the considered photon. For instance, if v_SO = 0 (Observer co-moving with S, both moving from E_p to S_T during the emission), the photon length, see Equation (16), is still λ', while its transit time (for the Observer and for S too) is T' = T, hence u' = λ'/T ≠ u, that is c' ≠ c.

Hereafter, to detect this variation, we describe a feasible experiment where the Observer (measuring the times), has to be in motion from the Emission point (taken as reference frame): usually, the measurements of c (through the method d/t), to be accurate, requires the Observer(s) to be fixed with the photon emission point), but, on our proposed experiment, the distance d, (variable during the experiment), is not involved into the evaluation of Δc.

4. Description of a Feasible Experiment Showing the Variation of the Speed of Light

To evaluate our predicted variation of c stated by an Observer O in motion from the initial Emission point E_p, we may assume, for simplicity, the source S fixed to E_p.

Thus, see Figure 2(a), at t = 0 (start of emission), let O be located in E_p (our reference frame) and let be the speed of O from E_p. So, at t = 0, it is: O and A₁ (front of the first emitted photon) both in E_p. At the end of the emission, lasting t_e (= nT), where n is the number of consecutive photons (A₁B₁-A_nB_n), the path covered by the front A₁ becomes L = nλ, the Observer has covered the path Δd = v_Ot_e, while the tail B_n is still in E_p. Then, when the tail B_n, at a certain time t_O, reaches O, the path covered by O is ΔL = v_Ot_O, where t_O corresponds to the (transit) time the n photons need to cross the Observer (that is from t = 0 to the time the tail B_n reaches O), hence we can write t_Oc = L + ΔL, so we get

(20)

giving

(21)

which, for, leads to

(valid for) (22)

and then

(23)

which is the variation of time stated by the Observer O between the transit time t_O and the emission time t_e where t_e is also the transit time for the Observer if this would be fixed to S. For instance, if v_O = 10 m/s and t_e = 3 s, one gets Δt = 10⁻⁷ s, well measurable.

Therefore the speed of light as stated by the Observer O (moving along the same direction as the light) becomes

(24)

while the speed stated by S (or by an Observer fixed to E_p) is:.

Referring to Figure 2(b), where the source S and the Observer O are duly represented in a different position, as for the clock of the Observer we have:

t = 0 (start of times, when the first photon, A₁-B₁, reaches O);

t = t_O (end of time, when the last photon, A_n-B_n, reaches O).

As for the clock of the source, not represented on figure (and not necessarily synchronized with the Observer clock), we have:

t_S = 0 (start of emission from S);

t_S = t_e (end of emission).

We point out that the value Δt given by Equation (23) does not depend univocally on the speed of the Observer, hence the predicted (by the Relativity) time dilation due to the Observer motion, cannot be claimed.

Now for an Observer, the frequency of photons of the same ray has to be defined as with n the number of photons crossing the Observer during the time t; for t = T' (generic transit time of one photon), it is n = 1, that is, therefore, from Equation (18), we get with the sign + when source and Observer are approaching to each other; in fact, for O and S at reciprocal rest, the number of photons emitted by S in a unit time has to be equal, in the same time, to the number of them crossing O, and this implies. Now we can summarize:

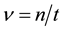
・ if S is moving from E_p, (as in Figure 1), while the Observer is fixed to E_p, he will state: c' = c and, hence and;

・ if the Observer is moving from E_p along the same direction as the photons (like in Figure 2(a)), while S is fixed to E_p, the Observer will state:, and, hence and.

5. Conclusion

We have seen that, on our bases, the speed of light (corresponding to the total escape speed) follows the Newtonian laws, and we have described a feasible experiment showing that the speed of light also follows the Galileo’s velocities composition law, if applied to these photons.

Cite this paper

AlfredoBacchieri, (2015) A Feasible Experiment Contrary to the 2^nd Postulate of SR. Journal of Modern Physics,06,1342-1349. doi: 10.4236/jmp.2015.69139

References