Received 3 June 2015; accepted 21 September 2015; published 24 September 2015

ABSTRACT

Models of the pointed interactions approximately describing real interactions of nuclear particles in quantum mechanics are considered. The concept of “a dot cluster”―a complex of charges which at the zero size create possibility of localization of a trial particle in the field of the final size is entered. States in one-dimensional systems, and also in three-dimensional systems with “a local isotropy” are studied. The conditions of dot systems characterized by the nonzero, including fractional, orbital moment were studied.

Keywords:

Shrӧdinger’s Equation, Dot Potential, Dot Claster

1. Introduction

For the model description of nuclear processes extensive literature―see, for example, [1] [2] is devoted to use of dot potentials. This circumstance is promoted by visible simplicity of the description with the help δ-poten- tials, connected with possibility of the analytical solution of complex challenges. Thus, however, the way of creation of the system characterized by the zero radius of interaction usually isn’t studied. It is possible to assume that at really small size of a positive charge, the defining role in behavior of system is played by one connected level, and then a way of creation δ-potential it is not essential. Works [3] [4] are devoted to detailed theoretical studying of properties of dot potentials. It is necessary to mention the works considering exact solutions of non-stationary tasks on the dispersing δ-potentials [5] -[7] , the illustrating possibilities of the considered model method. The complete self-coordinated description of systems with dot, or with δ-potentials can be of interest both with theoretical, and with experimental the points of view. In the real work, interaction of dot cters in one-dimensional systems and conditions of dot systems in symmetric systems three-dimensional are studied spherically.

2. 1-D System

We will consider, at first, the one-dimensional system described by Schrödinger’s equation of the following look:

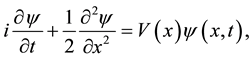(1)

where―psi-function of an electron,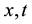―the coordinate and time, is used nuclear system of units:. If potential has an appearance, (1) has the decision:

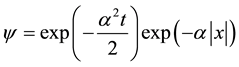, (2)

where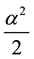―depth of the connected level The connected condition of the Equation (1) is the only thing, thus

there are also conditions of dispersion which are in detail studied in [8] . Only stationary solutions of the equation of Schrödinger designated will be studied further. We will consider how third-party charges can create the potential if interaction is electromagnetic. We will use Poisson’s equation which is written down in dimensionless variables:

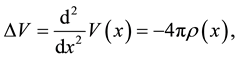(3)

where the 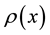-linear density of a charge of the object creating δ-potential, we will call this object further “cluster”. Density of a charge of a cluster satisfies to a ratio: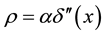. This equality means that the total

charge of a cluster q is equal to zero―the dipolar moment is also equal to zero―and only the square moment is other than zero: 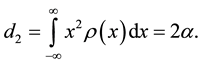Follows from the given considerations that for

deduction of charged particle (electron) in limited area existence of a charge of an opposite sign in the center of system isn’t obligatory―the electron can be localized if it interacts with the dot cluster characterized by a zero charge, but having the square moment, other than zero. At this field of a cluster everywhere, except the vicinity of a point 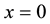equally to zero.

We will consider a situation when there are two δ―the center, i.e. potential has an appearance:

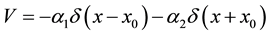(4)

The solution of the stationary equation of Schrödinger characterized by level depth 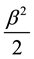can be looked for in a look (see [1] [2] ):

(5)

Substituting (5) in (1) taking into account (4) we will receive system:

Here a, b―constants. From a condition of existence of the nonzero decision of this system for a, b it is possible to receive a ratio for size:

. (6)

In a case when symmetric and antisymmetric decisions for -functions are possible. If,

that, and if that.

We will consider, further, impact of a field of the electron connected by two centers on these centers―dot clusters. The full force operating on a cluster is calculated as integral of the following look:

(7)

where cluster charge density,―the field created by the connected electron. This field is defined from the equation: where. I.e. the field has to satisfy to the equation:

(8)

This equation corresponds to symmetric distribution of electronic density,―a normalizing constant. As density of a charge of the cluster which is in a point is defined as, force operating is defined on this cluster by equality:

The derivative of integrand function has a gap in a point near which the cluster is loclized:

(9)

The difference between values on the right and to the left of a point makes that it is necessary to consider force operating on a cluster. Thus, however, it is supposed that the charges making a cluster are kept by not electromagnetic forces surpassing forces from electric charges. It is possible to show, further, that the full force operating on the cluster localized close, is equal in size and is opposite in the direction to force operating on a cluster in point. It is possible to show, further, that the full force operating on the cluster localized close is equal in size and is opposite in the direction to force operating on a cluster in a point and in case of symmetric on psi-function of an electron clusters make a start, and at antisymmetric psi-function clusters are attracted to each other.

In the absence of symmetry of system for forces operating on clusters it is possible to receive:

Forces are equal in size and are opposite in the direction.

We will note here that consideration of the real work makes sense at, thus sizes aren’t surely

positive. If that of (6) follows:. Relation.

3. Spherically Symmetric Clasters

The symmetric equation of Schrödinger stationary spherically at zero orbital quantum number has an appearance:

(10)

If the potential created by third-party charges has an appearance:, that to the Equation (10) is satisfied by function:. In case of spherically symmetric operator Laplace

.

Charge density in a spherical cluster is defined from the equation: from where. Calculation of a total charge of a cluster in this case gives infinite value for a charge. Besides, we

will notice that two separate clusters, “locally” spherically symmetric, located in different points, don’t influence at each other. Also it is necessary to notice that the determined higher than a potential doesn’t determine depth of the connected level, the equation is satisfied at any. Due to these circumstances the generalization of potential containing a distribution function derivative is usually used. In the Equation (10) it is replaceable

.

Let δ―the centers be located at. We will put

,

where.

We will substitute these expressions in (10), considering that. We will receive a ratio

. (11)

Equating of coefficients at leads to system:

(12)

The condition of existence of the nonzero decision of this system has an appearance:

(13)

The type of a ratio (13) is similar (6). (See also works [5] ). As well as in the case described by the equation (6) one of sizes α can be negative, however in the situation described (13) at rather small values both values α can be negative―two pushing away δ-centers can form the connected state.

4. Spherically Symmetric Clasters at Nonzero Orbital Quantum Number

If the orbital quantum number, spherically the symmetric equation of Schrödinger has an appearance:

(14)

We will make replacement in the Equation (14), including:. Then the equation will assume an air:

(15)

At the decision (15) has an appearance:, here― McDonald’s function. If, further, to use a ratio, the following from this that the differential operator in (15) has an appearance of radial part of a five-measured laplasian (see [9] ), it is possible to see that potential has to have an appearance:. It is also possible to use generalization of potential in a look Need of a capture of the second derivative is explained by the fact

that the first addresses in zero at. Potential in this case determines depth of the connected level. In this case disperses not only the size of a charge of a dot cluster, but also a charge of a trial particle―an electron (disperses at).

Due to these circumstance we will consider the Equation (14) in conditions when divergence of a charge of an electron at is absent. The solution of the Equation (14) with zero right part has an appearance:. If, at. I.e. if l is concluded in the specified interval, density of a charge of an electron has only the integrated feature. We will put. Then the equation will assume an air:. As the differential operator has an appearance of radial part of a laplasian in dimension space, (see [9] ), for V₂ equality follows: . At nonintegral l values size should be considered the potential created by a third-party charge. If, density of a third-party charge and a total charge disperses: , here―the minimum radius, trimming parameter. The size of a dot charge of a cluster, as well as in the previous cases, is dispersing. At certain values of parameters the total charge created distributed and dot charges is equal to zero. We will use the following expression for δ-functions: Then the total charge corresponding to potential V₂ is equal. If , the total charge is equal to zero. Thus, parameters and also have to be connected definitely among themselves. Unlike a one-dimensional case equality is impossible for zero full size of a third-party charge for the dot center in the absence of the distributed charge.

5. Conclusion

In summary, we will notice that in work problems of the theoretical description of systems with dot potentials in symmetric systems one-dimensional and three-dimensional spherically are considered.

Cite this paper

AlexanderChikhachev, (2015) Interaction of Dot Clasters. Journal of Modern Physics,06,1642-1646. doi: 10.4236/jmp.2015.611165

References