Journal of Modern Physics
Vol.06 No.05(2015), Article ID:56004,20 pages
10.4236/jmp.2015.65073
Scaling Transformation for Nonlocal Interactions
Hai-Jun Wang
Center for Theoretical Physics and School of Physics, Jilin University, Changchun, China
Email: whj@jlu.edu.cn
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 March 2015; accepted 25 April 2015; published 28 April 2015
ABSTRACT
In the light of their relationships with renormalization, in this paper we associate the scaling transformation with nonlocal interactions. On one hand, the association leads us to interpret the nonlocality with locally symmetric method. On the other hand, we find that the nonlocal interaction between hadrons could be test ground for scaling transformation if ascribing the running effects in renormalization to scaling transformation. The nonlocal interaction Lagrangian turns out to vary under scaling transformation, analogous to running cases in renormalization. And the total Lagrangian becomes scale invariant only under some extreme conditions. The conservation law of this extreme Lagrangian is discussed and a contribution named scalum appears to the spin angular momentum. Finally a mechanism is designed to test the scaling effect on nonlocal interaction.
Keywords:
Scaling Transformation, Renormalization, Conservation Law, Spin Crisis, Nonlocal Scattering

1. Introduction
Nowadays, on account of the developments of string theory [1] [2] , Lattice QCD [3] and the necessity to describe nonperturbatively the intermediate strong interaction between extended hadrons [4] , the construction of a consistent nonlocal theory is still called for [5] -[20] . The pioneering study of nonlocal interaction dates back to the 1930’s [21] when quantum field theory was in its infancy. And the phenomenology of nonlocal interaction commenced with the primary attempts to describe the interaction between extended particles (such as hadrons [22] [23] ), whilst to cope with the divergence appearing in local quantum field theories (LQFT). The development afterward purported mainly to give a consistently convergent theory in order to underlie the named “effective field theory”, whereof some form factors were usually employed [5] - [9] [24] - [36] . Whereas in such context one encounters the difficulty of unitarity and causality in formulating the S matrix [26] [36] , no matter the Feldman-Yang [37] method or conventionally canonical quantization method [26] . Some promising progresses on this issue [6] [7] [9] [32] [33] [38] - [43] in one way or another showed their accordance with the renormalization methods [44] - [47] .
In this paper we try to use the scaling transformation (dilatation of space-time), which is inspired by renormalization and assumed effective in nonlocal description of hadron physics, to unveil part of running effects in nonlocal interaction. More often than not, previous investigations on nonlocal interaction tried to fit certain results to those of renormalization [6] [9] [32] [33] . Reversely, in this paper we phenomenologically extract a scaling transformation from renormalization for nonlocal interaction based on their similar physical picture. With afterthought, the achievements of finding that nonlocal interaction is linked with renormalized interaction vertex may in one aspect owe to their common characteristic of effectively using form factors. For instance, in QED, the momentum-space vertex with renormalization is [48] [49]
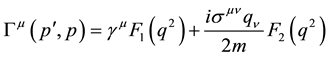 , (1)
, (1)
where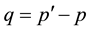 , with
, with 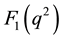 and
and 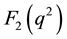 known as Dirac and Pauli form factors respectively. Similarly, the nonlocal interaction has its general form factors in coordinate-space [35] [36] ,
known as Dirac and Pauli form factors respectively. Similarly, the nonlocal interaction has its general form factors in coordinate-space [35] [36] ,
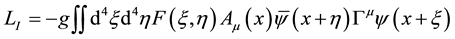 . (2)
. (2)
Here the vertex 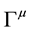 could be the usual vector
could be the usual vector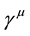 , tensor like
, tensor like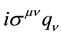 , or other forms to be determined. Its form
, or other forms to be determined. Its form
in momentum-space then is 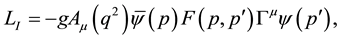 where
where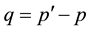 ,
, 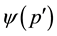 is the spinor
is the spinor
in momentum space and the expansion like 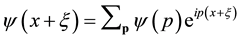 has been implicit. The
has been implicit. The 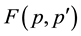 is defined as the Fourier transform of
is defined as the Fourier transform of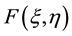 ,
,
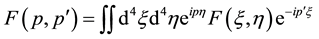 . (3)
. (3)
The renormalization group method (RGM) has its intrinsic relationship with scaling transformation if viewing
the differentiating operator 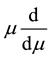 in group equation as scaling operator. In RGM, for a function
in group equation as scaling operator. In RGM, for a function 
presents a vertex function, a wave function or a propagator, its renormalized form and unrenormalized form are linked as [46]

whence the form factor 





where 

In the next section one may note that the operator 
apart from a coefficient i. The Equation (4) is a special form of renormalization group equation, and the well known form is [50] [51]

which is for any Green’s function of massless 






that is the essence of RGM. Besides the obvious application of spatial scaling-transformation to the nonlocal form factor
The scaling transformation, i.e. a freedom added to Poincare group to form Wely group [52] , belongs to a larger group called 4-dimension Conformal Group, which in mathematical side has been investigated thoroughly from different aspects, and its application to physics especially to quantum field once was also widely considered. However the application is not so satisfactory because hitherto no other perfect quantum system than photon field [53] [54] has been found so that the corresponding Lagrangian is scaling invariant, i.e. demanding the mass of involved particles to be null [55] - [60] . Furthermore, one inference of the scale invariance is that according to Noether’s theorem, if a Lagrangian is invariant under scaling transformation, then the trace of the energy-momentum tensor should be null [56] [58] . These two factors become obstacles to apply the scaling transformation to most material fields. Other efforts were also experienced to search for invariant fermion equation or scattering amplitude [57] [59] [61] , and even to apply it to nonlocal action [62] [63] . None of the results is pertinent to known material fields. In this paper we investigate the application by trying two new tentative methods. One is to consider the unitary representation and the coordinate representation of conformal group simultaneously. The other is to apply the scale transformation to hadron physics since, the hadrons have their own sizes with which the interactions between them to some extent vary. Accordingly the test bed for conformal transformation might be nonlocal interaction between hadrons. However, here the scaling transformation works not for invariance, but for running. The running effects of nonlocal interaction are just like those in renormalization.
In this paper we shall use the scaling feature of RGM, but we free us from the detail calculation of renormalization. Since we are looking for a transformation method to interpret the running effect in nonlocal interaction, once we already got an effective form of Lagrangian or Hamiltonian, we would just use tree-level form to do calculations. The further loop calculation will double count something, Born approximation is fine for most cases of interest. The calculation resembles that used in deep inelastic scattering, though we are involved just elastic processes. In summary, in the whole paper we focus more on the properties of scaling transformation/conformal group, and on how to apply them to nonlocal fields.
The rest of the paper is arranged as follows. Sect. II is dedicated to introducing the two representations of scale transformation, i.e. the coordinate/operator representation and spinor/unitary representation. In Sect. III we establish the physical relationship between the two representations, on condition that a scale invariant vertex exists. Subsequently in Sect. IV we discuss the conservation law for the derived scaling-invariant vertex, and the possibility that it relates to the nucleon’s polarizations is posed. In Sect. V according to the characteristics of applying the general vertex-form 
2. The Spatial and Spinor Representations for Scaling Transformation Based on Group Theory
It is well known that the scaling transformation belongs to a larger Conformal Group [52] [56] , therefore next we will learn first the properties of 4-dimensional Conformal Group, including its spatial/operator representation and unitary/spinor representation, as well as commutations among their generators. At the end of this section, we
will understand the role of operator 
rencing to that of Ref. [52] [64] and the unitary representation is derived by applying Cartan method [65] to 
Mostly the scaling transformation in 4-dimension is discussed as a subset of conformal group, and in previous literature its applications are seldom considered independently [56] . Here we start with the null vector space (Euclidean space),

reserving which gives the popular definition of conformal group [65] . A special expression of the differential forms in 4-dimension spatial representation can be derived directly from the above equation. In derivation we need to apply the following variables [52]

together with the differential form

to the definition of 6-dimensional angular-momentum

Then one gets the following generators for conformal group [52] [of which in Equation (56)]

The projected form (making K as constant boundary of Minkowski Space [66] ) with Minkowski convention then is

where 

Before using Cartan method to achieve the unitary representation of Conformal Group, let’s review first the steps of Cartan method with 


The trace 



immediately we have

thus 



matrix X acts as a mapping between 

by

with the solution 


which automatically satisfies 
From the above Cartan matrix X we can extract the Pauli matrices











And coincidentally the n-vectors form (defined in Equation (24)) based on Pauli matrices don’t generate new matrices, neither the multiplications nor the commutations among them, they themselves are closed. Now in what follows we would find the corresponding Cartan matrix from 

To achieve its unitary/spinor representation in 4-dimension, mimicking the relationship between the metric 

by the following matrix [67] ,

Count the degrees of freedom of the groups that conserve separately Equation (5) and Equation (18), one finds they are both 15. Next we only need to extract the coefficients before





and

the latter falls into Dirac spinor like
It can be examined that the matrix A in Equation (19) meets the invariant expression

just like the above 3-dimension example, while the 

it simultaneously reserves the metric Equation (18). The above method of linking real metric to a matrix is closely analogous to the Cartan method of constructing a spinor representation in any real space. Actually, the true spinor space for 4-d conformal group following Cartan method should be of 8-dimension instead of 4-dimension [65] [of which in pp. 88-89]. In what follows we would take over the process of deriving all of the n-vectors along the Cartan method [65] [of which in pp. 81-83], though we work in 4-dimension rather than 8-dimension. First we extract the matrices before

where

where P denotes different permutations. Apply the above formula to 2-vector, and use the corresponding subscripts to denote the 1-vectors involved, then
Similarly, let’s exhaust all possibilities, then obtain other nontrivial 2-vectors

We note that the new ones which are independent of



Computing the 4-vectors and the higher ones would not give new independent matrices. Finally, we can rearrange all above k-vector-produced matrices as follows [67] ,

where


kowski to Euclidean spaces while instead requiring


The route of inquiring the concrete matrices following Cartan method as above could be a shortcut that rarely mentioned in literature. It is can be checked that the commutations among




We use 

examined by computer. Now we recognize that the role of operator 

is equivalent to the scaling operator D, with its unitary form
3. The Physical Relationship between the Two Representations of Scaling Transformation
Enlightened by Lorentz transformation, in this section we try to link physically the spatial form of scaling transformation with its spinor/unitary form, the former representing the realistic expansions and contractions of space-time (dilatation and shrinkage means the same), the latter representing the intrinsic freedom very like spin angular momentum. Considering both representations in a sole frame is the main feature of this paper.
As for a nonlocal interaction






the transformed result 

transformation, our goal in this section is to search for the corresponding vertex-form 
transformation 



erator D, and 
Usually we perform the spatial Lorentz transformation on the vectors 




where 


While looking for 


where formally we have used 



hermit one. With the relation


Now let’s substitute 

From the experience of calculating 



we find out a possible form of

The coefficients 



By this way we set up the relationship between the operator D and its unitary counterpart 
The key element of linking the two operators D and 



operator D is responsible for acting on the real vector coupling to




Now we are interested in what if we perform the scaling transformation 



from which one notes that the vector vertex arrives at its limits 






Apart from these two extremes, the true vertex-form for nonlocal interaction would mostly be of mixture form like 







4. The Conservation Law for the Scale-Invariant Interaction
The necessity of studying the conservation law for the extreme vertices is that such vertices might exist for a very short moment in some scattering processes. According to Equation (38), to repeatedly perform the transformation succeedingly until 



Figure 1. The physics picture of performing finite steps of scaling transformation.
from the vertex-form




From a classical point of view, while a “soft” body (with definite mass m) rotating, its shrinkage or inflation (like zooming in or out) would not alter its total orbital angular momentum. However for a quantum particle, its shrinkage or inflation occurs only when it absorbs or releases a certain amount of energy. Such kind of energy exchange of course breaks the angular-momentum conservation by intuition. But this intuition is right only partially, since in what follows we recognize that only spin part is varied, and the spatial angular momentum is not varied due to the commutation 
A newly similar consideration of the scaling symmetry appears in Ref. [17] , in which the authors discuss the scaling symmetry in 2-dimension system by using the light-cone quantum field method. And the work [44] [45] treat the scaling transformation based on a first principle form from Wilsonian method, in which some of the renormalization processes are repeated. Here we don’t follow it in details of renormalization. We focus more on the application of scaling feature of renormalization to nonlocal interaction, and also on what we can infer based on such application. Earlier before there had been other efforts to associate scaling transformation to quantum field theory. None of them is satisfactory since, no perfect quantum system is found so that the corresponding Lagrangian is scaling invariant unless, the mass of involved particles are null and, the trace of energy-momen- tum of the system becomes zero [55] -[60] . I think a reason is that they didn’t consider the spatial representation and spinor representation simultaneously. For the same reason in what follows we derive a conservation law different from those in literature.
While discussing conservation law, in Lagrangian there are at least two other additional terms to be involved, namely the kinetic term 


here the 


In summary the Lagrangian without mass term yields

where
Here we mainly investigate the conserved angular momentum for Equation (41) under the transformation set
the usual spatial transformation, i.e. the translations and rotations. These 4-dimensional spatial transformations with infinitesimal forms are

where 





in which the matrices elements 


Take 

one gets a general conserved current (known as the Nöether current) [69] relating to angular momentum,
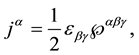
where

and

The current Equation (45) leads to angular momentum operator in four dimensions by

in which 

Since the orbital angular momentum is not affected by scaling transformation due to
only add the new ingredient 


(43). Thus the spinor part would vary with the change of


with

Since the part 





and we should caution that in the second term only the product of the constants 




Thus apart from the infinitesimal parameter

the constant 


Now it is evident that the angular momentum Equation (46) varies correspondingly with the transformation. In this sense we conclude that the nonlocal interaction entails the new internal freedom and becomes the particle intrinsic local property. Meanwhile it brings about the extrapolation of conventional spin angular-momentum. To put it in other words, the particles with shape and those point-like seem to follow different conservation laws.
For the extensive particles it is necessary to involve this correction term 
Thus when an extended particle (like proton) is smashed we shall not evaluate the polarizations of its initial state and its final state (smashed shreds of proton) in conventional way, since the initial state (proton) and the final states (smashed proton) all have their non-point size and thus the initial polarization might not be the sum of its final states (smashed proton) (Figure 2). Regarding this different conservation law may help us alleviate the spin crisis appearing in the polarized electron-nucleon scattering experiment [72] -[78] .
Figure 2. Schematic diagram for the colliding process between a point particle and an extended particle.
It has been a long-standing puzzle that how the nucleon spin originates from its constituent parts, namely, the angular momentum of quarks and gluons. The conflict arose from the estimation of the total spin of proton based on the experimental value of the antisymmetric structure function 







where






where the coefficients 


People once conceived gluons’ spin may contribute much to proton’s spin, but recent experimental analysis [85] supports merely small fraction of gluon’s contribution. Another recent flurry has been the focus on the decomposition of angular momentum of quark and gluon into spin part and orbital angular momentum part based on the gauge-invariant QCD dynamics [77] [83] [86] -[91] . But the ways to treat angular momentum of bounded quarks are so controversial that hitherto there has been no widely accepted scheme. In a very recent paper, Ji et al. [75] refined the sum rule using generalized parton distribution (GPD) method, which may improve further the evaluation of
Now let’s focus on the coefficients of 



in which 







5. The Impact of Vertex 
In this section we will discuss that after finite steps of scaling transformations, what is the contribution of the evolving vertex 




Firstly, let’s carry out the structure function of unpolarized cross-section by averaging over the initial spins and summing over the final spins [92] . Without losing generality, let’s suppose that it is the very case for an electron (a point fermion) incident on nucleon (an extended fermion) (Figure 3). By conventional steps, one finds that the evolving vertex-form 

and apart from the coefficient

and the result of the first term is well-known, it is

the second term is

and the third term results in the same

The last term has the same form as the first term, 

Figure 3. The Feynman graph for calculating the scattering cross-section for point particles, with the vertex- form
We note the new structure functions are from Equations (60), (61), whose contribution however, would vanish since the tensor 


Secondly, let’s consider the polarized cross-section. Now we do not fix the initial or the final spin states and leave the spin operator in the potential. With the same marks as in Figure 3 and without the propagator, we write the polarized amplitude (potential) by using the Dirac spinors as follows

Only the terms with coefficients 







where the indices 1, 2 represent respectively the first and the second particles. Substitute the concrete form of
Dirac spinor 


tion, and after lengthy calculation, it yields

here we use underlines to denote the inner product and

The second step follows while using the approximation 

approximation, one further gets

in the second step of the above equation we have used the following relations

and

Likewise, we obtain 

We note that the terms 

Lorentz-invariant currents




unless some of them are mixed. Thus we realize that 




We would like to present a simple gedanken experiment to test nonlocal effect due to the handedness terms, which are all proportional to helicity 

The proposed experiment is to use polarized electrons (or hydrogen atoms) colliding on polarized hydrogen- atom (polarized by magnetic field). Different from the previous calculations on polarized electron-electron (e-e) scattering [94] and e-H scattering [95] -[100] , the main results there are shown in Equations (67), (70), which is characterized by terms like




or

where




which has never been investigated in previous theoretical study [95] -[100] or experiments [101] -[104] . But this term may contribute even smaller fractions to total cross-section, since the sum of all spin-dependent terms have attributed just minor fraction in total cross-section. The calculation details can follow the paper [94] , concerning
additionally the present interaction. If any experiment gets a nontrivial parameter 



viate from former evaluations in literature if involving all of the handedness terms 
6. Conclusions and Discussions
In this paper we have discussed elaborately the role of scaling transformation in nonlocal interaction. This transformation pertains to describing the relationship of different energy/space-time scales in scattering between (fermion) hadrons. The scaling transformation is recognized/constructed based on the conclusions of RGM and the popular expressions of conformal group. The most significant feature of this paper is to combine its spinor representation 

tex 


vector vertex, 


Based on the knowledge that the transformation 

one finds the varying coefficients ahead of




We also call 

The extreme states as well as the extreme vertex may not exist in nature. However, by the inquiring and inferring process we recognize that the conformal group exists more like for running properties rather than for invariance of quantum fields. For an extended particle involved in a scattering at certain energy, we have to make corresponding scaling transformations to interpret locally its interaction vertex. Assume a nonlocal interaction interpreted initially/unphysically by exchanging vector bosons, then a general interaction-vertex 
Although the dynamics used in this paper mostly stems from the perturbative dynamics, it opens a door for our understanding to nonperturbative dynamics. There have been continuous efforts to study nonperturbative interaction ever since the birth of renormalization [106] -[108] . To apply somehow the scale parameter of renormalization to intermediate-strong-interaction was the primary goal of this paper. Furthermore an even stronger motivation is to develop an analytic non-perturbation method to understand such intermediate-strong-interaction. The motivation has driven us to apply transformation instead of solely the scale parameter to nonperturbative interactions. Some other nonlocal theories have made efforts to link the nonlocal interaction with renormalization, for instance in Ref. [6] [9] [31] [32] . But none of them used transformation method, which was laid there years before [109] [110] . In our results, the appearance of 

Acknowledgements
I am grateful to the hospitality of Prof. Y. B. Dong and Prof. P. Wang when I visited High Energy Institute of Chinese Academy, as well as the fruitful discussions with them. The Project Sponsored by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry and Fundamental Research Funds for the Central Universities.
References
- Ganor, O.J. (2007) Physical Review D, 75, Article ID: 025002. http://dx.doi.org/10.1103/PhysRevD.75.025002
- Minton, G. and Sahakian, V. (2008) Physical Review D, 77, Article ID: 026008. http://dx.doi.org/10.1103/PhysRevD.77.026008
- Fodor, Z. and Hoelbling, C. (2012) Reviews of Modern Physics, 84, 449-495. http://dx.doi.org/10.1103/RevModPhys.84.449
- Timofeyuk, N.K. and Johnson, R.C. (2013) Physical Review Letters, 110, Article ID: 112501. http://dx.doi.org/10.1103/PhysRevLett.110.112501
- Eliezer, D.A. and Woodard, R.P. (1989) Nuclear Physics B, 325, 389-469. http://dx.doi.org/10.1016/0550-3213(89)90461-6
- Moffat, J.W. (1989) Physical Review D, 39, 3654-3671. http://dx.doi.org/10.1103/PhysRevD.39.3654
- Evens, D., Moffat, J.W., Kleppe, G. and Woodard, R.P. (1991) Physical Review D, 43, 499-519. http://dx.doi.org/10.1103/PhysRevD.43.499
- Kleppe, G. and Woodard, R.P. (1992) Nuclear Physics B, 388, 81-112. http://dx.doi.org/10.1016/0550-3213(92)90546-N
- Moffat, J.W. (1990) Physical Review D, 41, 1177-1184. http://dx.doi.org/10.1103/PhysRevD.41.1177
- Neves, M.J., Farina, C. and Cougo-Pinto, M.V. (2010) Physical Review Letters, 105, Article ID: 211601. http://dx.doi.org/10.1103/PhysRevLett.105.211601
- Campo, D. (2010) arXiv:1004.5324. http://arxiv.org/abs/1004.5324
- Brüning, E. and Nagamachi, S. (2004) Journal of Mathematical Physics, 45, 2199. http://dx.doi.org/10.1063/1.1737055
- Haque, A. and Joglekar, S.D. (2009) Journal of Physics A: Mathematical and Theoretical, 42, Article ID: 065401. http://dx.doi.org/10.1088/1751-8113/42/6/065401
- Dowker, J.S. (2009) arXiv:0902.4180. http://arxiv.org/abs/0902.4180
- Barnaby, N. (2011) Nuclear Physics B, 845, 1-29. http://dx.doi.org/10.1016/j.nuclphysb.2010.11.016
- Calcagni, G., Montobbio, M. and Nardelli, G. (2008) Physics Letters B, 662, 285-289. http://dx.doi.org/10.1016/j.physletb.2008.03.024
- Hofman, D.M. and Strominger, A. (2011) Physical Review Letters, 107, Article ID: 161601. http://dx.doi.org/10.1103/PhysRevLett.107.161601
- Moffat, J.W. (2011) arXiv:1104.5706. http://arxiv.org/abs/1104.5706
- Zhou, L.-J., Wu, Q. and Ma, W.-X. (2008) Communications in Theoretical Physics, 50, 161-174. http://dx.doi.org/10.1088/0253-6102/50/1/33
- Pimikov, A.V., Bakulev, A.P. and Stefanis, N.G. (2010) Nuclear Physics B―Proceedings Supplements, 198, 182-185. Also at arXiv:0909.4624v1 [hep-ph].
- Wataghin, G. (1934) Zeitschrift für Physik, 88, 92-98. http://dx.doi.org/10.1007/BF01352311
- Yukawa, H. (1950) Physical Review, 80, 1047-1052. (ibid, 77, 849 (1950); ibid 76, 300 (1949))
- Yennie, D.R. (1950) Physical Review, 80, 1053-1061. http://dx.doi.org/10.1103/PhysRev.80.1053
- Kristensen, P., Moller, C. and Dan, K. (1952) Vidensk. Selsk. Mat.-Fys. Medd., 27.
- Bloch, C. and Dan, K. (1952) Vidensk. Selsk. Mat.-Fys. Medd., 27.
- Pauli, W. (1953) Il Nuovo Cimento, 10, 648-667. http://dx.doi.org/10.1007/BF02815288
- Hayashi, C. (1953) Progress of Theoretical Physics, 10, 533-548. ibid, 11, 226 (1954).
- Lee, T.D. and Yang, C.N. (1957) Physical Review, 108, 1611-1614. http://dx.doi.org/10.1103/PhysRev.108.1611
- Dirac, P.A.M. (1962) Proceedings of the Royal Society A, 268, 57-67. http://dx.doi.org/10.1098/rspa.1962.0124
- Kirzhnits, D.A. (1967) Soviet Physics Uspekhi, 9, 692-700. Translated from Uspekhi Fizicheskikh Nauk, 90, 129-142. (Sep. 1966).
- Efimov, G.V. (1967) Communications in Mathematical Physics, 5, 42-56. http://dx.doi.org/10.1007/BF01646357
- Efimov, G.V. (1972) Annals of Physics, 71, 466-485. http://dx.doi.org/10.1016/0003-4916(72)90127-3
- Alebastrov, V.A. and Efimov, G.V. (1973) Communications in Mathematical Physics, 31, 1-24. http://dx.doi.org/10.1007/BF01645588
- Alebastrov, V.A., Efimov, G.V. and Seltzer, S.Z. (1973) Annals of Physics, 76, 251-280. http://dx.doi.org/10.1016/0003-4916(73)90450-8
- Bloch, C. and Dan, K. (1950) Vidensk. Selsk. Mat.-Fys. Medd, 26.
- Marnelius, R. (1974) Physical Review D, 10, 3411. (Equation (2.3) and Equation (2.8); ibid, 8, 2472 (1973))
- Yang, C.N. and Feldman, D. (1950) Physical Review, 79, 972-978. http://dx.doi.org/10.1103/PhysRev.79.972
- Kleppe, G. and Woodard, R.P. (1992) Nuclear Physics B, 388, 81-112. http://dx.doi.org/10.1016/0550-3213(92)90546-N
- Clayton, M.A. (2001) Modern Physics Letters A, 16, 1117-1127. http://dx.doi.org/10.1142/S0217732301004327
- Calian, V. and Stoenescu, G. (2000) arXiv:hep-th/0011163. http://arxiv.org/abs/hep-th/0011163
- Raje Bhageerathi, P.C. and Eapen, K. (1998) International Journal of Modern Physics A, 13, 797-829. http://dx.doi.org/10.1142/S0217751X98000354
- Kleppe, G. and Woodard, R.P. (1993) Annals of Physics, 221, 106-164. http://dx.doi.org/10.1006/aphy.1993.1006
- Wang, P. (2011) Chinese Physics C, 35, 223-227. http://dx.doi.org/10.1088/1674-1137/35/3/003
- Cubero, A.C. and Orland, P. (2011) Physical Review D, 84, Article ID: 065034. http://dx.doi.org/10.1103/PhysRevD.84.065034
- Orland, P. and Xiao, J. (2009) Physical Review D, 80, Article ID: 016005. http://dx.doi.org/10.1103/PhysRevD.80.016005
- Su, J.-C., Yi, X.-X. and Cao, Y.-H. (1999) Journal of Physics G: Nuclear and Particle Physics, 25, 2325-2344. http://dx.doi.org/10.1088/0954-3899/25/12/303
- Su, J.-C. and Wang, H.-J. (2004) Physical Review C, 70, Article ID: 044003. http://dx.doi.org/10.1103/PhysRevC.70.044003
- Arrington, J., Blunden, P.G. and Melnitchouk, W. (2011) Progress in Particle and Nuclear Physics, 66, 782-833. http://dx.doi.org/10.1016/j.ppnp.2011.07.003
- Cloet, I.C., Roberts, C.D. and Thomas, A.W. (2013) Physical Review Letters, 111, Article ID: 101803. http://dx.doi.org/10.1103/PhysRevLett.111.101803
- Callan Jr., C.G. (1970) Physical Review D, 2, 1541-1547. http://dx.doi.org/10.1103/PhysRevD.2.1541
- Symanzik, K. (1970) Communications in Mathematical Physics, 18, 227-246. http://dx.doi.org/10.1007/BF01649434
- Budini, P. (1979) Czechoslovak Journal of Physics B, 29, 6-21.
- Bateman, H. (1910) Proceedings of the London Mathematical Society, s2-8, 223-264. http://dx.doi.org/10.1112/plms/s2-8.1.223
- Cunningham, E. (1910) Proceedings of the London Mathematical Society, s2-8, 77-98. http://dx.doi.org/10.1112/plms/s2-8.1.77
- Polchinski, J. (1988) Nuclear Physics B, 303, 226-236. http://dx.doi.org/10.1016/0550-3213(88)90179-4
- Nakayama, Y. (2013) arXiv:1302.0884 [hep-th]. http://arxiv.org/abs/1302.0884
- Gross, D.J. and Wess, J. (1970) Physical Review D, 2, 753-764. http://dx.doi.org/10.1103/PhysRevD.2.753
- Kastrup, H.A. (2008) Annalen der Physik, 17, 631-690. http://dx.doi.org/10.1002/andp.200810324
- Dirac, P.A.M. (1935) Annals of Mathematics, 37, 429-442. http://dx.doi.org/10.2307/1968455
- Luscher, M. and Mack, G. (1975) Communications in Mathematical Physics, 41, 203-234. http://dx.doi.org/10.1007/BF01608988
- Mack, G. and Salam, A. (1969) Annals of Physics, 53, 174-202. http://dx.doi.org/10.1016/0003-4916(69)90278-4
- Ryder, L.H. (1974) Journal of Physics A: Mathematical, Nuclear and General, 7, 1817-1828. http://dx.doi.org/10.1088/0305-4470/7/15/005
- Wheeler, J.A. and Feynman, R.P. (1945) Reviews of Modern Physics, 17, 157-181. (ibid, 21, 425 (1949))
- Budini, P., Furlan, P. and Raczka, R. (1979) IL Nuovo Cimento A, 52, 191-246. (21 Luglio 1979)
- Cartan, E. (1981) The Theory of Spinors. Dover Publications, Inc., Mineola. (This Is a Republication of the First Version Published by Hermann, Paris, 1966)
- Liu, Y.F., Ma, Z.Q. and Hou, B.Y. (1999) Communications in Theoretical Physics, 31, 481-490. http://dx.doi.org/10.1088/0253-6102/31/4/481
- Esteve, A. and Sona, P.G. (1964) IL Nuovo Cimento, 32, 473-485. http://dx.doi.org/10.1007/BF02733974
- Feynman, R.P. (1962) Quantum Electrodynamics―A Lecture Note and Preprint Volume. W. A. Benjamin, Inc., 44. (please refer to the Tenth Lecture on Equivalence Transformation)
- Mandl, F. and Shaw, G. (2010) Quantum Field Theory. 2nd Edition, John Wiley and Sons, Ltd., Hoboken. (page 93, Section 2.4 and Appendix A.7)
- Lurie, D. (1968) Particles and Fields. John Wiley and Sons, Inc., Hoboken. (Please refer to Eqs. (8.18)~(8.29) and context around)
- Scalum turns out to be a new inner degree of freedom. Yukawa and Yennie once contemplated that there should appear new “inner motion” degree of freedom in a nonlocal system, later it proved to be trivial due to their wrongly interpreting manner.
- Leader, E. (2011) Physical Review D, 83, Article ID: 096012. http://dx.doi.org/10.1103/PhysRevD.83.096012
- Wang, F., Chen, X.S., Lu, X.F., Sun, W.M. and Goldman, T. (2008) Physical Review Letters, 100, Article ID: 232002.
- Chen, X.-S., Sun, W.-M., Wang, F. and Goldman, T. (2011) Physical Review D, 83, Article ID: 071901.
- Ji, X.D., Xiong, X.N. and Yuan, F. (2012) Physical Review Letters, 109, Article ID: 152005. http://dx.doi.org/10.1103/PhysRevLett.109.152005
- Ji, X.D. (1997) Physical Review D, 55, 7114-7125. http://dx.doi.org/10.1103/PhysRevD.55.7114
- Ji, X.D. (1997) Physical Review Letters, 78, 610-613. http://dx.doi.org/10.1103/PhysRevLett.78.610
- Ma, B.Q. (1991) Journal of Physics G, 17, L53-L58. http://dx.doi.org/10.1088/0954-3899/17/5/001
- Kodaira, J., Matsuda, S., Muta, T., Uematsu, T. and Sasaki, K. (1979) Physical Review D, 20, 627-629. http://dx.doi.org/10.1103/PhysRevD.20.627
- Jaffe, R.L. (1995) Physics Today, 48, 24. http://dx.doi.org/10.1063/1.881473
- Kodaira, J., Matsuda, S., Sasaki, K. and Uematsu, T. (1979) Nuclear Physics B, 159, 99-124. http://dx.doi.org/10.1016/0550-3213(79)90329-8
- Bass, S.D. (2005) Reviews of Modern Physics, 77, 1257-1302.
- Jaffe, R.L. and Manohar, A. (1990) Nuclear Physics B, 337, 509-546. http://dx.doi.org/10.1016/0550-3213(90)90506-9
- Myhrer, F. and Thomas, A.W. (2010) Journal of Physics G: Nuclear and Particle Physics, 37, Article ID: 023101. http://dx.doi.org/10.1088/0954-3899/37/2/023101
- de Florian, D., Sassot, R., Stratmann, M. and Vogelsang, W. (2008) Physical Review Letters, 101, Article ID: 072001.
- Chen, X.S., Lu, X.F., Sun, W.M., Wang, F. and Goldman, T. (2008) Physical Review Letters, 100, Article ID: 232002. http://dx.doi.org/10.1103/PhysRevLett.100.232002
- Chen, X.S., Sun, W.M., Lu, X.F., Wang, F. and Goldman, T. (2009) Physical Review Letters, 103, Article ID: 062001. http://dx.doi.org/10.1103/PhysRevLett.103.062001
- Lorcé, C. (2013) Physical Review D, 87, Article ID: 034031. http://dx.doi.org/10.1103/PhysRevD.87.034031
- Wakamatsu, M. (2010) Physical Review D, 81, Article ID: 114010. http://dx.doi.org/10.1103/PhysRevD.81.114010
- Wakamatsu, M. (2011) Physical Review D, 83, Article ID: 014012. http://dx.doi.org/10.1103/PhysRevD.83.014012
- Hatta, Y. (2011) Physical Review D, 84, Article ID: 041701. http://dx.doi.org/10.1103/PhysRevD.84.041701
- Greiner, W., Schramm, S. and Stein, E. (2007) Quantum Chromodynamics. Third Revised and Enlarged Edition, Springer-Verlag, Berlin, Heidelberg and New York, 80-87.
- Su, J.C., Dong, Y.B. and Wu, S.S. (1992) Journal of Physics G: Nuclear and Particle Physics, 18, 1347-1354. http://dx.doi.org/10.1088/0954-3899/18/8/009
- Wang, H.-J. and Geng, W.T. (2007) Journal of Physics A: Mathematical and Theoretical, 40, 11617-11625. http://dx.doi.org/10.1088/1751-8113/40/38/012
- Blum, K. and Kleinpoppen, H. (1975) International Journal of Quantum Chemistry, 9, 415-424. http://dx.doi.org/10.1002/qua.560090851
- van Wyngaarden, W.L. and Walters, H.R.J. (1986) Journal of Physics B: Atomic and Molecular Physics, 19, 1827- 1842. http://dx.doi.org/10.1088/0022-3700/19/12/021
- Kelsey, E.J. (1979) Physical Review A, 19, 1062-1066. http://dx.doi.org/10.1103/PhysRevA.19.1062
- Edmunds, P.W., McDowell, M.R.C. and van de Ree, J. (1983) Journal of Physics B: Atomic and Molecular Physics, 16, L453-L458. http://dx.doi.org/10.1088/0022-3700/16/15/006
- Burke, P.G. and Schey, H.M. (1962) Physical Review, 126, C163-C168. http://dx.doi.org/10.1103/PhysRev.126.163
- Ohmura, T., Hara, Y. and Yamanouchi, T. (1958) Progress of Theoretical Physics, 20, 82-88. http://dx.doi.org/10.1143/PTP.20.82
- Crowe, D.M., Guo, X.Q., Lubell, M.S., Slevin, J. and Eminyan, M. (1990) Journal of Physics B: Atomic, Molecular and Optical Physics, 23, L325-L331. http://dx.doi.org/10.1088/0953-4075/23/13/010
- Fletcher, G.D., Alguard, M.J., Gay, T.J., Hughes, V.W., Tu, C.W., Wainwright, P.F., et al. (1982) Physical Review Letters, 48, 1671-1674. http://dx.doi.org/10.1103/PhysRevLett.48.1671
- Williams, J.F. (1975) Journal of Physics B: Atomic and Molecular Physics, 8, 1683-1692. http://dx.doi.org/10.1088/0022-3700/8/10/018
- Gay, T.J., Fletcher, G.D., Alguard, M.J., Hughes, V.W., Wainwright, P.F. and Lubell, M.S. (1982) Physical Review A, 26, 3664-3667. http://dx.doi.org/10.1103/PhysRevA.26.3664
- Wang, H.-J. (2008) Journal of Mathematical Physics, 49, Article ID: 033513. http://dx.doi.org/10.1063/1.2874556
- Mastropietro, V. (2008) Non-Perturbative Renormalization. World Scientific Publishing Co. Pte. Ltd., Singapore.
- Berges, J., Tetradis, N. and Wetterich, C. (2002) Physics Reports, 363, 223-386. http://dx.doi.org/10.1016/S0370-1573(01)00098-9
- Wang, D. and Bao, A.D. (2013) Journal of Modern Physics, 4, 35-38. http://dx.doi.org/10.4236/jmp.2013.41007
- Greenberger, D.M. (1963) Annals of Physics, 25, 290-308. http://dx.doi.org/10.1016/0003-4916(63)90015-0
- Takahashi, Y. (1971) Physical Review D, 3, 622-625. http://dx.doi.org/10.1103/PhysRevD.3.622









