Journal of Modern Physics
Vol.4 No.2(2013), Article ID:28342,5 pages DOI:10.4236/jmp.2013.42038
Critical Exponents of Quark Matter
Engineering Science Department, University of Tehran, Tehran, Iran
Email: gholizade@ut.ac.ir
Received November 21, 2012; revised December 20, 2012; accepted December 29, 2012
Keywords: Quark Matter; Critical Exponents; Exchange Interaction
ABSTRACT
I investigate the ferromagnetic phase transition inside strong quark matter (SQM) with one gluon exchange interaction between strong quarks. I use a variational method and the Landau-Fermi liquid theory and obtain the thermodynamics quantities of SQM. In the low temperature limit, the equation of state (EOS) and critical exponents for the second-order phase transition (ferromagnetic phase transition) in SQM are analytically calculated. The results are in agreement with the Ginzberg-Landau theory.
1. Introduction
The properties of Fermi systems have been investigated in several works [1-20]. One of the important cases is the study of the magnetic properties of an electron gas [3-20]. Spontaneous magnetization may appear at different densities for different temperatures and the polarization of the system is a function of the density and temperature. By assuming a spin-spin interaction inside the system, we can study its magnetic properties. For gaseous systems, statistical methods for an imperfect Fermi gas show that the system can be in its ferromagnetic phase [21-23]. All relations are written in the non-relativistic and low temperature limit, because in the ultra-relativistic region , the polarized states have greater energy than the un-polarized states [24,25]. The low temperature domain characteristic is Fermi energy of system. If the Fermi energy of system is greater than thermal energy, then we can use the low temperature limit. In SQM, the order of Fermi energy is greater than 20 MeV [25]; and low temperature means
, the polarized states have greater energy than the un-polarized states [24,25]. The low temperature domain characteristic is Fermi energy of system. If the Fermi energy of system is greater than thermal energy, then we can use the low temperature limit. In SQM, the order of Fermi energy is greater than 20 MeV [25]; and low temperature means  MeV. Therefore, the ferromagnetic phase can appear in the non-relativistic region [25]. Therefore only strange quarks are involved and the results of the present paper are applicable to SQM (The reason will be explained in Section II). The resulting scattering matrix elements in the non-relativistic region automatically have spin-dependent terms and we do not insert the spin-spin interaction manually [26]. I use a variational approach [27-35] to obtain the equation of state of the system. By varying the free energy with respect to p (the polarization parameter) and the effective mass at various densities and temperatures, we can minimize the free energy for a given density and temperature.
MeV. Therefore, the ferromagnetic phase can appear in the non-relativistic region [25]. Therefore only strange quarks are involved and the results of the present paper are applicable to SQM (The reason will be explained in Section II). The resulting scattering matrix elements in the non-relativistic region automatically have spin-dependent terms and we do not insert the spin-spin interaction manually [26]. I use a variational approach [27-35] to obtain the equation of state of the system. By varying the free energy with respect to p (the polarization parameter) and the effective mass at various densities and temperatures, we can minimize the free energy for a given density and temperature.
2. Exchange and Direct Contributions to the Energy Density
The Landau-Fermi liquid interaction function is related to the Lorentz invariant matrix element via
 (1)
(1)
If 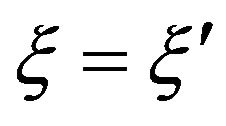 (parallel spins), we have the spin non-flip interaction and if
(parallel spins), we have the spin non-flip interaction and if 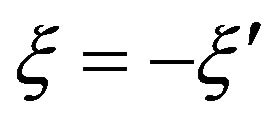 (antiparallel spins), we have the flip interaction. So the exchange energy density for the flip and non-flip interactions can be written as
(antiparallel spins), we have the flip interaction. So the exchange energy density for the flip and non-flip interactions can be written as
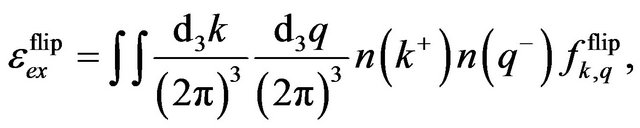 (2)
(2)
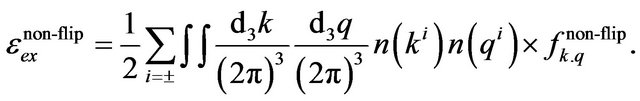 (3)
(3)
In the above equations,  correspond to
correspond to
 (4)
(4)
where the 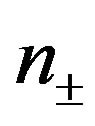 and p are the density of the spin up and spin down electrons and the polarization parameter, respectively.
and p are the density of the spin up and spin down electrons and the polarization parameter, respectively. 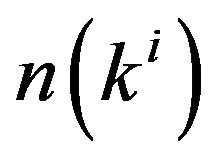 is the Fermi distribution functions. In the non-relativistic region, we can use the approximation
is the Fermi distribution functions. In the non-relativistic region, we can use the approximation  and then we have [23]
and then we have [23]
 (5)
(5)
Using Equation (5), if we have  then the Lorentz invariant matrix elements vanish, which means that in the non-relativistic region the spin flip contribution to the energy density vanishes. The spin non-flip exchange and kinetic energy density in the non-relativistic case at zero temperature is
then the Lorentz invariant matrix elements vanish, which means that in the non-relativistic region the spin flip contribution to the energy density vanishes. The spin non-flip exchange and kinetic energy density in the non-relativistic case at zero temperature is 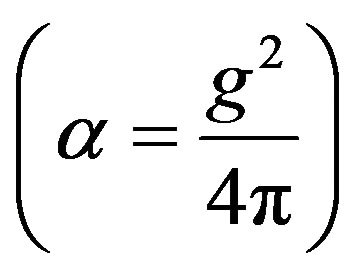
 (6)
(6)
In the ultra-relativistic region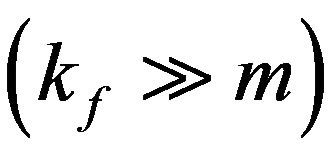 , the exchange energy density is proportional to
, the exchange energy density is proportional to
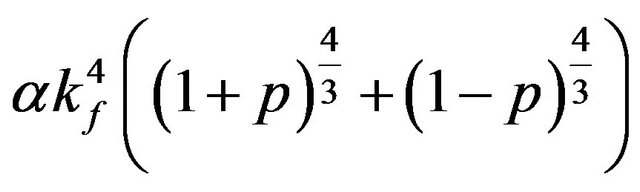 [24] and the kinetic energy is also proportional to
[24] and the kinetic energy is also proportional to . Thereforethe un-polarized state is energetically favorable and we will write all equations in the non-relativistic limit.
. Thereforethe un-polarized state is energetically favorable and we will write all equations in the non-relativistic limit.
3. Equation of State at Low Temperature
To obtain the equation of state at low temperature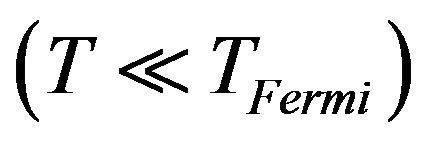 , I use the variational method with the following approximation to the single particle energy in the Fermi distribution function [2,27,35]:
, I use the variational method with the following approximation to the single particle energy in the Fermi distribution function [2,27,35]:
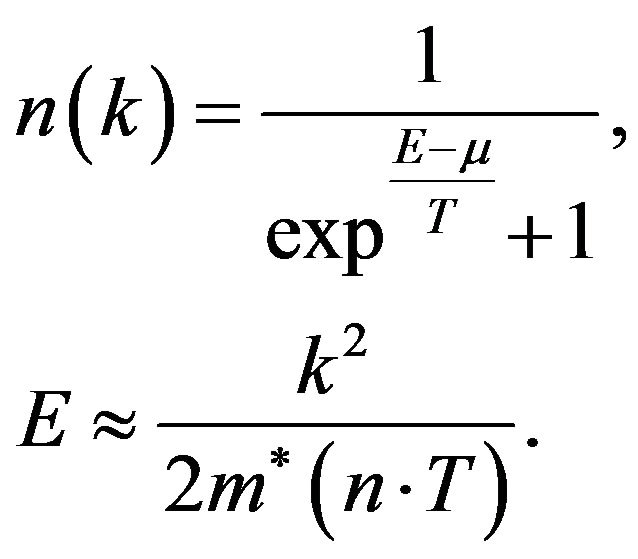 (7)
(7)
Using the above approximation, I use the redefined kinetic energy instead of the sum of kinetic and potential energy in the distribution function, and the kinetic energy in the other parts of the equations remains unchanged [2, 27,33,35]. For a fully polarized state p = 1 and an unpolarized state p = 0, I can describe the system with a single effective mass and chemical potential. For partially polarized states , we must use separate effective masses and chemical potentials for the spin up and spin down states. If we use the following relation,
, we must use separate effective masses and chemical potentials for the spin up and spin down states. If we use the following relation,
 (8)
(8)
(where  is the Lerch Phi function), we can write the kinetic energy as:
is the Lerch Phi function), we can write the kinetic energy as:
 (9)
(9)
To obtain the kinetic energy at low temperature, we use the relations
 (10)
(10)
Here, ± refers to spin up and down states. If we use the low temperature expansion of the chemical potential, then we have:
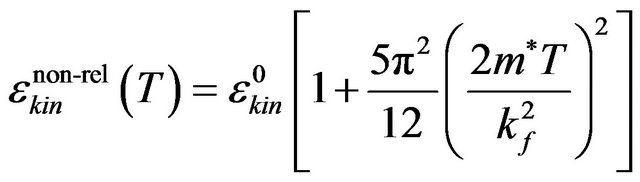 (11)
(11)
In Equation (11), 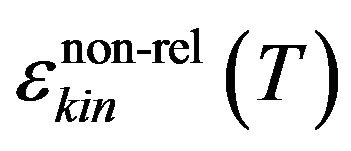 is the kinetic energy density of the system. Similar to the above, the exchange energy and entropy density of the system become
is the kinetic energy density of the system. Similar to the above, the exchange energy and entropy density of the system become
 (12)
(12)
Here, 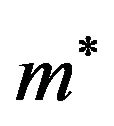 ,
, 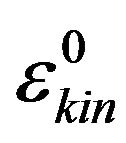 , and
, and 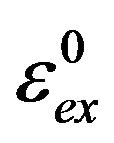 are the effective mass of the electrons, the non-relativistic kinetic and exchange energies at zero temperature, respectively. Using the results of Equation (12), it follows that the free energy density is
are the effective mass of the electrons, the non-relativistic kinetic and exchange energies at zero temperature, respectively. Using the results of Equation (12), it follows that the free energy density is
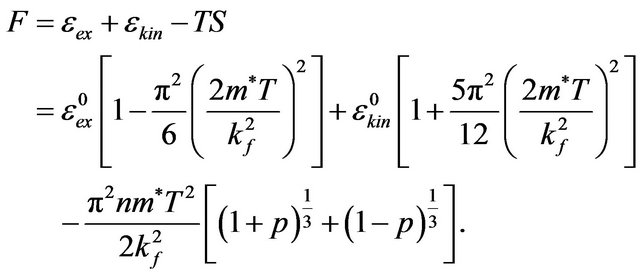 (13)
(13)
By minimizing the free energy, one can find  as a function of p:
as a function of p:
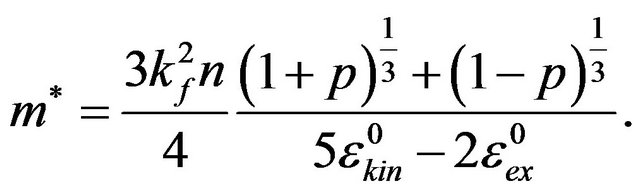 (14)
(14)
For p = 0 and non-interacting systems, Equation (14) simply yields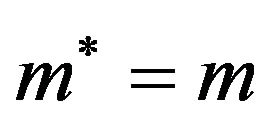 . We must notice here that if we set
. We must notice here that if we set  (non-interacting system), then p = 0. At zero temperature, minimization of the free energy becomes simpler, and one obtains
(non-interacting system), then p = 0. At zero temperature, minimization of the free energy becomes simpler, and one obtains
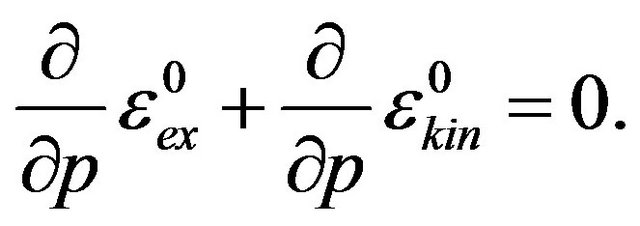 (15)
(15)
The resulting equation from Equation (15) is
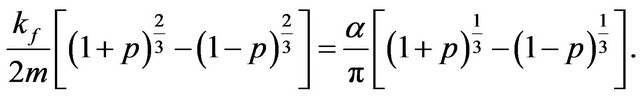 (16)
(16)
This result is very similar to the well-known results of the spontaneous magnetization of an imperfect Fermi gas [21]. But in our calculation, the interaction part of the Hamiltonian is not independent of the spin alignment, and this dependence changes the right side of Equation (16).
4. Critical Exponents
Similar to previous work on a Fermi gas [36], solving Equation (16) yields Figure 1. Also the results for nonzero temperature are similar to the results of [36]. Here I am interested in the density and temperature dependence of the polarization parameter and the other thermodynamic quantities. At zero temperature, we can expand the magnetic susceptibility 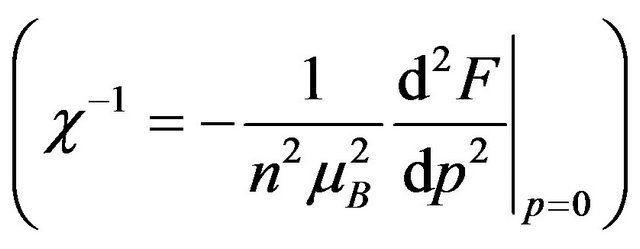 as follows:
as follows:
 (17)
(17)
As , the first term in Equation (17) becomes zero. So
, the first term in Equation (17) becomes zero. So
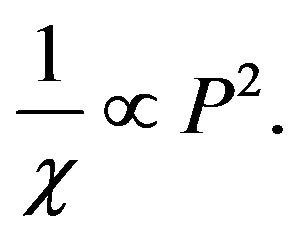 (18)
(18)
The magnetization is proportional to the polarization (p). The relation between 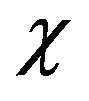 and the magnetization
and the magnetization  and magnetic field (J) is
and magnetic field (J) is
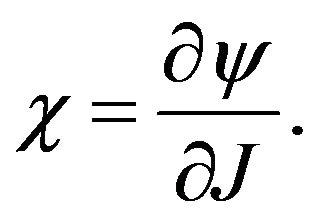 (19)
(19)
At  we have
we have
 (20)
(20)
Using (18) and (19), we find that . At non-zero temperature and
. At non-zero temperature and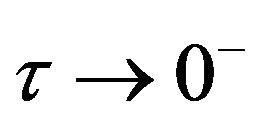 , we have
, we have
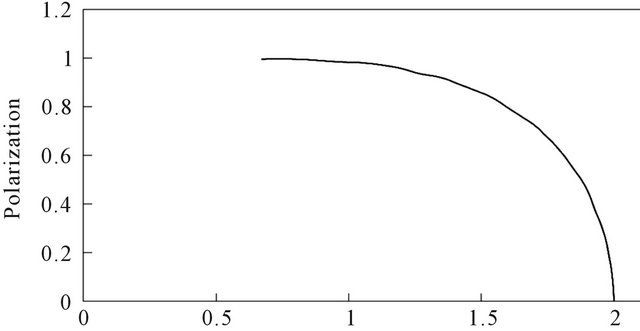

Figure 1. The polarization as a function of the Fermi momentum and coupling constant.
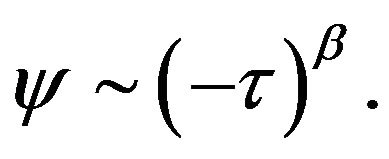 (21)
(21)
Expanding 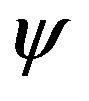 near
near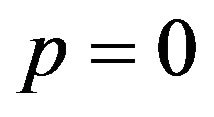 , we find
, we find
 (22)
(22)
So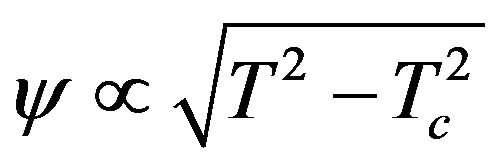 . As
. As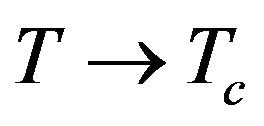 , we have
, we have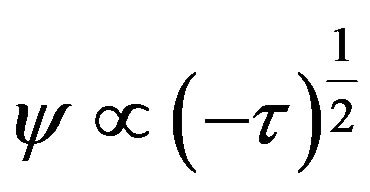 . Comparing with Equation (21), we find that
. Comparing with Equation (21), we find that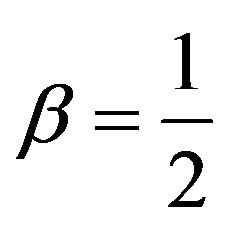 . It can be seen that the heat capacity
. It can be seen that the heat capacity 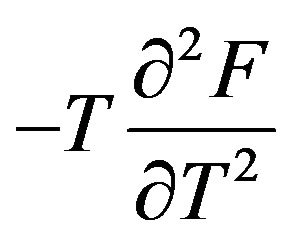 does not depend on
does not depend on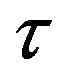 , so we have
, so we have .
.
5. Results and Discussion
I use the variational approach to obtain the critical exponents of quark matter. The method is based on the minimization of the free energy (corresponding to maximum entropy at equilibrium). Using this method, Fermi systems, such as an electron gas or quark matter, can be in a ferromagnetic phase for a specific value of the density and temperature. For quark matter, this can be happen at low temperature and high density. For SQM in chemical equilibrium, the density of the u, d, and s quarks can be calculated from the weak interactions between quarks [25]. The up and down quarks are in the ultra-relativistic region (because of their small mass) and only the s quarks can be in the ferromagnetic phase [25]. Therefore, all equations are for strange quarks. This phase transition is second order [36] and one can calculate the critical exponents of this phase transition. The results are the same as for the Landau mean field theory.
6. Acknowledgements
I would like to thank the Research Council of the University of Tehran and the Institute for Research and Planning in Higher Education for financial support under contract No. 138-569.
REFERENCES
- T. Tatsumi and K. Sato, “Non-Fermi-Liquid Effect in Magnetic Susceptibility,” Physics Letters B, Vol. 672, No. 2, 2009, pp. 132-135. doi:10.1016/j.physletb.2008.12.064
- M. Bigdeli, G. H. Bordbar and Z. Rezaei, “Temperature Dependence of Magnetic Susceptibility of Nuclear Matter: Lowest Order Constrained Variational Calculations,” Physical Review C, Vol. 80, No. 3, 2009, 8 p. doi:10.1103/PhysRevC.80.034310
- Y. Zhang and D. Sarama, “Exchange Instabilities in Electron Systems: Bloch versus Stoner Ferromagnetism,” Physical Review B, Vol. 72, No. 11, 2005, 9 p. doi:10.1103/PhysRevB.72.115317
- S. Ciccariello and A. De Col, “Zero-Temperature Perturbative Calculation of the Magnetic Susceptibility of the Free Fermion System,” European Journal of Physics, Vol. 22, No. 6, 2001, pp. 629-637. doi:10.1088/0143-0807/22/6/308
- A. Uldry and R. J. Elliott, “The Two-Particle Propagator and Magnetic Susceptibility in the Hubbard Model,” Journal of Physics, Vol. 17, No. 19, 2005, p. 2903.
- M. Ulmke, “Ferromagnetism in the Hubbard Model on Fcc-Type Lattices,” European Physics Journal B1, Vol. 1, No. 3, 1998, pp. 301-304. doi:10.1007/s100510050186
- D. Bodea, M. Crisan, I. Grosu and I. Tifrea, “Large n-Expansion Limit of the Three-Dimensional Ferromagnetic Quantum Phase Transition,” Journal of Low Temperature Physics, Vol. 146, No. 3-4, 2007, pp. 315-327. doi:10.1007/s10909-006-9251-3
- E. M. Chudnovsky, “Magnetic Susceptibility of Relativistic Fermi Gas,” Journal Physics A, Vol. 14, No. 8, 1981, pp. 2091. doi:10.1088/0305-4470/14/8/030
- V. T. Rajan, “Magnetic Susceptibility and Specific Heat of the Coqblin-Schrieffer Model,” Physical Review Letters, Vol. 51, No. 4, 1983, pp. 308-311. doi:10.1103/PhysRevLett.51.308
- L. Homorodean, “Magnetic Susceptibility of the Relativistic Boson Gas,” Modern Physics Letters B, Vol. 15, No. 25, 2001, p. 1147. doi:10.1142/S021798490100283X
- T. M. A. Khajil, “Magnetic Susceptibility of Liquid Metals,” International Journal of Modern Physics B, Vol. 16, No. 1, 2002, p. 2221. doi:10.1142/S0217979202011160
- N. Holden, B. T. Matthias, P. W. Anderson and H. W. Lewis, “New Low-Temperature Ferromagnets,” Physical Review, Vol. 102, No. 6, 1956, p. 1463. doi:10.1103/PhysRev.102.1463
- T. Izuyama, “General Theorems on Ferromagnetism and Ferromagnetic Spin Waves,” Physical Review B, Vol. 5, No. 1, 1972, pp. 190-203. doi:10.1103/PhysRevB.5.190
- K. Rajagopal and S. D. Mahanti, “Ferromagnetism of an Electron Gas,” Physical Review, Vol. 158, No. 2, 1967, pp. 353-355. doi:10.1103/PhysRev.158.353
- G. Fabricius and A. M. Llois, “Ferromagnetic Stability and Density of States,” Physical Review B, Vol. 48, No. 9, 1993, pp. 6665-6667. doi:10.1103/PhysRevB.48.6665
- P. C. Hemmer and D. Imbro, “Ferromagnetic Fluids,” Physical Review A, Vol. 16, No. 1, 1977, pp. 380-386. doi:10.1103/PhysRevA.16.380
- Baladie and A. Buzdin, “Thermodynamic Properties of Ferromagnet/Superconductor/Ferromagnet Nanostructures,” Physical Review B, Vol. 67, No. 1, 2003, 9 p. doi:10.1103/PhysRevB.67.014523
- Y. Kwon, D. M. Ceperly and R. M. Martin, “Quantum Monte Carlo Calculation of the Fermi-Liquid Parameters in the Two-Dimensional Electron Gas,” Physical Review B, Vol. 50, No. 3, 1994, p. 1684-1694. doi:10.1103/PhysRevB.50.1684
- C. Attaccalite, S. Moroni, P. G. Giorgi and G. B. Bachelet, “Correlation Energy and Spin Polarization in the 2D Electron Gas,” Physical Review Letters, Vol. 88, No. 25, 2002, Article ID: 256601.
- C. Attaccalite, S. Moroni, P. G. Giorgi and G. B. Bachelet, “Two-Dimensional Electron Gas: Correlation Energy versus Density and Spin Polarization,” International Journal of Quantum Chemistry, Vol. 91, No. 2, 2003, pp. 126- 130.
- K. Huang, “Statistical Mechanics,” 2nd Edition, John Wiley & Sons Ltd., Hoboken, 1987.
- Landau and E. Lifshitz, “Statistical Physics Part II,” 3rd Edition, Pergamon Press, Oxford, 1988.
- T. Tatsumi, “Ferromagnetism of Quark Liquid,” Physical Letters B, Vol. 489, No. 3-4, 2000, pp. 280-286. doi:10.1016/S0370-2693(00)00927-8
- G. Baym and S. A. Chin, “Landau Theory of Relativistic Fermi Liquids,” Nuclear Physics A, Vol. 262, No. 3, 1976, pp. 527-538. doi:10.1016/0375-9474(76)90513-3
- M. Modarres and H. Gholizade, “The Ferromagnetic Phase of Quark Matter in the Framework of One Gluon Exchange and Thermodynamics with the Density— Temperature-Dependent Particle Mass Mode,” Physica A: Statistical Mechanics and Its Applications, Vol. 387, No. 12, 2008, pp. 2761-2776. doi:10.1016/j.physa.2008.01.104
- J. Sakurai, “Advanced Quantum Mechanics,” Pearson, London, 1967.
- H. Kanzawa, K. Oyamatsu, K. Sumiyoshi and M. Takano, “Variational Calculation for the Equation of State of Nuclear Matter at Finite Temperatures,” Nuclear Physics A, Vol. 791, No. 1-2, 2007, pp. 232-250. doi:10.1016/j.nuclphysa.2007.01.098
- J. W. Clark, “Variational Theory of Nuclear Matter,” Progress in Particle and Nuclear Physics, Vol. 2, 1979, pp. 89-199. doi:10.1016/0146-6410(79)90004-8
- A. Akmal, V. R. Pandharipande and D. G. Ravenhall, “Equation of State of Nucleon Matter and Neutron Star Structure,” Physical Review C, Vol. 58, No. 3, 1998, pp. 1804-1828. doi:10.1103/PhysRevC.58.1804
- R. B. Wiringa, V. G. J. Stokes and R. Schiavilla, “Accurate Nucleon-Nucleon Potential with Charge-Independence Breaking,” Physical Review C, Vol. 51, No. 3, 1995, pp. 38-51. doi:10.1103/PhysRevC.51.38
- B. S. Pudliner, V. R. Pandharipande, J. Carlson and R. B. Wiringa, “Quantum Monte Carlo Calculations of A ≤6 Nuclei,” Physical Review Letters, Vol. 74, No. 22, 1995, pp. 4396-4399. doi:10.1103/PhysRevLett.74.4396
- V. R. Pandharipande and R. B. Wiringa, “Variations on a Theme of Nuclear Matter,” Review Modern Physics, Vol. 51, No. 4, 1979, pp. 821-861. doi:10.1103/RevModPhys.51.821
- B. Friedman and V. R. Pandharipande, “Hot and Cold, Nuclear and Neutron Matter,” Nuclear Physics A, Vol. 361, No. 2, 1981, pp. 502-520. doi:10.1016/0375-9474(81)90649-7
- K. E. Schmidt and V. R. Pandharipande, “Variational Theory of Nuclear Matter at Finite Temperatures,” Physics Letters B, Vol. 87, No. 1-2, 1979, pp. 11-14. doi:10.1016/0370-2693(79)90004-2
- M. Modarres, “LOCV Calculations of Pressure in Nuclear Matter at Finite Temperature,” Journal of Physics G: Nuclear and Particle Physics, Vol. 19, No. 9, 1993, pp. 1349-1358. doi:10.1088/0954-3899/19/9/013
- H. Gholizade and D. Momeni, “Stability of Landau Fermi Liquid Theory,” Journal of Statistical Physics, Vol. 141, No. 6, 2010, pp. 957-969. doi:10.1007/s10955-010-0091-9

