Journal of Modern Physics
Vol.3 No.9A(2012), Article ID:23110,8 pages DOI:10.4236/jmp.2012.329161
Approximation Method for the Relaxed Covariant Form of the Gravitational Field Equations for Particles
FaMAF, Universidad Nacional de Córdoba, Instituto de Fsica Enrique Gaviola (IFEG), CONICET, Ciudad Universitaria, Córdoba, Argentina
Email: emanuelgg@gmail.com
Received July 7, 2012; revised August 6, 2012; accepted August 14, 2012
Keywords: General Relativity; Approximation Methods; Particles
ABSTRACT
We present a study of the so called relaxed field equations of general relativity in terms of a decomposition of the metric; which is designed to deal with the notion of particles. Several known results are generalized to a coordinate free covariant discussion. We apply our techniques to the study of a particle up to second order.
1. Introduction
The notion of particle is fundamental to the Newtonian mechanics framework; in fact, this whole theoretical framework can be constructed in terms of the notion of test particles and massive particles. It is then natural to ask whether this notion can be translated to other frameworks, as is general relativity.
Within general relativity one understands Newtonian mechanics as the limit of weak field and slow motion. So we know that one can regain the notion of particle in this regime. Also in general relativity, the concept of test particle is a natural one, which allows to discuss several physically interesting situations.
At first sight it is not at all clear that one can extend the notion of particles (non-test) to the realm of general relativity. To begin with, if one imagines a process in which one shrinks the sizes of an object to obtain a point like object, one knows that at some moment in the process one would end up with the formation of a black hole, which has a characteristic size. However, the post-Newtonian approach to compact objects is frequently constructed in terms of the notion of particles; although post-Newtonian systems are normally required to have weak fields and slowly moving objects.
It is interesting to note that the most simple black hole, namely the one describing a vacuum spherically symmetric spacetime, can be expressed in terms of the so called Kerr-Schild decomposition. In this way, the Schwarzschild black hole, whose maximal analytic extension is described in terms of the well known causal conformal diagrams, when expressed in the Kerr-Schild decomposition shows a point like description in terms of the flat reference metric of the Kerr-Schild form.
This indicates that it might be possible to give a particle notion to a compact object in general relativity when expressed with respect to background reference metrics.
If one intends to study the problem of a systems composed of several compact objects, it appears as an appealing strategy to use approximation techniques for solving the field equations. Several problems are related to this.
In building approximation schemes for the study of the field equations in general relativity it is often useful to recur to the relaxed form of the field equations; that we recall below. Also, it frequently useful to decompose the physical metric in terms of a background metric. In this work we plan to study both techniques.
In the process of decomposing the metric a key issue is the notion of gauge, since in general one has more than one way to decompose the physical metric. In order to study this issue we bring the techniques used by Friedrich in his study of the hyperbolic nature of the gravitational field equations. We will present here a generalization of Friedrich’s results that is convenient for our discussion.
Although we work with coordinate independent expressions, we also relate our work with the widely used harmonic gauge condition; and take the opportunity to restate Anderson’s result in a coordinate independent fashion.
An approximation scheme is suggested in which the previous studies are taking into account.
We apply our techniques to the problem of a single particle up to the second order.
2. The Decomposition of the Metric
Let us express the metric  of the spacetime
of the spacetime 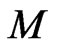 in terms of a reference metric
in terms of a reference metric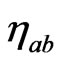 , such that
, such that
 (1)
(1)
Let 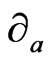 denote the torsion free metric connection of
denote the torsion free metric connection of 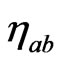 and
and 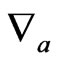 the torsion free metric connection of
the torsion free metric connection of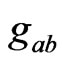 ; then one can express the covariant derivative of an arbitrary vector
; then one can express the covariant derivative of an arbitrary vector 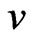 by
by
 (2)
(2)
and one can prove that
 (3)
(3)
Let us observe that
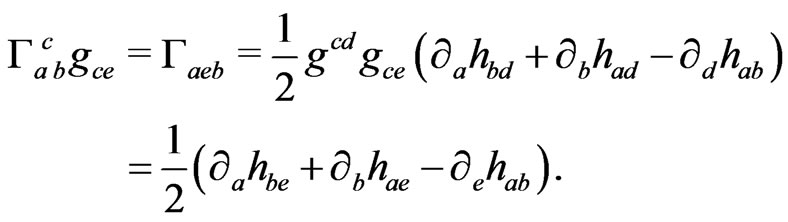 (4)
(4)
The relation between 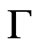 and the curvature tensor can be calculated from
and the curvature tensor can be calculated from
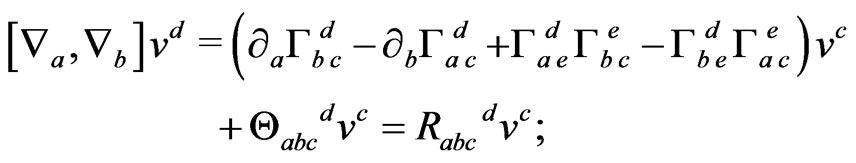 (5)
(5)
where  is the curvature of the
is the curvature of the 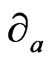 connection. Then the Ricci tensor can be calculated from
connection. Then the Ricci tensor can be calculated from
 (6)
(6)
where  is the Ricci tensor of the connexion
is the Ricci tensor of the connexion .
.
3. Auxiliary Functions or Gauge Vector
Let us consider four independent auxiliary functions , with
, with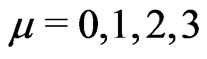 . Then let us observe that
. Then let us observe that
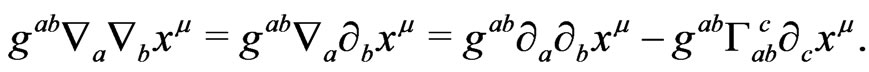 (7)
(7)
Then, if 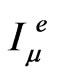 denotes the inverse of
denotes the inverse of , which exists by assumption of the independence of the set
, which exists by assumption of the independence of the set , one has
, one has
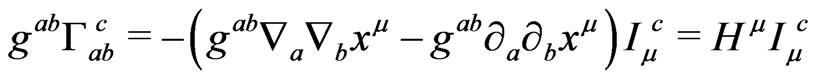 (8)
(8)
where we are using
 (9)
(9)
Alternatively, let us define the gauge vector 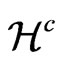
 (10)
(10)
which implies
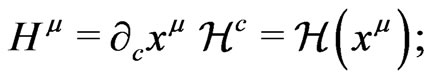 (11)
(11)
so that one also has
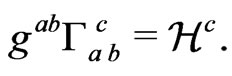 (12)
(12)
These equations show the relation that exist between working with a coordinate system, given by the set of functions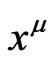 , and the gauge vector
, and the gauge vector ; which does not need any reference to coordinate systems at all. In what follows we will try to use the covariant approach that employs the use of the gauge vector
; which does not need any reference to coordinate systems at all. In what follows we will try to use the covariant approach that employs the use of the gauge vector . We emphasize that Latin indices are abstract; and therefore our expressions are coordinate independent and covariant.
. We emphasize that Latin indices are abstract; and therefore our expressions are coordinate independent and covariant.
Then, the Ricci tensor can be expressed by
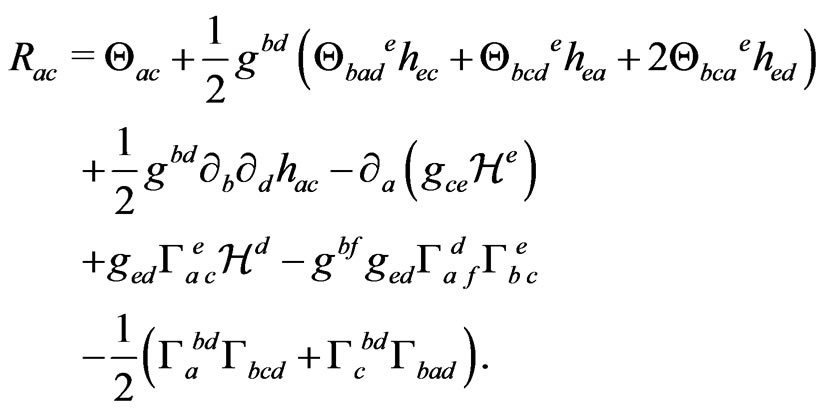 (13)
(13)
Let us note that if the vector field 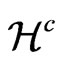 is given by (12), then for any function
is given by (12), then for any function 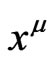 one has
one has
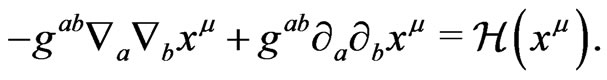 (14)
(14)
In the standard studies on approximations to the solution of the field equations, one frequently finds the choice of harmonic coordinates for the set of the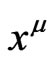 ’s; however, in Equation (13) one can see that only the vector field
’s; however, in Equation (13) one can see that only the vector field 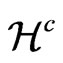 appears, without any reference to a choice of auxiliary functions. Therefore one could just refer to the gauge vector
appears, without any reference to a choice of auxiliary functions. Therefore one could just refer to the gauge vector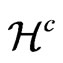 .
.
4. The Field Equations in Relaxed Covariant Form
Previous to the discussion of the relaxed covariant field equations, we would like to refer to the work of Friedrich [1] and its extension to this coordinate independent discussion.
4.1. Friedrich’s Theorem without the Use of Coordinates
The field equations are
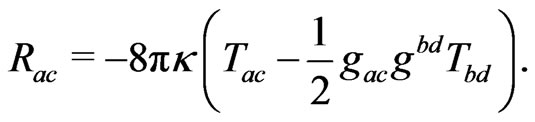 (15)
(15)
Equation (3.22) in reference [1] can be obtained from (13) by expressing it in a coordinate frame and neglecting the  terms. In this way, one would obtain the analogous expression where all the appearance of
terms. In this way, one would obtain the analogous expression where all the appearance of  derivatives are replaced by coordinate derivatives
derivatives are replaced by coordinate derivatives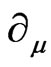 , the tensors
, the tensors 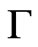 are replaced by the Chrirstoffel symbols and one uses
are replaced by the Chrirstoffel symbols and one uses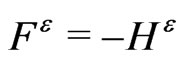 ; namely:
; namely:
 (16)
(16)
Friedrich has studied [1] this system introducing the notion of “coordinate gauge source’’
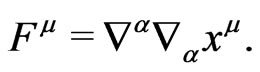 (17)
(17)
Subsequently, Friedrich studied the case in which 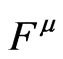 is given arbitrarily.
is given arbitrarily.
Then, we can rephrase Friedrich’s theorem in the following form:
Theorem 4.1 Let  be four independent functions that are used as a coordinate system. If
be four independent functions that are used as a coordinate system. If  is a solution of (16) together with the matter equations such that on the initial surface one has
is a solution of (16) together with the matter equations such that on the initial surface one has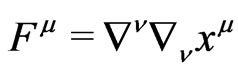 ,
,  , then
, then 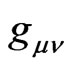 is in fact a solution of Einstein’s field equations.
is in fact a solution of Einstein’s field equations.
This theorem can be understood in two ways. In one of them, we think that the four coordinates 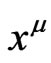 are given and then the theorem checks whether the
are given and then the theorem checks whether the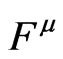 ’s satisfy the above equations. In the other way, one think that the
’s satisfy the above equations. In the other way, one think that the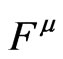 ’s are given and then the theorem checks whether there exists a coordinate system of
’s are given and then the theorem checks whether there exists a coordinate system of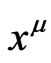 ’s such that the equations in the theorem are satisfied.
’s such that the equations in the theorem are satisfied.
From the fact that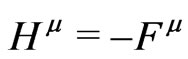 , one deduces, using the same techniques as in [1], that the generalized Friedrich’s theorem holds, namely, consider the four functions
, one deduces, using the same techniques as in [1], that the generalized Friedrich’s theorem holds, namely, consider the four functions 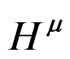 as given a priori, then:
as given a priori, then:
Theorem 4.2 If 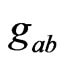 is a solution of (15), with the decomposition of the metric as in (1) and with the Ricci tensor as given by (13) with
is a solution of (15), with the decomposition of the metric as in (1) and with the Ricci tensor as given by (13) with , together with the matter equations such that on the initial surface one has
, together with the matter equations such that on the initial surface one has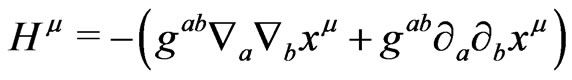 ,
,
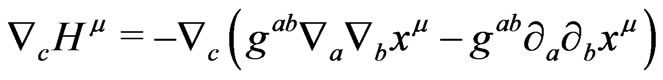 , where
, where 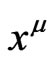 are four independent scalars, then
are four independent scalars, then 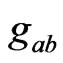 is in fact a solution of Einstein’s field equations.
is in fact a solution of Einstein’s field equations.
This result gives great freedom in the problem of finding solutions of the field equations in terms of a reference metric. Suppose that one solves (15) for a given vector field . Also assume that one can solve for the functions
. Also assume that one can solve for the functions 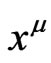 such that
such that . Then, let us build a flat metric
. Then, let us build a flat metric  so that
so that ; which in particular can be satisfied if the
; which in particular can be satisfied if the 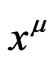 s are thought as Cartesian coordinates of
s are thought as Cartesian coordinates of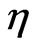 . In this way one would obtain
. In this way one would obtain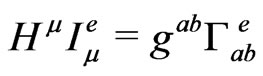 , and so have a solution of the field equations.
, and so have a solution of the field equations.
It also might be of interest to researchers in numerical relativity, since it provides the possibility to use any coordinate system; i.e., not necessarily an harmonic one.
Instead, one could have a proposition that does not refer to the auxiliary functions whatsoever; namely
Theorem 4.3 If 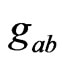 is a solution of (15), with the decomposition of the metric as in (1) and with the Ricci tensor as given by (13), together with the matter equations such that on the initial surface one has
is a solution of (15), with the decomposition of the metric as in (1) and with the Ricci tensor as given by (13), together with the matter equations such that on the initial surface one has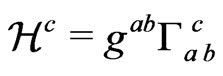 ,
, 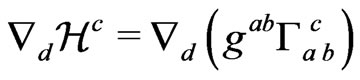 , then
, then  is in fact a solution of Einstein’s field equations.
is in fact a solution of Einstein’s field equations.
This theorem can be understood in two ways. In one of them, we think that the metric 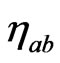 is given and then the theorem checks whether the vector
is given and then the theorem checks whether the vector 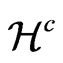 satisfies the above equations. In the other way, one think that the
satisfies the above equations. In the other way, one think that the  is given and then the theorem checks whether there exists a metric
is given and then the theorem checks whether there exists a metric  such that the equations in the theorem are satisfied.
such that the equations in the theorem are satisfied.
4.2. Relaxed Covariant Form of the Field Equations and a Generalization of Friedrich’s Theorem
Alternatively one can use the form of the field equations in terms of a slight different logic.
When we use the expression of the Ricci tensor as given by (13) in (15), without assuming that 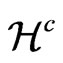 is
is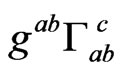 , namely
, namely
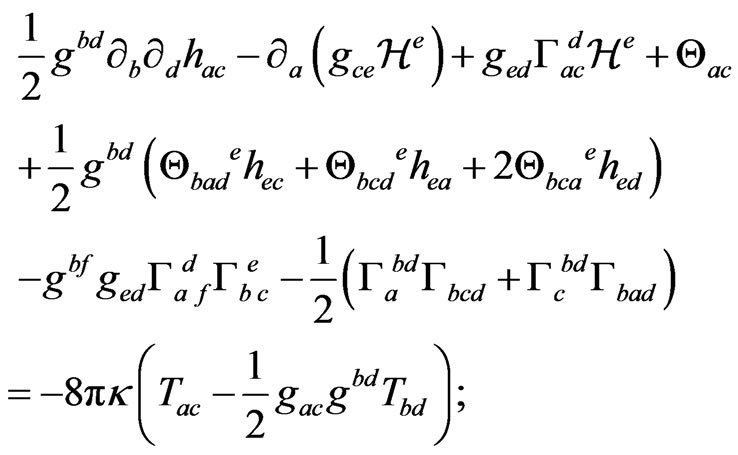 (18)
(18)
we will refer to these as the relaxed field equations [2].
Using the standard harmonic gauge technique, one would say: solve the relaxed field equation in the coordinate frame, with , and then require the equation
, and then require the equation
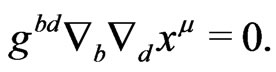 (19)
(19)
In the standard approach one makes use of coordinate basis; therefore the previous statement would be the complete story. However in our case, 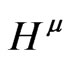 has a second term where two covariant derivatives of
has a second term where two covariant derivatives of 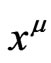 with respect to the metric
with respect to the metric 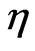 appears. At this point it is important to notice that if we have the solutions
appears. At this point it is important to notice that if we have the solutions  from (19) then, on constructing
from (19) then, on constructing  with this as a Cartesian coordinate system, one would obtain
with this as a Cartesian coordinate system, one would obtain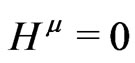 .
.
In some occasions it is preferable to work with a different set of equations. In this respect, several authors have indicated that actually to request Equation (19) is equivalent [2-4] to demand
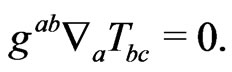 (20)
(20)
When dealing with Einstein equations in the relaxed form, and treating the vacuum case, Equation (20) is understood as the condition that the divergence of the Einstein tensor must be zero (which of course is identically zero in the non relaxed form).
Let us study the relation between the divergence of the energy-momentum tensor and the vector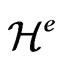 . One can write the relaxed field Equations (18) in the usual form in which on the right hand side we have just the standard term
. One can write the relaxed field Equations (18) in the usual form in which on the right hand side we have just the standard term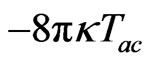 ; and so on the left hand side, the terms involving
; and so on the left hand side, the terms involving 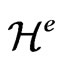 would be
would be
 (21)
(21)
where we have used that the term  contributes with the term
contributes with the term
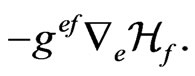 (22)
(22)
Then in taking its divergence, on the left hand side, the terms involving  are
are
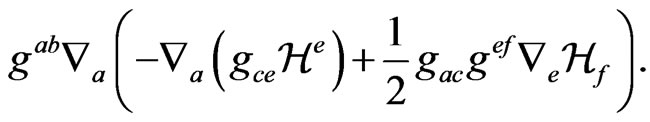 (23)
(23)
If we replace 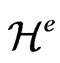 by
by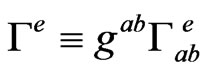 , the divergence of the left hand side would be identically zero, since the Einstein tensor has divergence zero. Therefore we conclude that the divergence of the stress energy-momentum tensor is
, the divergence of the left hand side would be identically zero, since the Einstein tensor has divergence zero. Therefore we conclude that the divergence of the stress energy-momentum tensor is
 (24)
(24)
Therefore, the stress energy-momentum is conserved if and only if
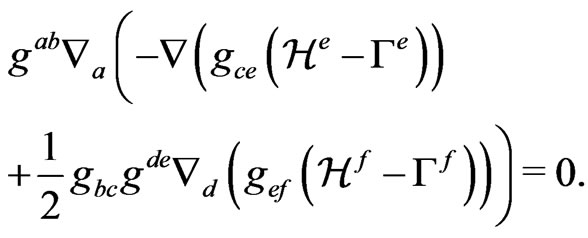 (25)
(25)
Working out the relations, one finds that the previous equation can be expressed as
 (26)
(26)
Which coincides with Friedrich calculation.
It follows that if one solves Equation (26) such that on an initial hypersurface  and
and , then the energy-momentum tensor will be conserved in the evolution of the system. Furthermore, one also deduces that:
, then the energy-momentum tensor will be conserved in the evolution of the system. Furthermore, one also deduces that:
Theorem 4.4 If, given the metric , one solves the relaxed field equations for
, one solves the relaxed field equations for 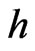 together with the matter equations, which include the conservation of the energymomentum tensor, such that
together with the matter equations, which include the conservation of the energymomentum tensor, such that 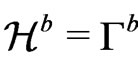 and
and 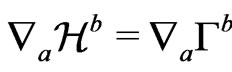 on an initial hypersurface, then
on an initial hypersurface, then  is a solution of Einstein equations.
is a solution of Einstein equations.
This is a rephrasing of Friedrich’s theorem applied to a decomposition of the metric and to its general relaxed covariant form of the field equations.
It is interesting to remark that Anderson [3], using a retarded integral expression for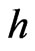 , was able to prove the equivalence between the conservation of the energymomentum tensor with the harmonic gauge condition. In relation to this let us remark that if the set of functions
, was able to prove the equivalence between the conservation of the energymomentum tensor with the harmonic gauge condition. In relation to this let us remark that if the set of functions 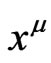 is obtained from the solutions of (19); and one uses them as harmonic coordinates of the metric
is obtained from the solutions of (19); and one uses them as harmonic coordinates of the metric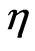 , then one deduces that
, then one deduces that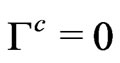 . And also, if
. And also, if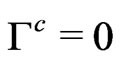 , then Cartesian coordinates of
, then Cartesian coordinates of 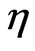 are harmonic coordinates of
are harmonic coordinates of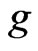 . This means that we can state Anderson’s result in a coordinate independent way, namely:
. This means that we can state Anderson’s result in a coordinate independent way, namely:
Theorem 4.5 Let  be the retarded solution, with respect to a flat metric
be the retarded solution, with respect to a flat metric  of the relaxed field equations together with the matter equations of state, such that
of the relaxed field equations together with the matter equations of state, such that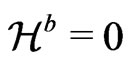 , then the conservation of the energy-momentum tensor implies that
, then the conservation of the energy-momentum tensor implies that 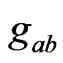 is a solution of Einstein equations.
is a solution of Einstein equations.
5. The Approximation Method and the Treatment of Particles
The approximation method that we introduce below, is adapted to the treatment of particles; therefore, it is convenient to begin by treating the problem of one single particle in the context of linearized gravity, in order to clarify some of the techniques.
5.1. The Gravitational Field from One Particle in Linearized Gravity
5.1.1. The Description of a Particle
Let us consider a massive point particle with mass 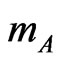 describing, in a flat space-time
describing, in a flat space-time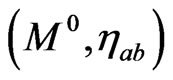 , a curve C which in a Cartesian coordinate system
, a curve C which in a Cartesian coordinate system 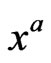 reads
reads
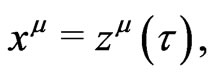 (27)
(27)
with 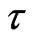 meaning the proper time of the particle along
meaning the proper time of the particle along .
.
The unit tangent vector to , with respect to the flat background metric is
, with respect to the flat background metric is
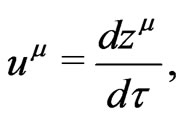 (28)
(28)
that is,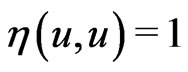 . Now, for each point
. Now, for each point 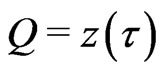 of
of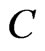 , we draw a future null cone
, we draw a future null cone 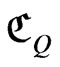 with vertex in
with vertex in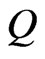 . If we call
. If we call 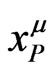 the Minkowskian coordinates of an arbitrary point on the cone
the Minkowskian coordinates of an arbitrary point on the cone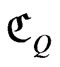 , then we can define the retarded radial distance on the null cone by
, then we can define the retarded radial distance on the null cone by
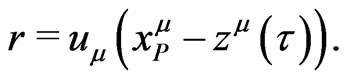 (29)
(29)
The energy momentum tensor 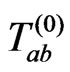 of a point particle is proportional to
of a point particle is proportional to ; where
; where 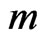 is the mass and
is the mass and 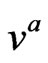 its four velocity. We are distinguishing between the unit tangent vector
its four velocity. We are distinguishing between the unit tangent vector 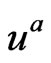 and the four velocity vector
and the four velocity vector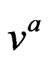 , because in future works we would like to consider the possibility to normalize the vector
, because in future works we would like to consider the possibility to normalize the vector 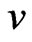 with respect to a different metric. In order to represent a point particle
with respect to a different metric. In order to represent a point particle  must also be proportional to a three dimensional delta function that has support on the world line of the particle.
must also be proportional to a three dimensional delta function that has support on the world line of the particle.
We will suppose that the particle does not have multipolar structure. Then, given an arbitrary Minkowskian frame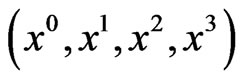 , we will express the energy momentum by
, we will express the energy momentum by
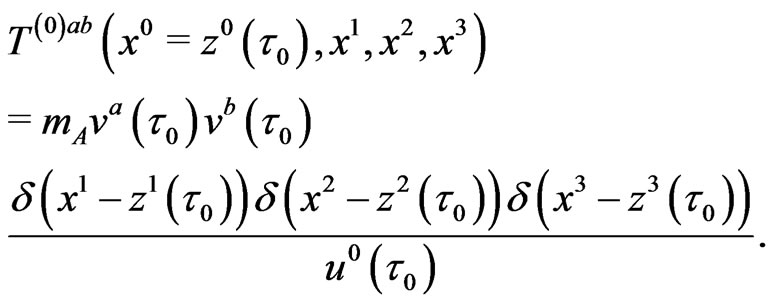 (30)
(30)
5.1.2. The First Order Solution
The retarded solution, in terms of Green functions, for the relaxed field Equations (18) for particle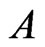 , in which we take
, in which we take  and
and 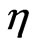 a flat metric, is
a flat metric, is
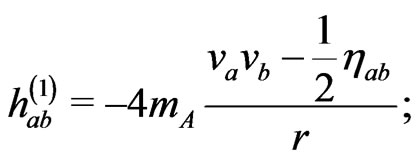 (31)
(31)
so that in general
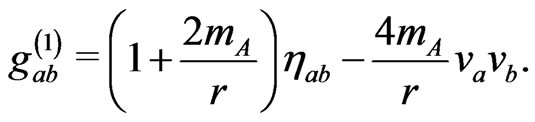 (32)
(32)
In these equations we have considered the definition
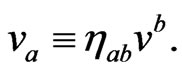 (33)
(33)
It is interesting to realize that the exact inverse of this metric is
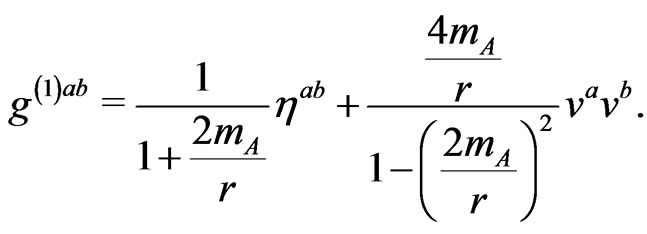 (34)
(34)
Note that one can solve for  for an arbitrary motion of the particle; however, the complete solution of the problem involves having to set also
for an arbitrary motion of the particle; however, the complete solution of the problem involves having to set also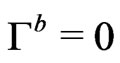 ; which in terms of a coordinate frame treatment is equivalent to the harmonic condition. Then, recalling, as mentioned previously, that Anderson has proved [3] the equivalence between the harmonic condition and the divergence free condition on the energy-momentum tensor; one deduces from this, that for the case of the energy-momentum tensor of a particle it implies its geodesic motion.
; which in terms of a coordinate frame treatment is equivalent to the harmonic condition. Then, recalling, as mentioned previously, that Anderson has proved [3] the equivalence between the harmonic condition and the divergence free condition on the energy-momentum tensor; one deduces from this, that for the case of the energy-momentum tensor of a particle it implies its geodesic motion.
5.2. Iterative Approximation Method
Now we present a general iterative method to solve the relaxed field equations.
First of all, let us note that given the decomposition (1) and defining the tensor 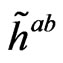 from
from
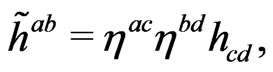 (35)
(35)
where
 (36)
(36)
that is 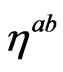 is the inverse of
is the inverse of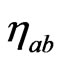 , one can always express the inverse
, one can always express the inverse 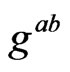 in the form
in the form
 (37)
(37)
Then making the contraction
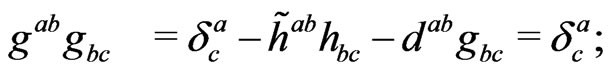 (38)
(38)
one finds
 (39)
(39)
which can be considered an implicit equation for ; but it also shows explicitly that
; but it also shows explicitly that  is quadratic in terms of
is quadratic in terms of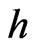 .
.
This suggests the natural series 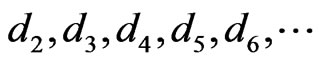 defined by
defined by
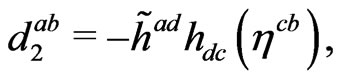 (40)
(40)
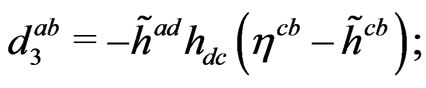 (41)
(41)
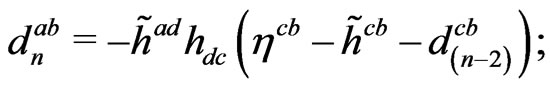 (42)
(42)
for natural numbers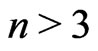 . It is clear that
. It is clear that 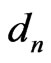 is order
is order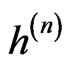 .
.
However, we have seen that in the first order solution for a single particle, the inverse of the metric has a term which is conformal to the flat metric ; which it will be convenient to take into account. For this reason we propose the following method of approximation where this issue is considered.
; which it will be convenient to take into account. For this reason we propose the following method of approximation where this issue is considered.
The idea is to express (18) and eventually (19) in the form
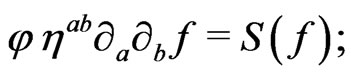 (43)
(43)
where 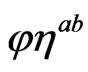 is the term proportional to
is the term proportional to 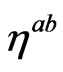 that is contained in
that is contained in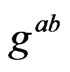 ; while the general case would be to consider just
; while the general case would be to consider just  for the left hand side. This equation can also be expressed by
for the left hand side. This equation can also be expressed by
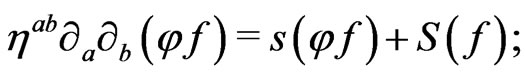 (44)
(44)
where
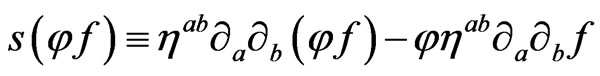 (45)
(45)
Now one would like to solve Equation (44) by iterations.
Let us define the sets 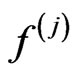 such that for
such that for , one takes
, one takes ,
, 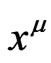 to be harmonic functions of the metric
to be harmonic functions of the metric 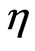 and
and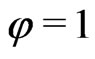 ; and for
; and for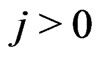 ,
, 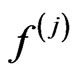 is the solution of
is the solution of
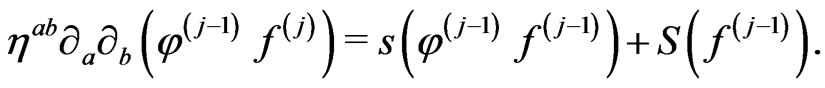 (46)
(46)
using the retarded Green function. As we have seen above, 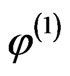 clearly arises in the first order calculation.
clearly arises in the first order calculation.
The application of this method to the first order, for a single particle, reproduces the calculation explained in Subsection 5.1.2. Next we study this case at second order.
5.3. The Second Order Solution
Let us remark that the first order solution is stationary and spherically symmetric. This structure transports to the second order solution.
The equation for 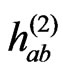 is
is
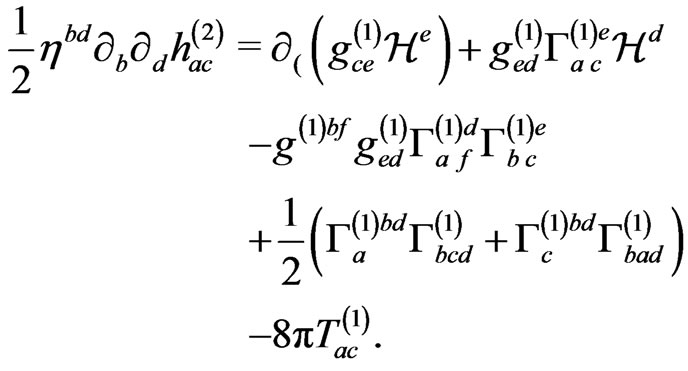 (47)
(47)
We will call the right hand side, the tensor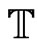 ; which has the structure
; which has the structure
 (48)
(48)
where we are using the three dimentional notation 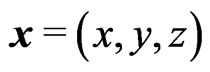 and where
and where
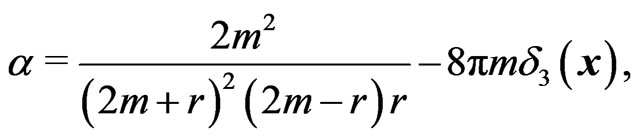 (49)
(49)
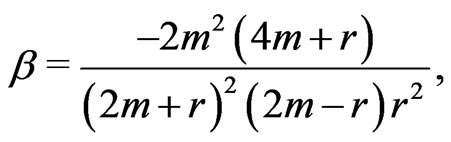 (50)
(50)
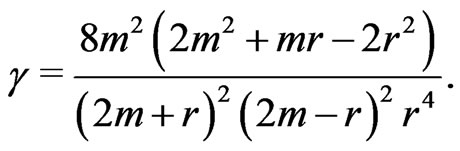 (51)
(51)
Therefore one assumes for 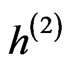 the same form, namely
the same form, namely
 (52)
(52)
In this way one has
 (53)
(53)
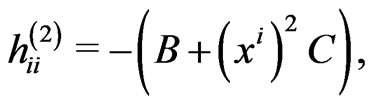 (54)
(54)
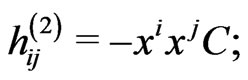 (55)
(55)
where the index 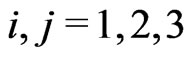 denote spatial coordinates.
denote spatial coordinates.
One can see then that the equations to solve are
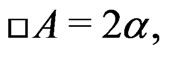 (56)
(56)
 (57)
(57)
 (58)
(58)
where we are using the symbol  to denote
to denote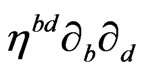 .
.
We can solve these equations in two ways, either using Green function techniques, or, recalling the stationary nature of the solution, just integrating the Laplace operator. For this presentation we choose the second option. Let us note that for any function 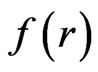 one has that
one has that
 (59)
(59)
Therefore one can find 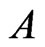 by two consecutive integrations, obtaining
by two consecutive integrations, obtaining
 (60)
(60)
Similarly one can see that the function 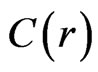 satisfies
satisfies
 (61)
(61)
which after integration gives
 (62)
(62)
Then the function 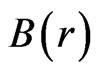 is given by
is given by
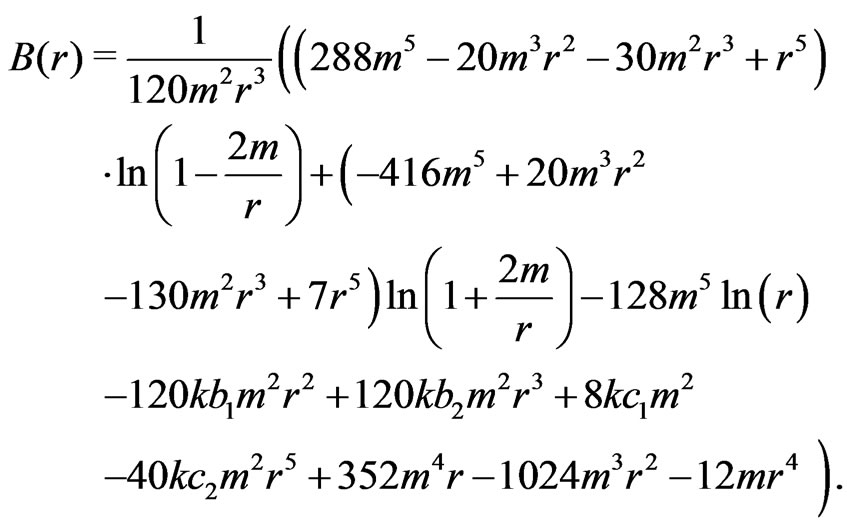 (63)
(63)
Our choice for the integration constants is: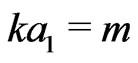 ,
,
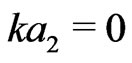 ,
,  ,
,  ,
,  and
and
 . This choice is made taking into consideration the exact solution and the integration of the solution coming from a Green function approach; that we will not discuss here due to considerations of space. By the exact functions we mean the metric components of the Schwarzschild spacetime in harmonic coordinates; which are
. This choice is made taking into consideration the exact solution and the integration of the solution coming from a Green function approach; that we will not discuss here due to considerations of space. By the exact functions we mean the metric components of the Schwarzschild spacetime in harmonic coordinates; which are
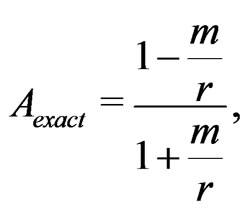 (64)
(64)
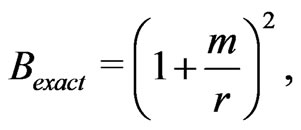 (65)
(65)
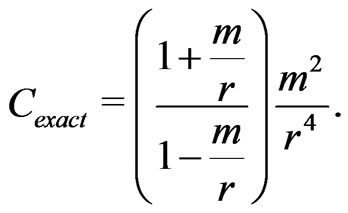 (66)
(66)
A graphical comparison with the exact functions of the Schwarzschild solution in harmonic coordinates are shown in Figure 1.
It can be observed that in second order one obtains anexcellent comparison of the solution with the exact values of the metric components; even for very small values of the radial coordinate. Although this comparison has limited value, it is in any case remarkable that it is only necessary to go only to second order to obtain such a good approximation.
6. Final Comments
We have presented an study of an approach to the gravitational field equation through the relaxed covariant form of them. The whole approach is intended to deal with the notion of compact objects.
The relaxed field equations was studied using Friedrich approach to the problem and we have also refer to Anderson’s result in the field of harmonic conditions.
We have generalized Friedrich results to a covariant formulation in terms of a decomposition of the metric.
Anderson’s result has been restated in a form that does not make reference to coordinate conditions.
We have presented an approximation method that can be applied to the notion of particles in general relativity; and which is successful in second order for the case of a solitary compact body.

Figure 1. Comparison of the functions calculated in the second iteration with the exact values.
It is our intention to apply these techniques to the problem of a binary system in general relativity.
7. Acknowledgements
We acknowledge support from CONICET and SeCyTUNC.
REFERENCES
- H. Friedrich, “On the Hyperbolicity of Einstein’s and Other Gauge Field Equations,” Communications in Mathematical Physics, Vol. 100, No. 4, 1985, pp. 525-543. Hdoi:10.1007/BF01217728
- M. Walker and C. M. Will, “The Approximation of Radiative Effects in Relativistic Gravity-Gravitational Radiation Reaction and Energy Loss in Nearly Newtonian Systems,” Astrophysical Journal, Vol. 242, 1980, pp. L129-L133. Hdoi:10.1086/183417
- J. L. Anderson, “Satisfaction of deDonder and Trautman Conditions by Radiative Solutions of the Einstein Field Equations,” General Relativity and Gravitation, Vol. 4, No. 4, 1973, pp. 289-297. Hdoi:10.1007/BF00759848
- A. Einstein, L. Infeld and B. Hoffmann, “The Gravitational Equations and the Problem of Motion,” Annals of Mathematics, Vol. 39, No. 1, 1938, pp. 65-100. Hdoi:10.2307/1968714

