Journal of Modern Physics
Vol.2 No.11(2011), Article ID:8645,17 pages DOI:10.4236/jmp.2011.211170
Capability of the Free-Ion Eigenstates for Crystal-Field Splitting
1Trzebiatowski Institute of Low Temperature and Structure Research, Polish Academy of Sciences, Wroclaw, Poland
2Institute of Physics, Wroclaw University of Technology, Wroclaw, Poland
E-mail: *Maciej.Mulak@pwr.wroc.pl
Received June 4, 2011; revised July 15, 2011; accepted July 29, 2011
Keywords: Crystal-Field Theory, Crystal-Field Splitting, Rare-Earth Free-Ion Eigenstates, Rare-Earth Ions
ABSTRACT
Any electronic eigenstate ![]() of the paramagnetic ion open-shell is characterized by the three independent multipole asphericities
of the paramagnetic ion open-shell is characterized by the three independent multipole asphericities 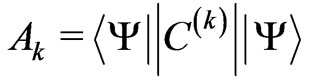 for
for  and 6 related to the second moments of the relevant crystal-field splittings by
and 6 related to the second moments of the relevant crystal-field splittings by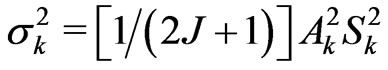 , where
, where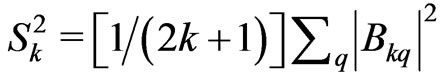 . The Ak as the reduced matrix elements can serve as a reliable measure of the state
. The Ak as the reduced matrix elements can serve as a reliable measure of the state ![]() capability for the splitting produced by the k-rank component of the crystal-field Hamiltonian. These multipolar characteristics allow one to verify any fitted crystal-field parameter set by comparing the calculated second moments and the experimental ones of the relevant crystal-field splittings. We present the multipole characteristics Ak for the extensive set of eigenstates from the lower parts of energy spectra of the tripositive 4 f N ions applying in the calculations the improved eigenfunctions of the free lanthanide ions obtained based on the M. Reid f-shell programs. Such amended asphericities are compared with those achieved for the simplified Russell-Saunders states. Next, they are classified with respect to the absolute or relative weight of Ak in the multipole structure of the considered states. For the majority of the analyzed states (about 80%) the Ak variation is of order of only a few percent. Some essential changes are found primarily for several states of Tm3+, Er3+, Nd3+, and Pr3+ ions. The detailed mechanisms of such Ak changes are unveiled. Particularly, certain noteworthy cancelations as well as enhancements of their magnitudes are explained.
capability for the splitting produced by the k-rank component of the crystal-field Hamiltonian. These multipolar characteristics allow one to verify any fitted crystal-field parameter set by comparing the calculated second moments and the experimental ones of the relevant crystal-field splittings. We present the multipole characteristics Ak for the extensive set of eigenstates from the lower parts of energy spectra of the tripositive 4 f N ions applying in the calculations the improved eigenfunctions of the free lanthanide ions obtained based on the M. Reid f-shell programs. Such amended asphericities are compared with those achieved for the simplified Russell-Saunders states. Next, they are classified with respect to the absolute or relative weight of Ak in the multipole structure of the considered states. For the majority of the analyzed states (about 80%) the Ak variation is of order of only a few percent. Some essential changes are found primarily for several states of Tm3+, Er3+, Nd3+, and Pr3+ ions. The detailed mechanisms of such Ak changes are unveiled. Particularly, certain noteworthy cancelations as well as enhancements of their magnitudes are explained.
1. Introduction
The spherical tensor operators 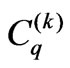 in the one-electron crystal-field (CF) Hamiltonian written as
in the one-electron crystal-field (CF) Hamiltonian written as
![]()
[1], or shortly as![]() , act on the angle coordinates
, act on the angle coordinates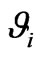 ,
, 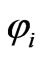 of individual unpaired electrons (i) of the central ion in its initial eigenstates
of individual unpaired electrons (i) of the central ion in its initial eigenstates 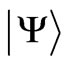 that are superpositions of the Russell-Saunders (RS) states
that are superpositions of the Russell-Saunders (RS) states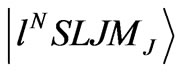 . The
. The 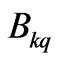 stand for the crystal-field parameters (CFP) for the above specified operators. For complex many-electron states the one-electron character of the
stand for the crystal-field parameters (CFP) for the above specified operators. For complex many-electron states the one-electron character of the 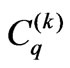 operators manifests itself by the 6-j symbols in their developed matrix elements [1-5] and the doubly reduced matrix elements of the unit tensor operator
operators manifests itself by the 6-j symbols in their developed matrix elements [1-5] and the doubly reduced matrix elements of the unit tensor operator ![]() [1-5] (Section 2, Equation (2)). They both reveal a decomposition of the coupled many-electron state into its one-electron spinorbitals. Thus, any matrix element
[1-5] (Section 2, Equation (2)). They both reveal a decomposition of the coupled many-electron state into its one-electron spinorbitals. Thus, any matrix element
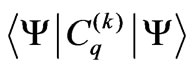 is concerned exclusively with the intrinsic properties of the central ion electronic eigenstate
is concerned exclusively with the intrinsic properties of the central ion electronic eigenstate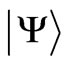 . The reduced (double bar) matrix elements is defined by [1-5]
. The reduced (double bar) matrix elements is defined by [1-5]
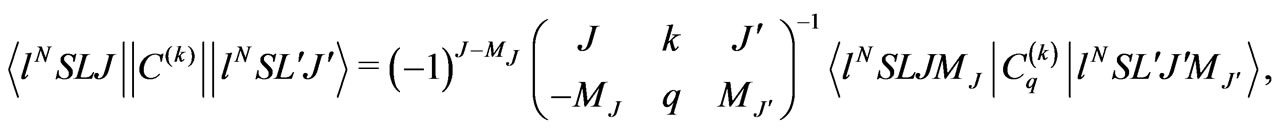 (1)
(1)
where the factor preceding the matrix element is the reciprocal of the 3-j symbol [1-5]. The reduced matrix element is independent of the reference frame orientation and hence also of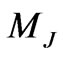 . The diagonal reduced elements
. The diagonal reduced elements 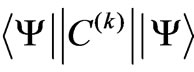 represent the 2k-pole asphericities
represent the 2k-pole asphericities ![]() (for
(for 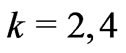 and 6) of the considered electronic state
and 6) of the considered electronic state 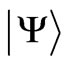 [6] and these dimensionless values can serve as a reliable measure of the state capability for CF splitting by the k-rank CF Hamiltonian (Section 3). The electron density distribution of the f-electron states is fully described by the first three multipoles with even
[6] and these dimensionless values can serve as a reliable measure of the state capability for CF splitting by the k-rank CF Hamiltonian (Section 3). The electron density distribution of the f-electron states is fully described by the first three multipoles with even 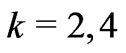 and 6. The asphericities
and 6. The asphericities 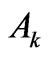 for 105 lower lying electron eigenstates of all the trivalent lanthanide ions are compiled in Table 1 (Section 2). They have been calculated for the corrected eigenstates including J-mixing effect [7] and the outstanding set of the free-ion data [8] and subsequently compared with those corresponding to the onecomponent RS states [6]. The
for 105 lower lying electron eigenstates of all the trivalent lanthanide ions are compiled in Table 1 (Section 2). They have been calculated for the corrected eigenstates including J-mixing effect [7] and the outstanding set of the free-ion data [8] and subsequently compared with those corresponding to the onecomponent RS states [6]. The 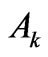 magnitudes and their possible variations due to the J-mixing of the RS states are thoroughly discussed. An inseparable entanglement of the asphericities
magnitudes and their possible variations due to the J-mixing of the RS states are thoroughly discussed. An inseparable entanglement of the asphericities 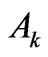 and the k-components of the CF strength
and the k-components of the CF strength 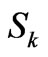 [9-12] seen in the expression for the second moment of the splitting
[9-12] seen in the expression for the second moment of the splitting 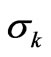 [10,13,14] (Section 3) justifies the
[10,13,14] (Section 3) justifies the 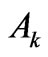 as a reliable capability of the relevant state for the
as a reliable capability of the relevant state for the 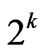 -pole partial CF splitting. By the fundamental law of additivity
-pole partial CF splitting. By the fundamental law of additivity  [10,13,14], resulting from the orthogonality of the 3-j symbols [3,4] (Equation (1)), the global
[10,13,14], resulting from the orthogonality of the 3-j symbols [3,4] (Equation (1)), the global 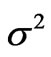 can be expressed by means of the
can be expressed by means of the 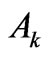 and
and 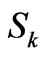 components. Tables 2-6 show the classification of the examined eigenstates with respect to their multipole structure (Section 4). The states distinguished by the strongest and the weakest
components. Tables 2-6 show the classification of the examined eigenstates with respect to their multipole structure (Section 4). The states distinguished by the strongest and the weakest 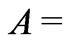
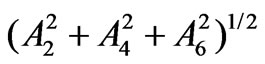 , by the strongest and the weakest
, by the strongest and the weakest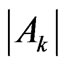 , and finally those with the largest and the smallest
, and finally those with the largest and the smallest 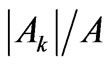 for
for  and 6 have been selected respectively. The relation between the defined capability of electronic state for CF splitting and correct parametrization of the involved CF Hamiltonian is explained by way of example for Tm3+:Y2O3 in Section 5. In turn, Section 6 gives a few instructive examples unveiling the mechanisms of the
and 6 have been selected respectively. The relation between the defined capability of electronic state for CF splitting and correct parametrization of the involved CF Hamiltonian is explained by way of example for Tm3+:Y2O3 in Section 5. In turn, Section 6 gives a few instructive examples unveiling the mechanisms of the  changes induced by the J-mixing of the RS states. A special attention has been paid to the strong enhancements and cancelations among the asphericities
changes induced by the J-mixing of the RS states. A special attention has been paid to the strong enhancements and cancelations among the asphericities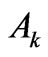 .
.
2. Multipole Characteristics of the 4 f N Tripositive Free-Ion Eigenstates including J-Mixing Effects
The k-rank multipole moment of an electronic eigenstate 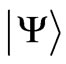 which is a superposition of the RS states with various L and S but the same J can be evaluated based on the reduced matrix element
which is a superposition of the RS states with various L and S but the same J can be evaluated based on the reduced matrix element 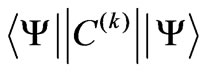 of the respective k-rank spherical tensor operator. According to the Wigner-Eckart theorem [5,15] such quantity is independent of the reference frame orientation and adequately expresses the 2k-pole type asphericity of the given eigenstate
of the respective k-rank spherical tensor operator. According to the Wigner-Eckart theorem [5,15] such quantity is independent of the reference frame orientation and adequately expresses the 2k-pole type asphericity of the given eigenstate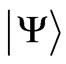 . For the spherical electronic density distribution the matrix element identically vanishes for
. For the spherical electronic density distribution the matrix element identically vanishes for 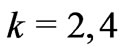 and 6. It plays also a crucial role as a scaling factor in the CF Hamiltonian interaction matrices and hence participates in both the calculational and fitting CFP procedures. In the case of J-mixing approach, i.e. for fixed J, the reduced matrix element can be expressed by the sum of all diagonal and off-diagonal matrix elements occurring in the
and 6. It plays also a crucial role as a scaling factor in the CF Hamiltonian interaction matrices and hence participates in both the calculational and fitting CFP procedures. In the case of J-mixing approach, i.e. for fixed J, the reduced matrix element can be expressed by the sum of all diagonal and off-diagonal matrix elements occurring in the 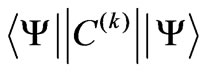 expansion [1,5,16]
expansion [1,5,16]
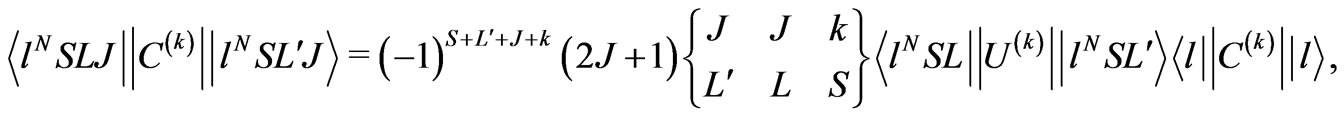 (2)
(2)
where the first factor on the right side, defining the sign of the reduced element, depends on the parity of the sum of four numbers, which are in principle autonomous, what leads to the sign randomness. The second factor stands for the degeneracy of the state, the third one is the 6-j symbol revealing what part of the final  function belongs to the orbital part
function belongs to the orbital part 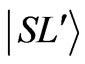 [17]. Finally, the double-bar matrix element of the unit tensor operator
[17]. Finally, the double-bar matrix element of the unit tensor operator ![]() depends on coupling of the N one-electron angular momenta 1 of the
depends on coupling of the N one-electron angular momenta 1 of the 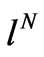 configuration into the resultant L [18]. The one-electron reduced matrix element
configuration into the resultant L [18]. The one-electron reduced matrix element 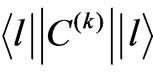 for
for 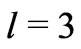 is equal to –1.3663, 1.1282, and –1.2774 for
is equal to –1.3663, 1.1282, and –1.2774 for 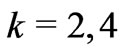 and 6, respectively.
and 6, respectively.
The  quantum numbers and the q index do not appear in Equation (2) (compare with Equation (1)). It clearly shows that the reduced matrix elements and in consequence the
quantum numbers and the q index do not appear in Equation (2) (compare with Equation (1)). It clearly shows that the reduced matrix elements and in consequence the 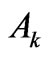 are independent of the reference frame choice. Any element of the
are independent of the reference frame choice. Any element of the 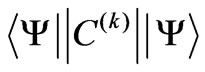 expansion includes additionally the product of amplitudes of the two involved components in the
expansion includes additionally the product of amplitudes of the two involved components in the 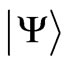 superposition together with their signs. The reduced matrix element (Equation (2)) differs from zero only for the same S quantum number (in the bra and ket) since
superposition together with their signs. The reduced matrix element (Equation (2)) differs from zero only for the same S quantum number (in the bra and ket) since 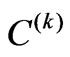 act exclusively on the configurational coordinates of the electrons, and for the states of the same parity L and L'. These requirements reduce the number of the non-zero off-diagonal matrix elements between various components of the J-mixed eigenfunctions.
act exclusively on the configurational coordinates of the electrons, and for the states of the same parity L and L'. These requirements reduce the number of the non-zero off-diagonal matrix elements between various components of the J-mixed eigenfunctions.
Such multipole characteristics have been evaluated earlier for the pure (one-component) RS open-shell electronic eigenstates [6]. In Table 1 we compare them with the corrected characteristics for the 4 f N tripositive ion
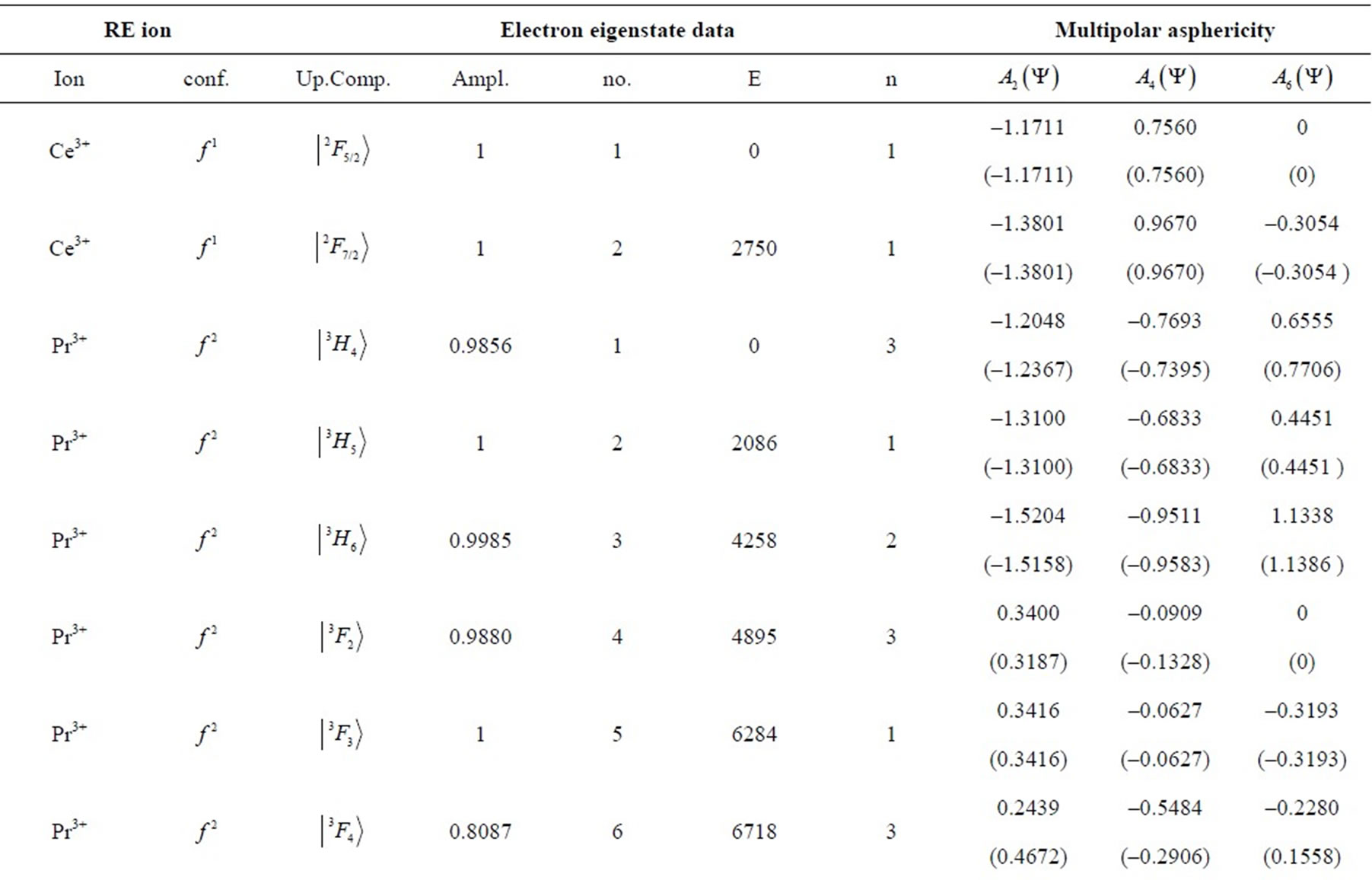

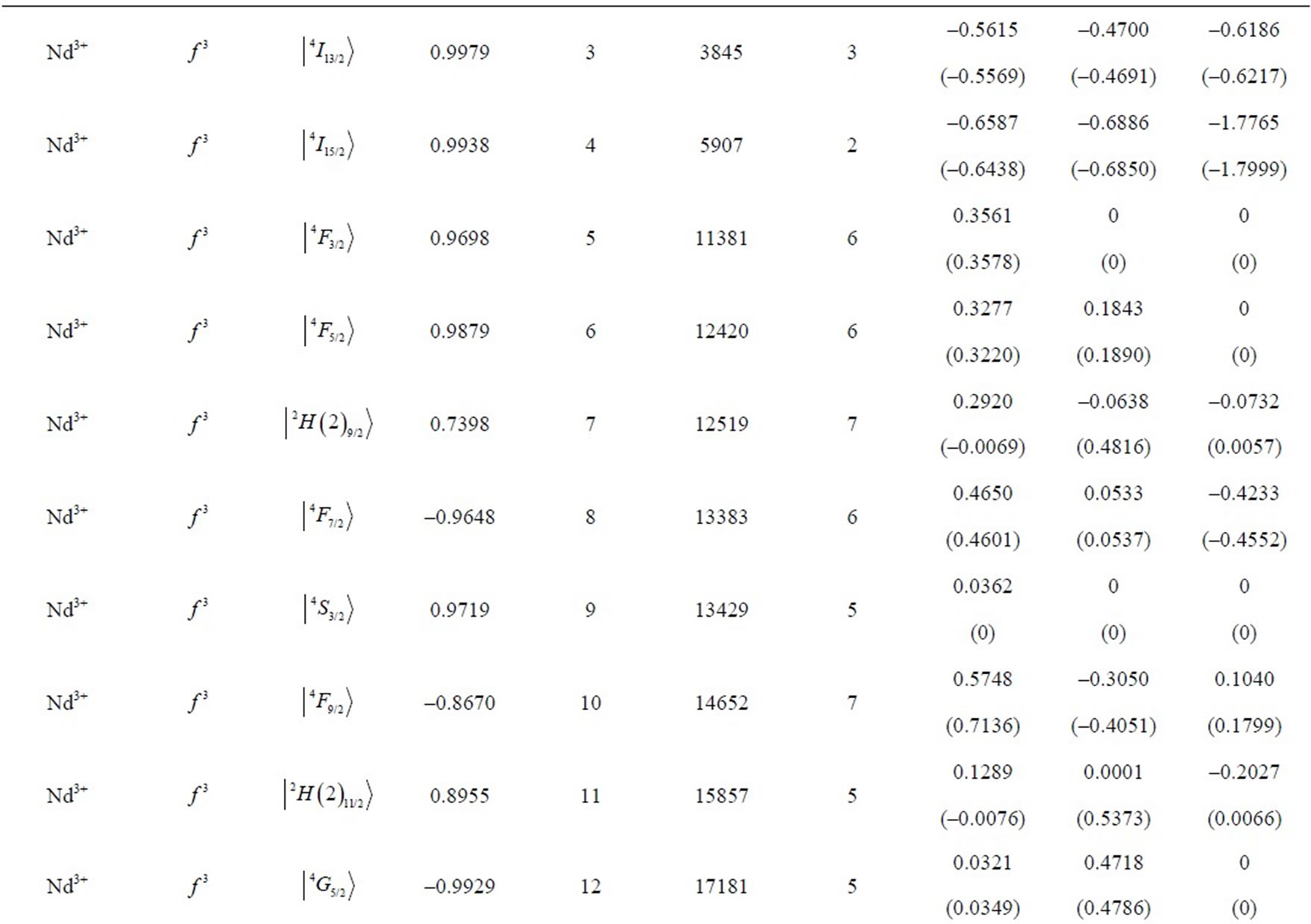
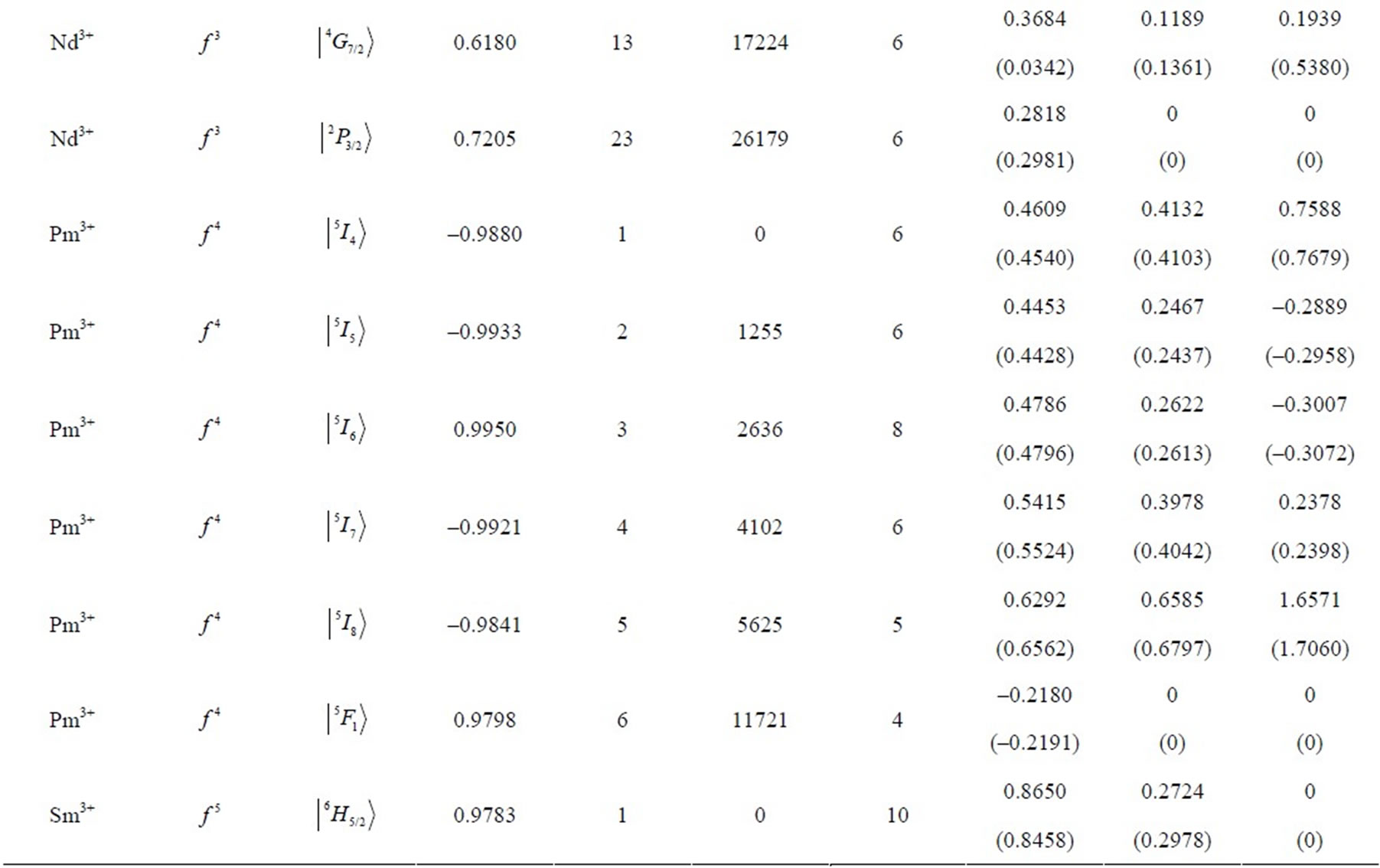
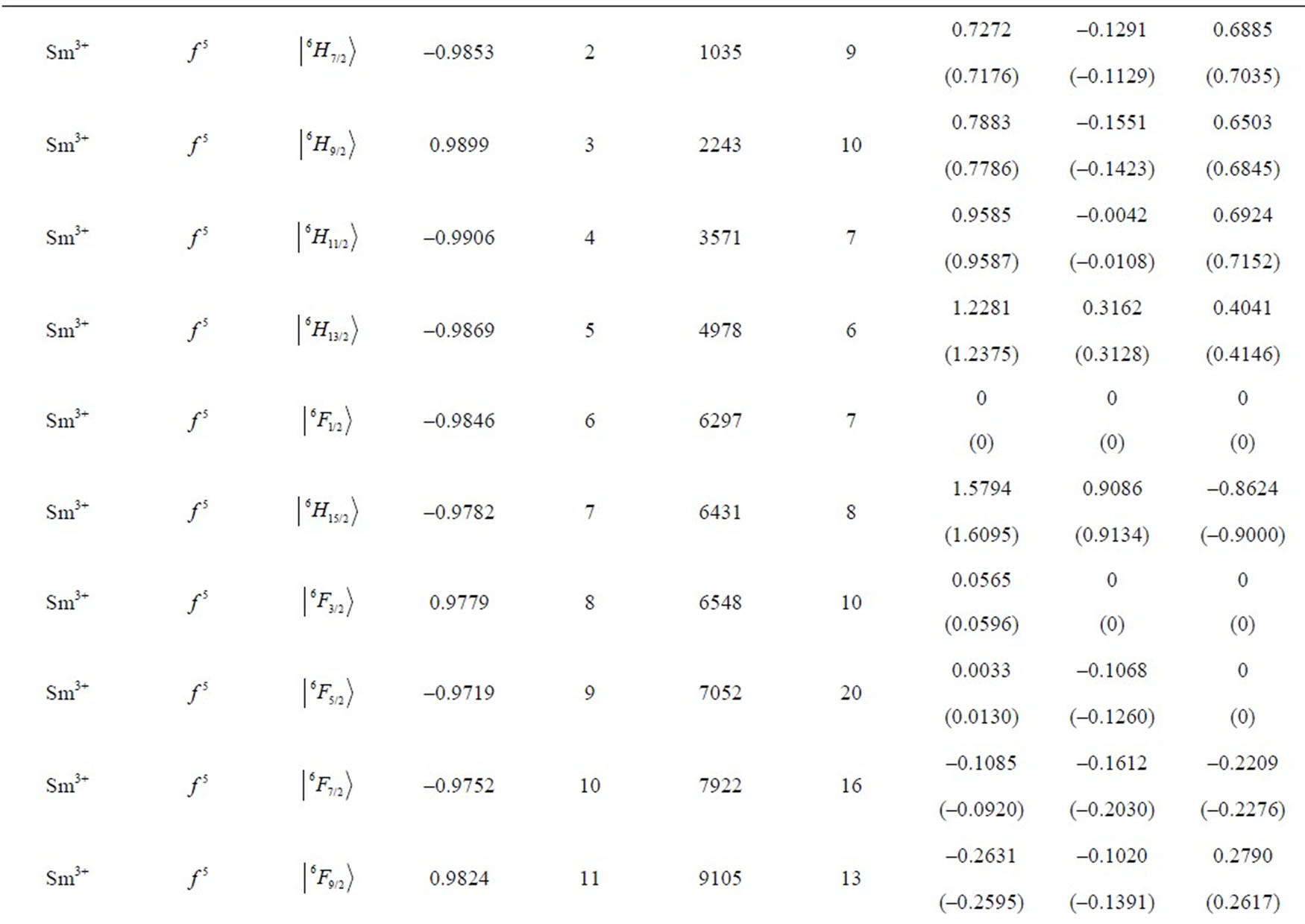

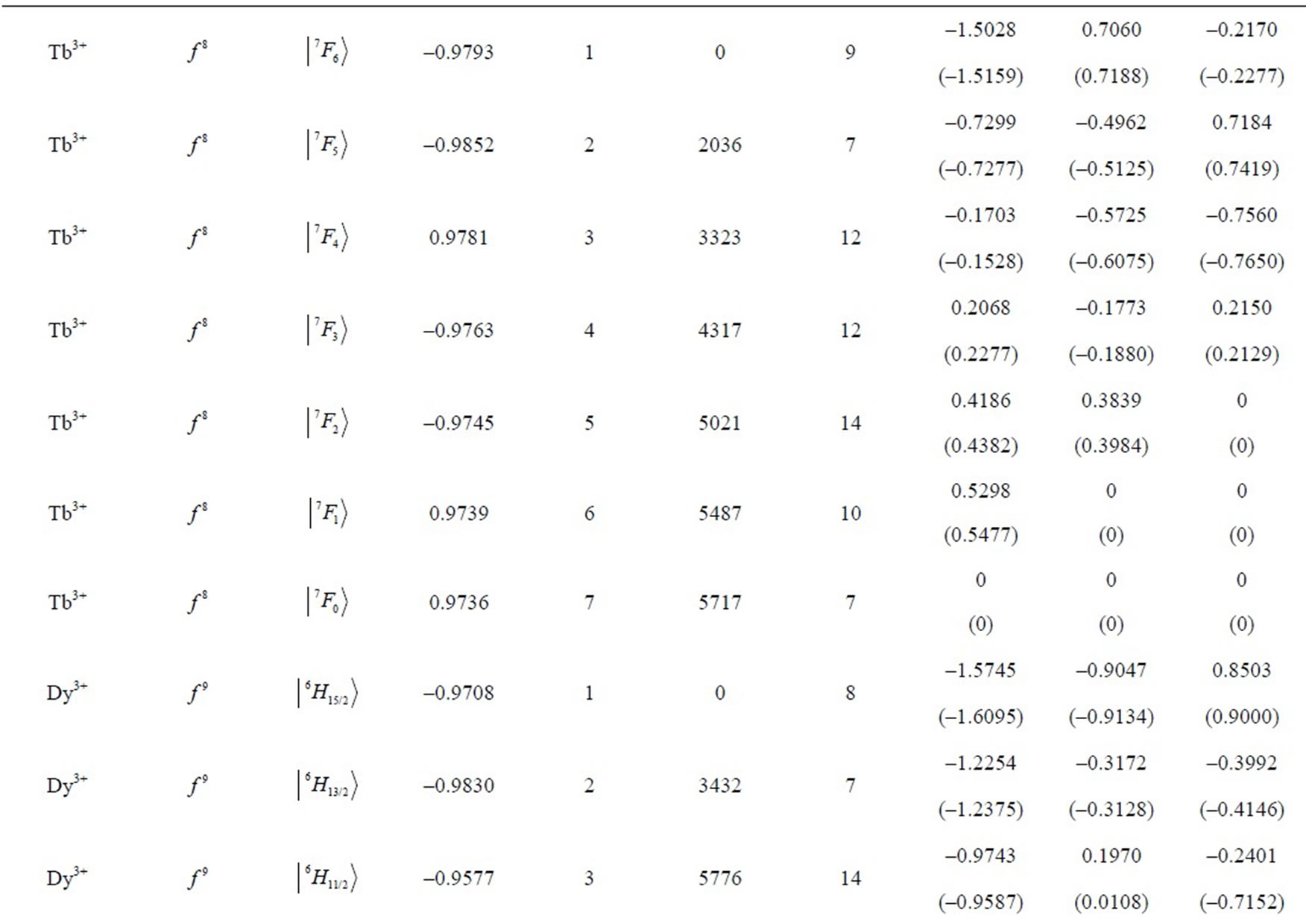
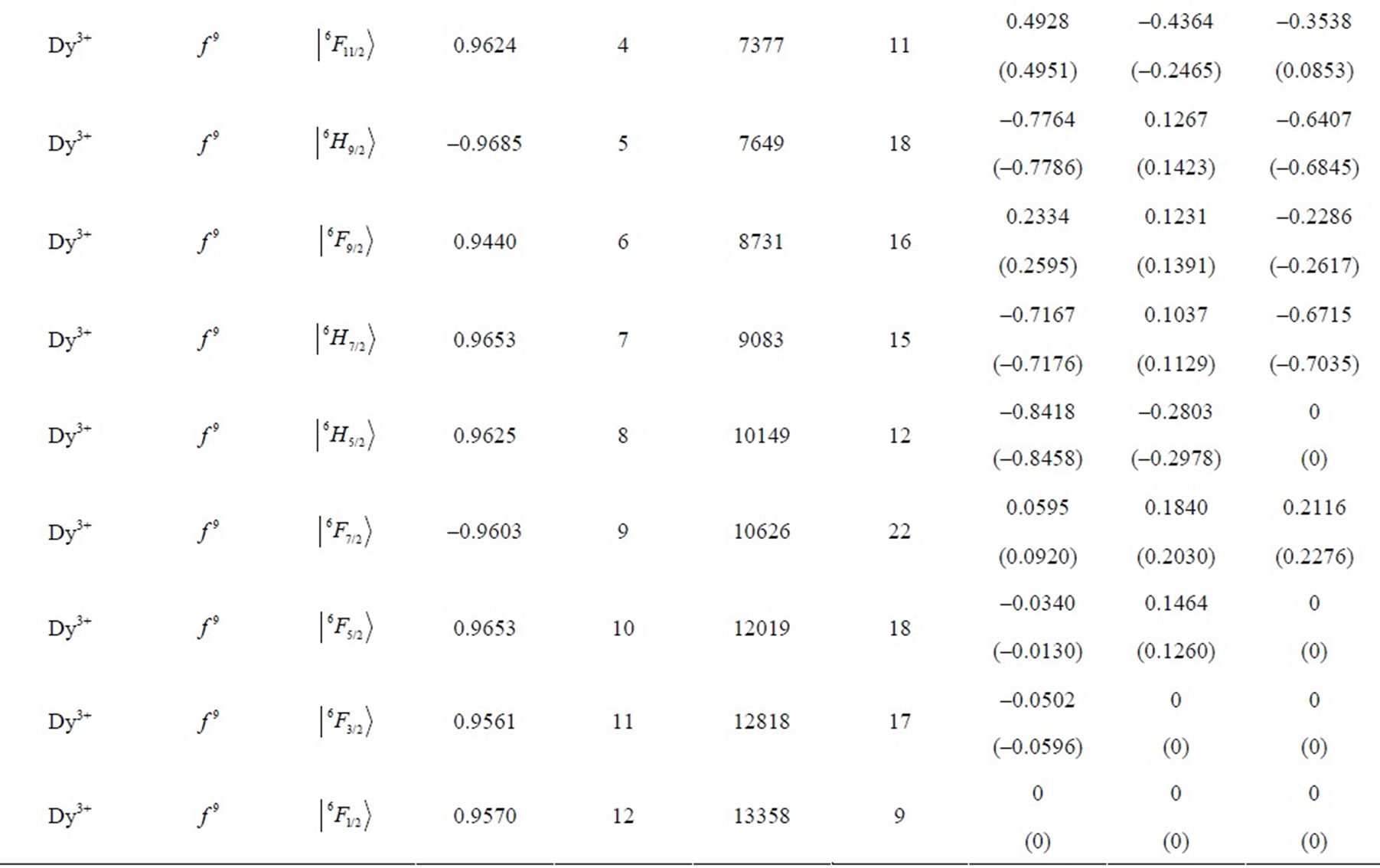
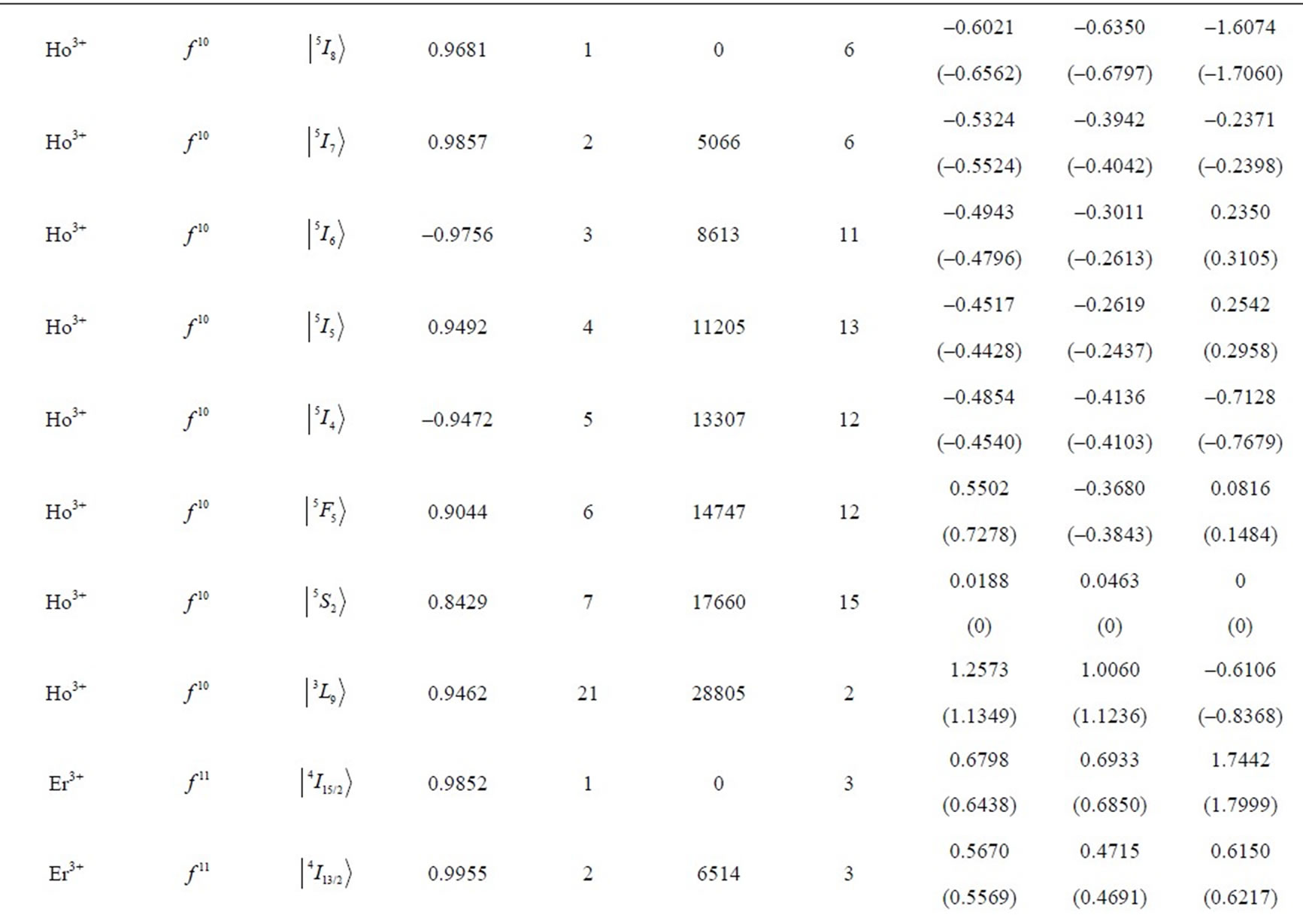
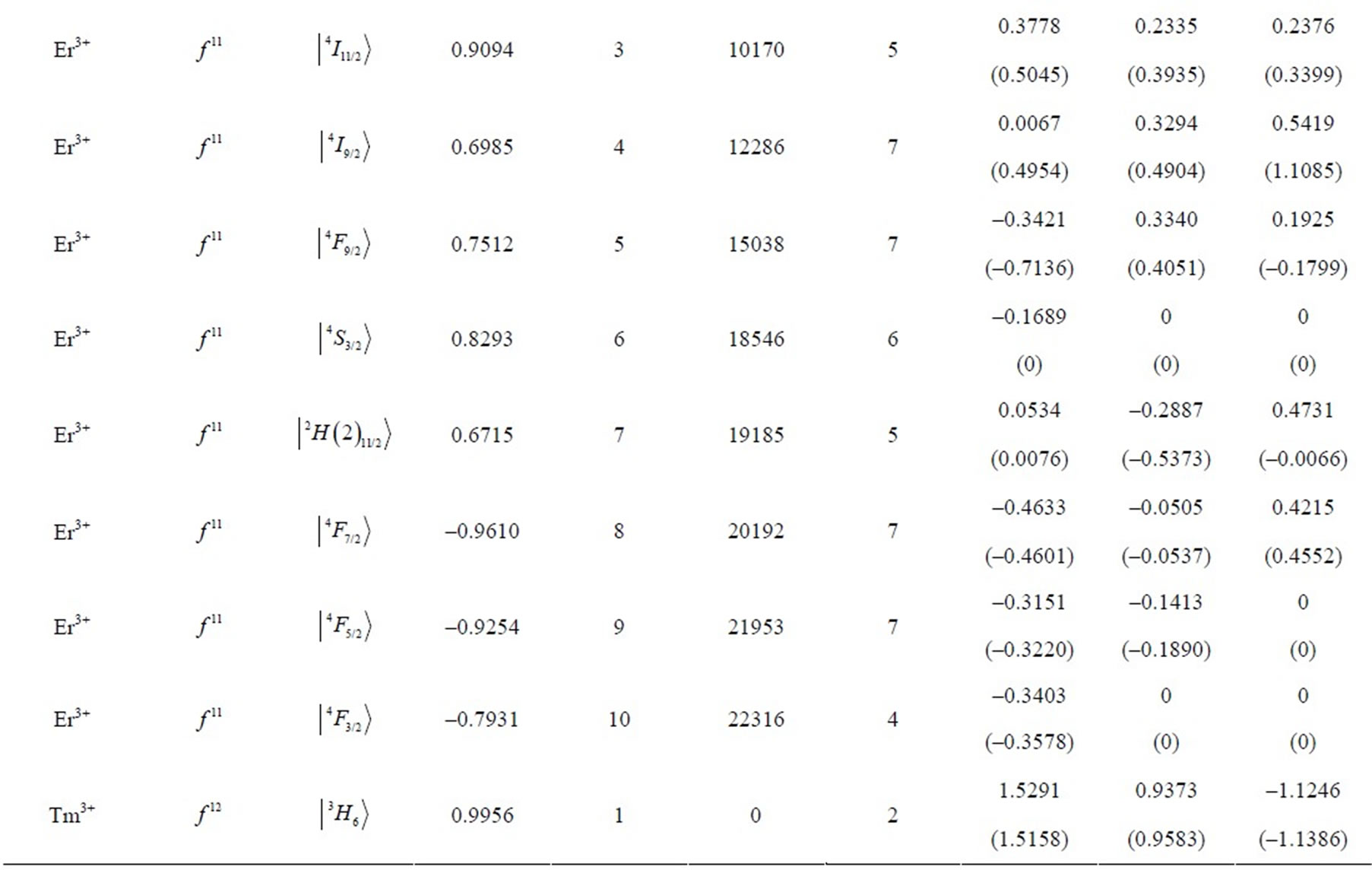
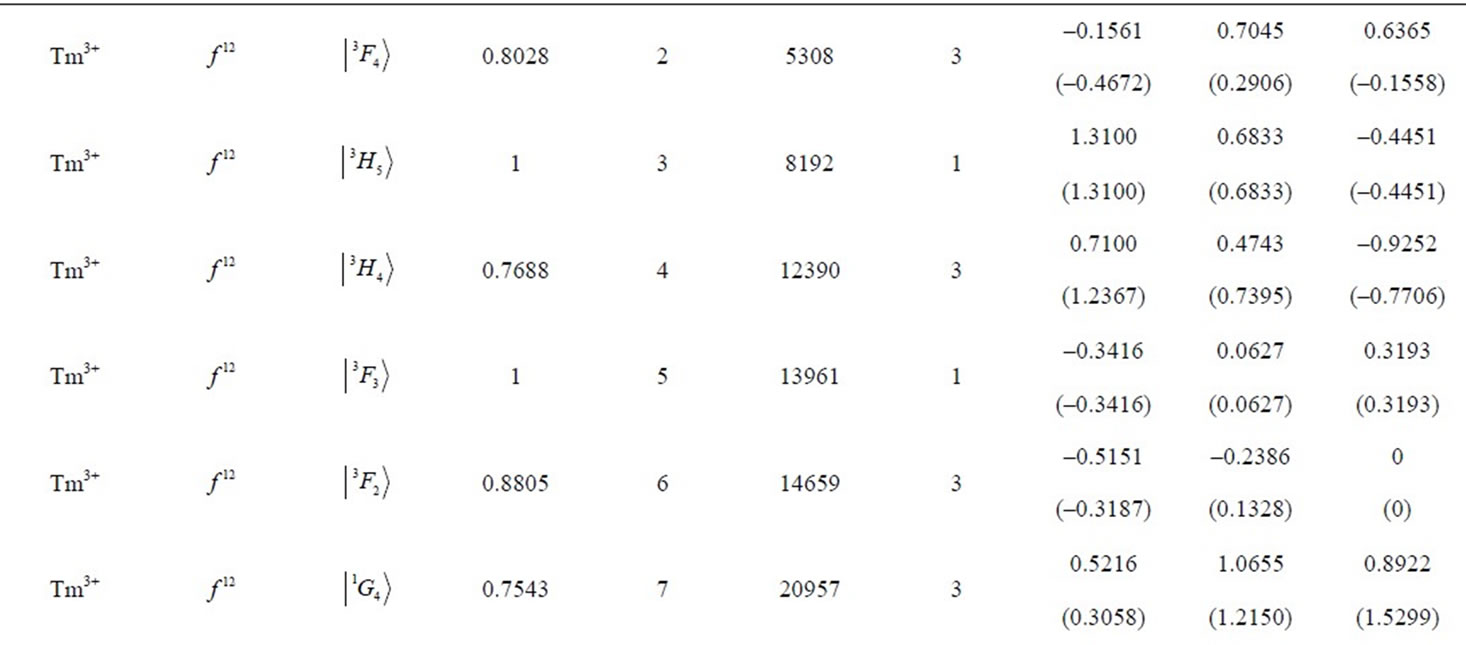

Table 1. Multipole character of the J-mixed electron eigenstates 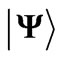 in RE free ions. The eigenfunctions and eigenvalues are calculated using M. Reid f-shell programs [7] and free-ion data reported by Carnall et al. [8]. The electron eigenstate data cover respectively: the upper component (Up.Comp.), its amplitude (Ampl.), consecutive no. in the spectrum [7] (no.), energy [cm–1] (E), number of components of amplitude >0.01 (n). The multipolar asphericities for the upper component of the state are given in the parentheses.
in RE free ions. The eigenfunctions and eigenvalues are calculated using M. Reid f-shell programs [7] and free-ion data reported by Carnall et al. [8]. The electron eigenstate data cover respectively: the upper component (Up.Comp.), its amplitude (Ampl.), consecutive no. in the spectrum [7] (no.), energy [cm–1] (E), number of components of amplitude >0.01 (n). The multipolar asphericities for the upper component of the state are given in the parentheses.
eigenstates obtained in the more accurate J-mixing approach based on the M. Reid f-shell programs [7] and the free-ion data reported by Carnall et al. [8]. In the considered J-mixed superpositions the average number of RS components is 7, whereas the average number of the constituent matrix elements is 13. In turn, the maximal number of the components reaches 22, whereas the maximal number of the matrix elements amounts to 64 (including 42 off-diagonal ones) what occurs for the 9th eigenstate of Dy3+ ion (Table 1) with 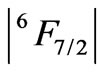 state as the upper component.
state as the upper component.
In total, we have taken into account 105 lower lying eigenstates of the three-valent RE ions from Ce3+ (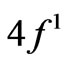 ) up to Yb3+ (
) up to Yb3+ (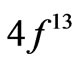 ). Table 1 lists also the basic attributes of the considered eigenstates: the upper RS component, its amplitude in the normalized superposition, the consecutive number in the ion’s spectrum [7], the eigenenergy in cm–1, and the number of components with the amplitude exceeding 0.01. It is instructive to compare the asphericities of the pure RS states [6] with those of the corrected J-mixed eigenstates. It turns out that from among the 105 analysed states only about 20% of them differ markedly in the asphericities from their RS counterparts, i.e. their upper states. Primarily, these are the states of the following ions: Tm3+ (
). Table 1 lists also the basic attributes of the considered eigenstates: the upper RS component, its amplitude in the normalized superposition, the consecutive number in the ion’s spectrum [7], the eigenenergy in cm–1, and the number of components with the amplitude exceeding 0.01. It is instructive to compare the asphericities of the pure RS states [6] with those of the corrected J-mixed eigenstates. It turns out that from among the 105 analysed states only about 20% of them differ markedly in the asphericities from their RS counterparts, i.e. their upper states. Primarily, these are the states of the following ions: Tm3+ (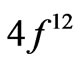 ), Er3+ (
), Er3+ (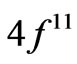 ), Nd3+ (
), Nd3+ ( ), and Pr3+ (
), and Pr3+ ( ) (Table 1). By sheer coincidence two various states of Tm3+ ion: the 8th and 12th are characterized by the same dominating component
) (Table 1). By sheer coincidence two various states of Tm3+ ion: the 8th and 12th are characterized by the same dominating component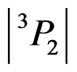 , but it does not lead to any misunderstanding because we do not use this ambiguous state description.
, but it does not lead to any misunderstanding because we do not use this ambiguous state description.
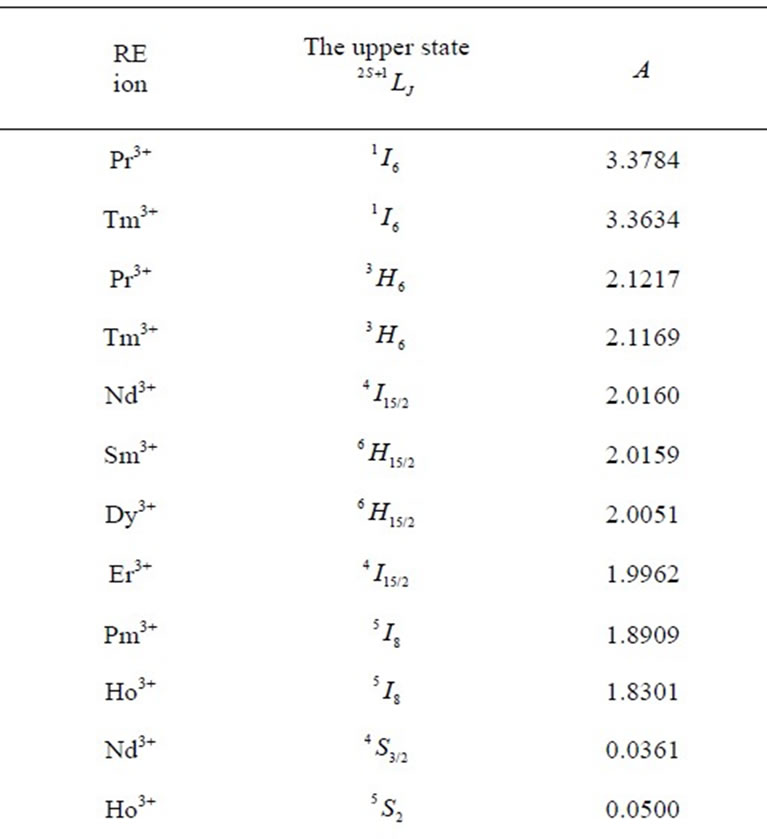
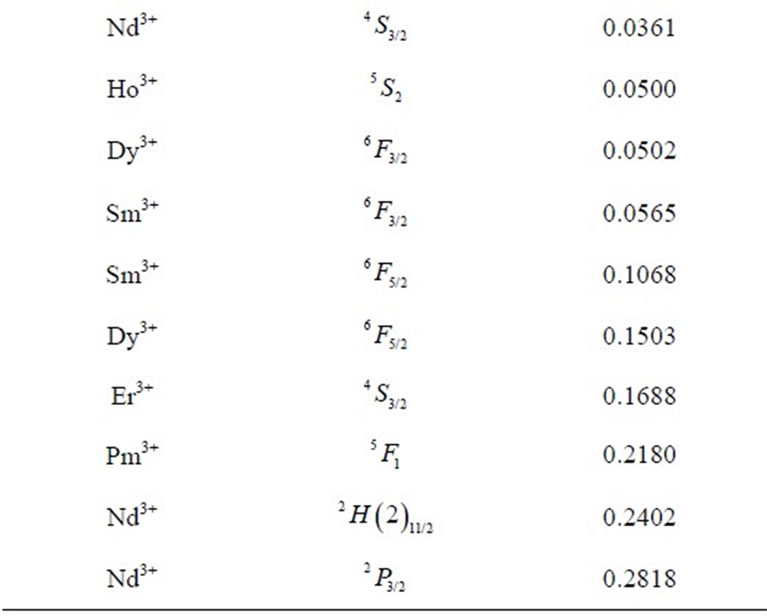
Table 2. Multipole characteristics of the RE+3 ion eigenstates (selected from Table 1) distinguished by the strongest (the upper half) and the weakest (the lower half) 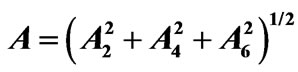 .
.
There exist the following J-mixing mechanisms that produce the observed changes in the asphericity of the states. Firstly, the normalization of any superposition of states reduces naturally the upper state amplitude, whereas its square determines the upper state asphericity input. Secondly, additional diagonal and off-diagonal terms in the the matrix element 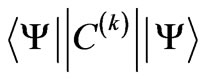 expansion differ in magnitudes and signs. The sign of each individual diagonal term is specified exclusively by the sign of the respective
expansion differ in magnitudes and signs. The sign of each individual diagonal term is specified exclusively by the sign of the respective 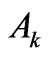 on the involved component. Its magnitude, however, comes from the product of
on the involved component. Its magnitude, however, comes from the product of  and the square of the component amplitude in the superposition. In turn, any off-diagonal term is a product of 6 factors including two involved amplitudes (Equation (2)).
and the square of the component amplitude in the superposition. In turn, any off-diagonal term is a product of 6 factors including two involved amplitudes (Equation (2)).
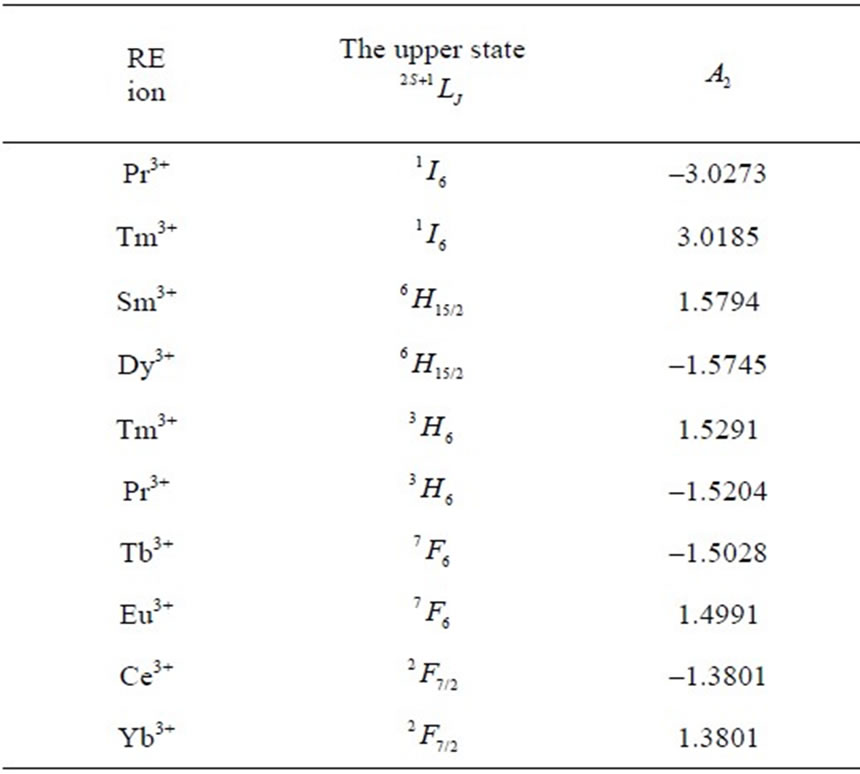
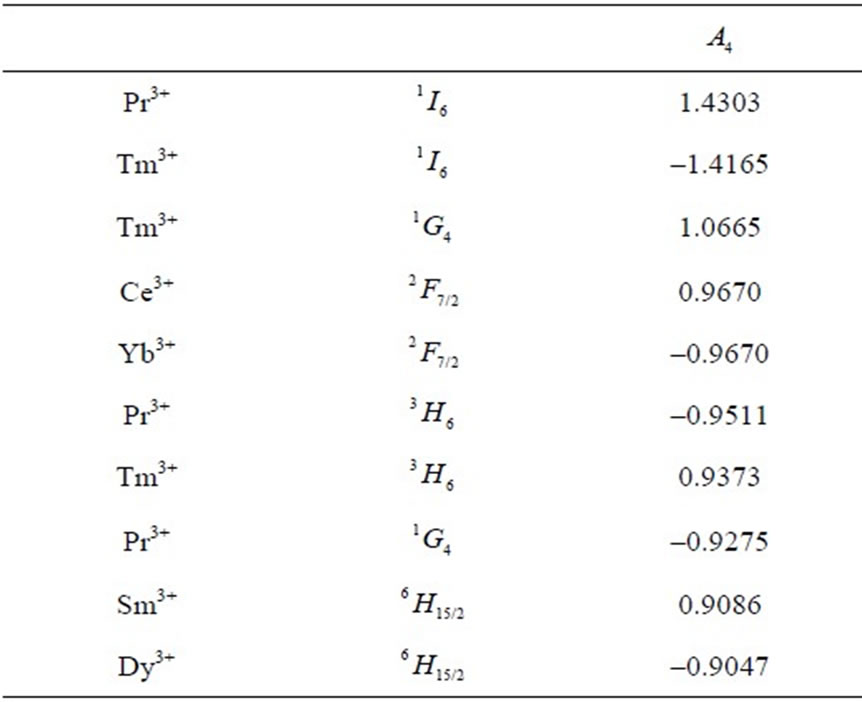
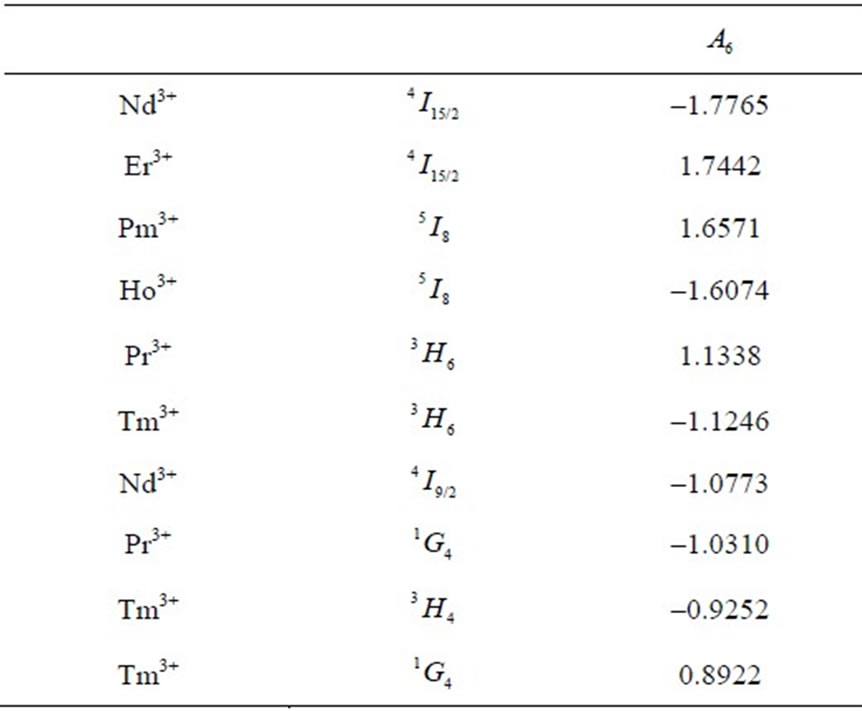
Table 3. Multipole characteristics of the RE+3 ion eigenstates (selected from Table 1) distinguished by the strongest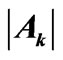 .
.
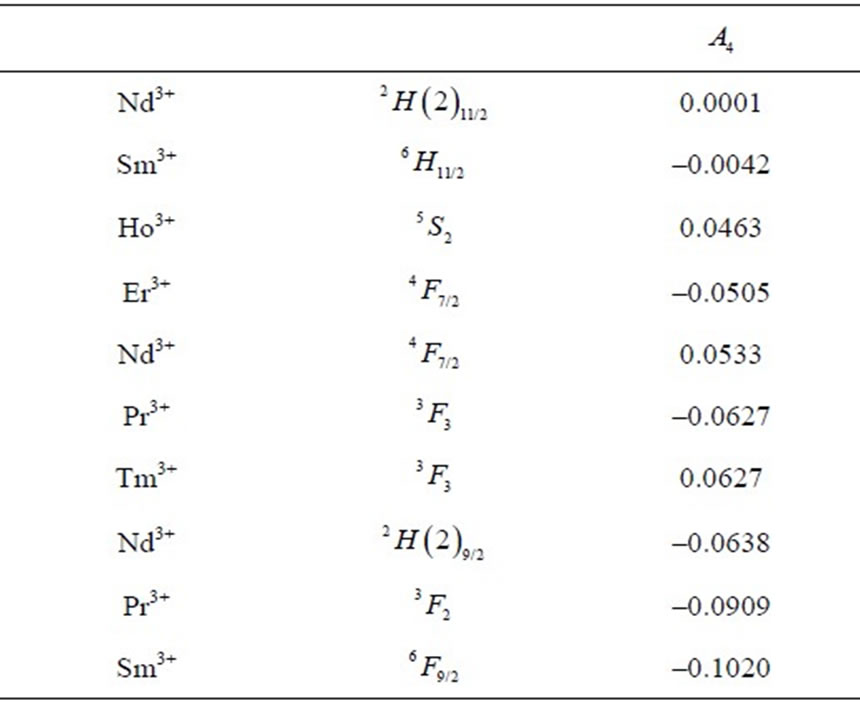

Table 4. Multipole characteristics of the RE+3 ion eigenstates (selected from Table 1) distinguished by the weakest .
.
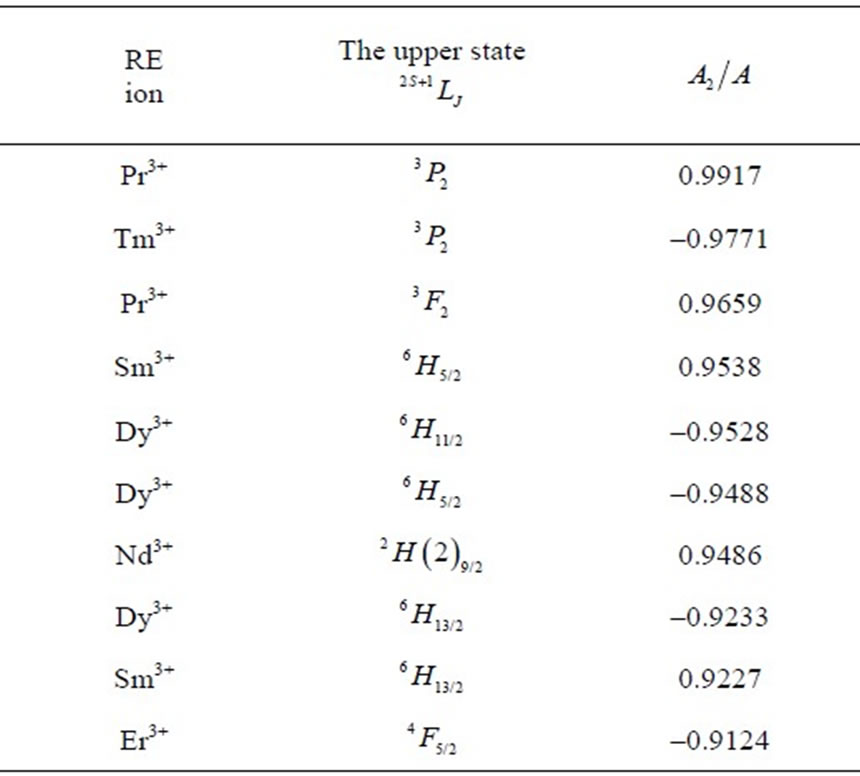
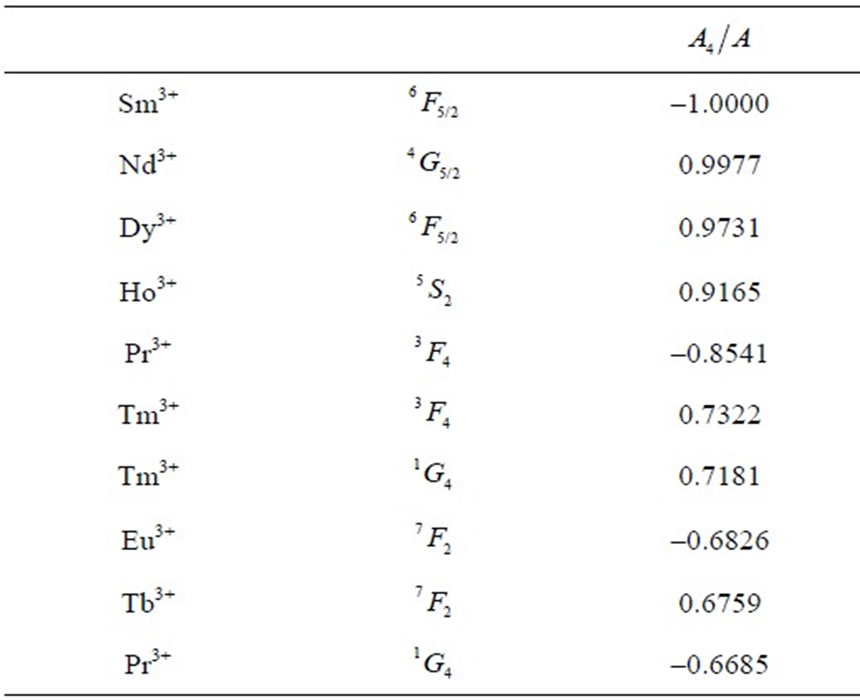

Table 5. Multipole characteristics of the RE+3 ion eigenstates (selected from Table 1) distinguished by the largest .
.
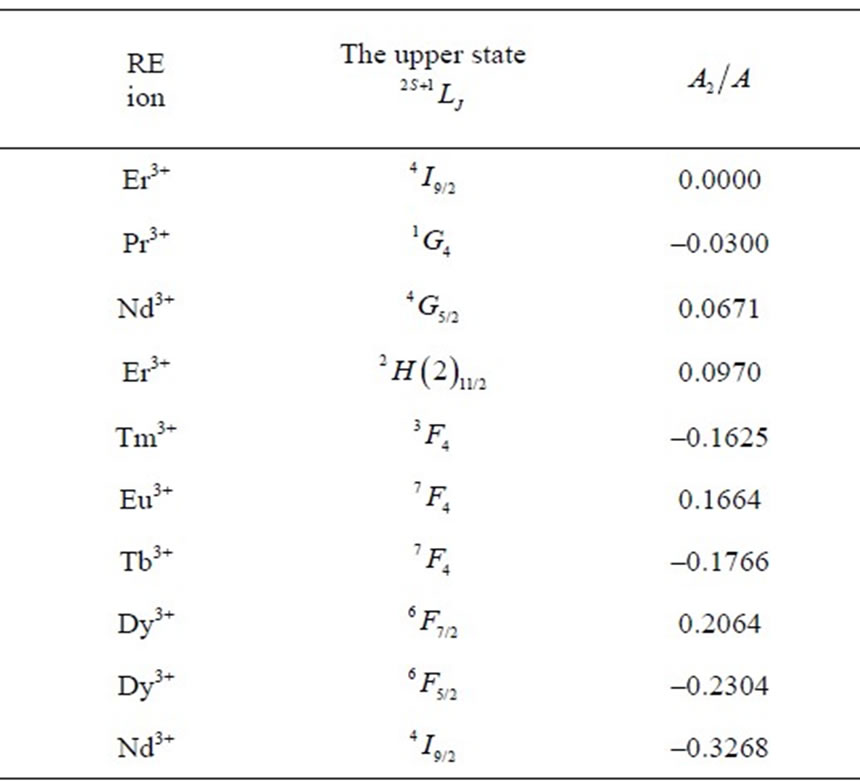
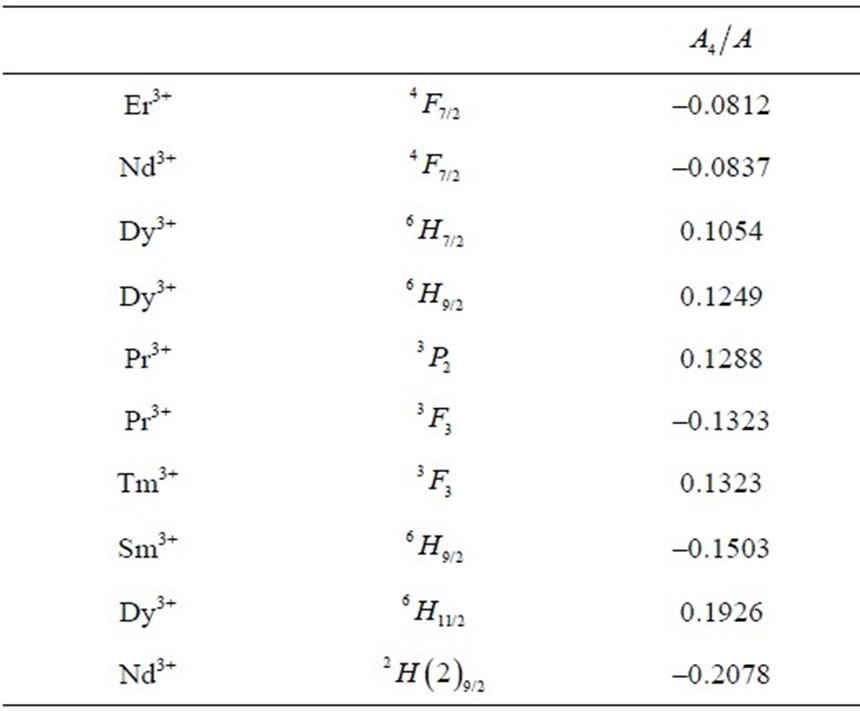
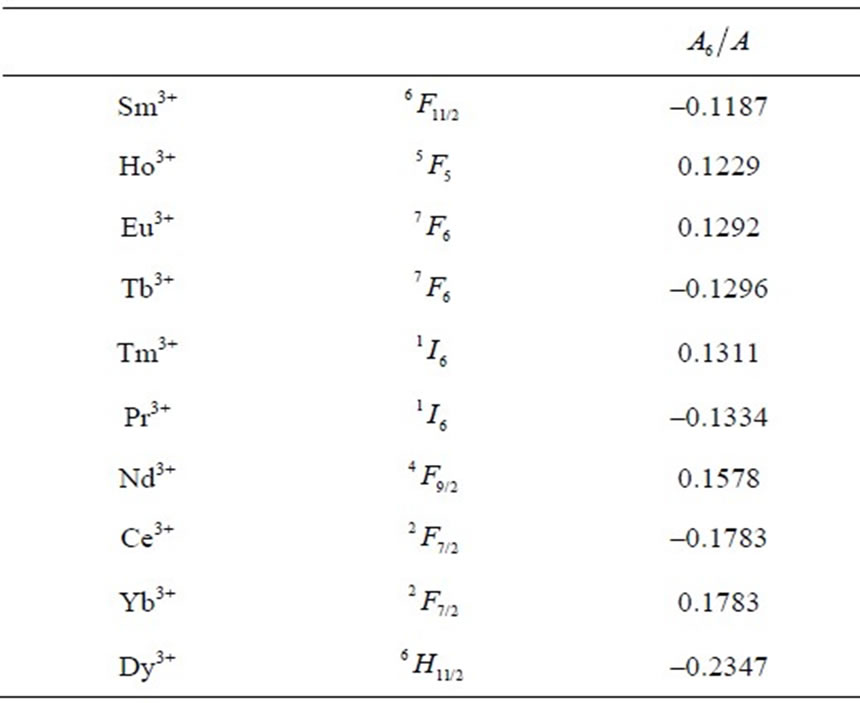
Table 6. Multipole characteristics of the RE+3 ion eigenstates (selected from Table 1) distinguished by the smallest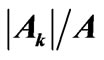 .
.
Its sign results from the product of 6 signs, and is in principle accidental. To cope with this matter effectively one should consider all the additional diagonal and offdiagonal contributions along with their various possible magnitudes and signs. Based on these investigations four types of the resultant Ak modifications can be noticed in Table 1.
· Due to insignificant J-mixing admixtures to the upper state only small changes (within a few percent) arise in the pertinent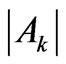 , which are the algebraic sum of the normalization effect and the additional diagonal and off-diagonal corrections. Such effect occurs for about 80% of the states listed in Table 1. However, the proximity of the Ak values for the RS and those for the corrected J-mixed states can be also accidental. For example, in the 23rd eigenstate of Nd3+ ion the amplitude of its upper state
, which are the algebraic sum of the normalization effect and the additional diagonal and off-diagonal corrections. Such effect occurs for about 80% of the states listed in Table 1. However, the proximity of the Ak values for the RS and those for the corrected J-mixed states can be also accidental. For example, in the 23rd eigenstate of Nd3+ ion the amplitude of its upper state 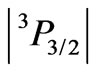 reaches merely 0.7205 and its contribution to
reaches merely 0.7205 and its contribution to 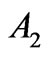 of the superposition is only
of the superposition is only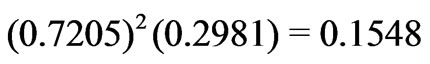 . Nevertheless, the remaining diagonal (0.2128) and off-diagonal (–0.0858) inputs are relatively large, and effectively lead to
. Nevertheless, the remaining diagonal (0.2128) and off-diagonal (–0.0858) inputs are relatively large, and effectively lead to  that accidentally is close to 0.2981, which is the value for the
that accidentally is close to 0.2981, which is the value for the 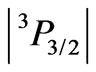 state.
state.
· The sum of the corrections is substantial with respect to Ak of the upper state and has the same sign as the Ak. Here an enhancement of 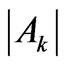 occurs. Such resultant effect is observed for the states: 13th of Nd3+, 7th of Er3+, 6th, 7th and 12th of Tm3+ in the case of
occurs. Such resultant effect is observed for the states: 13th of Nd3+, 7th of Er3+, 6th, 7th and 12th of Tm3+ in the case of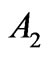 , for the states: 6th of Pr3+, 3rd and 4th of Dy3+, and 2nd of Tm3+ in the case of
, for the states: 6th of Pr3+, 3rd and 4th of Dy3+, and 2nd of Tm3+ in the case of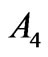 , and for the 4th state of Tm3+ in the case of
, and for the 4th state of Tm3+ in the case of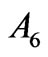 .
.
· The sum of the corrections is substantial but with the opposite sign than that of the upper state Ak. In this case a partial compensation of  (including the complete cancelation), or even the sign conversion of
(including the complete cancelation), or even the sign conversion of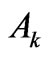 , takes place. Such result has been found in the case of
, takes place. Such result has been found in the case of 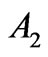 for the states: 6th and 7th of Pr3+, 7th, 10th and 11th of Nd3+, 6th of Ho3+, 3rd, 4th and 5th of Er3+, 2nd, 4th and 8th of Tm3+, in the case of
for the states: 6th and 7th of Pr3+, 7th, 10th and 11th of Nd3+, 6th of Ho3+, 3rd, 4th and 5th of Er3+, 2nd, 4th and 8th of Tm3+, in the case of 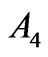 for the states: 7th and 8th of Pr3+, 7th, 10th and 11th of Nd3+, 4th, 5th and 7th of Er3+, 4th, 6th and 7th of Tm3+, and in the case of
for the states: 7th and 8th of Pr3+, 7th, 10th and 11th of Nd3+, 4th, 5th and 7th of Er3+, 4th, 6th and 7th of Tm3+, and in the case of 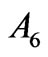 for the states: 1st, 6th and 7th of Pr3+, 7th, 10th, 11th and 13th of Nd3+, 3rd and 4th of Dy3+, 6th of Ho3+, 3rd, 4th, 5th and 7th of Er3+, 2nd and 7th of Tm3+.
for the states: 1st, 6th and 7th of Pr3+, 7th, 10th, 11th and 13th of Nd3+, 3rd and 4th of Dy3+, 6th of Ho3+, 3rd, 4th, 5th and 7th of Er3+, 2nd and 7th of Tm3+.
· The corrections generate the only contribution to Ak that for the initial state is equal to zero. It takes place for the states 12th of Pr3+ (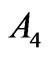 ), 9th of Nd3+ (
), 9th of Nd3+ (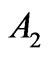 ), 7th of Ho3+ (
), 7th of Ho3+ ( ,
,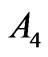 ), 6th of Er3+ (
), 6th of Er3+ (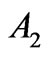 ), 8th and 12th of Tm3+ (
), 8th and 12th of Tm3+ (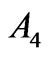 ).
).
The detailed mechanisms of the asphericity modifications induced by the J-mixing effect will be thoroughly analyzed for some representative examples in Section 6.
3. The Asphericity of an Electron Eigenstate and Its Crystal-Field Splitting
The asphericity Ak for 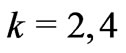 and 6 of any electronic state may serve as a reliable measure of its capability for CF splitting produced by the
and 6 of any electronic state may serve as a reliable measure of its capability for CF splitting produced by the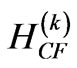 —the k-th component of the
—the k-th component of the![]() . It stems from the fundamental relationship between the CF splitting second moment
. It stems from the fundamental relationship between the CF splitting second moment 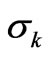 and the Ak [10,13,14]
and the Ak [10,13,14]
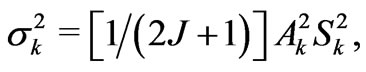 (3)
(3)
where 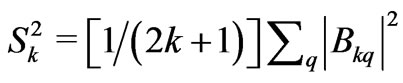 is the square of the CF strength of the 2k-pole
is the square of the CF strength of the 2k-pole ![]() component [9-12], and
component [9-12], and 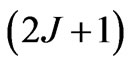 is the degeneracy of the given state with a good quantum number J. In fact, the above relationship (Equation (3)) arises from the spherical harmonic addition theorem [19] concerning the expansion of
is the degeneracy of the given state with a good quantum number J. In fact, the above relationship (Equation (3)) arises from the spherical harmonic addition theorem [19] concerning the expansion of  into the series of
into the series of ![]() components. They are the products of the conjugated spherical harmonics defined for the separated indices i and j. In the CF context the first factor refers to the electronic density angular distribution of the central ion unperturbed eigenstate, whereas the second refers to the surrounding charges. In fact, this separation lies in the background of the whole formalism exposing the scalar product nature of CF Hamiltonian.
components. They are the products of the conjugated spherical harmonics defined for the separated indices i and j. In the CF context the first factor refers to the electronic density angular distribution of the central ion unperturbed eigenstate, whereas the second refers to the surrounding charges. In fact, this separation lies in the background of the whole formalism exposing the scalar product nature of CF Hamiltonian.
As it is seen from Equation (3) the asphericity Ak can be treated as a potential capability of the considered state for the 2k-pole CF splitting since the second factor Sk represents a separate and unrelated external impact. The Ak can be either positive or negative (Section 2) what symbolically may be imagined as asphericities of convex or concave type. The Ak sign does not affect the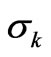 , but is crucial calculating the resultant asphericities of the superposition of states.
, but is crucial calculating the resultant asphericities of the superposition of states.
The question arises how the global second moment ![]() can be expressed by means of the asphericities of the involved electron eigenstate. As it is known, the square of the global second moment
can be expressed by means of the asphericities of the involved electron eigenstate. As it is known, the square of the global second moment 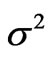 is a simple sum of the second moment squares of the individual components [6,10,13,14,20].
is a simple sum of the second moment squares of the individual components [6,10,13,14,20].
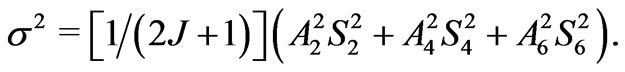 (4)
(4)
To describe 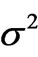 it is convenient to introduce two auxiliary vectors:
it is convenient to introduce two auxiliary vectors: 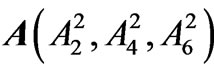 and
and 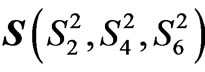 within the three-dimensional orthogonal reference frame based on the Ak (or Sk) axes. Then,
within the three-dimensional orthogonal reference frame based on the Ak (or Sk) axes. Then, 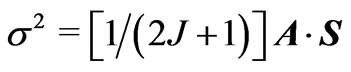 is defined by their scalar product. All the components of the A and S vectors are positive by definition and can be expressed by the spherical angular coordinates only within the ranges of
is defined by their scalar product. All the components of the A and S vectors are positive by definition and can be expressed by the spherical angular coordinates only within the ranges of 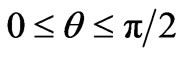 and
and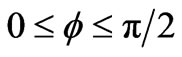 . Equation (4) shows that the CF splitting is determined by the two inseparable mutually entangled quantities Ak and Sk. The figurative vectors A and S may be orthogonal, what happens when both the vectors lie either along the two frame axes or one of them lies along an axis whereas the second belongs to the perpendicular plane. Then, always
. Equation (4) shows that the CF splitting is determined by the two inseparable mutually entangled quantities Ak and Sk. The figurative vectors A and S may be orthogonal, what happens when both the vectors lie either along the two frame axes or one of them lies along an axis whereas the second belongs to the perpendicular plane. Then, always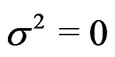 , in spite of some non-zero Ak and Sk. Simultaneously, Equation (4) enables us to critically verify the meaning of such quantities like
, in spite of some non-zero Ak and Sk. Simultaneously, Equation (4) enables us to critically verify the meaning of such quantities like 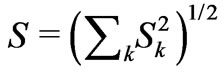 and
and ![]() [6]. In general, no apparent physical sense can be assigned to these quantities.
[6]. In general, no apparent physical sense can be assigned to these quantities.
4. The Range of Capability of the 4 f N Tripositive Free Ion Eigenstates for Crystal-Field Splitting
Similarly to the approximated RS states 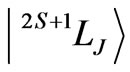 of triply ionized lanthanides [6], the eigenstates amended by the J-mixing [7] are characterized by an exceedingly diversified multipole structure both in qualitative and quantitative way (Table 1). Such random, to a large extent, diversity stems from a stochastic character with respect to the magnitude and sign of the multifactorial expression for the
of triply ionized lanthanides [6], the eigenstates amended by the J-mixing [7] are characterized by an exceedingly diversified multipole structure both in qualitative and quantitative way (Table 1). Such random, to a large extent, diversity stems from a stochastic character with respect to the magnitude and sign of the multifactorial expression for the 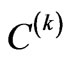 operator reduced matrix element (Equation (2)). The chaotic dispersion of the Ak magnitudes and signs is well exhibited in Tables 2-6 by the eigenstates chosen from among all the 105 studied ones: the top ten states of the strongest or weakest
operator reduced matrix element (Equation (2)). The chaotic dispersion of the Ak magnitudes and signs is well exhibited in Tables 2-6 by the eigenstates chosen from among all the 105 studied ones: the top ten states of the strongest or weakest 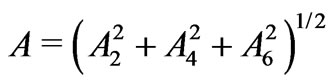 (Table 2), the ten of the strongest
(Table 2), the ten of the strongest 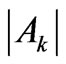 (Table 3), the ten of the weakest
(Table 3), the ten of the weakest 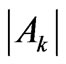 (Table 4), and finally the ten states of the highest
(Table 4), and finally the ten states of the highest 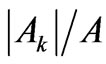 (Table 5), as well as the ten ones of the lowest
(Table 5), as well as the ten ones of the lowest 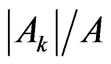 (Table 6). The
(Table 6). The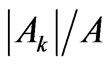 , which is a cosine of the angle between the
, which is a cosine of the angle between the  vector and the distinguished axis representing the Ak, gives the relative weight of the chosen 2k-pole in the eigenstate multipole structure. It is enough to notice that A takes values from 0 to 3.3784, whereas the entirely independent one of another
vector and the distinguished axis representing the Ak, gives the relative weight of the chosen 2k-pole in the eigenstate multipole structure. It is enough to notice that A takes values from 0 to 3.3784, whereas the entirely independent one of another  change within the ranges:
change within the ranges: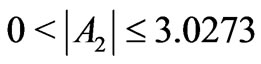 ,
, 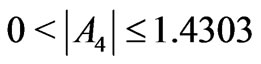 , and
, and . As it is seen, the multipole structure of the considered states is widely differentiated. In consequence, the states being characterized by only one prevailing multipole are not excluded. For example, the 12th eigenstate
. As it is seen, the multipole structure of the considered states is widely differentiated. In consequence, the states being characterized by only one prevailing multipole are not excluded. For example, the 12th eigenstate 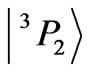 of Pr3+ ion is characterized by the predominant role of the 22-pole component
of Pr3+ ion is characterized by the predominant role of the 22-pole component 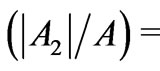
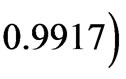 , the 9th eigenstate
, the 9th eigenstate 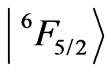 of Sm3+ ion by the 24-pole component
of Sm3+ ion by the 24-pole component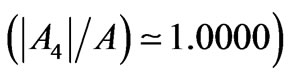 , and the 4th eigenstate
, and the 4th eigenstate 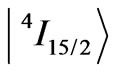 of Nd3+ ion by the prevailing 26-pole component
of Nd3+ ion by the prevailing 26-pole component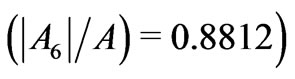 , however not so distinctly as in the two previous cases.
, however not so distinctly as in the two previous cases.
The highest total asphericities (the top A values), which represent the strongest total capabilities for the CF splitting, are found in the states with large L (and J) quantum numbers (Table 2). Such states are weakly disturbed by the J-mixing interaction due to a small number of the partner RS states of the same J and large energy gaps between them. Their calculated asphericities are close to those for the relevant upper states. On the contrary, the eigenstates with the weakest asphericities have quite often their Ak significantly changed with respect to those for their RS counterparts. In general, it results from a similar level of the J-mixing corrections in both the cases, and a substantial difference in their initial magnitudes.
Tables 1-6 indicate an evident correspondence between the calculated Ak for the pairs of the lanthanide ions with the complementary electron configurations 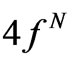 and
and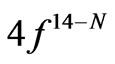 : (Ce3+, Yb3+), (Pr3+, Tm3+), (Nd3+, Er3+), (Pm3+, Ho3+), (Sm3+, Dy3+) and (Eu3+, Tb3+). The opposite Ak sign of the pair-partners results from the opposite sign of the related matrix elements of the
: (Ce3+, Yb3+), (Pr3+, Tm3+), (Nd3+, Er3+), (Pm3+, Ho3+), (Sm3+, Dy3+) and (Eu3+, Tb3+). The opposite Ak sign of the pair-partners results from the opposite sign of the related matrix elements of the ![]() operators [18], and is mainly a consequence of the Hund’s rules governing the eigenstates sequence, it means their location in the free-ion energy spectrum.
operators [18], and is mainly a consequence of the Hund’s rules governing the eigenstates sequence, it means their location in the free-ion energy spectrum.
The difference between the bottom parts of the energy diagrams of Pr3+ and Tm3+ ions serves as a good example of such case. In the energy spectrum of Pr3+ ion the RS states  and
and 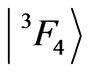 interacting via J-mixing are located one to another as far as possible: the
interacting via J-mixing are located one to another as far as possible: the 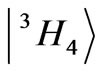 is the lowest state of the term
is the lowest state of the term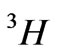 , whereas the
, whereas the 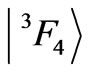 the highest one of the term
the highest one of the term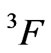 . In Tm3+ ion, in the reverse order, the
. In Tm3+ ion, in the reverse order, the 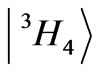 is the highest state of the
is the highest state of the 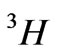 term, whereas the
term, whereas the 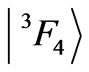 the lowest state of the term
the lowest state of the term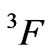 . In fact, the
. In fact, the 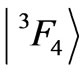 state lies below the state
state lies below the state 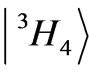 [16]. The energy gap between the states
[16]. The energy gap between the states 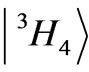 and
and , their so-called energy denominator, determines the efficiency of the J-mixing interaction.
, their so-called energy denominator, determines the efficiency of the J-mixing interaction.
5. Electronic State Capability for CF Splitting and Parametrization of the Involved CF Hamiltonian
Equations (3) and (4) reveal the direct relationship between the CF splitting second moments (![]() and
and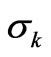 ) available from the experimentally fitted splitting diagrams, and the relevant Ak and Sk in the form of their products. Having known the capabilities Ak one gets the Sk which are consistent with the experimental data. Thus, we have an additional condition imposed on the CFPs for each individual multipole, i.e. for CFPs with a fixed k index. Therefore any correct fitting procedure must lead to CFPs obeying Equations (3) and (4). To fully realize the significance of the above defined capability of electronic states for CF splitting and its indispensability in practical CF calculations let us verify, as an example, the parametrization of the CF Hamiltonian for eight lower lying electronic states of Tm3+ ion doped into single crystal (C2 sites) of cubic yttrium oxide Y2O3 [21]:
) available from the experimentally fitted splitting diagrams, and the relevant Ak and Sk in the form of their products. Having known the capabilities Ak one gets the Sk which are consistent with the experimental data. Thus, we have an additional condition imposed on the CFPs for each individual multipole, i.e. for CFPs with a fixed k index. Therefore any correct fitting procedure must lead to CFPs obeying Equations (3) and (4). To fully realize the significance of the above defined capability of electronic states for CF splitting and its indispensability in practical CF calculations let us verify, as an example, the parametrization of the CF Hamiltonian for eight lower lying electronic states of Tm3+ ion doped into single crystal (C2 sites) of cubic yttrium oxide Y2O3 [21]: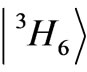 ,
, 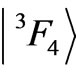 ,
, 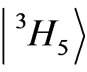 ,
, 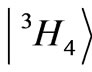 ,
, 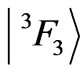 ,
, 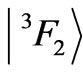 ,
, 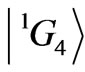 , and
, and 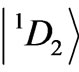 (Table 1). Mind the 8th state of Tm3+ ion (Table 1), the amplitude of the
(Table 1). Mind the 8th state of Tm3+ ion (Table 1), the amplitude of the 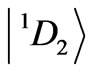 component is equal to 0.5871, so it is not the actual upper component.
component is equal to 0.5871, so it is not the actual upper component.
Based on Table IX in [21] all the eight 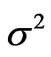 values for the considered states are known and amount to in [(cm–1)2]: 70205, 40019, 45836, 29941, 2965, 13548, 83061 and 10004 in order of the above mentioned states. Next, all the needed capabilities (asphericities)
values for the considered states are known and amount to in [(cm–1)2]: 70205, 40019, 45836, 29941, 2965, 13548, 83061 and 10004 in order of the above mentioned states. Next, all the needed capabilities (asphericities) 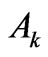 calculated for the corrected electronic states of Tm3+ ion by M. Reid [7] are compiled in Table 1. We have then the following set of eight linear equations (of Equation (4) type) for
calculated for the corrected electronic states of Tm3+ ion by M. Reid [7] are compiled in Table 1. We have then the following set of eight linear equations (of Equation (4) type) for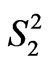 ,
, 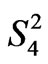 and
and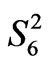 :
:
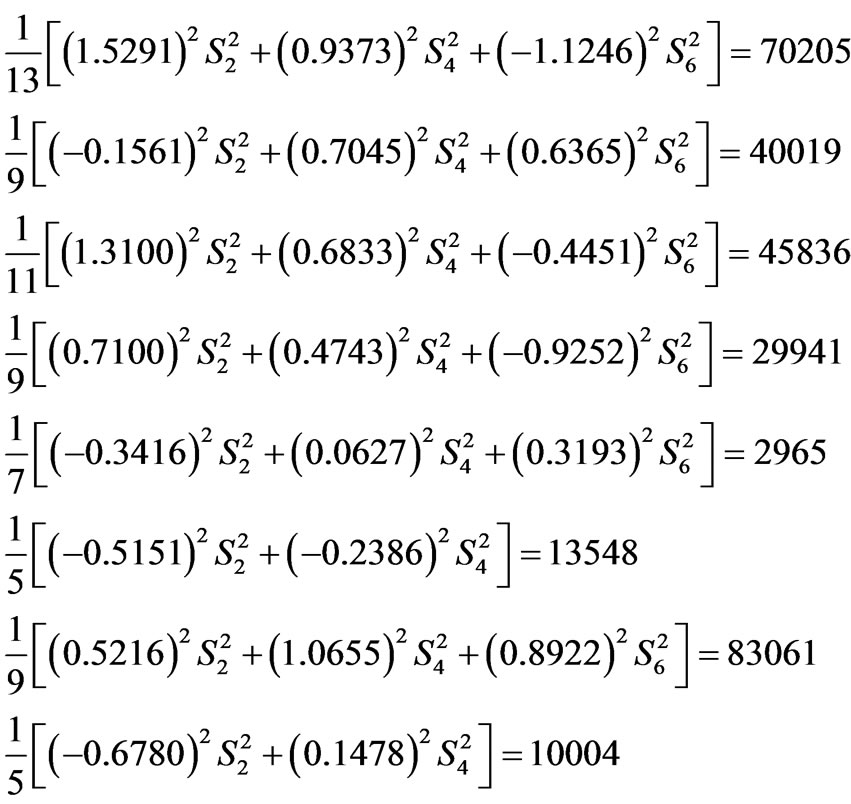 (5)
(5)
By definition, only positive solution is admitted, what is rather a strong requirement. For the corrected Tm3+ free-ion eigenstates we have found the proper solution of (Equation (5)). By means of the least square deviations Gauss method we have obtained in [(cm–1)2]: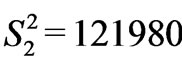 ,
, 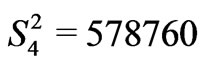 , and
, and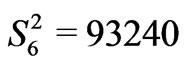 . The second moments calculated for these values of Sk are: 70120, 36440, 45280, 30170, 3715, 13060, 84940 and 13740, respectively. Taking into account all possible inaccuracies in the estimated
. The second moments calculated for these values of Sk are: 70120, 36440, 45280, 30170, 3715, 13060, 84940 and 13740, respectively. Taking into account all possible inaccuracies in the estimated 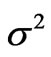 and in the calculated
and in the calculated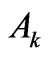 , as well as their wide ranges of variation, the presented calculations reproduce the observed
, as well as their wide ranges of variation, the presented calculations reproduce the observed 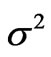 quite accurately.
quite accurately.
The role of the capabilities 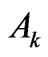 in the approach is readable. It is proper to add that there is no solution of Equation (5) in the case of
in the approach is readable. It is proper to add that there is no solution of Equation (5) in the case of 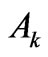 for the pure RS eigenstates of Tm3+ ion.
for the pure RS eigenstates of Tm3+ ion.
The presented example highlights the 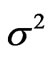 additivity principle which ensures the appropriate multipole moments yielded by the surroundings of Tm3+ ion in Y2O3 crystal lattice. Additionally, it evidences a good quality fitting of the CF levels given in [21] and the correctness of the RE3+ free-ion electronic eigenstates composition calculated by M. Reid [7].
additivity principle which ensures the appropriate multipole moments yielded by the surroundings of Tm3+ ion in Y2O3 crystal lattice. Additionally, it evidences a good quality fitting of the CF levels given in [21] and the correctness of the RE3+ free-ion electronic eigenstates composition calculated by M. Reid [7].
The CFPs for Tm3+:Y2O3 given in Table IV [21] yield the following ![]() in [(cm–1)2]:
in [(cm–1)2]: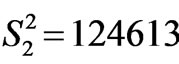 ,
, 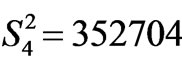 , and
, and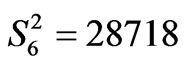 , which differ from those obeying the
, which differ from those obeying the 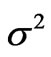 additivity. Although the corresponding CFPs reproduce the considered CF splitting diagrams [21] sufficiently well they do not represent the proper multipolar characteristics of the
additivity. Although the corresponding CFPs reproduce the considered CF splitting diagrams [21] sufficiently well they do not represent the proper multipolar characteristics of the 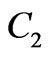 site in Y2O3.
site in Y2O3.
Similar breaking of the multipolar additivity of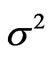 , calculated from the fitted parametrization of the corresponding CF Hamiltonian, has been evidenced previously for Nd3+:Y2O3 [20]. One can therefore suspect a remarkable part of published
, calculated from the fitted parametrization of the corresponding CF Hamiltonian, has been evidenced previously for Nd3+:Y2O3 [20]. One can therefore suspect a remarkable part of published ![]() parametrizations to suffer from this type of physical shortcoming. This can be also a source of the overwhelming inflation of formally good but non-equivalent
parametrizations to suffer from this type of physical shortcoming. This can be also a source of the overwhelming inflation of formally good but non-equivalent ![]() parametrizations. Concluding, the capabilities
parametrizations. Concluding, the capabilities 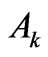 for the free-ion eigenstates of tripositive rare-earth ions given in Table 1 are crucial in order to verify any related CF Hamiltonian.
for the free-ion eigenstates of tripositive rare-earth ions given in Table 1 are crucial in order to verify any related CF Hamiltonian.
6. Discussion
The calculated asphericities 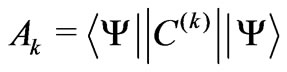 of the trivalent
of the trivalent 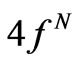 ions are not the actual ones due to approximate nature of the applied eigenfunctions
ions are not the actual ones due to approximate nature of the applied eigenfunctions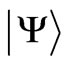 , but their reliability can be improved replacing the initial functions (e.g. those of the RS type) by their various superpositions. In the case of simultaneous diagonalisation of the interaction matrix including the Coulomb repulsion and the spin-orbit coupling these are the superpositions of the RS functions with the same J but different L and S quantum numbers [7]. The
, but their reliability can be improved replacing the initial functions (e.g. those of the RS type) by their various superpositions. In the case of simultaneous diagonalisation of the interaction matrix including the Coulomb repulsion and the spin-orbit coupling these are the superpositions of the RS functions with the same J but different L and S quantum numbers [7]. The 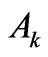 variations seen in Table 1 are limited mainly by the scale of the component admixtures. Additional role is played by magnitudes of the relevant diagonal and off-diagonal matrix elements of the
variations seen in Table 1 are limited mainly by the scale of the component admixtures. Additional role is played by magnitudes of the relevant diagonal and off-diagonal matrix elements of the  operator within the superposition, as well as the mutual competition between the corrections. In most cases the amplitudes of the admixtures are rather small. Therefore, for the majority of the lower lying eigenstates (about 80%) of the trivalent lanthanide ions there appear only insignificant differences between the
operator within the superposition, as well as the mutual competition between the corrections. In most cases the amplitudes of the admixtures are rather small. Therefore, for the majority of the lower lying eigenstates (about 80%) of the trivalent lanthanide ions there appear only insignificant differences between the  calculated for the model RS states [6] and those including their J-mixing (Table 1). Nevertheless, for certain part of the eigenstates, particularly the exited ones, the observed changes become essential, indeed. They illustrate well the types of the resultant J-mixing effects mentioned in Section 2. Some instructive mechanisms leading to such variations are analyzed in details for several chosen examples below.
calculated for the model RS states [6] and those including their J-mixing (Table 1). Nevertheless, for certain part of the eigenstates, particularly the exited ones, the observed changes become essential, indeed. They illustrate well the types of the resultant J-mixing effects mentioned in Section 2. Some instructive mechanisms leading to such variations are analyzed in details for several chosen examples below.
Let us consider the 6th state of Pr3+ ion (Table 1) of the composition:
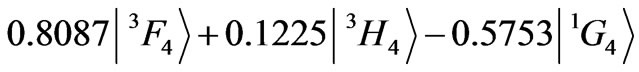
with the dominant  component. The diagonal contributions to the
component. The diagonal contributions to the  amount to:
amount to:
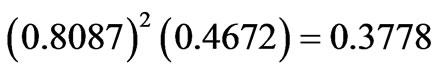 ,
,
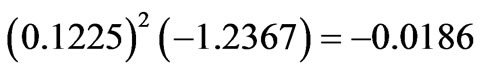 ,
,
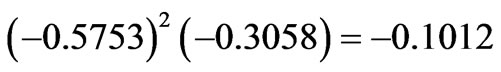 and the only off-diagonal input
and the only off-diagonal input
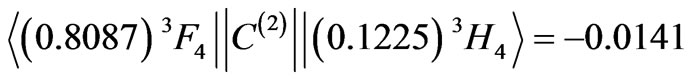 .
.
The accumulation of the three negative corrections reduces the 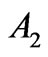 from 0.4672 down to 0.2439. The diagonal contributions to the
from 0.4672 down to 0.2439. The diagonal contributions to the  are negative and reach:
are negative and reach:
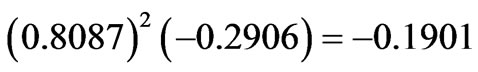 ,
,
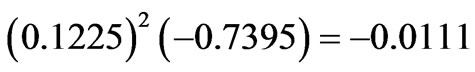 ,
,
 and the off-diagonal element
and the off-diagonal element
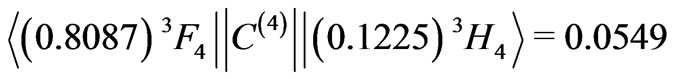 .
.
Here, the strong diagonal input of the 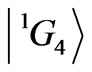 determines the magnitude and sign of the
determines the magnitude and sign of the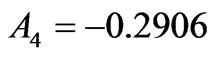 . In turn, the diagonal contributions to the
. In turn, the diagonal contributions to the 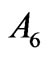 are equal to:
are equal to:
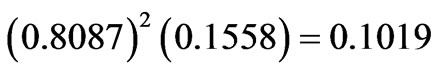 ,
,
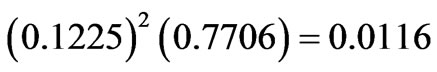 ,
,
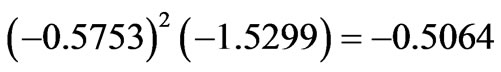 and the off-diagonal input is
and the off-diagonal input is
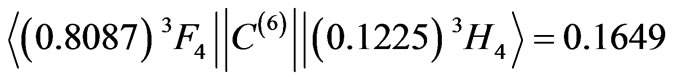 .
.
Again, as above, the diagonal negative input of the 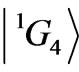 dominates and the ultimate
dominates and the ultimate 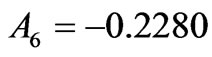 results from a partial compensation of all the contributions.
results from a partial compensation of all the contributions.
The 7th state of Nd3+ ion, is composed of
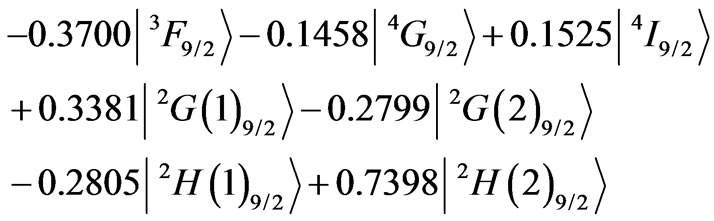
with the prevailing 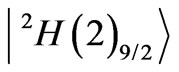 state. All the weak diagonal contributions to the
state. All the weak diagonal contributions to the 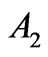 are almost compensated achieving in sum 0.0092 with respect to the dominant state input
are almost compensated achieving in sum 0.0092 with respect to the dominant state input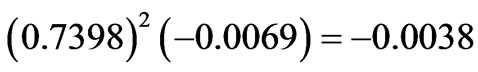 . The decisive are the positive off-diagonal terms
. The decisive are the positive off-diagonal terms
 along with
along with
 giving finally the
giving finally the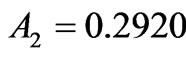 . Here, the dominant state input to the A4 amounts to
. Here, the dominant state input to the A4 amounts to 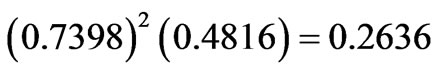 and the sum of all the seven diagonal elements 0.1675 is somewhat less. In this situation the relatively large and negative off-diagonal element
and the sum of all the seven diagonal elements 0.1675 is somewhat less. In this situation the relatively large and negative off-diagonal element
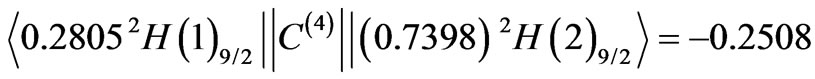
decides both on the magnitude and sign of the A4 = –0.0638. Similarly, for the very small positive sum of the partial diagonal elements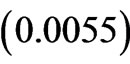 , the final A6 = –0.0732 is determined by the prevailing, as for the modulus, negative off-diagonal element
, the final A6 = –0.0732 is determined by the prevailing, as for the modulus, negative off-diagonal element
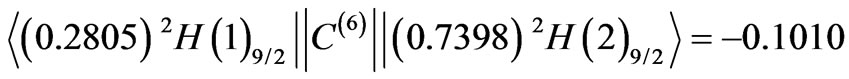 .
.
The 11th state of the Nd3+, is given by
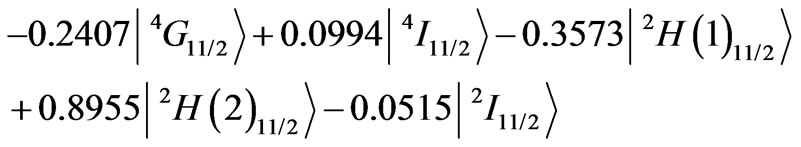
with the dominant 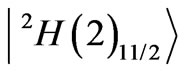 component. The sum of the diagonal contributions to the A2 is –0.0740, including the input –0.0632 from the
component. The sum of the diagonal contributions to the A2 is –0.0740, including the input –0.0632 from the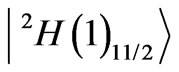 . The resultant
. The resultant 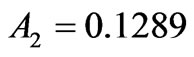 is the outcome of mutual competition of the positive off-diagonal term given by
is the outcome of mutual competition of the positive off-diagonal term given by
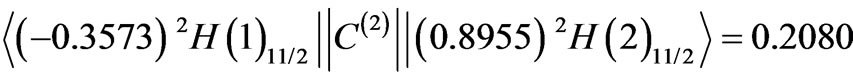
and the negative diagonal contribution coming mainly from the state . The sum of the diagonal elements combining to the A4 amounts to 0.4454 and is close to the contribution of the dominating
. The sum of the diagonal elements combining to the A4 amounts to 0.4454 and is close to the contribution of the dominating 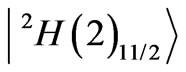 state, i.e.
state, i.e.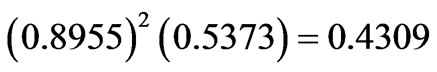 . However, it is practically entirely compensated
. However, it is practically entirely compensated  by the sum of two negative off-diagonal elements:
by the sum of two negative off-diagonal elements:
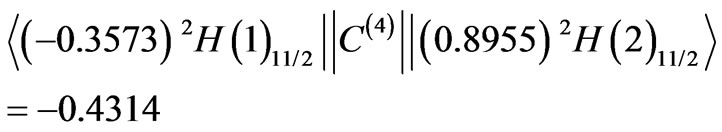
and
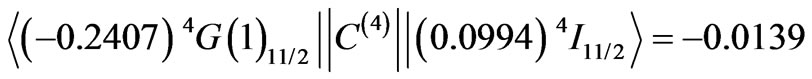 .
.
The resultant 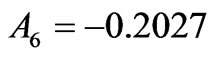 is determined by relatively strong off-diagonal input
is determined by relatively strong off-diagonal input
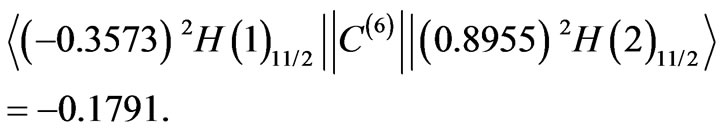
All the diagonal elements contribute only –0.0081.
The J-mixing of the RS states can activate some idle states making them susceptible to CF splittings. In other words, they lose their initial effective spherical symmetry. As an example let us examine the 6th state od Er3+ ion consisting of
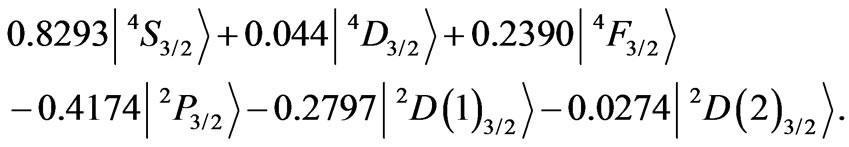
The prevailing element 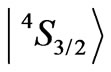 is characterized by zero asphericities
is characterized by zero asphericities ,
, 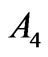 and
and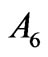 . However, the corrected eigenstate acquires the asphericity
. However, the corrected eigenstate acquires the asphericity 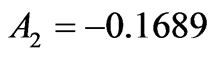 by accumulation of the negative diagonal contributions:
by accumulation of the negative diagonal contributions:
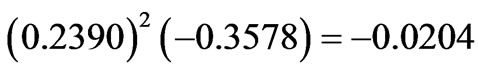 ,
,
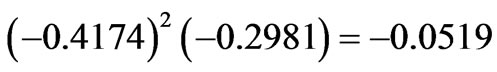 ,
,
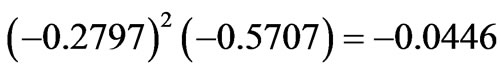 and the off-diagonal ones:
and the off-diagonal ones:
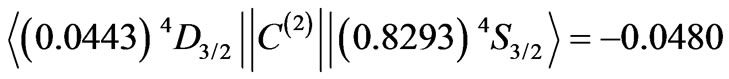 ,
,
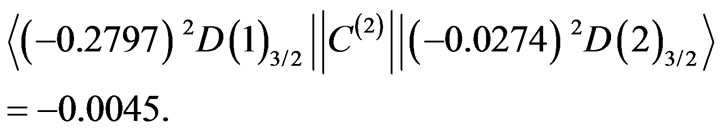
The states 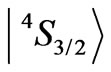 and
and 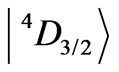 do not bring any diagonal inputs, and the state
do not bring any diagonal inputs, and the state 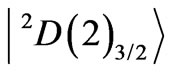 gives only 0.0005.
gives only 0.0005.
The ground state of Pr3+ ion is given by
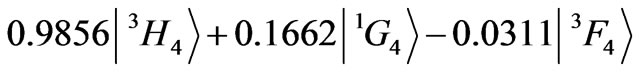
and its A2 and A4 asphericities change only slightly with respect to the parameters for the pure 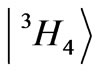 state. However, the
state. However, the ![]() asphericity is noticeably reduced. The diagonal contribution of the
asphericity is noticeably reduced. The diagonal contribution of the  state
state
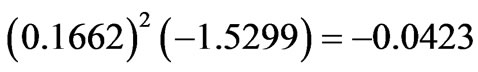 and the off-diagonal term
and the off-diagonal term

weaken the positive input of the 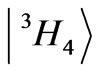 upper state
upper state 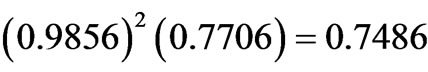 down to the value of 0.6555. It corresponds to attenuation of the state capability for the CF splitting by
down to the value of 0.6555. It corresponds to attenuation of the state capability for the CF splitting by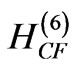 . An increase in both the
. An increase in both the 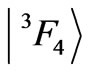 and
and 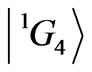 admixtures deepen the tendency. It is worth to remember analyzing the CF splitting of the
admixtures deepen the tendency. It is worth to remember analyzing the CF splitting of the 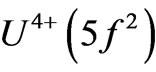 ion ground state.
ion ground state.
As is seen in Equation (3) the multipole characteristics of the electron eigenstates along with their CF splitting diagrams sheds a new light on the crystal matrix multipole structure and vice versa. Based on the CF splitting diagrams for several electron eigenstates of known multipole characteristics in a specified crystal matrix (with a definite![]() ), as well as the CF splitting diagrams of a specified eigenstate in various CF matrices, we can reconcile the actual
), as well as the CF splitting diagrams of a specified eigenstate in various CF matrices, we can reconcile the actual 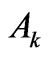 for the considered electronic states and the
for the considered electronic states and the 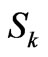 for the CF Hamiltonians, respectively. A great facilitation in such estimations is an incomplete multipolar structure of the analyzed eigenstates. Such incompleteness may result either from the triangle rule for J, J, k numbers (e.g. for
for the CF Hamiltonians, respectively. A great facilitation in such estimations is an incomplete multipolar structure of the analyzed eigenstates. Such incompleteness may result either from the triangle rule for J, J, k numbers (e.g. for 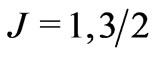 and
and 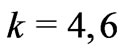 or
or 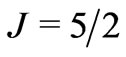 and
and ) or from accidental cancelation of some multipoles due to the J-mixing effect, as it is observed for the 11th state of Nd3+ and the 4th state of Er3+ ions in Table 1. Furthermore, in some CF Hamiltonians the three-component multipole structure is not always complete, like e.g. in the cubic
) or from accidental cancelation of some multipoles due to the J-mixing effect, as it is observed for the 11th state of Nd3+ and the 4th state of Er3+ ions in Table 1. Furthermore, in some CF Hamiltonians the three-component multipole structure is not always complete, like e.g. in the cubic ![]() which has no quadrupolar component.
which has no quadrupolar component.
In order to properly classify the multipolar characteristics of both the electronic eigenstates and the actual CF Hamiltonians we have to apply such kind of comprehensive reconciliations. The fitted CFP sets, that well reproduce the experimental spectrum of energy levels for intentionally approximated initial eigenfunctions, have by definition an effective character. Therefore, applying the same approximation for all eigenfunctions coming from different energy ranges will undoubtedly lead to errors. Presumably, this is the main reason for difficulties associated with minimization of rms deviations in fitted CFP sets. There are some phenomenological attempts to improve the fitting accuracy. In one of them the two-electron correlation CF is introduced, which may be simply expressed by an effective one-electron CF Hamiltonian being dependent on the considered electronic term. In another one the mean k powers of the unpaired electron radii 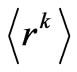 is made variable with respect to the electron term [5,22-24]. Both the above approaches are formally admissible, but they can be physically ungrounded.
is made variable with respect to the electron term [5,22-24]. Both the above approaches are formally admissible, but they can be physically ungrounded.
Yet another reflection arises. The dichotomic structure of the CF Hamiltonian [6] and random diversity of the asphericities by no means do not entitle us to exploit the concept of convergence of the ![]() multipole series. The
multipole series. The ![]() approximation reducing its multipole structure only to the first quadrupolar term is groundless. An exception could be perhaps a unique case when A2 = A4 = A6. Obviously, the
approximation reducing its multipole structure only to the first quadrupolar term is groundless. An exception could be perhaps a unique case when A2 = A4 = A6. Obviously, the ![]() three-multipole (k = 2, 4, 6) series is a finite one, and not truncated. The higher multipoles do not contribute at all. The second independent factor that controls to a similar extent as the external multipoles the resultant hierarchy of the three CF Hamiltonian terms is the capability
three-multipole (k = 2, 4, 6) series is a finite one, and not truncated. The higher multipoles do not contribute at all. The second independent factor that controls to a similar extent as the external multipoles the resultant hierarchy of the three CF Hamiltonian terms is the capability 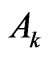 of the state for the CF splitting.
of the state for the CF splitting.
REFERENCES
- B. G. Wybourne, “Spectroscopic Properties of Rare Earths,” John Wiley, New York, 1965.
- B. R. Judd, “Operator Techniques in Atomic Spectroscopy,” Mc Graw-Hill, New York, 1963.
- A. R. Edmonds, “Angular Momentum in Quantum Mechanics,” Princeton University Press, Princeton, New York, 1960.
- M. Rotenberg, R. Bivins, N. Metropolis and J. K. Wooten Jr., “The 3-j and 6-j Symbols,” MIT Press, Cambridge, 1963.
- J. Mulak and Z. Gajek, “The Effective Crystal-Field Potential,” Elsevier, Amsterdam, 2000.
- J. Mulak and M. Mulak, “Multipole Characteristic of the Open-Shell Electron Eigenstates,” Physica Status Solidi B, Vol. 245, No. 6, 2008, pp. 1156-1164. doi:10.1002/pssb.200743527
- M. Reid, “f-Shell Programs,” Private Communication by Courtesy of Z. Gajek, 2010.
- W. T. Carnall, G. L. Goodman, K. Rajnak and R. S. Rana, “A Systematic Analysis of the Spectra of the Lanthanides Doped into Single Crystal LaF3,” Journal of Chemical Physics, Vol. 90, No. 7, 1989, pp. 3443-3457. doi:10.1063/1.455853
- F. Auzel and O. L. Malta, “A Scalar Crystal Field Strength Parameter for Rare Earth Ions: Meaning and Usefulness,” Journal of Physique, Vol. 44, No. 2, 1983, pp. 201-206. doi:10.1051/jphys:01983004402020100
- R. P. Leavitt, “On the Role of Certain Rational Invariants in Crystal-Field Theory,” Journal of Chemical Physics, Vol. 77, No. 4, 1982, pp. 1661-1663. doi:10.1063/1.444088
- C. Rudowicz and J. Qin, “Noether’s Theorem and Conserved Quantities for the Crystaland Ligand-Field Hamiltonians Invariant under Continuous Rotational Symmetry,” Physical Review B, Vol. 67, No. 17, 2003, Article ID 174420, pp. 1-14.
- C. Rudowicz and J. Qin, “Can the Low Symmetry Crystal (Ligand) Field Parameters Be Considered Compatible and Reliable,” Journal of Luminescence, Vol. 110, No. 1-2, 2004, pp. 39-64. doi:10.1016/j.jlumin.2004.04.003
- Y. Y. Yeung, “Invariants and Moments,” In: D. J. Newman and B. Ng, Eds., Crystal Field Handbook, Cambridge University Press, Cambridge, 2000, pp. 160-175. doi:10.1017/CBO9780511524295.010
- J. Mulak and M. Mulak, “On a Complementary Scale of Crystal-Field Parametrization,” Journal of Physics A: Mathematical and Theoretical, Vol. 40, No. 9, 2007, pp. 2063-2076. doi:10.1088/1751-8113/40/9/012
- I. G. Kaplan, “Symmetry of Many Electron Systems,” Academic Press, New York, 1975.
- S. Hüffner, “Optical Spectra of Transparent Rare Earths Compounds,” Academic Press, New York, 1978.
- S. G. Redsun, “3-j, 6-j, 9-j Symbol Calculators,” Accessed in January 2011. http://www.svengato.com (postware application).
- C. W. Nielson and G. F. Koster, “Spectroscopic Coefficients for pn, dn and fn Configurations,” MIT Press, Cambridge, 1963.
- J. S. Griffith, “The Theory of Transition-Metal Ions,” Cambridge University Press, Cambridge, 1961.
- J. Mulak and M. Mulak, “A Fundamental Requirement for Crystal-Field Parametrization,” Physica Status Solidi B, Vol. 248, No. 9, 2011, pp. 2159-2164.
- R. P. Leavitt, J. B. Gruber, N. C. Chang and C. A. Morrison, “Optical Spectra, Energy Levels, and Crystal-Field Analysis of Tripositive Rare-Earth Ions in Y2O3. II. NonKramers Ions in C2 Sites,” Journal of Chemical Physics, Vol. 76, No. 10, 1982, pp. 4775-4788. doi:10.1063/1.442796
- S. S. Bishton and D. J. Newman, “Parametrization of the Correlation Crystal Field,” Journal of Physics C: Solid State Physics, Vol. 3, No. 8, 1970, pp. 1753-1761. doi:10.1088/0022-3719/3/8/014
- D. J. Newman, “Theory of Lanthanide Crystal Field,” Advances in Physics, Vol. 20, No. 84, 1971, pp. 197-256. doi:10.1080/00018737100101241
- M. F. Reid, “Correlation Crystal Field Analyses with Orthogonal Operators,” Journal of Chemical Physics, Vol. 87, No. 5, 1987, pp. 2875-2884. doi:10.1063/1.453075

