Applied Mathematics
Vol.06 No.08(2015), Article ID:58299,13 pages
10.4236/am.2015.68125
Simulation Model of Wireless Channel
Huan Liu, Hanlin Chen
Southwest University of Science and Technology, Mianyang, China
Email: 897894201@qq.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 June 2015; accepted 21 July 2015; published 24 July 2015
ABSTRACT
The change of channel is caused by Doppler effect, and the degree of change is related to relative velocity in the condition of the certain carrier frequency. The multipath fading channel is independent of each other, whose amplitude obeys Rayleigh distribution and the phase obeys uniform distribution. The model of multipath time-varying transmission channel is built. Through the pro- cess of channel model building, the simulation results produced by the channel model verify the effect of the proposed model in the aspect of reducing test data. In a communication system, signal passing through the channel is involved with the process of digital modulation and demodulation. Binary sequence signal is modulated into a complex sequence in the process of modulation before the transmission in the channel, in order to accommodate the wireless channel transmission. With the increase of SNR, BER is overall slightly drops. However there exists violent fluctuation and it presents the random variation of details in the multipath channel. I employ the mathematical model of multipath time-varying channel, i.e. Jakes model to be simulated so as to compare with the AGWN channel in the same situation. Jakes model has the characteristics of the reference chan- nel compared with the AGWN. BER does not change with the increase of SNR significantly and coincides with multipath time-varying channel. The BER considerably decreases with the increase of SNR in the AGWN channel.
Keywords:
Doppler Effect, Multipath Fading Channel, Jakes Model

1. Introduction
In a communication system, the multipath reflection and attenuated change will cause random fluctuations of the signal when the signal is transmitted in a wireless channel. The Doppler effect caused by relative motion between mobile station and base station makes the channel characteristics change over time. The faster the movement speed is, the faster the change of channel is.
The channel change is caused by Doppler effect, and the degree of change is related to the relative velocity in the certain carrier frequency. The data is analyzed according to the test data of data file 1, 2 and 3. The laws are explored where velocity affects accuracy of constructed model. The fittings of Fourier model tree are verified at the velocities of 90 km/h, 270 km/h, 450 km/h. An analysis of how the change of velocity causes the change of fitting accuracy is made. I have published the article “Fast time-varying channel model research for data pro- cessing of wireless communication”. The method of Fourier model tree is introduced in detail in that paper. In this paper, with the increase of the experimental data, the method of employing the Fourier model tree to solve channel model at different rates can simulate data into graphs better for comparison. According to the channel parameters in the attachment file, multipath time-varying channel is simulated. The simulation results are fitted by the method of the Fourier model tree to check up the accuracy of the model tree. The variation of BER with SNR is calculated for the simulation of multipath fading channel. I make abstract mathematical model for multipath time-varying channel to compare with the AGWN channel. I also make a comparative analysis between the EBR of AGWN channel and the increase of the SNR [1] .
2. Doppler Frequency Shift and Multipath Effect
2.1. Doppler Frequency Shift
The mobile channel is a typical random channel. When the mobile station moves at the constant rate in the path of length d and terminals X and Y, it receives signals from signal source S, as shown in Figure 1. The radio waves start from signal source S and they are respectively accepted by the mobile station at points X and Y. So the difference between the two paths traveled by these two radio waves will be: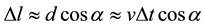 ,
, 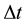 is the time consumed by the mobile station during its movement,
is the time consumed by the mobile station during its movement,  is angle between incident wave and X or Y. It is assumed that the X point and Y point share the same angle. The phase variation of the received signals
is angle between incident wave and X or Y. It is assumed that the X point and Y point share the same angle. The phase variation of the received signals
due to path difference will be: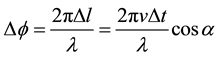 , where
, where 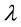 is the carrier wavelength. Thus Doppler
is the carrier wavelength. Thus Doppler
frequency shift can be drawn. There is a Doppler shift 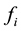 for each signal component arriving at antenna relative to the different angle of the movement speed [2] .
for each signal component arriving at antenna relative to the different angle of the movement speed [2] .
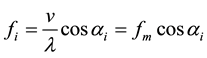 (1)
(1)
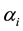 is the ith component’s angle.
is the ith component’s angle. 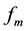 is the maximum Doppler frequency shift.
is the maximum Doppler frequency shift.
2.2. The Multipath Effect
The multipath effect is the delayed interference effect caused by the multipath transmission phenomenon of radio propagation channel. In the actual radio waves propagation channel (including all band), there are a lot of transmission paths with different time-delays. In the case of N paths, the channel output can be represented as:
Figure 1. Model of Doppler frequency shift.
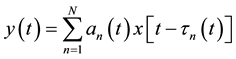 (2)
(2)
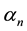 and
and 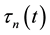 represent the attenuation and propagation-delay associated with the Nth multipath component and they are both the function of time. The complex envelope of the receiver’s input signal caused by the large amount of scattered components is the complex Gauss process. The expect is zero and there is a direct path. The amplitude obeys the Ricean Distribution. It is assumed that the channel input is a modulated signal [3] .
represent the attenuation and propagation-delay associated with the Nth multipath component and they are both the function of time. The complex envelope of the receiver’s input signal caused by the large amount of scattered components is the complex Gauss process. The expect is zero and there is a direct path. The amplitude obeys the Ricean Distribution. It is assumed that the channel input is a modulated signal [3] .
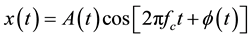 (3)
(3)
The form of the complex envelop is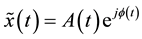 , take (3) into (2).
, take (3) into (2).
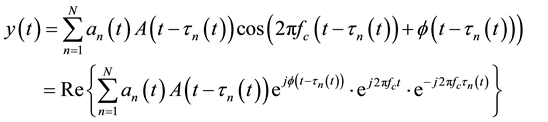 (4)
(4)
However, 

The complex path attenuation can be defined as, 

So the complex envelop of receiver’s input is
relationship of channel as a linear time-varying systems. The impulse response is:

where 
2.3. The Channel Model in Different Rate Is Solved by the Method of Fourier Model Tree
The data file 1, 2 and 3 are the tested impulse function values of channels. They are a series of impulse response sequences with an increasement during each unit sampling time, and the values are plural. I separate the real and imaginary parts.
According to data file 1, the actually measured data can be obtained at the velocity of 90 km/h and in the channel sampling frequency of 200 KHz. I use the method of Fourier model tree. Five steps of the regression tree of Fourier model are composed of data preprocessing, Fourier series approximation, model tree, pre-pruning and segmentation step. These steps are introduced in detail in the article “Fast time-varying channel model research for data processing of wireless communication.” Regression tree belongs to the improved method of decision tree. Generally speaking, the decision tree requires that data segmentation should be cut into small data set until they can’t be subdivided. Decision tree is a greedy algorithm, and with the given eigenvalues to partition the data, it will make the best choice in a given time but don’t care about whether the global optimum is reached or not. Data can be cut through the tree structure for complex data model, how to carry out effective data segmentation depends on the modeling way of the leaf node.
Firstly, I make model solving on imaginary parts of data and use the Fourier model tree to get the coefficients of the segmented Fourier series [4] .
{‘spInd’: 0, ‘spVal’: matrix([[673.]]),
‘right’: [matrix([[−0.00037289]]), matrix([[−0.00074577]]), matrix([[−0.01062968]])],
‘left’: [matrix([[0.00123526]]), matrix([[0.00247053]]), matrix([[0.01351784]])]}
The piecewise impulse response time is 673, the Fourier formula of the right part is:

The Fourier formula of the left part is:

And then draw the comparison picture of between the segmented Fourier series and the actually measured imaginary part data as shown in Figure 2.
As shown in Figure 2, the red line represents the fitting data, the blue line represents the actually measured data. Though the change trend can be fitted by the Fourier series with the change of velocity, the extension becomes more around the actually measured data and the data also gradually diffuse to surrounding due to the change of velocity. The deviation rate is calculated according to formula of variance.




I calculate the error of square difference, getting Devimg = 0.0594. The large deviation data appear much less likely making the square errors decrease because the actually measured data have a number of 72000. The Fourier coefficient is solved by the model tree according to the real part data of data file 1.
[matrix([[−7.57798329e−05]]), matrix([[−0.00015156]]), matrix([[ 0.04335678]])]
The Fourier formula is:

Figure 2. Comparison between the segmented Fourier series and the actually measured imaginary parts data.
Draw the comparison picture of between Fourier series and the actually measured real part data as shown in Figure 3.
The fitting data of Fourier series cover the actually measured data well as shown in Figure 3, and the extensions around are not many. According to formula (10), I calculate the error of square difference, obtaining Devreal = 0.0541. According to data file 2, the actually measured data can be obtained at the velocity of 270 km/h and in the channel sampling frequency of 200 KHz. I use the method of Fourier model tree. Firstly, I make model solving on imaginary parts of data and use the Fourier model tree to get the coefficients of the segmented Fourier series.
{‘spInd’: 0, ‘spVal’: matrix([[520.]]),
‘right’: [matrix([[−0.00013017]]), matrix([[−0.00026034]]), matrix([[0.008543]])],
‘left’: [matrix([[0.00037687]]), matrix([[0.00075373]]), matrix([[0.06409131]])]}
The Fourier series are:


Draw the comparison picture of between the Fourier series and the actually measured imaginary part data as shown in Figure 4.
As shown in Figure 4, the red line represents the fitting data, the blue line represents the actually measured data. According to the formula (10), I calculate square difference error of the Fourier series fitting data, getting Devimg = 0.0970. The square error is bigger because there are a few large deviation data points and the up and downs of curve movements do not coincide with each other also can be a reason. The Fourier coefficients are solved according to the real part data of data file 2.
[matrix([[−0.00016071]]), matrix([[−0.00032143]]), matrix([[0.03061008]])]
The Fourier series are:

Figure 3. Comparison between the Fourier series and the actually measured real parts data.
Figure 4. Comparison between the Fourier series and the actually measured imaginary parts data.
Draw the comparison picture of between the Fourier series and the actually measured real part data as shown in Figure 5.
The red line represents the fitting data, the blue line represents the actually measured data. According to the formula (10), I calculate square difference error of the Fourier series fitted data, getting Devreal = 0.0643. According to data file 3, the actually measured data can be obtained at the velocity of 450 km/h and in the channel sampling frequency of 200 KHz. I use the method of Fourier model tree. Firstly, I make model solving on imaginary parts of data and use the Fourier model tree to get the coefficients of the segmented Fourier series.
{‘spInd’: 0, ‘spVal’: matrix([[313.]]),
‘right’: [matrix([[−0.00054486]]), matrix([[−0.00108971]]), matrix([[0.00911897]])],
‘left’: [matrix([[0.00014312]]), matrix([[0.00028623]]), matrix([[0.09310624]])]}
The segmented Fourier series are:


Draw the comparison picture of between the Fourier series and the actually measured imaginary part data as shown in Figure 6.
The red line represents the fitting data, the blue line represents the actually measured data. According to the formula (10), I calculate square difference error of the Fourier series fitted data, getting Devimg = 0.1424.
The Fourier coefficients are solved according to the real part data of data file 3.
[matrix([[−0.00035213]]), matrix([[−0.00070427]]), matrix([[0.03083286]])]
The Fourier series are:

Draw the comparison picture of between the Fourier series and the actually measured real part data as shown in Figure 7.
Figure 5. Comparison between the Fourier series and the actually measured real parts data.
Figure 6. Comparison between the Fourier series and the actually measured imaginary parts data.
The red line represents the fitting data, the blue line represents the actually measured data. According to the formula (10), I calculate square difference error of the Fourier series fitted data, obtaining Devreal = 0.0641.
Imaginary parts Devimg and real parts Devreal are shown in Table 1 at the different velocities.
Making an illustration of velocity and offset is shown in Figure 8.
The cyan line represents deviation rate of imaginary parts, the red line represents deviation rate of real parts. With the increase of the velocity, the deviation rate of imaginary parts obviously increases and the deviation rate of real parts acts in the same way. With accelerating of the velocity, the deviation rate between the Fourier series fitted by the Fourier model tree and the actually measured data increases and so does the error.
2.4. The Simulation Model of Multipath Time-Varying Channel
In the condition of the certain carrier frequency of 3 GHz, the channel sampling frequency is 200 KHz and velocity is 90 Km/h. The maximum Doppler frequency shift can be solved in the condition of the velocity 90 Km/h according to the formula of Doppler frequency shift.

By the same token, the Doppler frequency shifts can be got on the conditions that the mobile station with speeds of velocity 180 Km/h, 270 Km/h and 450 Km/h, as shown in Table 2.
Figure 7. Comparison between the Fourier series and the actually measured real parts data.
Table 1. The deviation rate of imaginary parts and real parts.
The relevant parameters of channel including multipath numbers, multipath delay and multipath attenuation gain are chosen according to the typical urban model in the reference [5] ’s appendix B. Specific parameters are shown in Table 3.
2.5. The Simulation Results Are Solved by the Simulation Model of Time-Varying Channel to Verify the Method of the Fourier Model Tree
Three kinds of parameters as shown in Table 3 are substituted into the time-varying channel model to be simulated
Figure 8. Velocity and offset.
Table 2. Doppler frequency shifts at the different velocities.
Table 3. The typical urban model.
obtaining the impulse response sequence which depicts channel characteristics. The method of the Fourier model tree is used to fitting solution. Firstly, data preprocessing is made and the impulse response sequences are divided into real and imaginary parts. Then we deal with real parts and derive the coefficients of the segmented Fourier series from the model tree.
{‘spInd’: 0, ‘spVal’: matrix([[487.]]),
‘right’: [matrix([[0.04664147]]), matrix([[0.09328293]]), matrix([[−0.13159072]])],
‘left’: {‘spInd’: 0, ‘spVal’: matrix([[786.]]),
‘right’: [matrix([[0.01709217]]), matrix([[0.03418433]]), matrix([[0.01846343]])],
‘left’: [matrix([[−0.00485146]]), matrix([[−0.00970292]]), matrix([[0.14601979]])]}}
According to five steps of regression tree of Fourier model, the first demarcation point is 487, and the left branch branches again. The left second demarcation point is 786. The Fourier series in the interval [0, 487] are:

The Fourier series to the right side of the left branch’s second branching point in the interval (487, 786] are:

The Fourier series to the left side of the left branch’s second branching point in the interval (786, 1000] are:

Draw the comparison between the real part fitting and the actually measured curve as shown in Figure 9.
The blue line represents the actually measured data. The cyan line represents fitting data. The red line repre- sents fitting data. The yellow line represents fitting data. The two sections before have a certain deviation, but there is a good fitting cover when the impulse response time reaches 786. According to formula (10), getting Devreal = 0.2947. For the processing of imaginary parts, the coefficients of the segmented Fourier series are:
{‘spInd’: 0, ’spVal’: matrix([[484.]]),
‘right’: {‘spInd’: 0, ’spVal’: matrix([[103.]]),
Figure 9. Comparison between the real parts fitting and the actually measured curve.
‘right’: [matrix([[0.07269677]]), matrix([[0.14539348]]), matrix([[−0.06412545]])],
‘left’: [matrix([[0.01438901]]), matrix([[0.02877801]]), matrix([[0.03532326]])]},
‘left’: {‘spInd’: 0, ’spVal’: matrix([[838.]]),
‘right’: [matrix([[−0.03206781]]), matrix([[−0.06413562]]), matrix([[0.08239755]])],
‘left’: [matrix([[−0.02822166]]), matrix([[−0.0564433]]), matrix([[−0.03375118]])]}}
The level-one demarcation point is 484, the secondary right demarcation point is 103, and the secondary left demarcation point is 838. The segmented Fourier series are:




Draw the comparison between the imaginary part fitting and the actually measured curve in Figure 10.
As shown in Figure 10, the blue line represents the actually measured data. The cyan line represents fitting data. The red line represents fitting data. The yellow line represents fitting data. The pink line represents fitting data. According to formula (10), the fitting square difference deviation of the imaginary parts is Devimg = 0.1677.
The Fourier model tree of the simulation data is fitted, but the overall effect is general and the deviation value is large. There is the phenomenon of too many segmentations. The fitting of real parts is divided into three Fourier series sections. The fitting of imaginary parts is divided into five sections of the Fourier series. Too many segmentations are also the cause which introduce error.
3. The Main Orthogonal Amplitude Modulation QAM
The QAM signal employs two orthogonal carriers which is similar to the PSK signal. From the AWGN channel,
Figure 10. Comparison between the imaginary parts fitting and the actually measured curve.
the QAM bandpass signal received in a signal interval can be expressed as,



The output of two correlators generates the signal component which is contaminated by the noise signal. It can be expressed as,








3.1. The Simulation Model of the Multipath Fading Channel
I use the simulation model of multipath fading channel to perform the 16 QAM modulation and draw the relationship diagram of BER changing with SNR in a range from 0 to 40 db.
As shown in Figure 11, the channel is the random channel due to the characteristics of multipath time-vary- ing channel [6] . The influence of the signal transmission in it has a big fluctuation. The BER gains no much improvement at the high SNR. The BER more shows partially random features and the fluctuation is more severe. The BER value is lowered a little overall, but there are no obvious rules found in details.
I carry out the mathematical abstraction over the whole multipath time-varying channel model which makes it regarded as a common transmission channel in order to compare with the white Gaussian noise channel and compare with AGWN channel in the same condition. For the multipath time-varying channel, the abstract mathematical model usually employs the Jakes time-varying channel model.
Figure 11. The effect of SNR upon EBR in the multipath time-varying channel.
3.2. Jakes Time-Varying Channel Model

In the formula (30),


The formula (30), (31) and (32) are Jakes model.
I use the Jakes model to generate flat Rayleigh fading channel and compare it with the AGWN channel in the same SNR condition [7] .
As shown in Figure 12, the BER of AGWN channel will obviously decrease with the increase of SNR compared with the Jakes channel, while the one of the Jakes model channel basically maintain at the same level and has no obvious change, which coincides with the characteristics of the random channel.
4. Conclusions
The complexity of the problem is simplified by establishing the simulation model of multipath fading channel. The first one thousand actually measured data of each category are used to train the Fourier model tree and then the rest of the simulation data are used for fitting prediction. The deviation rate between the data field of algorithm fitting and the actually measured data increases with the increase of the mobile station’s velocity. According
Figure 12. The performance comparison of 16-QAM carrier modulation signal between AWGN channel multipath time-varying channel.
to the channel parameters, the simulation model of multipath time-varying channel is established at the velocity of 450 km/h. The impulse response sequence of channel is obtained. The first one thousand actually measured data are used to train the Fourier model tree and then the rest of the simulation data are used for fitting prediction. The deviation rate between the data field of algorithm fitting and the actually measured data is in a form of the real part Devreal = 0.2947 and the imaginary part Devimg = 0.1677.
The channel is simulated and modeled base on matlab in this paper. The synchronous scrambling is used to perform the linear feedback shift for the generated scrambling sequence. In the selection of the signal source, the random signal source model is employed in this paper. The standard 127-bit length scrambler sequence pro- cessing is applied for the data flow. At first, the data sequence is shunted and then bit mixed processing is implemented in the process of coding. BPSK modulation is used and the OFDM modulation is performed for the modulated data [8] .
The Jakes model can be better compared with the AGWN channel in the same condition by using the multipath time-varying channel model. But I only extract the channel parameters of typical urban model in the attachment file and make no analysis of channel parameters of vehicles and pedestrain models, thus the channel model may have certain limitations. Moreover, the Jakes model can’t fully reflect the characteristics of the simulation model of multipath fading channel.
Fund
National Natural Science Foundation Item Number 11372294.
Cite this paper
HuanLiu,HanlinChen, (2015) Simulation Model of Wireless Channel. Applied Mathematics,06,1318-1331. doi: 10.4236/am.2015.68125
References
- 1. Gao, B.K. and Wang, F.L. (2003) A Concise Deduction of Relativistic Doppler Effect. University Physics, 22, 15-16.
- 2. Jeong, J.W., Sampei, S. and Morinaga, N. (1995) Large Doppler Frequency Compensation Techniques for DS/CDMA LEO Mobile Satellite Communication Systems. Asia-PaciJlc Conf.Commun., 474-478.
- 3. Zhang, M.Y. and Lv, B.X. (1998) A Nalyses of Multipath Effects in the GPS System. Chinese Journal of Electronics, 26, 195-197.
- 4. Zhao, P.M. (2012) Thinking Python like Computer Scientists. People’s Posts and Telecommunications Press, Beijing.
- 5. Fan, C.X. (2013) The Principle of Communication. 6th Edition, Nation Defense Industry Press, 8.
- 6. Linnartz, J.P. and Gorokhov, A. (2000) New Equalization Approach for OFDM over Dispersive and Rapidly Time Varying Channel. Proceedings of IEEE International Symposium on Personal, Indoor Mobile Radio Communications, 1, 1375-1379.
http://dx.doi.org/10.1109/PIMRC.2000.881643 - 7. Zheng, Y.R. and Xiao, C. (2003) Simulation Models with Correct Statistical Properties for Rayleigh Fading Channels. IEEE Communications Letters, 51, 920-928.
http://dx.doi.org/10.1109/TCOMM.2003.813259 - 8. Pandharipande, A. (2002) Principles of OFDM. IEEE Potentials, 21, 16-19.
http://dx.doi.org/10.1109/45.997971














