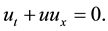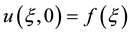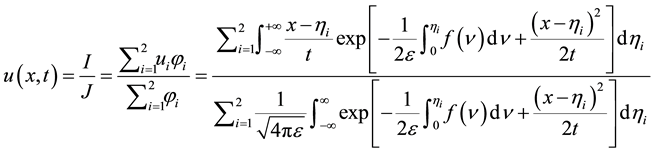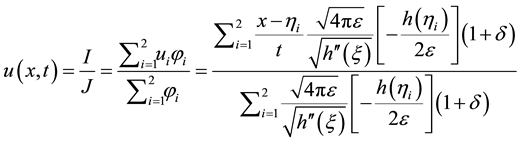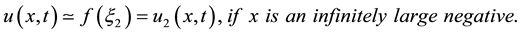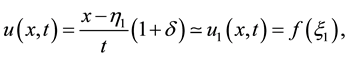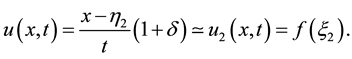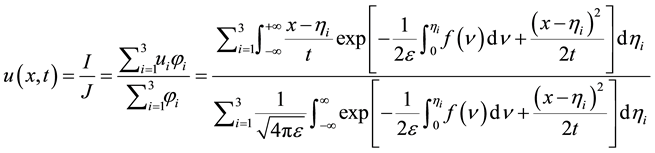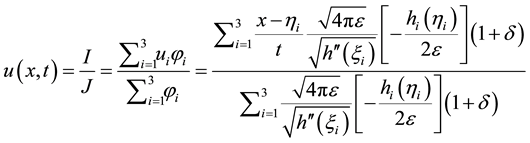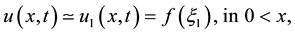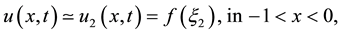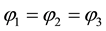Applied Mathematics
Vol.06 No.06(2015), Article ID:57042,12 pages
10.4236/am.2015.66099
Boundary Value Problems for Burgers Equations, through Nonstandard Analysis
Saida Bendaas
Department of Mathematics, Faculty of Sciences, University of Setif 1, Elbez, Algeria
Email: saida_bendaas@yahoo.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 April 2015; accepted 7 June 2015; published 10 June 2015
ABSTRACT
In this paper we study inviscid and viscid Burgers equations with initial conditions in the half plane . First we consider the Burgers equations with initial conditions admitting two and three shocks and use the HOPF-COLE transformation to linearize the problems and explicitly solve them. Next we study the Burgers equation and solve the initial value problem for it. We study the asymptotic behavior of solutions and we show that the exact solution of boundary value problem for viscid Burgers equation as viscosity parameter is sufficiently small approach the shock type solution of boundary value problem for inviscid Burgers equation. We discuss both confluence and interacting shocks. In this article a new approach has been developed to find the exact solutions. The results are formulated in classical mathematics and proved with infinitesimal technique of non standard analysis.
. First we consider the Burgers equations with initial conditions admitting two and three shocks and use the HOPF-COLE transformation to linearize the problems and explicitly solve them. Next we study the Burgers equation and solve the initial value problem for it. We study the asymptotic behavior of solutions and we show that the exact solution of boundary value problem for viscid Burgers equation as viscosity parameter is sufficiently small approach the shock type solution of boundary value problem for inviscid Burgers equation. We discuss both confluence and interacting shocks. In this article a new approach has been developed to find the exact solutions. The results are formulated in classical mathematics and proved with infinitesimal technique of non standard analysis.
Keywords:
Non Standard Analysis, Boundary Value Problem, Viscid Burgers Equation, Inviscid Burgers Equation, Heat Equation

1. Introduction
The nonlinear parabolic partial differential equation
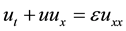 (1.1)
(1.1)
was first introduced by J. M. Burgers [1] [2] as the simplest model for fluid flow, this equation combining both nonlinear propagation effects and diffusive effect. If ε is not null, we approach to the Naveir’s Stokes equations in one dimension. Burgers equation has a wide variety of applications in the modeling of water in unsaturated soil, dynamics of soil water, statistics of flow problems mixing and turbulent diffusion cosmology and seismology.
When ε is null, this equation approaches to the Euler’s equations in one dimension who governs the flows of perfect fluids. It’s the viscid equation. it has the form
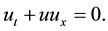 (1.2)
(1.2)
If the viscous term is dropped from the Burgers equation, discontinuities may appear in finite time; even if the initial condition is smooth, they give rise to the phenomenon of shock waves with important application in physics [3] . This property makes Burgers equation a proper model for testing numerical algorithms in flows where severe gradients or shocks are anticipated [4] -[6] . Discretization methods are well-known techniques for solving Burgers equation. Ascher and McLachlan established many methods as multi-symplectic box sheme. For the boundary value problem, Sinai [7] was interested to the initial condition case: null on  and Brownian on
and Brownian on . She, Aurell and Frich [8] with numerical calculations particularly examined the initial conditions of Brownian fraction nair to the asymptotic behavior.
. She, Aurell and Frich [8] with numerical calculations particularly examined the initial conditions of Brownian fraction nair to the asymptotic behavior.
A remarkable feature of viscid Burgers equation is that its solutions with initial conditions of the form
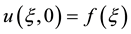 (1.3)
(1.3)
can be explicitly written down. Hopf [9] and Cole [10] independently showed that the Equation (1.1) can be linearized through the transformation
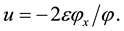 (1.4)
(1.4)
Then Hopf [9] showed that if 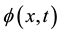 satisfies the linear heat equation
satisfies the linear heat equation
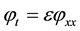 (1.5)
(1.5)
with initial condition
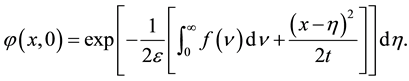 (1.6)
(1.6)
Then 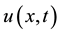 defined by Equation (1.4) solves (1.1) and (1.3). Conversely, if
defined by Equation (1.4) solves (1.1) and (1.3). Conversely, if 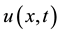 is a solution of problem (1.1) and (1.3) then
is a solution of problem (1.1) and (1.3) then 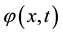 defined by Equation (1.4) is a solution of problem (1.5) and (1.6). Solving for
defined by Equation (1.4) is a solution of problem (1.5) and (1.6). Solving for 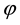 from (1.5) and (1.6) and substituting it into Equation (1.3) we obtained explicit formula for the solution of problem (1.1) and (1.2) namely:
from (1.5) and (1.6) and substituting it into Equation (1.3) we obtained explicit formula for the solution of problem (1.1) and (1.2) namely:
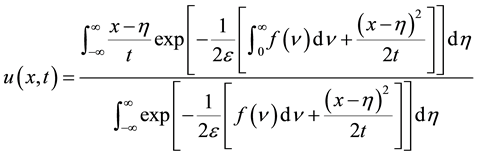 (1.7)
(1.7)
and studied the asymptotic behavior of .
.
Explicit solutions of the Burgers equation (1.1) in the quarter plane with integrable initial data and piecewise constant boundary data were constructed by [11] using Hopf-Cole transformation [9] . He obtained a formula for its weak limit as viscosity parameter goes to 0. Although, there are many results for initial value problem has been studied less. Using maximum principle, this formula for weak limit was extended to general boundary data. ε is a positive parameter small enough. The problem is considered by [12] . As the fact that ε multiplies the largest derivative, one is in the presence of a singular perturbation problem. The purpose of Singular Perturbation Theory is to investigate the behavior of solutions of (1.1) as
The aim of the present article is to study solutions of Inviscid and Viscid Burgers equation if the initial condition admits several singular points, i.e. in the case of a finite number of shocks. A simple formulation is given for the asymptotic behavior based on the evaluation of integrals which is a method of the non standard perturbation theory of differential equations proposed by Imm Van Den Berg [13] and improved by Lutz and Callot.
Historically the subject non standard was developed by Robinson, Reeb, Lutz and Goze [14] . The nonstan- dard perturbation theory of differential equations, which is today a well-established tool in asymptotic theory, has its roots in the seventies, when the Reebian school (see [14] [15] ) introduced the use of nonstandard analysis into the field of perturbed differential equations. Our goal in this paper is to generalize these techniques on EDP and our general purpose is to describe the asymptotic behavior of solutions in boundary value problem with a small parameter ε and to discuss in particular the cases of confluence and the interacting shocks with new technical infinitesimal of non-standard analysis. We can conclude that the solutions of the problem: (1.1) and (1.3) are infinitely close to the solutions of problems (1.2) and (1.3), as 
In Section 2, we treat the boundary value problem for inviscid Burgers equation, solve it and study it. Section 3 is devoted to useful lemmas for our main results. In Section 4, we study viscid Burgers equation, solve exactly the initial value problems for it, and describe the asymptotic behavior of solutions with a non standard form. Some components, such as multi-leveled equations, graphics, and tables are not prescribed, although the various table text styles are provided. The formatter will need to create these components, incorporating the applicable criteria that follow.
2. Initial Boundary Value Problem for Inviscid Burgers’ Equation
2.1. Shock Fitting
We consider the inviscid Burgers equation:
In: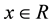
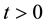
where 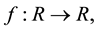
This problem not admits the regular solutions but some weak solutions with certain regularity exist. The Burgers equation on the whole line is known to possess traveling wave solutions. The solution of (1.2) and (1.3) may be given in a parametric form and shocks must be fitted in such that:
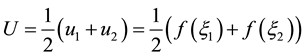
where 

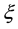
According to Equation (1.2), the solution at time t is obtained from the initial profile 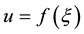
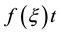
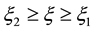



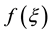
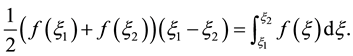
This is the differential equation for the line cord of shock that checks the condition of entropy such as [16] [17] Corresponding to the two inflection points.
2.2. Confluence of Shocks
When a number of shocks are produced, in general it is possible for one of them to overtake the shock ahead. Then they combine and continue as a single shock. This is also described by our shock solution.
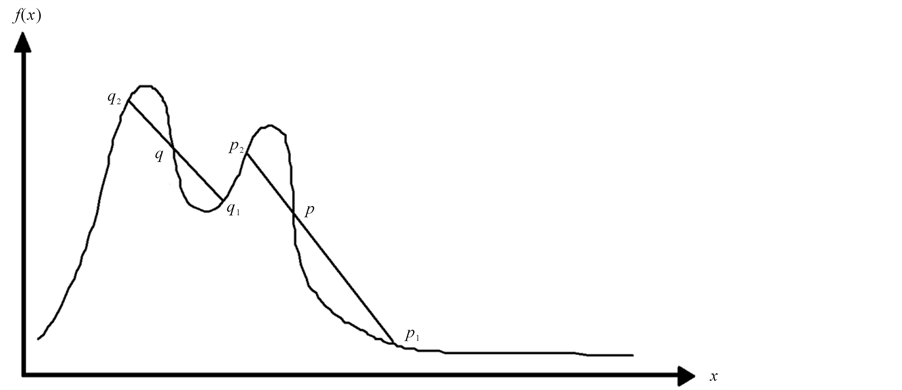
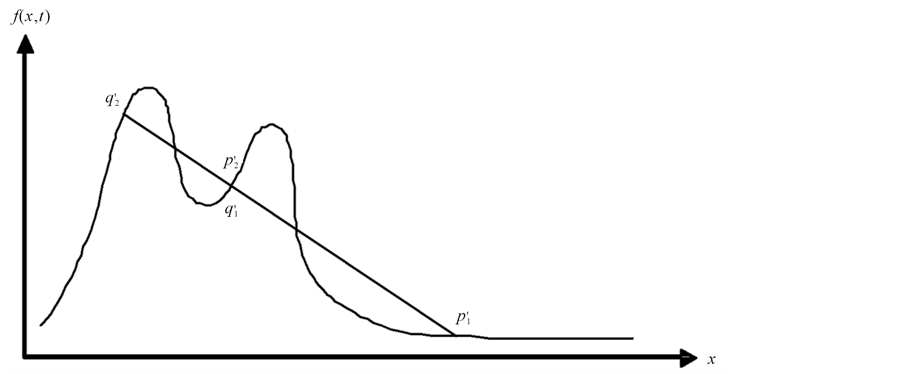
Consider the curve given by f Figure 1, then two shocks are formed corresponding to the inflection points p and q with families of equal area chords, typified by 
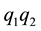
As time goes, the points 
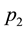
At this stage the characteristics corresponding to 
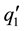
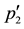

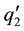

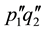
In the plane 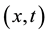
Figure 1. Graphic representation of the initial condition f.
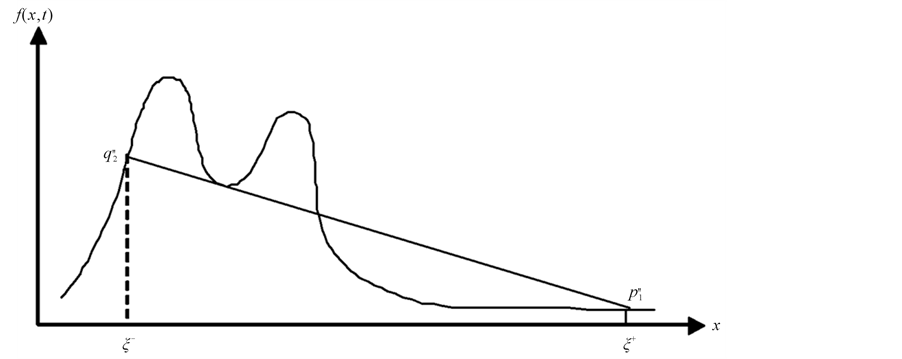
Figure 2. Graphical representation from the merger of the two shocks. The characteristics 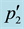

Figure 3. Construction for merging shocks in a final stage.
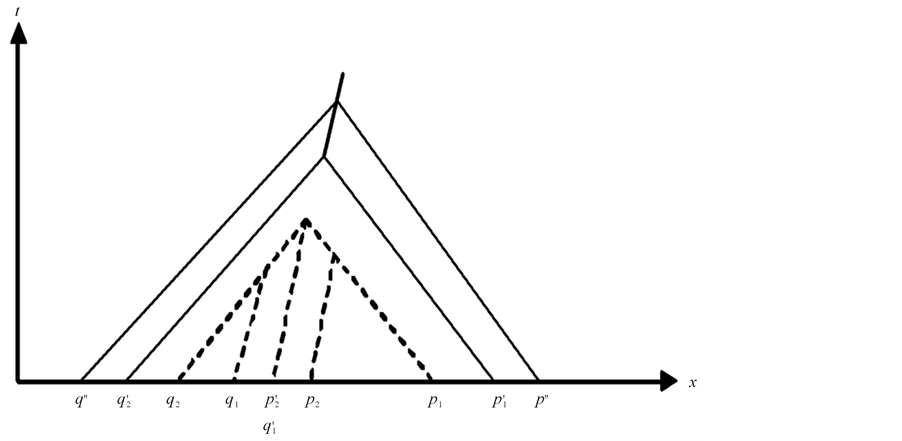
Figure 4. The (x, t) diagram for merging shocks corresponding to Figure 1.
3. Preliminaries
In this section we present some lemmas that are important to prove our main result.
Proposition 3.1. Let 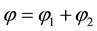
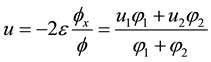
i.e.

Proof: When a shock overtakes another shock, they merge into a single shock of increased strength as described in inviscid solution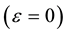
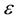

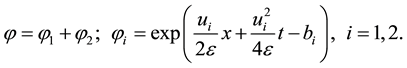
In the expression of solution for a single shock given in [3] [4] , the parameters b₁, b₂ witch locate the initial position of the shock are taken to be zero. The expressions 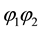
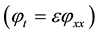

Corresponding to the initial conditions:
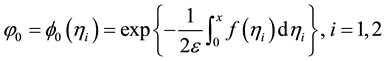
Then the solutions of the heat equation are given as:
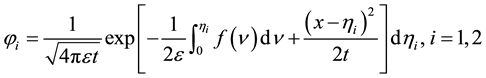
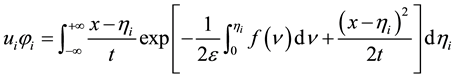
Using Equations (1.4) and (3.1) we obtain the expression (3.2).
And to prove our results, we use the non standard analysis techniques, for that we consider the following lemma.
Lemma 3.2. (The Van. Den. Berg lemma [14] ): Let h be a standard function, defined and increasing on [0,+∞[ such that 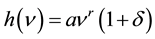

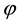
fined on ]0,+∞[ such that :
such that:
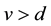

where a, r are positive standard, m and q are the both positive 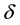
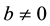
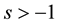
To give estimation to the solution, given by (3.2), we state the following lemma:
Lemma 3.3. Let ε be a positive real small enough. And let ϕ and h be two standard functions such that: h, is a C2 class function verified the Lemma 3, and admits on the ξ point a unique absolute minimum 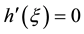

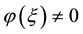

δ is an infinitesimal.
Proof: To prove this lemma, we use the “Van Den Berg” method, lemmas: (5.6), (5.7) [14] . It consists in the following steps
1) Search for the absolute minimum (maximum) of the function under the exponential sign and bring it out.
2) Bring back the minimum (maximum) to the zero.
3) Searching the galaxy as well as the main galaxy where the function in the exponential sign is appreciable.
4) Calculate the integral.
As consequence we have the following lemma.
Lemma 3.4. Let f the initial condition as Figure 1. Assume:
(H1): 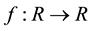
(H2): There exist a, b, c, d and e in R, with a < b < c < d < e, such that
Then for x and t fixed, the functions defined as:

has at most two minima 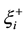

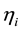
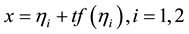
And the condition: 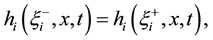
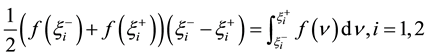
Proof: Let f the initial condition given as in Figure 1, two shocks are formed corresponding to the inflection points of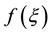
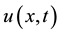
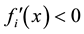
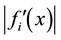
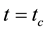
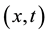

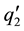



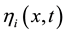
This equation is verified at the two minima 
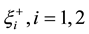
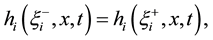
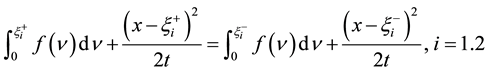
But 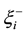
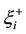
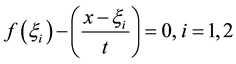
The condition of the shock is expressed by (3.12), is the same condition of shock given by (2.2) for invicid Burgers equation.
4. Initial Boundary Value Problem for Inviscid Burgers’ Equation
4.1. Confluence of Shocks
Our general purpose now is to show that the exact solution of (1.1) and (1.3) endorse the ideas regarding shocks in Section 2, we want to confirm that as 

Theorem 4.1. Under the assumptions: (H1), (H2) in lemma (3.4), the problem (1.1) and (1.3) admits a unique solution for 
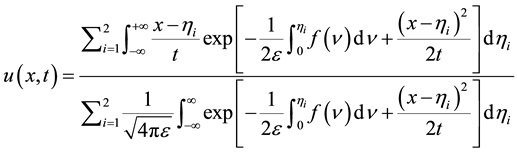
Such a solution is confluence of shocks and for ε sufficiently small, this solution is infinitely close to the solution of the reduced problem given in (2.2).
Proof: 1) From Figure 2 and Figure 3, after some time the two shocks combine and continue into one, and this is the lowest minimum that carries this amount to the case of a single shock. From the proposition (3.1), the problem (1.1) and (1.3) admits a single solution explicitly given by Formula (4.1). Uniqueness is due to the condition of entropy which restricts the set of solutions to one which is stable with a singular perturbation dissipative nature.
2) Let 


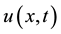
From the Lemma 3.2 we have
where δ > 0 is an infinitesimal. And we will have the following estimate
To conclude we have the following corollary.
Corollary 4.2. Let


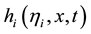
And the center of the shock when 
Proof: Using lemma (3.4), outside the region of each shock. For 

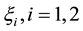

With 
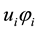
Using lemma (3.3) we obtain
And it follows that:
If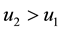

If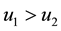
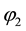
4.2. Interacting Shocks
In this section, we discuss the interacting shocks case; before going further in this case we need the following proposition and lemma.
Now since any 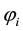
Proposition 4.3. Let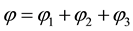
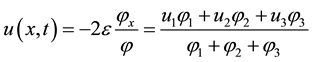
i.e.
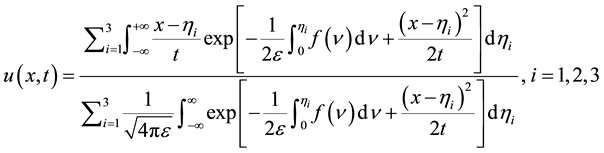
Proof: When a shock overtakes another, they merge into a single shock of increased strength as described in inviscid solution
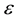
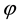
In the solution for a single shock given in [4] , the parameters 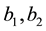
shock are taken to be zero and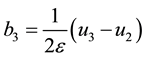
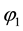


heat equation 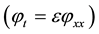

And
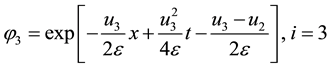
Corresponding to the initial conditions:
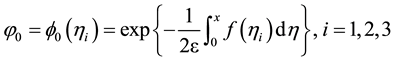
Then the solutions of the heat equation are given as:
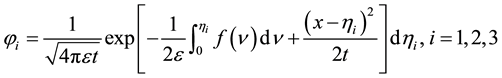
and

Using (1.4) and (4.4) we obtain the expression (4.3). Then we have the following.
Theorem 4.4. For
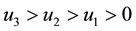
Such a solution is interacting shocks and for ε sufficiently small, it is infinitely close to the solution of the reduced problems (1.2) and (1.3).
Proof. 1) In the interacting shock case we have three shocks, when a shock overtakes another they merge into a single shock of increased strength and the lowest minimum dominating. Then we go back to the single shock case. Using the proposition (4.3), we deduce the uniqueness of solution explicitly given by (3.4). The uniqueness is due to the entropic condition [3] [4] , which restricts the set of solutions to one, who is stable with singular perturbation with dissipative nature.
2) Let 
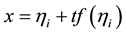

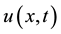
From the Lemma 3.2 we have:
where δ > 0 is an infinitesimal. And we will have the following estimate
from which the following corollary
Corollary 4.5. Let 


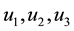

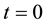

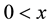



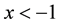
Proof: For 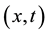


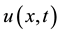

where 
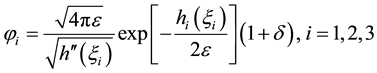
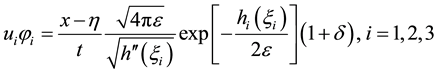
where δ is an infinitesimal positive real.
As shown in Figure 5, If 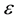


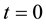
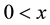
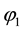
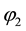
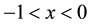
In: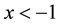

The symbol “≃” means infinitely close to [8] . Thus we have a shock transitions from 



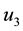
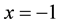
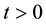
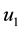


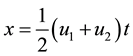
The transition from 

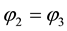
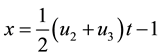
Since, 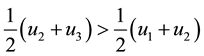

for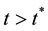
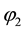
Figure 5. Merging shocks.
on the path determined by
Acknowledgements
I thank the editor and the referee for their comments.
References
- Burgers, J.M. (1948) A Mathematical Model Illustrating the Theory of Turbulence. In: Von Mises, R. and Von Karman, T., Eds., Advances in Applied Mechanics, Vol. 1, Academic Press, New York, 171-199. http://www.sciencedirect.com/science/article/pii/S0065215608701005 http://dx.doi.org/10.1016/s0065-2156(08)70100-5
- Burgers, J.M. (1975) The Non Linear Diffusion Equation Asymptotic Solution and Statistical Problems. http://www.amazon.it/The-Non-Linear-Diffusion-Equation-Statistical/dp/9027704945
- Kida, S. (1979) Asymptotic Properties of Burgers Turbulence. Journal of Fluid Mechanics, 93, 337-377. http://journals.cambridge.org/action/displayAbstract;jsessionid=0174C93AF976CBF18771FEB41E0FEFA9.journals?fromPage=online&aid=388434 http://dx.doi.org/10.1017/S0022112079001932
- Samokhin, A. (2014) Gradient Catastrophes and Saw Tooth Solution for a Generalized Burgers Equation on an Interval. Journal of Geometry and Physics, 85, 177-184. http://www.sciencedirect.com/science/article/pii/S0393044014000965 http://dx.doi.org/10.1016/j.geomphys.2014.05.007
- Samokhin, A.V. (2013) Evolution of Initial Data for Burgers Equation with Fixed Boundary Values. Sci Herald of MSTUCA, 194, 63-70. http://www.mstuca.ru/scientific_work/scientific_work/files/194.pdf
- Euvrard, D. (1992) Résolution Numérique des Equations aux Dérivées Partielles. Différences finies, Eléments finis. Masson, Paris.
- Sinai, G. (1992) Statistics of Shocks in Solutions of Inviscid Burgers Equation. Communications in Mathematical Physics, 148, 601-621. http://citeseerx.ist.psu.edu/showciting?cid=205153 http://dx.doi.org/10.1007/bf02096550
- She, Z.S., Aurell, E. and Frich, U. (1992) The Inviscid Burgers Equation with Initial Data of Brownian Type. Com- munications in Mathematical Physics, 148, 623-641. http://www.researchgate.net/publication/38331252_The_inviscid_Burgers_equation_with_initial_data_of_Brownian_type http://dx.doi.org/10.1007/BF02096551
- Hopf, E. (1950) The Partial Differential Equation: ut + uux= εuxx. Communications on Pure and Applied Mathematics, 3, 201-230. http://www.researchgate.net/publication/259149172_The_partial_differential_equation_ut__uux__xx http://dx.doi.org/10.1002/cpa.3160030302
- Cole, J.D. (1951) On a Quasilinear Parabolic Equation Occurring in Aerodynamics. Quarterly of Applied Mathematics, 9, 225-236. http://www.researchgate.net/publication/238286127_On_a_quasilinear_parabolic_equation_occurring_in_aerodynamics
- Joseph, K.T. (1988) Burgers Equation in the Quarter Plane, a Formula for the Weak Limit. Communications on Pure and Applied Mathematics, 41, 133-149. http://onlinelibrary.wiley.com/doi/10.1002/cpa.3160410202/abstract http://dx.doi.org/10.1002/cpa.3160410202
- Kevorkian, J. and Cole, J.D. (1981) Perturbation Methods in Applied Mathematics. Springer Verlag, New York. http://www.amazon.com/Perturbation-Methods-Mathematics-Mathematical-Sciences/dp/0387905073 http://dx.doi.org/10.1007/978-1-4757-4213-8
- Van Den Berg, I. (1987) Non Standard Asymptotic Analysis. Lecture Notes in Mathematics, 1249. http://www.researchgate.net/publication/44553479_Nonstandard_asymptotic_analysis__Imme_van_den_Berg
- Lutz, R. and Goze, M. (1981) Non Standard Analysis. A Practical Guide with Application. Lecture Notes in Mathe- matics, 861.
- Lutz, R. and Sari, T. (1982) Applications of Nonstandard Analysis in Boundary Value Problems in Singular Perturbatio Theory; Theory and Application of Singular Perturbation (Oberwolfach 1981). Lecture Notes in Mathematics, 942, 113-135. http://www.researchgate.net/publication/225547873_Applications_of_nonstandard_analysis_to_boundary_value_problems_in_singular_perturbation_theory
- Bendaas, S. (1994) Quelques applications de l’A.N.S aux E.D.P. Ph.D. Thesis, Haute Alsace University, France.
- Bendaas, S. (2008) L’équation de Burgers avec un Terme Dissipatif. Une approche non standard. Analele Universitatii din Oradea. Fascicola Matematica, 15, 239-252. http://stiinte.uoradea.ro/en/auofm/auofm_contents.htm