Received 14 November 2014; accepted 1 December 2014; published 19 January 2015

ABSTRACT

In this paper the estimates for norms of solutions to nonlinear systems are obtained via an integral inequality. As an application we considered affine control systems and systems of equations for synchronization of motions.

Keywords:

Nonlinear Systems, Novel Bounds for Solutions, Stability, Synchronization

1. Introduction

The problem of estimating the norms of solutions to nonlinear systems of ordinary differential equations remains urgent due to extensive application of the latter in the description of real processes in many mechanical, physical and other nature systems. Usually, to obtain the estimates of norms of solutions to linear and weakly nonlinear equations, the Gronwall-Bellman lemma is applied (see, for example, [1] -[3] and bibliography therein). The development of the theory of nonlinear inequalities has substantially widened the possibilities for obtaining the estimates of norms of solutions to nonlinear systems and has given an impetus to their application in the qualitative theory of equations (see, for example, [4] -[6] ).

Both linear and nonlinear integral inequalities are efficiently used for the development of the direct Lyapunov method, in particular, for the investigation of motion boundedness and stability of nonlinear weakly connected systems [7] .

The present paper is aimed at obtaining new estimates of norms of solutions for some classes of nonlinear equations of perturbed motion. The paper is arranged as follows.

In Section 2 the statement of the problem is given in view of some results of papers [1] [3] .

Section 3 presents main results on obtaining the estimates of norms of solutions for some classes of nonlinear systems of differential equations. In this regard, several results from [8] are taken into account.

In Section 4 two application problems are considered: a problem on stabilization of solutions to affine system (cf. [8] ) and a problem on estimation of divergence of solutions at synchronization (cf. [9] ).

In Section 5 the possibilities of application of this approach for solution of modern problems of nonlinear dynamics and systems theory are discussed.

2. Statement of the Problem

Consider a nonlinear system of ordinary differential equations of perturbed motion

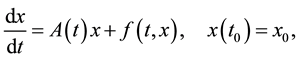(1)

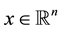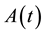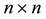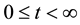where;, is an -matrix with the elements continuous on any finite interval. It is assumed that solution of problem (1) exists and is unique for all and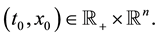

Equations of type (1) are found in many problems of mechanics (see, for example, [1] [10] and bibliography therein). Moreover, these equations may be treated as the ones describing the perturbation of the system of linear equations

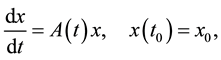(2)

In order to establish boundedness and stability conditions for solutions of system (1) it is necessary to estimate the norms of solutions under various types of restrictions on system (2) and vector-function of nonlinearities in system (1).

The purpose of this paper is to obtain estimates of norms of solutions to some classes of nonlinear ordinary differential Equations (1) in terms of nonlinear and pseudo-linear integral inequalities.

3. Main Results

First,we shall determine the estimate of the norm of solutions 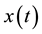of system (1) under the following assumptions:

A₁. For all there exists a nonnegative integrable function 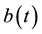such that

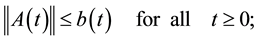
A₂. For all and 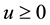there exists a continuous nonnegative integrable function, , such that (cf. [11] )

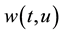for all.

Here and elsewhere an Euclidian norm of the vector x and a spectral norm of the matrix consistent with it are used.

Theorem 1. For system (1) let conditions of assumptions and be satisfied, then for any solution with the initial values, the inequality

(3)

holds for all.

If there exist:

(a) a continuous and nonnegative function for all and

(b) a continuous, nonnegative and nondecreasing function for such that

then for all the inequality

(4)

holds true, where is a function converse with respect to the function:

and the value is determined by the correlation

(c) If, additionally, there exists a constant such that

then inequality (4) is satisfied for all, i.e. for the values.

Proof. Let the right-hand part of inequality (3) be equal. Using inequality (3) and condition (b) of Theorem 1 we get

Since the function is nondecreasing and

we get the inequality

Hence, by the Bihari lemma (see [10] , p. 110) we have

for all. This implies estimate (4).

To prove the second assertion of Theorem 1 we note that the continuability condition for function is the inequality

or

This inequality is satisfied for any for which condition (c) of Theorem 1 holds true. Since, we have

Hence it follows that for the value. This proves Theorem 1.

Further we shall consider system (1) under the following assumption.

A₃. There exist a nonnegative integrable function for all and a constant such that

for all.

Theorem 2. For the system of Equations (1) let conditions of Assumptions and be satisfied. Then for the norm of solutions the estimate

(5)

holds true for all whenever

(6)

Proof. Let be the solution of system of Equations (1) with the initial conditions,. Under conditions and Equation (1) yields the estimate of the norm of solution in the form

(7)

We transform inequality (7) to the pseudo-linear form

(8)

and applying the Gronwall-Bellman lemma [1] arrive at the estimate

(9)

for all.

Further, for estimation of the expression

the following approach is applied (cf. [8] ).

Designate for all and from inequality (9) obtain

(10)

Multiplying both parts of inequality (10) by the expression

we get

This implies that

Integrating the obtained inequality between the limits and we arrive at

Under condition (6) this estimate implies

Moreover, inequality (10) becomes

This inequality yields estimate (5) for all for which condition (6) is satisfied.

This completes the proof of Theorem 2.

Inequality (7) is a partial case of inequality (3) and its representation in pseudo-linear form (8) allows us to simplify the procedure of obtaining the estimate of norm of solutions to system (1).

Theorem 2 has a series of corollaries as applied to some classes of systems of ordinary differential equations.

Corollary 1. Consider system (1) for for all

(11)

This is an essentially nonlinear system, i.e. a system without linear approximation. Such systems are found in the consideration of systems with dry friction, electroacoustic waveguides and in other problems. Systems with sector nonlinearity (see [12] ) are close to this type of systems.

If condition A₃ is fulfilled with the function such that

for any, , , then

Applying to this inequality the same procedure as in the proof of Theorem 2 it is easy to show that if

for all, then

(12)

for all.

Comment 1. Estimate (12) is obtained as well by an immediate application of the Bihari lemma (see [10] ) to the inequality

with the function, ,.

Corollary 2. In system (1) let, where is an -matrix continuous with respect to.

Consider a system of non-autonomous linear equations with pseudo-linear perturbation

(13)

Assume that condition is satisfied and there exists a nonnegative integrable function such that

(14)

for all.

Equation (13) implies that

(15)

Applying to inequality (15) the same procedure as in the proof of Theorem 2 we get the estimate

(16)

which holds true for the values of for which

(17)

Comment 2. If in inequality (15) functions for all, then Theorem 1 yields the estimate (see [4] )

for all, where is determined by the formula.

Corollary 3. In system (1) let, where for all. Further we shall consider the system of nonlinear equations

(18)

where are -matrices with the elements continuous on any finite interval and.

Assume that there exist nonnegative integrable on functions, , such that

(19)

In view of (19) we get from (18) the inequality

(20)

Inequality (20) is presented in pseudo-linear form

Hence

(21)

We shall find the estimate of the expression

Inequality (21) implies that the estimate

is true.

Multiplying both parts of this inequality by the negative expression

we get

Summing up both parts of this inequality from to we find

Integration of this inequality between 0 and t results in the following inequality

From this inequality we find that

Hence follows the estimate

(22)

which is valid for all such that

Estimate (5) allows boundedness and stability conditions for solution of system (1) to be established in the following form.

Theorem 3. If conditions and of Theorem 2 are satisfied for all and there exists a constant such that for all, where may depend on each solution, then the solu- tion of system (1) is bounded.

Theorem 4. If conditions A₁ and A₃ of Theorem 2 are satisfied for all and for, and for any and t₀? 0 there exists a such that if, then the estimate is satisfied for all, then the zero solution of system (1) is stable.

The proofs of Theorems 3 and 4 follow immediately from the estimate of norm of solutions in the form

of (5). The notations and mean that the right hand part of inequality (5) must sa-

tisfy these inequalities under appropriate initial conditions.

Similar assertions are valid for the systems of Equations (11), (13) and (18) in terms of estimates (12), (16) and (22).

4. Applications

4.1. Stabilization of Motions of Affine System

Consider an affine system with many controlling bodies

(23)

(24)

(25)

where, is an -matrix with continuous elements on any finite interval, is an - matrix, the control vectors for all, B is an -matrix and the control, C is a constant -matrix, is a vector of the initial states of system (23). With regard to system (23) the following assumptions are made:

A₄. Functions, , for all.

A₅. There exists a constant -matrix such that for the system

the fundamental matrix satisfies the estimate

for, where and are some positive constants.

A₆. There exist constants and such that

for all.

The following assertion takes place.

Theorem 5. Let conditions of assumptions - be satisfied and, moreover,

where.

Then the controls

stabilize the motion of system (23) to the exponentially stable one.

Proof. Let the controls and be used to stabilize the motions of system (23). Besides, we have

and

(26)

In view of conditions of Theorem 5 we get from (26) the estimate of norm of solution of system (23) in the form

(27)

We transform inequality (27) to the form

(28)

Applying Corollary 3 to inequality (28) we get

for all.

If condition

of Theorem 5 is satisfied, then

and for the norm of solution we have the estimate

for all, where

This completes the proof of Theorem 5.

4.2. Syncronization of Motions

The theory of motion synchronizations studies the systems of differential equations of the form (see [9] and bibliography therein)

(29)

where, is a function continuous with respect to, , and periodic with respect to with the period, and is a small parameter. Alongside system (29) we shall consider an adjoint system of equations

(30)

where

Assume that in the neighborhood of point for sufficiently small value of for any the vector-function and its partial derivatives are continuous. Designate

It is clear that the solutions of Equations (29) and (30) remain in the neighborhood for.

With allowance for

and

we compile the correlation

(31)

As it is shown in monograph [9] for the first and third summands in correlation (31) the following estimates hold true

(32)

(33)

To estimate the second summand we assume that there exist an integrable function such that for any

and such that

(34)

in the domain of values and.

In view of estimates (32)-(34) we find from (31)

(35)

for all.

Let there exist such that

(36)

for all. Then the norm of divergence of solutions and under the same initial conditions is estimated as follows

(37)

for all and for.

Estimate (37) is obtained from inequality (35) by the application of Corollary 1.

Comment 3. If in estimate (34) and, then the application of the Gronwall-Bellman lemma to inequality (35) yields the estimate of divergence between solutions in the form [9]

for all.

5. Concluding Remarks

In this paper the estimates of norms of solutions to differential equations of form (1), (11) and (13) are obtained in terms of nonlinear and pseudo-linear integral inequalities. This approach facilitates establishing the estimates of norms of solutions for some classes of systems of equations of perturbed motion found in various applied problems (see [11] [13] ). Efficiency of the obtained results is illustrated by two problems of nonlinear dynamics.

It is of interest to develop the obtained results in the investigation of solutions to dynamic equations on time scale (see [14] [15] ). In monograph [16] the integral inequalities on time scale form a basis of one of the methods of analysis of solutions to dynamic equations.

References