Applied Mathematics
Vol.5 No.10(2014), Article
ID:46591,11
pages
DOI:10.4236/am.2014.510148
Approximate Solutions to the Discontinuous Riemann-Hilbert Problem of Elliptic Systems of First Order Complex Equations
Guochun Wen1*, Yanhui Zhang2, Dechang Chen3#
1School of Mathematical Sciences, Peking University, Beijing, China
2Mathematics Department, Beijing Technology and Business University, Beijing, China
3Uniformed Services University of the Health Sciences, Bethesda, USA
Email: wengc@math.pku.edu.cn, zhangyanhui@th.btbu.edu.cn, dechang.chen@usuhs.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 March 2014; revised 23 April 2014; accepted 30 April 2014
ABSTRACT
Several approximate methods have been used to find approximate solutions of elliptic systems of first order equations. One common method is the Newton imbedding approach, i.e. the parameter extension method. In this article, we discuss approximate solutions to discontinuous RiemannHilbert boundary value problems, which have various applications in mechanics and physics. We first formulate the discontinuous Riemann-Hilbert problem for elliptic systems of first order complex equations in multiply connected domains and its modified well-posedness, then use the parameter extensional method to find approximate solutions to the modified boundary value problem for elliptic complex systems of first order equations, and then provide the error estimate of approximate solutions for the discontinuous boundary value problem.
Keywords:Discontinuous Riemann-Hilbert Problem, Elliptic Systems of First Order Complex Equations, Estimates and Existence of Solutions, Multiply Connected Domains

1. Introduction
Let 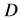 be an
be an 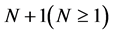 -connected bounded domain in
-connected bounded domain in  with the boundary
with the boundary
 . Without loss of generality, we assume that
. Without loss of generality, we assume that 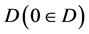 is a circular domain in
is a circular domain in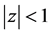 , bounded by the
, bounded by the 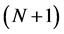 -circles
-circles 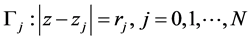 and
and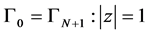 . In this article, the notations are the same as in references [1] -[12] . If the first order elliptic system with
. In this article, the notations are the same as in references [1] -[12] . If the first order elliptic system with 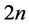 unknown real functions
unknown real functions
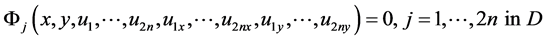 (1.1)
(1.1)
satisfies certain conditions, then (1.1) can be transformed into the complex form
 (1.2)
(1.2)
where 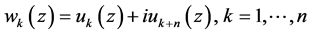 (see Section 4, Chapter 2 in [5] ). Its vector form is as follows:
(see Section 4, Chapter 2 in [5] ). Its vector form is as follows:
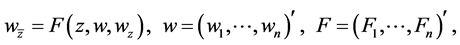 (1.3)
(1.3)
where 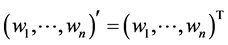 is the transposed matrix of
is the transposed matrix of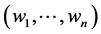 . We discuss the first order complex system (1.3) in the form
. We discuss the first order complex system (1.3) in the form
 (1.4)
(1.4)
in which 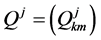 with
with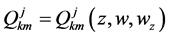 ,
,  with
with 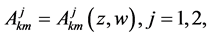
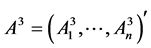 with
with 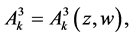
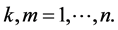
We assume (1.4) satisfies the following conditions:
Condition C 1)  are continuous in
are continuous in 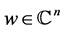 for almost every point
for almost every point 
2) The above functions are measurable in 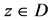 for all systems of continuous functions
for all systems of continuous functions 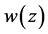 in
in  and any systems of measurable functions
and any systems of measurable functions 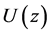 in
in 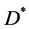 and satisfy
and satisfy
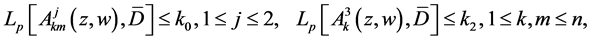 (1.5)
(1.5)
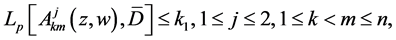 (1.6)
(1.6)
where  is as stated in (1.8) below,
is as stated in (1.8) below, 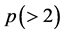 and
and 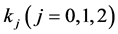 are non-negative constants.
are non-negative constants.
3) The complex system (1.4) satisfies the following ellipticity condition
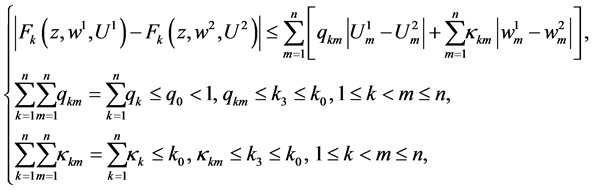 (1.7)
(1.7)
where 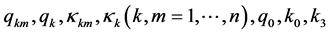 are non-negative constants.
are non-negative constants.
For convenience,  and
and  are used to indicate
are used to indicate 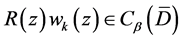 and
and 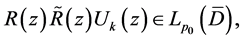 respectively,
respectively, 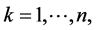 and we define the following:
and we define the following:
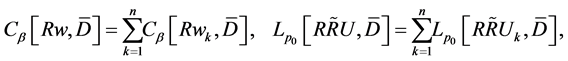
in which 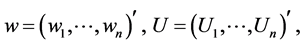 and
and 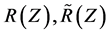 are stated as in (1.12), (2.1) below, and
are stated as in (1.12), (2.1) below, and
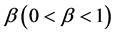 and
and  are non-negative constants.
are non-negative constants.
The so-called Riemann-Hilbert boundary value problem for the complex system (1.4) may be formulated as follows.
Problem A Find a system of continuous solutions 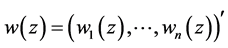 in
in 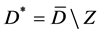 of (1.4), which satisfies the boundary condition
of (1.4), which satisfies the boundary condition
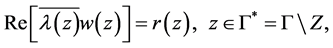 (1.8)
(1.8)
in which 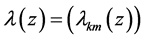 with
with 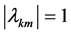 for
for 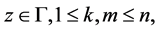
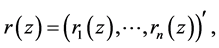 and
and
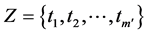 are the first kind of discontinuous points of
are the first kind of discontinuous points of 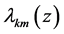 on
on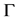 .
.
Denote by 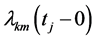 and
and 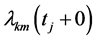 the left limit and right limit of
the left limit and right limit of 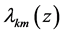 as
as 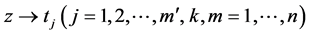 on
on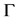 , and
, and
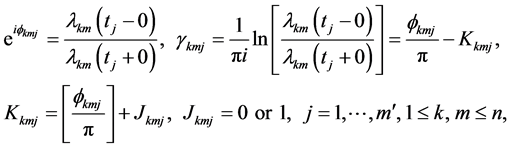 (1.9)
(1.9)
where  when
when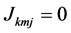 , and
, and 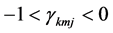 when
when . There is no harm in assuming that the partial indexes
. There is no harm in assuming that the partial indexes  of
of 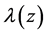 on
on 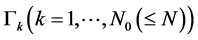 are not integers, and the partial indexes
are not integers, and the partial indexes 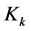 of
of 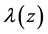 on
on 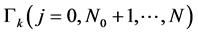 are integers. Set
are integers. Set
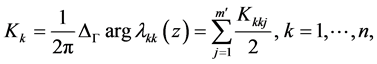 (1.10)
(1.10)
and we call 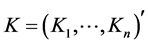 the index of Problem A.
the index of Problem A.
For problem A, we will assume  satisfy the conditions
satisfy the conditions
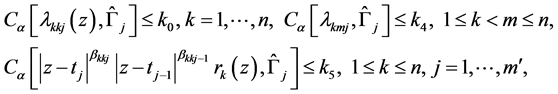 (1.11)
(1.11)
in which  is an open arc from the point
is an open arc from the point 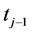 to
to 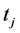 on
on 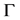
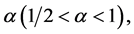
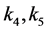 are non-negative constants,
are non-negative constants,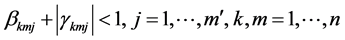 . Moreover, we require that the solution
. Moreover, we require that the solution 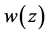 possess the property
possess the property
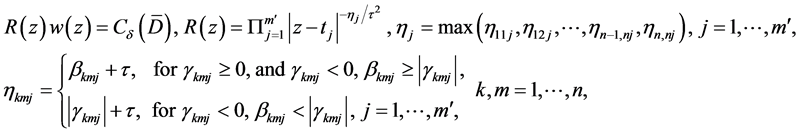 (1.12)
(1.12)
in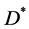 , where
, where 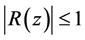 in
in 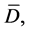 and
and  are small positive constants.
are small positive constants.
In general, Problem A may not be solvable. Hence we propose a modified problem as follows.
Problem B Find a system of continuous solutions 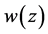 of the complex equation (1.4) in
of the complex equation (1.4) in , which satisfies the modified boundary condition
, which satisfies the modified boundary condition
 (1.13)
(1.13)
Here
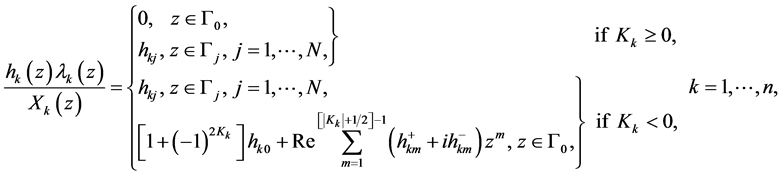 (1.14)
(1.14)
in which 
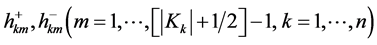 are unknown real constants to be determined appropriately, and
are unknown real constants to be determined appropriately, and , if
, if  is an odd integer. More description on
is an odd integer. More description on  and
and 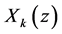 are given below. We begin with the following function
are given below. We begin with the following function

where 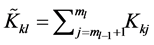 denotes the partial index on
denotes the partial index on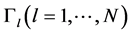 ,
, 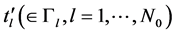 are fixed pointswhich are not the discontinuous points from
are fixed pointswhich are not the discontinuous points from . Note that the positive direction applies to the boundary circles
. Note that the positive direction applies to the boundary circles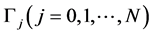 . Similarly to (1.7)-(1.12), Chapter V, [2] , we see that
. Similarly to (1.7)-(1.12), Chapter V, [2] , we see that
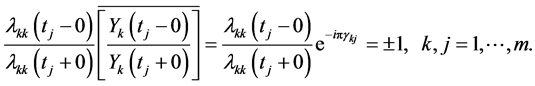
Clearly, with certain modification on the symbols on some arcs on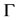 ,
, 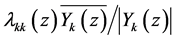 on
on 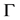 is seen to be continuous. In this case, its index
is seen to be continuous. In this case, its index
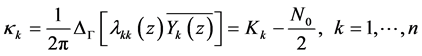
are integers. And we have the following:
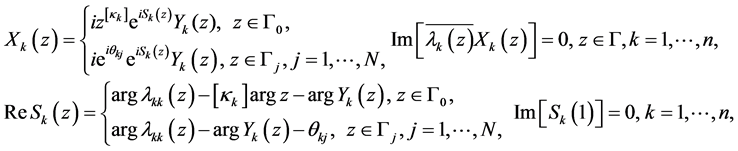
in which 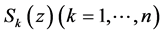 are solutions of the modified Dirichlet problems with the above boundary conditions for analytic functions,
are solutions of the modified Dirichlet problems with the above boundary conditions for analytic functions,  are real constants, and
are real constants, and .
.
In addition, we may assume that the solution 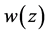 satisfies the following point conditions
satisfies the following point conditions
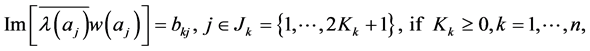 (1.15)
(1.15)
where  are distinct points, and
are distinct points, and 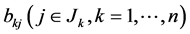 are all real constants satisfying the conditions
are all real constants satisfying the conditions
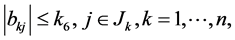 (1.16)
(1.16)
for a positive constant . Problem B with
. Problem B with  in
in ,
, 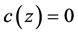 on
on  and
and 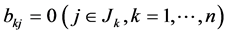 is called Problem
is called Problem .
.
If  then Problem B for (1.4) is the modified Dirichlet boundary value problem for (1.4). It is easy to see that the solutions of (1.4) include the generalized hyperanalytic functions as special cases. In fact, if (1.4) is linear, and
then Problem B for (1.4) is the modified Dirichlet boundary value problem for (1.4). It is easy to see that the solutions of (1.4) include the generalized hyperanalytic functions as special cases. In fact, if (1.4) is linear, and 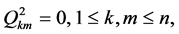
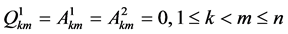 and
and 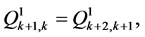
 then the solutions of (1.4) are called generalized hyperanalytic functions.
then the solutions of (1.4) are called generalized hyperanalytic functions.
2. Parameter Extension Method of the Discontinuous Riemann-Hilbert Problem for Elliptic Systems of First Order Complex Equations
We begin with the following estimates of the solution for problem B.
Theorem 2.1 Suppose that the complex system (1.4) satisfies Condition C and the constants 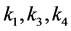 in
in
(1.6), (1.7), (1.11) are small enough. Then any solution 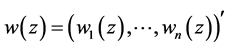 of Problem B for (1.4) satisfies the estimate
of Problem B for (1.4) satisfies the estimate
 (2.1)
(2.1)
where  with
with 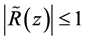 in
in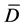 ,
, 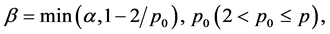
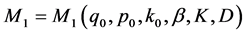
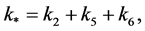 with
with 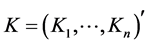 are non-negative constants.
are non-negative constants.
Proof There is no harm in assuming that 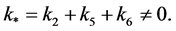 Let
Let  It can be seen that
It can be seen that  is a solution of the following boundary value problem
is a solution of the following boundary value problem
 (2.2)
(2.2)
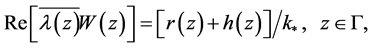 (2.3)
(2.3)
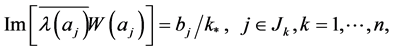 (2.4)
(2.4)
in which
 (2.5)
(2.5)
Following the proof of the Theorem 2.1 of Chapter VI in [1] , we can derive the estimate
 (2.6)
(2.6)
From the above estimate, it immediately follows that the estimate (2.1) is true.
In addition, we assume that (1.4) satisfies the following condition: For any continuous vectors  and any measurable vector
and any measurable vector 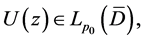
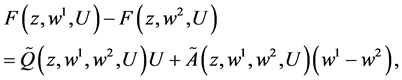 (2.7)
(2.7)
where  satisfy the condition
satisfy the condition
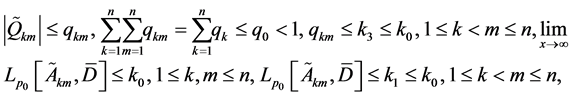 (2.8)
(2.8)
in which 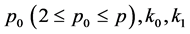 are non-negative constants.
are non-negative constants.
Now, we prove that there exists a unique solution of the modified Riemann-Hilbert problem (Problem B) for analytic vectors by the parameter extensional method.
Theorem 2.2 Let 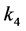 in (1.11) be a sufficiently small positive constant. Then Problem B for analytic vectors has a solution.
in (1.11) be a sufficiently small positive constant. Then Problem B for analytic vectors has a solution.
Proof We consider the modified Riemann-Hilbert problem (Problem ) for analytic vectors with the boundary conditions
) for analytic vectors with the boundary conditions
 (2.9)
(2.9)
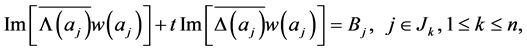 (2.10)
(2.10)
where

in which 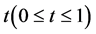 is a real parameter, and
is a real parameter, and 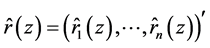 is any vector of real functions,
is any vector of real functions,  and
and 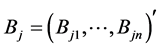 is any vector of constants. When
is any vector of constants. When , it is clear that Problem
, it is clear that Problem  for analytic vectors has a unique solution (see [1] ). If Problem
for analytic vectors has a unique solution (see [1] ). If Problem 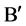 with
with 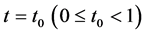 for analytic vectors is solvable, we shall prove that there exists a positive number
for analytic vectors is solvable, we shall prove that there exists a positive number 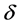 independent of
independent of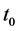 , such that Problem
, such that Problem 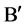 for every
for every 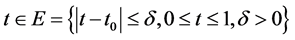 has a unique solution. In fact, the boundary conditions (2.9), (2.10) can be rewritten in the form
has a unique solution. In fact, the boundary conditions (2.9), (2.10) can be rewritten in the form
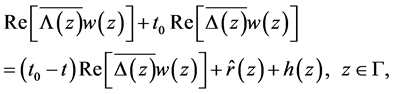 (2.11)
(2.11)
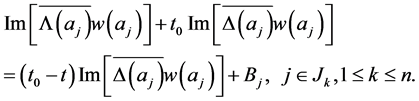 (2.12)
(2.12)
Substituting the zero vector 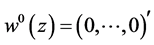 into the position of
into the position of  on the right hand side of (2.11) and (2.12), by the hypothesis, the boundary value problem (2.11), (2.12) for analytic vectors has a unique solution
on the right hand side of (2.11) and (2.12), by the hypothesis, the boundary value problem (2.11), (2.12) for analytic vectors has a unique solution 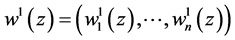 and
and  Using the successive iterationwe can find a sequence
Using the successive iterationwe can find a sequence 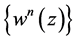 of analytic vectors, which satisfies the boundary conditions
of analytic vectors, which satisfies the boundary conditions
 (2.13)
(2.13)
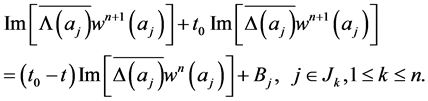 (2.14)
(2.14)
From (2.13) and (2.14), we have
 (2.15)
(2.15)
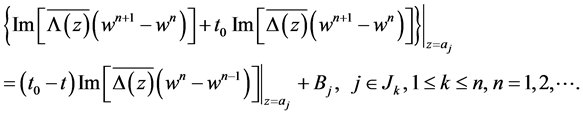 (2.16)
(2.16)
In accordance with Theorem 2.1, we can conclude
 (2.17)
(2.17)
where 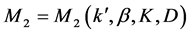 with
with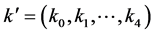 , and
, and 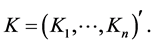 Choosing a positive constant
Choosing a positive constant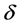 , such that
, such that 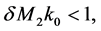 it is not difficult to see that
it is not difficult to see that
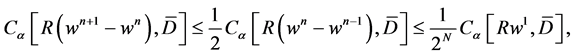
and

for  where
where 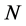 is a positive integer. This shows that
is a positive integer. This shows that
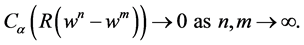
Hence, there exists an analytic vector 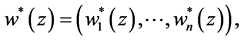 such that
such that
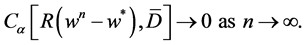 (2.18)
(2.18)
Thus 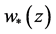 is a solution of Problem
is a solution of Problem 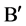 with
with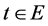 . From this we can derive that Problem
. From this we can derive that Problem 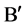 with
with  i.e. Problem B for analytic vectors is solvable.
i.e. Problem B for analytic vectors is solvable.
Next we prove the solvability of Problem B for the system (1.4).
Theorem 2.3 Let the nonlinear elliptic system (1.4) satisfy Condition C, and  in (1.6), (1.7), (1.11) be sufficiently small positive constants. Then Problem B for the complex system (1.4) is solvable.
in (1.6), (1.7), (1.11) be sufficiently small positive constants. Then Problem B for the complex system (1.4) is solvable.
Proof We consider the nonlinear elliptic complex system with the parameter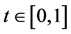 :
:
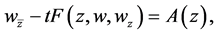 (2.19)
(2.19)
where 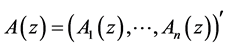 is any measurable vector in
is any measurable vector in 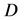 and
and 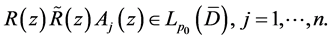 Applying Theorem 2.2, we see that Problem B for (2.19) with
Applying Theorem 2.2, we see that Problem B for (2.19) with  is solvable, and the solution
is solvable, and the solution  can be expressed as
can be expressed as
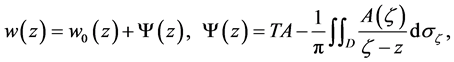 (2.20)
(2.20)
where 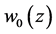 is an analytic vector satisfying the boundary conditions
is an analytic vector satisfying the boundary conditions
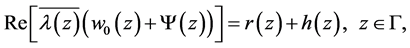 (2.21)
(2.21)
 (2.22)
(2.22)
Suppose that when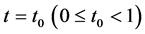 , Problem B for the system (2.19) has a unique solution. Then we shall prove that there exists a neighborhood of
, Problem B for the system (2.19) has a unique solution. Then we shall prove that there exists a neighborhood of 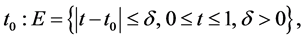 so that for every
so that for every 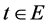 and any function
and any function 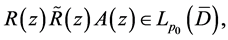 Problem B for (2.19) is solvable. In fact, the complex system (2.19) can be written in the form
Problem B for (2.19) is solvable. In fact, the complex system (2.19) can be written in the form
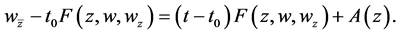 (2.23)
(2.23)
Suppose that Problem B for (2.13) with 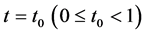 is solvable, by using the similar method as in the proof of Theorem 2.2, we can find a positive constant
is solvable, by using the similar method as in the proof of Theorem 2.2, we can find a positive constant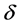 , so that for every
, so that for every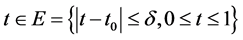 , there exists a sequence
, there exists a sequence 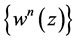 of solutions satisfying
of solutions satisfying
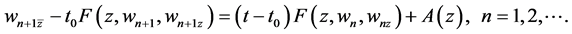 (2.24)
(2.24)
The difference of the above equations for 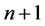 and
and 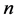 is as follows:
is as follows:
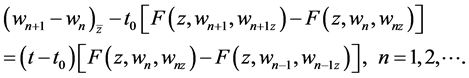 (2.25)
(2.25)
From Condition C, we can derive that
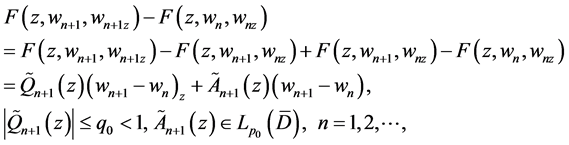
and
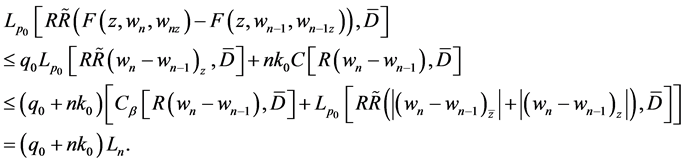
Moreover, 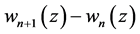 satisfies the homogeneous boundary conditions
satisfies the homogeneous boundary conditions
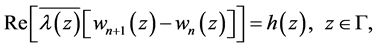 (2.26)
(2.26)
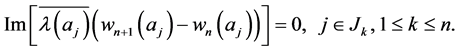 (2.27)
(2.27)
Similarly to Theorem 3.3, Chapter I, [1] , we have
 (2.28)
(2.28)
where 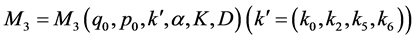 are positive constants. Provided
are positive constants. Provided 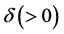 is small enough, so that
is small enough, so that 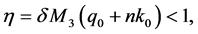 we can obtain
we can obtain
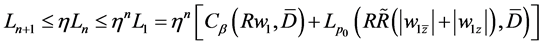 (2.29)
(2.29)
for every  Thus
Thus
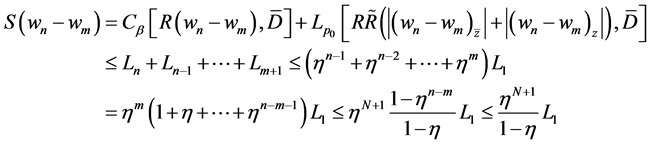
for  where
where  is a positive integer. This shows that
is a positive integer. This shows that 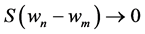 as
as 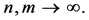 Thus there exists a system of continuous functions
Thus there exists a system of continuous functions  in
in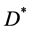 , such that
, such that

By Condition C, it follows that  is a solution of Problem B for the system (2.23), i.e. (2.19) for
is a solution of Problem B for the system (2.23), i.e. (2.19) for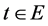 . It is easy to see that the positive constant
. It is easy to see that the positive constant 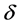 is independent of
is independent of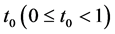 . Hence Problem B for the system (2.19) with
. Hence Problem B for the system (2.19) with 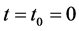 is solvable. Correspondingly we can derive that when
is solvable. Correspondingly we can derive that when , Problem B for (2.19) is solvable. Especially Problem B for (2.19) with
, Problem B for (2.19) is solvable. Especially Problem B for (2.19) with  and
and , namely Problem B for the system (1.4) has a solution.
, namely Problem B for the system (1.4) has a solution.
3. Error Estimates of Approximate Solutions of the Discontinuous Riemann Hilbert Problem for Elliptic Systems of First Order Complex Equations
In this section, we shall introduce an error estimate of the above approximate solutions.
Theorem 3.1 Under the same conditions as in Theorem 2.3, let  be a solution of Problem B for the complex system (1.4) satisfying Condition C in
be a solution of Problem B for the complex system (1.4) satisfying Condition C in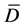 , and
, and 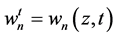 be its approximation as stated in the proof of Theorem 2.3 with
be its approximation as stated in the proof of Theorem 2.3 with 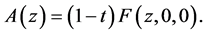 Then we have the following error estimate
Then we have the following error estimate
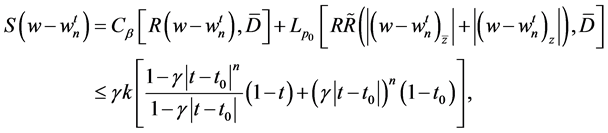 (3.1)
(3.1)
where 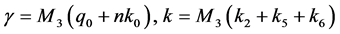 with
with 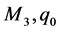 as in (2.28), and
as in (2.28), and 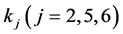 as in (1.6),(1.7), (1.11) and (1.16).
as in (1.6),(1.7), (1.11) and (1.16).
Proof From (1.4) and (2.24) with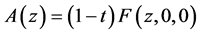 , we have
, we have
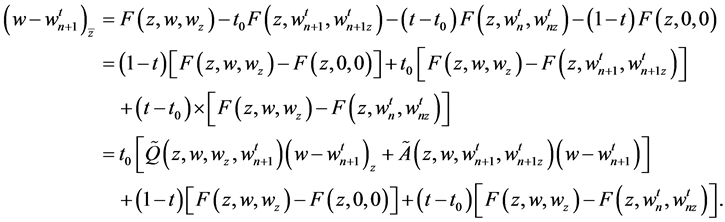 (3.2)
(3.2)
It is clear that 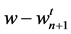 satisfies the homogeneous boundary conditions
satisfies the homogeneous boundary conditions
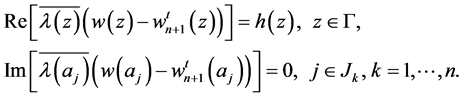 (3.3)
(3.3)
Noting that 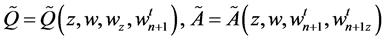 satisfy
satisfy , and
, and
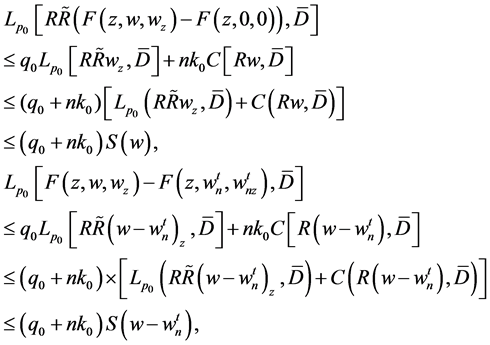
and then  is a solution of Problem
is a solution of Problem  for the complex equation
for the complex equation
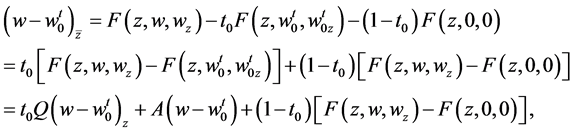 (3.4)
(3.4)
hence we have
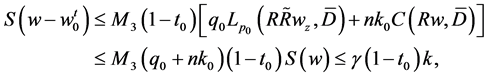 (3.5)
(3.5)
in which
 (3.6)
(3.6)
where the non-negative constants  are as stated in (2.28), (1.5), (1.11) and (1.12). Moreover according to the proof of Theorem 2.3, we can derive
are as stated in (2.28), (1.5), (1.11) and (1.12). Moreover according to the proof of Theorem 2.3, we can derive
 (3.7)
(3.7)
From (3.6) and (3.7), it follows that
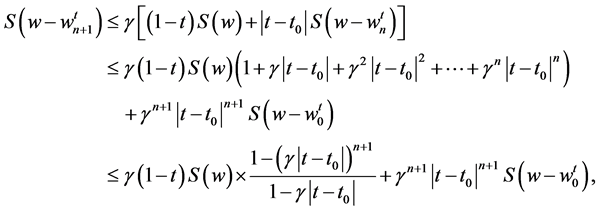
where 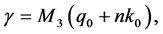 and
and 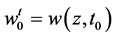 is the solution of Problem B for (2.24) with
is the solution of Problem B for (2.24) with 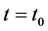 and
and 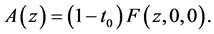 Finally, we obtain
Finally, we obtain
 (3.8)
(3.8)
This shows that (3.1) holds. If the positive constant  is small enough, so that when
is small enough, so that when 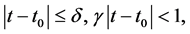
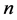 is sufficiently large and
is sufficiently large and 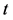 is close to 1, then the right hand side becomes very small.
is close to 1, then the right hand side becomes very small.
Note: The opinions expressed herein are those of the authors and do not necessarily represent those of the Uniformed Services University of the Health Sciences and the Department of Defense.
References
- Wen, G.C. and Begehr, H. (1990) Boundary Value Problems for Elliptic Equations and Systems. Longman Scientific and Technical Company, Harlow.
- Wen G.C. (1992) Conformal Mappings and Boundary Value Problems, Translations of Mathematics Monographs 106. American Mathematical Society, Providence.
- Wen, G.C., Tai, C.W. and Tian, M.Y. (1996) Function Theoretic Methods of Free Boundary Problems and Their Applications to Mechanics. Higher Education Press, Beijing (Chinese).
- Wen, G.C. (1986) Linear and Nonlinear Elliptic Complex Equations. Shanghai Scientific and Technical Publishers, Shanghai (Chinese).
- Wen G.C. (1999) Approximate Methods and Numerical Analysis for Elliptic Complex Equations. Gordon and Breach, Amsterdam.
- Wen, G.C. (1999 Linear and Nonlinear Parabolic Complex Equations. World Scientific Publishing Co., Singapore City.
- Wen, G.C. and Zou, B.T. (2002) Initial-Boundary Value Problems for Nonlinear Parabolic Equations in Higher Dimensional Domains. Science Press, Beijing.
- Wen, G.C. (2002) Linear and Quasilinear Complex Equations of Hyperbolic and Mixed Type. Taylor & Francis, London. http://dx.doi.org/10.4324/9780203166581
- Huang, S., Qiao, Y.Y. and Wen, G.C. (2005) Real and Complex Clifford Analysis. Springer Verlag, Heidelberg.
- Wen, G.C. (2008) Elliptic, Hyperbolic and Mixed Complex Equations with Parabolic Degeneracy. World Scientific, Singapore City.
- Wen, G.C., Chen, D.C. and Xu, Z.L. (2008) Nonlinear Complex Analysis and its Applications, Mathematics Monograph Series 12. Science Press, Beijing.
NOTES

*Deceased.
#I am very grateful for the guidance and help of Professor Guochun Wen, who served as my adviser for many years. 1 will always remember him because he inf1uenced me greatly.

