Applied Mathematics
Vol.5 No.3(2014), Article ID:42805,8 pages DOI:10.4236/am.2014.53050
Study of Delay and Loss Behavior of Internet Switch-Markovian Modelling Using Circulant Markov Modulated Poisson Process (CMMPP)
1Department of Mathematics, Medak College of Engineering and Technolgy, Medak, India
2Department of Mathematics, Kakatiya Institute of Technology and Science, Warangal, India
3Department of Mathematics, Kakatiya University, Warangal, India
Email: ranadheer.phdku@gmail.com, rameshrenikuntla@gmail.com, dsreddy.hari@gmail.com, mperati@yahoo.com
Received September 29, 2013; revised October 29, 2013; accepted November 7, 2013
ABSTRACT
Most of the classical self-similar traffic models are asymptotic in nature. Therefore, it is crucial for an appropriate buffer design of a switch and queuing based performance evaluation. In this paper, we investigate delay and loss behavior of the switch under self-similar fixed length packet traffic by modeling it as CMMPP/D/1 and CMMPP/D/1/K, respectively, where Circulant Markov Modulated Poisson Process (CMMPP) is fitted by equating the variance of CMMPP and that of self-similar traffic. CMMPP model is already the validated one to emulate the self-similar characteristics. We compare the analytical results with the simulation ones.
Keywords:CMMPP; Self-Similar Traffic; Mean Waiting Time; Packet Loss Probability; Traffic Intensity; Hurst Parameter; Time-Scale
1. Introduction
An effective traffic model has, at least, to reproduce the first and second order statistics of the original traffic trace. The second order statistics play an important role in traffic modeling, because traffic correlation is an important factor in packet losses due to buffer and bandwidth limitations. However, the first two order statistics may not be sufficient to characterize real data traces that are known to be bursty and spiky in nature. It has been shown through experimental evidence that network traffic may exhibit properties of self-similarity and/or long range dependence (LRD) [1-3]. Self-similar traffic shows identical statistics’ characteristics over a wide range of time scales, which have significant impact on network performance. Therefore, it is important to make frequent measurement of packet flows and to decide them through appropriate traffic models. Characterizing the statistical behavior of traffic is crucial for proper buffer design of switch in the network traffic to provide the quality of service (QoS). Various stochastic models have been proposed to emulate the statistical nature of self-similar network traffic over certain range of time scales. Traffic models such as Fractional Brownian Motion (FBM), Fractional Auto Regressive Integrated Moving Average (FARIMA) and Chaotic maps are proposed to characterize the self-similarity. These models describe the self-similar behavior in a relatively simple manner. Although these processes have less number of parameters, they are less effective in the context of queuing based performance evaluation. Traditional traffic models, such as Markovian models, can still be used to model traffic exhibiting LRD. In [4-7], Markovian arrival process (MAP) is employed to model the self-similar behavior over the desired time scales. These fitting models equate the second order statistics of self-similar traffic and superposition of several 2-state Interrupted Poisson Processes (IPPs). The said models hold well for voice traffic as IPP consists of two states talkspurt and silence. On the other hand, the Circulant Markov Modulated Poisson Process (CMMPP) is a Poisson process, the rate of which is changed according to circulant Markov chain [8]. The Circulant Markov Modulated Poisson Process is characterized by circulant stochastic transition matrix Q and non-negative vector λ. In the case of two states Circulant Markov Modulated Poisson Process (2-CMMPP) which is Switched Poisson process (2-state MMPP), two states are active unlike IPP and it is good model for arrival process in Internet traffic. The MMPP and CMMPP both are model classes which can be incorporated in queuing analysis. The CMMPP has several advantages over MMPP in terms of computational complexity [9,10]. The steady state probability distributions of this process are the normalized null vector of its generator matrix.
In addition to traditional data services, multimedia and real-time applications are becoming indispensable services offered by the best-effort Internet. The future Internet is expected to offer a certain QoS guarantee to some important applications, which are the best effort today. As is well understood, packets may suffer some delay and loss at the network nodes during their traversal across a packet-switched network. Therefore, packet loss and end-to-end delay are two crucial performance metrics for Internet QoS. In the present paper, we investigate delay and loss behavior of the resultant CMMPP/D/1/K queueing system and compare with that of simulation results.
The paper is organized as follows. In Section 2, we first overview the fundamentals of self-similar process and Circulant Markov modulated Poisson process. In Section 3, the generalized fitting procedure is given. In Section 4, Queuing systems and numerical results are presented. Finally, some conclusions are made in Section 5.
2. Self-Similar Process and Circulant Markov Modulated Poisson Process (CMMPP)
In this section, we first overview the definition of the exact second order self-similar process and summarize some characteristics of CMMPP and then, we make some remarks.
2.1. Self-Similar Process
The definition of exact second-order self-similar processes is given as follows. If we consider ![]() as a second -order stationary process with variance
as a second -order stationary process with variance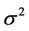 , and divide time axis into disjoint intervals of unit length, we could define
, and divide time axis into disjoint intervals of unit length, we could define 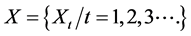 to be the number of points (packet arrivals) in the
to be the number of points (packet arrivals) in the ![]() interval. A new sequence
interval. A new sequence
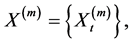 where
where 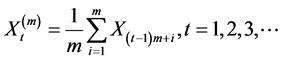 , is the average of the original sequence in m nonoverlapping blocks. Then the process
, is the average of the original sequence in m nonoverlapping blocks. Then the process ![]() is defined as an exact second order self-similar process with the Hurst parameter,
is defined as an exact second order self-similar process with the Hurst parameter, 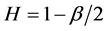 , if
, if
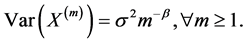 (1)
(1)
2.2. Circulant Markov Modulated Poisson Process (CMMPP)
CMMPP is a doubly stochastic process in which arrival rate is given by  where
where 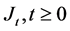 is an
is an 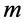 -state Markov process. The arrival rate can therefore take on only
-state Markov process. The arrival rate can therefore take on only 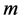 values, namely
values, namely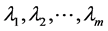 . It is equal to
. It is equal to ![]() whenever the Markov process is in the state
whenever the Markov process is in the state 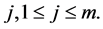 The CMMPP is fully parameterized by the infinitesimal generator
The CMMPP is fully parameterized by the infinitesimal generator  (Circulant Markovian) of the Markov process and the vector
(Circulant Markovian) of the Markov process and the vector 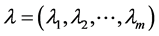 of the arrival rates. Let
of the arrival rates. Let 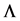 be the diagonal matrix with
be the diagonal matrix with 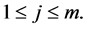
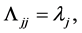 In the case of two state CMMPP,
In the case of two state CMMPP, 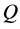 and
and 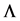 are given as follows:
are given as follows:
 (2)
(2)
The mean and variance of 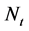 can be deduced from that of MMPP [7]. The mean arrival rate
can be deduced from that of MMPP [7]. The mean arrival rate ![]() of CMMPP is given by
of CMMPP is given by![]() , where
, where 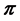 is the stationary probability vector of Q, i.e.
is the stationary probability vector of Q, i.e. 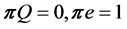 and
and 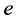 is an all 1 column vector with designated dimension. If we let
is an all 1 column vector with designated dimension. If we let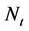 ,
, ![]() , be the number of arrivals in (0, t]The mean,
, be the number of arrivals in (0, t]The mean,
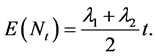 (3)
(3)
The variance of 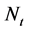 is given as follows
is given as follows
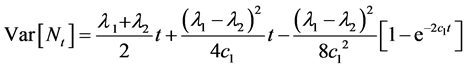 (4)
(4)
Since the index of dispersion for counts (IDC) is defined as

From (3) and (4), we can obtain
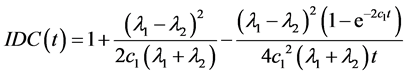 (5)
(5)
We then could obtain the following remarks:
1) 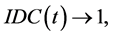 as
as ![]() , that is, CMMPP tends to a Poisson process.
, that is, CMMPP tends to a Poisson process.
2) 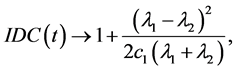 a constant , as
a constant , as 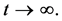
3) 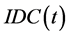 is monotonic increasing over a finite time interval and is bounded.
is monotonic increasing over a finite time interval and is bounded.
4) Steady state distribution of 2-state CMMPP is 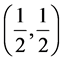 and is independent of transition rates.
and is independent of transition rates.
The first and second order statistics of Nt in the case of MMPP and CMMPP are listed in the following table.
3. Generalized Variance Based Fitting Procedure
Generalized variance-based fitting method is a procedure to find out the traffic model parameters, that match the variance of self-similar and that of model traffic [4-6,11]. The fitted model emulating self-similar traffic consists of a superposition of  2-CMMPPs and one Poisson process. We describe the ith 2-CMMPP as follows.
2-CMMPPs and one Poisson process. We describe the ith 2-CMMPP as follows.
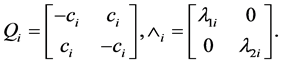 (6)
(6)
Superposition of above 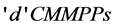 and a Poisson process is a transition rate matrix and is determined by
and a Poisson process is a transition rate matrix and is determined by
 (7)
(7)
In (7), ![]() means the Kroneker’s sum and
means the Kroneker’s sum and 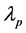 is the arrival rate of the Poisson process. The whole arrival rate,
is the arrival rate of the Poisson process. The whole arrival rate, ![]() , is then given by
, is then given by
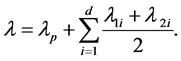 (8)
(8)
Let 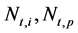 be the number of arrival packets from the ith CMMPP and Poisson process, respectively, during the tth time slot, and let
be the number of arrival packets from the ith CMMPP and Poisson process, respectively, during the tth time slot, and let 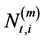 and
and  be the number of arrival from the averaged processes of ith CMMPP and Poisson process, respectively.
be the number of arrival from the averaged processes of ith CMMPP and Poisson process, respectively.
Put
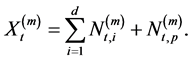 (9)
(9)
Using (4), we obtain the variance of the ith CMMPP as
 (10)
(10)
Also
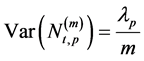 . (11)
. (11)
From (9)-(11) and using the fact that superposition of independent sub-processes preserves the variance, we obtain
 (12)
(12)
where
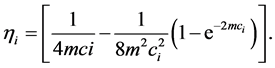 (13)
(13)
Using (1) and (12), we can match the variance at 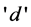 different points mi,
different points mi, 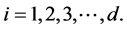 Let
Let 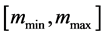
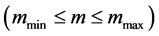 be the time interval over which we want the process to express self-similarity of the original process, then
be the time interval over which we want the process to express self-similarity of the original process, then 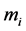 is given by
is given by
 (14)
(14)
where
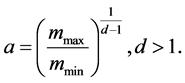 (15)
(15)
Now, we assume the following relations between 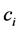 and
and 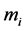
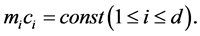
That is,  can be determined using
can be determined using
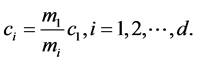 (16)
(16)
There are due to the fact that a Self-similar process takes the same in any time scale. Because of this assumption, we can reduce the number of parameters to be determined. That is, if we determine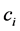 , we can obtain the values of
, we can obtain the values of 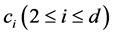 by using (16). Furthermore, we can obtain
by using (16). Furthermore, we can obtain 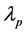 from (8) if we determine
from (8) if we determine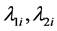 . The parameters we need to find are only
. The parameters we need to find are only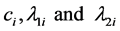 .
.
4. Queuing Systems and Numerical Results
In this section, synchronous input traffic of fixed length h (in time units) is modeled as CMMPP/D/1queuing system. In CMMPP/D/1 system, the packets of fixed length arrive according to CMMPP. The performance metrics in this case involve 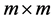 irreducible matrix
irreducible matrix 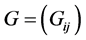 if CMMPP of
if CMMPP of 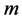 states [ ]">< a href="#r"> a href="#r">] ">12], where
states [ ]">< a href="#r"> a href="#r">] ">12], where 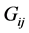 is the probability that a busy period starting with the CMMPP in state
is the probability that a busy period starting with the CMMPP in state ![]() and ends in state
and ends in state 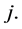 The matrix G is a key ingredient in obtaining mean waiting time. The mean waiting time (MWT) could be computed by the formula [11] .
The matrix G is a key ingredient in obtaining mean waiting time. The mean waiting time (MWT) could be computed by the formula [11] .
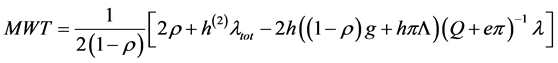 (17)
(17)
where  and
and 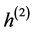 first and second moments of service time distribution, and here second moment
first and second moments of service time distribution, and here second moment 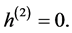 The steady state vector g of G satisfies
The steady state vector g of G satisfies 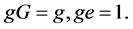 For the packet loss probability, the switch is modelled as finite buffer queueing system CMMPP/D/1/K [6, ]">]">12]. Packet loss probability against traffic intensity is computed using the procedure [6,] ">]">12]. We have fitted CMMPPs for the traffic parameters H = 0.7, H = 0.8, H = 0.9, λ = 1, σ2 = 0.6 over the time scales [102, 106] [102, 107] [102, 108]. In all the above cases, the number of two state CMMPPs, d, is equal to 4. Numerical calculations are performed using the MATLAB and the results are shown in the Figures 1-6. Figure 1 depicts the mean waiting time against traffic intensity for the case of H = 0.7 and the different time scales [102, 106], [102, 107] and [102, 108]. In this case, analytical results are validated with that of simulation. From this figure, it is clear that, the mean waiting time increases as the traffic intensity increases. Figure 2 depicts the mean waiting time against the traffic intensity for the case H = 0.8, and the time scales [102, 106], [102, 107], and [102, 108]. From the figure, it is clear that mean waiting time decreases as the time increases. Figure 3 depicts the mean waiting time against the traffic intensities for the case H = 0.7, H = 0.8, H = 0.9, over the time scale [102, 108]. From this we infer that the mean waiting time increases as H increases. Figure 4 depicts the packet loss probability against the traffic intensity for the case of H = 0.8 over the time scales [102, 106], [102, 107], and [102, 108]. From this figure, we conclude that packet loss probability increases as the traffic intensity increases. Figures 5-6 depict the packet loss probability against the traffic intensitiesfor the cases of H =
For the packet loss probability, the switch is modelled as finite buffer queueing system CMMPP/D/1/K [6, ]">]">12]. Packet loss probability against traffic intensity is computed using the procedure [6,] ">]">12]. We have fitted CMMPPs for the traffic parameters H = 0.7, H = 0.8, H = 0.9, λ = 1, σ2 = 0.6 over the time scales [102, 106] [102, 107] [102, 108]. In all the above cases, the number of two state CMMPPs, d, is equal to 4. Numerical calculations are performed using the MATLAB and the results are shown in the Figures 1-6. Figure 1 depicts the mean waiting time against traffic intensity for the case of H = 0.7 and the different time scales [102, 106], [102, 107] and [102, 108]. In this case, analytical results are validated with that of simulation. From this figure, it is clear that, the mean waiting time increases as the traffic intensity increases. Figure 2 depicts the mean waiting time against the traffic intensity for the case H = 0.8, and the time scales [102, 106], [102, 107], and [102, 108]. From the figure, it is clear that mean waiting time decreases as the time increases. Figure 3 depicts the mean waiting time against the traffic intensities for the case H = 0.7, H = 0.8, H = 0.9, over the time scale [102, 108]. From this we infer that the mean waiting time increases as H increases. Figure 4 depicts the packet loss probability against the traffic intensity for the case of H = 0.8 over the time scales [102, 106], [102, 107], and [102, 108]. From this figure, we conclude that packet loss probability increases as the traffic intensity increases. Figures 5-6 depict the packet loss probability against the traffic intensitiesfor the cases of H =
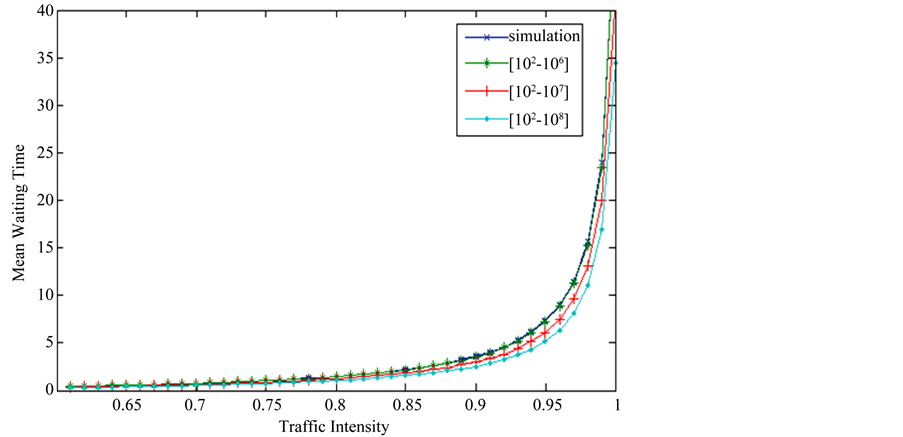
Figure 1. Mean waiting time of the resultant CMMPP/D/1 queue with d = 4, H = 0.7, λ = 1, σ2 = 0.6.
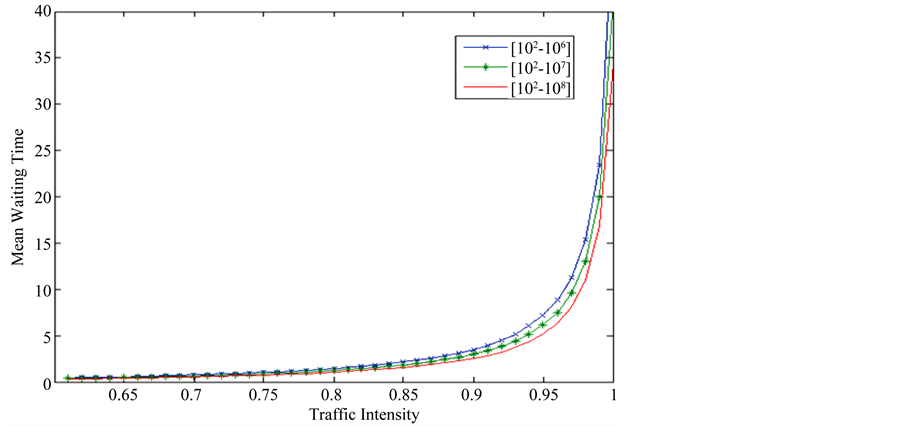
Figure 2. Mean waiting time of the resultant CMMPP/D/1 queue with d = 4, H = 0.8, λ = 1, σ2 = 0.6.
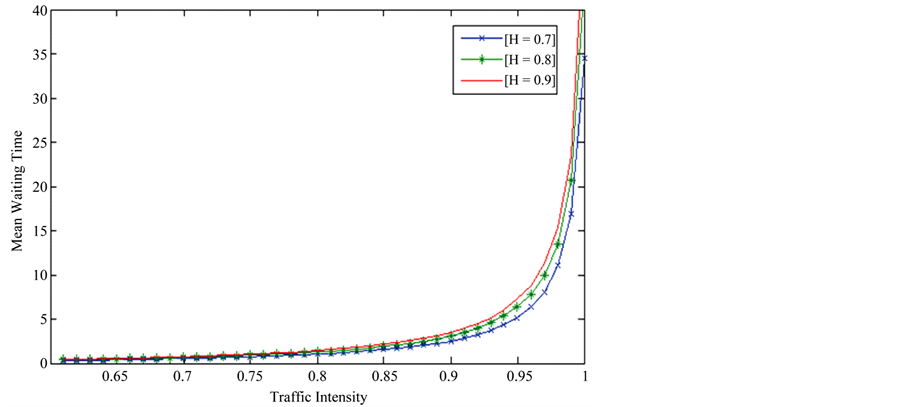
Figure 3. Mean waiting time of the resultant CMMPP/D/1 queue with d = 4, λ = 1, σ2 = 0.6 over the time scale [102, 108].

Figure 4. Loss probability of the resultant CMMPP/D/1/K queues with d = 4, λ = 1, H = 0.8, and K = 10.
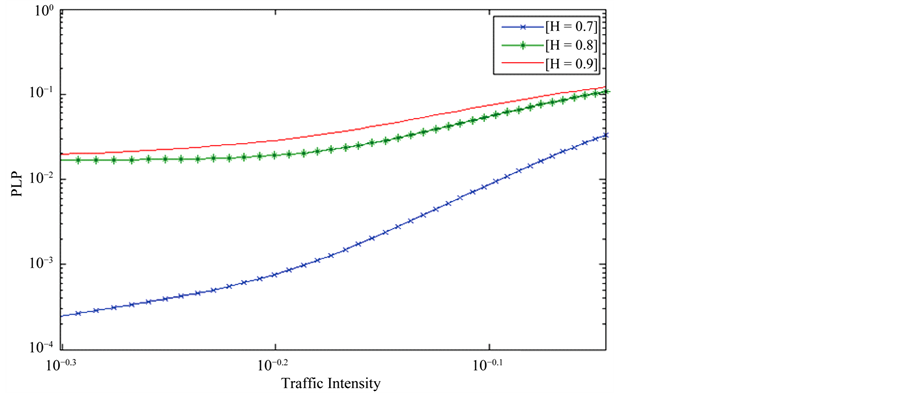
Figure 5. Loss probability of the resultant CMMPP/D/1/K queues with d = 4, λ = 1, and K = 10 over the time scale [102, 106].
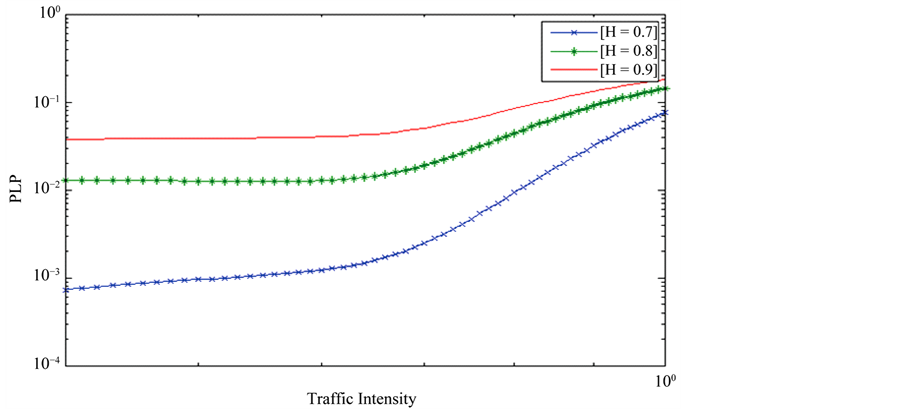
Figure 6. Loss probability of the resultant CMMPP/D/1/K queues with d = 4, λ = 1, and K = 10 over [102, 107].
0.7, H = 0.8, H = 0.9, over the time scales [102, 106], and [102, 107], respectively. From these figures, we conclude that packet loss probability decreases as the time scale increases, and packet loss probability decreases as the Hurst parameter decreases.
5. Conclusion
Most of the parsimonious self-similar traffic models proposed earlier are asymptotic in nature, therefore, they are less effective in the context of queuing based performance evaluation. Markovian models emulating selfsimilar traffic are proposed, as they hold well for queueing theory. These models are based on second order statistics. In this paper, we investigated queuing delay and loss behavior over different time scales and for different Hurst parameters. It is found from the numerical results that self-similar can be well represented by the proposed model. Our numerical results reveal that time-scale does have impact on packet loss probability. Packet loss probability increases as H and ρ increase. Based on the analysis presented in this paper, one could select the appropriate time-scale in the generalized variance based fitting method to meet the QoS requirement. This kind of analysis is useful in dimensioning the switch under self-similar input traffic.
REFERENCES
- W. E. Leland, M. S. Taqqu, W. Willinger and W. V. Wilson, “On the Self-Similar Nature of Ethernet Traffic (Extended Version),” IEEE/ACM Transactions on Networking, Vol. 2, No. 1, 1994, pp. 1-15. http://dx.doi.org/10.1109/90.282603
- V. Paxson and S. Floyd, “Wide Area Traffic: The Failure of Poisson Modelling,” IEEE/ACM Transactions on Networking, Vol. 3, No. 3, 1995, pp. 226-244. http://dx.doi.org/10.1109/90.392383
- M. Crovella and A. Bestavros, “Self-Similarity in World Wide Web Traffic: Evidence and Possible Causes,” IEEE/ACM Transactions on Networking, Vol. 5, No. 6, 1997, pp. 835-846. http://dx.doi.org/10.1109/90.650143
- A. Andersen and B. Nielsen, “A Markovian Approach for Modeling Packet Traffic with Long-Range Dependence,” IEEE Journal on Selected Areas in Communications, Vol. 16, No. 5, 1998, pp. 719-773. http://dx.doi.org/10.1109/49.700908
- T. Yoshihara, S. Kasahara and Y. Takahashi, “Practical Time-Scale Fitting of Self-Similar Traffic With Markov Modulated Poisson Process,” Telecommunication Systems, Vol. 17, No. 1-2, 2001, pp. 185-211. http://dx.doi.org/10.1023/A:1016616406118
- S. Kasahara, “Internet Traffic Modelling: Markovian Approach to Self-Similar Traffic and Prediction of Loss Probability for Finite Queues,” IEICE Transactions on Communication Special Issue on Internet Technology, Vol. E84-B, No. 8, 2001, pp. 2134-2141.
- S. K. Shao, P. Malla Reddy, M. G. Tsai, H. W. Tsao and J. Wu, “Generalized Variance-Based Markovian Fitting for Self-Similar Traffic Modeling,” IEICE Transactions on Communication, Vol. E88-B, No. 12, 2005, pp. 4659-4663.
- K. De and Cockand Bart DeMoor, “Identication of the First Order Parameters of a Circulant Modulated Poisson Process,” Proceedings of the International Conference on Telecommunications (ICT’98), Porto Carras, Vol. II, 1998, pp. 420-424.
- K. De Cock, T. Van Gestel and B. De Moo, “Identification of Circulant Modulated Poisson Process a Time Domain Approach,” Proceedings of MTNS, 1998, pp. 739-742.
- C. Blondia, “The N/G/l Finite Capacity Queue,” Communications in Statistics: Stochastic Models, Vol. 5, 1989, pp. 273-294.
- D. Ranadheer, R. Ramesh, D. Rajaiah and P. Malla Reddy, “Self-Similar Network Traffic Modeling Using Circulant Markov Modulated Poisson Process (CMMPP) (Manuscript),” Communicated to International Conference on Fractals and Wavelets, 2013.
- W. Fisher and K. S. Meier-Hellstern, “The Markov-Modulated Poisson Process (MMPP) Cookbook,” Performance Evaluation, Vol. 18, No. 2, 1992, pp. 149-171. http://dx.doi.org/10.1016/0166-5316(93)90035-S


