Applied Mathematics
Vol.3 No.12(2012), Article ID:25592,4 pages DOI:10.4236/am.2012.312268
On the Set of 2 − Common Consequent of Primitive Digraphs with Exact d Vertices Having Loop
School of Computer Science & Engineering, Zhanjiang Normal University, Zhanjiang, China
Email: cxiaogen@126.com
Received September 2, 2012; revised October 15, 2012; accepted October 23, 2012
Keywords: Boolean Matrix; Common Consequent; Primitive Digraph
ABSTRACT
Let ![]() and
and ![]() are positive integers,
are positive integers, 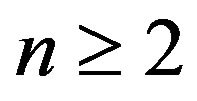 ,
, . In this paper we obtain that the set of the 2 − common consequent of primitive digraphs of order
. In this paper we obtain that the set of the 2 − common consequent of primitive digraphs of order ![]() with exact
with exact ![]() vertices having loop is
vertices having loop is .
.
1. Introduction
Let 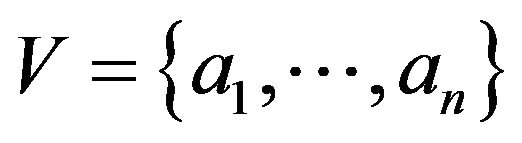 be a finite set of order
be a finite set of order![]() ,
, 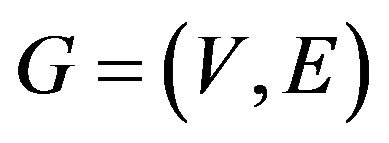 be a digraph. Elements of
be a digraph. Elements of 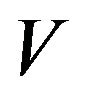 are referred as vertices and those of
are referred as vertices and those of 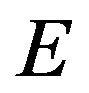 as arcs. The arc of
as arcs. The arc of 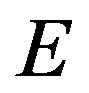 from vertex
from vertex ![]() to vertex
to vertex ![]() is denoted by
is denoted by . Let
. Let  be a
be a ![]() matrix over the Boolean algebra
matrix over the Boolean algebra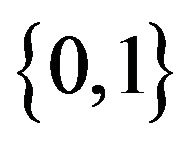 . If the adjacency matrix of
. If the adjacency matrix of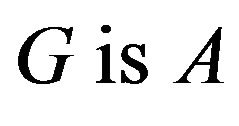 , where
, where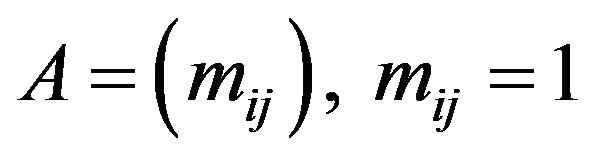 , if
, if 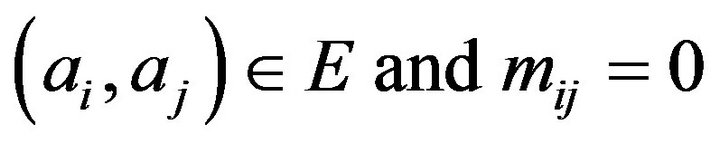 otherwise, then
otherwise, then  is Boolean matrix.
is Boolean matrix. 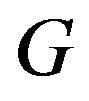 is called adjoint digraph of
is called adjoint digraph of .
.
The map:  is isomorphism.
is isomorphism.
Let 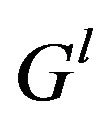 be a digraph corresponding to the
be a digraph corresponding to the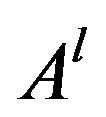 , and
, and
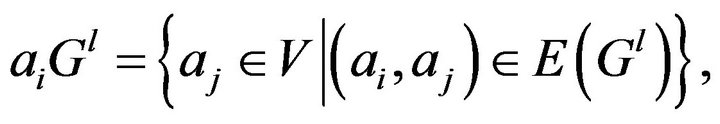
where l > 0 is an integer.
In 1983, Š. Schwarz [1] introduced a concept of the common consequent as follows.
Definition 1.1 Let 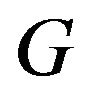 be a digraph. We say that a pair of vertices
be a digraph. We say that a pair of vertices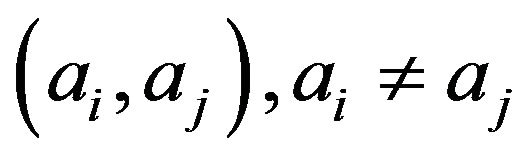 , has a common consequent
, has a common consequent 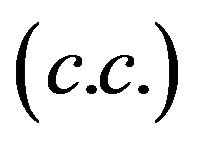 if there is an integer
if there is an integer  such that
such that
 (1)
(1)
If  have a
have a ![]() then the least integer
then the least integer  for which (1) holds is denoted by
for which (1) holds is denoted by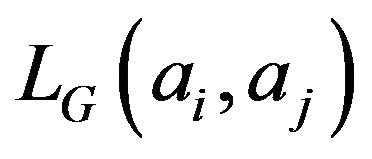 .
.
Definition 1.2 Let 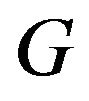 be a digraph. The generalized vertex exponent of
be a digraph. The generalized vertex exponent of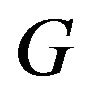 , denoted by
, denoted by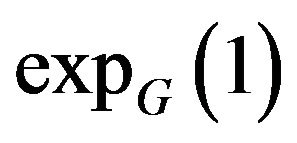 , is the least integer
, is the least integer 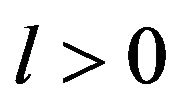 such that
such that
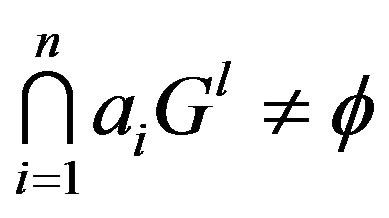 (2)
(2)
In 1996, Bolian Liu [2] extends the common consequent to the  common consequent
common consequent 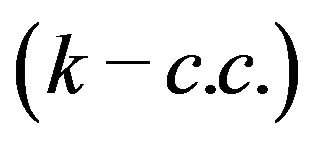 as follows.
as follows.
Definition 1.3 Let  be a digraph. We say that a group of vertices
be a digraph. We say that a group of vertices
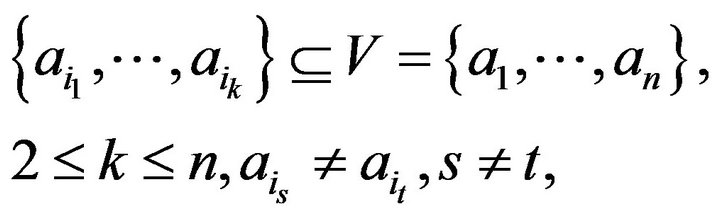
has a 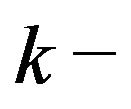 common consequent
common consequent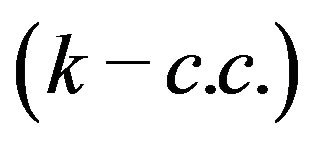 , if there is an integer
, if there is an integer 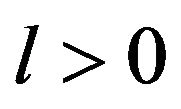 such that
such that
 (3)
(3)
If  have a
have a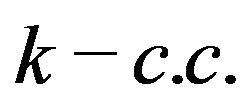 , then the least integer
, then the least integer  for which (3) holds is denoted by
for which (3) holds is denoted by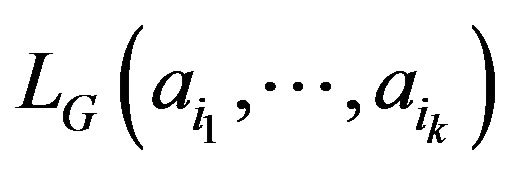 .
.
If there is at least one group 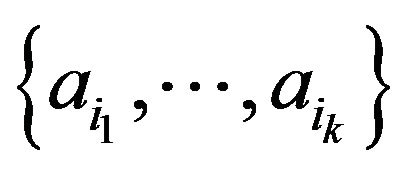 for which
for which
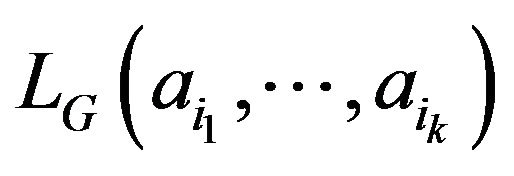 exists, we define
exists, we define
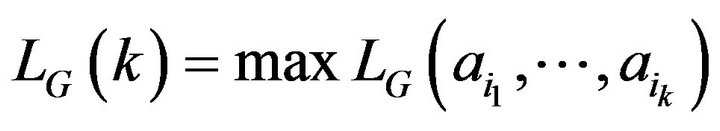 where
where 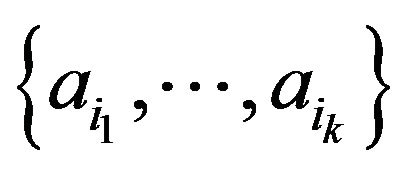 runs through all groups with
runs through all groups with 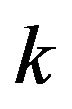 elements for which
elements for which 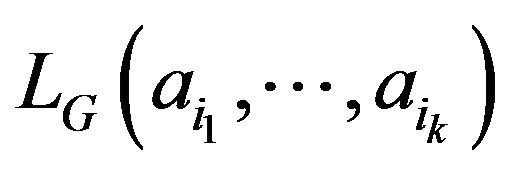 exists. If there is no group
exists. If there is no group 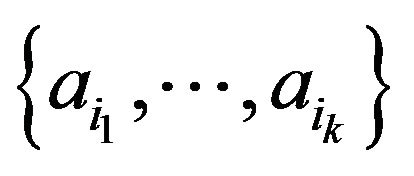 for which
for which 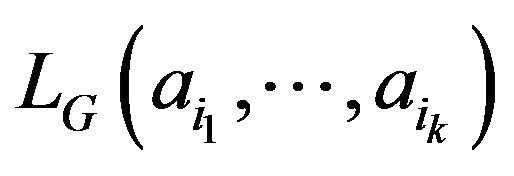 existswe define
existswe define .
. 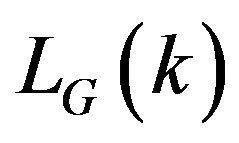 is called
is called 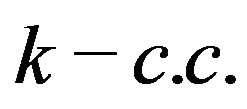 of
of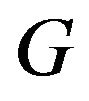 .
.
A digraph 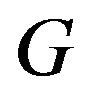 is said to be strongly connected if there exists a path from
is said to be strongly connected if there exists a path from ![]() to
to ![]() for all
for all . A digraph
. A digraph 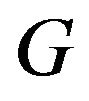 is said to be primitive if there exists a positive integer
is said to be primitive if there exists a positive integer  such that there is a walk of length
such that there is a walk of length ![]() from
from ![]() to
to ![]() for all
for all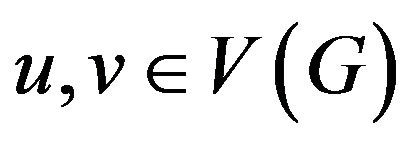 . The smallest such
. The smallest such ![]() is called the primitive exponent of
is called the primitive exponent of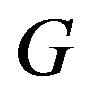 .
.
A digraph 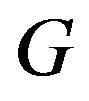 is primitive iff
is primitive iff 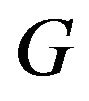 is strongly connected and the greatest common divisor of all cycle lengths of
is strongly connected and the greatest common divisor of all cycle lengths of 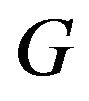 is
is .
.
Let 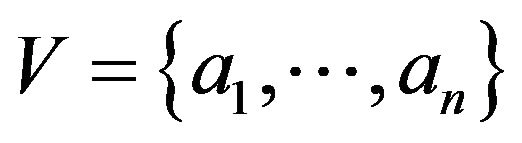 and
and  be the set of all primitive digraphs of order
be the set of all primitive digraphs of order ![]() with exact
with exact ![]() vertices having loop. It is obvious that if
vertices having loop. It is obvious that if , then
, then 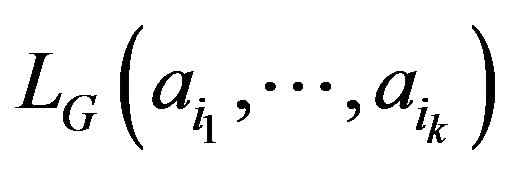 exists for any group
exists for any group
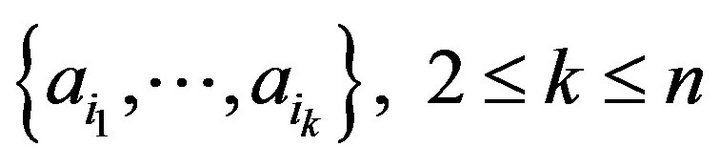 . We define
. We define
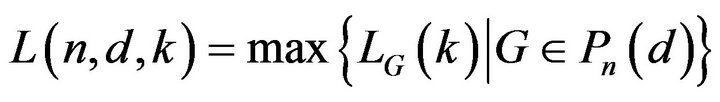 .
.
The properties of primitive digraphs and its  see [3-5]. In this paper we obtain that the set of the 2 − common consequent of primitive digraphs of order
see [3-5]. In this paper we obtain that the set of the 2 − common consequent of primitive digraphs of order ![]() with exact d vertices having loop is
with exact d vertices having loop is
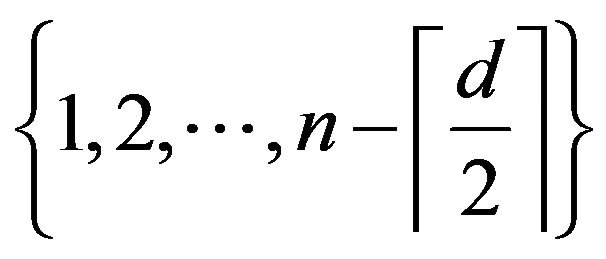 where
where ![]() and
and ![]() are positive integers,
are positive integers, 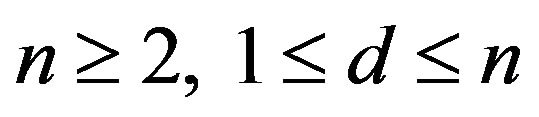 ,
, 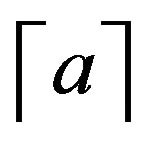 is the least integer greater or equal to a.
is the least integer greater or equal to a.
2. Preliminaries
It is easy to see that  exists by [1].
exists by [1].
Lemma 2.1 Let 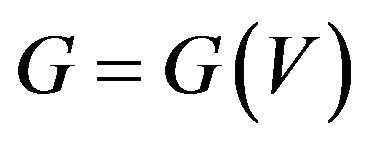 be a primitive digraph of order
be a primitive digraph of order 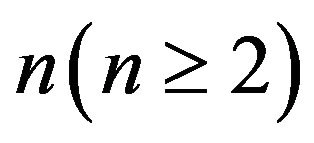 and
and 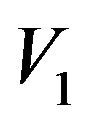 be a nonempty proper subset of
be a nonempty proper subset of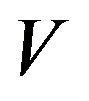 , then
, then 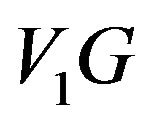 contains at least one element of
contains at least one element of 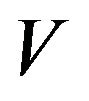 which is not contained in
which is not contained in .
.
Lemma 2.2 Let 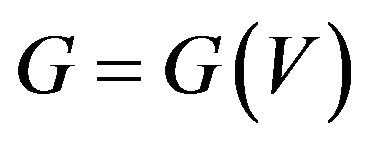 be a primitive digraph of order
be a primitive digraph of order 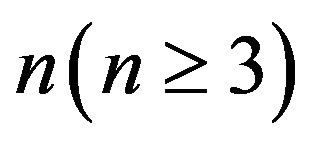 and
and , where vertex
, where vertex 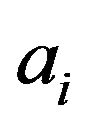 with having a loop,
with having a loop,  , then
, then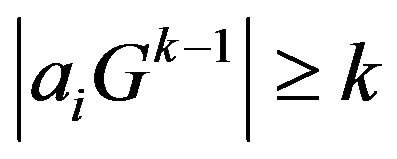 .
.
Proof: Since vertex 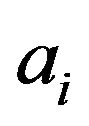 has a loop, hence
has a loop, hence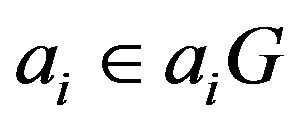 , and
, and 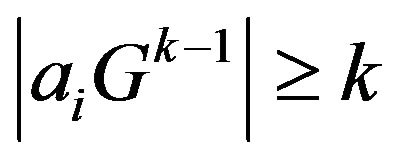 by lemma 2.1.
by lemma 2.1.
The follow lemma is obvious.
Lemma 2.3 [2] If ,
, 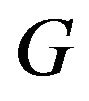 is a primitive digraph, then
is a primitive digraph, then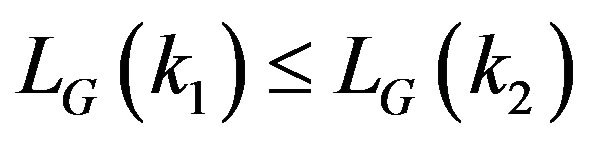 .
.
Lemma 2.4 Let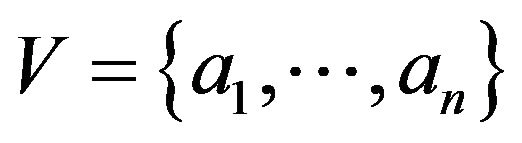 ,
,
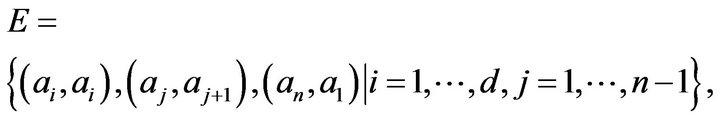
 where
where  are integers and
are integers and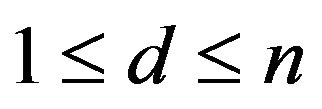 ,
, 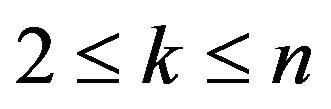 then
then
 .
.
Proof: First of all, It is obvious that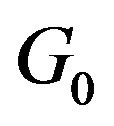 is belong to
is belong to .
.
Let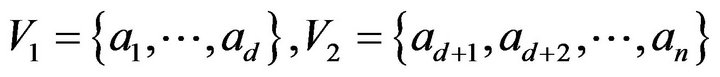 , then
, then 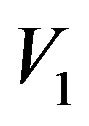 is a set in which every vertex have a loop, For all
is a set in which every vertex have a loop, For all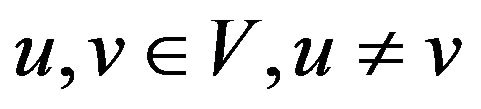 .
.
Case 1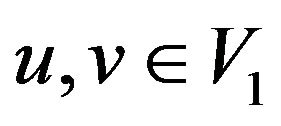 .
.
There exists a walk of length less than or equal to
 form
form ![]() to
to ![]() (or from
(or from ![]() to
to![]() ), and
), and
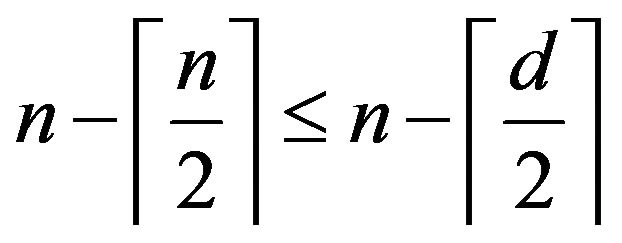 , then
, then .
.
Case 2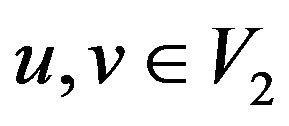 .
.
There exists a walk of length less than or equal to  form
form ![]() to
to 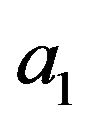 (and form
(and form ![]() to
to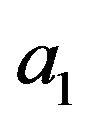 ),
),
 then
then
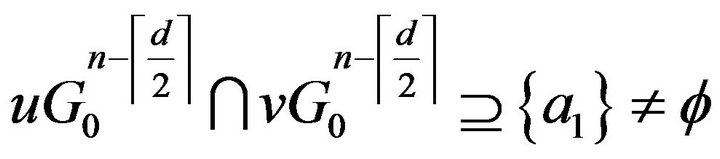 .
.
Case 3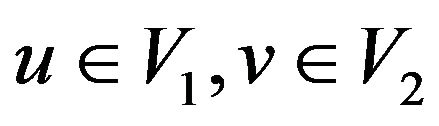 .
.
There exist a walk of length less than or equal to 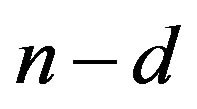 form
form ![]() to
to , by Lemma 2.2,
, by Lemma 2.2,

hence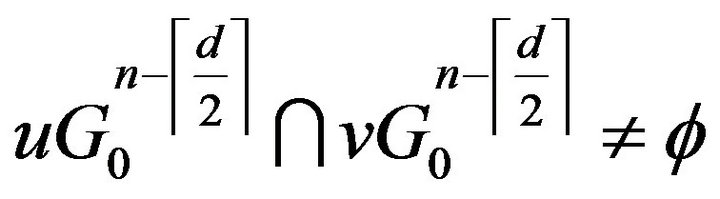 .
.
So we have 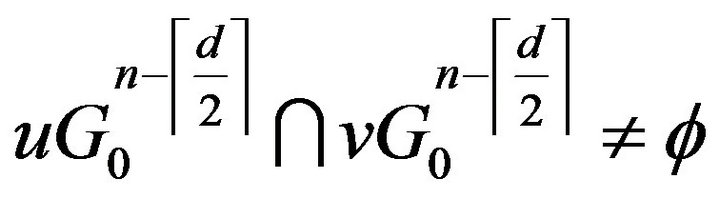 for all
for all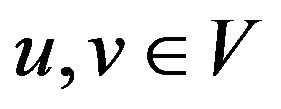 .
.
Note that if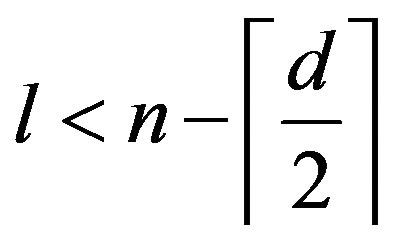 , then
, then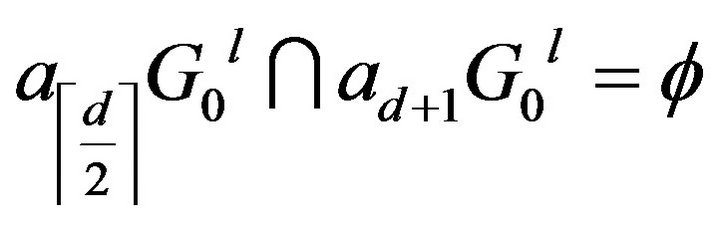 .
.
Hence 
Let ![]() be arbitrary vertex belong to
be arbitrary vertex belong to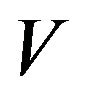 , then there exists a walk of length less than or equal to
, then there exists a walk of length less than or equal to 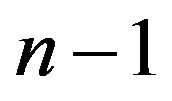 form
form
![]() to
to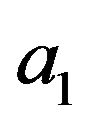 , then
, then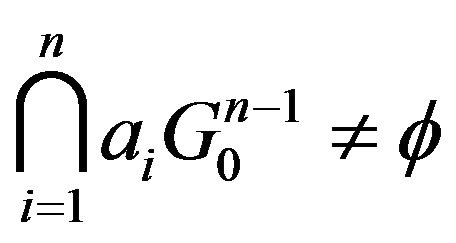 . It is easy to see that if
. It is easy to see that if
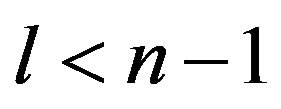 then
then .
.
Hence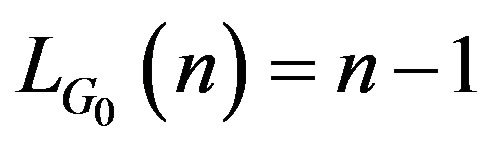 . The proof is now completed.
. The proof is now completed.
3. The Main Results
Theorem 3.1 Let 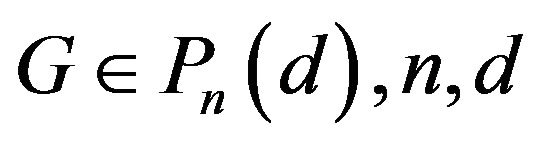 be integers,
be integers,
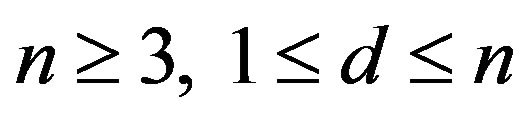 then
then 
Proof: Let 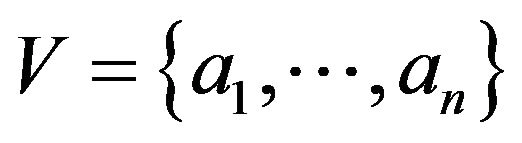 be set of vertices of
be set of vertices of 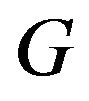 and
and 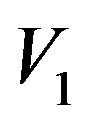 be subset of
be subset of 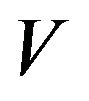 in which each vertex have a loop,
in which each vertex have a loop,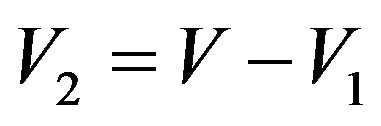 . for all
. for all .
.
Case 1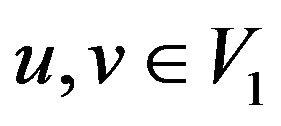 .
.
There exists a walk of length less than or equal to
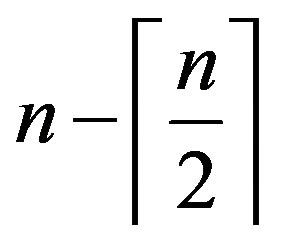 form
form ![]() to
to ![]() (or from
(or from ![]() to
to![]() ), and
), and
 , then
, then .
.
Case 2 .
.
Suppose that there be a walk of length equal to
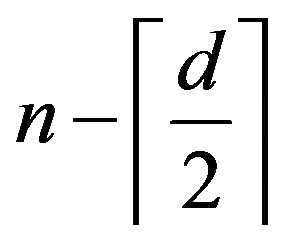 of
of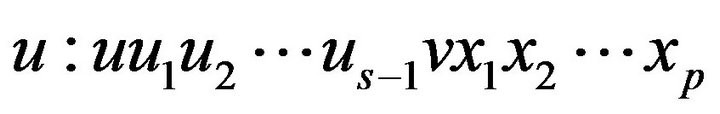 , and there be a walk of length equal to
, and there be a walk of length equal to  of
of
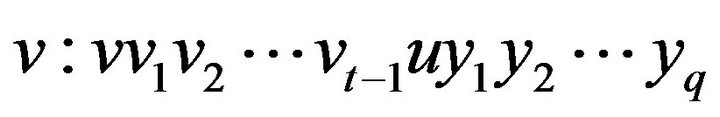 where
where .
.
Let 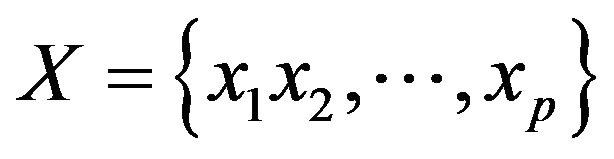 and
and . If there be one vertex of
. If there be one vertex of  or
or ![]() belong to
belong to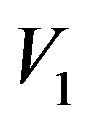 , then
, then
 .
.
Otherwise, 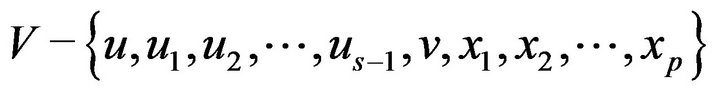 and
and
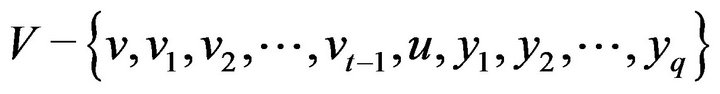 contains at most
contains at most 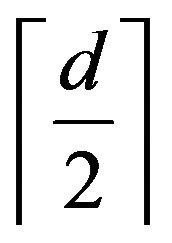 element of
element of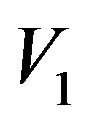 . In other word,
. In other word, 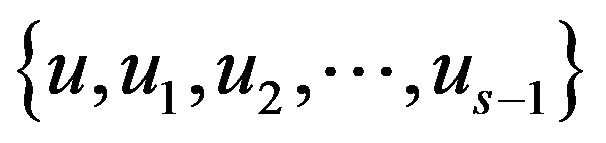 contains at least
contains at least 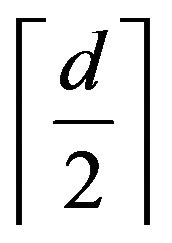 element of
element of . Note that
. Note that  is strongly connected,
is strongly connected, . There exists a walk of length less than or equal to
. There exists a walk of length less than or equal to 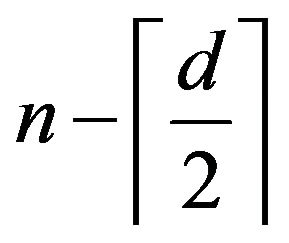 from
from ![]() to one vertex of
to one vertex of
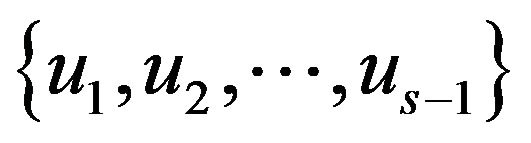 which belong to
which belong to . Therefore
. Therefore
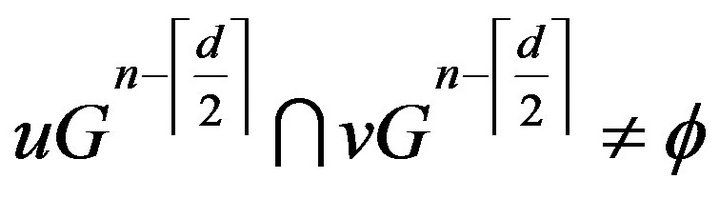 .
.
Case 3 .
.
There exist a walk of length less than or equal to 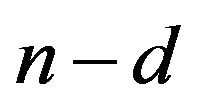 form
form ![]() to
to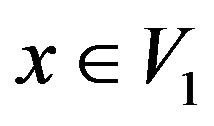 , by Lamma 2.2
, by Lamma 2.2
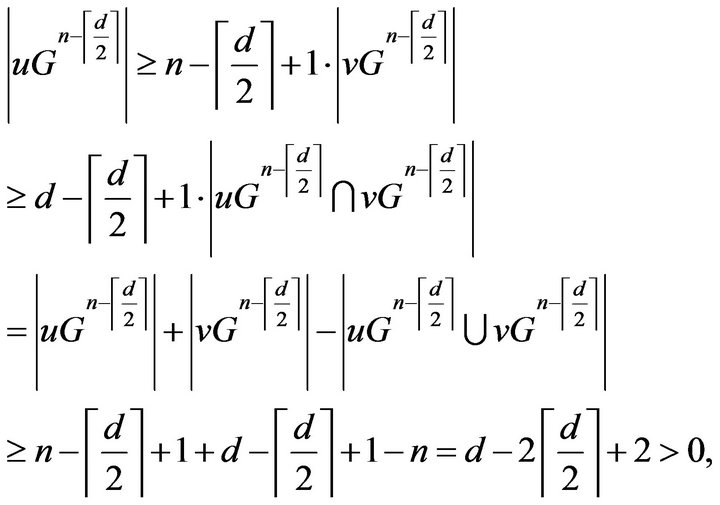
hence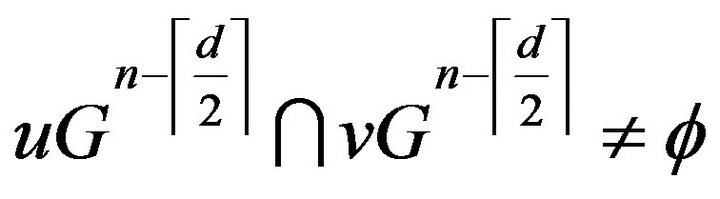 .
.
So we have  for all
for all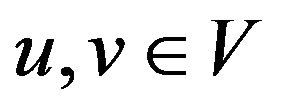 .
.
Hence
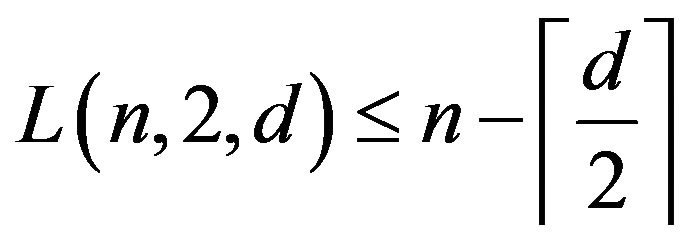 .
.
Note that
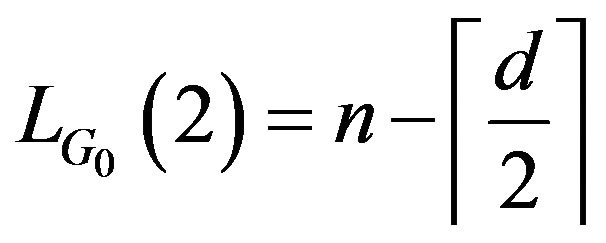 then
then
 .
.
The proof is completed.
Corollary 3.2 Let 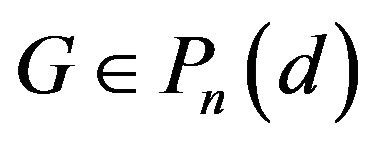 and
and  be integers,
be integers, 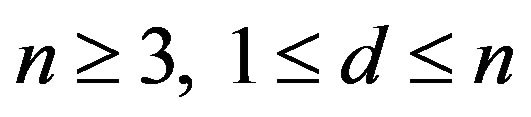 , then
, then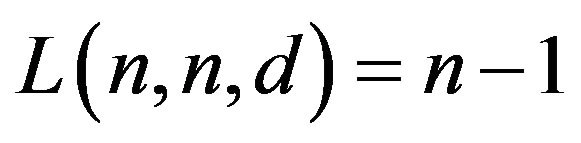 .
.
Proof: Let 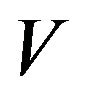 be a set of vertices of
be a set of vertices of 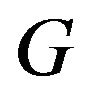 and let
and let ![]() be an arbitrary vertex belong to
be an arbitrary vertex belong to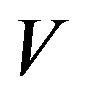 , then there exists a walk of length
, then there exists a walk of length 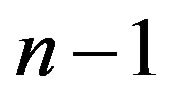 from
from ![]() to
to![]() , where
, where ![]() having a loop. Hence
having a loop. Hence
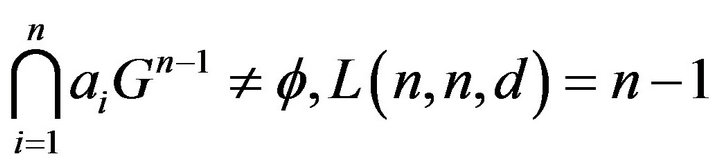
Note that  by Lemma 2.4, hence
by Lemma 2.4, hence
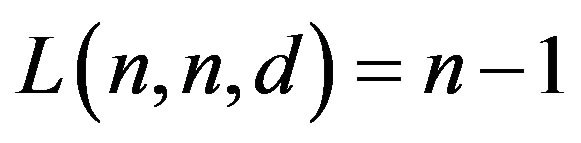 .
.
Applying Lemma 2.3, Theorem 2.1 and Theorem 2.2, we have conclusion.
Corollary 3.3 Let 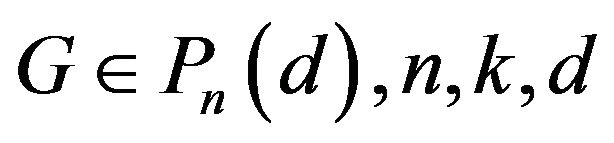 and be integers,
and be integers,  , then
, then
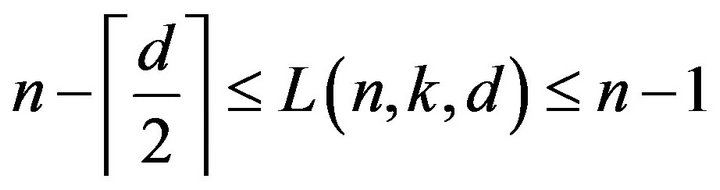 .
.
Corollary 3.4 Let  be a primitive digraph of order
be a primitive digraph of order ![]() with girth
with girth , then
, then
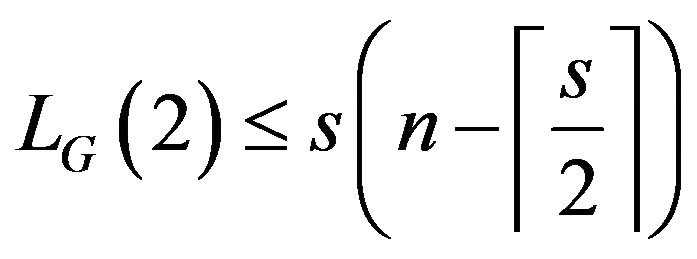 .
.
Proof: Since 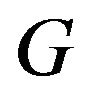 is a primitive digraph of order
is a primitive digraph of order ![]() with girth
with girth![]() , then
, then 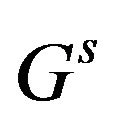 is a primitive digraph of order
is a primitive digraph of order ![]() with exact
with exact ![]() vertices having loop. By Theorem 3.1, we have
vertices having loop. By Theorem 3.1, we have
 .
.
Theorem 3.5 Let ![]() and
and ![]() be integers,
be integers, 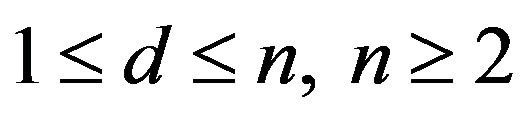 , then there exists
, then there exists 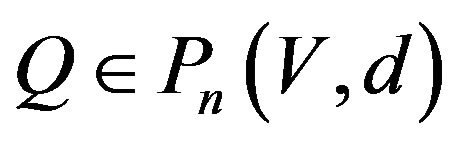 so that
so that
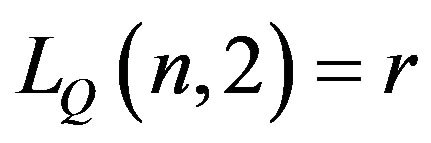 for arbitrary
for arbitrary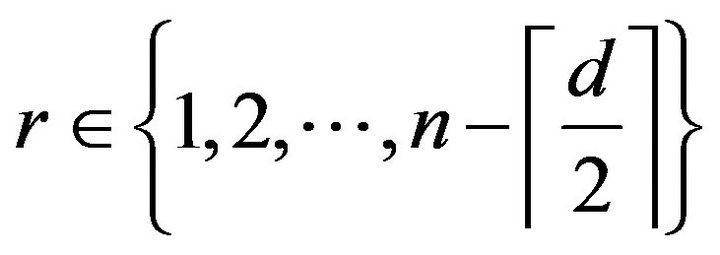 .
.
Proof: Let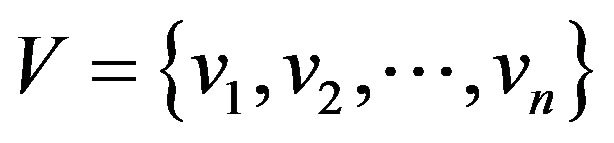 .
.
We construct  so that
so that 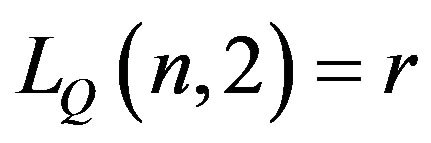 for arbitrary
for arbitrary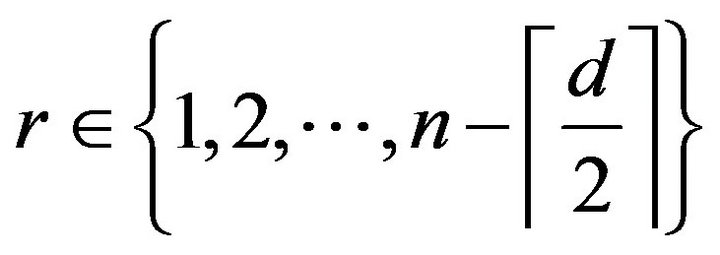 .
.
Case 1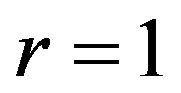 .
.
Let
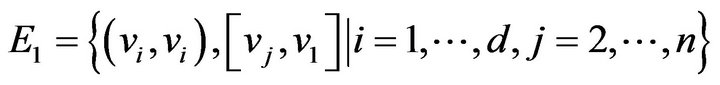 ,
,
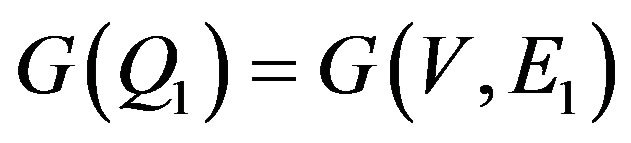 . It is obvious that
. It is obvious that  and
and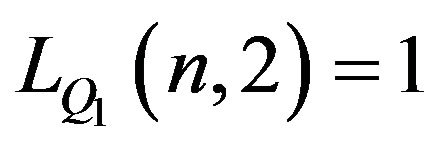 .
.
Case 2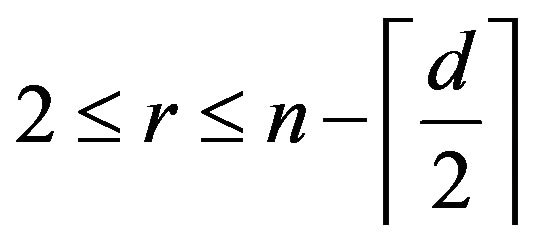 .
.
Case 2.1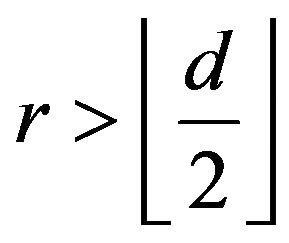 .
.
Let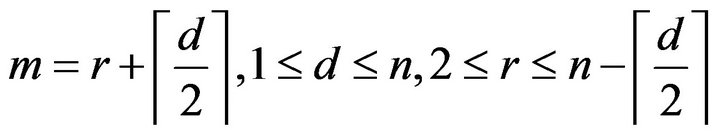 Hence
Hence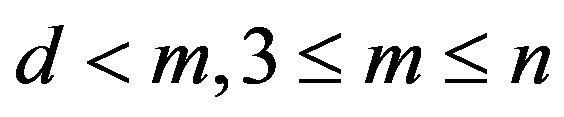 .
.
Let
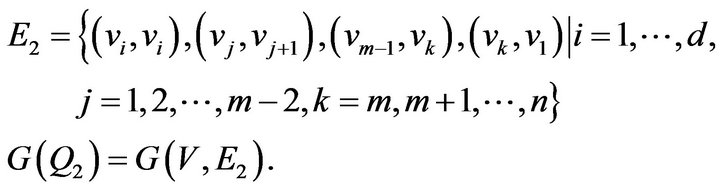
obviously,
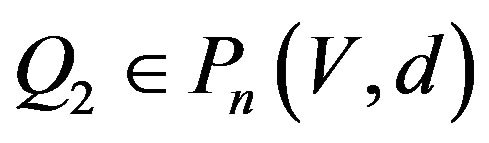 .
.
Let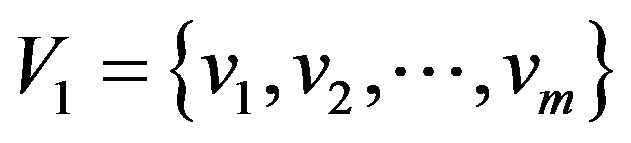 , then
, then 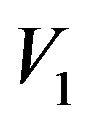 is the set of vertices which is in cycle lengths of
is the set of vertices which is in cycle lengths of![]() . Let
. Let , arbitrary vertex
, arbitrary vertex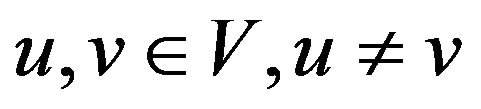 . If
. If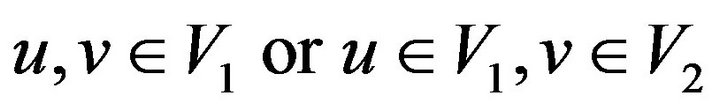 , by Lemma 2.4,
, by Lemma 2.4,
 .
.
If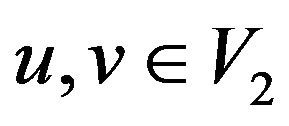 , then
, then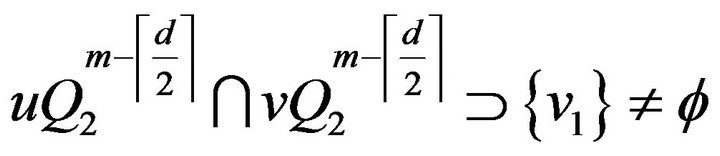 .
.
If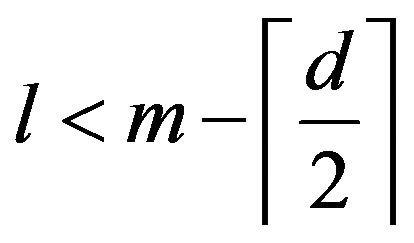 , then
, then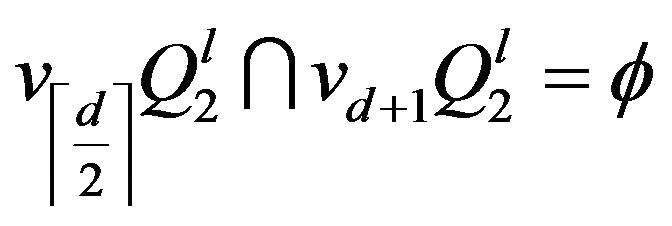 .
.
Hence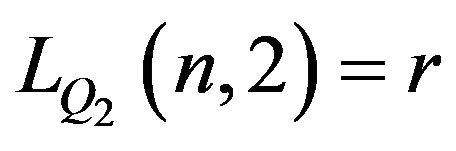 .
.
Case 2.2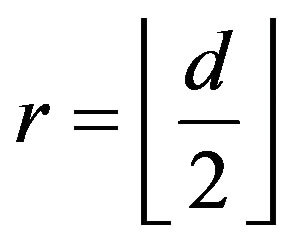 .
.
Let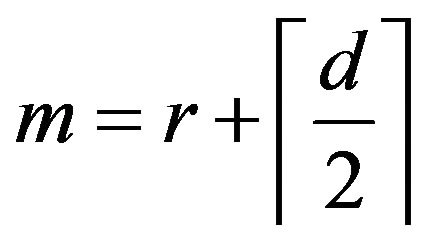 , then
, then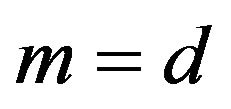 .
.
Let
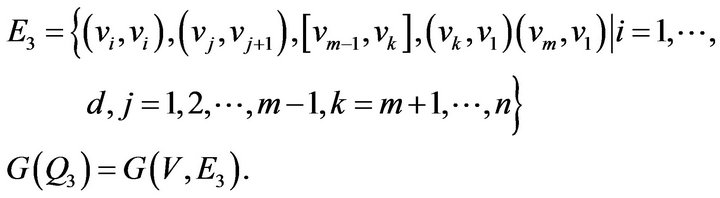
It is obvious that 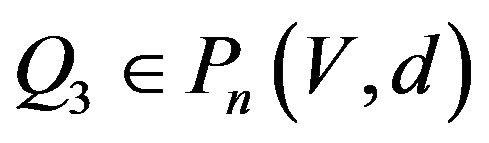 and
and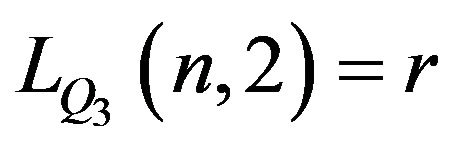 .
.
Case 2.3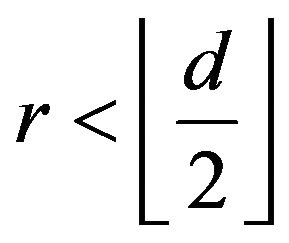 .
.
Let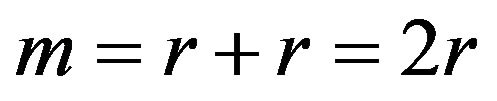 , then
, then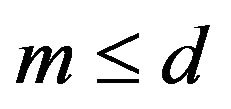 . Let
. Let
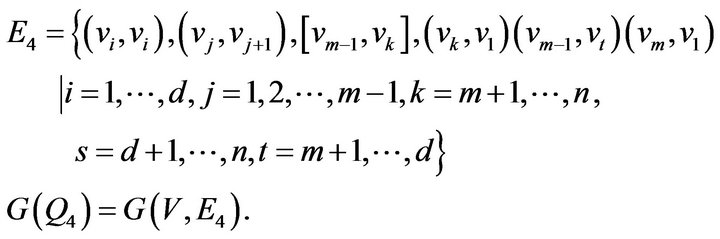
It is obvious that 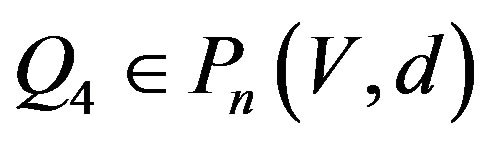 and
and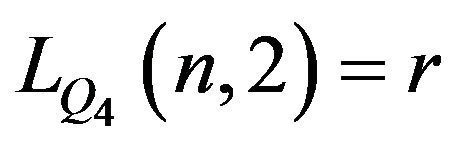 .
.
The proof is now completed.
Remark 3.6 By Theorem 3.5, we obtain that the set of the 2 − common consequent of primitive digraphs of order ![]() with exact
with exact ![]() vertices having loop is
vertices having loop is
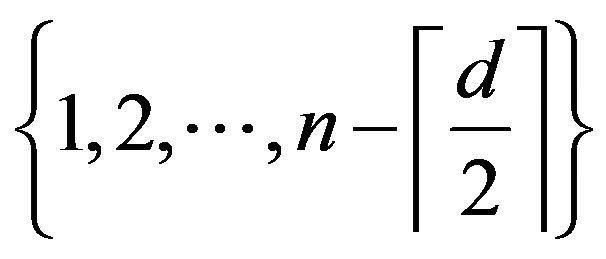 .
.
But, in Theorem 3.5, 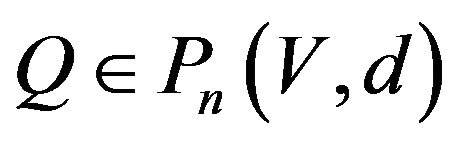 is not unique.
is not unique.
Example.
Let
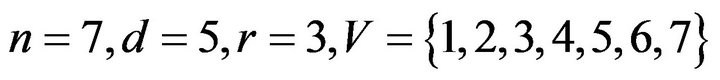 ,
,
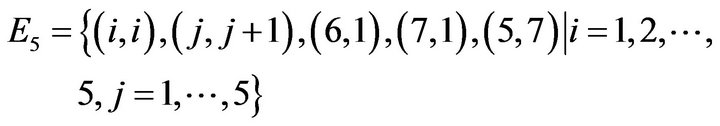

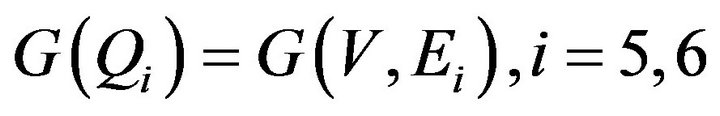 .
.
Obviously,
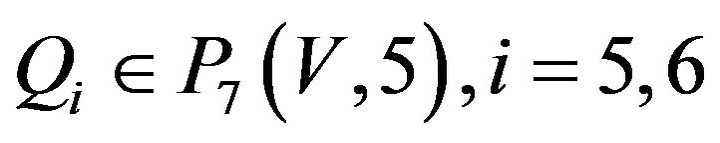 .
.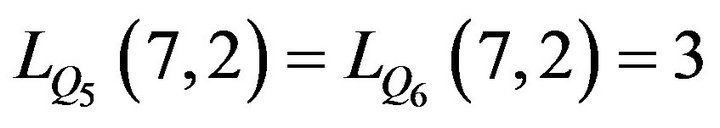 but
but 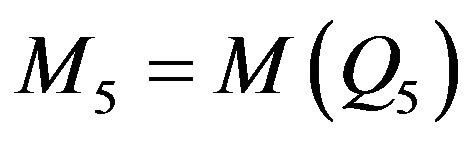 and
and 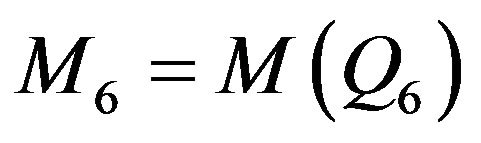 are not isomorphic digraph.
are not isomorphic digraph.
REFERENCES
- S. Schwarz, “Common Consequents in Directed Graphs,” Czechoslovak Mathematical Journal, Vol. 35, No. 110, 1985, pp. 212-246.
- B. L. Liu, “k − Common Common Consequents in Boolean Matrices,” Czechoslovak mathematical Journal, Vol. 46, 1996, pp. 523-536.
- R. A. Brualdi and B. L. Liu, “Generalized Exponents of Primitive Directed Graphs,” Journal of Graph Theory, Vol. 14, No. 4, 1990, pp. 483-499. doi:10.1002/jgt.3190140413
- S. Schwarz, “A Combinatorial Problem Arising in Finite Markov Chains,” Mathematica Slovaca, Vol. 36, 1986, pp. 21-28.
- B. Zhou, “The Upper Generalized Exponent of a Digraph,” Advances in Mathematics, Vol. 6, 2000, pp. 499- 506.

