Applied Mathematics
Vol.3 No.8(2012), Article ID:21477,4 pages DOI:10.4236/am.2012.38139
On Eccentric Connectivity Index and Polynomial of Thorn Graph
Department of Basic Science, Humanities and Social Science (Mathematics), Calcutta Institute of Engineering and Management, Kolkata, India
Email: de.nilanjan@rediffmail.com
Received February 19, 2012; revised July 4, 2012; accepted July 12, 2012
Keywords: Ecentricity; Eccentric Connectivity Index; Eccentric Connectivity Polynomial; Thorn Graphs
ABSTRACT
The eccentric connectivity index based on degree and eccentricity of the vertices of a graph is a widely used graph invariant in mathematics. In this paper we present the explicit generalized expressions for the eccentric connectivity index and polynomial of the thorn graphs, and then consider some particular cases.
1. Introduction
A topological index, based on degree and eccentricity of a vertex of a graph, known as eccentric connectivity index, first appeared for structure-property and structureactivity studies of molecular graphs [1] and shown to give a high degree of predictability of pharmaceutical properties. Now for any simple connected graph G = 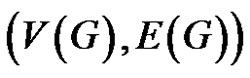 with n vertices and m edges, the distance between the vertices vi and vj of
with n vertices and m edges, the distance between the vertices vi and vj of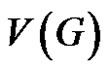 , is equal to the length that is the number of edges of the shortest path connecting vi and vj [2]. Also for a given vertex vi of
, is equal to the length that is the number of edges of the shortest path connecting vi and vj [2]. Also for a given vertex vi of  its eccentricity
its eccentricity 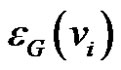 is the largest distance from vi to any other vertices of G [3-5]. The radius and diameter of the graph are respectively the smallest and largest eccentricity among all the vertices of G where as the average eccentricity of a graph is denoted by
is the largest distance from vi to any other vertices of G [3-5]. The radius and diameter of the graph are respectively the smallest and largest eccentricity among all the vertices of G where as the average eccentricity of a graph is denoted by 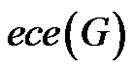 and is defined as
and is defined as
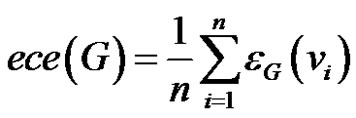
Analogues to Zagreb indices of a graph Vukičević and Graovac [6] introduced the Zagreb eccentricity indices 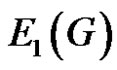 and
and 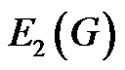 by replacing degree of the vertices by its eccentricity. The eccentric connectivity index of a graph G was proposed by Sharma, Goswami and Madan [1] and is defined as
by replacing degree of the vertices by its eccentricity. The eccentric connectivity index of a graph G was proposed by Sharma, Goswami and Madan [1] and is defined as
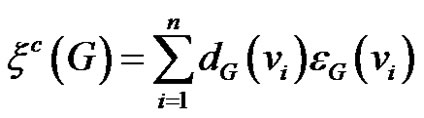 where
where 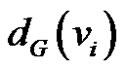 is the degree i.e. number of first neighbor of vi of
is the degree i.e. number of first neighbor of vi of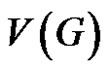 . Compare to other topological indices as the eccentric connectivity index has been found to have a low degeneracy [7], it subject to a large number of chemical [3,4,7-9] and mathematical studies [10,11]. Similar to other topological polynomials the eccentric connectivity polynomial of a graph G is defined as [11]
. Compare to other topological indices as the eccentric connectivity index has been found to have a low degeneracy [7], it subject to a large number of chemical [3,4,7-9] and mathematical studies [10,11]. Similar to other topological polynomials the eccentric connectivity polynomial of a graph G is defined as [11]

so that, the connection between the eccentric connectivity polynomial and the eccentric connectivity index is given by
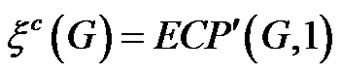 where
where 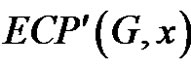 is the first derivative of
is the first derivative of .
.
The concept of thorn graphs was proposed by Gutman [2] and different applications have been studied by many others. Let 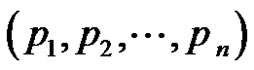 be an n-tuple on positive integers then the thorn graph
be an n-tuple on positive integers then the thorn graph 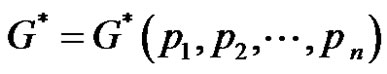 of the parent graph G on n vertices
of the parent graph G on n vertices 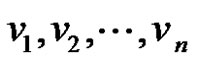 is formed by attaching pi (
is formed by attaching pi (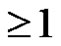 ),
),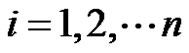 new vertices of degree one to each vertex vi of G. Various topological indices and polynomials such as wiener number [12,13], terminal Wiener index [14], modified Wiener index [15], altered Wiener index [16], Hosoya polynomial [17], Zagreb polynomial [18] and so on of the general and some particular thorn graphs and trees has already been studied.
new vertices of degree one to each vertex vi of G. Various topological indices and polynomials such as wiener number [12,13], terminal Wiener index [14], modified Wiener index [15], altered Wiener index [16], Hosoya polynomial [17], Zagreb polynomial [18] and so on of the general and some particular thorn graphs and trees has already been studied.
In this paper we present the expressions of the eccentric connectivity index and polynomials of thorn graph in terms of its underlying parent graph and consider some special cases for which the number of thorns that is pendant edges attached to any vertex of the parent graph is a linear function of its degree and eccentricity.
2. Main Results
Theorem 1 For any simple connected graph G the 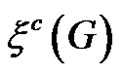 and
and 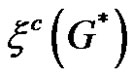 are related as
are related as
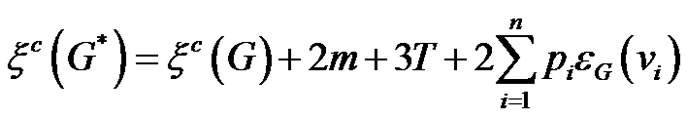 (1)
(1)
where G* is the thorn graph of G with parameters pi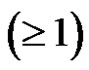 ,
, .
.
Proof Let 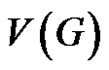 and
and  be the vertex set of G and its thorn graph G* respectively, so that
be the vertex set of G and its thorn graph G* respectively, so that
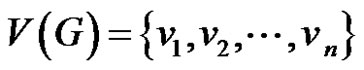
and
 where Vi are the set of degree one vertices attached to the vertices vi in G* and
where Vi are the set of degree one vertices attached to the vertices vi in G* and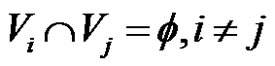 . Let the vertices of the set Vi are denoted by
. Let the vertices of the set Vi are denoted by 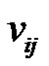 for j = 1, 2,···, pi and I =
for j = 1, 2,···, pi and I =
1, 2,···, n. Thus 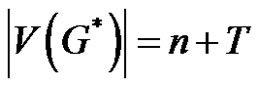 where,
where, .Then the degree of the vertices vi in G* are given by
.Then the degree of the vertices vi in G* are given by , for
, for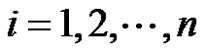 . Similarly the eccentricity of the vertices vi ,
. Similarly the eccentricity of the vertices vi , 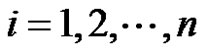 in G* are given by
in G* are given by , for
, for 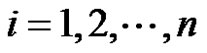 and the eccentricity of the vertices vij are given by
and the eccentricity of the vertices vij are given by 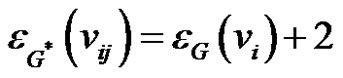 , for
, for 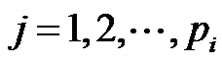 and
and . Then the eccentric connectivity index of G* is given by
. Then the eccentric connectivity index of G* is given by

Now since
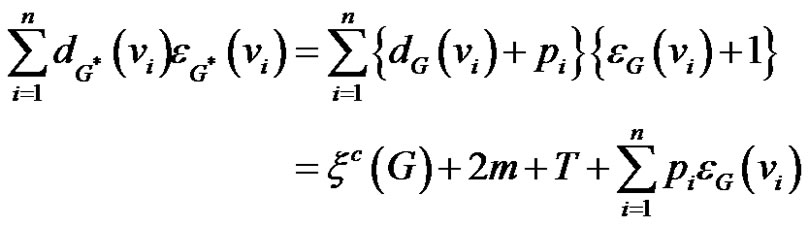
and
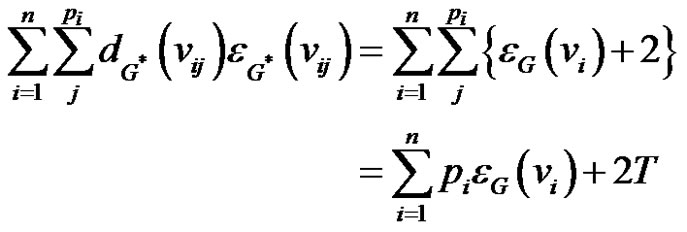
we get the desired result (1).
Theorem 2 For any simple connected graph G, eccentric connectivity polynomial 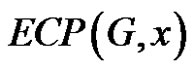 and
and 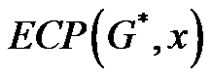 are related as
are related as
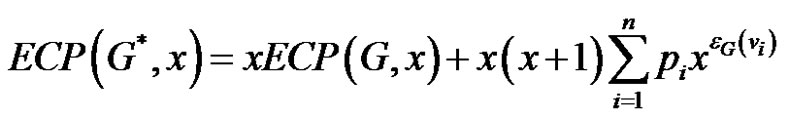 (2)
(2)
Proof Since G* is the thorn graph obtained from G by attaching pi new pendent vertices to the vertex vi of G (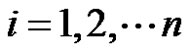 ), just analogues to Theorem 1 the eccentric connectivity polynomial of G* is given by
), just analogues to Theorem 1 the eccentric connectivity polynomial of G* is given by
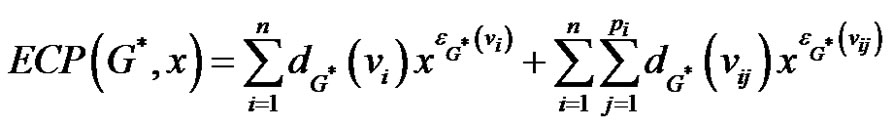
Now since
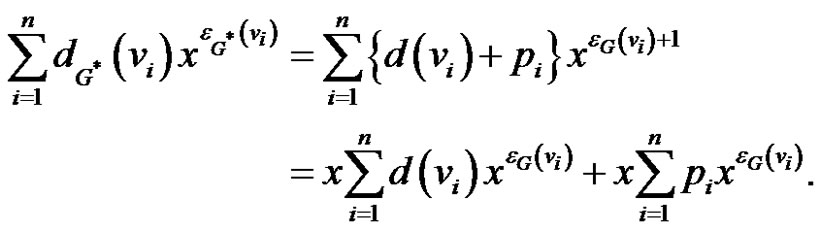
and
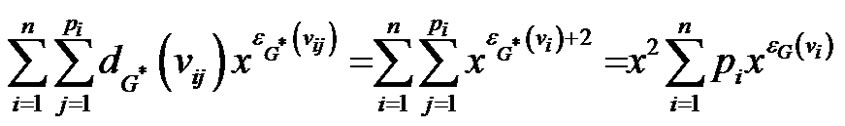
we get the desired result.
Corollary 1 Let G* is the thorn graph of G, with parameters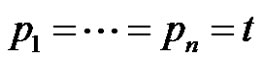 , then
, then
1) 
2) 
where 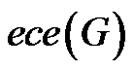 is the average eccentricity of G.
is the average eccentricity of G.
Proof 1) If 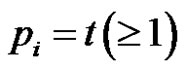 for
for 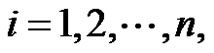 then
then
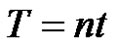 and
and . Thus from (1) we get the result as desired.
. Thus from (1) we get the result as desired.
2) Using the inequality between the arithmetic and geometric mean we have
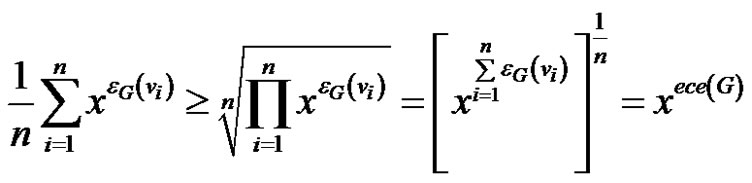 (3)
(3)
Then  and hence from (2) the desired result follows.
and hence from (2) the desired result follows.
Corollary 2 If the parameter pi is equal to the degree of the corresponding ith vertex, then
is equal to the degree of the corresponding ith vertex, then
1) 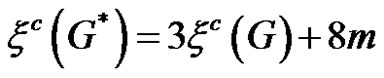
2) 
where m is the number of edges of G.
Proof 1) If  for
for 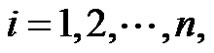 then
then
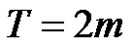 and
and . Thus from (1) the desired result is obtained.
. Thus from (1) the desired result is obtained.
2) Similarly, as in this case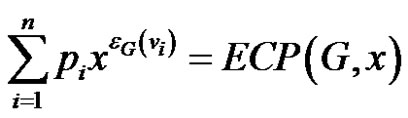 , from (2) the required result follows.
, from (2) the required result follows.
Corollary 3 Let 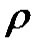 be any integer so that
be any integer so that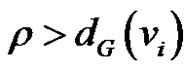 ,
,  and if G* is the thorn graph of G with parameters
and if G* is the thorn graph of G with parameters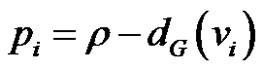 , then
, then
1) 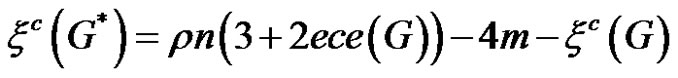
2)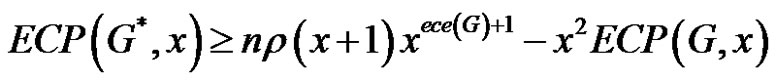 .
.
Proof 1) If 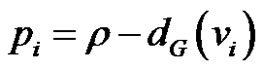 for
for 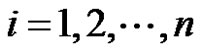 then
then
 and
and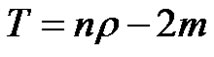 . Hence from (1) the desired result is obtained.
. Hence from (1) the desired result is obtained.
2) Since in this case as, applying (3)
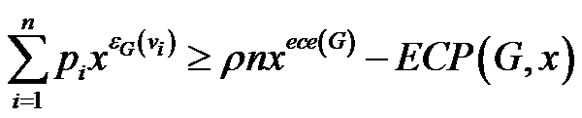
we get the desired result from (2).
Corollary 4 If the parameter pi  is equal to the eccentricity of the corresponding ith vertex, then
is equal to the eccentricity of the corresponding ith vertex, then
1) 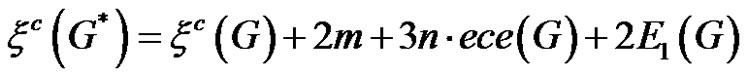
2) 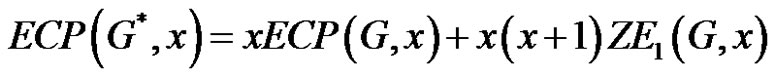
where  and
and  are Zagreb eccentricity index and polynomial of G.
are Zagreb eccentricity index and polynomial of G.
Proof 1) If 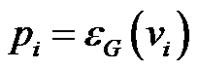 for
for 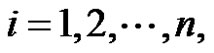 then
then
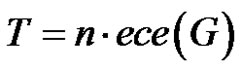 and
and 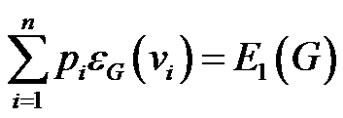 then from (1)
then from (1)
the desired result follows. Here  is the Zagreb eccentricity index [6].
is the Zagreb eccentricity index [6].
2) Again in this case since 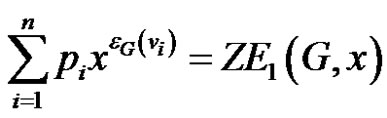 we get the desired result. Here
we get the desired result. Here 
is the Zagreb eccentricity polynomial corresponding to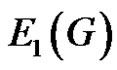 , such that
, such that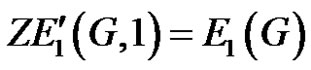 , where
, where 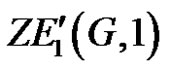 is the first derivative of
is the first derivative of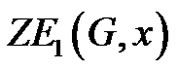 .
.
Corollary 5 Let τ be any integer so that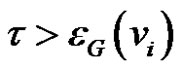 ,
, 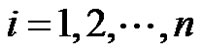 and if G* is the thorn graph of G with parameters
and if G* is the thorn graph of G with parameters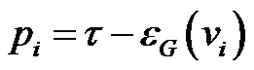 , then
, then
1) 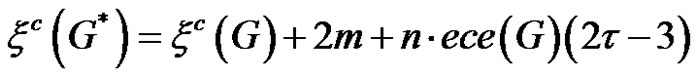
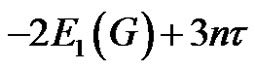
2) 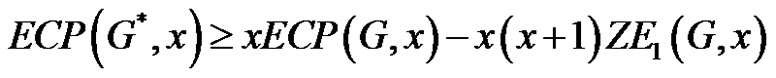
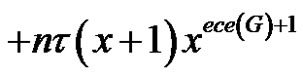
Proof 1) Since in this case 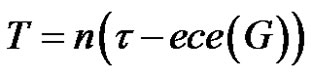 and
and
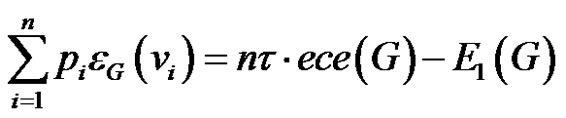 from (1) the desired result follows.
from (1) the desired result follows.
2) Similarly in this case since
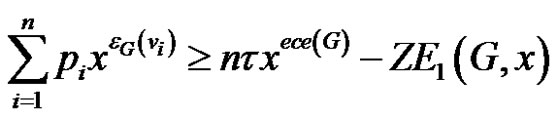
the desired result follows from (2).
Corollary 6 If G* is the thorn graph obtained from G with parameters 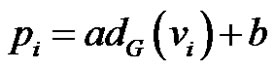 where a and b are integers such that
where a and b are integers such that 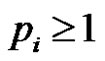 then
then
1) 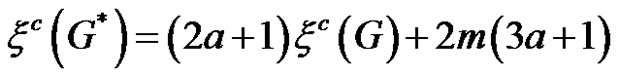
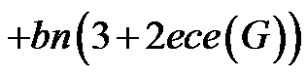
2) 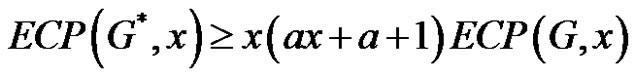
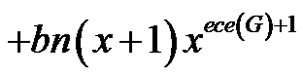
Proof 1) If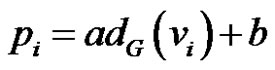 , then
, then 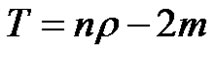 and so that from (1) the desired result follows.
and so that from (1) the desired result follows.
2) Again to find eccentric connectivity polynomial for this case we have

Hence from (2) the desired result follows.
Note that the Corollary 1, 2 and 3 can be obtained from above assuming a = 0, b = t; a = 1, b = 0 and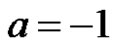 ,
,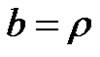 .
.
Corollary 7 If G* is the thorn graph obtained from G with parameters  where a and b are integers such that
where a and b are integers such that 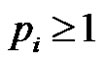 then
then
1) 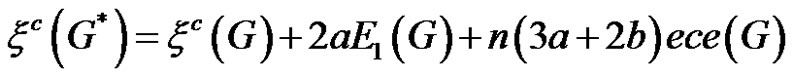
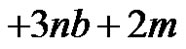
2) 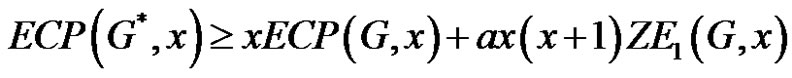
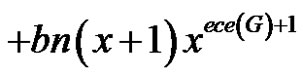
Proof 1) Since in this case, 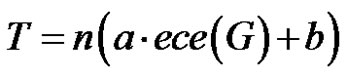 and
and
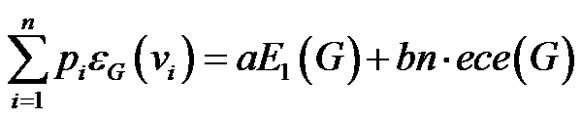 the desired result follows from (1).
the desired result follows from (1).
2) Similarly using (3) as
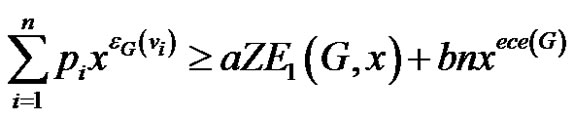
the desired result follows from (2).
Note that the Corollary 1, 4 and 5 can be obtained from Corollary 7 assuming a = 0, b = t; a = 1, b = 0 and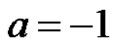 ,
,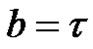 .
.
Corollary 8 If G* is the thorn graph obtained from G with parameters 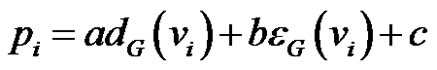 where a, b and c are integers such that
where a, b and c are integers such that  then
then
1) 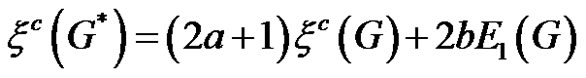
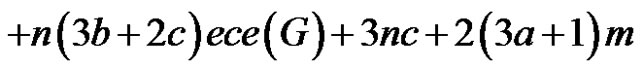
2) 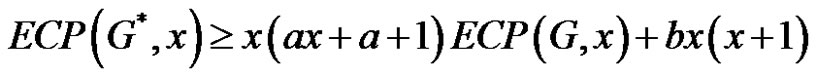
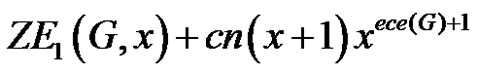
Proof 1) In this case, since

and

we get the desired result from (1).
2) Again since
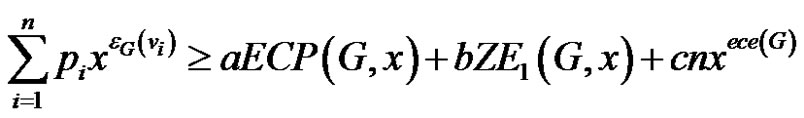 the desired result follows from (2).
the desired result follows from (2).
In all the above inequalities the equality holds when we differentiate it with respect to x and putting x = 1. Reader should note that the Corollary 6 and 7 can be obtained from Corollary 8 by putting b = 0, c = b and a = 0, b = a, c = b and hence all the previous Corollaries.
3. Conclusion
Using the relations derived above one can easily recursively obtained the eccentric connectivity index and polynomial for a particular type of thorn graph in terms of its parent graph i.e. the eccentric connectivity index and polynomial of a bigger graph is expressed in terms of a smaller graph. For example, using the relations (1) and (2) the eccentric connectivity index and polynomial of thorn cycle  obtained from a cycle
obtained from a cycle  by adding pi(
by adding pi( ),
), new vertices of degree one to each vertex vi are given by
new vertices of degree one to each vertex vi are given by

and
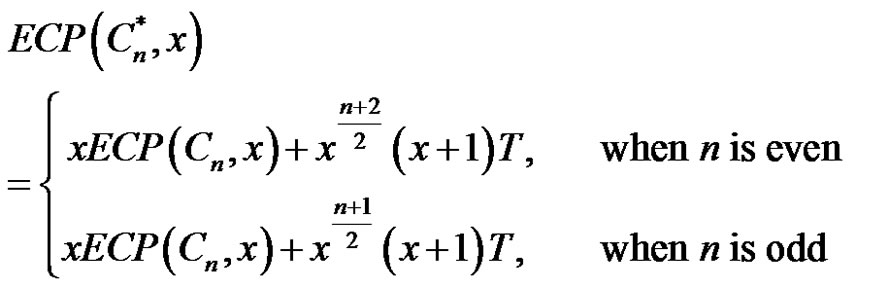
Similarly we can also find these results for other particular thorn graphs like thorn path, thorn star etc. Also note that all these results are true only when pi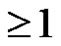 , for all
, for all , so these results can be extended to thorn graphs when some of pi = 0.
, so these results can be extended to thorn graphs when some of pi = 0.
REFERENCES
- V. Sharma, R. Goswami and A. K. Madan, “Eccentric Connectivity Index: A Novel Highly Discriminating Topological Descriptor for Structure-Property and StructureActivity Studies,” Journal of Chemical Information and Modeling, Vol. 37, No. 2, 1997, pp. 273-282. doi:10.1021/ci960049h
- I. Gutman, “Distance in Thorny Graph,” Publications de l’Institut Mathématique (Beograd), Vol. 63, 1998, pp. 31- 36.
- A. Ilić and I. Gutman, “Eccentric Connectivity Index of Chemical Trees,” MATCH—Communications in Mathematical and in Computer Chemistry, Vol. 65, 2011, pp. 731-744.
- B. Zhou and Z. Du, “On Eccentric Connectivity Index,” MATCH—Communications in Mathematical and in Computer Chemistry, Vol. 63, 2010, pp. 181-198.
- P. Dankelmann, W. Goddard and C. S. Swart, “The Average Eccentricity of a Graph and Its Subgraphs,” Utilitas Mathematica, Vol. 65, 2004, pp. 41-51.
- D. Vukičević and A. Graovac, “Note on the Comparison of the First and Second Normalized Zagreb Eccentricity Indices,” Acta Chimica Slovenica, Vol. 57, 2010, pp. 524- 528.
- T. Došlić, M. Saheli and D. Vukičević, “Eccentric Connectivity Index: Extremal Graphs and Values,” Iranian Journal of Mathematical Chemistry, Vol. 1, No. 2, 2010, pp. 45-56.
- K. C. Das and N. Trinajstić, “Relationship between the Eccentric Connectivity Index and Zagreb Indices,” Computers & Mathematics with Applications, Vol. 62, No. 4, 2011, pp. 1758-1764. doi:10.1016/j.camwa.2011.06.017
- L. Zhang and H. Hua, “The Eccentric Connectivity Index of Unicyclic Graphs,” International Journal of Contemporary Mathematical, Vol. 5, No. 46, 2010, pp. 2257-2262.
- J. Yang and F. Xia, “The Eccentric Connectivity Index of Dendrimers,” International Journal of Contemporary Mathematical, Vol. 5, No. 45, 2010, pp. 2231-2236.
- M. Ghorbani and M. Hemmasi, “Eccentric Connectivity Polynomial of C12n+4 Fullerenes,” Digest Journal of Nanomaterials and Biostructures, Vol. 4, No. 3, 2009, pp. 545-547.
- B. Zhou and D. Vukičević, “On Wiener-Type Polynomials of Thorn Graphs,” Journal of Chemometrics, Vol. 23, No. 12, 2009, pp. 600-604.
- D. Bonchev and D. J. Klein, “On the Wiener Number of Thorn Trees, Stars, Rings, and Rods,” Croatica Chemica Acta, Vol. 75, No. 2, 2002, pp. 613-620.
- A. Heydari and I. Gutman, “On the Terminal Wiener Index of Thorn Graphs,” Kragujevac Journal of Science, Vol. 32, 2010, pp. 57-64.
- B. Zhou, “On Modified Wiener Indices of Thorn Trees,” Kragujevac Journal of Mathematics, Vol. 27, 2005, pp. 5-9.
- D. Vukičević, B. Zhou and N. Trinajstić, “Altered Wiener Indices of Thorn Trees,” Croatica Chemica Acta, Vol. 80, No. 2, 2007, pp. 283-285.
- H. B. Walikar, H. S. Ramane, L. Sindagi, S. S. Shirakol and I. Gutman, “Hosoya Polynomial of Thorn Trees, Rods, Rings, and Stars,” Kragujevac Journal of Science, Vol. 28, 2006, pp. 47-56.
- S. Li, “Zagreb Polynomials of Thorn Graphs,” Kragujevac Journal of Science, Vol. 33, 2011, pp. 33-38.

