Modern Economy
Vol.09 No.04(2018), Article ID:84191,35 pages
10.4236/me.2018.94055
Welfare Impact of Wheat Farmers Participation in the Value Chain in Tanzania
William Barnos Warsanga1, Edward Anthony Evans2
1Moshi Co-Operative University, Moshi, Tanzania
2University of Florida, Gainesville, Florida, USA

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 1, 2018; Accepted: April 27, 2018; Published: April 30, 2018
ABSTRACT
The paper examines the link between value chain participation and welfare changes for wheat farmers in Tanzania. Specifically, the paper analyzes the wheat value chain from production to consumption, explores participation in the value chain, and examines the net effect of farmers’ participation in the value chain. A logistic model is used to explore the factors influencing farmers’ participation in the value chain and to estimate propensity scores to match the covariates for participants and nonparticipants. Applying the nearest neighbor and caliper radius matching algorithms found that only a few farmers are vertically (~17%) and horizontally (~39%) coordinated based on participation in contracts and associations, respectively. At the vertical coordination level, characteristics are significantly different for farmers with and without contracts in terms of land size, technical efficiency, allocative efficiency, output per acre, frequency of extension visits, frequency of village meetings attendance, and off-farm income. At the horizontal coordination level, farmers who join associations differ significantly from nonmembers in terms of level of education, frequency of village meetings attendance, output per acre, technical efficiency, and allocative efficiency. Vertical coordination participants receive a profit of 126 TSh/kg more for wheat than nonparticipants, with the difference significant at the 1% level. Horizontal coordination participants receive a profit of 46 TSh/kg more for wheat than nonparticipants, with the difference significant at the 5% level. The sensitivity analysis reveals that farmers’ participation in the value chain is generally insensitive to unobserved covariates. The findings suggest that establishing more contracts and stronger associations that specifically deal with wheat production has a positive impact on farmers’ welfare.
Keywords:
Wheat, Value Chain, PSM, Tanzania

1. Introduction
The rapid growth in the consumption of wheat in Tanzania and more importantly the widening of the gap between consumption and domestic wheat production have become a major concern for the Tanzanian government. The situation is troubling given the additional burden that wheat imports place on the demands for the country’s scarce foreign exchange and the fact that there are areas of the country agronomically suitable for the production of the crop that are underutilized. Of equal concern is the fact that past efforts by the government to spur domestic production have not generated the intended effect. Between 2005 and 2010, the Tanzanian government implemented the East African Community Common External Tariff (35% ad valorem) and expensive import procedures at the Dar es Salaam port in Tanzania with the hope that increasing the domestic wheat prices farmers received would boost domestic production. Despite these efforts, growth in production failed dismally to keep pace with that of consumption. The failure of many of the small-scale to medium-scale farmers to participate in the value chain hinders farmers from accessing high-value wheat markets and obtaining the returns that would enable them to increase their productivity and profitability. For example, most small-scale farmers in Tanzania sell their crops at the farm gate to intermediaries (brokers), often at a low price [1] . Lack of strong linkages between farmers and postharvest actors in the wheat value chain marginalizes farmers’ welfare gain because prices received from intermediaries are much lower and rarely cover the cost of production.
There are two types of linkages within the value chain literature: horizontal and vertical. Horizontal linkage for farmers refers to their membership and participation in farm associations. Farmers’ participation in horizontal coordination has shown progressive outcomes through their collective actions as documented in the literature. Acting collectively enables farmers to reduce their transaction costs for accessing inputs and transporting outputs, ease their access to market information and extension services, and improve their bargaining power with postharvest actors [2] [3] [4] [5] [6] . Despite such apparent advantages to farmers, the findings in the literature are not clear-cut regarding the value of participation in associations to farmers’ welfare due to differences in production locations and agro-economics [7] .
Vertical linkage refers to various associations between farmers and postharvest actors that entail formal and informal contracts that secure market outlets for farmers’ output and make it easier for smallholders to overcome constraints such as inadequate or limited access to improved inputs, modern technology, and credit [8] - [17] . Masakure and Henson [18] list the benefits of contracts in reducing market uncertainty, enhancing knowledge acquisition, and increasing farmers’ income.
Despite the economic importance of associations and contracts, most small-scale farmers in Tanzania do not participate in the formal value chain. Rather, they operate within a framework/system that is characterized by weak or poor coordination with little or no legal enforcement of contracts between the postharvest actors. Moreover, few farmers belong to associations that could help them gain access to guaranteed markets and collective bargaining to influence the market [19] .
This article makes two major contributions to the literature. First, a review of the literature indicates that there has been no prior formal comprehensive assessment of the value chain participation of wheat farmers in Tanzania based on horizontal and vertical coordination as key indicators for farmers’ value chain participation. For example, SAGCOT [20] only maps the value chain to trace the flow of inputs, goods, and services from production point to the ultimate consumer, and a USAID [21] report on staple-food value chain analysis focuses mainly on production and consumption trends, constraints, and opportunities. Second, this study is the first to demonstrate a plausible explanation for the Tanzanian farmers’ lackluster response to what appears to be a market opportunity to satisfy domestic demand for wheat and wheat products. It also offers useful policy suggestions to address the situation.
In addition, not controlling endogeneity caused by unobservables could result in biased estimates, especially when the unobservables affects participation in the value chain [22] [23] [24] [25] [26] . These unobservable factors as pointed out by Barrett et al. [12] may include individual risk aversion behavior, social capital, and trust/distrust of associations and contracts. To control for unobservables, we conducted a sensitivity analysis on outcome results, given that the propensity score matching (PSM) can only solve observed factor bias, thus producing less biased results in assessing the impact of value chain participation on wheat farmers’ welfare in Tanzania.
Following the introduction, section 2 provides an overview of the concept of value chain, as well as a discussion of the theoretical underpinnings of the analysis undertaken. In particular, we discuss the rationale for using the propensity scoring technique and the additional steps needed to improve the robustness of the technique. Section 3 lays out in detail the methodological framework, including the specifications used in the analysis and the source of the data used in the analysis. The results of the investigation are presented and discussed in section 4. Section 5 provides the concluding remarks.
2. Concept of Value Chain and Theoretical Framework
2.1. Brief Overview of the Concept of Value Chain and Value Chain Development
The value chain concept carries various definitions based on the question the researcher wants to address. Based on Kaplinsky and Morris [27] and Donovan et al. [28] , a value chain can be defined as an organized system of transforming products in various forms from production to consumption.
As the product moves along the value chain, it increases its value through transformation/processing, relocation, and distribution. In agriculture, food safety and food functionality also add value to the products through product differentiation. The incremental value of the resultant products can be identified by their price differences. Value Chain Development (VCD) is geared toward analyzing the value chain and addressing key weaknesses in a manner that contributes to the development or improvement in the value chain. Therefore, VCD is a positive or desirable change in a value chain to extend or improve productive operations and generate socioeconomic benefits toward poverty reduction, income and employment generation, economic growth, environmental performance, gender equity, and other development goals [29] .
The value chain concept in agriculture involves linkages of actors and their agri-food products toward adding value for consumers. The features of value chain development include mapping, coordination, governance, upgrading, meeting consumer demand, and competitiveness. Products gain value as they move along the value chain to various actors, say from input suppliers (such as seed providers) to farmers, then to intermediaries such as processors, wholesalers, retailers, and ultimately to consumers. Therefore, there must be linkages between actors to facilitate the movements of these products. These links need to be effective so that the benefits of the value chain are distributed among the chain actors. The value chain is not sustainable if only one actor receives all the benefits.
Often, farmers receive the lowest share of the consumer dollar, which is attributed to several factors, including the risk of product damage, high product transport costs to urban markets, and weak linkages with actors farther up the value chain. To deal with these challenges, value chain actors need to be organized and have external support to participate effectively in the high-value markets, including better rural infrastructures, educational institutions, and research and extension services.
Many studies have shown the impact of value chain participation in various farm aspects, including farmers’ welfare. For example, the study by Birthal et al. [30] on vertical coordination in high-value commodities found that contracts reduce transaction costs and improve market efficiency to benefit smallholders. Coordinated farmers were paid better prices and enjoyed the benefit of assured procurement of their products. Valkila et al. [31] employed the value chain approach to assess whether the Fair Trade system empowers traders. They found that despite the premium prices set by Fair Trade, farmers still received the lowest price share in the value chain. Warsanga [32] employed marketing margins to assess price variations among actors within the banana value chain in Tanzania and found that farmers received the lowest price share. Unlike these studies, this paper examines the impact on farmer’s welfare by comparing identical groups of participant and nonparticipant farmers in the value chain. The findings are used to explain the lacklustre response of farmers to opportunities in the wheat market in Tanzania.
2.2. Theoretical Framework
A frequent problem encountered by social scientists in the quest to determine the impact of a decision taken by a particular group (treated) vs. a group that has not made that decision (untreated) is self-selection. Apart from statistical estimation issues, this presents a challenge to the researcher who in most cases only observes the outcome of the choice made by the individual (self-selection) but not the effect had that same individual been randomly assigned to a group. Comparisons are easier for randomized data (experiments) than for nonrandomized data (observations).
In light of the above, several approaches have been advanced in the literature aimed at circumventing this issue. In general, the aim is to evaluate the treatment effect by selecting a control unit (untreated group) that is identical in terms of characteristics to the self-selected unit (treated group) in order to make inferences about the choices made. Moreover, it is important to account for observable and unobservable factors when evaluating the treatment effect in order to make good inferences about a choice. Failure to do so could result in selection bias (endogeneity) problems, thus leading to faulty inferences being drawn regarding the choice or particular treatment. As a result, Rosenbaum and Rubin [33] proposed using propensity score matching (PSM) to estimate the probability (propensity score) of participating in the value chain.
2.2.1. Propensity Score Matching
PSM is a statistical technique in which treatment individuals (beneficiaries of the program) are matched with one or more of the controlled individuals based on scores obtained from the function of covariates. For PSM to yield unbiased inferences, conditional independence must exist between the participants and nonparticipants of the program.
Statistical inference about the treatment effect on the individual outcome involves having prior information before an individual’s participation in the program. The missing information (unobserved outcome) is referred to as a counterfactual outcome. Because estimating individual treatment effect is impossible, one needs to consider either obtaining the average treatment effect (ATE) or the average treatment effect on the treated (ATT) where consideration is given to the entire sample population. For policy implications, the focus should be on the intended group (ATT) rather than the entire group (ATE).
The expected value of ATT is the difference between the expected value of “with” and “without” treatment. That is, the ATT parameter is the actual gain from participation in the program and can be compared with its cost to determine whether the program should proceed, assuming it has a positive impact [23] . Accordingly, this paper focuses on ATT by fixing counterfactual information from the untreated group using PSM [33] . The major assumption of the treatment effect for evaluation studies is that the treatment satisfies the exogeneity condition, referred to in the literature by several names. The Unconfoundedness assumption states that
(1)
where ⊥ denotes independence, if treatment was received, and if no treatment was received. The expression above implies that with a given set of covariates K unaffected by treatment, the potential outcomes R0, R1 would be independent of treatment assignment. Further, it implies that all covariates that might affect the treatment and the outcome simultaneously must be observed to reduce any biasness that could alter inference. The overlap assumption states that
, (2)
implying that participants and nonparticipants with the same K values both have a positive probability of being treated [23] . Assumptions 1 and 2 are strongly ignorable [33] , where ATE and ATT can be defined for all values of K. In this paper, the logit model is chosen due to the presence of binary dependent variables [24] .
2.2.2. Matching Algorithms
After the propensity scores have been obtained, the second necessary step is to choose matching algorithms. The most common matching algorithm techniques are Nearest Neighbor Matching (NN), Caliper and radius, stratification and interval, and Kernel and Local linear [24] . All these types techniques can be done with or without replacement. “With replacement” means an individual from the control group can be matched more than once, while “without replacement” means the individuals from the control group are matched once only with individuals in the treated group. Both “with” and “without” involve a tradeoff between bias and efficiency (variance). “With replacement” is useful for dispersed propensity score distribution between the control and treated groups. The choice will depend on the nature and availability of the data. It would make sense to use “with” when there are more observations for the treated group than for the control group, and to use “without” in the opposite situation.
Of the various matching techniques, NN is the one most frequently used, often in combination with others. NN matches individuals with the closest propensity score from the control group to those in the treated group. Caliper and radius matching resolve the problem of NN when the closest neighbor is far away. Caliper imposes a common support condition, whereby observations that are out of radius are dropped [34] . One advantage of the caliper technique is that it uses all the individuals within the caliper range. When there are suitable matches within the range, extra-individuals can be used; otherwise fewer individuals are used. Thus, caliper shares the attractive feature that avoids the risk of unsuitable matches [24] . Once the matching algorithms and their combinations have been chosen, the next stage of the process is to check for overlap between participants and nonparticipants.
2.2.3. Overlap
Overlap (common support condition) ensures that only comparable observations are used in the matching algorithm before proceeding with the analysis [26] . Several techniques to accomplish this can be found in the literature, including visual distribution of propensity scores before and after matching, minima and maxima comparison, and trimming [25] . Determining overlap involves identifying and retaining those individuals inside the region of a suitable match and discarding those outside the region. In other words, once the minimum and maximum propensity scores from both groups have been determined, individuals below the minimum or above the maximum of the control (untreated) group are discarded [23] . The next step requires revisiting the covariates and assessing the quality of matching. The process of doing so is discussed in the next subsection.
2.2.4. Testing the Matching Quality
Testing the matching quality involves checking all the covariates to determine if the balancing property is achieved from relevant variables of both the control and treated group. Specifically, the intent is to determine whether any systematic differences between the groups remain after the matching is completed (i.e., after conditioning on the propensity scores). The matching quality checks if
, (3)
where K are the covariates that are independent to treatment (D) after conditioning to their probability of participation:
(4)
If there is still a dependency on K covariates, then it can be concluded that either the model is misspecified or lacks good matches between the groups [35] . That is, there should be no more new significant information about the treatment decision. In applying the test, various methods have been suggested, including standardized bias, t-test, joint significance and pseudo R2, and the stratification test [36] [37] [38] . This paper uses the t-test method for participants and nonparticipants for the reasons described below.
The t-test, which is used to test the means of covariates before and after matching, is the preferred test because it gives statistically significant results. After the matching quality has been checked and tested, the impact of participation is measured using the matched sample. The parameter value is the ATT (the average treatment effect on the treated). Because the PSM only reduces the observable bias, there is the need to conduct a sensitivity test for endogeneity or unobservable bias.
2.2.5. Sensitivity Analysis
The last step for this analysis is to check the sensitivity of confounders on our results. The treatment effect estimation is based on two major assumptions: unconfoundedness and overlap. The unconfoundedness assumption is a strong assumption that can lead to bias estimates if there are confounders that affect both participation and the outcome simultaneously [39] . This is because the estimators from matching will not be robust to the hidden bias. While the magnitude of selection bias cannot be estimated with nonexperimental data, it can be addressed by sensitivity analysis. A sensitivity analysis gives answers on whether the inference about the outcome can be altered by unobservables or confounders. Stated slightly differently, it tells how strongly the unmeasured variables could alter the inference made from the analyzed model. That is, the participation probability, say, , is determined by observables and unobservables such that
, (5)
where γ shows the extent to which could affect the participation decision of individual i. Then if there is no hidden bias and is only determined by . If , this implies there is an unobserved effect on participation and that two observations, say, i and j, with the same k (identical value) differ in their probability of receiving treatment. The sensitivity of the results from hidden bias can be checked by varying the value of γ. By varying the values of γ, the bounds for significance and the confidence interval can be generated [39] [40] [41] .
Rosenbaum’s technique of sensitivity analysis depends on the sensitivity parameter, γ, which determines the degree of departure from treatment or participation. Thus, two individuals, i and j, with the same covariates k differ in their odds of participation in the program by at most a factor, γ. In experimental studies, the randomization ensures that the γ value is always 1 to control for bias [42] .
In the odds criteria, values of γ are normally generated and tested in the model to see whether the findings will change. The odds ratio in sensitivity analysis is used because it shows how great the differences in π would need to be to change our estimated results. If is the probability of participation for individual i, then the odds that individual i participates in the program is . The odds ratio is bounded by gamma (γ) such that
(6)
The expression implies that there would be a hidden bias if two individuals with the same covariate values k have a different probability of participating in the program. That is, we would have hidden bias if but for individuals i and j. The basic process for a sensitivity analysis has two steps. First, is the selection of values for γ. Second, the γ values can either be used on p values or on the effect (outcome) to see how the values change as gamma increases. For binary outcomes, the sensitivity analysis is based on McNemar’s test. For other outcomes, we use the sensitivity test based on the Hodges-Lehmann point estimate for the signed rank test because the outcome is a continuous variable.
3. Method and Data
3.1. Method
Participation of farmers in the value chain is associated with linkages among themselves (horizontal coordination) and between postharvest actors (vertical coordination). An experimental approach (treatment and control) is used to determine the extent to which farmers benefit from value chain participation and to identify a causal relationship between participation and an outcome or set of outcomes. PSM is used to evaluate the impact of participation in contracts (C) and associations (A) on wheat farmers’ welfare. Based on Heckman et al. [33] and Dehejia and Wahba [34] ), the propensity scores were estimated using logistic probability regression, the algorithms for matching were selected, common support conditions were checked for variables that influenced both vertical and horizontal coordination participation, the ATT was estimated, and a sensitivity analysis was conducted to check for any confounder effect.
The treatment groups for this study are the participants in contracts and associations, while the control groups are the nonparticipants in contracts and associations. The outcome (R) is the wheat net profit per kilogram (kg). The impact of participation in contracts and associations on household wheat profit (R) is estimated by taking the average difference for R across both the treatment and control groups after controlling for differences in participation due to observable variables (k). First, we use the logit model to estimate the probability of farmers’ participation, assuming that the error term is logistically distributed [43] . The logit model for C and A are specified as
(7)
(8)
where C represents contracts (dummy), and A represents membership in an association (dummy). C takes on a value of 1 if the farmer had a contract during the wheat sales, and zero otherwise. Likewise, A takes on a value of 1 if the farmer belonged to a wheat association, and a value of zero if not. Following the probability estimation, the nearest neighbor (NN) and caliper algorithms with varied radii are used, respectively, to match the control and treatment groups based on propensity scores. The matched sample is used to determine the average treatment effect on treated (ATT) group for net profit R. Explicitly, the treatment effect for individual i is written as
(9)
where Ri is the outcome of an ith individual with treatment, and R0 is the outcome of the same ith individual without treatment. However, because R0 is not observed the counterfactual profit is used. In this case, the expected treatment effect of participation or average treatment effect on treated (ATT) is the difference between the actual profit and the profit if the farmer did not participate in the contract (C) or association (A).
(10)
(11)
where and are the observed net profit, and and are the counterfactual net profits for contract participation and membership in a farmer’s association, respectively.
A proxy is needed for the counterfactual. A ready candidate for the proxy is to use an outcome observed from the untreated group (or a subset of the group). Comparing the average difference in the outcome of the treated vs the proxy as counterfactual, the estimated ATT is
(12)
(13)
where and are the net profit proxies for contract and membership participation, respectively, as obtained from the matched control group. The difference between the true ATT and the estimated ATT is the estimation bias due to some farmers being selected (or self-selected) for the treated group and others for the untreated group such that proxies have to be used for counterfactual outcomes. This bias is referred to as “selection bias” in the econometric literature and is given by
(14)
(15)
where and are biases given by unobserved pre-existing differences between the groups. Thus, the true parameter of ATT is only identified if the counterfactual net profit is similar to proxy net profit without considering unobserved biases. That is
(16)
(17)
After the ATT is obtained, we can now further check for the unobserved effect. Let the probability of participation in value chain for individual i be and for the matched individual j be . Assuming each individual i is exactly matched by individual j, their treatments odds are given by
(18)
(19)
The odds ratio for the paired matched individuals is given by
(20)
where γ is the treatment odd ratio in Rosenbaum’s sensitivity analysis and represents the probability ratio of participants to the matched nonparticipants of the value chain. From
(21)
Assume the F function has a logistic distribution. Then odds ratio equation becomes
(22)
Since the values of after matching, then
(23)
The individuals still differ in their odds of participation by a factor γ and their unobserved covariate w. If there are no differences in unobserved variables or if unobserved variables have no influence on the probability of participating , the odds ratio is 1, implying the absence of hidden or unobserved selection bias. Following Rosenbaum [39] and Aakvik [40] , the bounds for the odds ratio in equation 23 above is given by
(24)
where
represents individual i participating in the value chain, while 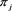 represents individual j not participating in the value chain despite the similarity in the covariate value with individual i. Similarly, γ shows the difference in the odds of treatment and unobservable covariates between two individuals of the same covariate values.
represents individual j not participating in the value chain despite the similarity in the covariate value with individual i. Similarly, γ shows the difference in the odds of treatment and unobservable covariates between two individuals of the same covariate values.
In this case, 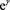 is the measure of the degree of departure from participation that is free of hidden bias. The package rbound in the r-program is used such that γ is the log odds of the differential assignment to treatment due to unobserved factors. The profit outcome is a continuous variable; thus the sensitivity test for p-value is conducted using the Wilcoxon signed rank p-value test. For the profit effect due to participation, the Hodges-Lehmann point estimate test is used. The null hypothesis is
is the measure of the degree of departure from participation that is free of hidden bias. The package rbound in the r-program is used such that γ is the log odds of the differential assignment to treatment due to unobserved factors. The profit outcome is a continuous variable; thus the sensitivity test for p-value is conducted using the Wilcoxon signed rank p-value test. For the profit effect due to participation, the Hodges-Lehmann point estimate test is used. The null hypothesis is , implying that there is no unobserved bias that would badly affect our inference (ATT).
, implying that there is no unobserved bias that would badly affect our inference (ATT).
3.2. Data
Data were collected through a field survey in northern highland area of Tanzania where 90% of the total cultivated wheat is produced. Arusha and Kilimanjaro, which are two relatively homogenous regions in agricultural land use, production practices, and ecological condition, were chosen. Two districts from Arusha (Karatu and Monduli) and one from Kilimanjaro (Hai) were selected based on their level of wheat production. Next, the Mbulumbulu and Rhotia wards were selected in the Karatu District, the Mondulijuu Ward was selected in the Monduli District, and the Ngarenairobi Ward was selected in the Hai District to form a more homogenous stratum by location to represent the variability in wheat growing conditions by the wards. The sampling frame was obtained from village officials who provided lists of farmers who grew wheat during the 2014/15 crop season. The combination of random and snowball sampling techniques were used select the survey respondents. Trained enumerators administered a pre-tested questionnaire to farmers to obtain information related to production, costs, and marketing practices. Demographic information was collected on solicited heads of households that included household size, age, gender, education, and occupation of the respondents, as well as information on the number of wheat contracts, membership in a group/association, and production and marketing of wheat challenges that the survey respondents had encountered during the 2014/15 wheat season. In addition, formal discussions with key informants such as government officials and traders were conducted to solicit their opinions about the 2014/15 wheat crop. This information supplemented the data collected from the structured questionnaire for farmers.
The final sample included 350 farmers despite several farmers switching from wheat production to barley production or significantly reducing their wheat production. Barley competes directly with wheat in Tanzania since both crops are grown under the same conditions using the same inputs. The differences include seeds and buyers. Barley has the advantage in that it sells for a slightly higher price than wheat and receives full support from private brewery companies. Such support includes the provision of inputs, assistance with harvesting and transporting the crop. Despite the difficulty encountered, a total of 310 out of 350 farmers completed the questionnaires and participated in the analysis. Incomplete questionnaires were discarded. The focus of this study was small-scale farmers who are the majority of farmers in Tanzania, with land size ranging from 0.2 to 2 hectares (the equivalent of 0.5 to 5 acres).
4. Results and Discussions
4.1. Value Chain Structure
The wheat value chain in the study area consists of four main value chains: wheat input, wheat grain, wheat flour, and wheat product. We focus mainly on farmers’ participation in the wheat grain value chain, which consists of producers, brokers, wholesalers, and retailers.
Although landholdings in the study area range from 0.5 acres to more than 50 acres, the bulk of farmers represented in the survey are small-scale farmers with land averaging about 5 acres. Figure 1 depicts the wheat grain value chain. As can be seen in Figure 1, the farmers sell wheat grain to local retailers, brokers, and wholesalers. The wheat brokers in the study area are the major/dominant players in the wheat grain value chain because they are involved in organizing most of the transactions between the traders and the farmers. They participate in the harvesting and transporting of crops to the urban market/warehouse “godown” where they meet with wholesalers or processors.
Brokers and traders visit at the farm gate to bid for prices shortly before the harvest. Sometimes brokers and traders agree to harvest the crops themselves in exchange for one bag (100 kgs) of wheat to every acre harvested as the cost of harvesting. The brokers and traders harvest and transport the wheat to the processors for further value adding activities. Once the wheat is sold, the brokers and traders then deduct their costs and give the cash balance to the farmers.
One disadvantage that farmers face in selling their wheat to the brokers and traders at the farm gate is that each bag of wheat actually holds from 110 kgs to 130 kgs, depending on how much extra (overflow) the bags can extend. In the Swahili language, the overflow bags are called “lumbesa” (extended bags).
4.2 Value Chain Coordination
Coordination along the chain is achieved by means of contracts and associations
Figure 1. Wheat grain value chain map.
between and within actors. Two types of coordination are identified: vertical (contracts with brokers and traders) and horizontal (membership in associations). Table 1 shows that only 16.5% of all the farmers surveyed had a contract with traders, and most of those were verbal agreements only. This implies that the majorities of small-scale farmers are not coordinated vertically and sell their wheat grain to spot markets or at the farm gate. The small percentage of farmers with contracts implies weak vertical coordination between farmers and other actors of the wheat grain value chain. Because the relationship between farmers and traders starts at harvest time, there are no set predetermined prices or forward contracts. Neither is there any type of arrangement that would compel buyers to provide agricultural inputs nor farmers to supply wheat. In addition, verbal contracts do not force the wheat buyer to provide technical or extension support, which leaves farmers in a dilemma during high peak/good harvests. This is in sharp contrast to the situation that exists for barley, whereby the companies purchasing the barley also finance the inputs and provide extension and transportation services. Barley contracts are a type of centralized agreement where the buyers take care of almost everything while the farmer only takes care of the operations costs (land preparation, planting, spraying, and fertilization). As a result, many farmers have exchanged/reduced wheat cultivation for barley.
Table 2 shows that 39.4% of the total producers surveyed belonged to wheat associations. The fact that the vast majority were not part of associations indicates weak horizontal coordination. Most of these associations are not formed officially; oftentimes it is just a group of farmers working together on various economic and community activities.
4.3. Mean Characteristics of Participants and Nonparticipants of Value Chain
The participants and nonparticipants of vertical coordination differ significantly
Table 1. Farmers’ vertical coordination by wards.
~Values in bracket are percentages.
Table 2. Farmers’ horizontal coordination by wards.
~Values in brackets are percentages.
in farm and farmer characteristics. Nonparticipants are more experienced in farming, have a larger number of household members, and a larger number of adults in the household. Participants are characterized by larger numbers of farmers leasing the land, higher frequency of extension visitations, higher attendence atvillage meetings, higher off-farm income, larger proportion of land used for wheat production more output per acre, and fewer seeds planted per acre. Further, participants have a higher technical efficiency (TE scores) and allocation efficiency (AE scores) compared to nonparticipants at the 1% significance level (Table 3). For the rest of the characteristics, the differences between participant and nonparticipant farmers were not significant. This implies that relatively suitable matches would be available for vertical coordination participants and nonparticipants to analyze the impact of vertical coordination participation on farmer’s welfare as measured by wheat profit per kg.
Table 4 shows the characteristics of participants and nonparticipants of associations. Many variables are insignificant, which implies that the mean differences between participants and nonparticipants in associations are not associated with farm and farmer characteristics. Table 4 demonstrates that participants differ positively and significantly from nonparticipants in the level of education (10% significance level), frequency of meetings attendance (5% significance level), output per acre (1% significance level), technical efficience (1% significance level), and allocative efficiency (1% significance level). Conversely, nonparticipants differ positively and significantly from participants on better farm equipment ownership and number of herbicide applications at the 10% and 5% significance level, respectively. Since most of the variables are either not significant or have a weak significance level, there is a good match from nonparticipants to analyze the impact of horizontal coordination participation on farmer’s welfare as measured by wheat profit per kg.
4.4. Factors Influencing Farmers’ Participation in Value Chain
As mentioned earlier, a logit model was used to determine the factors that influence the farmer’s participation in contracts and associations to generate the fitted values (estimated coefficients) that were used to create the propensity scores. Table 5 shows that age of the household head, land leased, frequency of extension visits, frequency of meetings attendance, off-farm income, land size allocated for wheat, and technical efficiency are significant factors that determine farmers’ participation in vertical coordination. Unlike younger farmers, older farmers might have long-time partners who buy their wheat, and thus are more likely to participate in vertical coordination. Farmers who receive more extension visitations are more likely to participate in vertical coordination,
Table 3. Characteristics for vertical coordination, participants and nonparticipants.
*significant at 10% level, ** at 5% level, *** at 1% level.
Table 4. Characteristics for horizontal coordination, participants and nonparticipants.
*significant at 10% level, ** at 5% level
perhaps because the extension officers provide both technical and marketing information, including identifying traders willing to negotiate contracts. Farmers who attend village meetings are more likely to participate in contracts because the meetings allow farmers to gain access to various production and marketing information and to meet traders interested in establishing contractual arrangements. Farmers with off-farm activities have a greater opportunity of meeting wheat traders at off-farm workplaces or in the marketplace. The larger the land size allocated for wheat production, the higher the probability of participating in vertical coordination. This is probably because traders prefer contracting with farmers with larger acreages. Not surprisingly, farmers with higher technical efficiency have a greater chance of participating in vertical coordination due to contract participation. The marginal effect for age indicates
Table 5. Logit estimates of propensity score model for contracted farmers.
*significant at 10% level, ** at 5% level, *** at 1%level
that all other factors being held constant, older farmers are more likely (by 0.3%) to participate in contracts than younger farmers. The marginal effect of the extension visits is 1.1% more for visited farmers than for non-visited farmers. Higher attendance at village meetings increases a farmer’s probability of participating in contracts by 3.0%.The marginal effect for off-farm income shows that farmers with higher off-farm income have a 6.3% greater chance of participating in vertical coordination than their counterparts. Farmers with larger land size are 0.8% more likely to participate in vertical coordination. Farmers with higher technical efficiency scores are 48% more likely to participate in vertical coordination. However, in general, the low probability of farmers’ participation in contracts suggests a weak vertical coordination in the value chain. It is possible that if there had been better institutional arrangements, more farmers would have participated in contracts.
Horizontal coordination is associated with farmers’ formation of groups for collective actions in agricultural activities. Table 6 shows the farm and farmer characteristics influencing participation in horizontal coordination. Few factors significantly influence farmers’ participation, such as meetings attendance (5%), farm equipment (5%), and output (5%). Farmers with high-tech farm equipment are less likely to participate in associations. Village meetings attendance and level of output positively and significantly influence participation in horizontal coordination by 5% each. Meetings attendance influences farmers’ participation in associations because of the camaraderie and the sharing of information and expenses, which encourages others to join/form associations. The marginal effect of meetings attendance indicates a 7% increase in the probability of farmers who attend village meetings to participate in horizontal coordination.
Table 6. Logit estimates of propensity score model for farmers’ membership.
*Significant at 10% level, ** at 5% level, *** at 1% level.
4.5. Covariate Balancing Property
Overlapping of propensity scores between participants and nonparticipants is one of two basic assumptions in PSM. The estimates that lie between 0 and 1 are used to determine the common support region and to check whether this assumption has been met. Results for both vertical and horizontal coordination are provided in Table 7 and Table 8, respectively, to show the covariate balances of observables. Visual proofs of histogram distribution (Figures 2-10) are also provided to show the balances of the matched treated and control samples. Checking the overlap assumption before further analysis is necessary to ensure that reliable estimates are presented. Table 7 shows that the matching for the control and treated groups is properly overlapped for the selected variables. That is, there is no significant difference between the means of the control and treated groups after matching. As indicated in Table 7, all of the “after matching” mean value differences between the treated and control groups are insignificant.
Figures 2-6 show the visual look of the distribution before and after matching for various caliper levels and nearest neighbor matching. The histograms’ distributions before and after matching for treated (contract) and control (noncontract) groups reveal that after matching, the shapes for the treated and control groups are similar and that there are no significant differences between the two groups, thus suggesting that we can further use the matched sample group to examine the effect of farmers’ participation in vertical coordination on wheat profit per kg. Table 8 shows that the matching for the control and the treated groups under horizontal coordination were properly overlapped. That is, there is no significant difference between the means of the control and treated groups after matching.
Figures 7-10 show the visual distribution before and after matching for the control and treated groups. The histograms for the nearest neighbor and caliper algorithms indicate that the after matching distributions are similar between the control and treated groups. This implies that there are no significant differences between the two groups. Thus, the matched sample can be used for analyzing the effect of horizontal coordination participation on wheat profit per kg.
4.6. Impact of Vertical and Horizontal Coordination on Wheat Farmers’ Net Profit
The vertical coordination effect was measured using both the nearest neighbor and caliper radius matching algorithms. As seen in Figure 6, the nearest neighbor visual distribution did not result in the best matches, so its profit effect of 130 TSh/kg in Table 9 will still be biased. Caliper radius matching is a flexible form of an algorithm that checks matching at various radii. A caliper radius of 0.01 showed a profit effect of 136 TSh/kg and was significant at the 1% level. Despite the visual diagram (Figure 2) showing similar distribution between the matched treated and control groups, few treated farmers were used for the analysis. Possible increases in the samples were checked further by increasing the
Table 7. Covariate balancing for contract and noncontract farmers (caliper 0.07).
Table 8. Covariate balancing for members and nonmembers farmers (caliper 0.022).
Figure 2. Distribution of propensity scores before and after matching the contract and noncontract farmers by caliper radius of 0.01.
Figure 3. Distribution of propensity scores before and after matching the contract and noncontract farmers by caliper radius of 0.03.
Figure 4. Distribution of propensity scores before and after matching the contract and noncontract farmers by caliper radius of 0.05.
Figure 5. Distribution of propensity scores before and after matching the contract and noncontract farmers by caliper radius of 0.07.
Figure 6. Distribution of propensity score before and after matching the contract and noncontract farmers by nearest neighbor algorithm 1:1 but not good match.
Figure 7. Distribution of propensity scores before and after matching the members and nonmembers by caliper radius of 0.005.
Figure 8. Distribution of propensity scores before and after matching the members and nonmembers by caliper radius of 0.02.
Figure 9. Distribution of propensity scores before and after matching the members and nonmembers by caliper radius of 0.022.
Figure 10. Distribution of propensity score before and after matching the members and nonmembers by nearest neighbor algorithm of 1:1 ratio but not a good match.
Table 9. Vertical coordination effect (ATT).
caliper radius. A caliper radius of 0.07 gave the maximum number of treated farmers that matched with the control group and the visual look after matching showed a similarity between the matched treated and matched control groups. A caliper radius of 0.07 showed a profit effect of 126 TSh/kg and was significant at the 1% level for a sample of 43 treated farmers included in the analysis. This finding implied that vertical coordination participants earn a higher net profit than nonparticipants by over 126 TSh/kg. Because the unobserved confounder effect was not considered in the outcome, a sensitivity analysis needed to be conducted to see how the unobserved confounding factors might alter our inference. For horizontal coordination, the analysis also revealed a positive and significant impact of farmers’ participation in the value chain through membership in associations. The nearest neighbor matching for vertical coordination did not show suitable matches for horizontal coordination (Figure 10), thus the profit result in Table 10 of Tsh 41/kg was not unbiased. Caliper matching radii of
Table 10. Horizontal coordination effect (ATT).
0.005, 0.02, and 0.022 were used to check the visual balances of the matched sample. The caliper radius of 0.022 accommodated the maximum sample of 100 treated farmers out of 122 participants. The average net profit effect on treated (ATT) was found to be 46 TSh/kg more for participants than for nonparticipants and was significant at the 5% level. We further checked the robustness of our result from unobserved exposures (confounders) by conducting a sensitivity analysis
4.7. Sensitivity Analysis
The results in the previous section relied only on the assumption of unconfoundedness, or conditional independence. That is, no systematic differences in the distribution of the covariates between the two groups were caused by observable or unobservable (hidden bias) factors. Hidden bias can arise by the non-inclusion of variables that may affect both the value chain participation and the profit, simultaneously [22] [39] [41] [42] . Thus, this study performed a sensitivity analysis to check the extent to which the inferences made from vertical and horizontal coordination participation could be altered by unobservables. Table 11 shows the Rosenbaum bounds sensitivity analysis from Wilcoxon’s signed rank test and Hodges-Lehmann point estimate test for vertical coordination. The Hodges-Lehmann test gives the median range of ATT for every value of gamma while the Wilcoxon provides their corresponding ranges of significance levels for each ATT generated from gamma values. The parameter values generated from gamma for unobserved covariates explain how hidden biases of various magnitudes could alter the profit effect of value chain participation. The values of 




Table 11. Vertical coordination Rosenbaum sensitivity test.
sensitive to hidden bias That is, our significant result would become questionable due to unobservables if 



5. Conclusions
The objective of this study was to assess the impact of value chain participation on wheat farmers’ welfare in Tanzania. The postulation was that the slow response to wheat production could be due to the failure of wheat growers in Tanzania to formally participate in the value chain. Nonparticipation breaks the information flow about this market opportunity and restricts the potential contribution of this crop to the welfare of farmers. In exploring that broad objective,
Table 12. Horizontal coordination Rosenbaum sensitivity test.
we described the wheat grain flows from production point to ultimate consumption, analyzed the coordination of wheat actors, explored factors that influence participation in the value chain, and examined the net effect of farmers’ participation in the value chain. The wheat value chain in the study area consists of four main chains: the wheat input chain, the wheat grain chain, the wheat flour chain, and the wheat products chain. Focusing on the wheat grain chain, we observed that farmers sell wheat grain to local retailers, brokers, and wholesalers at the farm gate. The wheat brokers in the study area are the major/dominant players in the wheat grain value chain because they are involved in organizing most of the transactions between traders and the farmers.
This study found that only a few farmers are vertically (~17%) and horizontally (~39%) coordinated as indicated by participation in contracts and associations, respectively. At the vertical coordination level, farmers with contracts had characteristics that were significantly different from those without contracts in terms of wheat land size, technical efficiency, allocative efficiency, output/acre, frequency of extension visits, frequency of village meetings attendance, and off-farm income. At the horizontal coordination level, similar findings were obtained in that the farmers who were members of associations differ significantly with nonmembers in terms of level of education, frequency of meetings attendance, output per acre, technical efficiency, and allocative efficiency.
The propensity scoring technique (PSM) was used to explore the causal relationship between participation and nonparticipation in the wheat value chain and the impact on the welfare of wheat farmers as reflected in wheat profits per kg. A logistic model was used to explore the factors influencing farmers’ participation in the value chain and to estimate the propensity scores that were later used to match the covariates for participants and nonparticipants. The results indicate that participation in vertical coordination was influenced by the age of the farmer, land leased, frequency of extension service visits, frequency of meetings attendance by farmers, off-farm income, land size allocated for wheat, and technical efficiency. On the other hand, participation in horizontal coordination was influenced by the frequency of meetings attendance, farmers’ location, farm equipment ownership, and technical efficiency. The fitted values from the logit model generated propensity scores that were used to match the participants and nonparticipants of the value chain. The overlapping and unconfoundedness assumptions were fulfilled by applying the nearest neighbor and caliper radius matching algorithms. The vertical coordination participation impact on farmers’ welfare revealed that participants received 126 TSh/kg more for wheat than nonparticipants and the difference was significant at the 1% level. Horizontal coordination participants received 56 TSh/kg more for wheat more than nonparticipants and the difference was significant at the 5% level. The sensitivity analysis revealed that our statistical inference on farmers’ participation in the value chain is generally insensitive to unobserved covariates. However, we cannot ignore the fact that horizontal coordination is somewhat more sensitive to hidden bias than is vertical coordination. In this connection, it should be noted that one limitation of the study lies in the fact that the propensity score methodology can only ensure balance in measured, not unmeasured, confounders.
The overall concern of this investigation revolves around the failure of Tanzanian farmers to respond to what appears to be a market opportunity to satisfy domestic demand for wheat and wheat product. Our study suggests that even in the face of relatively weak contracts, farmers who participated in contracts (vertically or horizontally) received added benefits compared to nonparticipants. However, the number of farmers who formally participate in contracts is relatively small, implying that the level of support for the hypothesis posited that this could be one of the major factors responsible for the lackluster response to wheat market opportunity. An implication of our findings is that policy makers and other beneficiaries should take steps to encourage and nurture contracts through upfront investments to wheat farmers in order to facilitate production through binding contracts. Further, more emphasis is needed on offering farmers more extension services, better agricultural-related meetings, greater land size for wheat production, more off-farm work opportunities, and higher levels of technical efficiency. There should also be more emphasis on improving the efficiency of horizontal coordination to improve farmers’ welfare.
Cite this paper
Warsanga, W.B. and Evans, E.A. (2018) Welfare Impact of Wheat Farmers Participation in the Value Chain in Tanzania. Modern Economy, 9, 853-887. https://doi.org/10.4236/me.2018.94055
References
- 1. Fafchamps, M. and Hill, R.V. (2005) Selling at the Farmgate or Travelling to Market. American Journal Agricultural Economic Association, 87, 717-734. https://doi.org/10.1111/j.1467-8276.2005.00758.x
- 2. Holloway, G., Nicholson, C., Delgado, C., Staal, S. and Ehui, S. (2000) Agro Industrialization through Institutional Innovation: Transactions Costs, Cooperatives, and Milk Market Development in the Ethiopian Highlands. Agricultural Economics, 23, 279-288. https://doi.org/10.1111/j.1574-0862.2000.tb00279.x
- 3. Thorp, R., Stewart, F. and Heyer, A. (2005) When and How Far Is Group Formation a Route Out of Chronic Poverty? World Development, 33, 907-920. https://doi.org/10.1016/j.worlddev.2004.09.016
- 4. Wollni, M. and Zeller, M. (2007) Do Farmers Benefit from Participating in Specialty Markets and Cooperatives? The Case of Coffee Marketing in Costa Rica. Agricultural Economics, 37, 243-248. https://doi.org/10.1111/j.1574-0862.2007.00270.x
- 5. Roy, D. and Thorat, A. (2008) Success in High Value Horticultural Export Markets for the Small Farmers: The Case of Mahagrapes in India. World Development, 36, 1874-1890. https://doi.org/10.1016/j.worlddev.2007.09.009
- 6. Abebaw, D. and Haile, M.G. (2013) The Impact of Cooperatives on Agricultural Technology Adoption: Empirical Evidence from Ethiopia. Food Policy, 38, 82-91. https://doi.org/10.1016/j.foodpol.2012.10.003
- 7. Hoken, H. and Su, Q. (2015) Measuring the Effect of Agricultural Cooperatives on Household Income Using PSM-DID: A Case Study of a Rice-Producing Cooperative in China. IDE Discussion Paper 539, Institute of Developing Economies, Chiban, Japan.
- 8. Boger, S. (2001) Quality and Contractual Choice: A Transaction Cost Approach to the Polish Hog Market. European Review of Agriculture Economics, 28, 241-261. https://doi.org/10.1093/erae/28.3.241
- 9. Reardon, T., Timmer, P. and Berdegue, J. (2004) The Rapid Rise of Supermarkets in Developing Countries: Induced Organizational, Institutional, and Technological Change in Agrifood Systems. Journal of Agricultural and Development Economics, 1, 168-183.
- 10. Gulati, A., Minot, N., Delgado, C. and Bora, S. (2006) Growth in High-Value Agriculture in Asia and the Emergence of Vertical Links with Farmers. In: Swinnen, J., Ed., Global Supply Chains, Standards, and Poor Farmers, CABI Press, London, 91-108.
- 11. Miyata, S., Minot, N. and Hu, D. (2009) Impact of Contract Farming on Income: Linking Small Farmers, Packers, and Supermarkets in China. World Development, 37, 1781-1790. https://doi.org/10.1016/j.worlddev.2008.08.025
- 12. Barrett, C.B., Bachke, M.E., Bellemare, M.F., Michelson, H.C., Narayanan, S. and Walker, T.F. (2012) Smallholder Participation in Contract Farming: Comparative Evidence from Five Countries. World Development, 40, 715-730. https://doi.org/10.1016/j.worlddev.2011.09.006
- 13. Abebe, G.K., Bijman, J., Kemp, R., Omta, O. and Tsegaye, A. (2013) Contract Farming Configuration: Smallholders’ Preferences for Contract Design Attributes. Food Policy, 40, 14-24. https://doi.org/10.1016/j.foodpol.2013.01.002
- 14. Bolwig, S., Gibbon, P. and Jones, S. (2009) The Economics of Smallholder Organic Contract Farming in Tropical Africa. World Development, 37, 1094-1104. https://doi.org/10.1016/j.worlddev.2008.09.012
- 15. Dries, L., Germenji, E., Noev, N. and Swinnen, J.F.M. (2009) Farmers, Vertical Coordination, and the Restructuring of Dairy Supply Chains in Central and Eastern Europe. World Development, 37, 1742-1758. https://doi.org/10.1016/j.worlddev.2008.08.029
- 16. Maertens, M. and Swinnen, J.F.M. (2009) Trade, Standards, and Poverty: Evidence from Senegal. World Development, 37, 161-178. https://doi.org/10.1016/j.worlddev.2008.04.006
- 17. Rao, E.J.O. and Qaim, M. (2011) Supermarkets, Farm Household Income, and Poverty: Insights from Kenya. World Development, 39, 784-796. https://doi.org/10.1016/j.worlddev.2010.09.005
- 18. Masakure, O. and Henson, S. (2005) Why Do Small-Scale Producers Choose to Produce under Contract? Lessons from Nontraditional Vegetable Exports from Zimbabwe. World Development, 33, 1721-1733. https://doi.org/10.1016/j.worlddev.2005.04.016
- 19. Narrod, C., Roy, D., Okello, J., Avendano, B., Rich, K. and Thorat, A. (2009) Public-Private Partnerships and Collective Action in High Value Fruit and Vegetable Supply Chains. Food Policy, 34, 8-15. https://doi.org/10.1016/j.foodpol.2008.10.005
- 20. SAGCOT (2009) Value Chain and Market Analysis. http://www.sagcot.com/uploads/media/Appendix_IV-_Value_Chain_and_Market_Analysis_03.pdf
- 21. USAID (2010) Staple Foods Value Chain Analysis: Country Report, Tanzania. United States Agency for International Development, Washington DC.
- 22. Rosenbaum, P. and Rubin, D. (1983) Assessing Sensitivity to an Unobserved Binary Covariate in an Observational Study with Binary Outcome. Journal of the Royal Statistical Society, 45, 212-218.
- 23. Heckman, J., Ichimura, H. and Todd, P. (1997) Matching as an Econometric Evaluation Estimator: Evidence from Evaluating a Job Training Programme. The Review of Economic Studies, 64, 605-654. https://doi.org/10.2307/2971733
- 24. Caliendo, M. and Kopeinig, S. (2008) Some Practical Guidance for the Implementation of Propensity Score Matching. Journal of Economic Survey, 22, 31-72. https://doi.org/10.1111/j.1467-6419.2007.00527.x
- 25. Smith, J.A. and Todd, P.E. (2005) Does Matching Overcome LaLonde’s Critique of Nonexperimental Estimators? Journal of Econometrics, 125, 305-353. https://doi.org/10.1016/j.jeconom.2004.04.011
- 26. Dehejia, R.H. and Wahba, S. (1999) Causal Effects in Nonexperimental Studies: Reevaluating the Evaluation of Training Programs. Journal of the American Statistical Association, 94, 1053-1062. https://doi.org/10.1080/01621459.1999.10473858
- 27. Kaplinsky, R. and Morris, M. (2001) A Handbook for Value Chain Research. Institute of Development Studies, Univeristy of Sussex, Brighton, UK.
- 28. Donovan, J., Franzel, S., Cunha, M., Gyau, A. and Mithofer, D. (2015) Guides for Value Chain Development: A Comparative Review. Journal of Agribusiness in Developing and Emerging Economies, 5, 2-23. https://doi.org/10.1108/JADEE-07-2013-0025
- 29. UNIDO (2011) Pro-Poor Value Chain Development. United Nations Industrial Development Organization, Vienna, Austria.
- 30. Birthal, P.S., Joshi, P.K. and Gulati, A. (2005) Vertical Coordination in High-Value Food Commodities: Implication for Smallholders. MTID Discussion Paper 85, IFPRI, Washington DC.
- 31. Valkila, J., Haaparanta, P. and Niemi, N. (2010) Empowering Coffee Traders? The Coffee Value Chain from Nicaraguan Fair Trade Farmers to Finnish Consumers. Journal of Business Ethics, 97, 257-270. https://doi.org/10.1007/s10551-010-0508-z
- 32. Warsanga, W.B. (2014) Coordination and Structure of Agri-Food Value Chains: Analysis of Banana Value Chain Strands in Tanzania. Journal of Economics and Sustainable Development, 5, 71-79.
- 33. Rosenbaum, P.R. and Rubin, D.B. (1983) The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika, 70, 41-55. https://doi.org/10.1093/biomet/70.1.41
- 34. Dehejia, R.H. and Wahba, S. (2002) Propensity Score-Matching Methods for Nonexperimental Causal Studies. Review Economics and Statistics, 84, 151-161. https://doi.org/10.1162/003465302317331982
- 35. Blundell, R., Dearden, L. and Sianesi, B. (2005) Evaluating the Effect of Education on Earnings: Models, Methods and Results from the National Child Development Survey. Journal of the Royal Statistical Society, 168, 473-512. https://doi.org/10.1111/j.1467-985X.2004.00360.x
- 36. Lechner, M. (1999) An Evaluation of Public-Sector-Sponsored Continuous Vocational Training Programs in East Germany. IZA Discussion Paper 93, Institute of Labor Economics, Bonn, Germany.
- 37. Sianesi, B. (2004) An Evaluation of the Swedish Sytem of Active Labor Market in the 1990s. Review of Economics and Statistics, 86, 133-155. https://doi.org/10.1162/003465304323023723
- 38. Caliendo, C., Guida, M. and Parisi, A. (2007) A Crash-Prediction Model for Multilane Roads. Accident Analysis and Prevention, 39, 657-670. https://doi.org/10.1016/j.aap.2006.10.012
- 39. Rosenbaum, P.R. (2002) Design of Observational Studies. Springer, New York. https://doi.org/10.1007/978-1-4757-3692-2
- 40. Aakvik, A. (2001) Bounding a Matching Estimator: The Case of a Norwegian Training Program. Oxford Bulletin of Economics and Statistics, 63, 115-143. https://doi.org/10.1111/1468-0084.00211
- 41. Becker, S. and Caliendo, M. (2007) Sensitivity Analysis for Average Treatment Effects. Stata Journal, 7, 71-83.
- 42. Keele, L. (2010) An Overview of Rbounds: An R Package for Rosenbaum Bounds Sensitivity Analysis with Matched Data. White Paper, Ohio State University, Columbus, Ohio.
- 43. Saigenji, Y. and Zeller, M. (2009) Effect of Contract Farming on Productivity and Income of Smallholders: The Case of Tea Production in Northwestern Vietnam. International Association of Agricultural Economists, Beijing.












