Advances in Pure Mathematics
Vol.3 No.1(2013), Article ID:27390,4 pages DOI:10.4236/apm.2013.31018
Fuzzy δ*-Continuity and Fuzzy δ**-Continuity on Fuzzy Topology on Fuzzy Sets
Department of Mathematics, College of Education, Al-Mustansiriya University, Baghdad, Iraq
Email: mssm_1975@yahoo.com
Received September 1, 2012; revised October 17, 2012; accepted November 19, 2012
Keywords: Fuzzy δ*-Continuity; Fuzzy δ**-Continuity; Quasi-Neighbourhood; Fuzzy δ-Open; Quasi-Coincident
ABSTRACT
The concept of a fuzzy topology on a fuzzy set has been introduced in [1]. The aim of this work is to introduce fuzzy δ*- continuity and fuzzy δ**-continuity in this in new situation and to show the relationships between fuzzy continuous functions where we confine our study to some of their types such as, fuzzy δ-continuity, fuzzy continuity, after presenting the definition of a fuzzy topology on a fuzzy set and giving some properties related to it.
1. Introduction
The concept of a fuzzy topology on a fuzzy set has been introduced by Chakrabarty and Ahsanullah [1]. Neighbourhood systems, quasi-neighbourhood system, subspaces of such fuzzy topology space and quasi-coincidence in this new situation have also been discussed by them. Also, the concepts of fuzzy continuity, Hausdorffness, regularity, normality, compactness, and connectedness have been introduced by Chaudhuri and Das [2]. The concepts of fuzzy δ-closed sets, fuzzy δ-open sets fuzzy regular open, fuzzy regular closed, fuzzy δ- continuity and the relation between fuzzy continuity and fuzzy δ-continuity in this new situation was introduced by Zahran [3]. These functions have been characterized and investigated mainly in light of the notions of quasineighborhood, quasi-coincidence. In our rummage we confined ourselves to the study of some kinds of these functions, the fuzzy continuous function, fuzzy δ-continuity and some types of fuzzy regular. In this paper, we introduce the concepts of a fuzzy δ*-continuity, fuzzy δ**- continuity and to show the relationships between types of fuzzy continuous functions in this situation and we examine the validity of the standard results.
2. Preliminaries
Let X and Y be sets and  and
and  be two subsets of X, Y respectively. Let I denote the closed unit interval
be two subsets of X, Y respectively. Let I denote the closed unit interval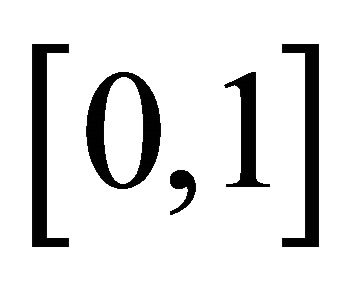 . Let
. Let  and
and 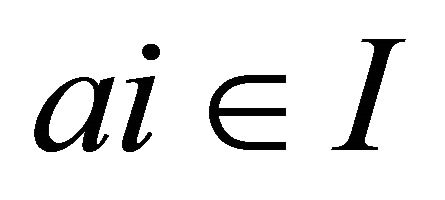 for
for 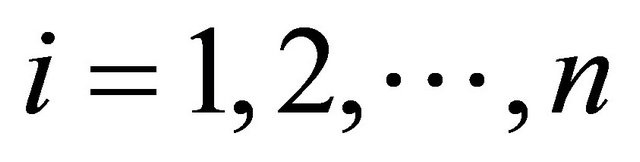 By
By 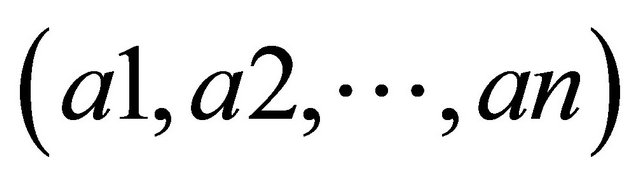 we shall mean the fuzzy subset
we shall mean the fuzzy subset  of X and the value of a fuzzy set
of X and the value of a fuzzy set  at some
at some 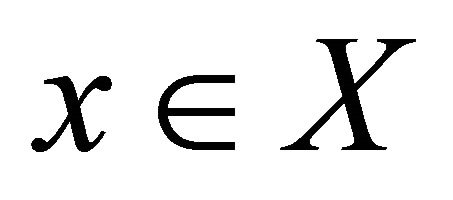 will be denoted by
will be denoted by 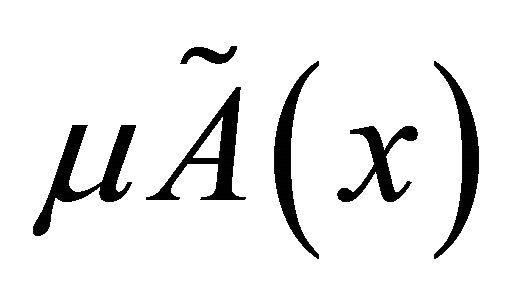 such that
such that 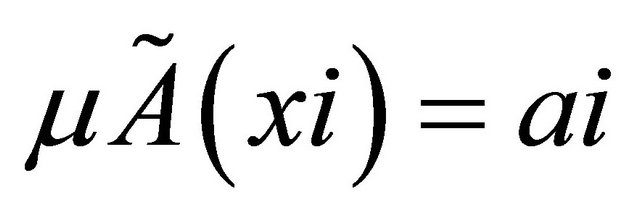 for
for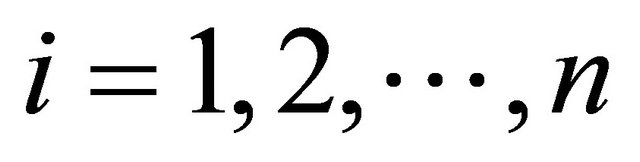 , and the support of a fuzzy set
, and the support of a fuzzy set  in X will be denoted by
in X will be denoted by  such that
such that 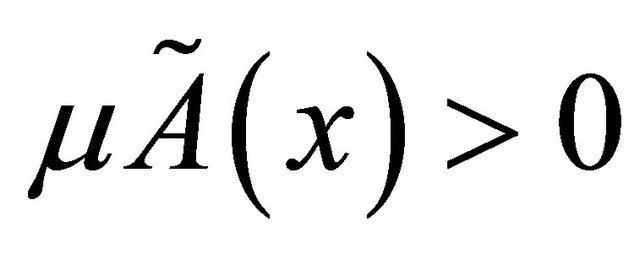 for all x in X. If
for all x in X. If  and
and  are fuzzy sets and
are fuzzy sets and  for all x in X, then
for all x in X, then  is said to be a fuzzy subset of
is said to be a fuzzy subset of  and denoted by
and denoted by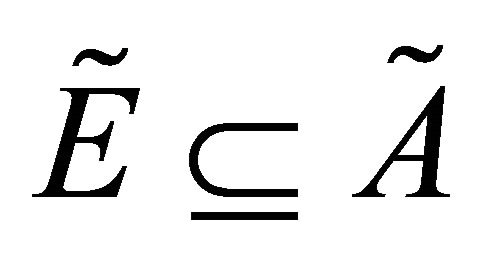 . The set of all fuzzy subsets of a nonempty set
. The set of all fuzzy subsets of a nonempty set  is denoted by
is denoted by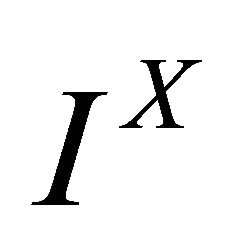 .
.
Definition 2.1. [2] Let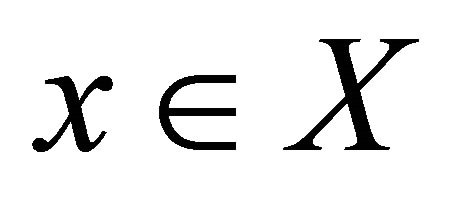 ,
, . A fuzzy set
. A fuzzy set  of the form
of the form
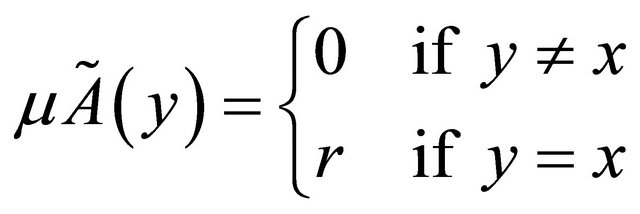
is called a fuzzy point with support x and value r.  is often denoted by
is often denoted by .
.
For a fuzzy point 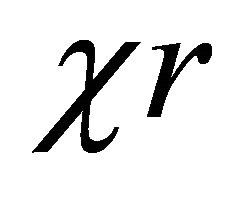
1)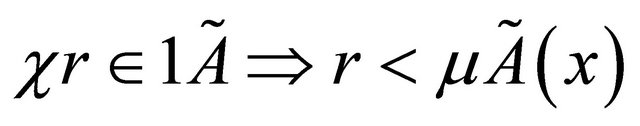 .
.
2)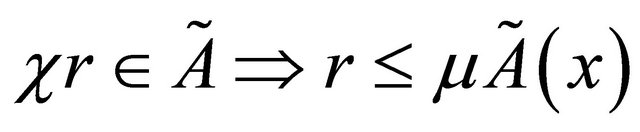 .
.
Definition 2.2. [1] If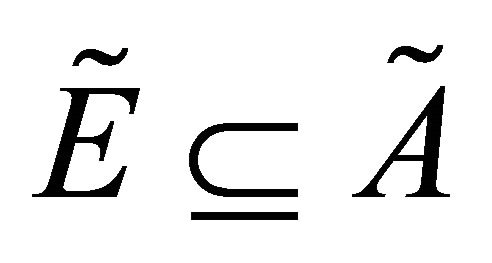 , the complement of
, the complement of 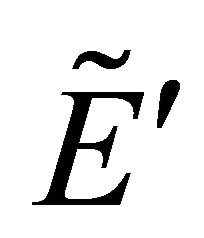 referred to
referred to , denoted by
, denoted by  is defined by
is defined by 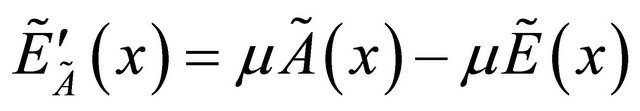 , for each
, for each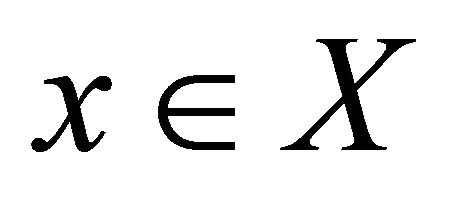 .
.
Definition 2.3. [2] ,
, 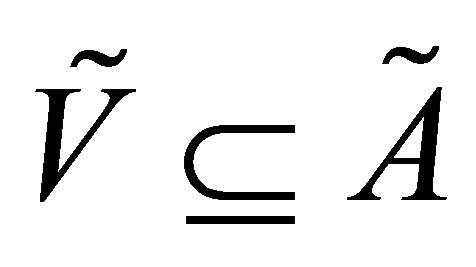 are said to be quasicoincident (q-coincident, for short) referred to
are said to be quasicoincident (q-coincident, for short) referred to  written as
written as 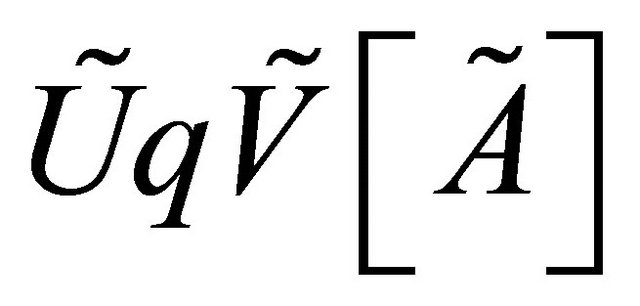 if there exists
if there exists 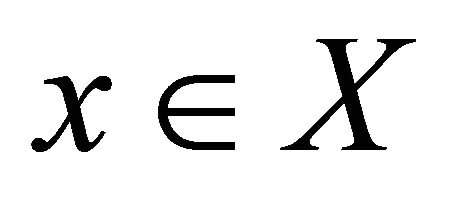 such that
such that
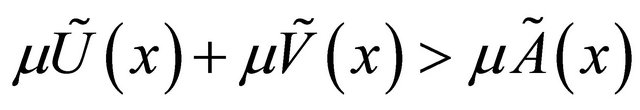 . If
. If  and
and 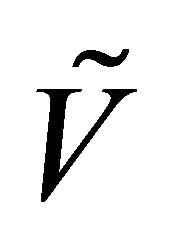 is not quasicoincident referred to
is not quasicoincident referred to , we denoted for this by
, we denoted for this by .
.
3. Basic Definitions and Properties
In [4,5] fuzzy function have been introduced in a different way considering them as fuzzy relations with special properties. A special kind of fuzzy functions had been called fuzzy proper functions or proper functions that would be the morphisms in the proposed category FUZZY TOP.
Definition 3.1. [1] A fuzzy subset  of
of 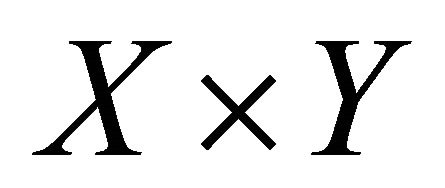 is said to be a proper function from
is said to be a proper function from  to
to  if 1)
if 1)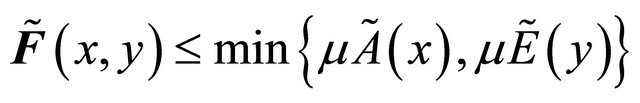 , for each
, for each 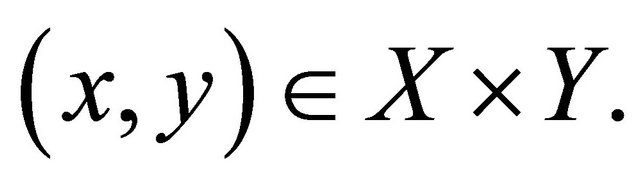
2) For each , there exists a unique
, there exists a unique 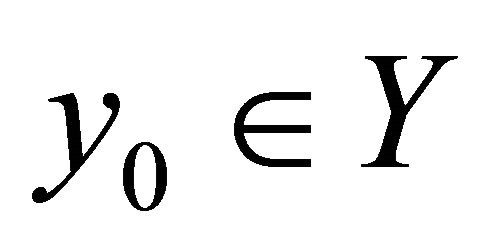 such that
such that 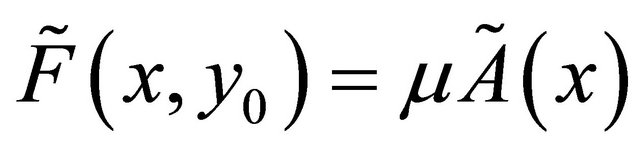 and
and 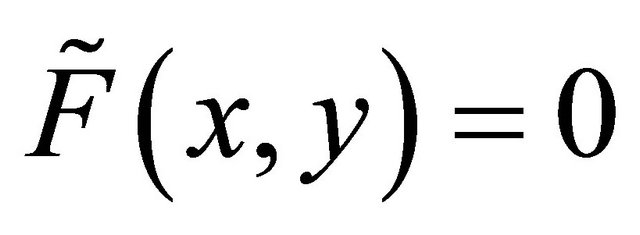 if
if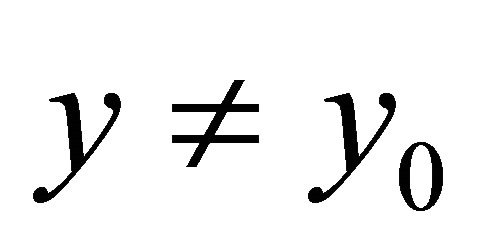 .
.
Let  be a proper function from
be a proper function from  to
to .
.
Definition 3.2. [1] If , then
, then 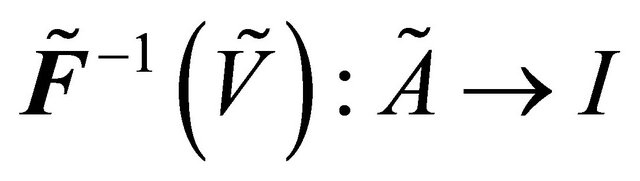 is defined by
is defined by
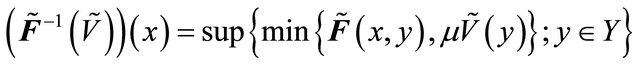
for each .
.
Definition 3.3. [2] If , then
, then 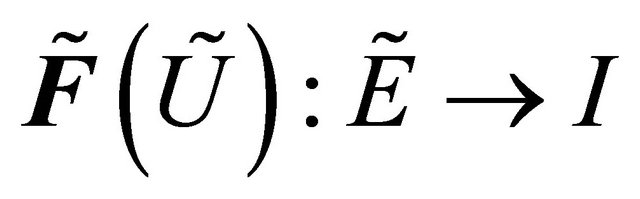 is defined by
is defined by

for each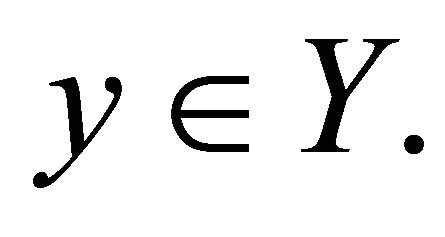
Proposition 3.4. [2] For a proper function 
1) , for each
, for each .
.
2)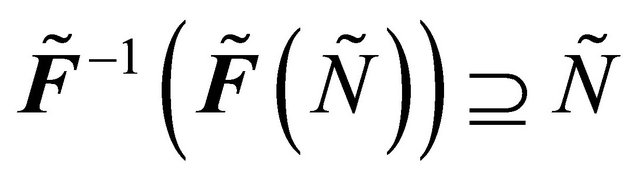 , for each
, for each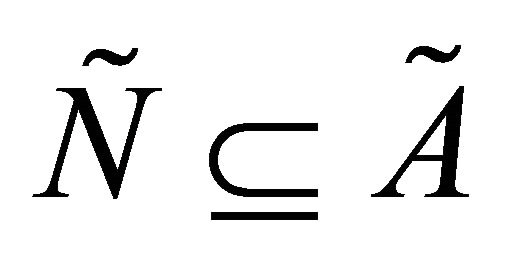 .
.
3) 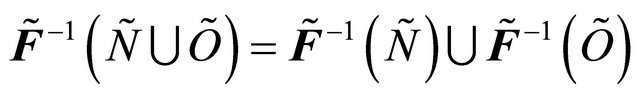 and
and
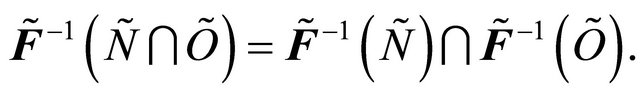
Definition 3.5. [2]  is said to maximal if for each
is said to maximal if for each 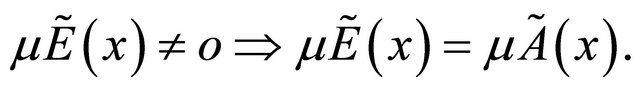
Proposition 3.6. [2] If 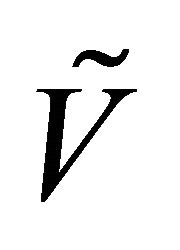 is a maximal fuzzy subset of
is a maximal fuzzy subset of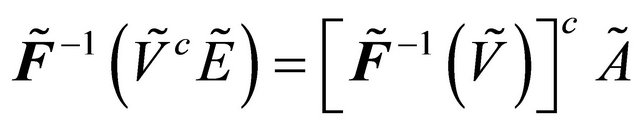 .
.
Definition 3.7. [2] Let 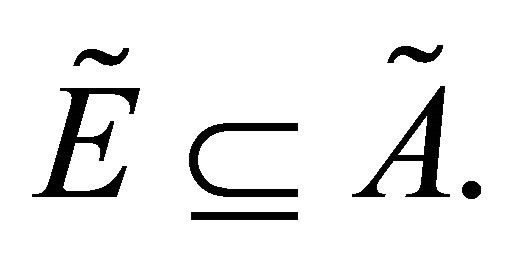 Then
Then 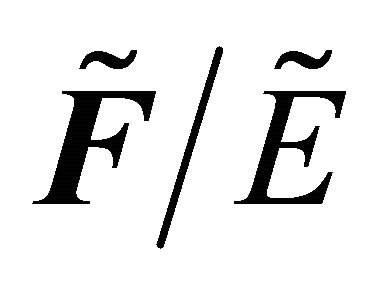 defined by
defined by
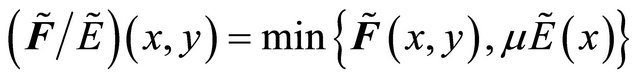 for each
for each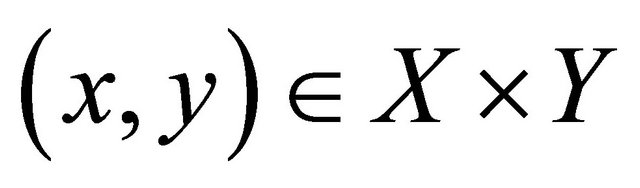 , is said to be the restriction of
, is said to be the restriction of  to
to .
.
Proposition 3.8. [2] If 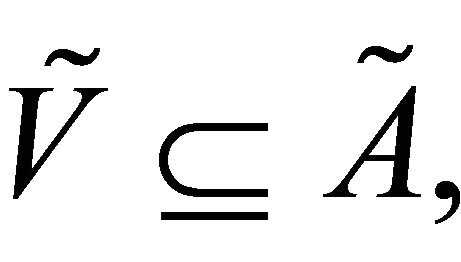 then for each
then for each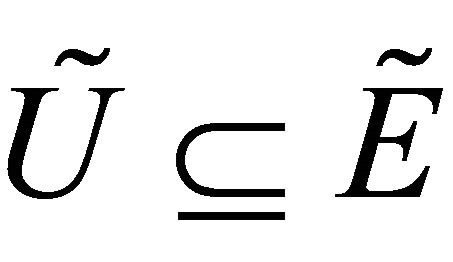 ,
, .
.
Definition 3.9. [1] A collection  of fuzzy subsets of a fuzzy set
of fuzzy subsets of a fuzzy set  is said to be a fuzzy topology on
is said to be a fuzzy topology on  if 1)
if 1) .
.
2)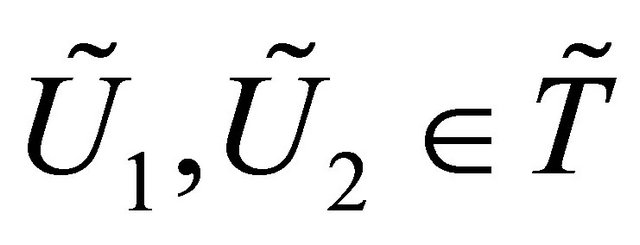 , then
, then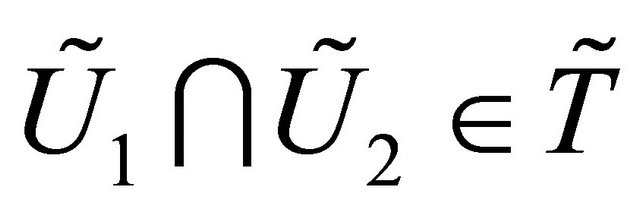 .
.
3) 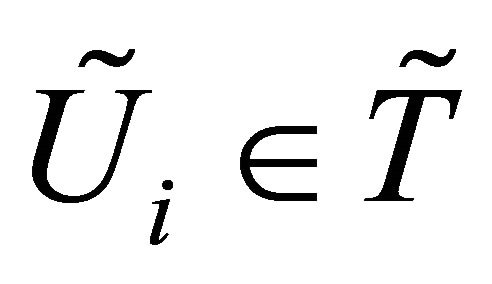 for each
for each , then
, then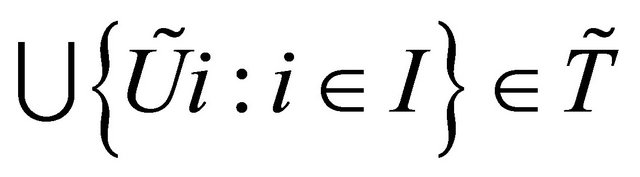 .
.
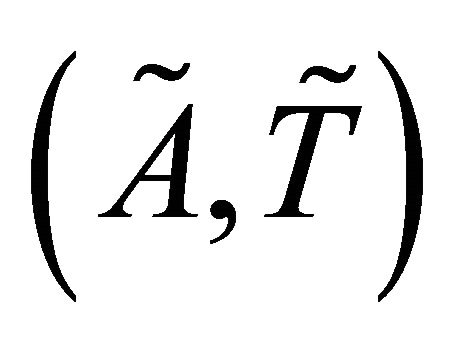 is said to be a fuzzy topological space (fts, for short). The members of
is said to be a fuzzy topological space (fts, for short). The members of  are called fuzzy open sets in
are called fuzzy open sets in . The complement of the members of
. The complement of the members of  referred to
referred to  are called the fuzzy closed sets in
are called the fuzzy closed sets in . The family of all fuzzy closed sets in
. The family of all fuzzy closed sets in  will be denoted by
will be denoted by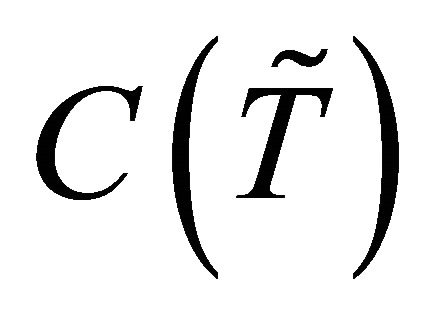 .
.
Definition 3.10. [1] If ,
, 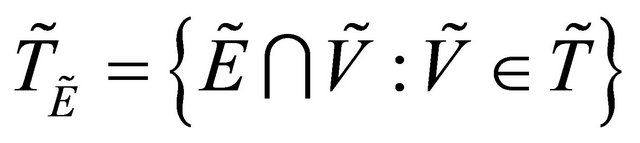
is a fuzzy topology on ,
,  is called a subspace of
is called a subspace of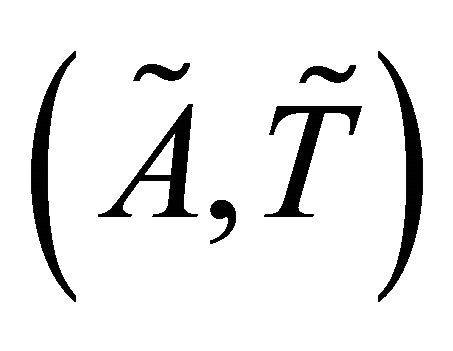 .
.
Definition 3.11. [1] Let 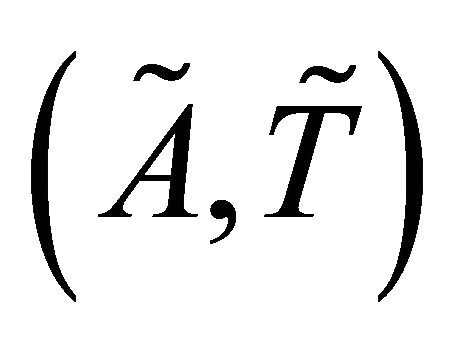 be a fts and
be a fts and  then the closure of
then the closure of  denoted by
denoted by 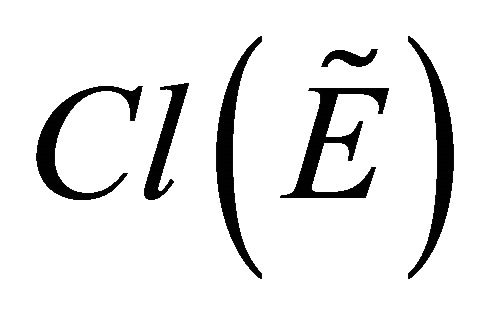 is defined by
is defined by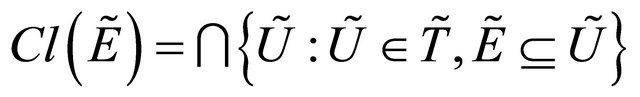 . i.e.
. i.e. 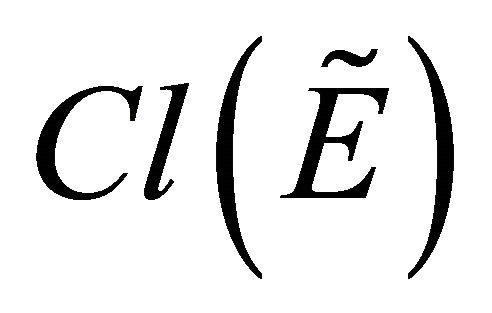 is the intersection of all closed fuzzy subsets of
is the intersection of all closed fuzzy subsets of  containing
containing .
.
Definition 3.12. [3] Let  be a fts and
be a fts and 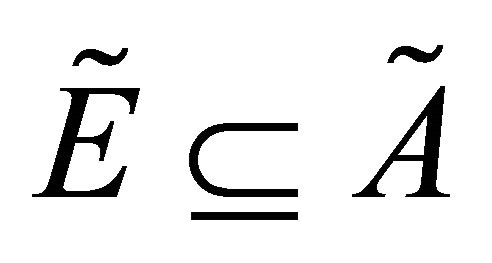 then the interior of
then the interior of  denoted by
denoted by
 . i.e.
. i.e.  is the union of all open fuzzy subsets of
is the union of all open fuzzy subsets of  which contained in
which contained in .
.
Definition 3.13. [1] Let 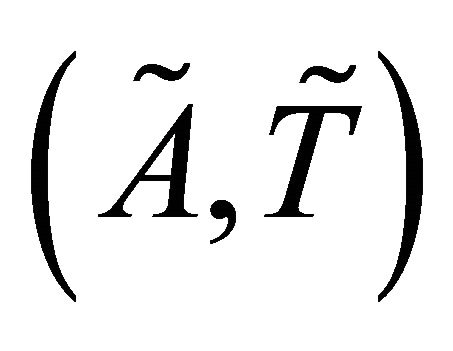 be a fts, a fuzzy subset
be a fts, a fuzzy subset  of
of  is called 1) Neighbourhood (nbd, for short) of the fuzzy point
is called 1) Neighbourhood (nbd, for short) of the fuzzy point 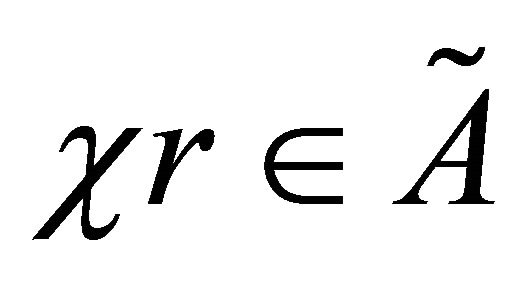 if there exists
if there exists 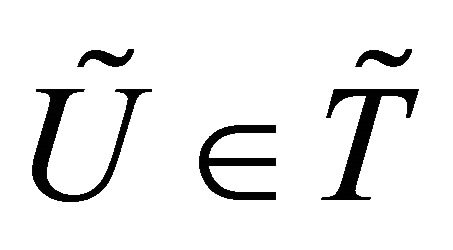 such that
such that 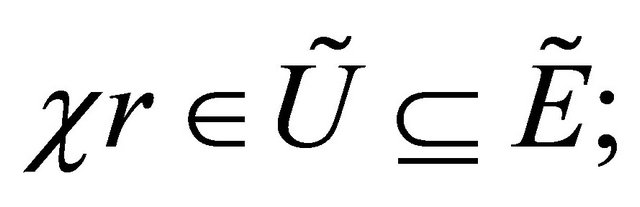 2) Quasi-neighbourhood (q-nbd, for short) of the fuzzy point
2) Quasi-neighbourhood (q-nbd, for short) of the fuzzy point 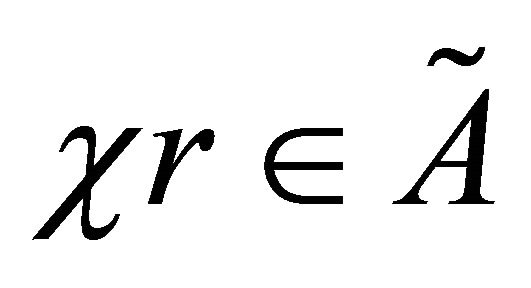 if there exists
if there exists 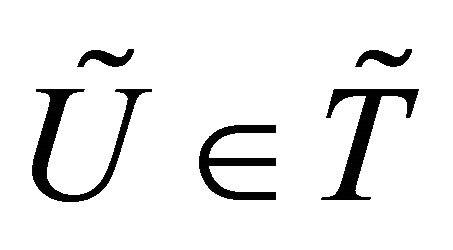 such that
such that
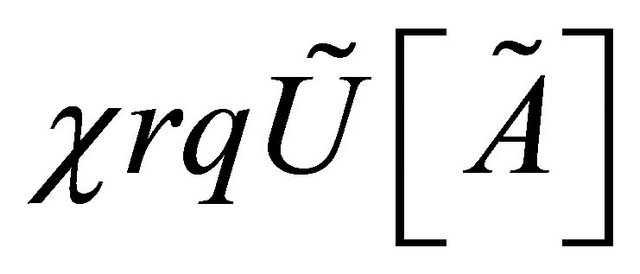 ,
,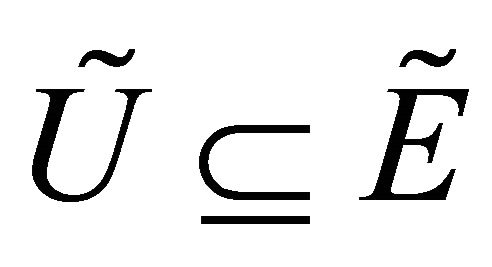 .
.
The set  of all q-neighbourhood of
of all q-neighbourhood of 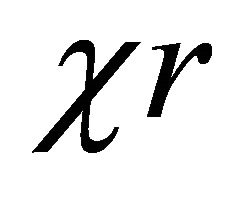 is called the system of q-nbd of
is called the system of q-nbd of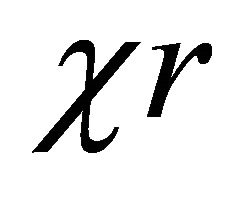 .
.
Proposition 3.14. [2] If 
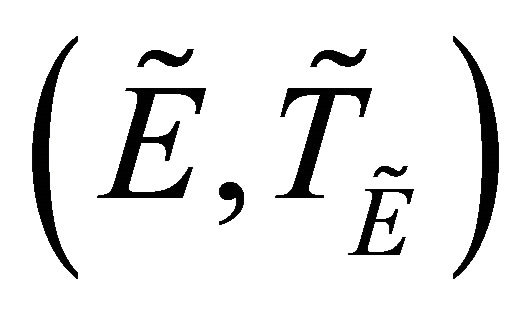 is a maximal subspace of
is a maximal subspace of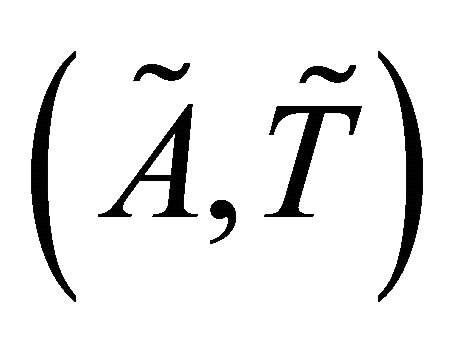 , then
, then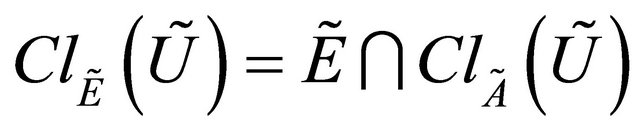 , where
, where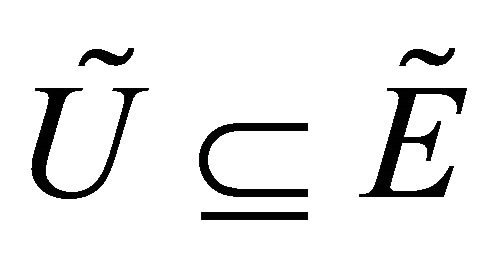 .
.
Definition 3.15. [3]
1)  is said to be a fuzzy regular open set in a fts
is said to be a fuzzy regular open set in a fts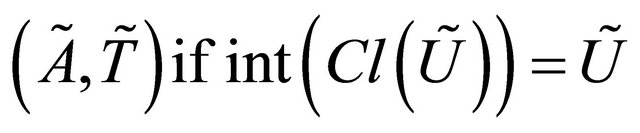 .
.
2) 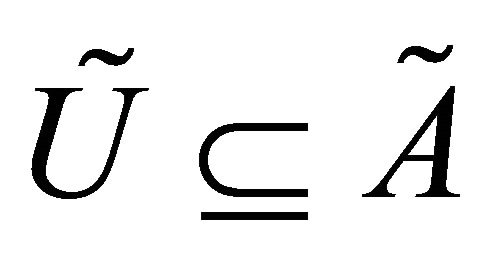 is said to be a fuzzy regular closed set in a fts
is said to be a fuzzy regular closed set in a fts  if
if 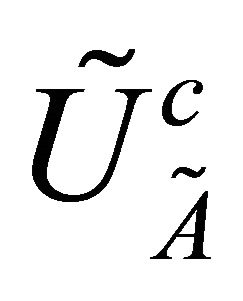 is fuzzy regular open.
is fuzzy regular open.
Definition 3.16. [3] A fuzzy point  is said to be a fuzzy δ-cluster (resp. θ-cluster) point of a fuzzy subset
is said to be a fuzzy δ-cluster (resp. θ-cluster) point of a fuzzy subset 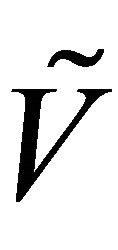 of
of  if for each fuzzy regularly open (resp. fuzzy open) q-nbd of
if for each fuzzy regularly open (resp. fuzzy open) q-nbd of 
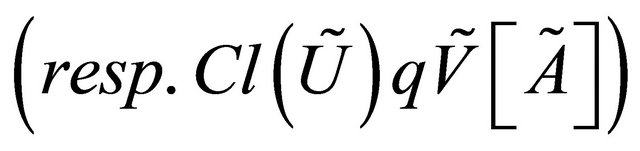 . The set of all fuzzy
. The set of all fuzzy  -cluster
-cluster
(resp. fuzzy θ-cluster) points of 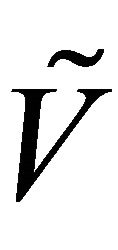 is called fuzzy
is called fuzzy  - cluster (resp. fuzzy θ-closure) and is denoted by
- cluster (resp. fuzzy θ-closure) and is denoted by
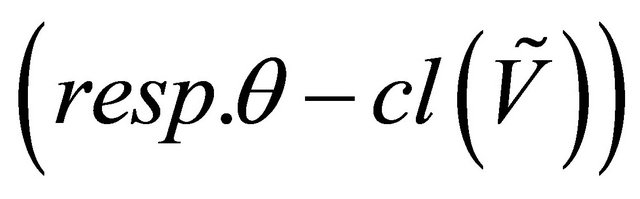
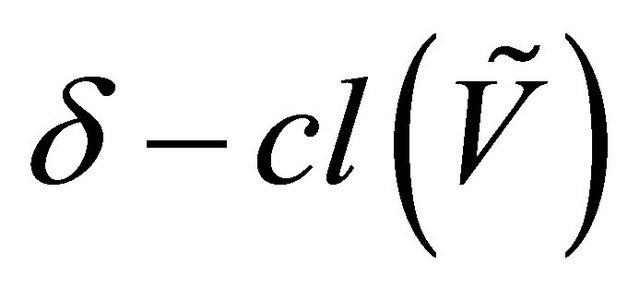 . A fuzzy subset
. A fuzzy subset  is called a fuzzy δ-closed (resp. θ-closed) if
is called a fuzzy δ-closed (resp. θ-closed) if 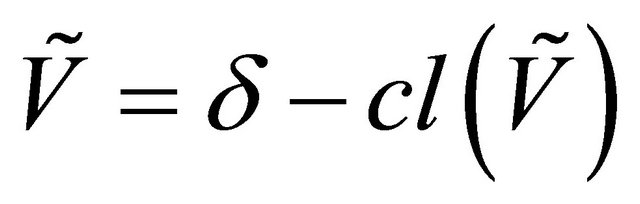 (resp.
(resp.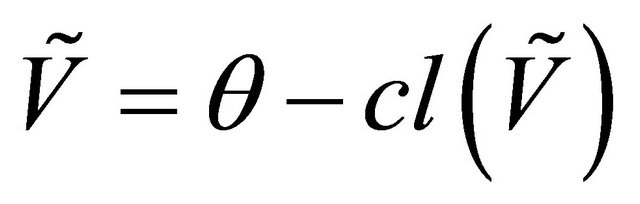 ) and the complement of a fuzzy δ-closed (resp. θ-closed) set is called fuzzy δ-open (resp. θ-open).
) and the complement of a fuzzy δ-closed (resp. θ-closed) set is called fuzzy δ-open (resp. θ-open).
Remark 3.17. [3] It is clear that fuzzy regular open (fuzzy regular closed) implies fuzzy δ-open (fuzzy δ- closed) implies fuzzy open (fuzzy closed) but the converses are not true in general.
In this paper, the family of all fuzzy regular open (resp. fuzzy regular closed, fuzzy δ-open, fuzzy δ-closed, fuzzy open, fuzzy closed) sets in  will be denoted by
will be denoted by


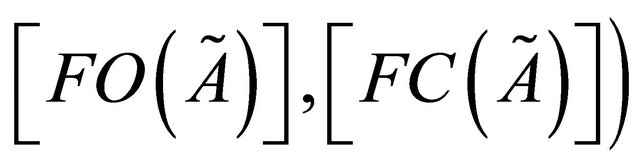 .
.
4. Fuzzy δ*-Continuity
Unless otherwise mentioned 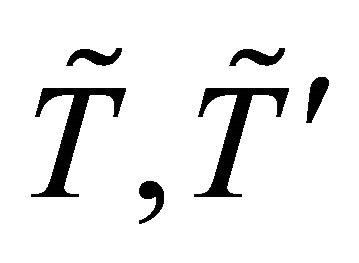 are two fuzzy topologies on
are two fuzzy topologies on ,
,  respectively, and
respectively, and  a proper function from
a proper function from  to
to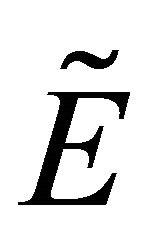 .
.
Definition 4.1. A proper function
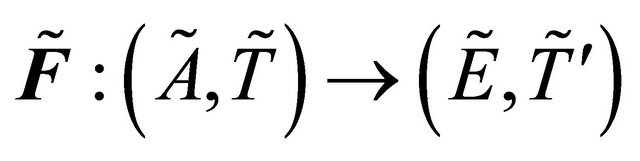 is called fuzzy
is called fuzzy  -continuous if
-continuous if
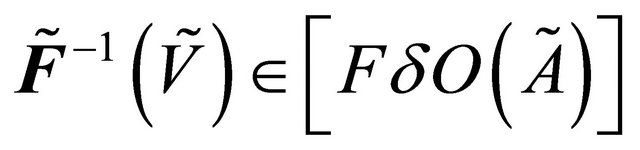 for each
for each .
.
Example 4.2. Let
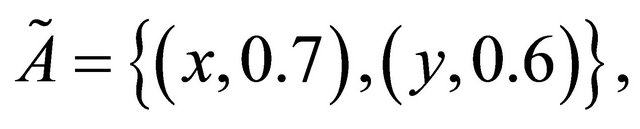


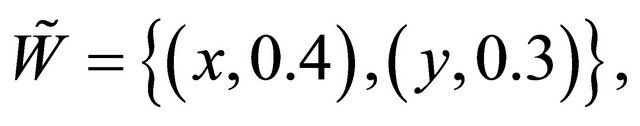
and
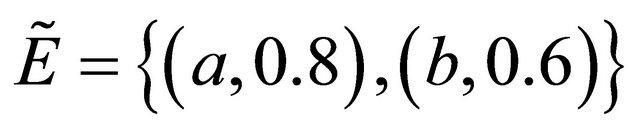 ,
,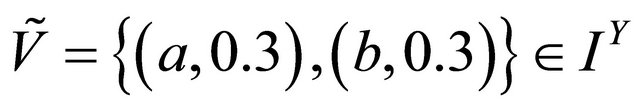 .
.
Consider the fuzzy topologies on ,
, 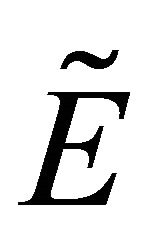 resp.
resp.
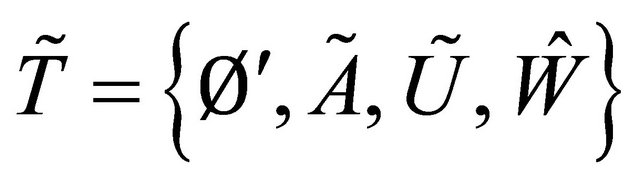 and
and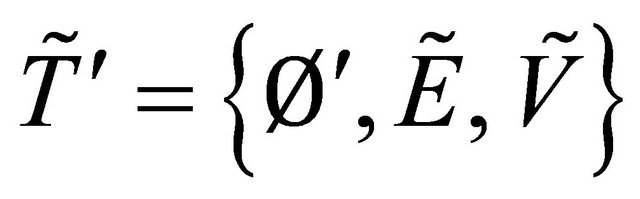 . Let the proper function
. Let the proper function 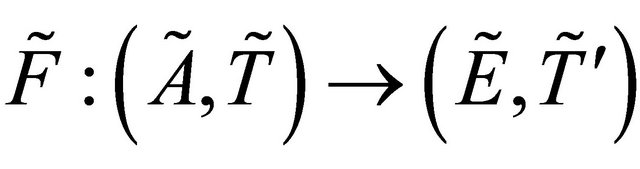 defined by
defined by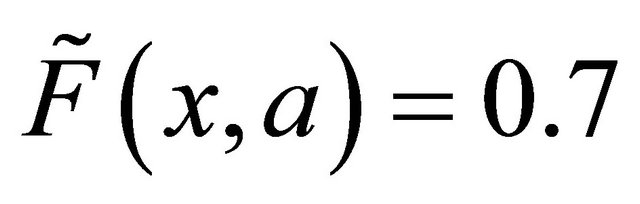 ,
,
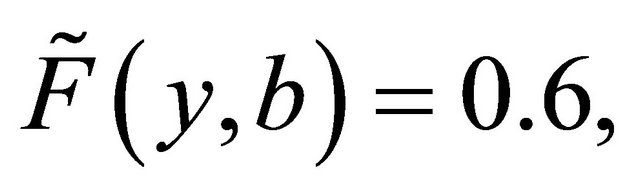
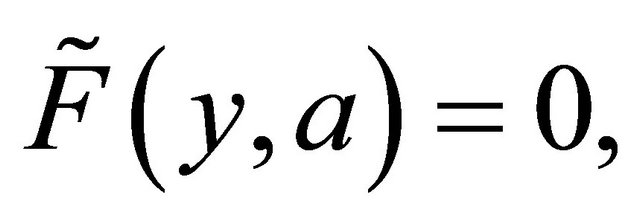
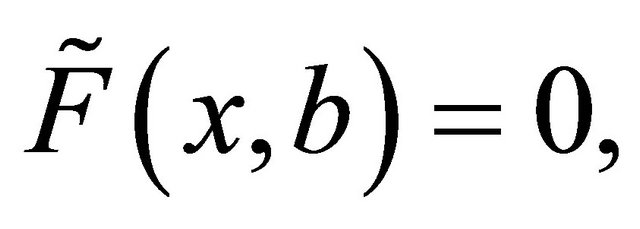 one may notice that the only fuzzy open sets in
one may notice that the only fuzzy open sets in 
 are
are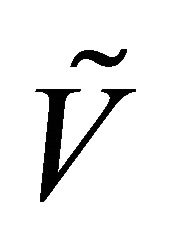 ,
,  and
and 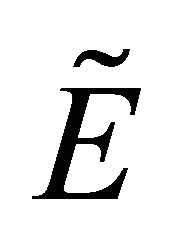 but
but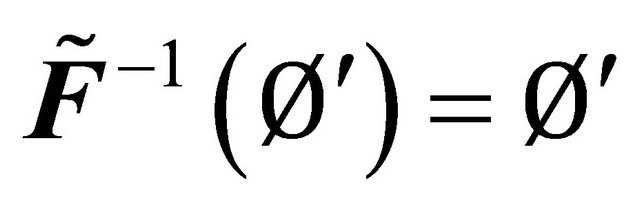 ,
,  ,
,  and
and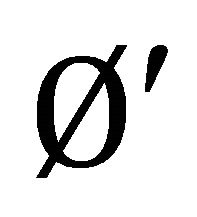 ,
,  ,
, . Hence
. Hence  is fuzzy δ*- continuous.
is fuzzy δ*- continuous.
Theorem 4.3. If 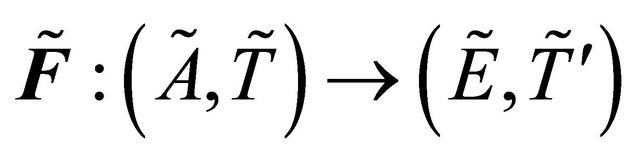 be fuzzy δ*- continuous and
be fuzzy δ*- continuous and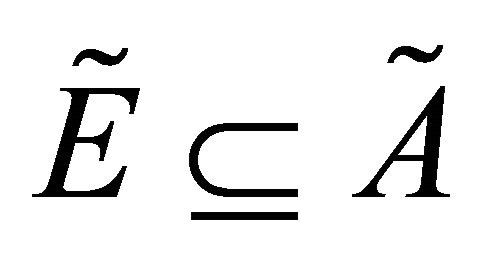 , then
, then
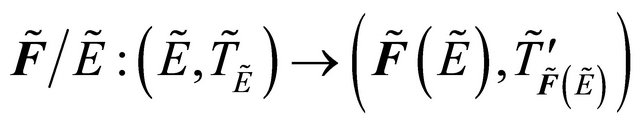
is fuzzy δ*-continuous .
Proof: Let 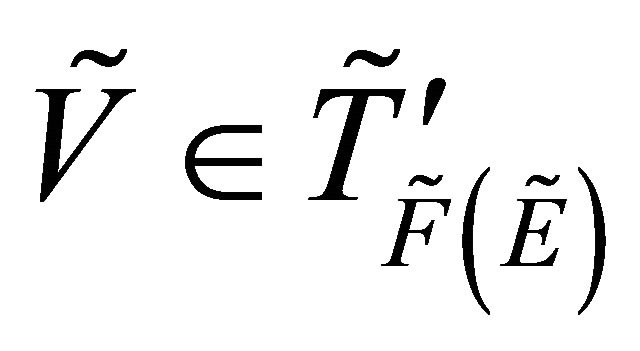 such that
such that
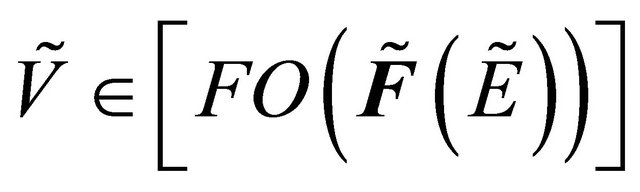 .
.
Then there exists fuzzy open 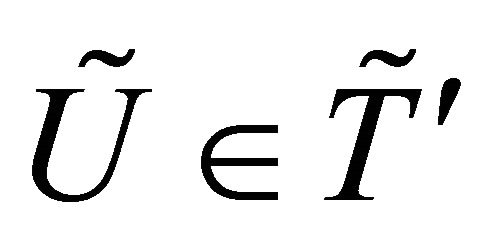 such that
such that 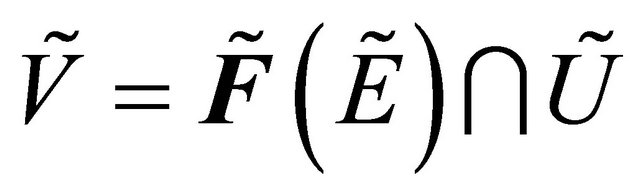 .
.
Now
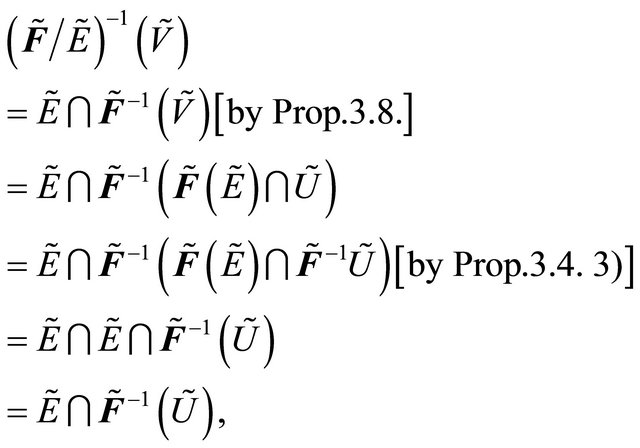
but  be fuzzy δ*-continuous such that
be fuzzy δ*-continuous such that 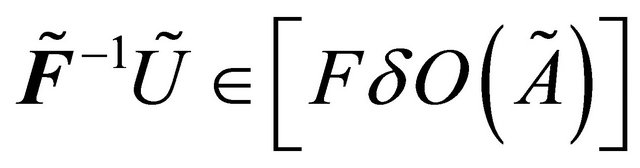 . Therefore
. Therefore
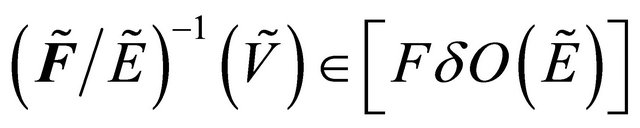 .
.
Hence  is fuzzy δ*-continuous.
is fuzzy δ*-continuous.
Definition 4.4. [2] 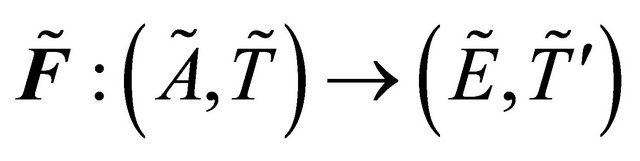 is said to satisfy property
is said to satisfy property  if
if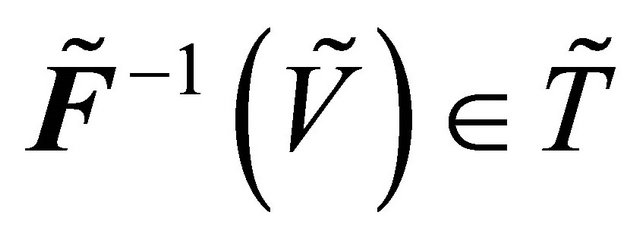 , for each
, for each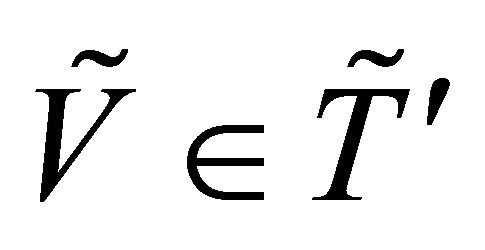 .
.
Henceforth such functions will be called fuzzy continuous proper function.
Theorem 4.5. If a proper function  is fuzzy δ*-continuous then, it is fuzzy continuous.
is fuzzy δ*-continuous then, it is fuzzy continuous.
Proof: Let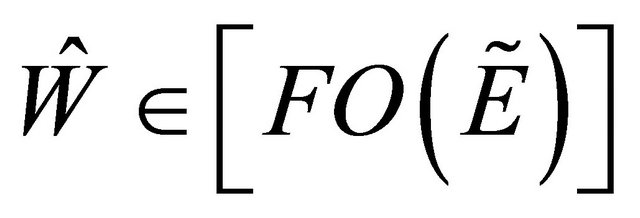 , but
, but  is fuzzy δ*-continuous. Hence
is fuzzy δ*-continuous. Hence 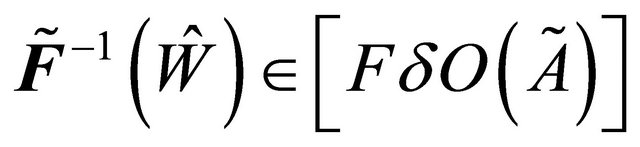 and by (Remark (3.17)) every fuzzy δ-open implies fuzzy open. (i.e.
and by (Remark (3.17)) every fuzzy δ-open implies fuzzy open. (i.e.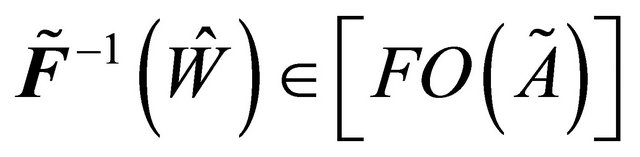 ). Hence
). Hence  is fuzzy continuous.
is fuzzy continuous.
We can see from Example (4.2) such that
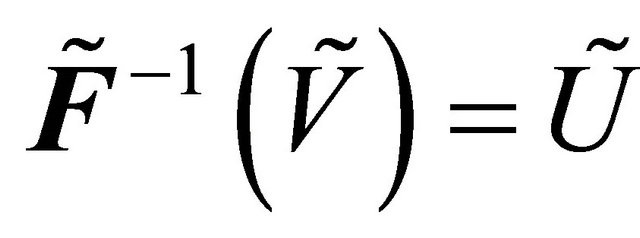
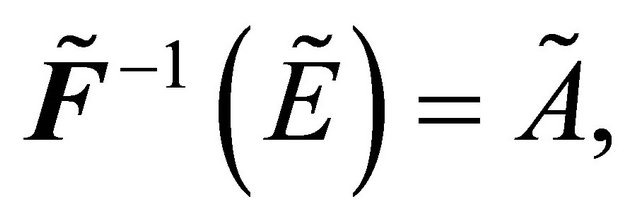
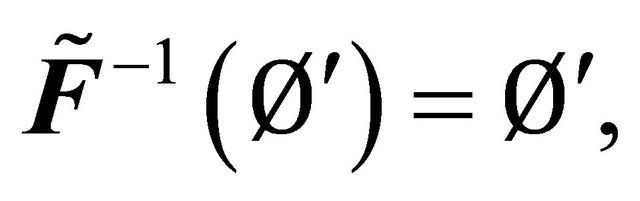 and
and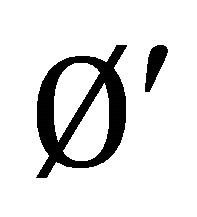 ,
,  ,
,
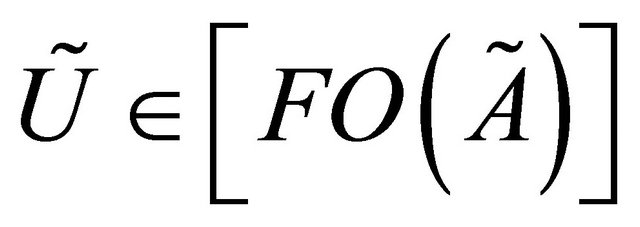 but
but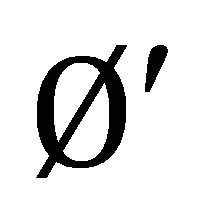 ,
, 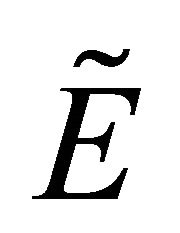 ,
,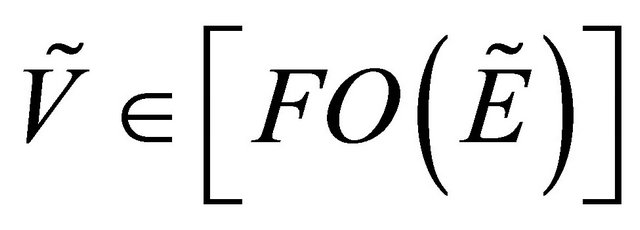 .
.
Definition 4.6. [3] A proper function  is called fuzzy δ-continuous if
is called fuzzy δ-continuous if
 for each
for each .
.
Remark 4.7. [3] The concepts of fuzzy δ-continuous and fuzzy continuous are independent to each other .
Theorem 4.8. If  be fuzzy δ- continuous and
be fuzzy δ- continuous and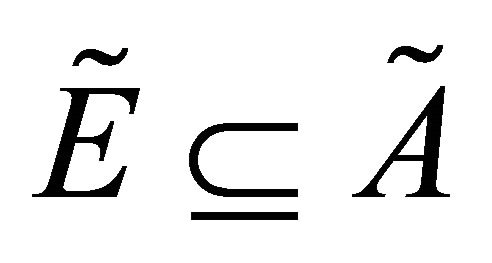 , then
, then
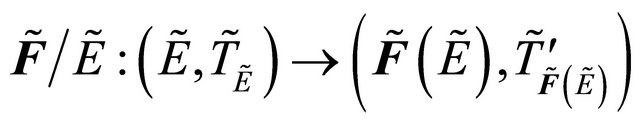 is fuzzy δ-continuous.
is fuzzy δ-continuous.
Proof: Let 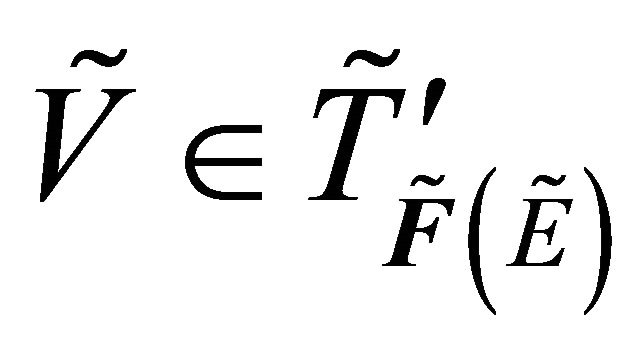 such that
such that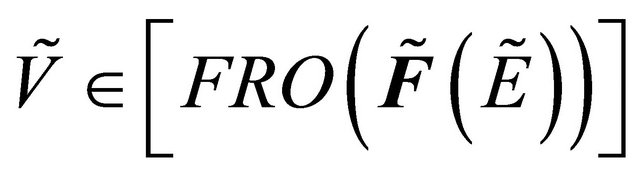 .
. 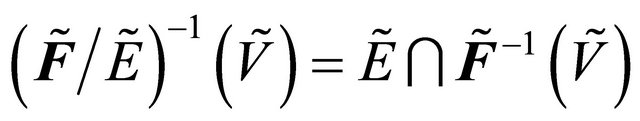 [by Prop. 3.8]. But
[by Prop. 3.8]. But  is fuzzy δ-continuous such that
is fuzzy δ-continuous such that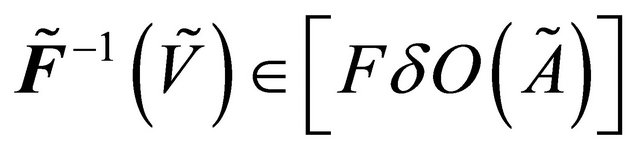 . Therefore
. Therefore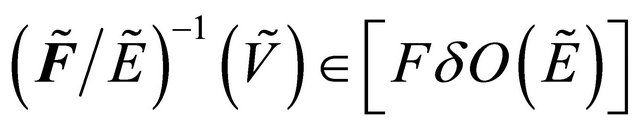 . Hence
. Hence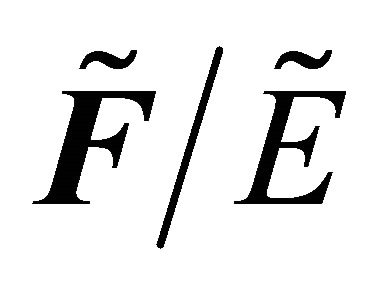 is fuzzy δ-continuous.
is fuzzy δ-continuous.
Theorem 4.9. If a proper function 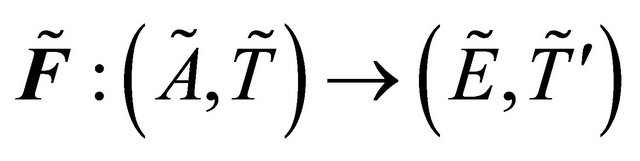 is fuzzy δ*-continuous, then it is fuzzy δ-continuous.
is fuzzy δ*-continuous, then it is fuzzy δ-continuous.
Proof: Let . And by Remark 3.17 every fuzzy regular open implies fuzzy δ-open implies fuzzy open. (i.e.
. And by Remark 3.17 every fuzzy regular open implies fuzzy δ-open implies fuzzy open. (i.e. 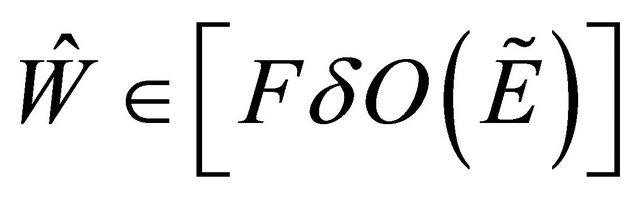 and
and  but
but  is fuzzy δ*-continuous). Hence
is fuzzy δ*-continuous). Hence 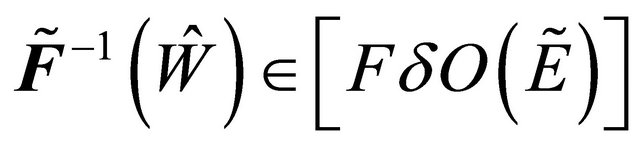 . Therefore
. Therefore  is fuzzy δ-continuous.
is fuzzy δ-continuous.
5. Fuzzy δ**-Continuity
Definition 5.1. A proper function 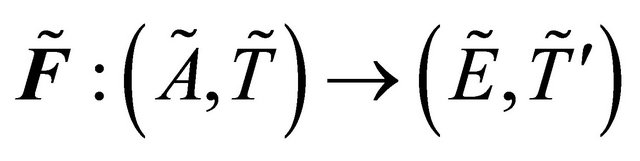 is called fuzzy
is called fuzzy  -continuous if
-continuous if  for each
for each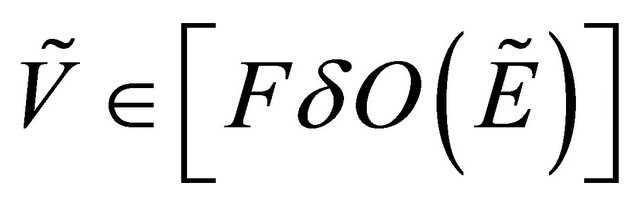 .
.
Example 5.2. Let
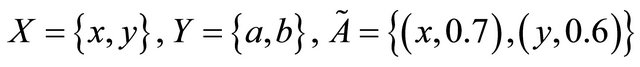

and
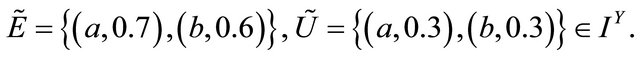
Consider the fuzzy topologies on  and
and  resp.
resp. 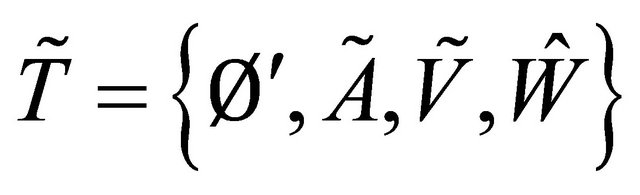 and
and . Let the proper function
. Let the proper function 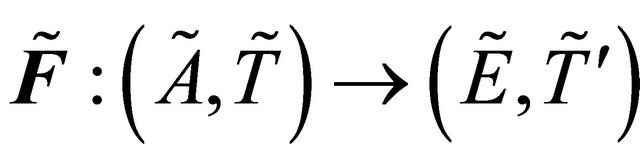 defined by
defined by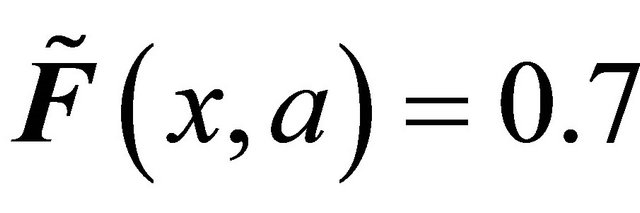

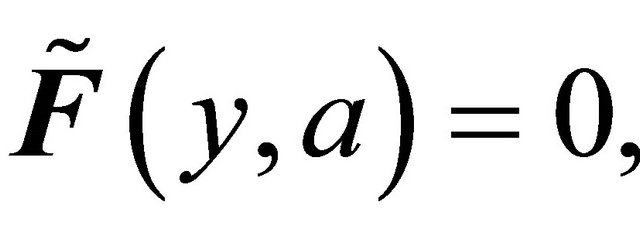
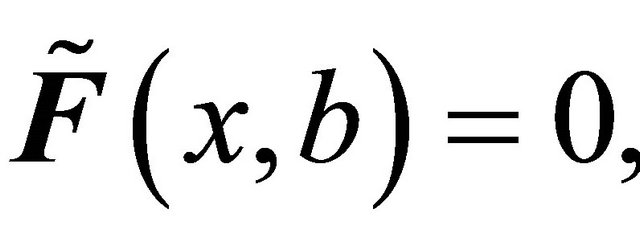 . One may notice that the only fuzzy δ-open sets in
. One may notice that the only fuzzy δ-open sets in 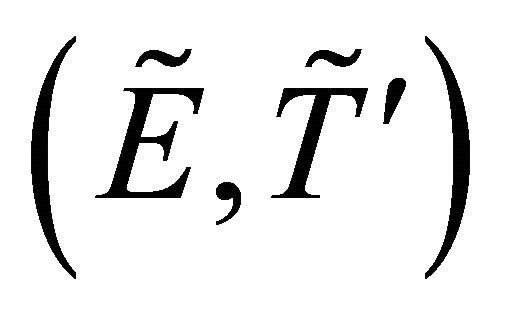 are
are ,
, 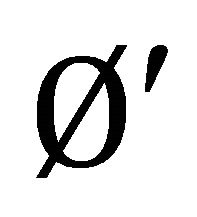 and
and  and
and


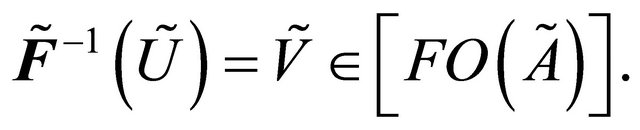
Hence  is fuzzy δ**-continuous.
is fuzzy δ**-continuous.
Theorem 5.3. If 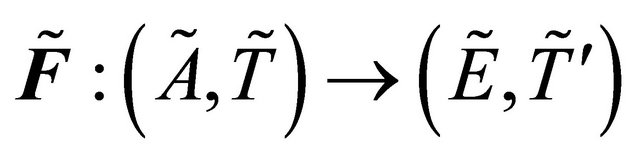 be fuzzy δ**- continuous and
be fuzzy δ**- continuous and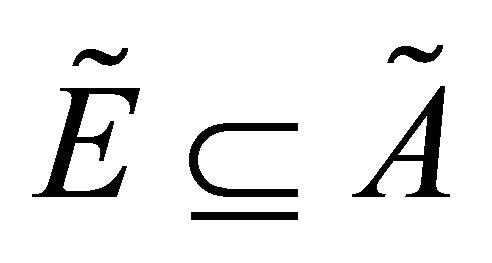 , then
, then
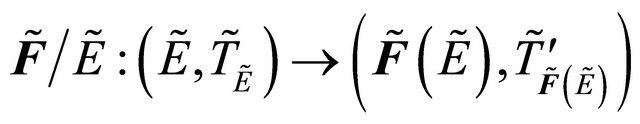 is fuzzy δ**-continuous.
is fuzzy δ**-continuous.
Proof: Let  such that
such that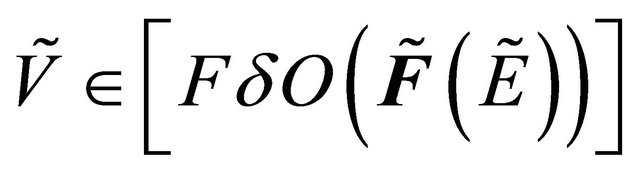 .
.
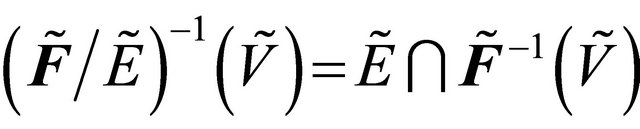 [by Prop. 3.8]. But
[by Prop. 3.8]. But 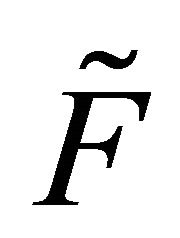 is fuzzy δ**-continuous such that
is fuzzy δ**-continuous such that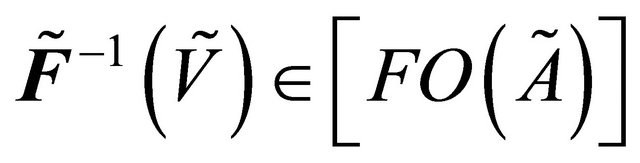 . Therefore
. Therefore 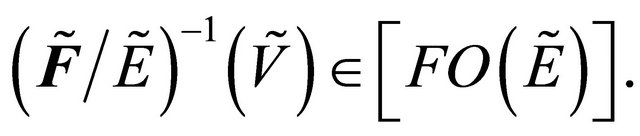 Hence
Hence 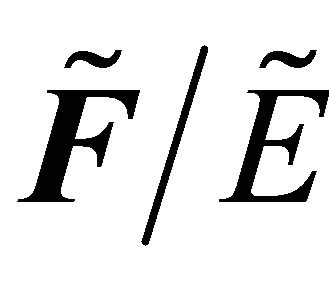 is fuzzy δ**-continuous.
is fuzzy δ**-continuous.
Theorem 5.4. If a proper function 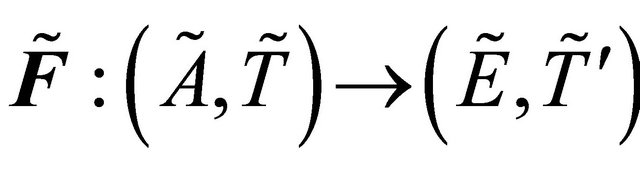 is fuzzy δ-continuous, then it is fuzzy δ**-continuous.
is fuzzy δ-continuous, then it is fuzzy δ**-continuous.
Proof: Let  and (by Remark 3.17 every fuzzy regular open implies fuzzy δ-open), i.e.
and (by Remark 3.17 every fuzzy regular open implies fuzzy δ-open), i.e.
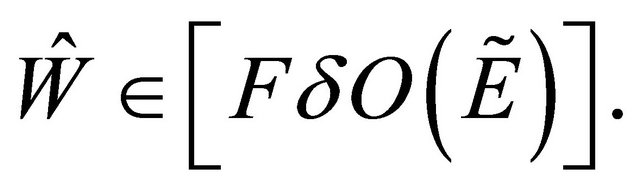 But
But  is fuzzy δ-continuous. Hence
is fuzzy δ-continuous. Hence
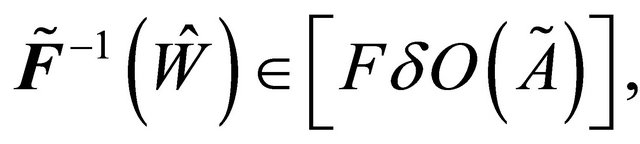 and (by Remark 3.17 every fuzzy δ-open implies fuzzy open). Therefore,
and (by Remark 3.17 every fuzzy δ-open implies fuzzy open). Therefore, 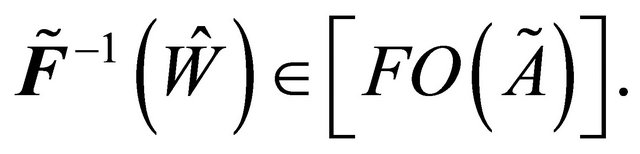 (i.e.
(i.e.  is fuzzy δ**-continuous).
is fuzzy δ**-continuous).
Theorem 5.5. If a proper function 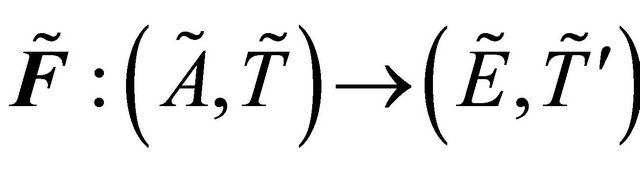 is fuzzy continuous, then it is fuzzy δ**-continuous.
is fuzzy continuous, then it is fuzzy δ**-continuous.
Proof: Let 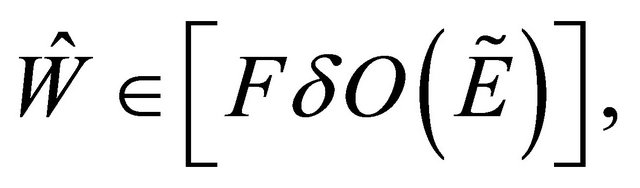 and (by Remark 3.17 every fuzzy δ-open implies fuzzy open), i.e.
and (by Remark 3.17 every fuzzy δ-open implies fuzzy open), i.e.
 But
But  is fuzzy continuous. Hence
is fuzzy continuous. Hence 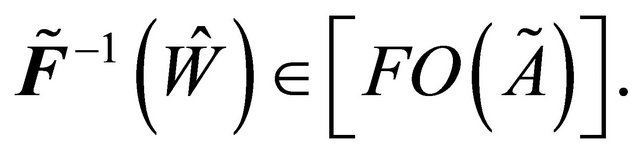 Therefore
Therefore  is fuzzy δ**-continuous.
is fuzzy δ**-continuous.
We can see from Example (5.2.).
Remark 5.6. It is clear that not every fuzzy δ**-continuous may be fuzzy δ*-continuous and we can see from example.
Example 5.7. Let
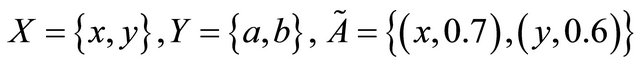
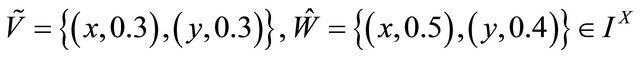
and
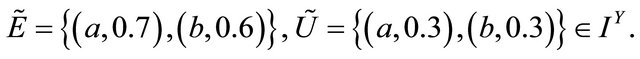
Consider the fuzzy topologies on  and
and  resp.
resp.
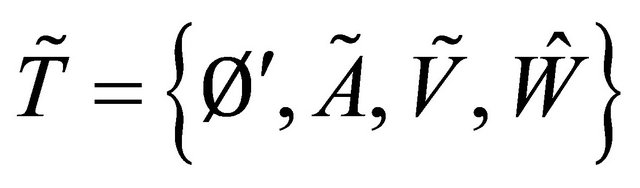 and
and . Let the proper function
. Let the proper function  defined by
defined by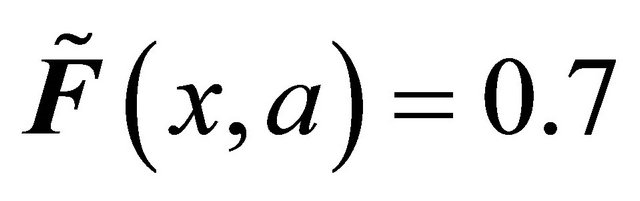 ,
, 
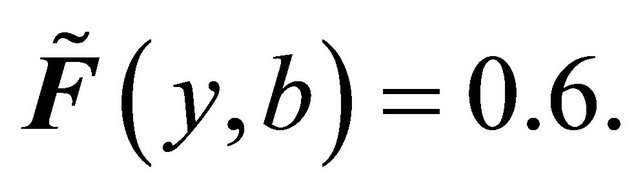
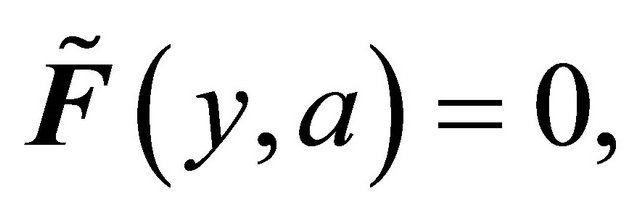
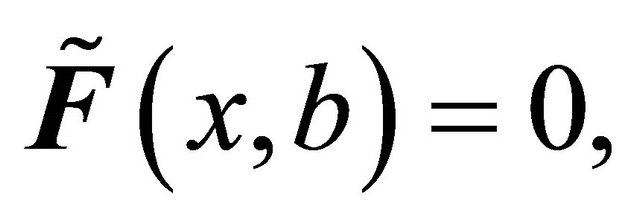 is fuzzy δ**-continuous but not fuzzy δ*-continuous such that the only fuzzy δ-open sets in
is fuzzy δ**-continuous but not fuzzy δ*-continuous such that the only fuzzy δ-open sets in 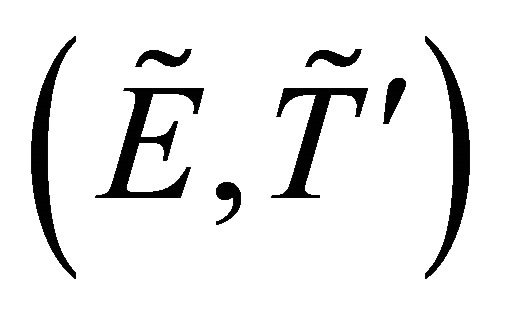 are
are ,
, 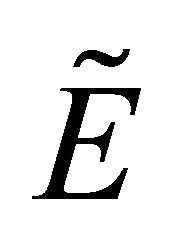 and
and 
but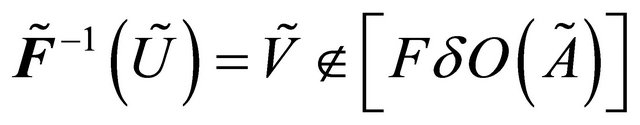 .
.
From what we have deduced so far, we now obtain:
Fuzzy continuous ® Fuzzy δ**-continuous;
Fuzzy δ-continuous ® Fuzzy δ**-continuous;
Fuzzy δ*-continuous ® Fuzzy continuous;
Fuzzy δ*-continuous ® Fuzzy δ-continuous.
6. Conclusion
The main purpose of this paper introduces a new concept in fuzzy set theory, namely that of a fuzzy δ*-continuity and fuzzy δ**-continuity. On the other hand, fuzzy topology on a fuzzy set is a kind of abstract theory of mathematics. First, we present and study fuzzy δ*-continuity and fuzzy δ**-continuity from a fuzzy topological space on a fuzzy set into another. Then, we present the relationships between types of fuzzy continuous functions.
7. Acknowledgements
The author is thankful to the referee for his valuable suggestions.
REFERENCES
- M. K. Chakraborty and T. M. G. Ahsanullah, “Fuzzy Topology on Fuzzy Sets and Tolerance Topology,” Fuzzy Set and Systems, Vol. 45, No. 1, 1990, pp. 103-108. doi:10.1016/0165-0114(92)90096-M
- A. K. Chaudhari and P. Das, “Some Results on Fuzzy Topology on Fuzzy Sets,” Fuzzy Set and Systems, Vol. 56, No. 3, 1993, pp. 331-336. doi:10.1016/0165-0114(93)90214-3
- A. M. Zahran, “Fuzzy δ-Continuous, Fuzzy almost Regularity (Normality) on Fuzzy Topology No Fuzzy Sets,” Fuzzy Mathematics, Vol. 3, No. 1, 1995, pp. 89-96.
- M. K. Chakraborty and S. Sarkar, “On Fuzzy Functions, Homorelations, Homomophisms etc.,” IFSAEURO Proceeding, Warsaw, 1986.
- M. K. Chakraborty, S. Sarkar and M. Das, “Some Aspects of [0,1]—Fuzzy Relation and a Few Suggestions towards Its Use,” In: Gupta, et al., Eds., Approximate Reasoning in Expert Systems, North-Holland, Amsterdam, 1985, pp. 156-159.

