Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:25018,5 pages DOI:10.4236/apm.2012.26070
Some Properties on the Error-Sum Function of Alternating Sylvester Series
Science College of Hunan Agricultural University, Changsha, China
Email: Huiping_J@126.com, *lum_s@126.com
Received July 11, 2012; revised September 21, 2012; accepted September 29, 2012
Keywords: Alternating Sylvester Series; Error-Sum Function; Hausdorff Dimension
ABSTRACT
The error-sum function of alternating Sylvester series is introduced. Some elementary properties of this function are studied. Also, the hausdorff dimension of the graph of such function is determined.
1. Introduction
For any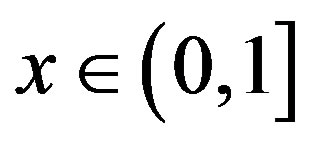 , let
, let 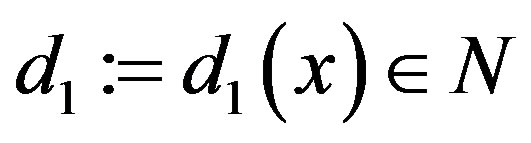 and
and 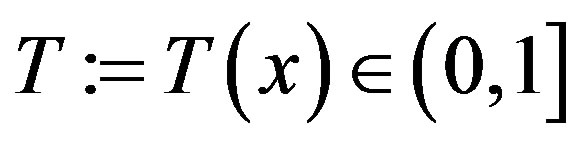 be defined as
be defined as
 (1)
(1)
where  denote the integer part. And we define the sequence
denote the integer part. And we define the sequence 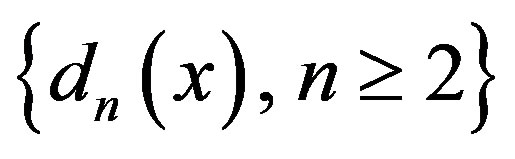 as follows:
as follows:
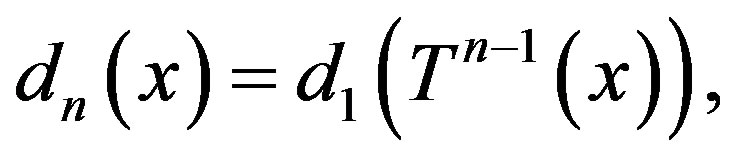 (2)
(2)
where 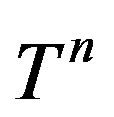 denotes the nth iterate of
denotes the nth iterate of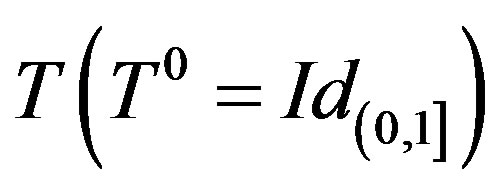 .
.
It is well known that from the algorithm (1), all 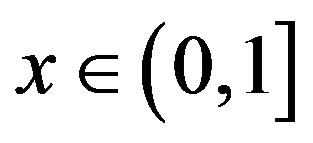 can be developped uniquely into an infinite or finite series
can be developped uniquely into an infinite or finite series
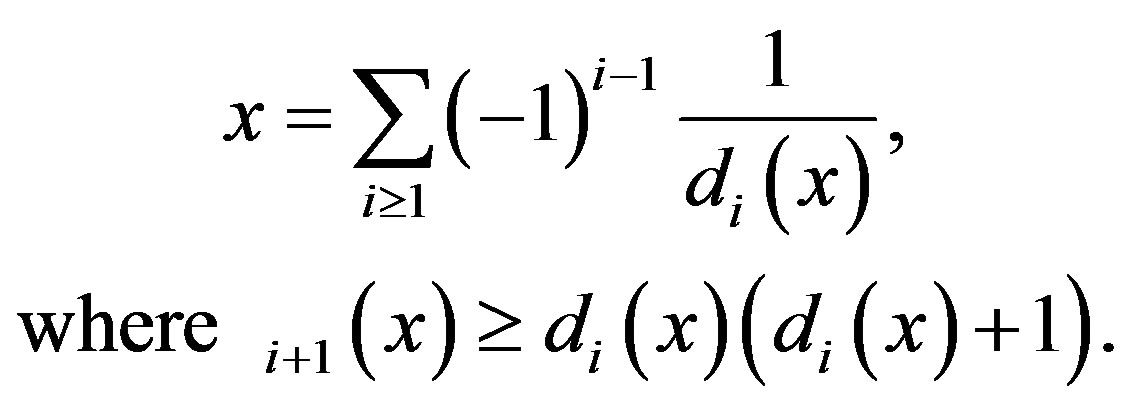 (3)
(3)
In the literature [2], (3) is called the Alternating Balkema-Oppenheim expansion of x and denoted by 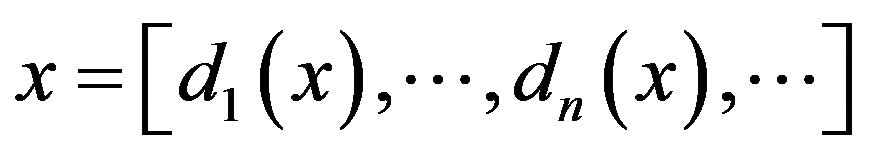 for short. From the algorithm, one can see that T maps irrational element into irrational element, and the series is infinite. While for rational numbers, in fact, we have
for short. From the algorithm, one can see that T maps irrational element into irrational element, and the series is infinite. While for rational numbers, in fact, we have 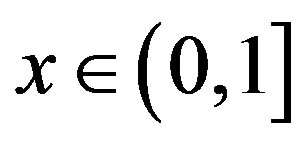 is rational if and only if its sequence of digits
is rational if and only if its sequence of digits 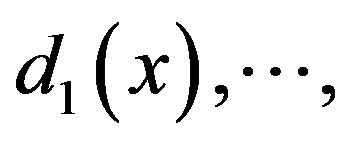 is terminate or periodic, see [1-3].
is terminate or periodic, see [1-3].
For any 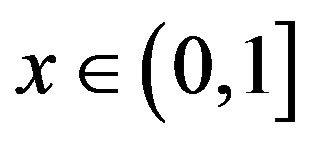 and
and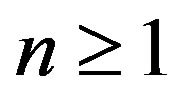 , define
, define
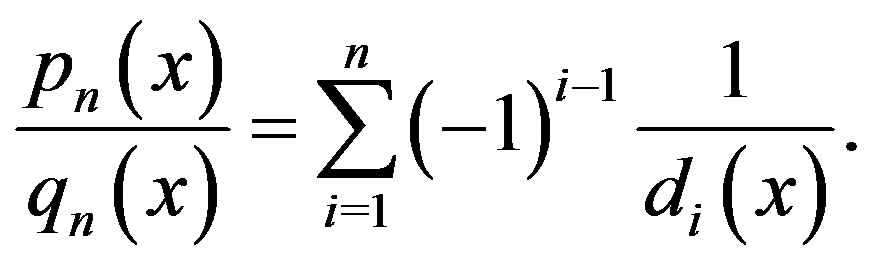
From the algorithm of (1), it is clear that
 (4)
(4)
For any , let
, let 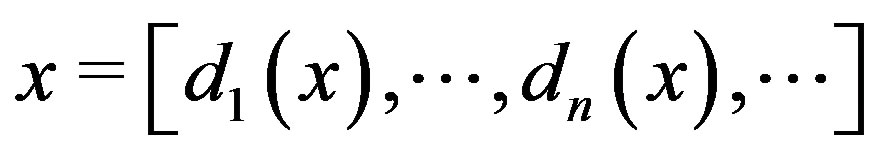 be its Alternating Sylvester expansion, then we have
be its Alternating Sylvester expansion, then we have
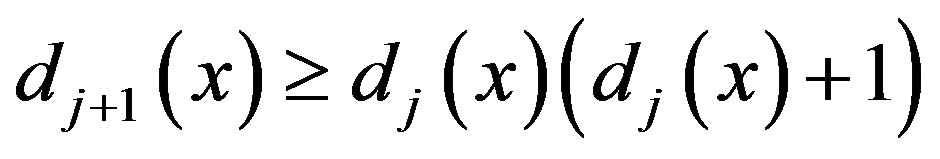 for any
for any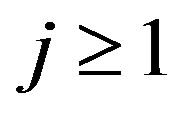 . On the other hand, any
. On the other hand, any  of integer sequence satisfying
of integer sequence satisfying
 for all
for all 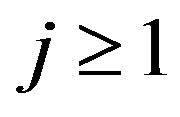 is a Sylvester admissible sequence, that is, there exists a unique
is a Sylvester admissible sequence, that is, there exists a unique 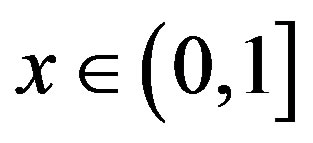 such that
such that 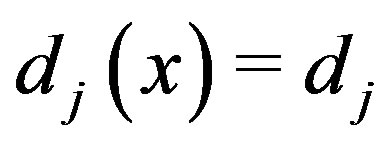 for all
for all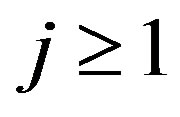 , see [9].
, see [9].
The behaviors of the sequence 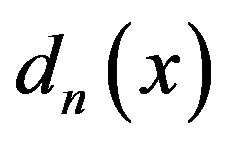 are of interest and the metric and ergodic properties of the sequence
are of interest and the metric and ergodic properties of the sequence 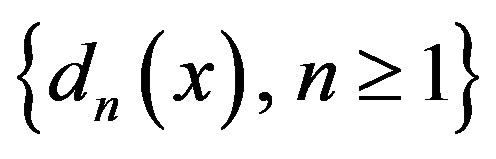 and
and 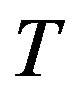 have been investigated by a number of authors, see [1-3].
have been investigated by a number of authors, see [1-3].
For any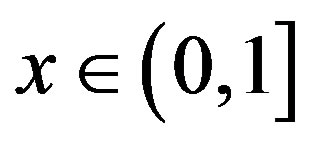 , define
, define
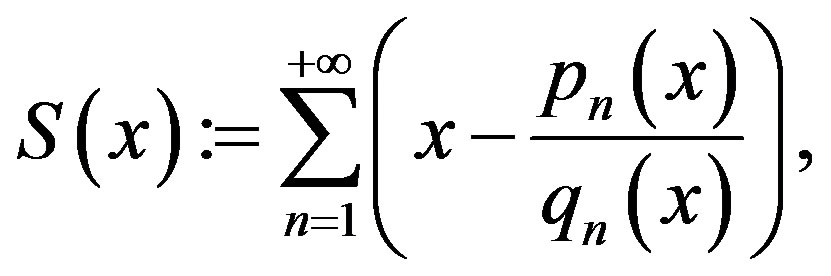 (5)
(5)
and we call 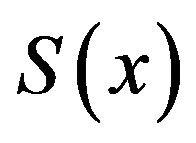 the error-sum function of Alternating Sylvester series. By (4), since
the error-sum function of Alternating Sylvester series. By (4), since  for all
for all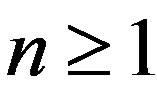 , then
, then 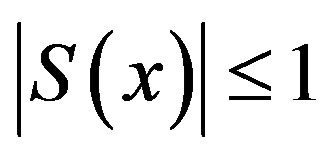 and
and 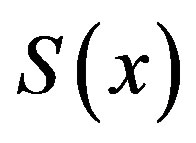 is well defined. In this paper, we shall discuss some basic nature of
is well defined. In this paper, we shall discuss some basic nature of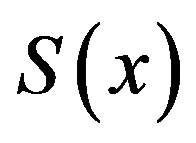 , also the Hausdorff dimension of the graph of
, also the Hausdorff dimension of the graph of 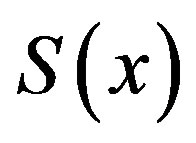 is determined.
is determined.
2. Some Basic Properties of 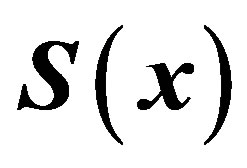
In what follows, we shall often make use of the symbolic space.
For any , let
, let

Define
For any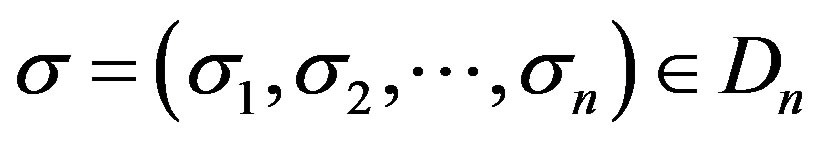 , write
, write
 (6)
(6)
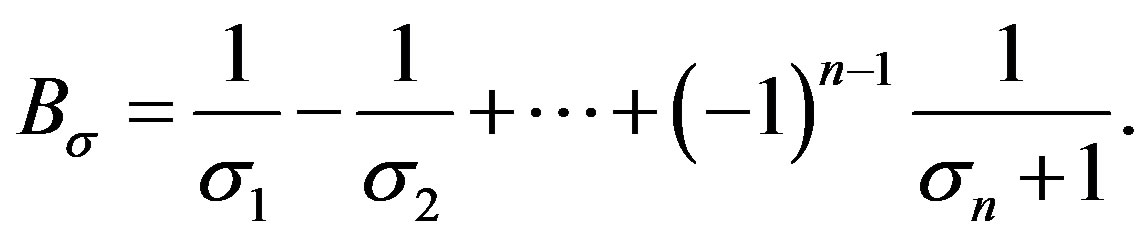 (7)
(7)
We use 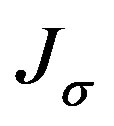 to denote the following subset of (0,1],
to denote the following subset of (0,1],
 (8)
(8)
From theorem 4.14 of [8], we have 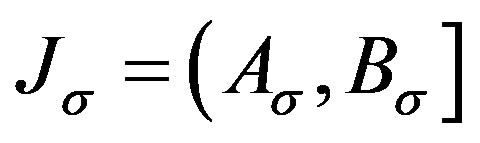 when
when 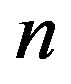 is even, and
is even, and 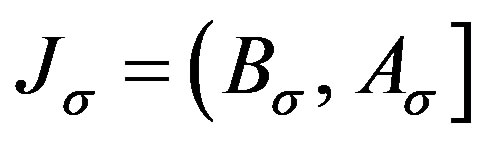 when
when 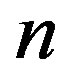 is odd. Finally, define
is odd. Finally, define
 (9)
(9)
Lemma 1. For any 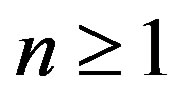 and
and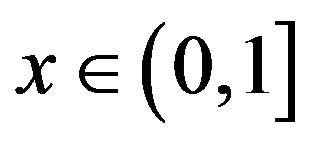 1)
1)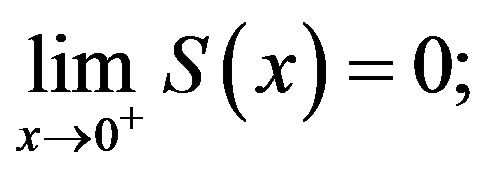 (10)
(10)
2)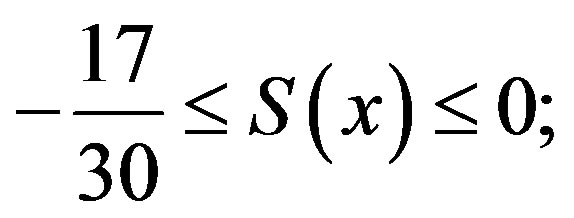 (11)
(11)
3) 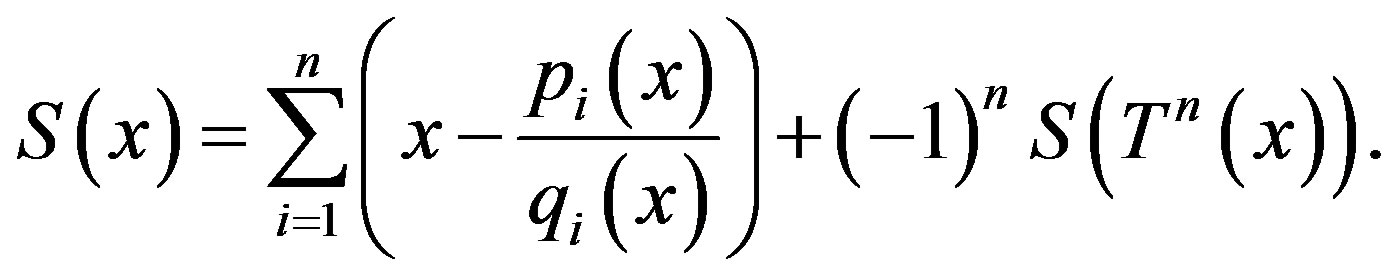 (12)
(12)
Proof. 1) Since 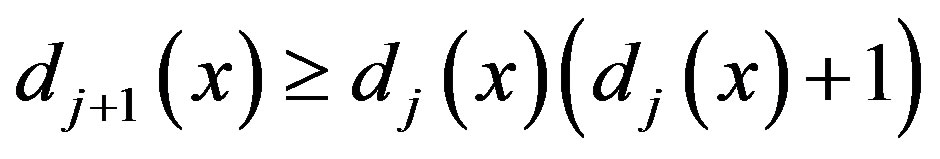 and
and 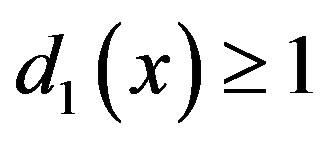 , so when
, so when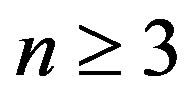 , we can get
, we can get
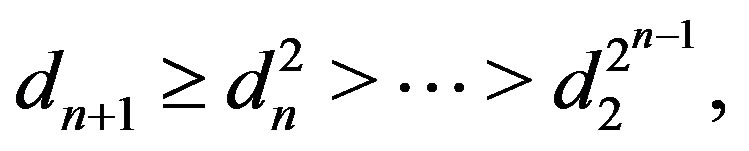
accordingly
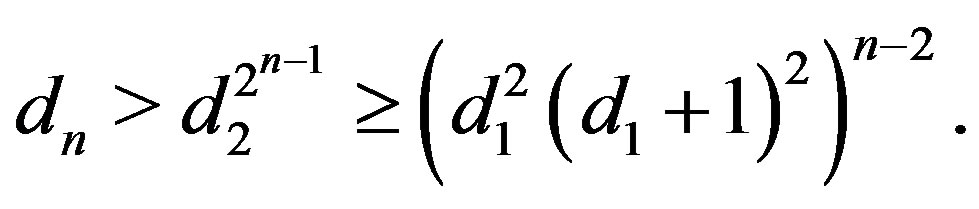
we write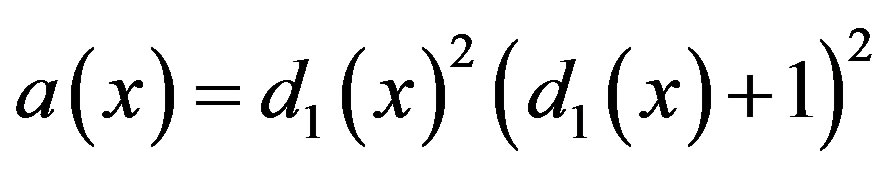 , so
, so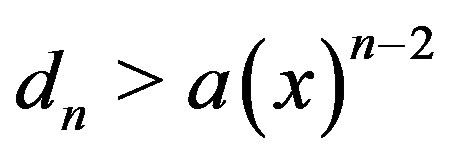 .
.
Now 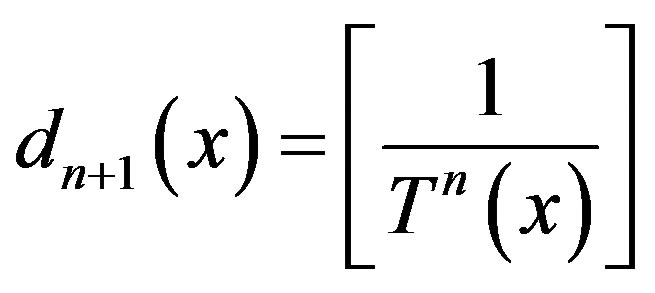 implies
implies
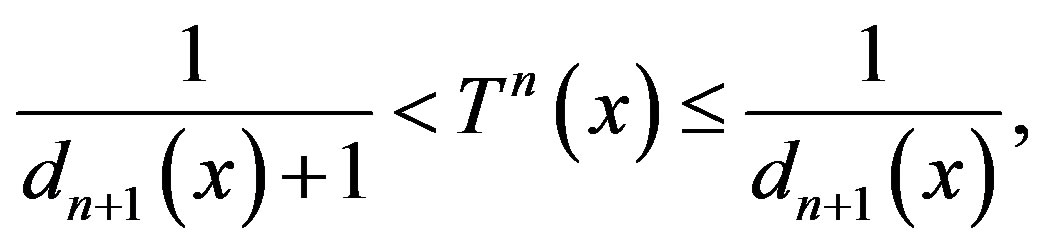 for
for 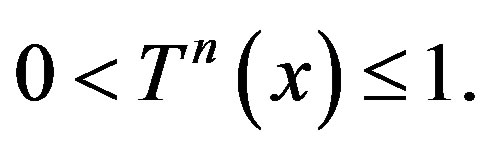
Thus
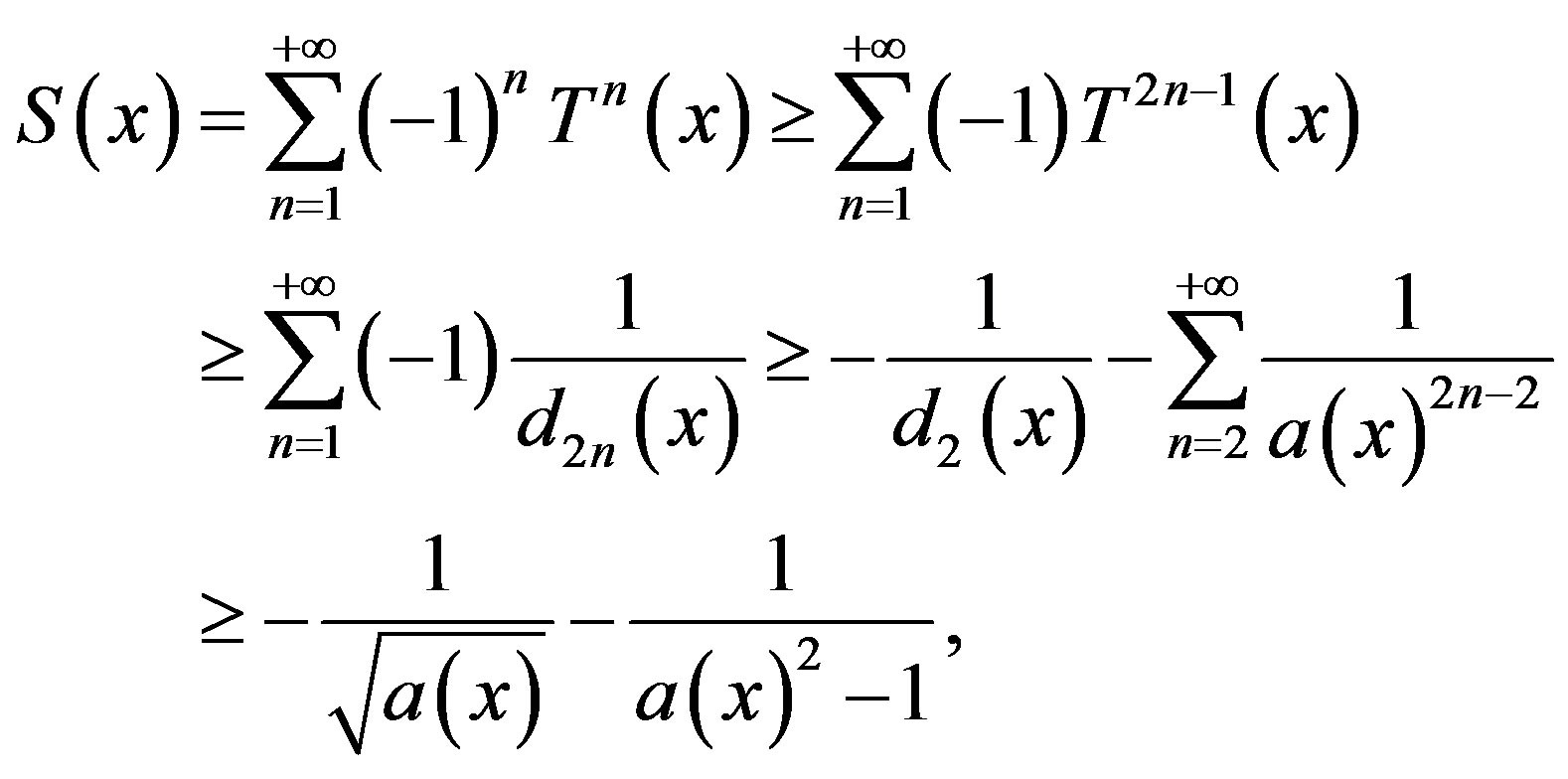
let , we have
, we have 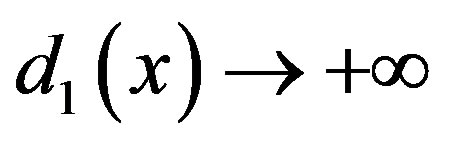 and
and , thus
, thus
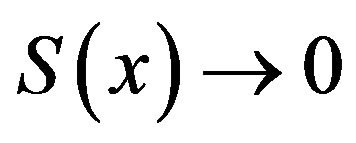
2) From 1) we know that
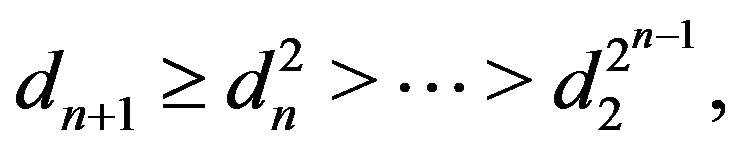
from the definition of 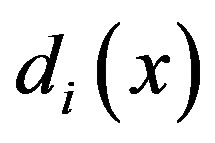 we also know that
we also know that , so
, so 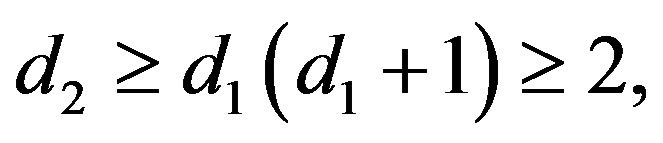
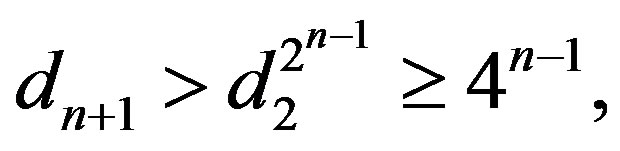
thus
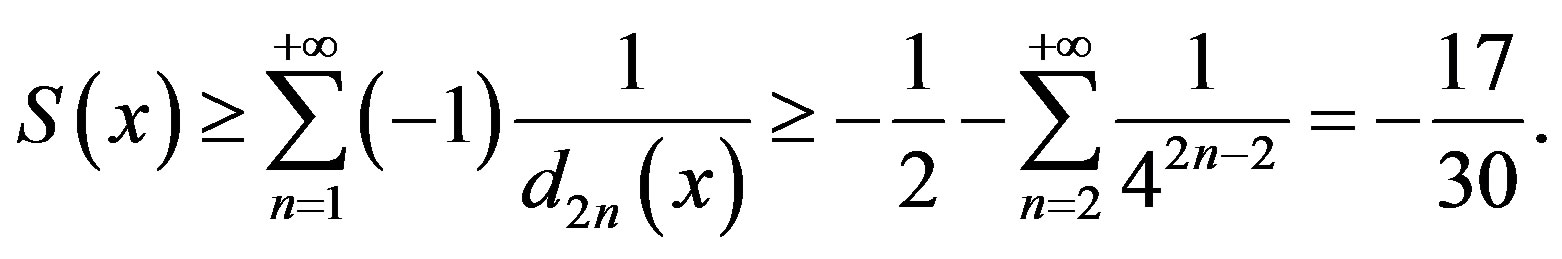
3) Since as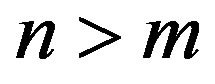 ,
,
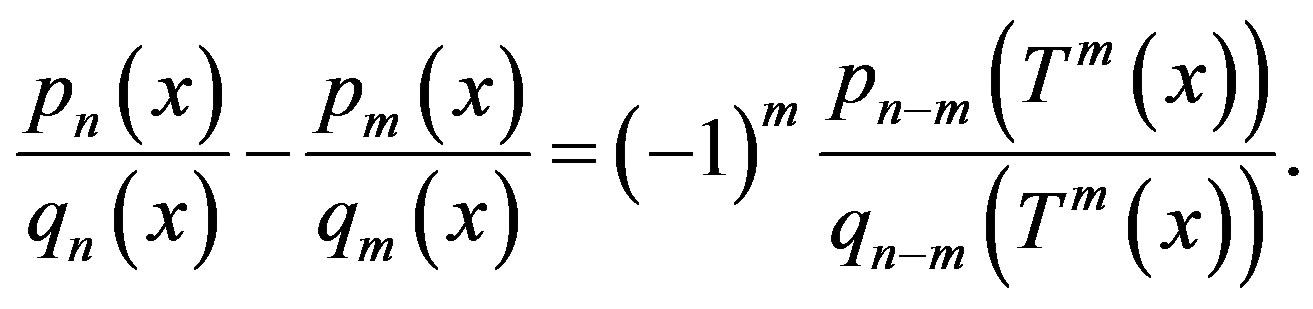
Thus
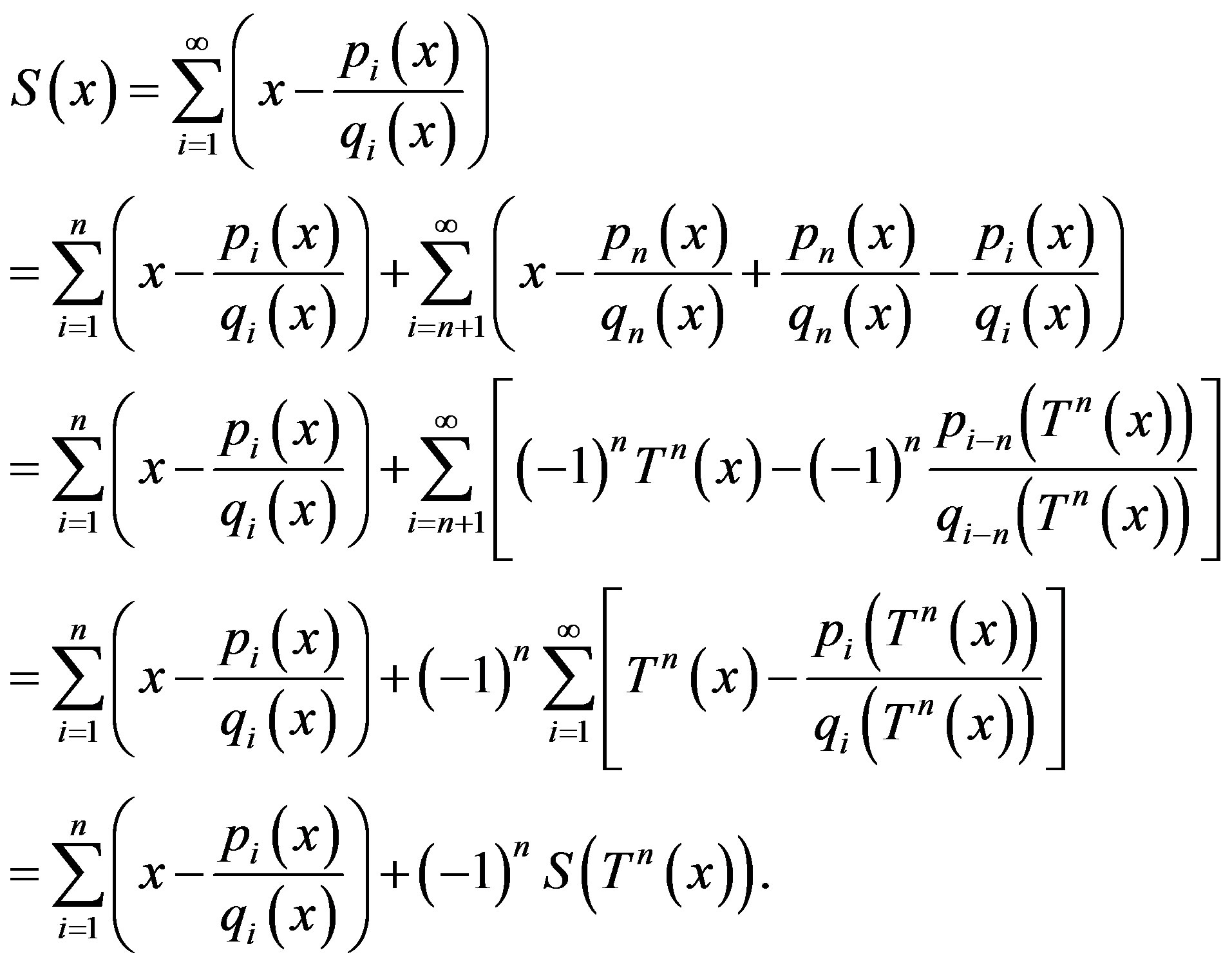
Let
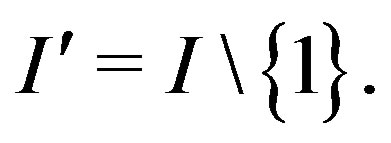
Proposition 2. For any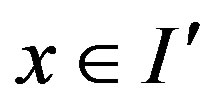 , if
, if 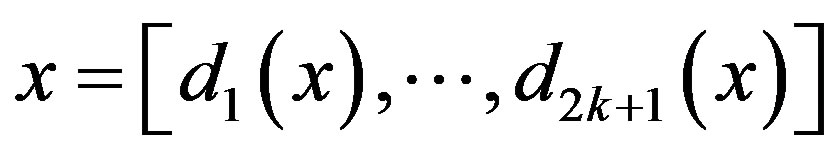 , then
, then 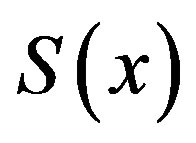 is left continuous but not right continuous. If
is left continuous but not right continuous. If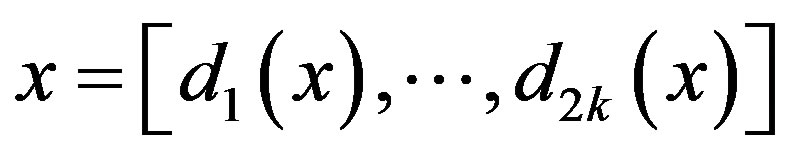 , then
, then 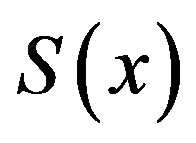 is right continuous but not left continuous.
is right continuous but not left continuous.
Proof. For any 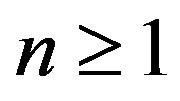 and
and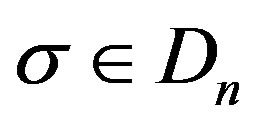 , write
, write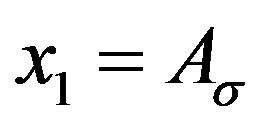 ,
, 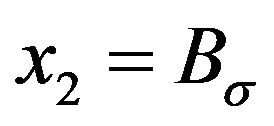 , where
, where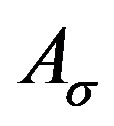 ,
,  are given by (6) and (7).
are given by (6) and (7).
Case I, 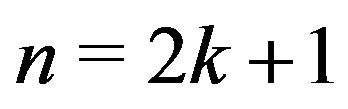 , then
, then
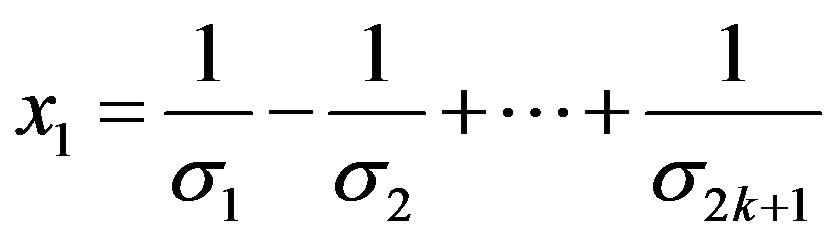 (13)
(13)
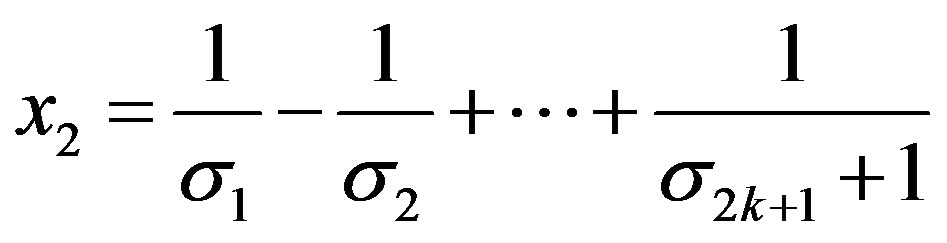 (14)
(14)
and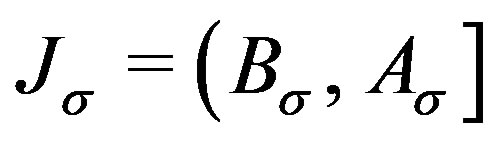 . For any
. For any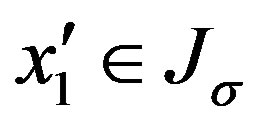 , since when
, since when 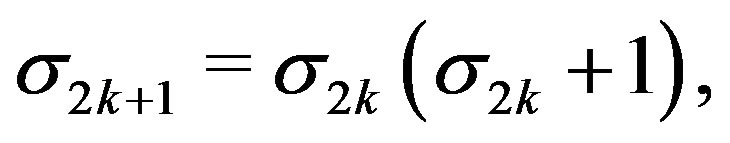
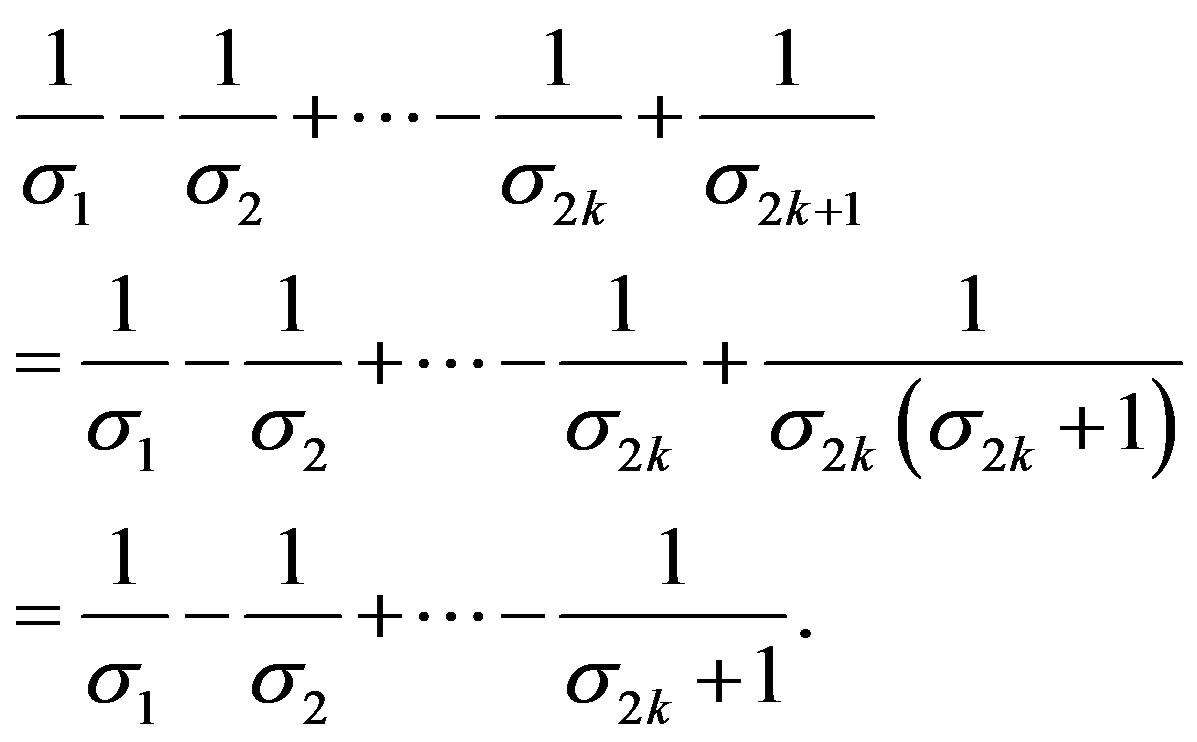
This situation is included in Case II, so we can take 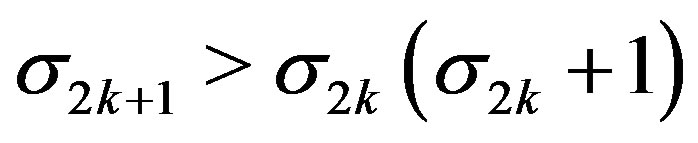 and
and
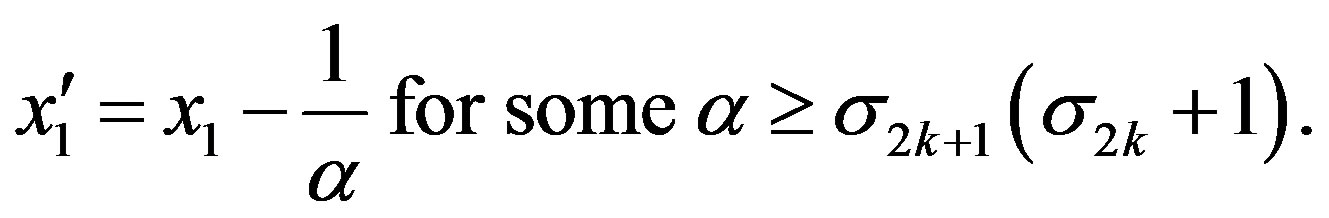
i.e.
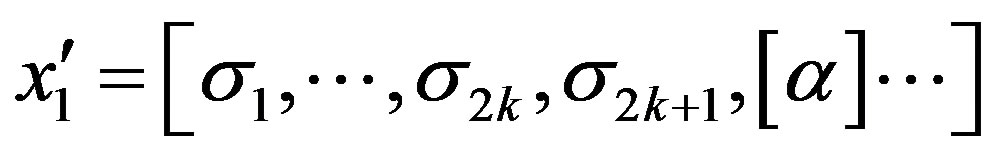
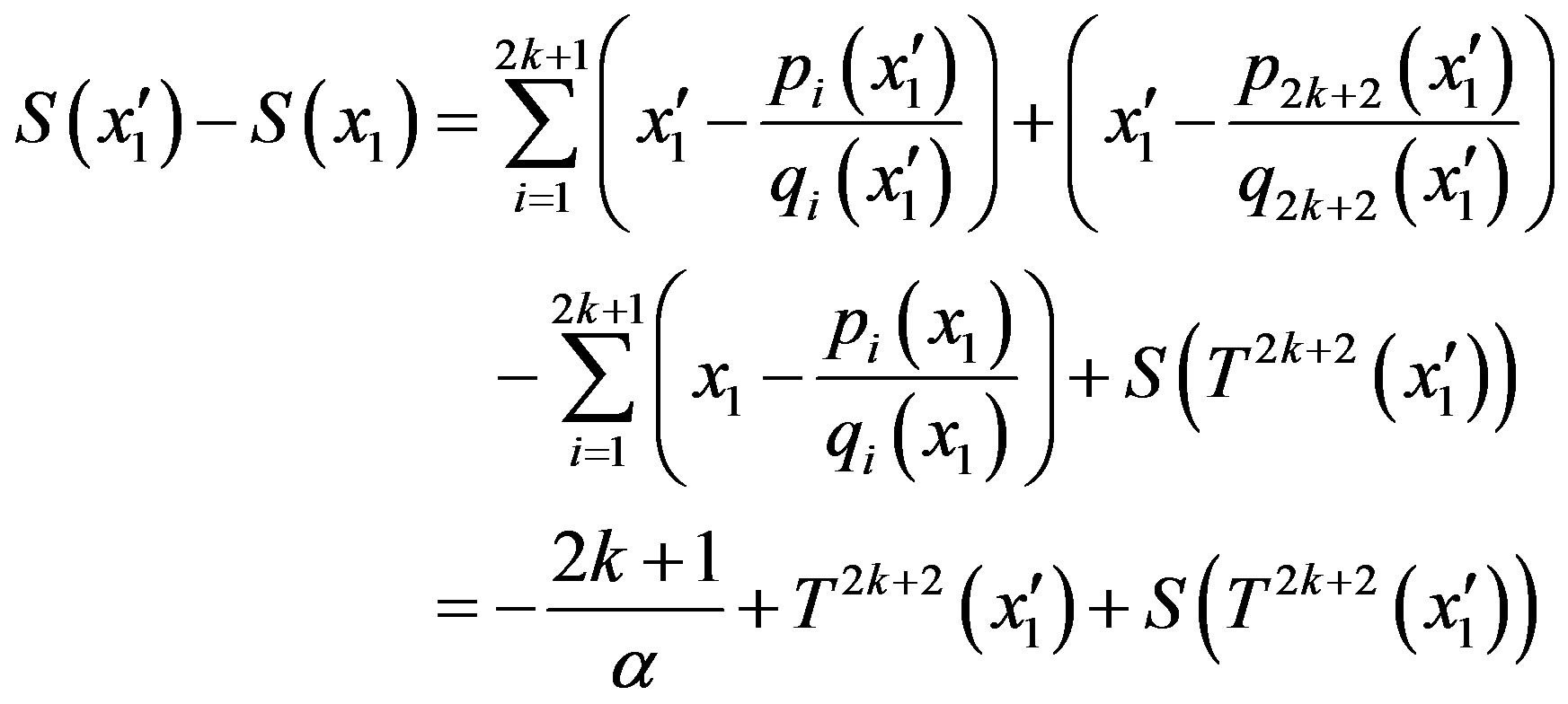
By (2),
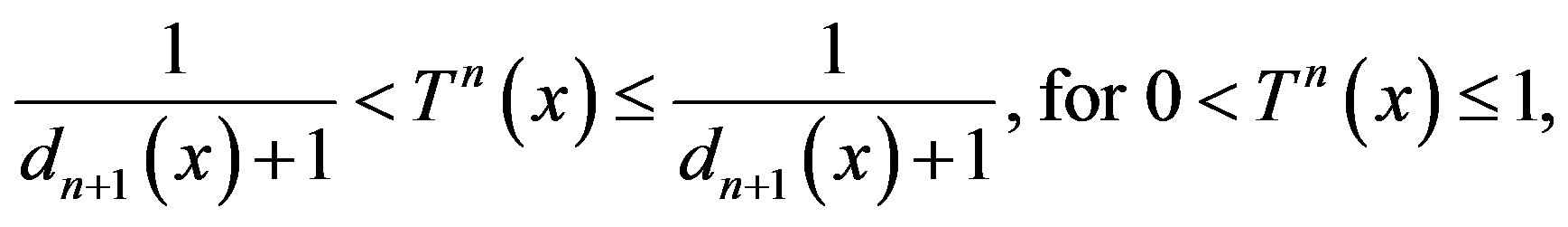
which implies
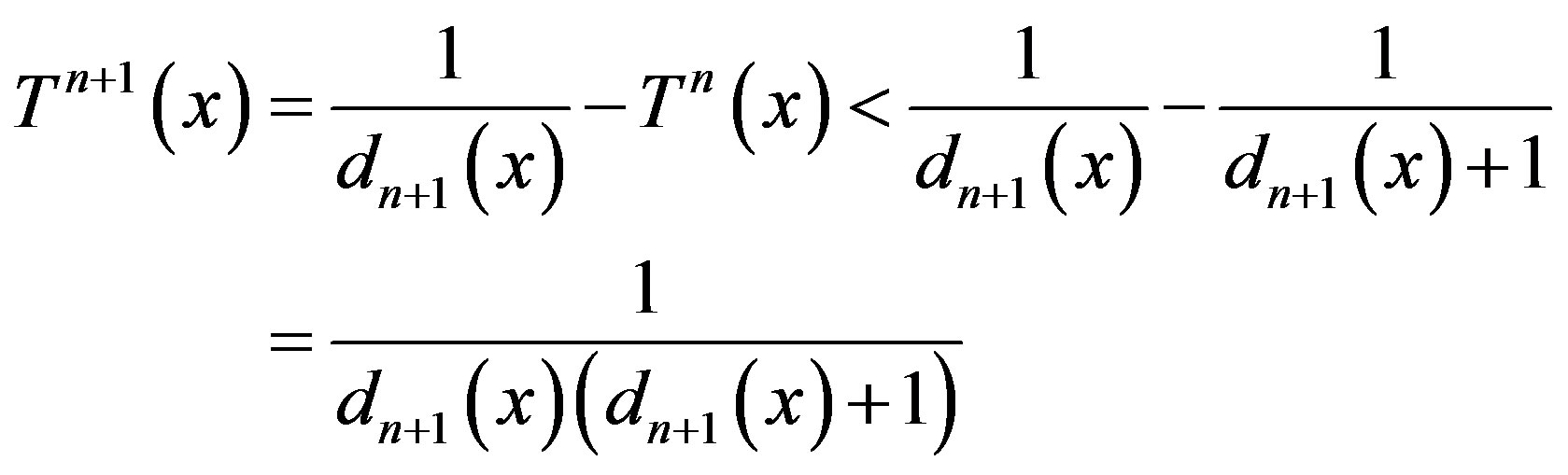
and

Let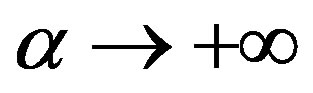 , we get
, we get 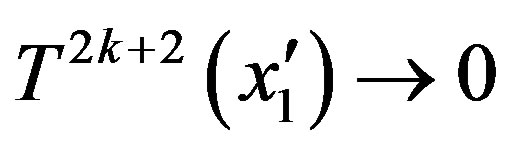 and
and , thus
, thus
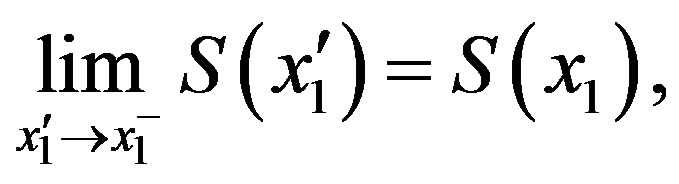
and this implies 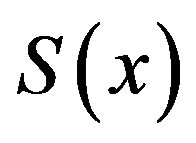 is left continuous at
is left continuous at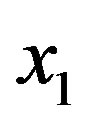 .
.
Let
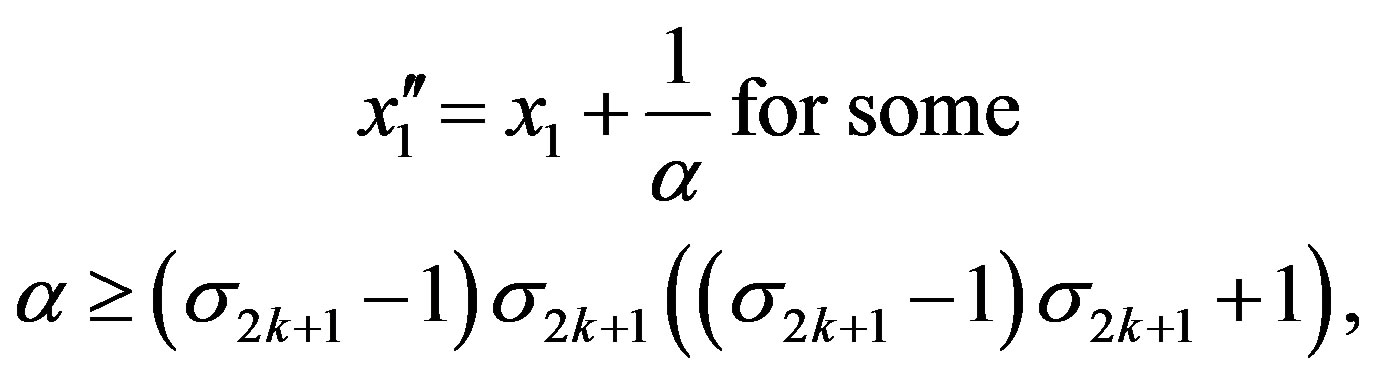
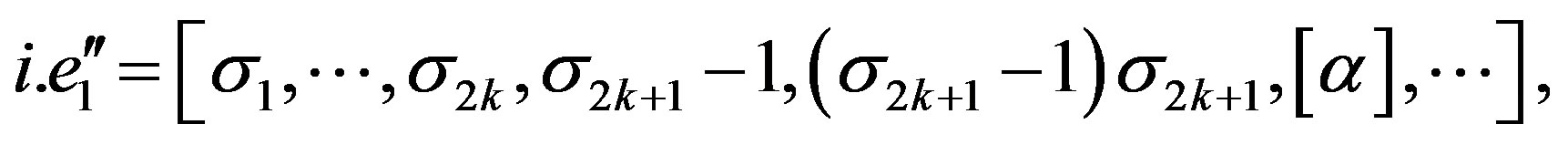
then
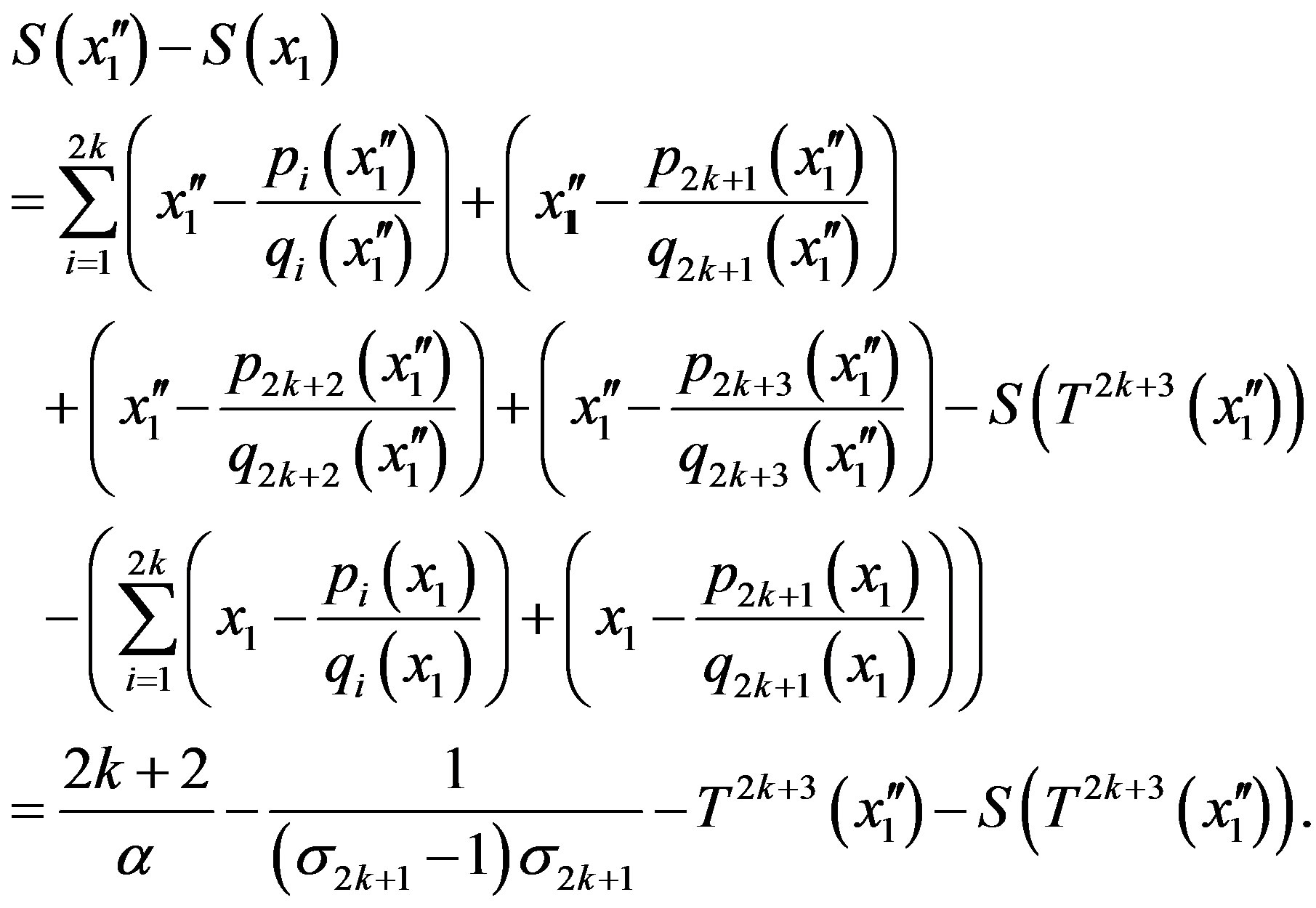
Let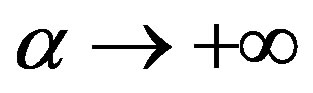 , we have
, we have

and this implies 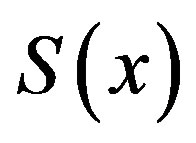 is not right continuous at
is not right continuous at . For
. For
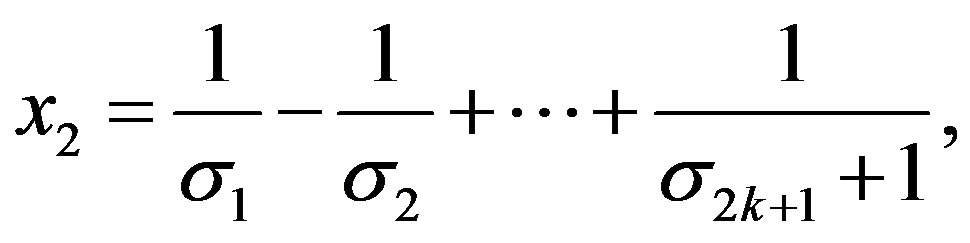 (15)
(15)
following the same line as above, we have

Case II 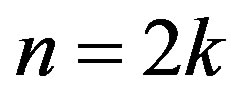
Let
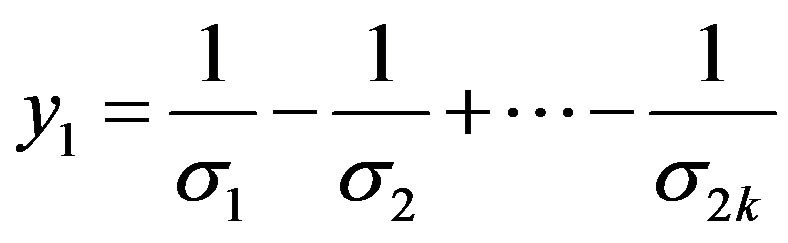 (16)
(16)
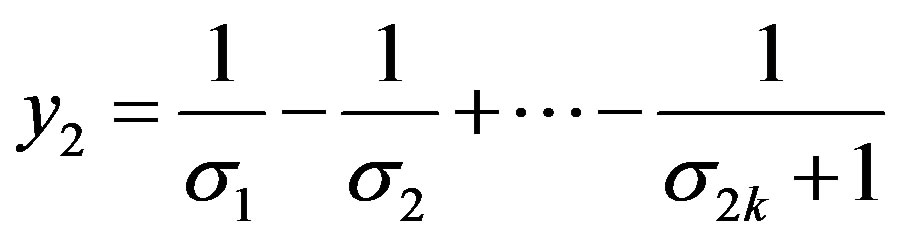 (17)
(17)
Following the same line as above, we have
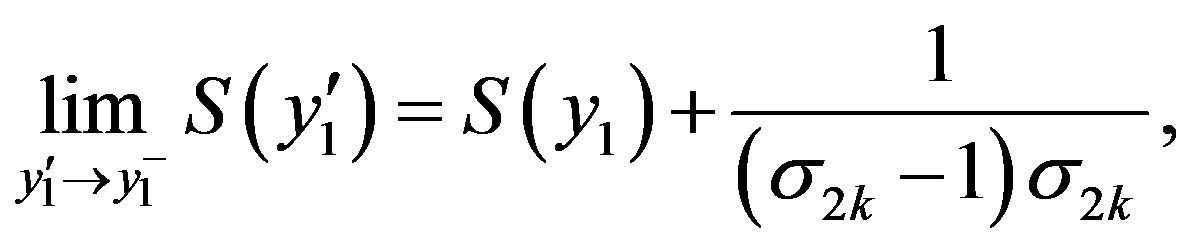
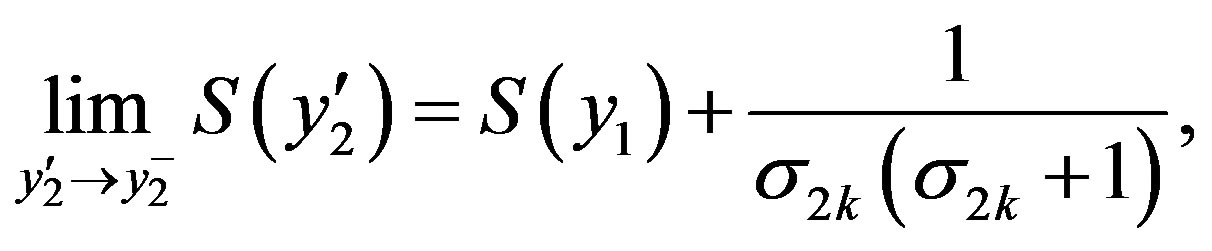
and 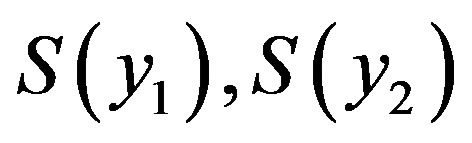 is right continuous.
is right continuous.
Corollary 3. For any 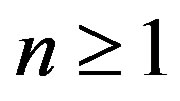 and
and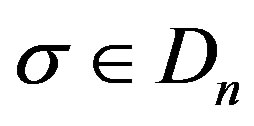 , write
, write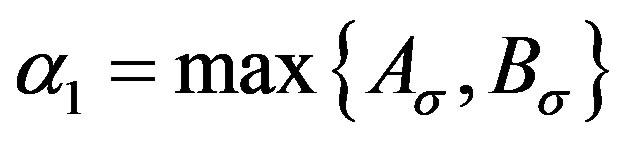 ,
,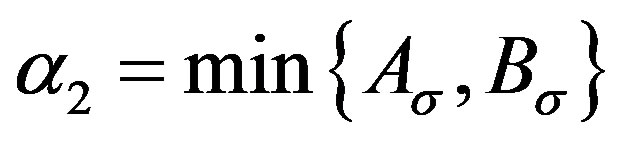 . Then for any
. Then for any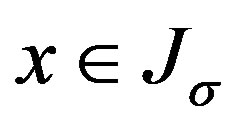 , if
, if 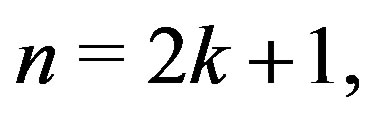 then
then
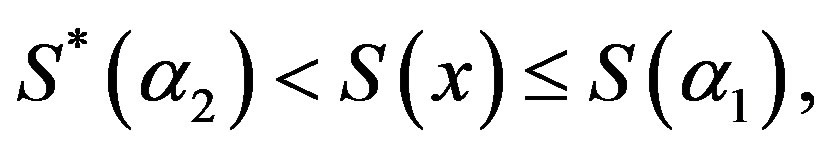
where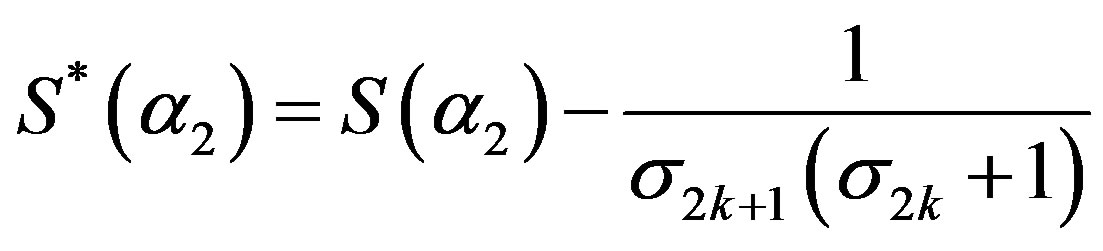 .
.
From the corollary, for any 
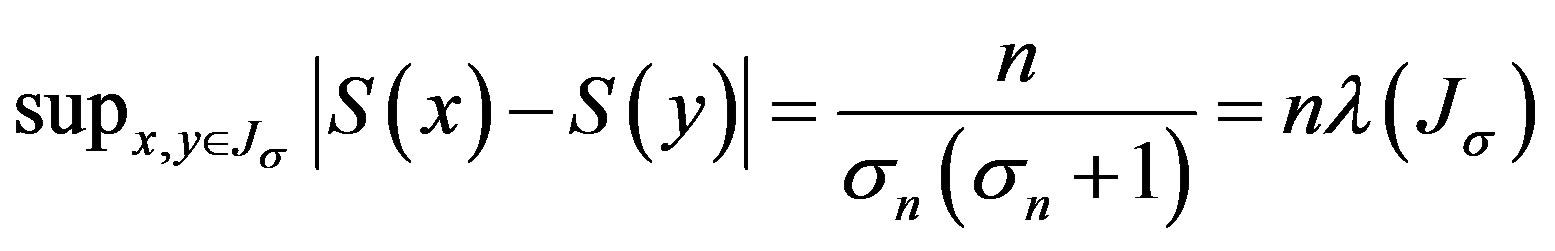
where 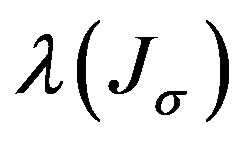 is the Lebesgue measure of
is the Lebesgue measure of .
.
Theorem 4. 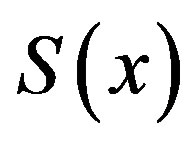 is continuous on
is continuous on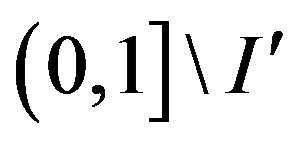 .
.
Proof: For any 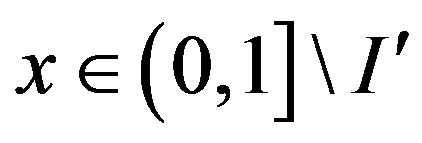 and
and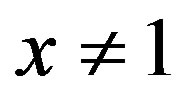 , let
, let 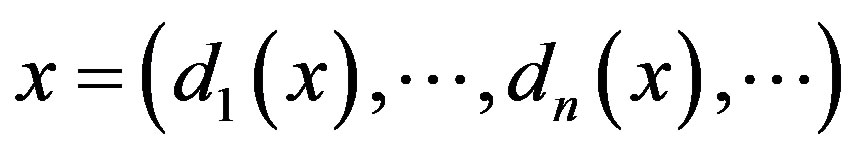 be its Alternating Sylvester expansion. For any
be its Alternating Sylvester expansion. For any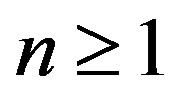 , write
, write 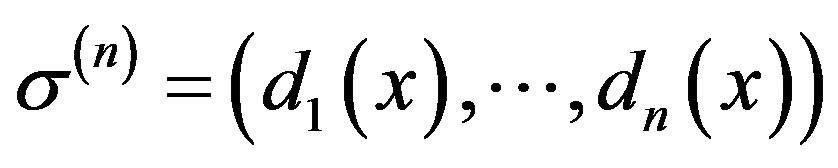 . By (Corollary 3), for any
. By (Corollary 3), for any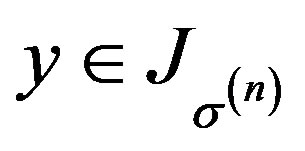 , we have
, we have

Write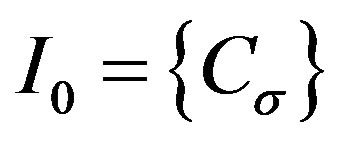 , where
, where
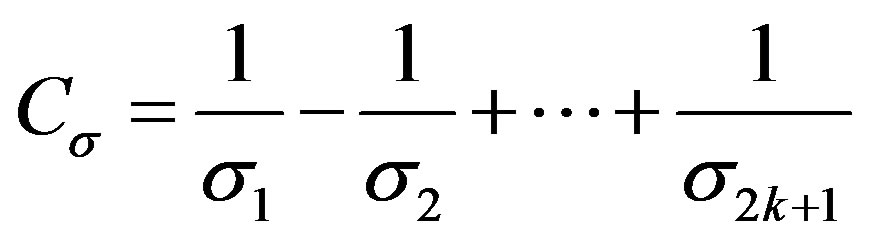
Theorem 5. If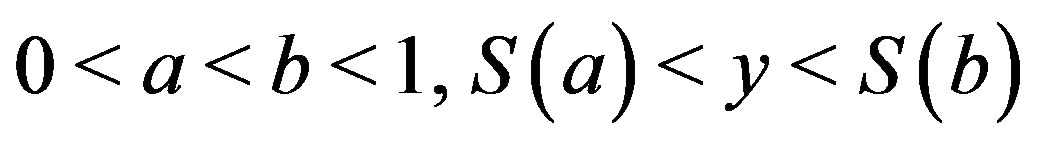 , then there exists
, then there exists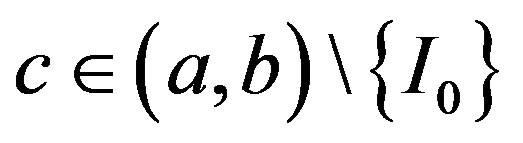 , such that
, such that 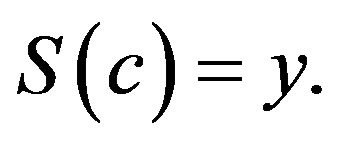
Proof. Set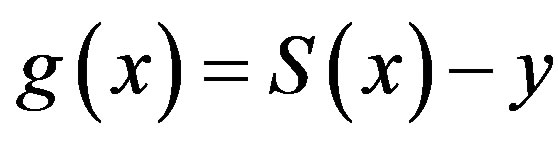 , then
, then  has the same continuity as
has the same continuity as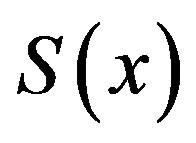 . Write
. Write
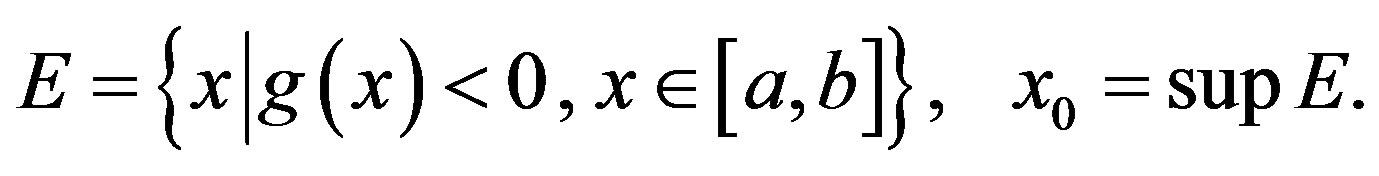
trivially, 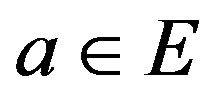 , then the set is well defined.
, then the set is well defined.
If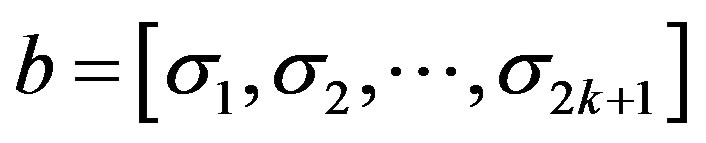 , then by the left continuity of
, then by the left continuity of , we have
, we have
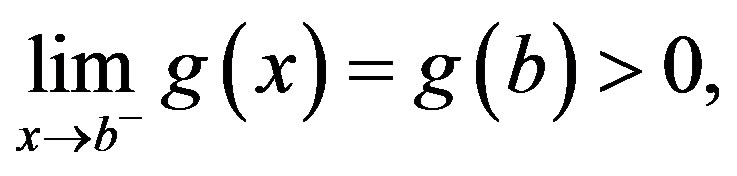
As a result, there exists a  such that for any
such that for any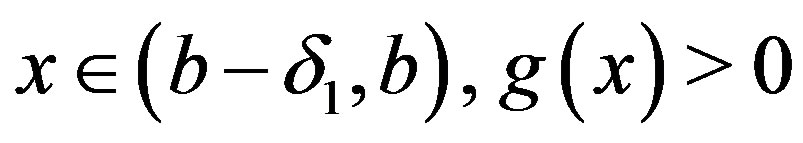 .
.
If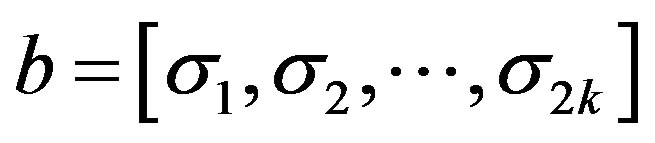 , since
, since 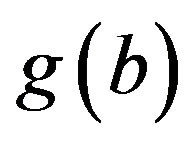 is not left continuous, then
is not left continuous, then 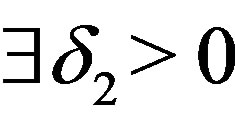 such that for any
such that for any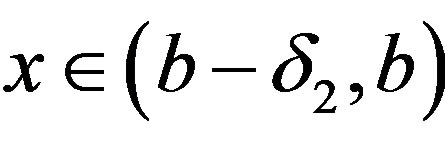 ,
, 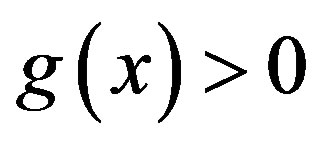 , that is
, that is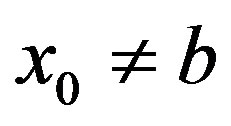 .
.
Following the same line as above, we can prove .
.
Now we shall prove that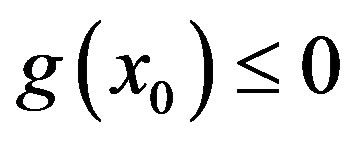 . We can choose
. We can choose 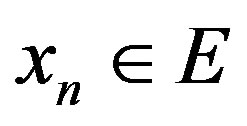 such that
such that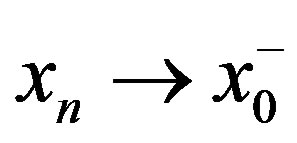 , if
, if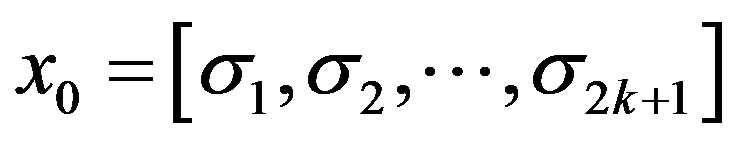 , then
, then
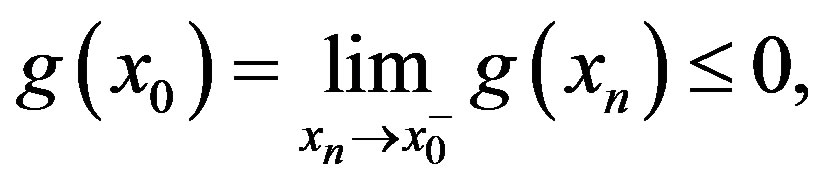
if , then
, then

In both case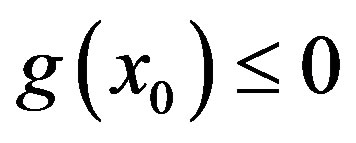 . Following the same line as above, we can prove
. Following the same line as above, we can prove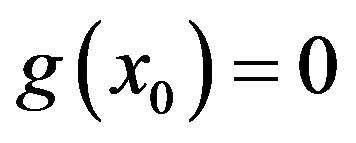 , and
, and 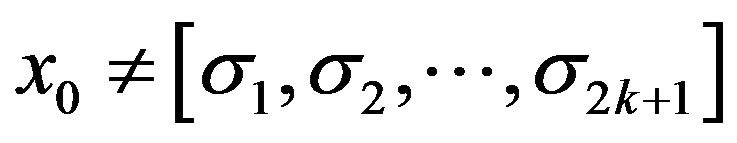 .
.
Therefore, there exists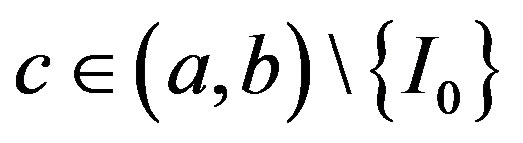 , such that
, such that 
Theorem 6.  and
and 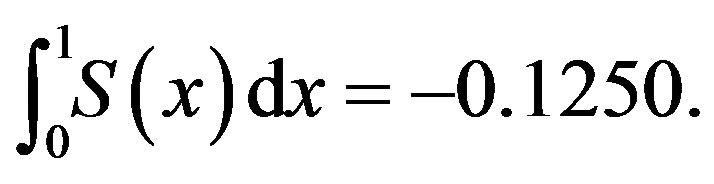
Proof.
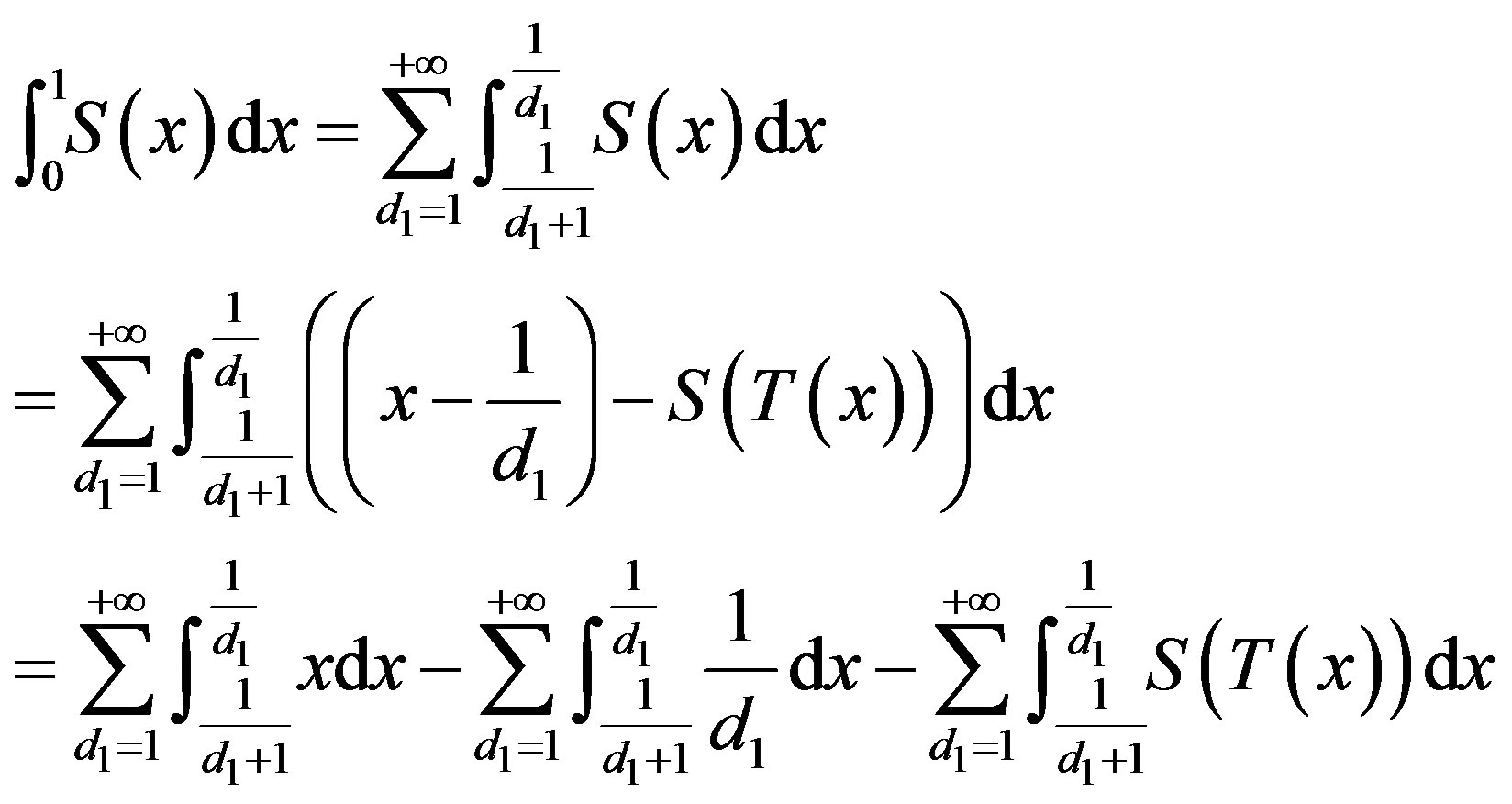
Let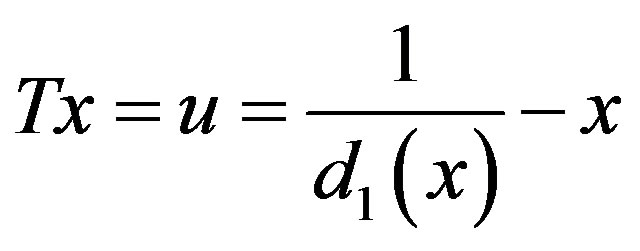 , then
, then 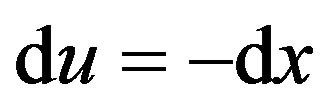 thus
thus
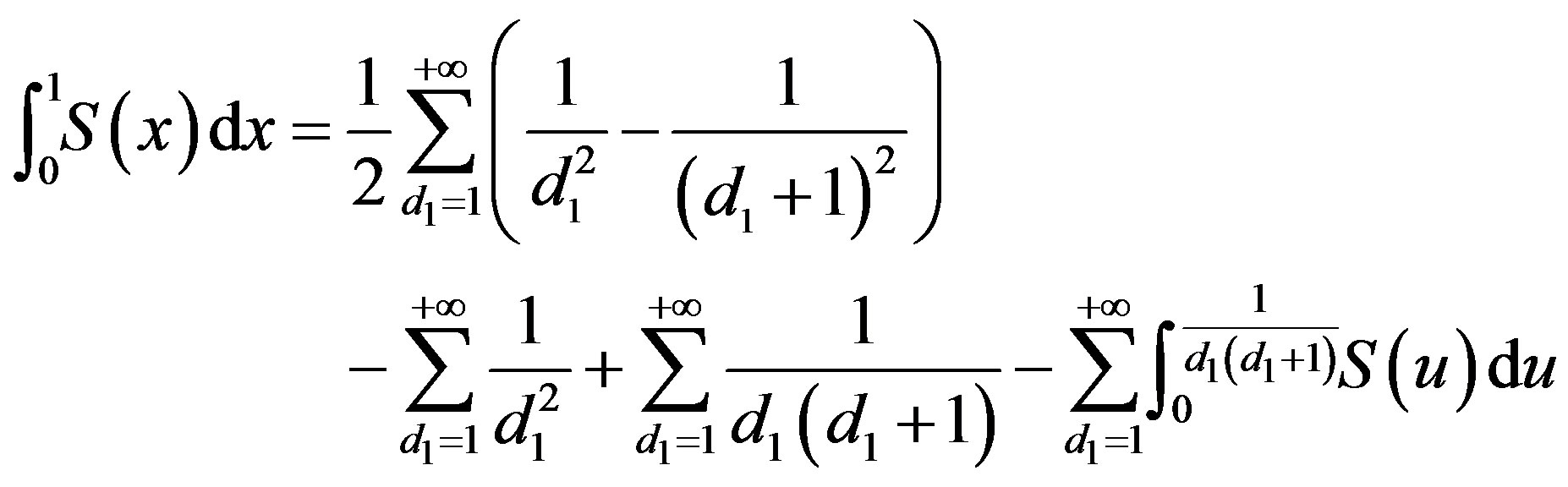
thus,
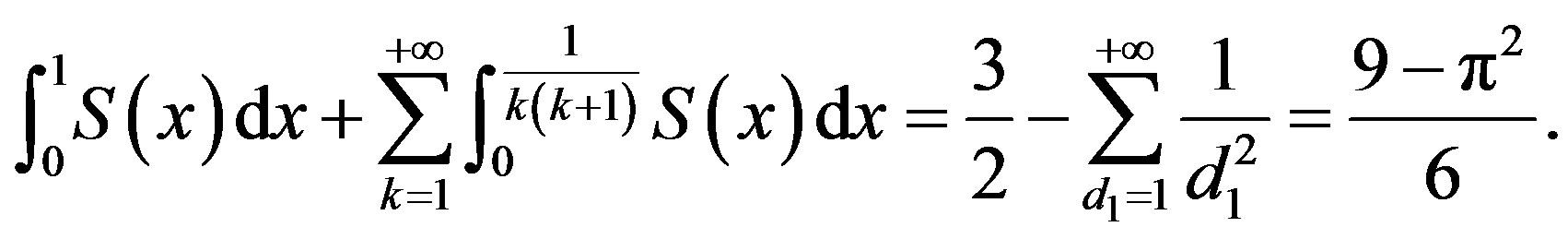
Through the MATLAB program we can get the definite integration

3. Hausdorff Dimension of Graph for 
Write
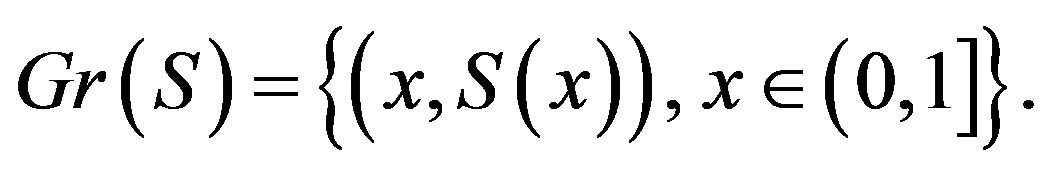
Theorem 7. .
.
Proof. For any ,
, 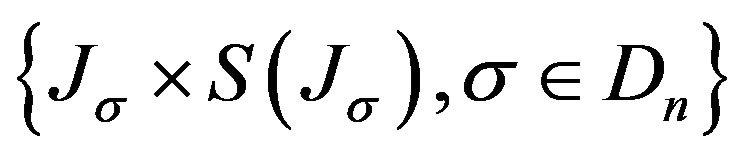 is a covering of
is a covering of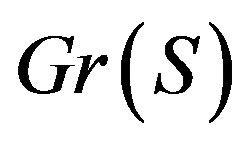 . From (Cor 3),
. From (Cor 3),  can be covered by
can be covered by  squares with side of length
squares with side of length . For any
. For any ,
,
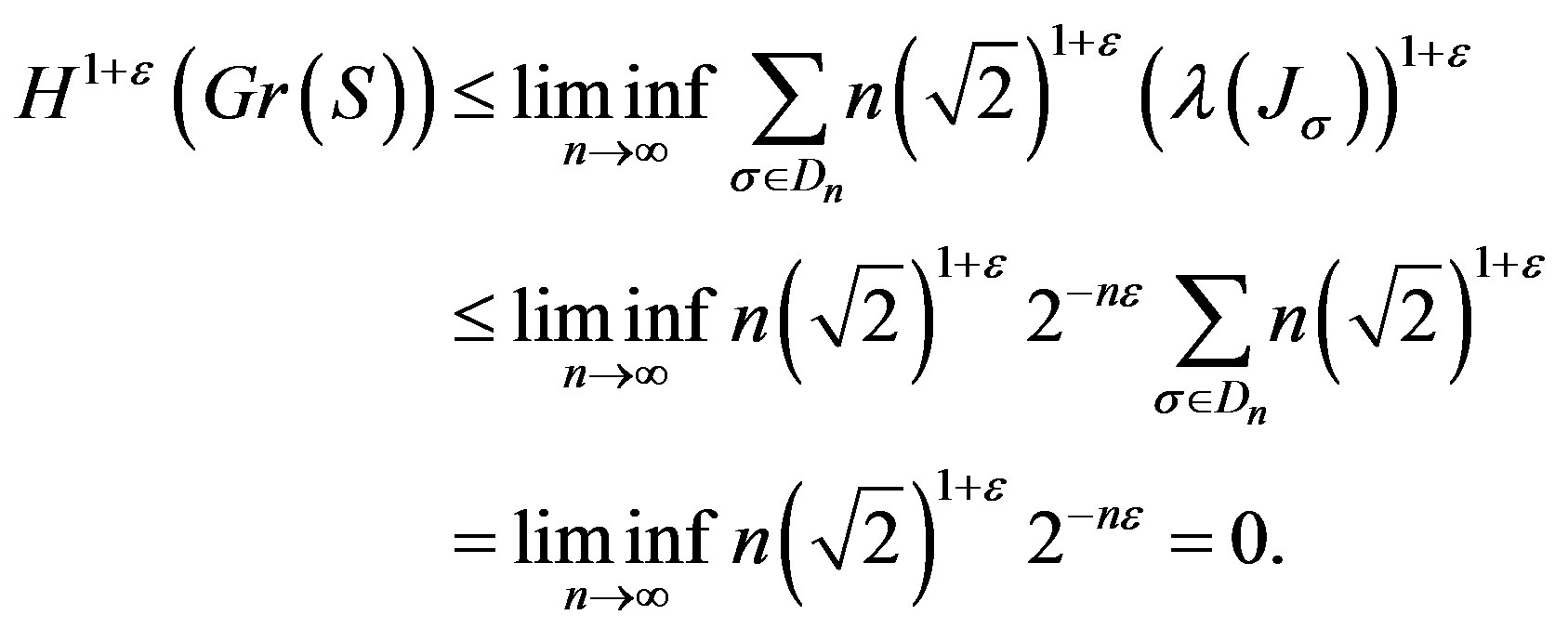
Thus, 
Since
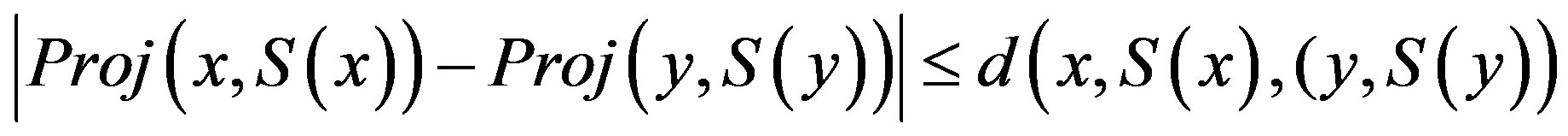 then
then
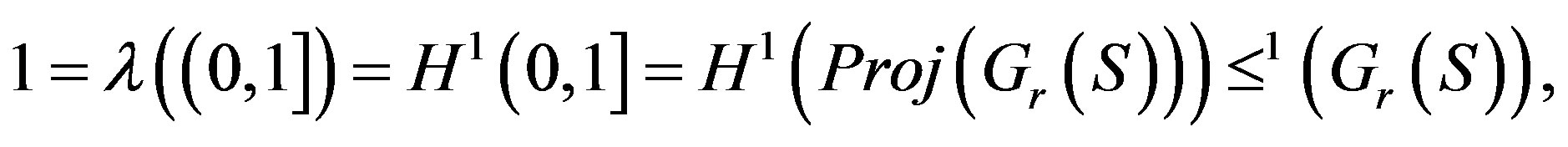
so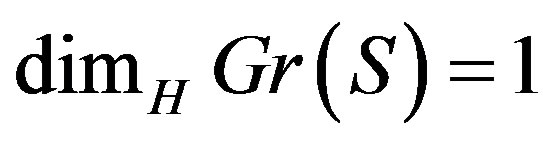 .
.
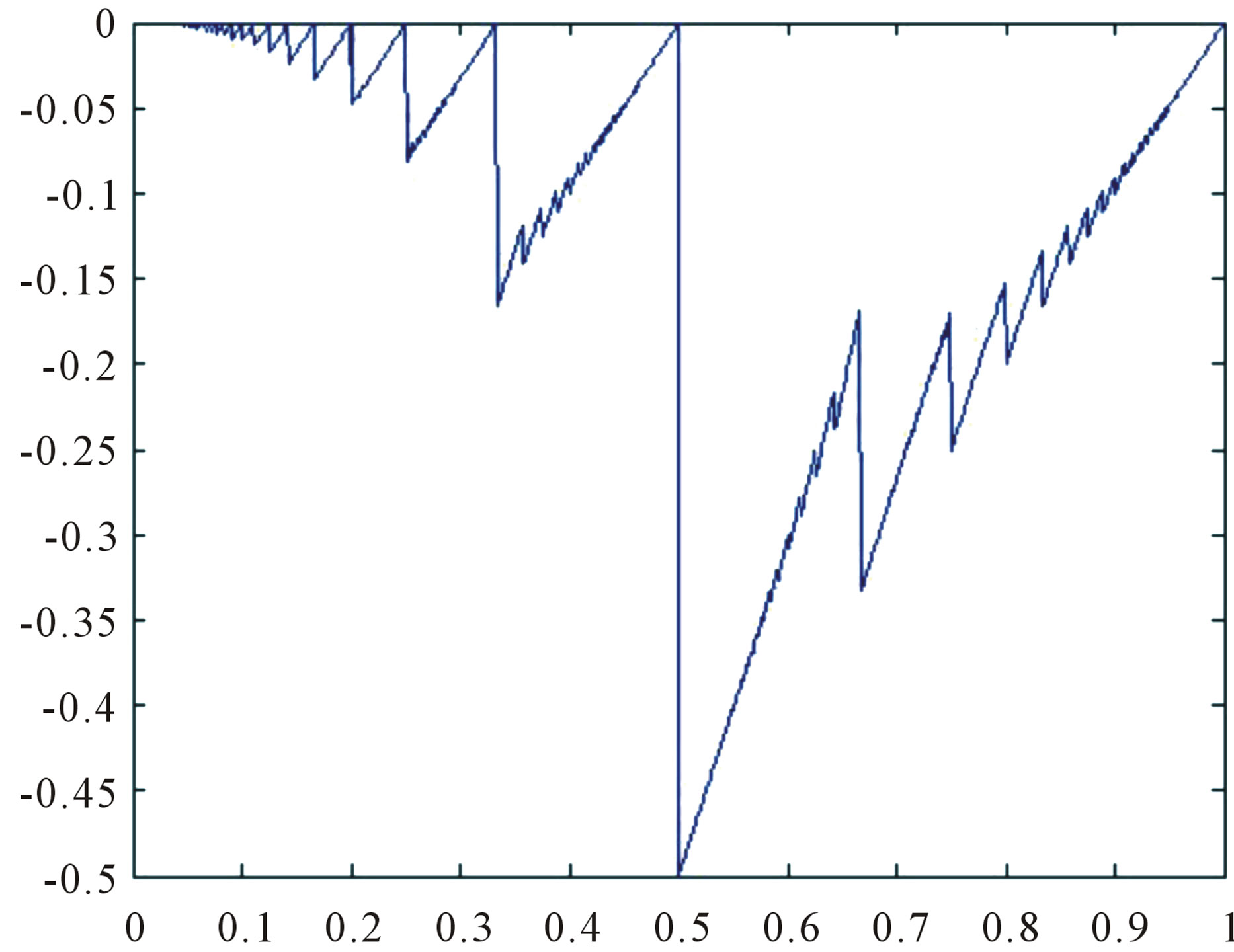
Figure 1. The graph of S(x).
4. Acknowledgements
This work is supported by the Hunan Education Department Fund (11C671).
REFERENCES
- S. Kalpazidou, A. Knopfmacher and J. Knopfmacher, “Lü- roth-Type Alternating Series Representations for Real Numbers,” Acta Arithmetica, Vol. 55, No. 4, 1990, pp. 311-322.
- K. H. Indiekofer, A. Knopfmacher and J. Knopfmacher, “Alternating Balkema-Oppenheim Expansions of Real Numbers,” Bulletin de la Société Mathématique, Vol. B44, 1992, pp. 17-28.
- S. Kalpazidou, A. Knopfmacher and J. Knopfmacher, “Metric Properties of Alternating Lüroth Series,” Potugaliae Mathematica, Vol. 48, No. 3, 1991, pp. 319-325.
- J. Barrionuevo, M. Burton-Robert, Dajani-Karma and C. Kraaikamp, “Ergodic Properties of Generalized Lüroth Series,” Acta Arithmetica, Vol. 74, No. 4, 1996, pp. 311- 327.
- K. Dajani and C. Kraaikamp, “On Approximation by Lü- roth Series,” Journal de Théorie des Nombres de Bordeaux, Vol. 8, No. 2, 1996, pp. 331-346. doi:10.5802/jtnb.172
- K. J. Falconer, “Fractal Geometry, Mathematical Foundations and Applications,” Wiley, Hoboken, 1990.
- K. J. Falconer, “Techniques in Fractal Geometry,” Wiley, Hoboken, 1997.
- J. Galambos, “Reprentations of Real Numbers by Infinite Series,” Lecture Notes in Math, Springer, Berlin, 1976.
- L. M. Shen and J. Wu, “On the Error-Sum Function of Lüroth Series,” Mathematics Analysis and Applications, Vol. 329, No. 2, 2007, pp. 1440-1445.
- L. M. Shen, C. Ma and J. H. Zhang, “On the Error-Sum Function of Alternating Lüroth Series,” Analysis in Theory and Applications, Vol. 22, No. 3, 2006, pp. 223-232. doi:10.1007/s10496-006-0223-x
- T. Sálat and S. Znám, “On the Sums of Prime Powers,” Acta Universitatis Palackianae Olomucensis of Mathematica, Vol. 21, 1968, pp. 21-25.
NOTES
*Corresponding author.

