World Journal of Condensed Matter Physics
Vol. 2 No. 4 (2012) , Article ID: 25070 , 4 pages DOI:10.4236/wjcmp.2012.24045
Domain Suppression in the Negative Differential Conductivity Region of Carbon Nanotubes by Applied AC Electric Field
![]()
1Department of Physics, Laser and Fibre Optics Centre, University of Cape Coast, Cape Coast, Ghana; 2Department of Physics, The Pennsylvania State University, Altoona, USA; 3Materials Research Institute, The Pennsylvania State University, University Park, USA; 4National Centre for Mathematical Sciences, Ghana Atomic Energy Commission, Accra, Ghana; 5Department of Mathematics, University of Cape Coast, Cape Coast, Ghana; 6Department of Applied Physics, University for Development Studies, Navorongo, Ghana.
Email: *profsymensah@yahoo.co.uk
Received January 4th, 2012; revised February 26th, 2012; accepted March 9th, 2012
Keywords: Carbon Nanotubes; Negative Differential Conductivity; Generation of Terahertz Radiation
ABSTRACT
We study theoretically the electron transport properties in achiral carbon nanotubes under the influence of an external electric field E(t) using Boltzmann’s transport equation to derive the current-density. A negative differential conductivity (NDC) is predicted in quasi-static approximation i.e., ωτ << 1, similar to that observed in superlattice. However, a strong enhancement in the current density intensity is observed in NDC of the achiral carbon nanotubes. This is observed at where the constant electric field E0 is equal to the amplitude of the AC electric field E1. The peak of the NDC intensity occurs at very weaker fields than that of superlattice under the same conditions. The peak intensity decreases and shifts to right with the increase in the amplitude of the ac field. This mechanism suppresses the domain formation and therefore could be used in terahertz frequency generation.
1. Introduction
Carbon nanotubes (CNTs) were first discovered by Iijima in 1991 [1], and since then there has been exponential growth in the interest of the quasi-one-dimensional monomolecular structure due to their unique and outstanding electrical, mechanical, and chemical properties. Nonlinear effects on CNTs are of great interest for potential applications in nanoelctronics and negative differential conductivity (NDC) has been predicted at room temperature under the condition, when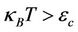 ,
, 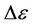 in a certain range of electric field strength [2]. The NDC is believed to provide current instability in CNTs [2] which is destructive for the formation of terahertz (THz) radiation as in semiconducting superlattices (SLs). Simultaneous application of both dc-and ac-fields to the CNTs will result in nonlinear phase of the instability [2] as observed in semiconducting superlattices (SL). Mensah [3] studied the NDC effect in a semiconductor SL in the presence of an external electric field and showed that the NDC occurred in the current density characteristics when
in a certain range of electric field strength [2]. The NDC is believed to provide current instability in CNTs [2] which is destructive for the formation of terahertz (THz) radiation as in semiconducting superlattices (SLs). Simultaneous application of both dc-and ac-fields to the CNTs will result in nonlinear phase of the instability [2] as observed in semiconducting superlattices (SL). Mensah [3] studied the NDC effect in a semiconductor SL in the presence of an external electric field and showed that the NDC occurred in the current density characteristics when  i.e. near where the constant electric field is equal to the amplitude of the ac electric field and the peak decreases with increasing the amplitude of the ac field. The theory agrees fairly well with an experiment [4] that indicated “right shift” of the current density versus static electric field characteristics, which is typical for a SL without domain formation. Klappenberger and coworkers [4] demonstrated ultrafast creation and annihilation of space-charge domains in a semiconductor superlattice using terahertz fields. Up to now, NDC has been observed only in a d.c electric field in both doped and undoped CNTs [2]. However, there is no report on simultaneous application of dc and ac fields to CNT to date. In this paper, we report a systematic theoretical investigation of effect of simultaneous application of dc and ac field to armchair CNT (a-SWCNT) and zigzag CNT (z-SWCNT) using the Boltzmann’s transport equation to derive the current density and analyze the behavior of the normalized current density as a function of dc electric field.
i.e. near where the constant electric field is equal to the amplitude of the ac electric field and the peak decreases with increasing the amplitude of the ac field. The theory agrees fairly well with an experiment [4] that indicated “right shift” of the current density versus static electric field characteristics, which is typical for a SL without domain formation. Klappenberger and coworkers [4] demonstrated ultrafast creation and annihilation of space-charge domains in a semiconductor superlattice using terahertz fields. Up to now, NDC has been observed only in a d.c electric field in both doped and undoped CNTs [2]. However, there is no report on simultaneous application of dc and ac fields to CNT to date. In this paper, we report a systematic theoretical investigation of effect of simultaneous application of dc and ac field to armchair CNT (a-SWCNT) and zigzag CNT (z-SWCNT) using the Boltzmann’s transport equation to derive the current density and analyze the behavior of the normalized current density as a function of dc electric field.
2. Theory
We consider a response of electrons in an undoped achiral single-wall carbon nanotubes (a-SWCNT and z-SWCNT) (a-SWCNT), to the action of a strong pumping electric field.
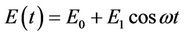 (1)
(1)
where the dc bias 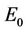 is small and the ac field is quasi static
is small and the ac field is quasi static The investigation is done within the semiclassical approximation in which the motion of π-electrons is considered as classical motion of free quasi-particles in the field of the crystalline lattice with dispersion law extracted from quantum theory. Taking into account the hexagonal crystalline structure of a rolled graphene in a form of SWCNT and using the tight binding approximation, the energy dispersion for z-SWCNT and aSWCNT are expressed respectively, as [2]
The investigation is done within the semiclassical approximation in which the motion of π-electrons is considered as classical motion of free quasi-particles in the field of the crystalline lattice with dispersion law extracted from quantum theory. Taking into account the hexagonal crystalline structure of a rolled graphene in a form of SWCNT and using the tight binding approximation, the energy dispersion for z-SWCNT and aSWCNT are expressed respectively, as [2]
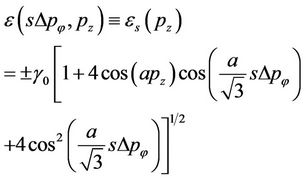 (2)
(2)
and
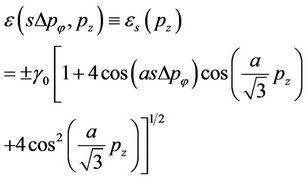 (3)
(3)
where 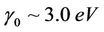 is the overlapping integral,
is the overlapping integral, 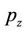 is the axial component of quasimomentum,
is the axial component of quasimomentum, 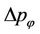 is transverse quasimomentum level spacing and s is an integer. The expression for
is transverse quasimomentum level spacing and s is an integer. The expression for  in Equations (2) and (3) is given as
in Equations (2) and (3) is given as ,
, 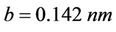 is the C-C bond length. The – and + signs correspond to the valence and the conduction bands respectively. Due to the transverse quantization of the quasi-momentum, its transverse component can take n discrete values,
is the C-C bond length. The – and + signs correspond to the valence and the conduction bands respectively. Due to the transverse quantization of the quasi-momentum, its transverse component can take n discrete values,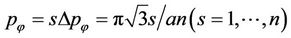 . Unlike transverse quasimomentum
. Unlike transverse quasimomentum  , the axial quasimomentum
, the axial quasimomentum  is assumed to vary continuously within the range
is assumed to vary continuously within the range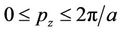 , which corresponds to the model of infinitely long SWCNT
, which corresponds to the model of infinitely long SWCNT . This model is applicable to the case under consideration because of the restriction to the temperatures and /or voltages well above the level spacing [5], i.e.
. This model is applicable to the case under consideration because of the restriction to the temperatures and /or voltages well above the level spacing [5], i.e.  where
where 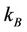 is Boltzmann constant, T is the temperature,
is Boltzmann constant, T is the temperature,  is the charging energy. The energy level spacing
is the charging energy. The energy level spacing  is given by
is given by
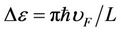 (4)
(4)
where 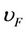 is the Fermi velocity and L is the carbon nanotube length [6].
is the Fermi velocity and L is the carbon nanotube length [6].
Employing Boltzmann equation with a single relaxation time approximation
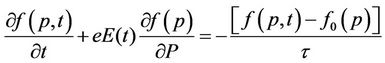 (5)
(5)
where e is the electron charge, 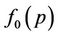 is the equilibrium distribution function,
is the equilibrium distribution function, 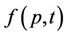 is the distribution function, and
is the distribution function, and 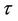 is the relaxation time. The electric field E is applied along the SWCNT axis. In this problem the relaxation term
is the relaxation time. The electric field E is applied along the SWCNT axis. In this problem the relaxation term 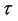 is assumed to be constant. The justification for
is assumed to be constant. The justification for 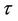 being constant can be found in ref [7]. The relaxation term of Equation (5) describes the effects of the dominant type of scattering (e.g. electron-phonon and electron-twistons) [8]. For the electron scattering by twistons (thermally activated twist deformations of the tube lattice),
being constant can be found in ref [7]. The relaxation term of Equation (5) describes the effects of the dominant type of scattering (e.g. electron-phonon and electron-twistons) [8]. For the electron scattering by twistons (thermally activated twist deformations of the tube lattice), 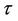 is proportional to m and the
is proportional to m and the 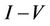 characteristics have shown that scattering by twistons increases
characteristics have shown that scattering by twistons increases 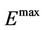 and decreases
and decreases 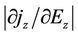 in the NDC region. The effect is stronger for smaller ms. Quantitative changes of the
in the NDC region. The effect is stronger for smaller ms. Quantitative changes of the 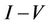 curves turn out to be insignificant in comparison with the case of
curves turn out to be insignificant in comparison with the case of  = constant [7,8].
= constant [7,8].
Expanding the distribution functions of interest in Fourier series as;
 (6)
(6)
and
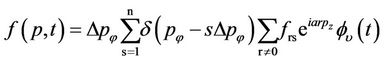 (7)
(7)
where the coefficient,  is the Dirac delta function,
is the Dirac delta function,  is the coefficient of the Fourier series and
is the coefficient of the Fourier series and 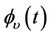 is the factor by which the Fourier transform of the nonequilibrium distribution function differs from its equilibrium distribution counterpart.
is the factor by which the Fourier transform of the nonequilibrium distribution function differs from its equilibrium distribution counterpart.
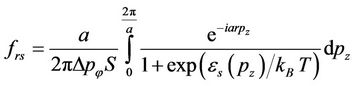 (8)
(8)
Substituting Equations (6) and (7) into Equation (5), and solving with Equation (1) we obtain
 (9)
(9)
where
 , and
, and 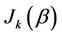 is the Bessel function of the kth order and
is the Bessel function of the kth order and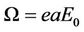 .
.
Similarly, expanding 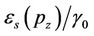 in Fourier series with coefficients
in Fourier series with coefficients 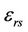
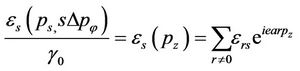 (10)
(10)
where
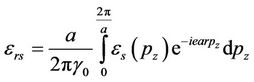 (11)
(11)
and expressing the velocity as
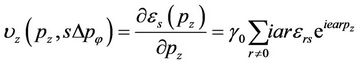 (12)
(12)
we determine the surface current density as
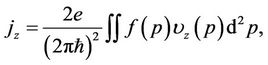
or
 (13)
(13)
where the integration is taken over the first Brillouin zone. Substituting Equations (7), (9) and (12) into (13) we find the current density for the z-SWCNT after averaging over a period of time t, as
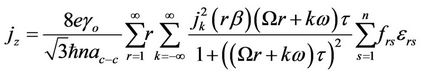 (14)
(14)
which is similar to expression (8) in ref. [3]. See Figure 1.
Where 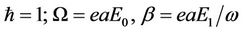 for z-SWCNT and
for z-SWCNT and 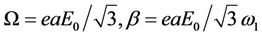 for a-SWCNT.
for a-SWCNT.
3. Results and Discussion
The current density expression for z-SWCNT subjected to dc bias field 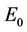 and quasi static-field
and quasi static-field 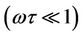 is obtained by using the solution to the Boltzmann equation with constant relaxation time
is obtained by using the solution to the Boltzmann equation with constant relaxation time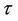 . The behavior of the normalized current density
. The behavior of the normalized current density 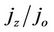 as a function of the dimensionless parameter
as a function of the dimensionless parameter 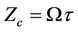 (Equation 14) for given
(Equation 14) for given  and
and 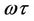 values was analyzed using a Matlabversion 7.6 2008a.
values was analyzed using a Matlabversion 7.6 2008a.
The normalized current density of the nanotubes structures (z-SWCNT, a-SWCNT) exhibits linear dependence on 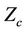 at weak applied external static electric field strengths (i.e. the region of ohmic conductivity). As Zc increases, the current density
at weak applied external static electric field strengths (i.e. the region of ohmic conductivity). As Zc increases, the current density  increases and researches a maximum then drops off, and hence experiencing negative differential conductivity (NDC) i.e.
increases and researches a maximum then drops off, and hence experiencing negative differential conductivity (NDC) i.e.
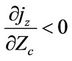 . We observed that as the amplitude increases the normalized current density maximum decreases and shifts towards large electric field values. This “right shift” of the current density maximum is due to a nonlinearity of the Esaki-Tsu characteristics (i.e. nonlin
. We observed that as the amplitude increases the normalized current density maximum decreases and shifts towards large electric field values. This “right shift” of the current density maximum is due to a nonlinearity of the Esaki-Tsu characteristics (i.e. nonlin
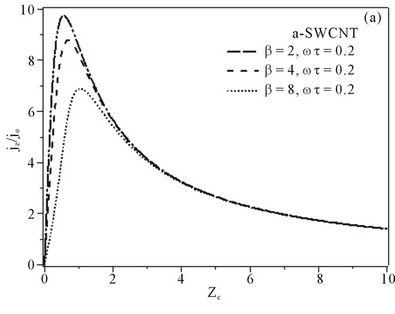
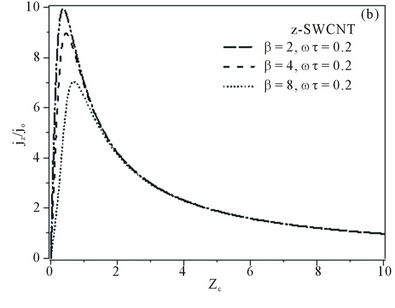

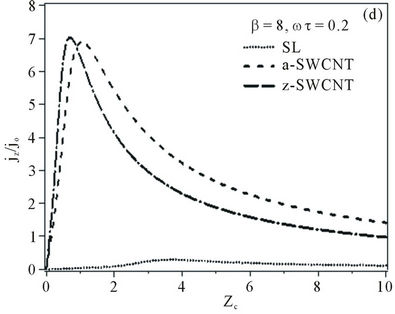
Figure 1.  curves for (a) armchair; (b) zigzag ; (c) superlattice when: ωτ = 0.2 and β = 2, 4, and 8; (d) superlattce; armchair; and zigzag for β = 0.8, ωτ = 0.2.
curves for (a) armchair; (b) zigzag ; (c) superlattice when: ωτ = 0.2 and β = 2, 4, and 8; (d) superlattce; armchair; and zigzag for β = 0.8, ωτ = 0.2.
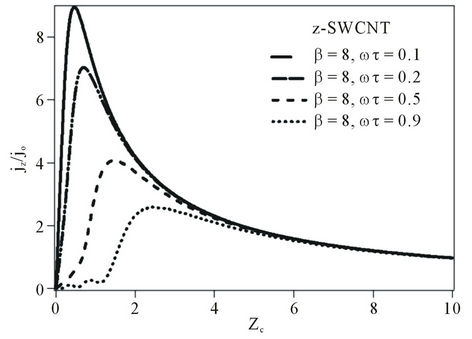
Figure 2.  curves for (a) Expression (14); when: β = 0.8, and ωτ = 0.1, 0.2, 0.5 and 0.9 respectively.
curves for (a) Expression (14); when: β = 0.8, and ωτ = 0.1, 0.2, 0.5 and 0.9 respectively.
earity associated with the non-parabolicity of the electron energy band) which is very strong in SWCNT because of the high stark component (summation over r). We noted that the nonlinearity in SWCNT is much higher than in SL [9,10]. See Figure 1.
The current density-electric field characteristics curves for the nanotubes structures are qualitatively similar to those of SL. However, the NDC effect on the SL appeared at larger electric field strengths in comparison with the nanotubes. See Figures 1(a)-(c).
We sketched also the graph of 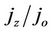 against
against 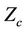 for
for 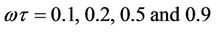 when
when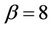 . See Figure 2. We observed that when
. See Figure 2. We observed that when , the normalized current density
, the normalized current density 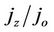 for the nanotubes structures (z-SWCNT, a-SWCNT) linearly depends on
for the nanotubes structures (z-SWCNT, a-SWCNT) linearly depends on 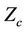 at weak applied external static electric field strengths. On the other hand for
at weak applied external static electric field strengths. On the other hand for  the normalized current density oscillates at weak applied external static electric field strengths.
the normalized current density oscillates at weak applied external static electric field strengths.
The estimations of the restrictions to the theoretical approach can be found in [11].
4. Conclusion
We have studied theoretically the current-density electric field characteristic in the presence of ac-dc driven field and negative differential conductivity was observed. The current-density electric field characteristic shows a negative differential conductivity when 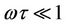 (quasi-static case). We suggest that this phenomenon can also be used for the generation of terahertz radiation without electric current instability.
(quasi-static case). We suggest that this phenomenon can also be used for the generation of terahertz radiation without electric current instability.
REFERENCES
- S. Iijima, “Helical Microtubules of Graphitic Carbon,” Nature (London), Vol. 354, 1991, pp. 56-58. doi:10.1038/354056a0
- A. S. Maksimenko and G. Ya. Slepyan, “Negative Differential Conductivity in Carbon Nanotubes,” Physical Review Letters, Vol. 84, No. 2, 2000, pp. 362-365. doi:10.1103/PhysRevLett.84.362
- S. Y. Mensah, “The Negative Differential Effect in a Semiconductor Superlattice in the Presence of an External Electric Field,” Journal of Physics: Condensed Matter, Vol. 4, No. 22, 1992, pp. L325-329. doi:10.1088/0953-8984/4/22/001
- F. Klappenberger, K. N. Alekseev, K. F. Renk, R. Scheurer, E. Schomburg, S. J. Allen, G. R. Ramian, J. S. S. Scott, A. Kovsh, V. Ustinov and A. Zhokov, “Ultrafast Creation and Annihilation of Space-Charge Domains in a Semiconductor Superlattice Observed by Use of Terahertz Fields,” The European Physical Journal B, Vol. 39, No. 4, 2004, pp. 483-489. doi:10.1140/epjb/e2004-00221-y
- C. Kane, L. Balents and M. P. A. Fisher, “Coulomb Interactions and Mesoscopic Effects in Carbon Nanotubes,” Physical Review Letters, Vol. 79, No. 25, 1997, pp. 5086- 5089. doi:10.1103/PhysRevLett.79.5086
- M. F. Lin and K. W. K. Shung, “Magnetization of Graphene Tubules,” Physical Review B, Vol. 52, No. 11, 1995, pp. 8423-8438. doi:10.1103/PhysRevB.52.8423
- C. L. Kane, E. J. Mele, R. S. Lee, J. E. Fischer, P. Petit, H. Dai, A. Thess, R. Smalley, E. A. R. M. Verscheueren, S. J. Tans and C. Dekker, “Temperature-Dependent Resistivity of Single-Wall Carbon Nanotubes,” Europhysics Letters, Vol. 41, No. 6, 1998, pp. 683-688. doi:10.1209/epl/i1998-00214-6
- R. A. Jishi, M. S. Dresselhaus and G. Dresselhaus, “Electron-Phonon Coupling and the Electrical Conductivity of Fullerene Nanotubules,” Physical Review B, Vol. 48, No. 15, 1993, pp. 11385-11389. doi:10.1103/PhysRevB.48.11385
- F. G. Bass and A. A. Bulgakov, “Kinetic and Electrodynamic Phenomena in Classical and Quantum Semiconductor Superlattices,” Nova Science, New York, 1997.
- O. M. Yevtushenko, G. Ya. Slepyan, S. A. Maksimenko, A. Lakhtakia and D. A. Romanov, Physical Review Letters, Vol. 79, 1997, p. 1102.
- G. Ya. Slepyan, S. A. Maksimenko, V. P. Kalosha, J. Herrmann, E. E. B. Campbell and I. V. Hertel, “Highly Efficient High-Order Harmonic Generation by Metallic Carbon Nanotubes,” Physical Review A, Vol. 60, No. 2, 1999, pp. 777-780. doi:10.1103/PhysRevA.60.R777
NOTES
*Corresponding author.

