ABSTRACT

Data from a recently discovered long Gamma Ray Burst (GRB 090102) by NASA’s Swift satellite revealed that such GRBs may not be fireballs as usually presumed, but instead they are powered and collimated by organized strong magnetic fields generated by the compact object, a neutron star (NS) created at the core of the associated supernova explosion (SNeII). A mechanism for the generation of such strong surface magnetic fields where power NSs result from the deaths of massive progenitor stars is described based on a non-conventional model for pulsar magnetic fields, namely, spinning polarization charge that I recently developed in [1]. I show that this could give rise to scenarios involving long GRB events as the one captured by the Swift satellite during GRB 090102 in January 2, 2009. The model predicts that the magnetic moment of a NS has a dynamical feature which makes it different from that of a simple pulsar. I show this could have serious consequences on the statistics of observing long GRBs and also help explain such scenarios as the steep decline in the photon count-rate and the subsequent shutoff in the Swift/XRT X-ray data from GRB 070110.

1. Introduction

GRBs are events related to highly beamed or pulsed brief bursts of radiation that randomly appear on the sky releasing energy in the order of 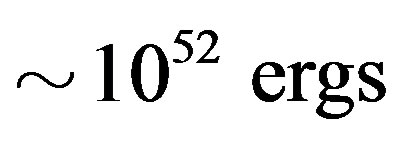[2-4]. GRBs have been the subject of intense research ever since they were first discovered in 1967. According to observational data from the CGRO (1,2), the spatial distribution of these events is almost isotropic. Current understanding of GRBs is that they are phenomena produced by the dissipation of the kinetic energy of a relativistically expanding wind or a “fireball”. A recent 10% ± 1% polarization measurement of the optical emission from GRB 090102, however, showed that GRBs related to SNeII are powered and collimated by strong magnetic fields that originate from the NSs at the cores of the exploding stars. Actually, model fits to the observations from GRB 090102 suggest large-scale magnetic fields present throughout the relativistic outflow. Following this, the speculation now is that GRBs from SNeII may not be fireballs after all as originally thought but rather are driven by strongly magnetized NSs.

The origin and evolution of NS magnetic fields have been strongly debated on for decades and until now there is no any self-consistent theory able to address these critical issues. At present there seems to be no clear knowledge on how these fields are produced and where they are actually located inside the star [5,6]. The current understanding is that NS magnetic fields could either be fossil remnants from progenitors found in the form of Abrikosov fluxoids of the core proton super-conductor [7] or be crustal fields created by thermoelectric instabilities after the birth of the NS [8]. Regardless of this, however, it has been pointed out by several authors that supernova bounce and the related core stability require magnetic fields in excess of 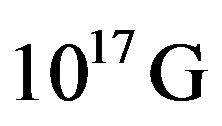[9]. It is known that a shock wave powered by released gravitational binding energy will not lead to prompt core collapse supernova because the shock looses a substantial fraction of its energy in the outer part of the Iron core. No simulation predicts a successful SN for a Fe—core progenitor star with. Moreover, general relativistic magnetohydrostatic calculations show that magnetic field strength up to 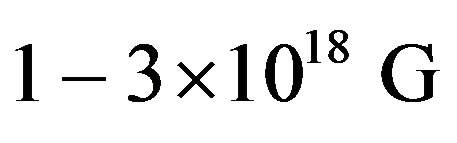is not large enough to influence particle compositions or matter pressure considerably [10].

In this issue, I will, based on the new model, show (see next section) that, at birth, NSs could have very strong surface magnetic fields, up to, and these fields are the engines that drive the observed long Gamma Ray Bursts in SNeII such as the one detected by the Swift satellite in GRB 090102. I will relate the dynamic properties of pulsar magnetic moment to some of the known properties of long GRBs from SNeII as well as attempt to give valid interpretations to some of the related observations from such sources.

2. Magnetic Moments of NSs and Their Dynamic Properties

Findings of the Swift satellite seem to link the burst observed in GRB 090102 to a possible strong magnetic field 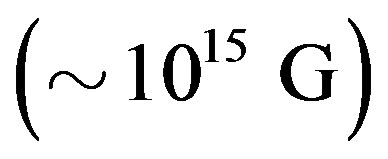from the compact object (NS) centered at the core of the related SNeII. However, as already mentioned in the introduction, the sources for these fields are not very well known. Determination of the actual sources for NS magnetic fields, in general, has been and still is the biggest challenge to current pulsar theory. The following is a short description of how spinning polarization surface charge could give rise to the observed NS magnetic fields first outlined by [1,11].

The structure of a NS is believed to consist of a solid crust, a superfluid interior and an inner core, presumably also solid (neutron solid) as pointed out by [12] and some others. The constituents of NS matter are mostly nucleons, ions and electrons in the solid crust; neutrons, proton and electrons in the outer core suggesting that a NS may be treated as a compact object in a plasma state. However, since the electrons are the lightest species in the plasma and they will be the quickest to respond to any driving force. For this reason we will consider the plasma as a one component (electron) plasma in the rest of this manuscript.

Calculations show that a NS generally has a surface density of 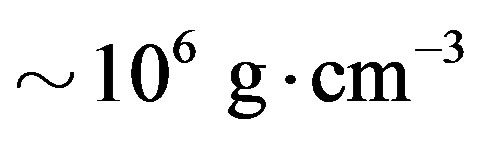[13,14] and a central density ranging between 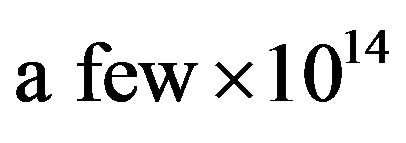and depending on the mass of the NS. These figures clearly indicate that, under normal circumstances, there is a huge radial plasma density gradient within any NS. For example, using a crude approximation of singly ionized crustal atoms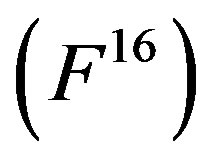, the free electron density near the NS surface may be estimated to be. On the other hand at the bottom of the crust, [15] estimates a plasma density of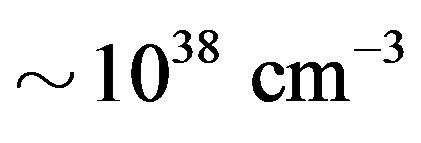. From these figures alone we easily derive a radial plasma density gradient of 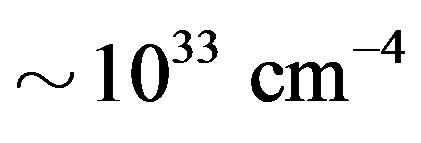threading the crust of the NS alone. The rest of the NS parts are expected to be threaded by even much stronger plasma density gradients.

The plasma density gradient, in general, is modeled as [1]

(1)

where, (see Equation (2) below)

and. These relations are expected to hold true even at the early stages (proto-NS stage) of the compact object.

The plasma density gradient generates the force that drives the electrons with an acceleration

(3)

where, is the electron Fermi energy (or chemical potential). This acceleration is many orders of magnitude stronger than the gravitational acceleration even at a location close to the proto-NS surface and gives rise to a spherically symmetric current which is our ultimate interest in this particular issue. However, if we also would like to consider general relativistic effects including that from the rotation of the frame, the current equation should be modeled as, [1],

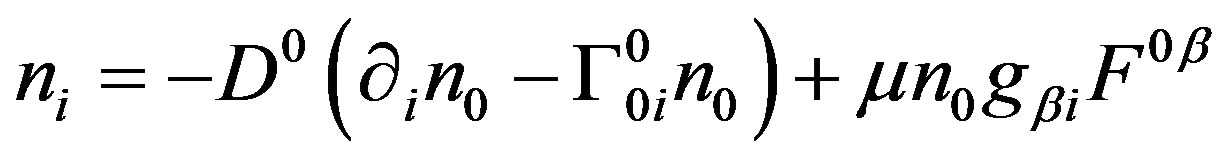(4)

where,.

The spherically symmetric current driven by Equation (3) establishes a polarization field (or charge) [11] which will restore hydrodynamic equilibrium inside the compact object (the proto-NS). For the surface plasma density of 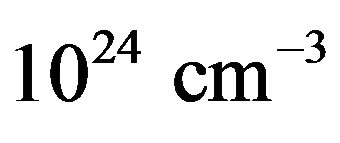we have calculated earlier, the magnitude of the surface charge required to restore hydrodynamic equilibrium, in all cases, will be small enough to be locally drawn from the material found within a depth not more than a couple of centimeters into the proto-NS surface, in a rather very short time. Generally, the spinning surface charge not only generates the kinds of fields we mentioned earlier but the fields in return will ensure supernova bounce and the stability of the proto-NS.

If we ignore the rotation of the frame and other gravitational effects, the polarization field associated with the separated charge will be

(2)

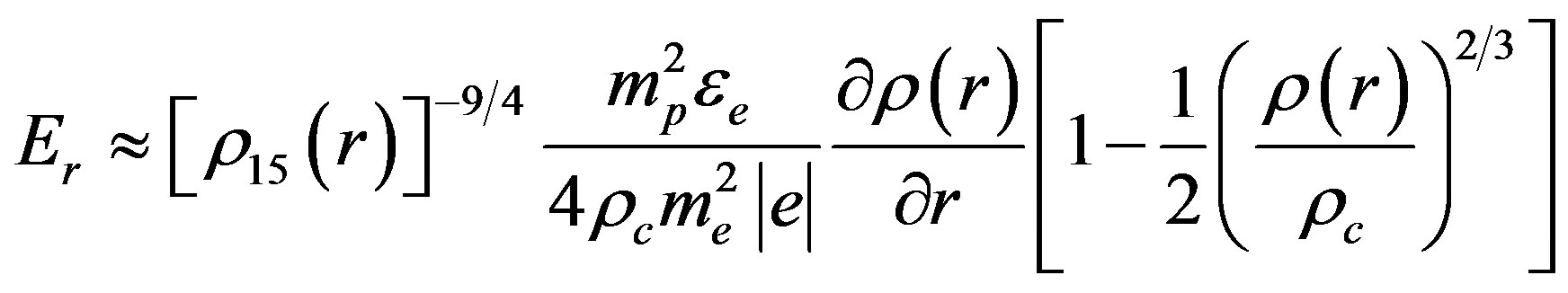(5)

where, is the critical density.

Since NSs normally rotate very fast, the spinning polarization (surface) charge is expected to generate a strong magnetic field. I have, in a previous issue [1], shown that a TI star with mass of, central density of 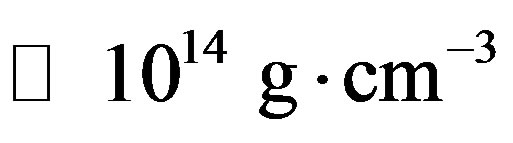and spinning at a rate of only will, as a result of the spinning of polarization charge, attain a surface magnetic field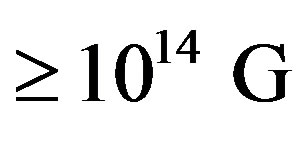. If we leave out the effect of the rotation of the NS, the resulting magnetic field of such a rotator, assuming the NS surface is spherical, will be purely dipolar [1]. This result is in excellent agreement with experimental estimates of the main component of NS surface magnetic field [16-18]. However, if the effect of the rotation of the frame is also included into the calculations early on, it can easily be shown that there will be higher poles appearing alongside the main dipole term suggesting that, according to the new model, NS surface magnetic fields are naturally multipolar in agreement with what current experimental findings seem to indicate.

The intensity of the dipole field is determined not only by the magnitude of the polarization (surface) charge which itself is strongly core plasma density (or central density) dependent, but also by the spin frequency [1]. Realistic equations of state predict that NSs could have masses, central densities and radii in the range

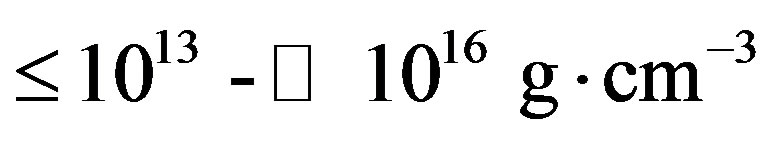, , and

respectively [19]. This, coupled with the fact that massive progenitors are capable of giving birth to NSs with spin periods [20]¹, means that these objects could, at birth, be powered by very strong surface magnetic fields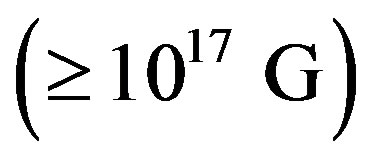. Such fields ensure a successful bounce of the remnant. They are also expected to catastrophically decay by 2 - 3 orders of magnitude in a matter of couple of minutes or so, mainly, as a result of magnetic dipole radiation. It will take additional thousands of years for them to decay to 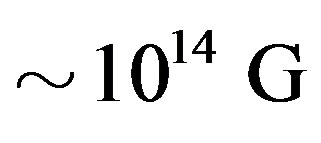and their rotational period increase by about four orders of magnitude as a result. See Section 3 for the time evolution of such fields. In general, the intensity of the magnetic field at the time of a NS birth could be anywhere between and depending on the mass of the progenitor star. Long GRBs from SNeII such as GRB 090102 are most likely powered by fields in the range.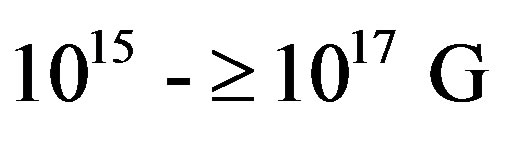

In the new model for NS surface magnetic fields, differential rotation between the crust and the core of the NS is assumed. Misalignment between their axes of rotation is also considered as a possibility. This could be due to asymmetry in supernova bounce or kicks [22]. These assumptions lead to a natural oblique rotator possessing dynamical features different from that of the commonly expected simple pulsar [11]. According to the findings listed in this paper, the dynamics of the NS magnetic moment, beginning with the event of a supernova explosion, passes through three distinct phases, namely, the chaotic phase (deterministic and slow [11]), the pulsar phase and the quiescent phase. Under normal circumstances, these dynamical features will be exhibited by every NS during its life time in the exact sequence listed above. In the first phase, the magnetic moment will assume random orientations in space. In the second phase the NS will emit periodic pulses into space whereas in the last phase the magnetic moment will be aligned along the NS spin axis as a result of which there will be no radiation coming from the NS. The transition from one phase to the next is mediated by the change in the viscosity of NS matter which comes as a result of cooling via neutrino and photon emissions. The chaotic phase may last for thousands of years depending on how fast the NS material cools. In this same issue the chaotic phase was employed to address such standard problems in current pulsar Astrophysics as that of missing pulsars and delayed pulsar onset.

3. Application of the New Model to GRBs from SNeII

Until very recently one point of controversy about the nature of GRBs from SNeII was the extent in which magnetic fields rather than matter generated forces are involved in accelerating and collimating the jets of material emitted at relativistic velocities from the expanding remnant. In the standard baryon dominated scenario ([23,24] magnetic fields are generated in situ by way of plasma instabilities [25] in mainly relativistic shocks and they are not considered as dynamically important even though there is a wealth of recent evidence (from Swift data, for example) hinting otherwise. The IS model is known to have its difficulties of low efficiency, lacking bright photospheres, fast cooling, etc. [26].

Currently there is a proposal variant to the IS model suggesting that the GRB ejecta carries a strong magnetic field which dissipates its energy within the ejecta that later on powers the GRB radiation throughout the relativistic flow [27]. Swift data from GRB 090102 seems to strongly support the involvement of large scale magnetic fields in GRBs from SNeII. Model fits to the observations from this particular burst suggest large-scale magnetic fields present throughout the relativistic outflow, originating from the start inside the “central engine—not the surrounding plasma” driving the explosion, accelerating and collimating the jet.

This is the kind of large-scale magnetic field the new model is presenting, a field originating from a central engine (NS) and not from the surrounding plasma like all fields related to MHD sources are. The model indicates that there exists a direct (one-to-one) relationship between the strength of the surface magnetic field and the rotation frequency of the associated NS. This means, due to conservation of angular momentum, the kinds of strong magnetic fields indicated in the preceding section are connected to extremely rapidly rotating high mass progenitor stars. Consequently, the very large angular momentum connected to these stars together with the strong magnetic radiation pressure from the central compact object (proto-magnetar) can cause most of the matter and the energy from the SNeII to be focused into an extremely fast (with a speed of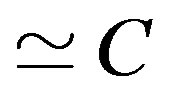) and narrow GRB jet so much so that the energy emitted in our direction almost matches that picked up by measuring instruments during a GRB event. This clearly shows that the new model for pulsar fields is in complete coherence with current understanding of relativistic jet formation and GRB generation in SNeII.

GRB jets from SNeII are threaded by strong magnetic fields 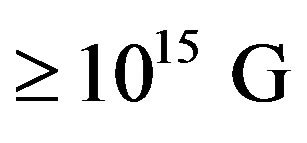as polarization measurements from GRB 090102 indicated, for example. A scenario for the ejection of magnetic field through the stellar envelop has been discussed by several authors [28,29] which will explain the presence of a large scale magnetic field throughout the relativistic outflow observed in GRB 090102.

It has already been indicated above that the surface magnetic field of NSs, according to the current model, is spin frequency dependent which makes the decay of these fields to be extremely catastrophic particularly early in the life time of the NS if it is initially strongly magnetized (see next section). Based on this we conclude that the surface magnetic field of the compact object for the event in GRB 090102 that was measured a couple or so minutes after the explosion must have been.

According to current understanding, to power a GRB event such as the one displayed in GRB 090102, the millisecond young magnetar must have a surface magnetic field and spin frequency such that its dipole spin down luminosity is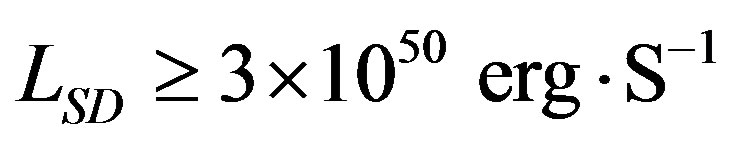. This will require a surface dipole field, minimum, that being the field which was driving GRB 090102, and a spin frequency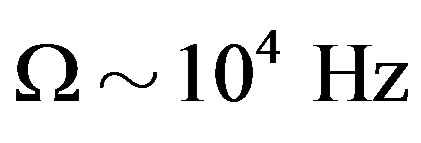. Just for the record, a new born magnetar will be referred to as a proto-magnetar hereafter, and not a magnetar, because, according to the new model, it requires thousands of years (after the supernova event) for it to transit into a pulsar mode and eventually become a magnetar [11] (Table 1).

One specific property of GRBs from SNeII is that they very seldom repeat and the reason for it is not that well

known. However, it is already indicated above that according to the new model the magnetic moment of a proto-magnetar begins its life in a chaotic mode something that stays with it for many thousands of years [11]. I suggest, this could be one of the main reasons why GRBs from SNeII do not repeat. Because of its chaotic motion, the magnetic moment may not assume its original orientation in the frame of reference of the compact object and get captured by the instrument one more time so soon. This does not rule out the possibility to repeat, however.

Under normal circumstances a GRB event associated with SNeII may be generated after the proto NS cools and a Poynting flux dominated outflow is launched, typically several seconds later ([30,31]. According to the present model, however, such a proto NS is formed following a supernova explosion mediated by a strong magnetic field which ensures the SN bounce and at the same time maintains the stability of the core. Actually, in the preceding section, it was indicated that massive progenitors give rise to proto NSs with very high surface magnetic fields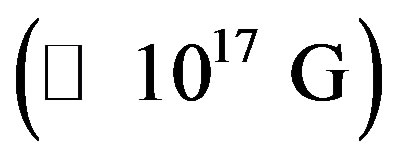. Once the remnant thins out, a long GRB event is expected to launch. These GRBs are known to be related to those massive progenitors whose masses are in the range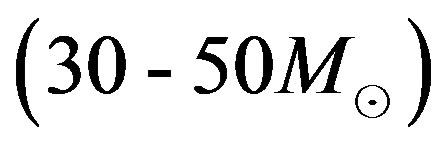. This seems to be in a very good agreement with what was just discussed above and the physical ground on which the present model is built. Accordingly, then all supernovae should produce long GRBs.

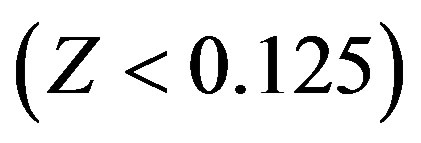Regardless of expectations, however, long GRBS remain to be very rare phenomena as compared to SNeII, in general. Even such close by long GRBs as GRB 060505 and GRB 060614 do not have SNe. [4] indicated that at most, of supernovae are GRBs even though all SNeII are believed to have jets. This longstanding issue regarding the disparity between the number of SNe and observed long GBBs can be resolved using, once again, the chaotic nature of the dynamics of the magnetic moment of pre-magnetars. This involves the unpredictable nature of its start-off direction. Most probable is that it might not even drive a GRB event in our direction initially; but its motion will ultimately take it to the origin. Refer to Figure 2 [11]. However, it will be undecided when it comes out of the origin because its state of motion after that will all depend on the initial conditions at the origin. The situation is like a ball sitting on top of a sphere. Initial conditions matter a lot on the subsequent motion after the origin. There is a probability for the magnetic moment to come into view after sometime, but it may not have the magnetic field strength enough to generate a GRB event on the scale of GRB 090102. This is mainly because of the fast decay it experiences during transition.

A descent to the origin is expected to involve a relatively quick change in the direction of the magnetic moment and consequently a fast reduction in the X-ray afterglow count rate. Following this, there will be an immediate shut-off since, as indicated just above, the state of motion of the magnetic moment immediately after passing through the origin will not have the memory of its past. Such a scenario can be used to understand Swift/ XRT data from GRB 070110.

There are those who like to consider that some premagnetars like the one responsible for GRB 070110 are formed before the final collapse of the system leading to an unusual plateau and steep decay in the afterglow X-ray light-curve. [32,33] suggest that the abrupt dropoff in the X-ray light-curve could be related to the spindown of the pre-magnetar. However, after being in action for some fifteen minutes or so, the magnetic field is not expected to undergo a fast decay for the rest of the several weeks needed to completely kill-off the X-ray countrate, as the data from this particular GRB shows (refer to Table 1).

4. Magnetic Field Evolution and Spin Down of a Pre-Magnetar

Our new model for pulsars clearly shows that NS magnetic fields are spin frequency 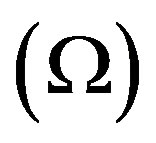dependent [1] and should decay as a result of known braking mechanisms such as gravitational quadrupole and magnetic dipole radiation as well as neutrino emission. The time rate of energy loss due to magnetic dipole radiation will be

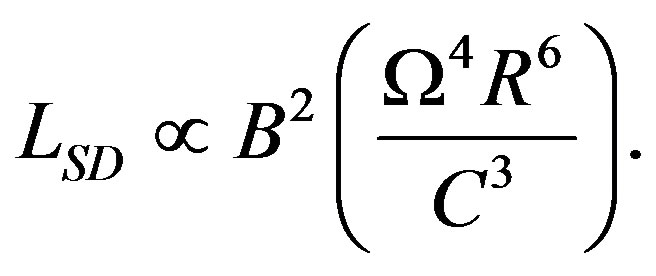(6)

According to the present model, [1] where and are the magnitude of the separated charge and the spin frequency respectively. This leads to a pulsar field decay law due to magnetic braking alone. The results are listed in Tables 1 and 2, for those pulsars commonly referred to as field pulsars and pre-magnetars as well.

5. Discussion

Many aspects of long GRBs are still not very well understood regardless of recent advances following the launch of Swift and Fermi. The physics behind the possible

sources for the strong magnetic fields required to power the core engines (NSs) believed to drive long GRBs was discussed in Section 2. The diversity of the initial premagnetar surface magnetic fields which is directly related to the diversity of the masses of the progenitor stars (or the pre-magnetars themselves) suggested by the new model gives us the extra advantage to have a better look at the longstanding issue of pulsar field decay. Regarding this, current understanding is that magnetic fields of Isolated Pulsars (IPs) will show very little decay in the first 10⁶ yrs and then totally stop decaying there on for up to 10⁸ yrs [34,35]. The decision was made based on simulation studies which limit the initial pulsar fields to within the canonical value of. Very high field pulsars are not fairly represented in the study.

 The findings of the present model indicate that pulsar fields continually decay as a result of magnetic dipole radiation suggesting that all pulsars, including Anomalous X-ray Pulsars (AXPs) and Soft Gamma-ray Repeaters (SGRs) (Table 1), are driven by their respective magnetic fields. Recent observations of a number of very high magnetic field radio luminous pulsars [36,37] support this conclusion. Their findings clearly tie AXPs and SGRs to potential radio sources. In good agreement to this is also the finding of [38] from their studies on period 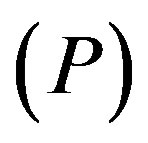and period derivative 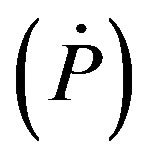distribution of pulsars. They have shown that there exists a strong correlation for field pulsars including AXPs and SGRs.

I hold that the pulsars that are indicated to have not decayed [35] could have began their lives with widely different initial surface fields ranging between 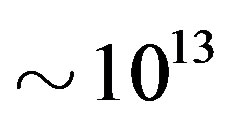and. These fields eventually decayed down to their present strengths 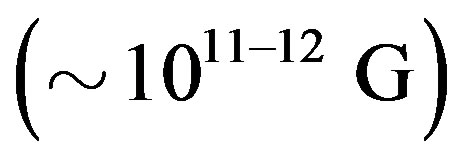each through a time window comparable to their respective ages. Their initial spin periods could have been anywhere between 5 - 10 ms [20]. In general, any discussion on magnetic field decay must refer to the initial surface field strength which, according to the present model, may not necessarily be the canonical value of.

Finally, it will not be hard to imagine that the intensity of the surface magnetic field of a proto-NS at the core of a massive progenitor star increases during core collapse as a direct result of flux conservation of some commonly assumed seed field threading the star. Since the current model for proto-NS surface magnetic fields relies on inherent plasma density gradient, within such kinds of compact objects, these fields should also show growth in intensity during collapse. Notice, however, that the two processes for field growth are totally different. The latter process seems to indicate that the magnetization of the core of the progenitor star begins early in its life, that is long before (a few × 10⁶ yrs. before) its collapse.

The Astrophysics of pre-supernova evolution of massive stars predicts that the cores of these stars get progressively hot and dense as they age. Massive stars are normally believed to have ages between 5 - 10 million years. The changes within their cores take place as a result of gravitational contraction marked by halts that signal the onset of the nuclear burning of the next fuel in the succession of those available. The core of a massive star will consist of mostly Helium at about 85% - 90% into the star’s life. At every stage of the evolutionary process, however, the core not only gets denser and hotter than it was in the previous stage but, will also spin much faster as a unit. Some sort of differential rotation between its innermost region and the surface could be assumed as this is also the case with the rest of the star in general. More importantly, however, the massive star will gradually develop larger and larger radial plasma density gradient within the core which demands a progressively increasing polarization field to re-establish the disrupted hydrodynamic equilibrium that comes along with the change. This could then give rise to a possible core magnetic field. The situation becomes more and more aggressive towards the end of the massive star’s life since the duration of the nuclear burning phase in this case is very short. In particular the last phases before catastrophe are extremely short.

In the new model for pulsar fields, focus is made on these cumulative processes that lead to a progressively stronger core magnetic field through the millions of years of the star’s life time even though the largest contribution to the surface magnetic field of the Proto—NS comes in the very short span of time during which the core gets compacted as a result of gravitational collapse. It is the largest contribution because it comes as a result a huge plasma density of (see Section 2) created by the extremely compacted NS matter at the very end of the dying progenitor star’s life. It has already been indicated in the same section that the polarization charge required to restore the disrupted hydrodynamic equilibrium caused by the radial plasma density gradient is small enough to be locally drawn from the NS material found within a depth not more than a couple of centimeters or so into the NS-surface in quite a very short time essentially because of the huge driving force which is proportional to the plasma density gradient 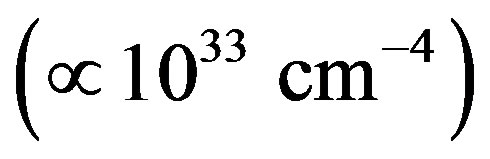inside the crust (see Section 2). The final core magnetic field is NS mass dependent. Obviously, the mass of the NS is the main factor that determines the magnitude of the plasma density gradient.

6. Conclusions

This paper demonstrates the fact that Long GRBs from SNeII are related to massive progenitors which according to the current model for pulsar fields [2,11] would mean that these GRBs are driven by initial surface field strengths of the order. Measurements related to GRB 090102 have already indicated this. These progenitors are expected to have a central density of 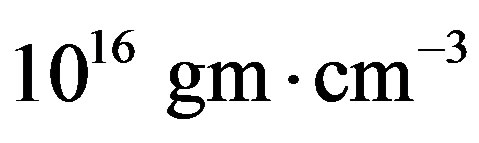which gives rise to a huge plasma density gradient or a very big driver for the strong fields indicated above. This is central to the predictions of the current model.

The fact that the measurements from GRB 090102 indicated that the relativistic plasma flow responsible for the afterglow is driven and collimated by the strong magnetic field of the compact object situated at the very core of the explosion, that is, the NS created by the implosion, strongly supports the mechanism for the generation of NS surface magnetic fields as outlined in this model. This would mean the spinning of separated charges forced by the current shown in Equation (4). As shown in [2], this eventually will give rise to a natural oblique rotator with a built-in or inherent chaotic behavior, a property that was used to explain such aspects of Long GRBs as the disparity between the number of observed SNeII and the number of Long GRBs associated to these explosions.

Even though it is not of current interest to us, it is good to know, however, that a thorough investigation of the model equation for the currents given in Equation (4) will show that magnetic field reconnection comes natural to a strongly magnetized NS leading to X-Ray flares. Anomalous X-Ray Pulsars (AXPs) and Soft Gamma-Ray Repeaters (SGRs) are known to flare in X-Ray. The production of the X-Ray flares is similar to those operating in the Solar Corona, namely, energy dissipation from simulated magnetic reconnection models [39] normally accompanied by particle acceleration mechanisms such as shock acceleration responsible for the flares [40].

REFERENCES

NOTES

¹The theoretical NS breakup period is ~0.1 mS [21].