American Journal of Plant Sciences
Vol.4 No.5(2013), Article ID:32155,7 pages DOI:10.4236/ajps.2013.45135
New Method for Measurement of Plant Roots Specific Surface
![]()
Institute of Agrophysics of Polish, Academy of Sciences, Lublin, Poland.
Email: jozefaci@demeter.ipan.lublin.pl
Copyright © 2013 Grzegorz Jozefaciuk, Malgorzata Lukowska. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 4th, 2013; revised April 10th, 2013; accepted May 10th, 2013
Keywords: Adsorption Isotherm; Plant Roots; Specific Surface Area; Cation Exchange Capacity
ABSTRACT
To provide enough space to carry all surface charges responsible for high cation exchange capacity of plant roots, large area of the root specific surface is necessary, however all experimental methods used up to date give too small surface area values. In this paper, we propose to measure the plant roots surface area using water vapor adsorption isotherm. This method gives roots specific surface areas compatible to CEC. Methodical aspects of the measurements are described along with theoretical background for calculating specific surface area on the example of roots of barley grown in nutrient solution.
1. Introduction
Most interactions between plant and soil take place at root-soil interface. One side of this interface consists from soil solid particles, air and solution, and the second side from root surface being in contact with soil constituents. Therefore the extent of root surface is extremely important for understanding plant-soil processes, especially these of water and nutrient uptake by plants [1,2].
The cation exchange capacity (CEC) of roots, expressing available surface charge at a given pH, ranges from a few to a few tens of cMol kg−1 (mMol per 100g) of the dry material [3]. The total charge carried by plant roots is around two times higher. Jozefaciuk and SzatanikKloc [4] determined the total charge of roots of cereal plants from 40 (rye) to 85 (barley) cMol kg−1. Assuming that the total charge of a plant root is only 50 cMol kg−1 one can calculate that 1g of such roots carries 3.01 × 1020 elementary charges. The molecular dimension of even a simple molecule is around one nanometer: the cross dimension of one of the simplest amino acid alanine is 0.75 nm as calculated from molecule volume data given by Cooper et al. [5], and of galacturonic acid that is a basic component of polymeric cell walls structure is around 0.6 nm, as calculated from Density Functional Theory using PQSMol program provided by Parallel Quantum Solutions (http://pqs-chem.com/). Thus taking the cross dimension of a charge generating molecule on the root surface as 0.6nm and of the area of 0.36 nm2, the 50 cMol kg−1 charges of plant roots have to occupy 108,4 m2 of the specific surface of one gram of the roots, even if the surface charge generating groups are located in a closest arrangement and no other molecules are present between.
Usually the surface area of plant roots of a few square centimeters to a few square meters per gram, measured by immersion of roots in water or in electrolyte solutions, is reported [6,7] that is far too small to provide enough space for surface charged groups. In these methods a very thick layer of water (solution) adhered to the surface is taken as a measure of the surface area that shades real surface details. Certainly the finest roots do not contribute to this value and the external geometrical surface of the thickest roots is measured. Therefore in this paper application of adsorption isotherm to characterize plant roots specific surface area is proposed.
Despite the usefulness of adsorption isotherm for estimation of surface areas of soils, clays, minerals, soil organic matter, industrial and chromatographic adsorbents, powders and many other solids, confirmed by enormous amount of results published, adsorption isotherms are rarely used for determination of plant roots specific surfaces. Some results showing their applicability for assessment of changes of plant roots surfaces under aluminum and heavy metals stresses can be found in [4,8-11].
The adsorption isotherm is a function relating the amount of gas or vapor (adsorbate) adsorbed on a surface of a bare solid (adsorbent) to the equilibrium pressure of the adsorbate during the pressure increase at a constant temperature [12,13]. The adsorption isotherm can be measured using either instrumental equipment (sorptomates, Dynamic Vapor Sorption DVS apparatuses) or manually in a vacuum chamber. Instrumental methods measure the isotherm for one sample in one experimental cycle, whereas the number of the samples studied simultaneously in the same cycle in manual method is practically limited only by the chamber space. The vacuum chamber method is easiest, most convenient and most cost-effective. Among many adsorbates used for adsorption isotherms measurements the most popular are nitrogen (the measurement is performed at liquid nitrogen temperature) and water vapor. Because water vapor adsorption better relates to plant behavior in natural conditions than nitrogen adsorption, the present paper is designed to present methodical theoretical aspects of plant roots surface area measurements from water vapor adsorption isotherms using vacuum chamber method.
2. Material
Roots of barley Hordeum (Ars) Stratus grown in the Marschner and Romheld [14] nutrient solution, harvested at the occurrence of a Flag Leaf were used. After harvesting, the surface of the roots was standardized to a homoionic form, because water adsorption processes strongly depend on the kind and amount of surface ions [15]. Since acid washing removes surface exchangeable ions and replaces them by protons, the harvested roots were rinsed 3 times in 0.01 moldm−3 HCl and 5 times in distilled water. No basic cations in the third HCl extract was detectable by AAS, so it was assumed that the homoionic hydrogen form of the roots was obtained.
To check the effect of the state of the root material on the isotherms, the roots in a fresh state just after harvesting and washing (abbreviated further as F), lyophilized just after harvesting and stored in a closed vessel by 2 weeks (L), air dried and stored in the laboratory atmosphere by 2 weeks (AD) and dried at 105˚C by 24 h 6 days before the isotherms measurements (D105) were studied.
The adsorbent samples should be homogenic. For nonhomogenic samples the isotherms replicates may be quite different. To check the effect of root material homogeneity on the isotherms the whole roots (W) and roots cut to around 1mm length pieces (C) were used, assuming that the latter material is well homogenized.
3. Method
3.1. General Description of the Method
The method is based on equilibration of the adsorbent (plant root) sample with water vapor of a given relative pressure, p/p0 (p is the vapor pressure at the equilibrium and p0 is the saturated water vapor pressure at the temperature of the measurements), estimation of the adsorbed vapor amount (weighing) and repeating the cycle for the same sample at other pressure values and at the same temperature. After completing all measurements the dry mass of the samples, md (kg), is measured (to estimate the weight of the bare root adsorbent) and the amount of the adsorbed vapor on a unit dry mass of the sample, a(p/p0) [kg kg−1] at each p/p0 value is determined:
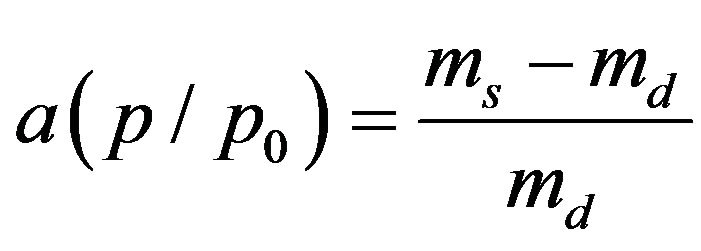 , (1)
, (1)
where ms [kg] is the mass of the sample with the adsorbed vapor, and the isotherm being the dependence of a(p/p0) against p/p0 is plotted. Principally this method may be applied to study any of plant materials as leaves, stems, tissues, cell walls etc.
3.2. Methodical Aspects of the Measurements
3.2.1. Controlling Relative Water Vapor Pressure
The chamber atmosphere should have different p/p0 level at each step of the measurements. The p/p0 values can be controlled by a number of saturated salts solutions or by a series of sulfuric acid solutions of different concentrations. The p/p0 value depends on the kind of salt or on the density (concentration) of the acid, that can be find in physicochemistry handbooks. For the choice of convenience sulfuric acid was used in the present experiments. The relationship of water vapor relative pressure against density of sulfuric acid based on measurements performed in our Laboratory and on handbooks is presented in Figure 1.
Stepwise decreasing densities are used to measure adsorption points. In the adsorption chamber, the sulfuric acid of a given density should be placed in a large vessel poured to a quarter of its volume and covered by a layer of glass wool to avoid eventual splattering of the acid drops while it eventually boils under vacuum. Because of this and the water consumption during adsorption process, the acid concentration changes, the water vapor pressure in the chamber should be determined from the density of the acid measured after completing each step of the measurement. To avoid this, in fact not very precise step, using the internal standard is recommended: the sample of a material of known adsorption isotherm is measured together with the studied roots and the p/p0 is estimated from the adsorbate amount.
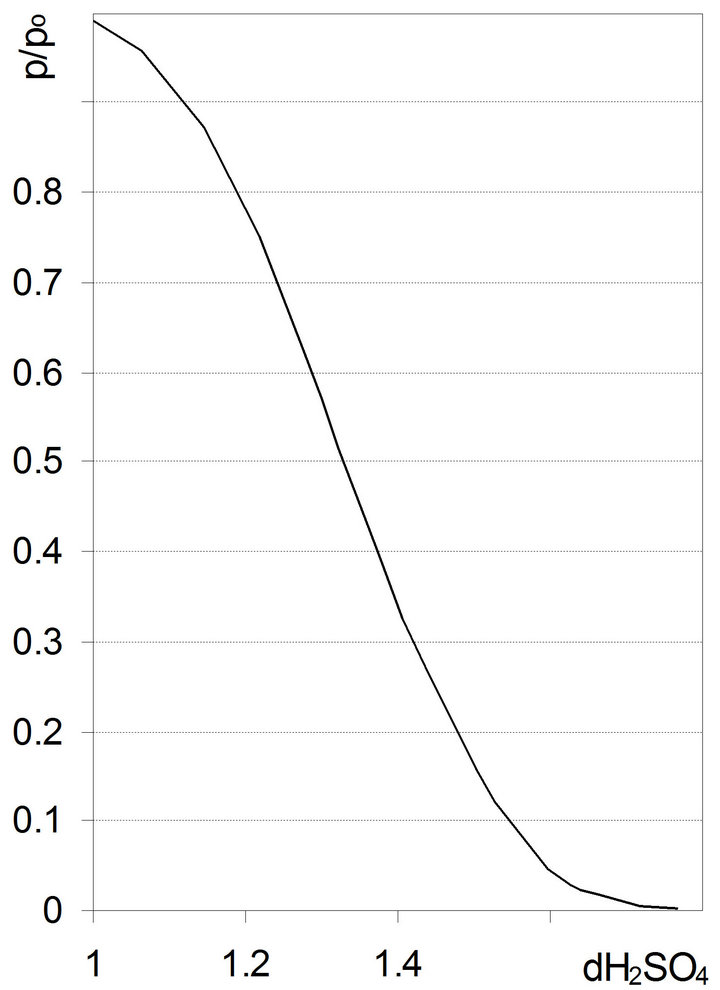
Figure 1. Relative water vapor pressure dependence on density of sulfuric acid solution. d = 1 accounts for pure water.
3.2.2. Adsorption/Desorption Equilibrium time
Because the equilibration of the roots at the lowest p/p0 involves the desorption of water vapor from the roots (stored previously at the laboratory atmosphere) the kinetics of desorption and adsorption equilibriums should be known to establish the proper time of roots contact with water vapor. These kinetics were estimated for root samples placed directly on a balance closed in the measuring chamber. As this is rather obvious, the kinetics of adsorption/desorption and so the equilibration time depends on the difference of relative water vapor pressure at which the sample was stored and of this in the chamber, that is presented in Figure 2.
As this is seen, regardless the starting roots moisture, 30 h equilibration time is enough to reach the equilibrium at all vapor pressures studied. To be sure that the equilibrium conditions are gained while studying more samples in the same cycle, the samples are equilibrated by 48 h at each p/p0 value during adsorption and desorption measurements, and at the starting point, this time is doubled.
3.2.3. Estimation of Dry Mass of the Sample
Usually the dry mass is taken as the adsorbent mass after 24 h heating at 105˚C, assuming that such procedure removes physically adsorbed water. This does not necessarily mean that the samples are dehydrated fully. For example drying of a montmorillonite mineral at temperatures from 100˚C up to 500˚C results in a consecutive removal of water molecules linked to the exchangeable cations. An amount of this kind of water can account of c.a. 3% of the final mass. At higher temperatures the further lost of c.a. 5% of the final mass represents dehydroxylation of the structure [16]. Therefore even for mineral materials the dry mass is defined rather operationally and not by strong physical principles. The lost of mass during drying of the studied roots at increasing temperatures is shown in Figure 3.
The roots mass decreases consecutively with the increase of the drying temperature, more rapidly above 150˚C. From the presented data one can not decide which temperature should be selected to estimate the dry mass of the sample, therefore standard drying at 105˚C, similarly as this is done for other materials (e.g. soils) was applied. This operation mode allows for comparison of the water adsorption on roots with this on soils which is important to study plant-soil relations.
3.3. Manual Remarks
The constraint of the constant temperature during adsorption measurements requires it to be adjusted as precisely as possible, however variations of ±2 K do not practically affect the results. To control the p/p0 level sulfuric acid solutions of different concentrations is used most frequently. Samples of the adsorbate (for plant roots 100 - 200 mg) are placed the in the chamber (a glass desiccator may be applied) in weighing vessels over sulfuric acid of the highest concentration (lowest p/p0). This is important the vessels are not heavy and their lids are tight. The vessels are open and their lids are placed
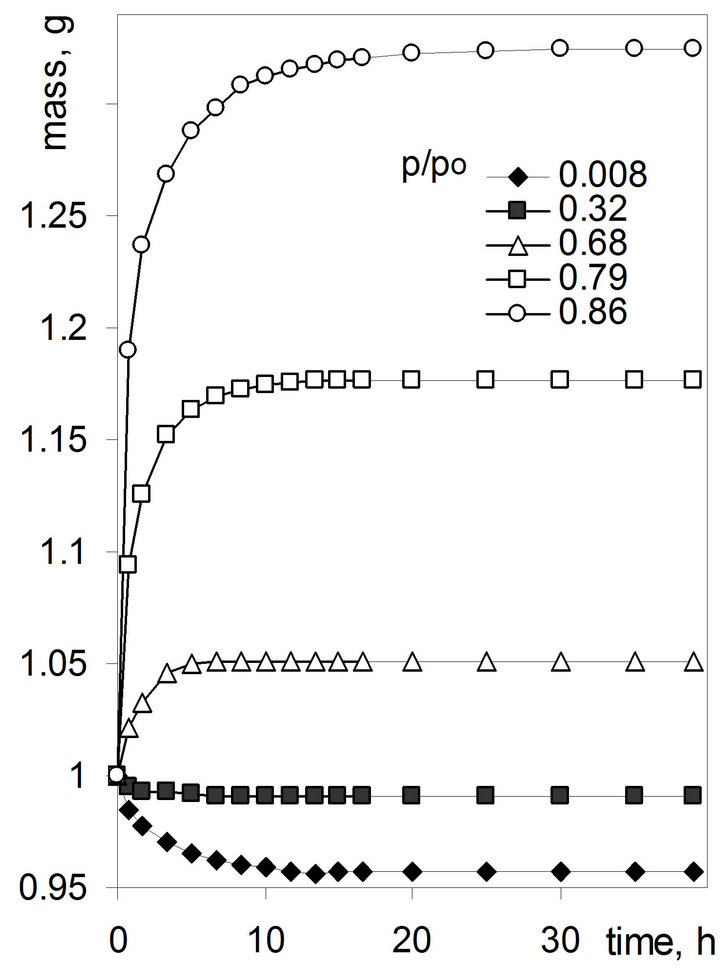
Figure 2. Kinetics of water vapor adsorption and desorption on air dry root sample at different p/p0 levels (marked in the Figure). Initial p/p0 at time = 0 was around 0.4.
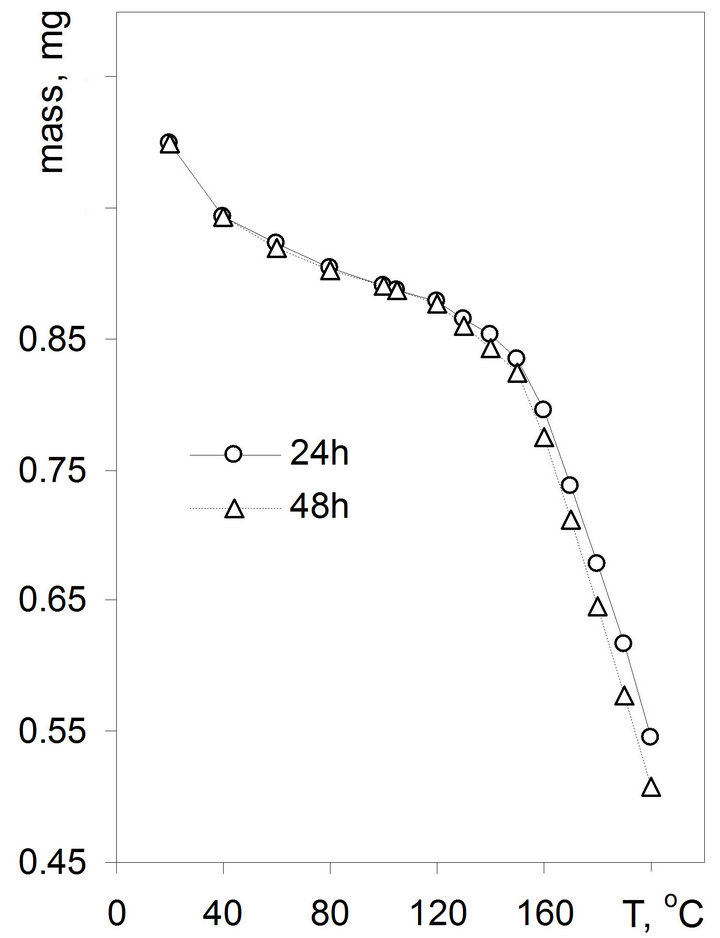
Figure 3. Changes in air dry roots mass during drying at different temperatures. The curves represent drying by 24 and 48 hours. The initial mass of the roots was 100 mg.
upon them diagonally to keep the connection of the sample with the chamber atmosphere. Next the chamber is closed and outgassed to accelerate the adsorption equilibrium. No special requirements for the vacuum level is necessary, standard vacuum pump outgassing the chamber to around 1hPa is sufficient. After reaching the equilibrium, the chamber is slowly filled with the dry air and opened. Now the weighing vessels are closed with the lids as quickly as possible to avoid mixing the chamber atmosphere with humid laboratory air that may cause (slight) changes in adsorbed vapor. To avoid this, after opening one may close the chamber with a transparent plastic cover having operating holes with surgical gloves and close the vessels using these gloves. Now the gross mass of the samples (sample + vessel + lid + adsorbed vapor) is measured with 0.1 mg accuracy (1/1000 of the sample mass). Knowing the mass of the vessel + lid, the ms value can be easily calculated. After weighing the samples, the whole procedure is repeated using more diluted sulfuric acid solution (increase of p/p0). Too small differences between subsequent steps leads in practice to scattering of experimental points, too large provide not enough experimental data. From the experience of our Laboratory, to measure specific surface areas 6 - 7 experimental points measured in the p/p0
range of 0.1 to 0.6 is enough.
3.4. Calculating the Specific Surface Area
The water vapor adsorption process on most natural adsorbents, including plant roots has polymolecular character. The idea of the estimation of the surface area from polymolecular adsorption data is to find a number (mass) of adsorbate molecules which cover the adsorbate surface as a monolayer (monolayer capacity), and to multiply this number by the area occupied by a single molecule. To calculate surface area, usually the standard Brunauer-Emmett-Teller model [17] is applied. However, the BET equation is thermodynamically incorrect and works properly only in a narrow range of a relative humidity, therefore the other, in fact very similar, Aranovich [18] equation, which is thermodynamically correct and fits to the experimental adsorption data in a broader vapor pressure range (BET from 0.05 to 0.35 and Aranovich from 0.05 to 0.6) is recommended. In linear form this equation reads: p
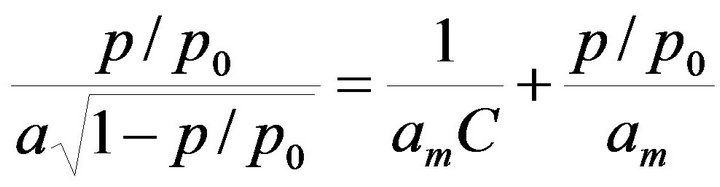 (2)
(2)
where a [kg kg−1] is the amount of the adsorbed vapor at the relative vapor pressure p/p0 and at the temperature T [K], am [kgkg−1] is a monolayer capacity (defined as the quantity of an adsorbate which can be accommodated in a completely filled, single layer of molecules on the surface of the solid), C = exp ((Ea − Ec)/RT is a constant related to the adsorption energy, Ea [J mol−1], and the condensation energy of water, Ec [J mol−1], and R [J mol−1 K−1] is the universal gas constant. The adsorption data are plotted in the coordinates of Equatuion (2) and am values are calculated from the slopes (1/am) of the linear part of the plot. The surface areas of the studied samples, S [m2 g−1], are calculated as:S
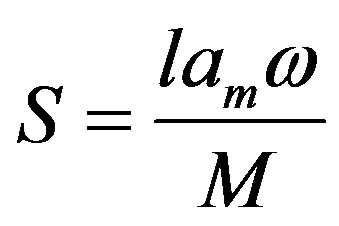 (3)
(3)
where L [mol−1] is Avogadro number, M [kg] is molecular mass of water and w is the area occupied by a single water molecule equal to 1.08 × 10−19 m2.
3.5. The Procedure in Brief
a) place the sulfuric acid of the density corresponding to p/p0 ~ 0.1 in a measuring chamber;
b) place the root sample in a weighing vessel (the lid open) to the chamber;
c) close and outgas the chamber;
d) wait until the equilibrium;
e) fill the chamber with dry air;
f) open the chamber;
g) close the weighing vessel with the root sample;
h) measure the gross mass of the sample (sample + vessel + lid + adsorbed vapor) and save data;
i) estimate p/p0 from the acid density (or from the standard sample of known isotherm placed in the chamber) and save data;
j) place new sulfuric acid (next concentration) in a measuring chamber;
k) repeat steps b) to j) for range of acids corresponding to p/p0 up to ~ 0.6;
l) estimate the dry mass of the sample;
m) use Equation 1 and saved adsorption data to find a(p/p0) against p/p0 dependence;
n) use Equations (1)-(3) to calculate surface area.
4. Measurements and calculations
The water vapor adsorption isotherms for all root materials were measured at the temperature 298 ± 0.5 K using the vacuum chamber method as described above. Because the fresh roots were too wet and some fungi infection occurred during the adsorption measurements and equilibrium at the initial adsorption point was hard to reach this material was not studied further. The other root samples of c.a. 0.2 g were used. The measurements were performed in 3 independent adsorption runs for 3 replicates each. The obtained average isotherms are illustrated in Figure 4. For illustration purposes the isotherms measured in full range of p/p0 are shown despite only the 01 - 06 p/p0 range is important for surface area calculation.
This was observed that the isotherms for whole and cut material are very similar so practically the sample state does not markedly influence the results. Similar isotherms are measured also for air dry and 105˚C dried roots what may indicate that severe decomposition of the plant root

Figure 4. Water vapor adsorption isotherms on variously pretreated roots. Abbreviations for the pretreatments: Wwhole roots, C-cut roots, AD-air dried, D105-dried at 105˚C, L-lyophilized. The isotherms show average data from 9 isotherms (3 independent adsorption/desorption runs for 3 replicates each).
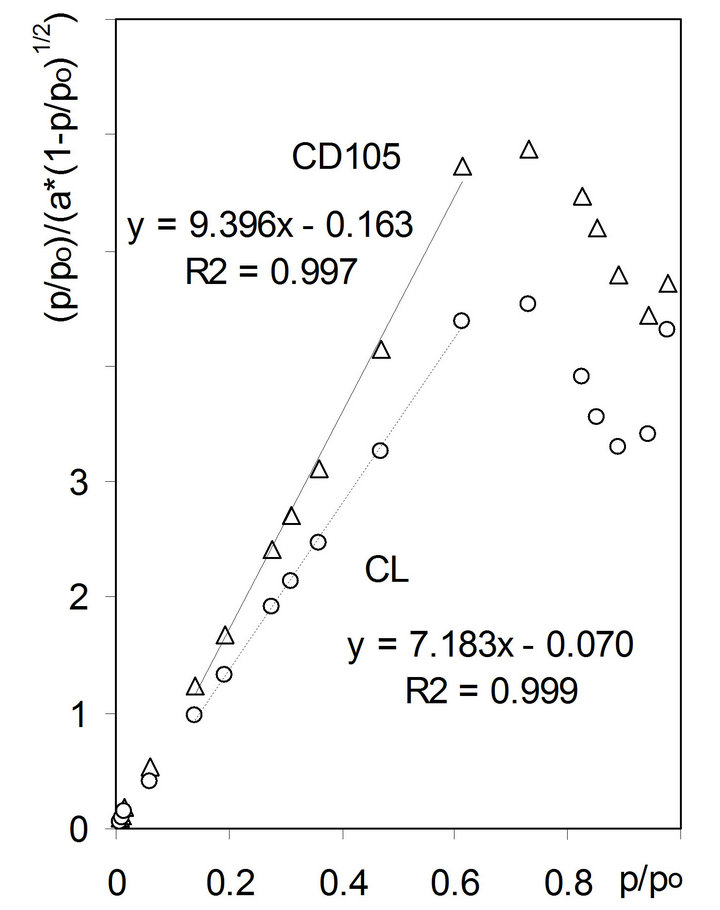
Figure 5. Plot of the Aranovich equation (Eqution (2)) for adsorption data of the studied root samples. Lines shows linear fits to the data points plotted in the range of the equation linearity. Abbreviations for the pretreatments: C-cut roots, D105-roots dried at 105˚C, L-lyophilized roots.
constituents does not occur during moderate heating and that estimation of the dry mass of the roots after drying at 105˚C is a good choice. The isotherms measured for lyophilized material differ from the previous what most probably may be due to slight differences in the geometrical structure of the dried and lyophilized roots. Lyophilization may better preserve the plant material natural structure.
Monolayer capacities of the studied roots were estimated from the plots of Equation 2 in the range of p/p0 from 0.141 to 0.614 that are presented in Figure 5. This Figure, for clarity of presentation, shows only the data for cut roots dried at 105˚C (CD105) and lyophilized cut roots (CL). Knowing monolayer capacities, roots surface areas were calculated from Equation (3).
5. Results and Discussion
Values of specific surface areas of the studied roots calculated from the measured adsorption isotherms are presented in Table 1.
Surface area of the studied roots estimated from water vapor adsorption isotherm is large, around 400 m2 g−1. Similarly large values are reported in [8,9,11] for other cereal plants. Surface area measured by water vapor adsorption characterizes the overall extent of the surface and not the external one. Therefore all spaces of the roots that are available for water molecules can participate in the adsorption process, including internal root tissues. This is rationale to state that all surfaces available for

Table 1. Surface areas of the studied roots. Data show average values calculated from 9 isotherms ±95% coincidence intervals. Abbreviations for the root material: W-whole roots, C-cut roots, AD-air dried, D105-dried at 105˚C, Llyophilized.
water vapor are also available for the liquid water (soil solution) and so the surface area measured by water vapor adsorption characterizes the real extent of the active root surface.
As far as the surface area is a key parameter for description of water and nutrients uptake by plants, we expect that the surface area measured by water vapor adsorption should better relate to the above processes than the (much lower) external root surface area.
For the soil rhizosphere material, depending on the soil type, surface areas vary from a few to around hundred m2g−1. So the root adsorbent strongly competes with the soil in water adsorption. Somewhat higher surface areas of lyophilized roots can indicate that the mode of pretreatment has some influence on the material structure. As the above effects are not high, air drying seems to be more convenient choice for preparation of root material for studying adsorption/desorption isotherms.
6. Conclusion
Water vapor adsorption isotherm measurement is proposed to estimate plant roots specific surface. The indicator of the validity of this method is that the resulted root surface area provides enough space to carry all root surface charges together with other no charged molecules. However, the practical and theoretical usefulness of this method for characterizing root surface as well as to study and model plant processes needs more further evidences.
7. Acknowledgements
This work was supported by the European Regional Development Fund through the Innovative Economy Program for Poland 2007-2013, project WND-POIG. 01.03. 01-00-101/08 POLAPGEN-BD “Biotechnological tools for breeding cereals with increased resistance to drought”. The project is realized by POLAPGEN Consortium coordinated by Institute of Plant Genetics, Polish Academy of Sciences in Poznan. Further information about the project can be found at www.polapgen.pl.
REFERENCES
- P. H. Nye, “The Relation between the Radius of a Root and Its Nutrient-Adsorbing Power,” J. Exp. Bot., Vol. 24, 1973, pp. 783-786. doi:10.1093/jxb/24.5.783
- M. Siberbrush and S. A. Barber, “Sensitivity of Simulated Phosphorus Uptake to Parameters Used by a MechanisticMathematical Model,” Plant and Soil, Vol. 74, No. 1, 1983, pp. 93-100. doi:10.1007/BF02178744
- S. E. P. R. Troelstra and F. Berendse, “Root CEC Determinations to Establish Root Biomasses of Two Plant Species Grown in Mixtures,” Plant and Soil, Vol. 64, No. 2, 1982, pp. 277-281. doi:10.1007/BF02184262
- G. Jozefaciuk and A. Szatanik-Kloc, “Decrease in Variable Charge and Acidity of Root Surface under Al Treatment Are Correlated with Al Tolerance of Cereal Plants,” Plant and Soil, Vol. 260, No. 1-2, 2004, pp. 137-145. doi:10.1023/B:PLSO.0000030175.23904.5a
- T. W. Cooper, W. Jones, S. Motherwell and G. M. Day, “Database Guided Conformation Selection in Crystal Structure Prediction of Alanine,” CrystEngComm, Vol. 9, No. 7, 2007, pp. 595-602. doi:10.1039/b702136d
- H. E. Carley and R. D. Watson, “A New Gravimetric Method for Estimating Root-Surface Areas,” Soil Science, Vol. 102, No. 5, 1996, pp. 289-291. doi:10.1097/00010694-196611000-00001
- S. A. Ansari, P. Kumar and B. N. Gupta, “Root Surface Area Measurements Based on Adsorption and Desorption of Nitrite,” Plant Soil, Vol. 175, No. 1, 1995, pp. 133-137. doi:10.1007/BF02413018
- G. Jozefaciuk and A. Szatanik-Kloc, “Aluminium-Induced Changes in the Surface and Micropore Properties of Wheat Roots: A Study Using the Water Vapor AdsorptionBdesorption Technique,” Plant Soil, Vol. 233, No. 1, 2001, pp. 95-108. doi:10.1023/A:1010373116199
- G. Jozefaciuk and A. Szatanik-Kloc, “Changes in Specific Area and Energy of Root Surface of Cereal Plants in Al-Solution Cultures. Water Vapor Adsorption Studies,” Plant and Soil, Vol. 250, No. 1, 2003, pp. 129-140. doi:10.1023/A:1022813018940
- Szatanik-Kloc, “Effect of pH and Zn-Stress on Micropore System of the Rye Roots,” International Agrophysics, Vol. 26, 2012, pp. 311-316.
- Szatanik-Kloc and G. Jozefaciuk, “Effect of pH and Aluminium on Surface Properties of Barley Roots as Determined from Water Vapor Adsorption,” Acta Physiologiae Plantarum, Vol. 19, No. 3, 1997, pp. 327-332. doi:10.1007/s11738-997-0009-6
- S. J. Gregg and K. S. W. Sing, “Adsorption, Surface Area and Porosity,” Academic Press, London/New York, 1967.
- K. S. W. Sing, “Reporting Physisorption Data for Gas/ Solid Systems with the Special Reference to the Determination of Surface Area and Porosity,” Pure and Applied Chemistry, Vol. 54, No. 11, 1982, pp. 2201-2218. doi:10.1351/pac198254112201
- J. Oscik, “Adsorption,” Ellis Horwood, Chichester, 1982.
- H. Marschner and V. Romheld, “In Vivo Measurement of Root-Induced pH Changes at the Soil-Root Interface: Effect of Plant Species and Nitrogen Source,” Z. Pflanzenphysiology, Vol. 111, 1983, pp. 249-254.
- P. L. Hall and D. M. Astill “Adsorption of Water by Homoionic Exchange Forms of Wyoming Bentonite (SWy1),” Clays and Clay Minerals, Vol. 37, 1989, pp. 355-363. doi:10.1346/CCMN.1989.0370409
- J. M. Cases, I. Berend, M. Francois, J. P. Uriot, L. J. Michot and F. Thomas, “Mechanism of Adsorption and Desorption of Water Vapor by Homoionic Montmorillonite. 3. The Mg, Ca, Sr, and Ba Exchanged Forms,” Clays and Clay Minerals, Vol. 45, 1997, pp. 8-22.
- doi:10.1346/CCMN.1997.0450102
- S. Brunauer, P. H. Emmet and E. Teller, “Adsorption of Gases in Multimolecular Layers,” Journal of the American Chemical Society, Vol. 60, No. 2, 1938, pp. 309- 314. doi:10.1021/ja01269a023
- G. L. Aranovich, “The Theory of Polymolecular Adsorption,” Langmuir, Vol. 8, No. 2, 1992, pp. 736-739. doi:10.1021/la00038a071

