ABSTRACT

This work analyzes the technical efficiency of maize farmers and its influencing factors in Ombella Mpoko, Central African Republic, using the data from primary source of the farmers in the region of Boali and Damara. Data was collected using a structured questionnaire, on farmers’ output of maize, inputs used in the production process (land, capital, labor, fertilizer and cuttings) on each plot, and the socio-economic and plot-specific characteristics. This included farmer’s age, level of education, household size, and farm size, membership in cooperative and producer organizations as well as other relevant variables. The study employed the Stochastic Frontier Analysis (SFA) Approach and the Tobit model. The result shows that socio-economic factors, environmental factors and physical and technical factors have a significant influence on maize production in study area. In other words, this shows that technical inefficiency effects do make a significant contribution to the level and variation of maize production in Boali, Damara, and Ombella. That is why the final null hypothesis explores the test that specifies each farm is operating on the technically efficient frontier and that the systematic and random technical efficiency in the inefficiency effects are zero. This is rejected in favor of the presence of inefficiency effects.

Keywords:

Maize, Efficiency, Factors, Stochastic Frontier Analysis, Tobit Model, Central African Republic

1. Introduction

Agriculture of the Central African Republic (CAR) is one of the major sectors of the economy. It is dominated by the cultivation and sale of food crops, such as cassava, peanuts, maize, sorghum, millet, sesame, and plantain. Agriculture (including forestry and fisheries) accounted for 54% of GDP in 2016 [1] , and it employed about 74% of the labor force. The FAO estimates that about 2,020,000 hectares (4,991,000 acres, or 3.2% of the total land area) [1] , are arable or under permanent crops, and 3,000,000 hectares (7,400,000 acres, or 4.8% of total land area) are in permanent pasture. The CAR is nearly self-sufficient in food production and has potential as an exporter.

Maize is the most-produced cereal worldwide. In Africa alone, more than 300 million people depend on maize as their main food crop [2]. In addition, maize is also very important as feed for farm animal. Currently, approximately 1 billion tons of maize is grown in more than 170 countries on about 180 million hectares of land. 90% of the world’s production is yellow maize, but in Africa, 90% of the total maize production is white maize [3]. Maize production in Africa is very low: while the average yield worldwide is approximately 5.5 tons/hectare/year, production in Africa stagnates at around 2 tons/hectare/year [4]. According to FAO, the 2018 cereal crop harvest in CAR concluded by late November or early December, while in some areas of the south, the harvest of the secondary season crops is expected to start in December [5]. Satellite-based rainfall estimates indicate that, in the southern maize-producing areas, above average amounts were received across the country since the beginning of the cropping season in February until the third decade of October. However, despite adequate weather conditions, persisting civil insecurity continues to negatively constrain crop production as the area planted significantly declined due to the abandonment of a substantial number of farms. Moreover, the reduced aggregate output in the past five consecutive years has led to the depletion of the already inadequate households’ productive assets, particularly seeds and farming tools. As a result, the 2018 aggregate output is preliminarily estimated to be below average and significantly reduced compared to the pre-crisis levels in 2013.

Faced with the new ecological situation, farmers in the region of Boali and Damara have developed new habits. Maize crops, formerly developed for self-consumption, have become the main income-generating crops. Farmers in this region are not only the essential producers, but also the recipients of income. Yet, despite the massive presence of corn farmers, no empirical study has evaluated, to our knowledge, the technical efficiency of these farmers to really determine their production capacity.

Faced with the new challenge of fighting poverty, especially in rural areas, what are the main constraints to raise in order to substantially improve the income of maize farmers in this region of the Central African Republic? The answer to this question requires an empirical analysis of the real efforts of maize farmers in this region through the evaluation of their level of technical efficiency and to examine the determinants of it. Admittedly, numerous studies have made it possible to evaluate the level of economic and technical efficiency of African farmers in general and, in particular, that of Central African farmers. But with regard to the technical efficiency of maize farmers in the Ombella M’Poko, particularly those of Boali and Damara, these studies are apparently non-existent. This article proposes to achieve a number of specific objectives:

- To analyze the efficiency of maize farmers in Ombella M’Poko;

- To determine the factors that influence corn production in the region;

- And to make recommendations likely to fill the probable shortcomings.

In this article, the first part presents a review of the literature. Then the data collection and analysis methodology is explained in the second part; the third part presents the results. Finally, the conclusion offers some technical and institutional recommendations.

2. Literature Review

The output of a firm is expressed by the production function, which gives the maximum quantity of output that can be obtained by a combination of factors. In other words, this function characterizes all the relationships between the quantities produced and the quantities of factors used with the possible techniques [6]. The change in output when increasing the use of a factor of production while keeping the other factors of production unchanged is the marginal productivity of this factor. It decreases when the use of the factor is increased, the quantities used of the other factors being maintained in the same way. This observation is general and qualified by the marginalists as “the law of decreasing marginal returns” [7]. Work on farm performance is widespread in developed countries and even in developing countries. [8] evaluated the level of technical efficiency of Polish farms and found that farms geared towards breeding are more efficient than specialized farms and mixed farms. Then she examined the determinants of this technical efficiency. This was a plus because the existing studies on estimating the technical efficiency of Polish farms were limited to analyzing the results of efficiency without identifying the determinants of it.

[9] estimated the technical efficiency of rice-producing farms in Vietnam, using successively a Data Envelopment Method (DEA) and a stochastic frontier approach to production. The result of this work is that, technical efficiency is significantly influenced by primary education of farmers and regional factors.

Africa has not remained on the margins of this trend. Thus, [10] analyzes the growth of the global productivity of the factors of production and its decomposition in technological evolution and evolution of the efficiency. Through a Data Envelopment Method (DEA), using data from 16 countries over the period 1970-2001, the study concludes that technological change has been the main obstacle to achieving high levels of factor productivity in sub-Saharan Africa during the review period. Finally, the results indicate that institutional and agro-ecological factors play a key role in the growth of agricultural productivity. He deduces a rule of specialization of individuals according to their relative productivity (the best performing to specialize where it is relatively best placed) by focusing on the “difference productive faculties” of workers. It explains the fundamental movements in commodity prices of an industry by changes in labor productivity in this industry relative to labor productivity in the precious metals industry [11].

By studying the factors that may affect the technical efficiency of the coffee sector in the west central region of Côte d’Ivoire, [12] used the DEA method to measure the technical efficiency of 81 coffee farms. The analysis shows that the average technical efficiency level is 36% in constant returns to scale and 47% in variable returns of scale, which gives a level of efficiency of scale of 76.6%.

[13] studied the production and technical efficiency of Guinea rice farmers by a stochastic parametric estimation. Thus, the author shows that the levers of improvement exist for the Guinean rice sector, even if the production and the technical efficiency do not seem yet linked to the introduction of modern inputs.

The notion of family farming is rooted in the organization of agricultural production in Europe [14]. The main characteristic of this is the work force, which is often family in nature. However, it is essential to specify as [15] that “the African family farm is different from the European agricultural family farm”. Thus, the African family farm is a family team of workers who together cultivate at least one common main field with or without one or more secondary fields of varying importance depending on the case and having their decision centers, [16].

In Cameroon, [17] assessed the technical efficiency of 450 smallholder groundnuts and maize in monoculture and these crops in association across 15 villages. The average level of technical efficiency obtained by the three types of producers is 0.77, 0.73 and 0.75, respectively. The causes of the differences in their technical efficiency are mainly due to credit, soil fertility, access to supervision and the road.

[18] used a stochastic model with individual and temporal fixed-effect panel data. In this model, the non-negative term representing technical inefficiency is assumed to be a function of firm-specific variables and time. It follows a truncated normal distribution of constant variance and whose mean is a linear function of the observed variables included in the model [19]. Empirical data are on paddy rice farms in India. These panel data cover a period of ten years.

[19] analyzed the economic efficiency of rice seed producers facing the problem of food security in Benin. For them, rice production is one of the best ways of achieving food security in West Africa. Indeed, statistics of the last decade show a significant increase in rice production in West Africa in general and specifically in Benin. About 70% of this increase is explained by the use of improved seed varieties [19]. However, a major constraint is the availability of improved seeds. To overcome this situation several countries including Benin have adopted a new policy of decentralization of seed production with the direct involvement of producers. Therefore, producers have been trained for the production of certified rice seeds. To analyze the efficiency and sustainability of this new activity, this study aims to estimate the technical, allocative and economic efficiency of certified seed rice producers. To achieve these objectives, data were collected from a random sample of 128 producers of certified rice seeds in southern Benin. The stochastic frontier production function and the cost function as well as the Bootstrap Tobit regression model were used to estimate the efficiencies. The results show that the average technical, allocative and economic efficiency are respectively 0.72; 0.83 and 0.62. This study suggests that quality controls of seed production should be accompanied by technical support, training and periodic capacity building to allow producers of certified rice seeds to improve their productivity, while producing good quality seeds and satisfying demand. These actions will participate greatly to ensure increasing of rice production and consequently contribute to food security.

Special Report “FAO/WFP Food Security Assessment Mission to the Central African Republic. This report states that the unprecedented political-military crisis, which began in the Central African Republic (CAR) in December 2012, devastated the national economy. It resulted in a 37 per cent reduction in gross domestic product (GDP) in 2013 compared to 2012. The agricultural sector, the backbone of the economy, experienced a contraction of 46 per cent in 2013. In 2014 agricultural activities have experienced serious disruption: areas planted at levels well below pre-crisis levels due to persistent insecurity and scarcity of essential inputs such as seeds and tools. The 2014 crop, estimated at 762,690 tonnes, which is 58 percent lower than the pre-crisis average, increased by 11 percent over 2013 due to an increase in cassava production. However, cereal production is down by 54 percent in 2014 compared with 2013. FAO’s support for agricultural production has mitigated the negative impact of the crisis on food production, with some 111,750 households assisted with food production. seeds (maize, rice, peanut, sesame, millet, sorghum, legumes) and tools, while 100 seed multiplier groups received maize, rice and groundnut seeds [20]. WFP supported the operation by providing seed protection rations.

The Mission estimates cereal import requirements at 134,356 tonnes for the 2014-2015 food year (November-October). Assuming a projected commercial import of 29,000 tonnes and 48,000 tonnes of food assistance [20] , the Mission estimates a cereal deficit of some 57,000 tonnes. Livestock numbers are estimated to have fallen by up to 77 percent from pre-crisis levels following looting and slaughter. Fish catches are down by 40 percent due to insecurity in fishing grounds and loss of equipment. The severe disruption in the functioning of markets and commercial activities has resulted in the scarcity of commodities including staple foods, causing price increases in Bangui, where inflation rose by 3.5 percent in January 2014 at 12 percent in August 2014, limiting the food access of a large number of people. In Bangui, maize, millet and groundnut prices increased by 30 to 70 percent between March-April and August 2014. In contrast, cassava prices fell 13 percent from February to August. The crisis has caused a serious deterioration of food security. Food reserves in rural areas are estimated at between 40 and 50 percent of their usual level because of looting and insecurity, and a drop in the frequency and quality of meals is already observed. IDPs and landlocked people face emergency food insecurity, 50 percent of these households consume a poor diet and face high nutritional risk.

For non-displaced groups, food assistance will be needed during the 2015 lean season (April-July). A safety net should be put in place to prevent and treat acute malnutrition. It is urgent to provide support for food production (through the distribution of seeds, small equipment, the promotion of market gardening, fish farming and small livestock). Strong support to the agricultural sector, in line with the PNIASAN National Agricultural Investment, Food and Nutrition Security Program, would promote inclusive economic growth and generate jobs and income opportunities. The establishment of an information system on agriculture and food security is strongly recommended to allow regular and timely monitoring of the situation.

[21] measured the technical efficiency of women farmers of food crops in Côte-d’Ivoire. The purpose of this article is to evaluate the technical efficiency of women farmers of food crops in Côte-d’Ivoire and to analyze the determinants. The stochastic production frontier is used. The sample was randomly drawn and its size is 458 women farmers (301 cassava and 157 yam) across 19 villages. The analysis of the production frontiers shows that the two food crops are very labor intensive. From the analysis of the technical efficiency of women farmers, yam and cassava farmers operate respectively at 88% and 80% of their productive capacity. This shows that there is still scope for increasing production without any additional inputs. In addition, analysis of the determinants shows that household size, access to extension and credit are major determinants of improving the efficiency of these women farmers. In view of these results, it is recommended that extension and agricultural credit structures intensify their support.

3. The Stochastic Frontier Analysis (SFA) Approach and the Tobit Model

3.1. The SFA

The Stochastic Frontier Analysis searches for the production function, which represents the maximum output attainable given a certain quantity of inputs [22].

The first stage of SFA consists in the specification and in the estimation of the stochastic frontier production function and in the estimation of technical inefficiency effects, under the assumption that these inefficiency effects are identically distributed [23]. The SFA methodology allows functional form and the breakdown of the inefficiency from a specified set of inputs, given the existing technology.

The problem is to determine empirically the maximum potential of a production unit. The ratio of the observed value to the maximum potential output obtainable from a particular set of inputs is the technical efficiency of a production unit.

The model of the Stochastic Frontier Analysis [22] is:

$\ln y_i={x^{\prime }}_i\beta +{\nu }_i-{\mu }_i$ (1)

where $y_i$ is the output of producer I; $x_i$ is a vector of inputs; $\beta$ is a vector of $k+1$ parameters to be estimated.

We assume that:

・ ${\nu }_i=iid$ $N\left(0,{\sigma }_{\nu }^2\right)$ is the noise or error term or the measure of effects independent by producer; ${\nu }_i$ is assumed to have constant variance (homoskedasticity);

・ ${\mu }_i$ is non-negative random variable measuring the technical inefficiency, iid, with $N^{+}\left(0,{\sigma }_{\mu }^2\right)$ (half-normal or $N^{+}\left(0,{\sigma }_{\mu }^2\right)$ normal-truncated or exponential or gamma);

・ ${\nu }_i$ and ${\mu }_i$ are distributed independently of each other and of the regressors.

3.2. The Technical Efficiency

We can define the Technical Efficiency (TE) as the ratio of realized output to the stochastic frontier output:

$\ln T{E}_i=\ln y_i-\ln {\widehat{y}}_i=\ln \left(y_i/{\widehat{y}}_i\right)=-{\mu }_i$ ( $0\le T{E}_i\le 1$ ) (2)

The parameters of stochastic frontier function are estimated by the maximum likelihood method. As estimation of stochastic frontier is facilitated by the use the reparameterization proposed by [24] :

${\sigma }^2={\sigma }_{\nu }^2+{\sigma }_{\mu }^2$ $\gamma =\frac{{\sigma }_{\mu }^2}{{\sigma }^2}$ ( $0\le \gamma \le 1$ ). (3)

The prediction of individual technical efficiencies involves the unobservable technical inefficiency effects ${\mu }_i$ . The best predicator of ${\mu }_i$ is the conditional expectation of ${\mu }_i$ , given the value of ${\epsilon }_i={\nu }_i-{\mu }_i$ [25].

If the predicator $\gamma =0$ then the variance of the technical inefficiency effect is zero and so the model reduces to the traditional mean response function, a specification with parameters that can be consistently estimated using OLS.

If $\gamma$ is close to one, it indicates that the deviations from the frontier are due mostly to the technical inefficiency.

When $\gamma =1$ , one-sided error component dominates the symmetric error component and the model is the deterministic production function with no noise.

3.3. The Tobit Model

The second stage consists in the specification of a regression model for the predicated effects of the technical inefficiency. The Tobit model by [26] is an appropriate tool since the inefficiency scores are censored, and they cannot exceed 1 nor be lower than 0. The idea at the basis of the Tobit model is that it observes the variable only within bounded limits. If the value of an unobservable dependent variable lies outside the limits, we let it equals to the value at the limit. Inefficiency effects are simultaneously conditioned on several specific factors and estimated using the parameterization with mean [18] :

${\widehat{TE}}_i={\delta }_0+{z^{\prime }}_i\delta$ (4)

where $z_i$ is the vector of the explanatory variables and ${\delta }_0$ and ${\delta }_j$ ( $j=1,2,\dots ,J$ ) are respectively a parameter and a vector of J parameters to be estimated. The technical inefficiency effects ${\mu }_i$ are frequently estimated in a first step and the determinants of inefficiency are obtained in a second-stage regression. However, this may induce both bias and inefficiency in the estimations. To assess the Technical IN efficiency $\widehat{TIN}$ instead of technical efficiency $\widehat{TE}$ in order to directly assess the relationship between inefficiency and other variables, $\widehat{TIN}$ can be calculated using the following formula:

$\widehat{TIN}=\frac{1-\widehat{TE}}{\widehat{TE}}$ (5)

and then the Tobit regression method must be applied using $\widehat{TIN}$ instead of $\widehat{TE}$ . The technical inefficiency scores ( $\widehat{TIN}$ ) assume values between 0 and infinity. Although the two-step approach seems reasonable, assuming that any inefficiencies that have been found can be explained by additional factors in a second stage, it contradicts the assumption made in the first stage of identically distributed inefficiency effects on the stochastic frontier [27].

The main hypotheses of interest of the Stochastic Frontier Analysis are:

$H_0:{\beta }_1=\dots ={\beta }_q=0$ $q\le K$ (6)

The omission of ${\mu }_i$ is equivalent to impose the constraint specified in the null hypotheses, i.e.:

$H_0:\gamma ={\delta }_0=\dots ={\delta }_J=0$ (7)

This indicates that the inefficiency effects in the frontier model are not present (no efficiency).

Null hypotheses of interest are tested using the generalized likelihood ratio. The generalized likelihood-ratio statistic $\lambda$ is given by:

$\lambda =-2\ln \left[L\left(H_0\right)/L\left(H_1\right)\right]=-2\left[\ln L\left(H_0\right)-\ln L\left(H_1\right)\right]$ (8)

where $L\left(H_0\right)$ and $L\left(H_1\right)$ are the values of the likelihood function under the specifications of the null and the alternative hypotheses, $H_0$ and $H_1$ respectively. Special care must be taken when the likelihood test involves a null hypothesis that includes $\gamma =0$ .

The null hypothesis $H_0:\gamma =0$ specifies that the effects of the technical inefficiency are not stochastic. We reject the null hypothesis of no technical inefficiency effects given the specifications of the stochastic frontier and of the inefficiency effect model. In this case that $H_0$ is true, the generalized likelihood-ratio statistics, LR has an asymptotic distribution which is a mixture of chi-square distribution [28].

4. Data and Methodology

4.1. Data Collection

Data collection was conducted in May 2018 in the study area. It should be remembered that the area of study initially chosen is the prefecture of Kemo (chief town Sibut). When we arrived in Bangui, the security situations due to the rebel groups that pillaged, raped, killed and massacred the population since the coup of March 24, 2013, did not allow us to reach the locality of Sibut. In agreement with my supervisor and since the prefecture of Ombella M’Poko is also renowned in the maize culture and is closer to Bangui capital of the Central African Republic, we have seen fit to guide our study in the Sub-prefectures of Boali and Damara.

After the sub-prefectures, the villages in which the survey took place were randomly drawn. These are ten villages. They were distributed as follows: five villages in the first and five in the last.

For maize farmers, who are randomly selected, we looked at different parcels with different sizes. Thus, the statistical unit is the crop plot led by the farmer. The type of plot considered is that of maize. Two components make up the questionnaire: a household component and a component, physical and economic. The first identifies the producer with all the basic information. The second component related to the unit of production or physical and economic factors analyzes production activities, soil quality, temperature, factor costs and access to extension services. The questionnaire collected both quantitative and qualitative data. Quantitative variables include production, price of products, quantities of inputs used, quantity of products sold, age of farmer, size of household, etc. Qualitative variables are represented by the level of education of the farmer, his marital status, access to extension services, whether or not he belongs to an economic interest group, whether credit is obtained or not, impact of socio-political crises. At the end of our survey, 905 farmers were selected and are distributed as follows.

4.2. Data Analysis

After the data collection, the questionnaires were collected, verified coded and converted into electronic form. In addition, data clarification is done using Microsoft Excel. Subsequently, the data was exported to the Statistical Package for Social Science Researchers (PSCSS), which is the statistical software of simple descriptions, and frequency analyzes, then econometrics (STATA) was also used.

Secondly, the analysis of maize farmers’ technical efficiency from the Stochastic Border Analysis (SFA) approach and the Tobit model were used to determine average technical efficiency levels and regress independent factors selected against the score of efficiency. The main statistics of the input and output variables are shown in Table 1.

The descriptive analysis of the sample is presented above. These descriptive statistics results describe the socio-economic factors, environmental factors, and physical and technical factors. The socio economic factors bring together issues of existence of groups or associations, membership of groups or associations, attendance at agricultural extension advisory services, contraction of loans or credits

for corn production, recipients of government or agency grants, the existence of other sources of revenue to finance production. These factors have enormous influences on the technical efficiency of farmers in the agricultural sector in general, and maize farming in particular. The Physical and technical factors take in consideration issues of land tenure, area of the field, amount of seed planted, type of seed planted, location of supply of certified grain, and use of inputs. Like the previous ones, these physical and technical factors play an important role in the efficiency of a farmer. The environmental factors take into account average annual temperature, average annual rainfall, soil types, pests and diseases in study areas, natural disasters.

The majority of farmers are males, with an average age of 33 years. The age of the farmer is an important factor as it determines whether the farmers benefits from the experience of older farmers or the risk-taking attitude of younger farmers. 52% of the farmers are males against 48% females.

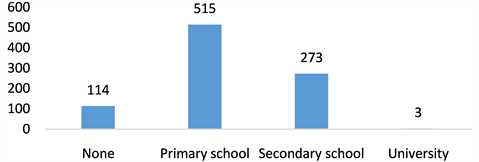
The highest level of education of the farmers varied greatly. The results shows that 114 farmers are not attended the formal education, 515 farmers attended primary school, 273 among of 905 farmers have the level of secondary school and only three of them attended university.

In the planting season, farmers produced an average of 0.846 metric tons of maize with largest producer producing 13.25 metric tons. The average farm size was 0.608 hectares and 243.49 kg of cutting was used per farmer. All famers did not use the chemical fertilizer to produce an average of 0.846 metric tons of maize, does it mean the used soils (clayey, sand-clay, stony, gravelly, black soil). The main information is shown in Figure 1 and Figure 2.

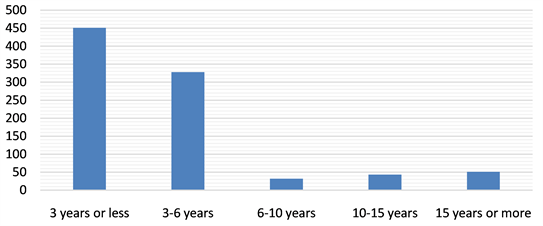
The result of the analysis shows that more than 451 or 49.9% of maize farmers have less than three years’ experience and 328 or 36.2% of other farmers have experience ranging from 3 to 6 years. These data confirm the age of farmers who are younger in the study area. 32 or 3.5% others have experience of 6 to 10 years, then 43 or 4.8% have experience of 10 to 15 years, and finally, 51 farmers or 5.6% have more than 15 years old.

4.3. The Model Specification

This paper uses the stochastic frontier production function model, which has the advantage that it allows for simultaneous estimation of individual technical efficiency of the respondent farmers as well as determinants of technical efficiency [18]. Following [29] , technical efficiencies and their determinants were estimated using a one-step maximum likelihood estimates (MLE) procedure [30]. This is done by incorporating the model for technical efficiency effects into the production function. This study specifies the stochastic frontier production function the flexible translog specification and later carries out a log likelihood ratio test to determine if the translog reduces to Cobb-Douglas production function. The translog model is specified as follows:

$\begin{array}{l}\ln y={\beta }_0+{\beta }_1\ln x_1+{\beta }_2\ln x_2+{\beta }_3\ln x_3+{\beta }_4\ln x_1^2+{\beta }_5\ln x_2^2+{\beta }_6\ln x_3^2\\ +{\beta }_7\ln x_1\ln x_2+{\beta }_8\ln x_1\ln x_3+{\beta }_9\ln x_2\ln x_3+\nu -\mu \end{array}$ (9)

where ln is the natural logarithm, y is output of i-th farmer, x₁ and x₂ are respectively Quantity of cuttings planted and Farm size, $\beta$ ’s are parameters to be estimated. Maximum likelihood estimation of Equation (9), provides the estimators for $\beta$ ’s and variance parameters ${\sigma }^2$ and $\gamma$ . The inefficiency model is estimated from equation given below.

${\mu }_i={\delta }_0+{\delta }_1{z}_1+{\delta }_2{z}_2+{\delta }_3{z}_3+{\delta }_4{z}_4+{\delta }_5{z}_5+{\delta }_6{z}_6+{\delta }_7{z}_7+{\delta }_8{z}_8+{\delta }_9{z}_9+{\delta }_{10}{z}_{10}+{\delta }_{11}{z}_{11}$ (10)

where z’s are various operational and farm, specific variables described in Table 1 and ${\delta }_i$ ’s are unknown parameters to be estimated.

5. Results and Discussions

5.1. Parameter Estimates

The maximum likelihood estimates (MLE) of the parameters of stochastic frontier production function output obtained using the program FRONTIER (version 4.1c) as present in Table 2.

The gamma parameter (0.05) associated with variances in the stochastic production frontier is not close to 1, this indicates that the deviations from the frontier are due mostly to the technical inefficiency. In other words, this shows that technical inefficiency effects do make a significant contribution to the level and variation of maize production in Boali, Damara, and Ombella.

5.2. Technical Inefficiency Model

The coefficients in the technical inefficiency model are presented in Table 3 using Stata 13 below.

A likelihood test was conducted to test the null hypothesis that the translog stochastic frontier production function can be reduced to a Cobb Douglas. The test statistic: $H_0:{\beta }_{ij}=0$ ’s, $H_0:{\beta }_{ij}\ne 0$ , as shown in Table 4 has a likelihood ratio value of which implies a reject of the null hypothesis at 1% significance. In other words, the translog model does not reduce to a Cobb Douglas model and is hence the ideal model.

*Significant at 95% confidence level.

Testing the model specification for technical inefficiency in Table 4 shows that both null hypothesis that the technical inefficiency effects are absent (hypothesis 1) and that inefficiency effects are not stochastic (hypothesis 2) are rejected, which implies that the traditional production function is not an adequate

representation of maize production data used in this study. In this case, it is can be said that inefficiencies are present and they are stochastic. This third null hypothesis determines whether the variables included in the inefficiency effects model have no effect on the level of technical inefficiency. $H_0:{\delta }_0={\delta }_1=\dots ={\delta }_{12}=0$ , the null hypothesis is rejected confirming that the joint effect of these variables on technical inefficiency is statistically significant. The final null hypothesis explores the test that specifies each farm is operating on the technically efficient frontier and that the systematic and random technical efficiency in the inefficiency effects are zero. This is rejected in favor of the presence of inefficiency effects.

6. Conclusion and Suggestion

The aim of this article was to assess the level of technical efficiency of maize producers in the Boali, Damara and Ombella regions, and to analyze its influence factors on corn production in the study area. At the end of the investigations, it appears that the producers are technically inefficient in maize. Indeed, the average index of technical inefficiency is 0.99. Maize production in Boali, Damara and Ombella is a labor-intensive and low-capital intensive activity. The areas are rather small because the pressure on the labor to be divided between the various agricultural activities is strong; each producer practices at the same time several agricultural activities.

As for the analysis of the determinants of technical efficiency, it shows that socio-economic factors, environmental factors and physical and technical factors improve the technical efficiency of producers in the study area. Socio-economic factors include problems with the existence of groups or associations, membership of groups or associations, assistance with agricultural extension advisory services, contraction of loans or credits for the production of maize, beneficiaries of government subsidies or agencies, and the existence of other sources of income to finance production, insecurity in the country, conflicts between farmers and pastoralists. These factors have a considerable influence on the technical efficiency of farmers in the agricultural sector in general and maize cultivation in particular. Physical and technical factors take into account issues of land tenure, area of the field, amount of seed planted, type of seed planted, location of grain supply certified, and use of inputs. Like the previous ones, these physical and technical factors play an important role in the efficiency of a farmer. Environmental factors take into account average annual temperature, average annual precipitation, soil types, pests and diseases in study areas, natural disasters.

Based on these findings, the study makes recommendations at three levels: extension services, formal microfinance institutions, and the Government of Central African Republic.

Extension services: It is recommended that these services intensify the technical supervision. In terms of production, emphasis should be placed on the use of the most cost-effective techniques, such as respect of planting periods for the addition of soil amendments to the Damara savanna zone where found soil depletion in some areas. In addition, extension services should encourage maize producers in the study area to join economic interest groups.

Formal microfinance institutions: Reducing poverty in rural areas requires vigorous action [31]. In this context, financial assistance must be provided in local agricultural development projects to maize producers in Boali, Damara and Ombella regions to allow the use of agricultural labor. Since the use of such labor is the key factor in the production of these areas, general councils should encourage financial support to enable producers to use them. To this end, the development of decentralized financial institutions should be encouraged.

The Government of the Central African Republic: Because it is often very difficult to see a climate of trust between farmers and pastoralists, and this climate of mistrust is due to the fact that farmers accuse the Peulh cattle herders of devastating sometimes their fields, and the government must reinforce the policy of the communes of breeding to separate the farmers from the breeders, and that the cleansing of armed groups that have been plundering, raping and killing farmers since 2012 would allow farmers to go about their farming activities freely.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

Payang, R.S.O., Poyearleng, C., Ngaisset, F.J.D. and Xia, X.L. (2019) Analysis of the Technical Efficiency of Maize Farmers and its Influencing Factors in Ombella Mpoko, Central African Republic. Open Journal of Social Sciences, 7, 216-232. https://doi.org/10.4236/jss.2019.72018

References