Journal of Applied Mathematics and Physics
Vol.04 No.02(2016), Article ID:63845,14 pages
10.4236/jamp.2016.42047
Numerical Simulation of Interaction of a Current with a Circular Cylinder near a Rigid Bed
M. Y. Abdollahzadeh Jamalabadi1,2, M. Oveisi1
1Chabahar Maritime University, Chabahar, Iran
2Department of Mechanical, Robotics and Energy Engineering, Dongguk University, Seoul, Republic of Korea

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 December 2015; accepted 23 February 2016; published 26 February 2016
ABSTRACT
The numerical modeling of a 2D flow around a horizontal cylinder near a rigid bed with the gap ratios G/D = 0, 0.2, 0.3 at Reynolds numbers 840, 4500, 9000, and 9500 is investigated by using weakly compressible smoothed particle hydrodynamics. The velocity field and the separation angles from the present simulations are compared with those obtained from the experimental measurements and are in a good agreement. The results show that the maximum value of shear stress on the bed increases as the cylinder closes the bed and suddenly decreases when the cylinder contact the wall.
Keywords:
Vortex Shedding, Circular Cylinder, Wall Proximity, Seabed Erosion, Weakly Compressible Smoothed Particle Hydrodynamics (WCSPH) Method

1. Introduction
Vortex shedding past slender bluff bodies near a wall occurs in many engineering and environmental flow situations such as flow past pipelines near the ground [1] -[3] . The prediction of dynamic loading on the bodies and influence of the vicinity of wall near it is of great practical importance. The shedding is a function of the distance between the wall and the cylinder [4] - [7] . The severe grid-resolution constraint in Eulerian formulation in the near wall region has been the major barrier to the use of the finite-volume of practical applications. This arises because of the presence of boundary layer effects in the near-wall region. To resolve this, the Lagrangian method is used [8] - [10] . Weakly compressible smoothed-particle hydrodynamics (WCSPH) is a numerical approach used for modeling fluid flows. It has been used in many fields of research, including astrophysics, ballistics, volcano-logy, and oceanography [11] . It is a mesh-free Lagrangian method (where the co-ordinates move with the fluid), and the resolution of the method can easily be adjusted with respect to variables such as the density. So this method is very convenient for modeling of free surface flows.
Study of the current interacted with circular cylinders near the sea bed is of importance to the design of offshore structures and submarine pipelines. The cylinders with circular cross-sections are the most common submerged structural elements in civil, mechanical, coastal and ocean engineering practices. In coastal and ocean engineering, the design of submarine pipelines is one of the most important practical examples [12] . When a pipeline is initially placed on an erodible bed, the interaction of the disturbed flow field with the sea floor may create erosion problems. Scour may occur below the pipe and, as a result, the pipeline may become a free-span- ning structure. Pipelines, either resting on the seabed or suspended above the bed with a small gap, may be subjected to transverse flowing steady currents in deep, intermediate and shallow water conditions. The dynamic forces exerted by the fluid flow on submerged cylindrical elements and their response to these forces are the primary concerns in engineering design. Also the shear stress imposed by the flow under the circular cylinder on the bed is the main cause of erosion. Hence, a study on the effects of geometry characteristics on the amount of shear stress imposed by the velocity gradient near the bed gain an outstanding importance.
Flow structures affected by cylindrical bodies near solid boundaries have been the subject to numerous experimental and theoretical investigations [13] - [17] . Furthermore, the experimental and theoretical analyses of the flow field affected by the cylinders near the solid boundaries have been the subject of numerous investigations [18] - [20] . Solving the Navier-Stokes equations using the discrete vortex method to model the mean and instantaneous features of flow past a circular cylinder at ReD = 1.4 × 105 is the subject of the some papers [19] . Their results for mean velocity and shear stress profiles demonstrated good agreement with the experiments. Hansen and Forsythe [20] used a cell-centered finite volume approach to solve the 3D compressible Navier-Stokes equations for the flow perpendicular to a cylinder’s axis at ReD = 3900. They investigated the effect of mesh density for unstructured and structured meshes on the velocity, cylinder surface pressure coefficient and Reynolds stress distribution; and compared the results with measurements. They concluded that unstructured-mesh algorithms can be successfully applied to geometrically complex problems, and simultaneous refinement in all radial, azimuthal and axial directions, is the best method to achieve mesh convergence. Further studies on the numerical analysis of the flow around the cylinders near plane boundaries would be useful to experimentally validate and enhance the reliability of the numerical simulations for different conditions. In this article we have used the experimental data that have used the PIV technique of the flow around the cylinder for verification of these study numerical results [21] .
The studies have mostly focused on the determination of the hydrodynamic forces on cylinders; velocity and pressure fields, vortex formation and turbulence characteristics of the flow past a cylinder; vortex shedding frequencies behind the cylinder; and the flow interaction between the wake and the plane boundary layer. The past experimental information reveals that the major variables affecting the flow past a circular cylinder are the free-stream velocity u0, depth h, and boundary layer thickness 𝛿 of channel flow, cylinder diameter D, the vertical ddistance between the cylinder and plane G. Therefore, numerical analysis of flow around a circular cylinder near the solid boundaries in free surface flows is considered. External flows past objects have been studied extensively because of their many practical applications. Since the issue has an important relevance to design of offshore structures, several theoretical and experimental approaches have been improved in order to find the interaction of current with circular cylinder near rigid boundaries [22] - [35] . This problem is also solved by some grid-base numerical methods that their results for mean velocity and shear stress profiles showed good agreement with experiments [11] . As a new approach, Weakly Compressible Smoothed Particle Hydrodynamics (WCSPH), a Lagrangian mesh-free method, is employed to simulate flow around a circular cylinder near the sea bed.
In this study the effect of gap ratio (the minimum vertical distance of the cylinder from the bed and the cylinder diameter ratio) on the flow field and the fluid velocity profile is considered. Hydrodynamic forces exerted on the cylinder by current are obtained and the influence of the gap ratio on the velocity field is studied. Also, the influence of geometry on the shear stress distribution of the solid bed and the circular cylinder are investigated for low Reynolds numbers (Re = 840, 4150, 9500).
2. Governing Equations and Numerical Method
Compressible Smoothed-particle hydrodynamics (WCSPH) is being progressively more used to model fluid motion as well. This is due to several benefits over conventional grid-based techniques. First, WCSPH guarantees the conservation of mass without extra computation since the particles they represent mass. Second, WCSPH computes pressure from weighted contributions of neighboring particles rather than by solving linear systems of equations. Finally, unlike the grid-base technique which must track fluid boundaries, WCSPH creates a free surface for two-phase interacting fluids directly. For these reasons it is possible to simulate fluid motion using WCSPH in real time. Furthermore, between SPH methods WCSPH have superiority because of its explicit method in finding pressure field. A classical method which solves weakly compressible equations in primitive variables (density ρ, velocity u, v) is presented in this subsection. At low Reynolds number the flow behavior around the cylinder is time-independent and is assumed 2D; and the governing equations of it, continuity and Navier-Stokes equations can be written in the following form in Cartesian coordinate system:
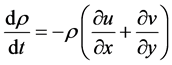 (1)
(1)
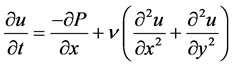 (2)
(2)
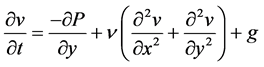 (3)
(3)
in which, u and v is the velocity components in x and y directions respectively, g is the body force due to gravity, p is pressure, μ is kinematic viscosity, ρ is the density of fluid. The system composed of continuity and momentum Equations are closed by a relation between ρ and P taking the form of an appropriate equation of state for water (Batchelor, 1974):
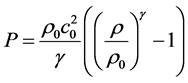 (4)
(4)
where γ = 7, ρ0 = 1000 kg∙m−3 is a reference density and c0 is a numerical speed of sound which is normally taken 10 times higher than the maximum fluid velocity in order to reduce the density fluctuation down to 1% (Monaghan, 1994). Each iteration step in the numerical procedure consists of the following steps:
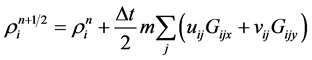 (5)
(5)
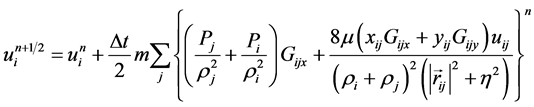 (6)
(6)
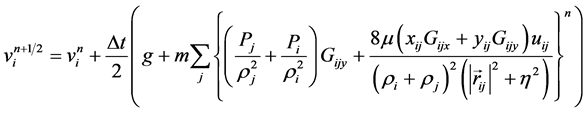 (7)
(7)
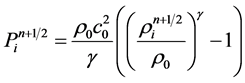 (8)
(8)
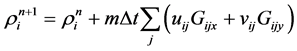 (9)
(9)
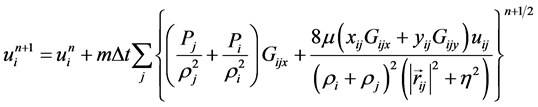 (10)
(10)
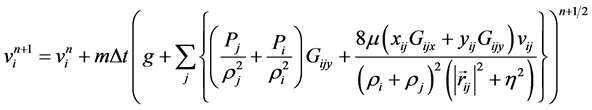 (11)
(11)
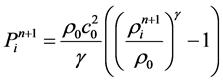 (12)
(12)
in which m is the particle mass , η is a small number to avoid singularity, xij = xi − xj and yij, rig, wig, vij are calculated in the same manner and the following kernel based on the spline function and normalized in 2-D is adopted (Monaghan, 1992):
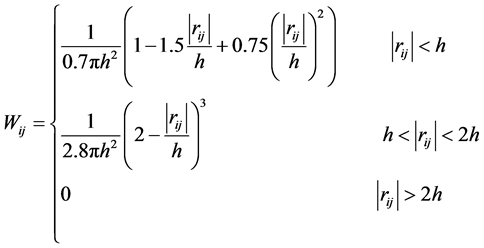 (13)
(13)
Here h, kernel smoothing distance, is taken 1.2 times of initial minimum distance between particles and. In order to define an appropriate model, a 2-D free surface flow with the presence of a circular cylinder near a rigid bed is considered. The inlet flow condition is considered fully developed with log wind profile under neutral stability conditions:
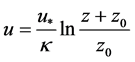 (14)
(14)
in which, where 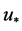 is the friction (or shear) velocity (m∙s−1), κ is von Karman’s constant (~0.41), z0 is the surface roughness (~0.0002 m). Outlet flow boundaries are outflow and the rigid surface is simulated as a solid wall. To discretize the domain some movable smoothed particles are defined as fluid particles and some fixed particles as solid boundaries. Fluid particles move according to Navier-Stokes equations and particles which include solid bed and circular cylinder are fixed in space. Lennard-Jones forces are utilized to prevent the fluid particles penetrate into the solid boundaries. The Morris equation is employed to predict the pressure distribution and an artificial viscosity is used for fluid viscosity. The numerical method used in time marching is performed using a predictor and corrector scheme in order to obtain velocity components of the fluid. The repulsive-particle method has been used which was first introduced by Monaghan (Monaghan, 1994).
is the friction (or shear) velocity (m∙s−1), κ is von Karman’s constant (~0.41), z0 is the surface roughness (~0.0002 m). Outlet flow boundaries are outflow and the rigid surface is simulated as a solid wall. To discretize the domain some movable smoothed particles are defined as fluid particles and some fixed particles as solid boundaries. Fluid particles move according to Navier-Stokes equations and particles which include solid bed and circular cylinder are fixed in space. Lennard-Jones forces are utilized to prevent the fluid particles penetrate into the solid boundaries. The Morris equation is employed to predict the pressure distribution and an artificial viscosity is used for fluid viscosity. The numerical method used in time marching is performed using a predictor and corrector scheme in order to obtain velocity components of the fluid. The repulsive-particle method has been used which was first introduced by Monaghan (Monaghan, 1994).
3. Results and Discussion
Figure 1 shows a schematic diagram of the present configuration, the boundary condition, and the coordinate system. The x and y coordinates are fixed on the wall in the flow direction and perpendicular to it respectively. The origin is located on the wall for all cases except the case of an isolated cylinder without a wall, for which the origin is located at the center of the cylinder.
At the first step, the problem is solved analytically by the assumption of 2-D invisid flow. The flow passed from a cylinder in free stream is the linear summation of a uniform flow and a doublet:

Here the image method used for the consideration of free surface and rigid body. The velocity vectors, pres-
Figure 1. Problem definition.
sure field and streamlines for potential flow for zero distance ratio is illustrated in Figure 2. The deflection of the fluid flow and its departure from symmetry due to the wall proximity can be understood by the isocontours of streamwise velocity. Further, because there is no boundary layer, just the inner shear layer accounts for the deflection of the streamlines and the downstream separation is not observed. It is clear that by increase of distance between cylinder and rigid bed (distance between two doublets in analytical solution) the maximum velocity decreased, the angle of attack has a tendency to zero and the streamlines have a habit of free stream solution. Furthermore, the maximum pressure occurs at the behind of the cylinder, the streamlines are independent of fluid viscosity, and there is no circulation in the fluid flow. Because of high Reynolds number simulation required in this investigation the creep flow analysis is not sufficient too. If the Stokes flow analysis used here the streamlines the velocity vectors would be less than the free stream velocity and the effect of body perturbation in the fluid flow remains longer than potential flow.
As known the potential flow just can show the general characteristics of the problem and the formation of a vortex queue is normally well thought-out to be the consequence of a coupling of Kelvin-Helmholtz instabilities with separated shear layers. The flow curvature, defined as the upward deflection of lower shear layer and the downward deflection of the upper shear layer, is larger than that of the viscous fluid flow and the recirculation length is considerably shorter than that of it. In each shear layer, the instabilities lead to vortex-sheet roll-up. Therefore, each sheet can be simulated as an infinite train of co-rotating vortices via the simulation of the problem with full Naier-Stokes equations. An in-house computer program with a non-linear time stepping procedure for the free water surface is developed and used to solve the governing equations by WCSPH models are examined. The geometry of problem and boundary condition is like (Oner et al., 2008). In the Figure 3 the schematic of particle arrangement for the SPH method at initial condition are plotted. As shown, some of the particles are fixed to simulate the effect of solid walls. The boundary condition here is in correspondence of Marrone et al. [14] . This problem is solved for G/D = 0, 0.2, 0.3 and ReD = 840, 4150, 9500 by the SPH method. The values of G/D because at the far wall regime, the flow and shedding characteristics are similar to a stand-alone cylinder, but for G/D less than 0.3 there is a strong coupling between the lower shear layer and the wall boundary layer and the vortex shedding is suppressed. Figure 4 shows the process of the vorticity dynamics for these small gap ratios which particle vector lines for G/D = 1 and ReD = 840 after 50, 100, 150, and 200 time steps. As presented, by increase of time the velocity is developed about the cylinder body and the vortexes are formed. The most obvious feature of the flow field of the oscillatory flow is vortex shedding. For the sake of increasing reliability of results the velocity vectors are calculated for 6000 particles for a finer mesh. The velocity vector for G/D = 1 and ReD = 840 at 200 time steps after the start of the problem are shown in Figure 5. It is obvious that the Strouhal number increases with the velocity gradient. By increasing of Strouhal number the four regions in the flow around the cylinder are detected as: the upstream retarded, the boundary layers, the accelerated sidewise and the wake. In the upstream retarded flow region flow is held back and blocked by the front of the cylinder. So the effect of boundary layer is neglected. After this region the boundary layers gradually develop along the cylinder surface to separation point. Because of curved form of solid body flow accelerated and the boundary layer is separated from the cylinder surface. The downstream separated flow region called the wake. The wake section is the most complex part of the disturbed flow field. At one fell swoop, it is the most significant in the interaction between the fluid and the solid body.
The steady velocity is acquired by averaging the oscillatory flow velocity over one flow period. Figure 6 and Figure 7 show calculated ensemble-average velocity contours at Reynolds number up to 9500 within one shed-
Figure 2. Velocity vectors, pressure field and streamlines for potential flow.
Figure 3. Particles arrangement for a coarse mesh.
Figure 4. Velocity vectors for G/D = 1 and ReD = 840 for 50, 100, 150, and 200 time steps for a coarse mesh.
ding period for the cylinder to wall gap height 0.0 and 0.3 times the cylinder height (G/D = 0.0 to 0.3). The vertical distributions of horizontal velocity at ReD = 4150 and ReD = 9500 are shown in Figure 6 and Figure 7 respectively. These results are similar to the figures of Oner et al. 2008.
Figure 5. Velocity vectors for G/D = 1 and ReD = 840 for 200 time steps and 6000 particles for a fine mesh.
Figure 6. Vertical distributions of horizontal velocity at ReD = 4150 and various distances from the bed (D = 0.05).
Figure 7. Vertical distributions of horizontal velocity at ReD = 9500 and various distances from the bed (D = 0.05).
Table 1 shows the Cylinder boundary layer separation angles with G/D at different ReD. The results of above Table are confirmed by the laboratory experiment and shows good agreement with experiments [11] . The separation angles were found to be displaced upward rapidly with an increasing gap ratio and increase of the boundary layer thickness, δ/D, caused an upward displacement of the separation angles on the cylinder. The values of separation angles in the table show that the flow separation points on the cylinder shift in a clockwise direction as the cylinder moves away from the bottom. At the θ = 90˚ and ReD = 4150, the distribution of velocity is in fairly good agreement with the measurement, but then the predicted velocity also settles at a lower value than observed. The four typical disturbed regions of the flow around the cylinder may be detected from the velocity profiles provided in Figure 6 and Figure 7. Profiles are rather flat and locations of peak velocities occur for relativistic large values of length to diameter ratio (x/D). Also, the maximum values of the peaks are low. This indicates that both the lower and upper shear layers are more straightened in the fluid stream direction. Therefore the momentum exchange between fluids in the free stream and those in the gap is relatively low.
Streamline contours at two Reynolds Numbers and various distances from the bed is illustrated in Figure 8. From the velocity distributions in Figure 8, it is seen that the disturbed velocity field around the cylinder is nearly symmetrical about its horizontal axis. That means the influence of the solid bed on the velocity field around the cylinder becomes weak when the gap ratio increases. In addition, by the increase of Reynolds Num-
Figure 8. Streamline contours at various Reynolds Number, and various distances from the bed.
Table 1. Cylinder boundary layer separation angles.
ber the length of the wake region decreased and the streamlines are more parallel to the free stream. The formation of von Karman vortex street and shedding of vortices in the rear of the cylinder at this gap height is obvious from the Figure 8. The boundary layer on the wall separates and forms a recirculation region, which inspirations the vortex shedding process behind the cylinder. The wall vortex creates from the wall boundary layer and attaches to the wall over the whole shedding cycle without separating from it. We find that in the sequence of the period of vortex shedding, the wall recirculation zone is conveyed downstream without separating from the wall. The recirculation zone of the wall also increases as time evolutions.
The Strouhal number calculated in terms of the free-stream velocity is more stable than that in terms of the velocity at the cylinder surface. Therefore, it is suggested that the free-stream velocity be used for the calculation of the Strouhal number. In the present study the Strouhal number is decreased smoothly from 0.215 to 0.205 with an increase of the Reynolds number from 850 to 9500. Total Pressure distribution at two Reynolds Numbers and various distances from the bed is illustrated in Figure 9. As shown, the maximum pressure of the flow field occurs at the bottom of the cylinder. Moreover, by increase of Reynolds Number a small flow jump transpire at the free surface top of the cylinder. Two counter rotating vortices (clockwise in upper side) that have shed can be realized beyond downstream. It is notable that the vortex shed from the upper side is strong and circular, even though, because of the wall the vortex shed from the lower side is smaller, weaker, and considerably
Figure 9. Total Pressure distribution at various Reynolds Number, and various distances from the bed (D = 0.05).
stretched in the flow direction. But by the increase of the gap size, there is less interaction between the vortex- shedding motion and the wall boundary layer and the upper and lower vortexes have the same strength and shape. Both velocity and pressure fields at two Reynolds Numbers and various distances from the bed is illustrated in Figure 10. As presented, the maximum velocity of the flow field takes place at the bottom of the cylinder. It is noticeable in Figure 10 that the effect of the boundary layer on the mean pressure distribution around the cylinder is more distinct at lesser gap ratios than that at larger gap ratios. The positive pressure area shifts upward as the boundary layer is thickened by moving the cylinder away from the leading edge of the plane boundary. The shift of the pressure distribution results in a displacement of the stagnation point away from the gap side. The main consequence of the existence of the increase of the Reynolds number is to create the stagnation point move upward further, especially at small gap ratios the upward shift of the stagnation point has also been detected when the gap ratio is increased.
Shear stress on bed at two Reynolds Numbers and various distances from the bed is illustrated in Figure 11. The negative shear layer from the cylinder upper surface appears just about horizontally into the near wake and positive shear layer from the cylinder wall face reattached with the cylinder. Below the cylinder a recirculation zone alongside the wall. The boundary layer along the wall separates further downstream. The decrease of the skin friction coefficient is because of the boundary layer separation and the recirculation region are captured rather well, indicating that they are not strongly affected by the upstream vortexes. The values of the periodic stresses in the wall are generally smaller in the region of the vortex centers, because in the vortex frame there is no motion at the centers. When there is not a gap between cylinder and bed, there are two peaks in the shear stress profile at the front and at the behind of the cylinder. But by the increase of the distance between body and horizontal wall there is just one maximum point in the shear stress profile. The maximum value of shear stress on the bed wall increases as the cylinder body approaches the bed. But it suddenly decreased when the cylinder contact the wall. In the results the sensitivity of the flow to perturbations due to surface roughness and free- stream turbulence is not considered.
4. Conclusion
Using the WCSPH technique, numerical investigation of steady, two-dimensional flows around a horizontal smooth circular cylinder near a plane wall were performed. The main conclusion to be drawn from this study is that the WSPH method can predict the vortex-shedding flow past a circular cylinder in the presence of an adja-
Figure 10. Velocity and pressure fields at various reynolds number, and various distances from the bed (D = 0.05).
Figure 11. Shear stress on bed at various Reynolds Number, and various distances from the bed (D = 0.05).
cent wall while the laminar method was applied for the Reynolds number up to 9000. The calculations allow the details of the interaction between the vortex-shedding motion and the boundary layer developing on the adjacent wall. Using three different gap ratios, G/D = 0, 0.2, 0.3 for the flow conditions at Reynolds number ReD = 840, 4150, 4500, 9000, and 9500. From the calculated velocity fields, the effects of wall proximity to various flow properties were investigated. The results revealed that four distinct regions may be identified for describing the flow the observed flow dynamics. The maximum value of shear stress on the bed increases as the cylinder closes the bed and suddenly decreased when the cylinder contact the wall. Also the results for the velocity field show that the numerical modeling using WCSPH is reasonably successfully and more convenient on free surface boundary condition rather than common CFD methods. Moreover, WCSPH method has superiority to other common SPH method because of its explicit approach to finding pressure.
Cite this paper
M. Y. AbdollahzadehJamalabadi,M.Oveisi, (2016) Numerical Simulation of Interaction of a Current with a Circular Cylinder near a Rigid Bed. Journal of Applied Mathematics and Physics,04,398-411. doi: 10.4236/jamp.2016.42047
References
- 1. Baggett, J.S., Jim_enez, J. and Kravchenko, A.G. (1997) Resolution Requirements in Large Eddy Simulations of Shear Flows. Annual Research Briefs––1997. Center for Turbulence Research, Stanford University/NASA Ames, 51-66.
- 2. Balaras, E., Benocci, C. and Piomelli, U. (1996) Two-Layer Approximate Boundary Conditions for Large Eddy Simulation. AIAA Journal, 34, 1111-1119.
http://dx.doi.org/10.2514/3.13200 - 3. Bearman, P.W. and Zdravkovich, M.M. (1978) Flow around a Circular Cylinder near a Plane Boundary. Journal of Fluid Mechanics, 89, 33-47.
- 4. Beaudan, P. and Moin, P. (1994) Numerical Experiments on the Flow past Circular Cylinder at Subcritical Reynolds Number. Report No. TF-62, Department of Mech. Engr., Stanford University.
- 5. Chen, H.C. and Patel, V.C. (1988) Near-Wall Turbulence Models for Complex Flows including Separation. AIAA Journal, 26, 641-648.
http://dx.doi.org/10.2514/3.9948 - 6. Hansen, P. and Forsythe, J. (2004) A Grid Convergence Study of a Highly Separated Turbulent Flow. Computing in Science & Engineering, 6, 30-37.
http://dx.doi.org/10.1109/MCSE.2004.59 - 7. Oner, S.M., Oner, A.A. and Akoz, M.S. (2009) Numerical Modeling of Interaction of a Current with a Circular Cylinder near a Rigid Bed. Advances in Engineering Software, 40, 1191-1199.
http://dx.doi.org/10.1016/j.advengsoft.2009.03.019 - 8. Liang, D. and Cheng, L. (2005) Numerical Modeling of Flow and Scour below a Pipeline in Currents. Part I: Flow Simulation. Coastal Engineering, 52, 25-42.
http://dx.doi.org/10.1016/j.coastaleng.2004.09.002 - 9. Marrone, S., Colagrossi, A., Antuono, M., Colicchio, G. and Graziani, G. (2013) An Accurate SPH Modeling of Viscous Flows around Bodies at Low and Moderate Reynolds Numbers. Journal of Computational Physics, 245, 456-475.
http://dx.doi.org/10.1016/j.jcp.2013.03.011 - 10. Monaghan, J.J. (1992) Smoothed Particle Hydrodynamics. Annual Review of Astronomy and Astrophysics, 30, 543-574.
http://dx.doi.org/10.1146/annurev.aa.30.090192.002551 - 11. Monaghan, J.J. (1994) Simulating Free Surface Flows with SPH. Journal of Computational Physics, 110, 399-406.
http://dx.doi.org/10.1006/jcph.1994.1034 - 12. Salih Kirkgoz, M., Alper Oner, A. and Sami Akoz, M. (2009) Numerical Modeling of Interaction of a Current with a Circular Cylinder near a Rigid Bed. Advances in Engineering Software, 40, 1191-1199.
>http://www.sciencedirect.com/science/article/pii/S0965997809000830
http://dx.doi.org/10.1016/j.advengsoft.2009.03.019 - 13. Oner,A.A., Kirkgoz, M.S. and Akoz, M.S. (2008) Interaction of a Current with a Circular Cylinder near a Rigid Bed. Ocean Engineering, 35, 1492-1504.
http://dx.doi.org/10.1016/j.oceaneng.2008.06.005 - 14. Richmond-Bryant, J. and Flynn, M.R. (2004) Applying the Discrete Vortex Method in Environmental Fluid Mechanics: A Study of the Time-Averaged near Wake behind a Circular Cylinder. Environmental Fluid Mechanics, 4, 455-463.
http://dx.doi.org/10.1007/s10652-005-0896-2 - 15. Saghatchi, R., Ghazanfarian, J. and Gorji-Bandpy, M. (2014) Numerical Simulation of Water-Entry and Sedimentation of an Elliptic Cylinder Using Smoothed-Particle Hydrodynamics Method. Journal of Offshore Mechanics and Arctic Engineering, 136, Article ID: 031801.
http://dx.doi.org/10.1115/1.4026844 - 16. Shih, W.C.L., Wang, C., Coles, D. and Roshko, A. (1993) Experiments on Flow Past Rough Circular Cylinders at Large Reynolds Numbers. Journal of Wind Engineering & Industrial Aerodynamics, 49, 351-368.
http://dx.doi.org/10.1016/0167-6105(93)90030-R - 17. Travin, A., Shur, M., Strelets, M. and Spalart, P. (1999) Detached Eddy Simulations Past a Circular Cylinder. Flow, Turbulence and Combustion, 63, 269-291.
- 18. Warschauer, K.A. and Leene, J.A. (1971) Experiments on Mean and Fluctuating Pressures of Circular Cylinders at Cross Flow at Very High Reynolds Numbers. Proceeding of International Conference on Wind Effects on Buildings and Structures, Tokyo, 305-315.
- 19. Yim, S.C., Challa, R, Idichandy, V.G. and Vendhan, C.P. (2014) Rigid-Object Water-Entry Impact Dynamics: Finite-Element/Smoothed Particle Hydrodynamics Modeling and Experimental Validation. Journal of Offshore Mechanics and Arctic Engineering, 136, Article ID: 031102.
- 20. Zdravkovich, M.M. (1997) Flow around Circular Cylinders. Fundamentals, Vol. 1, Oxford University Press, Oxford, Chapter 6.
- 21. Zdravkovich, M.M. (1985) Forces on a Circular Cylinder near a Plane Wall. Applied Ocean Research, 7, 197-201.
http://dx.doi.org/10.1016/0141-1187(85)90026-4 - 22. Zovatto, L. and Pedrizzetti, G. (2001) Flow about a Circular Cylinder between Parallel Walls. Journal of Fluid Mechanics, 440, 1-25.
http://dx.doi.org/10.1017/S0022112001004608 - 23. Abdollahzadeh Jamalabadi, M.Y. and Park, J.H. (2014) Thermal Radiation, Joule Heating, and Viscous Dissipation Effects on MHD Forced Convection Flow with Uniform Surface Temperature. Open Journal of Fluid Dynamics, 4, 125-132.
http://dx.doi.org/10.4236/ojfd.2014.42011 - 24. Abdollahzadeh Jamalabadi, M.Y. (2013) Electrochemical and Exergetic Modeling of a Combined Heat and Power System Using Tubular Solid Oxide Fuel Cell and Mini Gas Turbine. Journal of Fuel Cell Science and Technology, 10, Article ID: 051007.
- 25. Shadloo, M.S., Poultangari, R., Jamalabadi, M.Y.A. and Rashidi, M.M. (2015) A New and Efficient Mechanism for Spark Ignition Engines. Energy Conversion and Management, 96, 418-429.
http://dx.doi.org/10.1016/j.enconman.2015.03.017 - 26. Shadloo, M.S., Weiss, R., Yildiz, M. and Dalrymple, R.A. (2015) Numerical Simulation of Long Wave Run-Up for Breaking and Non-Breaking Waves. International Journal of Offshore and Polar Engineering, 25, 1-7.
- 27. Shadloo, M.S., Kimiaeifar, A. and Bagheri, D. (2013) Series Solution for Heat Transfer of Continuous Stretching Sheet Immersed in a Micropolar Fluid in the Existence of Radiation. International Journal of Numerical Methods for Heat & Fluid Flow, 23, 289-304.
http://dx.doi.org/10.1108/09615531311293470 - 28. Hadjadj, A., Ben-Nasr, O., Shadloo, M.S. and Chaudhuri, A. (2015) Effect of Wall Temperature in Supersonic Turbulent Boundary Layers: A Numerical Study. International Journal of Heat and Mass Transfer, 81, 426-438.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2014.10.025 - 29. Rahmat, A., Tofighi, N., Shadloo, M.S. and Yildiz, M. (2014) Numerical Simulation of Wall Bounded and Electrically Excited Rayleigh-Taylor Instability Using Incompressible Smoothed Particle Hydrodynamics. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 460, 60-70.
http://dx.doi.org/10.1016/j.colsurfa.2014.02.044 - 30. Shadloo, M.S., Hadjadj, A. and Hussain, F. (2015) Statistical Behavior of Supersonic Turbulent Boundary Layers with Heat Transfer at M∞ = 2. International Journal of Heat and Fluid Flow, 53, 113-134.
http://dx.doi.org/10.1016/j.ijheatfluidflow.2015.02.004 - 31. Fatehi, R., Shadloo, M.S. and Manzari, M.T. (2014) Numerical Investigation of Two-Phase Secondary Kelvin-Helmholtz Instability. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 228, 1913-1924.
http://dx.doi.org/10.1177/0954406213512630 - 32. Shadloo, M.S., Hadjadj, A. and Chaudhuri, A. (2014) On the Onset of Postshock Flow Instabilities over Concave Surfaces. Physics of Fluids, 26, Article ID: 076101.
- 33. Mabood, F., Ibrahim, S.M., Rashidi, M.M., Shadloo, M.S. and Lorenzini, G. (2016) Non-Uniform Heat Source/Sink and Soret Effects on MHD Non-Darcian Convective Flow past a Stretching Sheet in a Micropolar Fluid with Radiation. International Journal of Heat and Mass Transfer, 93, 674-682.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2015.10.014 - 34. Shadloo, M.S., Zainali, A., Sadek, S.H. and Yildiz, M. (2011) Improved Incompressible Smoothed Particle Hydrodynamics Method for Simulating Flow around Bluff Bodies. Computer Methods in Applied Mechanics and Engineering, 200, 1008-1020.
http://dx.doi.org/10.1016/j.cma.2010.12.002 - 35. Shadloo, M.S., Rahmat, A. and Yildiz, M. (2013) A Smoothed Particle Hydrodynamics Study on the Electrohydrodynamic Deformation of a Droplet Suspended in a Neutrally Buoyant Newtonian Fluid. Computational Mechanics, 52, 693-707.
http://dx.doi.org/10.1007/s00466-013-0841-z
Nomenclature













