Journal of Applied Mathematics and Physics
Vol.2 No.7(2014), Article
ID:47025,9
pages
DOI:10.4236/jamp.2014.27072
Application of the Two Nonzero Component Lemma in Resource Allocation
Morteza Seddighin
Mathematics Department, Indiana University East, Richmond, IN, USA
Email: mseddigh@indiana.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2014; revised 16 May 2014; accepted 21 May 2014
ABSTRACT
In this paper we will generalize the author's two nonzero component lemma to general self-reducing functions and utilize it to find closed from answers for some resource allocation problems.
Keywords:Two Nonzero Component Lemma, Resource Allocation, The Distribution of the Search Effort

1. Introduction
The technique we will use in this paper was first applied by this author to problems in matrix inequalities and matrix optimization. Historically, many researchers have established matrix inequalities by variational methods. In a variational approach one differentiates the functional involved to arrive at an “Euler equation” and then solves the Euler Equation to obtain the minimizing or maximizing vectors of the functional. The same technique is also often used in matrix optimization. Solving the Euler equations obtained are tedious and generally provide little information. Others have established inequalities for matrices and operators by going through a two-step process which consists of first computing upper bounds for suitable functions on intervals containing the spectrum of the matrix or operator and then applying the standard operational calculus to that matrix. This method, which we refer to as “the operational calculus method”, has the following two limitations: First,it does not provide any information about vectors for which the established inequalities become equalities (a matrix optimization problem). Second, the operational calculus method is futile in extending Kantorovich-type inequalities to operators on infinite dimensional Hilbert spaces. See [1] for examples using each of the two methods mentioned above. In his study of matrix inequalities and matrix optimization, the author has discovered and proved a lemma called the Two Nonzero Component Lemma or TNCL for short. In this paper we will state an extension of the author’s Two Nonzero Component Lemma and utilize it to solve some resource allocatoin problems. While resource allocatoin problems are not generally formulated in terms of matrices, as we will see, there are some similarities between matrix optimization problems and resource allocation problems Let us first state the TNCL as it was used in author's previous papers on matrix inequalities and matrix optimization.
2. The Two Nonzero Component Lemma
It was in his investigation on problems of antieigenvalue theory that the author discovered and proved the Two Nonzero Component Lemma (see [2] -[4] ). Although this lemma is utilized effectively by the author in matrix theory, it is by nature a dimension reducing optimization lemma which has potential applications in all areas of mathematics and physics. While TNCL was implicitly used in all of the papers just cited, it was not until 2009 that the author stated a formal description of the lemma in his paper titled, “Antieigenvalue Techniques in Statistics” (see [4] ). Below is the statement of the lemma. For the proof of the lemma please see the author’s work cited above.
Lemma 1 (The Two Nonzero Component Lemma) Let 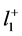 be the set of all sequences with nonnegative terms in the Banach Space
be the set of all sequences with nonnegative terms in the Banach Space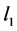 . That is, let
. That is, let
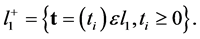 (1)
(1)
Let
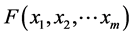 (2)
(2)
be a function from 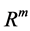 to
to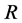 . Assume
. Assume 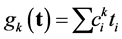 for
for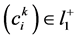 ,
, 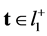 , and
, and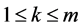 . Then the minimizing vectors for the function
. Then the minimizing vectors for the function
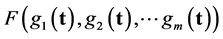 (3)
(3)
on the convex set 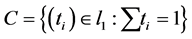 have at most two nonzero components.
have at most two nonzero components.
What make the lemma possible are the following two facts: First, the fact that the set
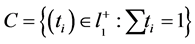 (4)
(4)
is convex. Second, a special property that the functions
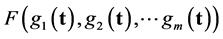 (5)
(5)
involved possess. If we set
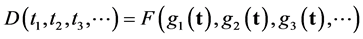 (6)
(6)
then all restrictions
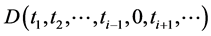 (7)
(7)
of
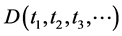 (8)
(8)
obtained by setting one component 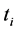 equal to zero, have the same algebraic form as
equal to zero, have the same algebraic form as 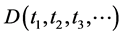 itself. We call functions with this property self-reducing functions. Please note that TNCL is valid for both finite and infinite variable cases. Let us look at an example of a self-reducing function where there are only a finite number of variables
itself. We call functions with this property self-reducing functions. Please note that TNCL is valid for both finite and infinite variable cases. Let us look at an example of a self-reducing function where there are only a finite number of variables 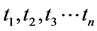 involved. Considered the function
involved. Considered the function
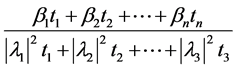 (9)
(9)
where 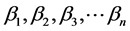 are real numbers and
are real numbers and 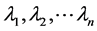 are complex numbers (this function appeared in [2] ).
are complex numbers (this function appeared in [2] ).
Let
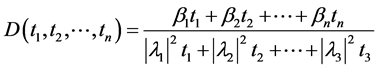 (10)
(10)
then we have
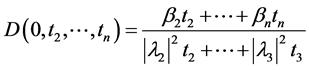 (11)
(11)
which has the same algebraic form as
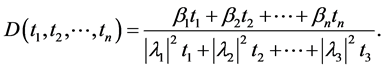 (12)
(12)
Indeed, for any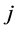 ,
,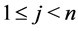 ; all restrictions of the function
; all restrictions of the function
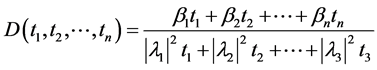 (13)
(13)
obtained by setting an arbitrary set of 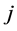 components of
components of 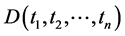 equal to zeros have the same algebraic form as
equal to zeros have the same algebraic form as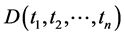 .
.
Obviously, not all functions have this property. For instance, for the function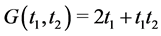 , we have
, we have
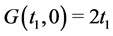 , which does not have the same algebraic form as
, which does not have the same algebraic form as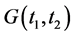 . Note that functions
. Note that functions 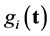 appearing in the statement of TNCL above are finite or infinite linear combinations of
appearing in the statement of TNCL above are finite or infinite linear combinations of 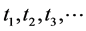 The lemma was originally stated this way because when we deal with a matrix or operator optimization problem each
The lemma was originally stated this way because when we deal with a matrix or operator optimization problem each 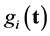 is either a finite or infinite linear combination of variables
is either a finite or infinite linear combination of variables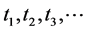 .
.
Example 2 In Theorem 1 of [4] we used TNCL to find the minimum of a Rayleigh quotient. A Rayleigh quotient of a positive operator  over positive operators
over positive operators 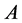 and
and 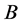 is a quotient of the form
is a quotient of the form
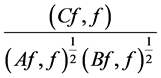 (14)
(14)
The unit vectors 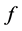 for which the minimum in
for which the minimum in
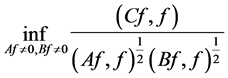 (15)
(15)
is attained are called stationary values for (14). In Theorem 1 of [4] the minimum of (14) was found by converting the problem to the problem of finding the minimum of
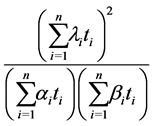 (16)
(16)
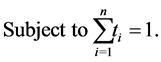 (17)
(17)
In this case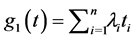 ,
, 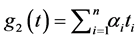 , and
, and 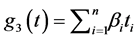 The sets
The sets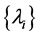 ,
, 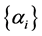 ,
, 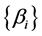 are the set of eigenvalues of
are the set of eigenvalues of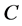 ,
, 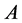 , and
, and 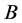 respectively.
respectively.
3. A Generalization of TNCL (GTNCL)
In this section we will show how a generalization of TNCL can be formulated. In the proof of the TNCL in [2] and [3] we took advantage of the facts that the set
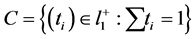
is a convex set and the function
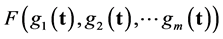
is a self-reducing function. A function
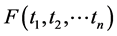
can be a self-reducing function without being composed of linear combinations of the form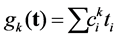 .
.
Example 3 Consider the function
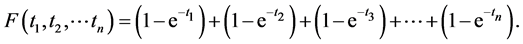
This function is self-reducing but is not a composition of linear combinations. A close look at our arguments in [3] shows that the only property used was the fact that the function to be minimized was self-reducing and the set 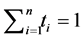 was convex. Therefore, we can state the following lemma which is a generalization of TNCL.
was convex. Therefore, we can state the following lemma which is a generalization of TNCL.
We state the lemma for the case that the number of variables in finite (a case which occurs in many applied problems) but the arguments used in [3] show that the lemma is also valid in the case where the number of variables is infinite.
Lemma 4 If the function
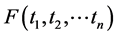 (18)
(18)
is a positive self-reducing function on the convex set
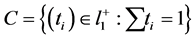 (19)
(19)
then the minimizing vectors
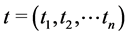
have at most two nonzero components.
We call the lemma stated above the General Two Nonzero Component Lemma or GTNCL for short.
Remark 5 We can also use TNCL and GTNCL to find the maximum of a positive self-reducing function on (19). To see this please note that if
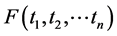 (20)
(20)
is a positive self-reducing function so is
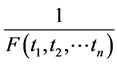 (21)
(21)
and maximum of (20) on (19) is the reciprocal of the minimum of (21) on (19).
A general resource allocation problem is stated as
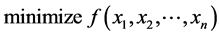
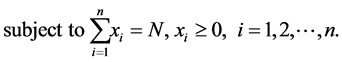
which can be converted to
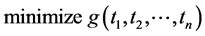
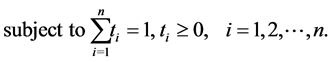
In the following sections we will use GTNCL to compute a closed form answer for the distribution of the search effort problem.
4. The Distribution of the Search Effort
This problem is formulated as
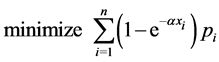
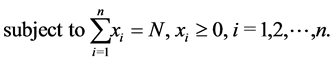
where 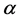 is a positive number,
is a positive number, 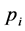 is the probability of an object being at position
is the probability of an object being at position 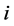 and
and 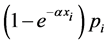 is the conditional probability of detecting the object at position
is the conditional probability of detecting the object at position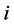 . If we define
. If we define
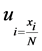
then the distribution of the search effort problem will be transformed into
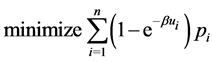
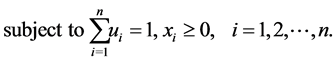
Theorem 6 The minimum of
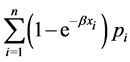 (22)
(22)
subject to
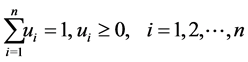 (23)
(23)
is either
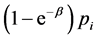 (24)
(24)
for some 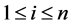 or
or
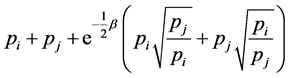 (25)
(25)
for a a pair of 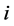 and
and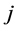 ,
, 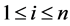 and
and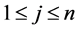 .
.
Proof. Since
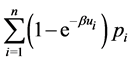 (26)
(26)
is a self -reducing function, the GTNCL can be used to find the minimum of this function subject to
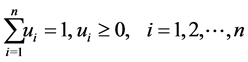 (27)
(27)
Since 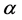 is positive so is
is positive so is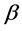 . Suppose
. Suppose 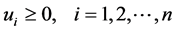 are components of a minimizing vector on the feasible set (27). By GTNCL either there is an
are components of a minimizing vector on the feasible set (27). By GTNCL either there is an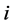 ,
, 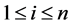 so that
so that 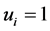 and
and 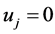 for
for 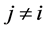 and
and  or there is a pair of
or there is a pair of 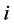 and
and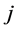 ,
, 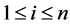 ,
, 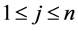 such that
such that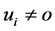 ,
, 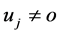 and
and 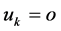 for
for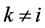 ,
, 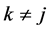 ,
,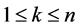 . In the first case the minimum of (26) on (27) is obviously (24). In the second case the minimum of (26) on (27) is the same as the minimum of
. In the first case the minimum of (26) on (27) is obviously (24). In the second case the minimum of (26) on (27) is the same as the minimum of
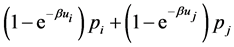 (28)
(28)
subject to
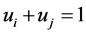 (29)
(29)
Expression (28) can be simplified to
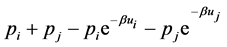 (30)
(30)
Substituting 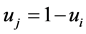 in (30) we have
in (30) we have
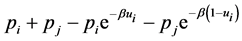 (31)
(31)
If we differentiate (31) with respect to 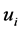 and put the derivative equal to zero we have
and put the derivative equal to zero we have
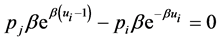 (32)
(32)
If we solve (32) for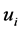 , we obtain
, we obtain
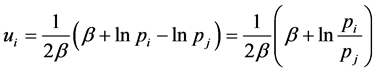 (33)
(33)
Substituting 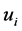 from (33) in (29) gives us
from (33) in (29) gives us
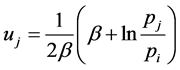 (34)
(34)
If we substitute (33) and (34) in (30) we have
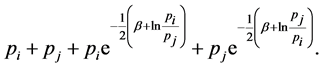 (35)
(35)
The last expression is equivalent to
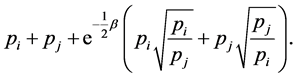 (36)
(36)
Please note that the derivative of the function
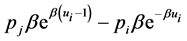 (37)
(37)
with respect to 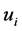 is
is
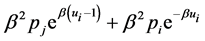 (38)
(38)
which is positive for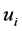 ,
,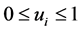 . Therefore, by the second derivative test (36) is a minimum value not a maximum value for the objective function in the resource allocation problem. ■
. Therefore, by the second derivative test (36) is a minimum value not a maximum value for the objective function in the resource allocation problem. ■
Although the GTNCL states two components 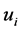 and
and 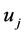 are nonzero but in general we do not know exactly which pair of
are nonzero but in general we do not know exactly which pair of 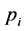 and
and 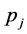 expresses (36). When applying TNCL to problems of matrix optimization, the author was able to determine exactly which component or which pair of components of the optimizing vectors are nonzero (see [5] ) under certain conditions. The same can be done here.
expresses (36). When applying TNCL to problems of matrix optimization, the author was able to determine exactly which component or which pair of components of the optimizing vectors are nonzero (see [5] ) under certain conditions. The same can be done here.
Theorem 7 Suppose the probabilities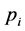 ,
, 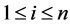 are ordered such that
are ordered such that
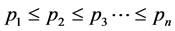
Then the minimum of
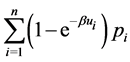
subject to
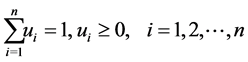
is
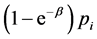
Proof. Assume
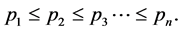 (39)
(39)
Since 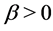 (39) implies that
(39) implies that
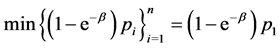
Furthermore, in (25) assume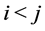 . Let
. Let 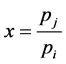 and
and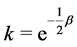 . Obviously
. Obviously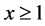 . Now (25) can be written as
. Now (25) can be written as
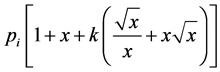 (40)
(40)
Note that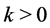 . If we define
. If we define
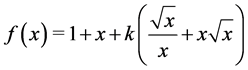 (41)
(41)
then
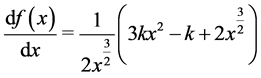 (42)
(42)
Since 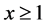 then
then
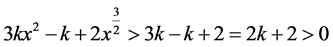 (43)
(43)
This shows that 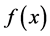 is an increasing function on
is an increasing function on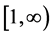 . Hence on the finite set
. Hence on the finite set
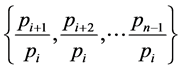
the function
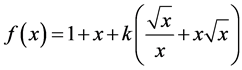
has its minimum at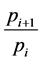 . Therefore, if two components
. Therefore, if two components 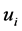 and
and 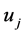 are nonzero, we must have
are nonzero, we must have 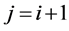
and in this case the minimum of the objective function is
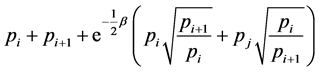
for some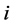 ,
,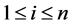 . Next notice that
. Next notice that
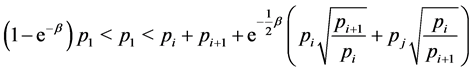
for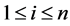 . Hence the minimum of the objective function is
. Hence the minimum of the objective function is
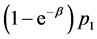 . ■
. ■
Since both TNCL and GTNCL are valid for infinite number of variables, these techniques can be used to solve resource allocatoin problems involving an infinite number of variables as well. For example, in the distribution of the search effort problem we can assume the search is for an object on the plane that can be potentially detected at an infinite set of locations (such as points with integer 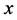 and
and 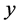 coordinates).
coordinates).
5. Optimal Portfolio Selection
There are other resource allocation problems that we are able to tackle with GTNCL, One of these problems is the problem of optimal portfolio selection. One model for this general problem is formulated as finding the maximum of
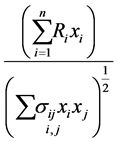
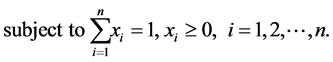
(see [6] ). Here 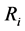 is expected return on security
is expected return on security 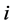 and
and 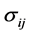 is the covariance between securities
is the covariance between securities 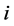 and
and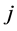 .
.
If the correlation coefficients between 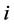 and
and 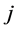 are constant
are constant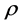 , with
, with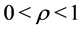 , then
, then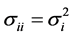 ,
,
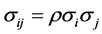 and from Karush-Kuhn-Tucker conditions the problem is reduced to
and from Karush-Kuhn-Tucker conditions the problem is reduced to
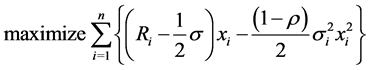 (44)
(44)
Notice that (44) is a self-reducing function and one can again apply the GTNCL to find a maximum value for it.
The problems of distribution of search effort and optimal portfolio selection are both examples of separable resource allocation problems. A separable resource allocation problem is a problem where we want to minimize or maximize
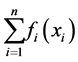
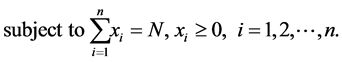
where each  is continuously differentiable over an interval including
is continuously differentiable over an interval including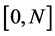 . The GTNCL can be applied to such a problem if
. The GTNCL can be applied to such a problem if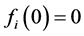 , for each
, for each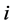 ,
,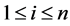 . This condition is not satisfied for a number of resource allocation problems including optimal sample allocation in stratified sampling, and production planning (see [5] ).
. This condition is not satisfied for a number of resource allocation problems including optimal sample allocation in stratified sampling, and production planning (see [5] ).
Remark 8 In a broader sense, each Kantorovich-type matrix optimization problem such as the one in Example 2 can be regarded as a resource allocation problem where our resource is just the set of pure numbers on the interval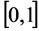 . For instance in Example 2 the problem is reduced to finding minimum of
. For instance in Example 2 the problem is reduced to finding minimum of
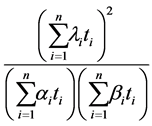
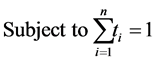
Each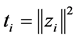 , where each
, where each 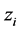 is a component of a minimizing vector
is a component of a minimizing vector 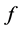 of norm
of norm 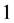 for the operator optimization problem (15). Indeed nonzero components of a minimizing vector
for the operator optimization problem (15). Indeed nonzero components of a minimizing vector 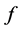 are important in applications. Historically, the optimization problem (15) was first discussed by R. Cameron and B. Kouvartakis in an effort to minimize the norm of output feedback controllers used in pole placement (see [7] ).
are important in applications. Historically, the optimization problem (15) was first discussed by R. Cameron and B. Kouvartakis in an effort to minimize the norm of output feedback controllers used in pole placement (see [7] ).
Remark 9. The author is not aware of any other theorem that provides closed form answers for resource allocation problems. The results we obtain might be of interest for instance in signal analysis where one needs to minimize the resource spent finding a signal that is probable to detected at a certain location. Computer models are used for solving such problems and it is interesting to investigate how consistent the results of computer models are with our results here. Also, many theories in portfolio selection suggest that diversification maximizes the profit. At the first glance this might sound inconsistent with the results one might obtain using the two nonzero theorem. However, we have to remember that the over theory also ensures diversification increases profit. If the profit is maximized for one or two securities, then the more the number of securities, the more pairs of securities we have.
References
- Gustafson, K. and Rao, D. (1997) Numerical Range. Springer, New York.http://dx.doi.org/10.1007/978-1-4613-8498-4
- Gustafson, K. and Seddighin, M. (1989) Antieigenvalue Bounds. Journal of Mathematical Analysis and Applications, 143, 327-340. http://dx.doi.org/10.1016/0022-247X(89)90044-9
- Seddighin, M. (2002) Antieigenvalues and Total Antieigenvalues of Normal Operators. Journal of Mathematical Analysis and Applications, 274, 239-254. http://dx.doi.org/10.1016/S0022-247X(02)00295-0
- Seddighin, M. (2009) Antieigenvalue Techniques in Statistics. Linear Algebra and Its Applications, 430, 2566-2580.http://dx.doi.org/10.1016/j.laa.2008.05.007
- Seddighin, M. and Gustafson, K. (2005) On the Eigenvalues which Express Antieigenvalues. International Journal of Mathematics and Mathematical Sciences, 2005, 1543-1554. http://dx.doi.org/10.1155/IJMMS.2005.1543
- Ibaraki, T. and Katoh, N. (1988) Resource Allocation Problems. The MIT Press, Cambridge.
- Cameron, R. and Kouvartakis, B. (1980) Minimizing the Norm of Output Feedback Controllers Used in Pole Placement: A Dyadic Approach. International Journal of Control, 32, 759-770.http://dx.doi.org/10.1080/00207178008922889

