Theoretical Economics Letters
Vol.05 No.04(2015), Article ID:59225,7 pages
10.4236/tel.2015.54069
Welfare Improvement and the Extension of the Income Gap under Monopoly
Yuhki Hosoya1, Soh Kaneko2
1Department of Economics, Kanto-Gakuin University, Yokohama, Japan
2Faculty of Economics, Keio University, Tokyo, Japan
Email: stairlimit@moon.cims.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 August 2015; accepted 25 August 2015; published 28 August 2015
ABSTRACT
This study constructs a model of a monopoly where investors are also actors, and shows that, in contrast to traditional models, this model admits the welfare improvement caused by monopoly. This study also reveals that if a huge income gap exists in the initial stage, then monopoly exacerbates the expansion of the income gap caused by market trades. Moreover, we show that this exacerbation occurs in general situations under some additional (but natural) assumptions.
Keywords:
Monopoly, Income Gap, Total Surplus

1. Introduction
Economics traditionally considers a monopoly to be bad for an economy. The most famous research indicating that monopolies are bad is the classical partial equilibrium analysis performed by Hicks [1] . This research indicates that a monopoly lowers the total surplus, and thus, the economy with a monopoly is not Pareto efficient. The result of this research is summerized in most of the textbook in microeconomics, e.g. Varian (1992), Okuno (2008) or Mas-Colell, Whinston, and Green (1995) [2] -[4] .
This research focuses on monopoly from a fresh perspective. The traditional monopoly model includes two characters: the monopolistic firm and the consumer. However, a real monopolistic situation necessarily involves a third character, namely, the investor. Under capitalism, investors are also consumers. Therefore, in our model, consumers invest in the monopolistic firm, which distributes its profit into its investors.
We formalize the above circumstance in a model, and analyze its model. We find that the total surplus of an economy may improve under a monopoly, which contradicts the traditional rationale for monopolies being bad. Meanwhile, in such a case the income gap often is expanded by market trade. If the initial income gap is sufficiently large, then a monopoly exacerbates this expansion of the income gap. The reason for this is as follows. Consider there are two consumers, where one is poor and another is rich. Both consumers invest in a firm that sells their own products and transfers its margin to investors in the form of dividends. However, the poor consumer has only limited ability to invest, and thus receives only a small share of the margin on product sales. The bulk of the margin is expropriated by the rich consumer. In this scenario, monopoly exacerbates this expansion of the income gap by enlarging firm’s profit.
This is the case in which the initial income gap is very high. In the case where the initial income gap is not so high, under certain assumptions monopoly also exacerbate the expansion of the income gap. Although these assumptions are not clear in the theoretical sense, we believe that these assumptions are intuitively natural.
In Section 2, we introduce our model and show the results. Section 3 is the conclusion.
2. The Model
We construct two models, named model 1 and model 2, to compare the competitive case with the monopolistic case. Model 1 corresponds with the competitive case, while model 2 corresponds with the monopolistic case. Both models consist of two consumers and one firm. Both consumers have a utility function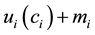 , where
, where
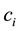 denotes private consumption and denotes the amount of money. We assume that
denotes private consumption and denotes the amount of money. We assume that
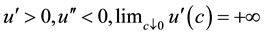 , and
, and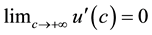 . In the beginning of the model, consumer
. In the beginning of the model, consumer
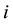 has
has
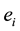 units of money and one unit of labor. Without loss of generality, we assume
units of money and one unit of labor. Without loss of generality, we assume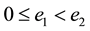 . In the first-stage of the model, consumer
. In the first-stage of the model, consumer
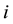 determines the amount of investment
determines the amount of investment
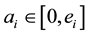 at same time. Then the stock ratio
at same time. Then the stock ratio
 is defined as
is defined as
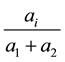 and the capital of the firm
and the capital of the firm
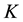 is defined as
is defined as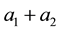 . The product function of the firm is denoted as
. The product function of the firm is denoted as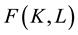 . We assume that
. We assume that
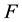 is homogeneous of degree one,
is homogeneous of degree one,
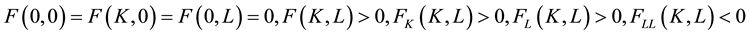 for all
for all



The second-stage is different from each model. In model 1, each consumer and firm participates in the competitive market and the equilibrium arises. In model 2, the firm determines the price of consumption


2.1. The First Model
First, we solve the second-stage. The first-order condition of consumer

Hence,
and thus,

and,
Hence, the equilibrium price is
Next, the first-order condition of the firm is,
Thus, the equilibrium wage is
Then, the profit of firm is2
where the subscript 1 represents that it is the profit of the first model. Hence,


Therefore, the payoff function of this model

In the first-stage, consumer


Define
and



Hence,





We show the following proposition:
Proposition 1: There exists a Nash equilibrium






Proof: We first suppose



















To show that










Next, suppose















2.2. The Second Model
The demand function of consumer

Hence, the total demand is


Now, we introduce an assumption.
ASSUMPTION 1: For any



By first-order condition, we have
Recall that


Then, the payoff function of this model

We want to focus on the case where the equilibrium of the first stage is well-defined. Therefore, we introduce an additional assumption:
ASSUMPTION 2:


Here, we provide a sufficient condition of ASSUMPTION 2 to show this assumption is not too strong.
Proposition 2: Suppose that ASSUMPTION 1 holds. Then, ASSUMPTION 2 holds if


Proof: By ASSUMPTION 1 and the second-order necessary condition, we have
Meanwhile, since

By homogeneity of degree one on
Further, both


and thus,
Hence,
and thus, ASSUMPTION 2 holds. This completes the proof.
It can be easily verified that

Define
and











We will show the following proposition:
Proposition 3: Under ASSUMPTIONS 1-2, there exists a Nash equilibrium





Proof: It can be verified in the same way as Proposition 1.
2.3. Example: Improvement of Total Welfare
Suppose


and thus,
Therefore, we have
In model 2, we have
and thus,
Therefore,
This example demonstrates that the existence of the case where monopoly improves the total surplus.
2.4. Comparative Statics
First, we argue the following result.
Proposition 4: Suppose that


Then, we have




Proof: It suffices to show that our claim holds if






which completes the proof.
Later, 2) of Proposition 5 says that under ASSUMPTION 3, the restriction of proposition 4 is removed. Here we introduce additional assumptions.
ASSUMPTION 3:


ASSUMPTION 4:


Remark: ASSUMPTIONS 3-4 are not clear in the theoretical view. However, we think both conditions are natural in the real world. Usually, the bigger the capital obtained, the richer the firm becomes. Also, if the monopolistic power of the firm becomes strong, then we can expect wages to decrease. Note that by definition,
Proposition 5: Suppose ASSUMPTIONS 1-2 hold, and choose any Nash equilibria


1)


2) Under ASSUMPTION 3,




3) Under ASSUMPTIONS 3-4,





Proof: If

Suppose ASSUMPTION 3 holds. By easy calculation,
and thus,
Recall that



Since



Note that








If
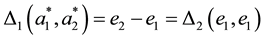






Lastly, suppose ASSUMPTIONS 3-4 hold. If


whenever

and thus,

and thus,
3. Conclusion
We constructed a model of a monopoly with investors, and showed that monopoly did not necessarily decrease total welfare. Meanwhile, under mild assumptions monopoly exacerbated the expansion of the income gap. Therefore, we revealed a new aspect of the negative influence of monopoly.
Acknowledgements
We are grateful for Eisei Ohtaki for his comments and suggestions.
Cite this paper
YuhkiHosoya,SohKaneko, (2015) Welfare Improvement and the Extension of the Income Gap under Monopoly. Theoretical Economics Letters,05,590-597. doi: 10.4236/tel.2015.54069
References
- 1. Hicks, J.R. (1938) Value and Capital. Oxford University Press, Oxford.
- 2. Mas-Colell, A., Whinston, M.D. and Green, J.R. (1995) Microeconomic Theory. Oxford University Press, Oxford.
- 3. Okuno, M. (2008) Microeconomics. Tokyo University Press, Tokyo.
- 4. Varian, H.R. (1992) Microeconomic Analysis. W. W. Norton and Company, New York.
Notes
1In the second-stage, we assume that the consumption space of each consumer is

2Use the Euler equation
3If


4For example, to differentiate




5Actually, we think that there may exist a weaker condition than ASSUMPTION 2 ensuring the following Propositions. However, since ASSUMPTION 2 itself is not too strong, we satiate this assumption, at least in this paper.















































