Theoretical Economics Letters
Vol.04 No.09(2014), Article ID:52309,7 pages
10.4236/tel.2014.49110
The Effect of Environmental Taxes on Steady-State Consumption
Bidisha Lahiri
Department of Economics and Legal Studies, Oklahoma State University, Stillwater, USA
Email: bidisha.lahiri@okstate.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 October 2014; revised 28 November 2014; accepted 12 December 2014
ABSTRACT
This paper examines the effects of environmental taxes on the demand and supply sides of the economy and uncovers two opposite forces on long-term production. An increase in the environmental tax stimulates abatement behavior as producers lower production from the same capital stock but simultaneously lower per-unit emissions increases consumers’ demand for the cleaner goods hence increasing the capital stock. Starting from a low level of environmental taxes, my model finds that initially the demand-driven positive relationship dominates while at a higher level of environmental taxes, the production lowering negative effect dominates; the transition occurs before the economy reaches the optimal tax rate.
Keywords:
Environmental Tax, Steady State, Production, Emission

1. Introduction
It is commonly recognized that a higher pollution tax lowers the marginal productivity of resources and has a negative effect on long-term production. However, there exists a specialized segment of the literature recognizing that stricter abatement policies could also have some positive effects. A tighter environmental policy can potentially operate through different mechanisms such as investment, education, R&D, productivity improvement of inputs, etc., to influence the long-term growth rate. Thus the final effect of these two forces determines whether the net effect of a stricter environmental policy is to increase or decrease long-term production levels. Examples of some articles exploring the positive effects of higher pollution taxes are as follows. Bovenberg and Smulders [1] [2] show that a higher pollution tax improves the quality of the environment, which increases productivity and hence has a positive effect on production in the long term. Ono [3] determines that a higher pollution tax leads to a higher quality of environmental capital bequeathed to future generations, which is equivalent to greater environmental wealth. For future generations, this is equivalent to the positive income effect of a high pollution tax in the long run. Grimaud and Rouge [4] assume that emissions generated during production have a negative effect on welfare. Using an endogenous growth model, they find that a carbon tax has a negative impact on short-term production and consumption but has a positive impact on long-term growth.
In a slightly different approach, Gupta and Ray Burman [5] consider the allocation of government income tax revenue across abatement expenditures and productive public expenditures. In their model, a higher share of abatement expenditures improve the efficiency of productive public expenditures, generating the positive effect of pollution control. Acemoglu et al. [6] consider the effect of environmental policies toward endogenous technology. When stricter environmental policies encourage technological innovation, a positive effect on production emerges.
This theoretical literature shows that a stricter environmental policy is not incompatible with a positive effect on economic production; however, in showing this result, the studies rely on strong assumptions that may appear to favor such results. In the current paper, I uncover the positive (and negative) effects of stricter environmental policies in a simple model that is not based on a priori assumptions regarding the positive effect of the policies. Instead, the model derives its results based on the observation that for consumers the trade-off between consumption and environmental quality is such that richer consumers prefer lower pollution while poorer consumers are more accepting of higher pollution if that affords them marginally more consumption. This results in a negative relationship between consumption and pollution. On the resource constraint side, a positive relationship exists between pollution and production. Introducing a change in environmental taxes in the setting of these positive and negative relationships between production and pollution generates very interesting comparative statics results.
The rest of the paper is stet-up as follows. I set-up the model in Section 2 where I first elaborate the production conditions which coupled with the resource constraint underlies the negative relation between environmental taxes and consumption. Next I develop the demand side of the model that leads to the positive relation between environmental taxes and consumption. Finally I put together the demand and supply dimensions to characterize the steady state equilibrium. The effects of changes in environmental taxes are explored as comparative statics for the steady state equilibriums. Finally Section 3 concludes with a summary of the current findings and directions for future research.
2. Model
To capture the final effect of an environmental policy on long-term equilibrium (steady-state) output, I will focus on how emission taxes affect both supply and demand within the economy. I introduce emissions and environmental taxes in the Neoclassical Growth Model with an endogenous savings rate developed by Ramsey [7] , Cass [8] and Koopmans [9] . The price of the produced commodity
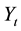 is normalized to one; return to capital
is normalized to one; return to capital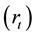 , environmental taxes
, environmental taxes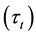 , and the value of marginal disutility from pollution
, and the value of marginal disutility from pollution
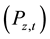 are all expressed relative to this normalized price1.
are all expressed relative to this normalized price1.
2.1. Supply
Production
 is a decreasing function of capital
is a decreasing function of capital
 and emits pollution
and emits pollution
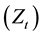 as a byproduct. In the absence of any abatement activity, production and emissions are given by Equation (1).
as a byproduct. In the absence of any abatement activity, production and emissions are given by Equation (1).
 . (1)
. (1)
Emissions can be abated if some resources are diverted for this purpose. Following the approach popularized by Copeland and Taylor [10] , the production of output and of the emission byproduct are combined into a single function using abatement technology. If
 is the fraction of resources spent for abatement activity in sector
is the fraction of resources spent for abatement activity in sector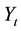 , then the output level after abatement activity is:
, then the output level after abatement activity is:
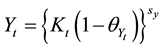 . (2)
. (2)
The emission level after abatement activity is:
 . (3)
. (3)
Here
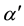 is the parameter from abatement technology in the
is the parameter from abatement technology in the
 sector. Combining (2) and (3) by eliminating
sector. Combining (2) and (3) by eliminating
 between the above two production functions results in the Cobb-Douglas form of production relationship.
between the above two production functions results in the Cobb-Douglas form of production relationship.
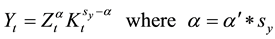 (4)
(4)
Emissions appear as an input for production; higher emissions are associated with a higher production level, implying that fewer resources are diverted for abatement of the pollution.
Suppose that the government imposes a tax


Using this condition to eliminate emission level



I assume that emission tax revenues collected by the government are distributed back in a lump-sum manner so that they do not affect the national budget constraint. The only role of the emission tax is to ensure abatement activity by producers. Under optimal taxation where the tax level is set equal to consumers’ disutility from emissions, the optimal tax ensures that the marginal cost to producers of emission reduction equals consumers’ valuation of the marginal disutility from emissions.
2.2. Resource Constraint
Next I turn to the resource constraint of the economy that matches demand and supply. The total quantity produced every period



Using (5) to represent production in the above resource constraint, I rewrite it as Equation (6).

2.3. Demand
On the demand side, I assume an infinitely lived consumer whose life-time welfare is the discounted sum of every period’s welfare:

In any given period, the consumer derives positive but decreasing marginal utility from consumption and disutility from emissions2. If


Equation (9) is the Euler equation that embodies the first-order condition for maximizing intertemporal welfare (7) with respect to


2.4. Steady State
The steady-state versions of resource constraint (6) and consumption Euler Equation (9)-presented as Equations (10) and (11), respectively-together determine steady-state equilibrium. At the steady state, the aggregate capital stock remains constant, as shown in Equation (10).

Equation (11) below, derived from Equation (9), is the constant consumption equation. Consumption attains a steady level when the welfare cost of delaying consumption by one period equals the next period return from current investment. In this model with environmental externality, the next period return from investment requires that the emission disutility associated with additional capital in the next period be subtracted from the marginal productivity of capital. Equation (11) is the corresponding zero consumption growth equation.

In standard growth models with no environmental externality, the return from investment is the marginal product of capital without necessitating the deduction of the disutility of emissions. Hence the steady-state consumption locus is a constant capital stock line in standard models; in the current model with emission disutility, it is a negatively sloped relationship between capital stock and consumption, as captured by Equation (11). If

2.5. Comparative Statics of an Emission Tax Change
On the steady-state locus for resource constraint (10), steady-state consumption demand equals its production or supply. A higher environmental tax

Table 1. Parameter interpretations and values.
Figure 1. Effect of higher environmental tax on steady state capital locus.
In the steady-state version of consumption Euler Equation (11), the welfare cost of delaying consumption by
one period

tion, the marginal valuation of emission disutility is significant. Hence the above equality can be achieved either by a smaller capital stock accompanied by a relatively lax environmental tax


To see the long-term effect of an increase in environmental taxes, I look at the simultaneous effect of the shifts of both loci in Figure 3.
While Figure 3 suggests that the change in the equilibrium could be in either direction, the solution emerging from solving equations (10) and (11) provides an interesting analytical result4.
The tightening of environmental standards has two opposite effects. On one hand, it makes production associated with each unit of capital cleaner, so a higher capital stock becomes acceptable from the consumers’ perspective. On the other hand, a higher environmental tax lowers the marginal product of capital, lowering production. In equilibrium, the resource constraint identifies an equilibrium where the positive and negative forces balance each other. The derivative



The optimal emission tax is defined as the shadow cost of emissions to producers that equals the marginal disutility to consumers

Figure 2. Effect of higher environmental tax on steady state consumption locus.
Figure 3. Effect of higher environmental tax on steady state equilibrium.
tween production and the environmental tax turns negative before environmental taxes reach the optimal level except in the case of constant returns to scale
3. Conclusions and Future Directions
While the production-lowering effects of stricter environmental policies remain the mainstream result, this paper contributes to the segment of literature that seeks to investigate the positive effects of higher emission taxes on long-term income and consumption. Instead of adding special characteristics to the model, this model uncovers the interaction of the positive and negative relationships between environmental taxes and consumption arising from basic demand and supply relationships. The role of the emission tax is to ensure abatement activity by the producers. Stricter environmental policy lowers supply from any given capital stock, but simultaneously the tighter policy increases demand for the cleaner good and hence increases the capital stock raising production and consumption. I consider the above forces at the steady state and uncover the transitional level of environmental tax where the relationship between environmental policy strictness and consumption turns from positive to negative. This switch happens before the attainment of the optimal environmental tax, defined as the level of taxation that equals consumers’ valuation of pollution disutility. Hence the incentive to raise environmental taxes in order to increase steady state consumption is not sufficient to induce policymakers to set the environmental tax as high as the socially optimal level.
There are some aspects that need to be addressed in future work. For example, the environmental quality addressed in this paper is a flow variable while many environmental quality variables are stock variables. Second, the international aspect both in terms of international spillovers of environmental externalities and international outsourcing of production are real-world complexities that need to be addressed in future extensions of this model.
References
- Bovenberg, A.L. and Smulders, S. (1995) Environmental Quality and Pollution Augmenting Technological Change in a Two Sector Endogenous Growth Model. Journal of Public Economics, 57, 369-391. http://dx.doi.org/10.1016/0047-2727(95)80002-Q
- Bovenberg, A.L. and Smulders, S. (1996) Transitional Impacts of Environmental Policy in an Endogenous Growth Model. International Economic Review, 37, 861-893. http://dx.doi.org/10.2307/2527315
- Ono, T. (2003) Environmental Tax Policy and Long Run Economic Growth. Japanese Economic Review, 54, 203-217. http://dx.doi.org/10.1111/1468-5876.00254
- Grimaud, A. and Rouge, L. (2014) Carbon Sequestration, Economic Policies and Growth. Resource and Energy Economics, 36, 307-331. http://dx.doi.org/10.1016/j.reseneeco.2013.12.004
- Gupta, M.R. and Ray Barman, T. (2009) Fiscal Policies, Environmental Pollution and Economic Growth. Economic Modelling, 26, 1018-1028. http://dx.doi.org/10.1016/j.econmod.2009.03.010
- Acemoglu, D., Aghion, P., Bursztyn, L. and Hemous, D. (2012) The Environment and Directed Technological Change. American Economic Review, 102, 131-166. http://dx.doi.org/10.1257/aer.102.1.131
- Ramsey, F. (1928) A Mathematical Theory of Saving. Economic Journal, 38, 543-559. http://dx.doi.org/10.2307/2224098
- Cass, D. (1965) Optimum Growth in an Aggregative Model of Capital Accumulation. Review of Economic Studies, 32, 233-240. http://dx.doi.org/10.2307/2295827
- Koopmans, T.C. (1965) On the Concept of Optimal Economic Growth. Econometric Approach to Development Planning, North-Holland Publishing Company, Amsterdam, 225-287.
- Copeland, B.R. and Taylor, M.S. (1997) A Simple Model of Trade, Capital Mobility and the Environment. NBER Working Paper 5898.
Appendix: Effect of Higher Environmental Tax on Steady State Consumption
Solve for steady-state consumption using Equations (10) and (11):
Total differentiation of the above equation to see the effect of a change in environmental taxes on steady state consumption:
NOTES
1Although the output, capital, emission, and welfare variables are presented in levels, they are open to percapita interpretation.
2Copeland and Taylor (1997), “A Simple Model of Trade, Capital Mobility and the Environment,” NBER Working Paper 5898.
3As the valuation of pollution disutility becomes larger as




4Derivation in Appendix.
5Refer to Equation (8).

















