Theoretical Economics Letters
Vol.2 No.3(2012), Article ID:21517,7 pages DOI:10.4236/tel.2012.23060
Optimal Costly Information Gathering in Public Service Provision
1School of Economics and Finance, Massey University, Auckland, New Zealand
2Department of Accounting and Finance, University of Auckland, Auckland, New Zealand
Email: p.geertsema@auckland.ac.nz, *c.schumacher@massey.ac.nz
Received May 23, 2012; revised June 25, 2012; accepted July 27, 2012
Keywords: Costly Information Gathering; Signal Extraction; Service Provision
ABSTRACT
Imperfect information regarding the true needs of recipients is a common problem for governmental or not-for-profit service providers. This can lead to potentially dangerous under-provision or wasteful over-provision of services. We provide a method for optimally improving a service provider’s information regarding true client need through costly information gathering. Our contribution is to allow providers to endogenously and optimally choose the intensity of information gathering. Providers do so by specifying the level of correlation between observed and true recipient need, subject to an arbitrary cost function over the specified correlation. We derive the conditions that characterize the choice of optimal correlation for providers with quadratic utility. Using a realistic exponential correlation cost function, we show that there exists a critical value of true client need variance below which it is never optimal to engage in information gathering. Further, for true client variance above this critical level the optimal correlation will always exceed 0.5. Our findings have a wide range of policy implications in areas such as health care, social wellfare and even counterterroism.
1. Introduction
Most commercial firms are motivated to some degree by profit; government providers and NGO’s, on the other hand, do not generally subscribe to a profit motive. Instead, these providers are motivated by a desire to assist a target group of recipients as best as their resources allows. In some cases the level of need faced by potential recipients is clear and the more pressing concern for providers is the acquisition of resources, or the rationing of resources amongst recipients if available resources fall short of observed needs. However, the provider may not be able to observe the true needs of recipients perfectly. For example, in treating a certain health condition, it may not be clear what the true need of the patient is. In such cases the provider risks under-treating or over-treating the patient. Or in a counter-terrorism setting an intelligence agency may not know the true risk of a suspect, and may inefficiently commit to the costly surveillance of a low-threat suspect while inadequately monitoring a high-threat suspect. In general, this sort of problem is likely to occur in settings where a provider wishes to provide a service to a large number of recipients but cannot accurately determine the efficient level of services for individual recipients, due to imperfect information regarding each recipient’s true need for the service.
To reduce the level of imperfect information, the provider can engage in information gathering. At times, this can be straight-forward. Imagine, for example, a public health care provider that has to provide care for a patient that presents herself with an injury to her arm after a fall. An X-ray is likely to provide a sufficient amount of information to determine the patient’s true need for service. But what if a patient presents herself with a raised temperature, loss of appetite and mild abdominal pain? The initial diagnosis could include mild gastroenteritis, appendicitis or even cancer. In a world of limitless resources the provider would simply perform as many tests as necessary to determine the true need for care. However, in an environment of severe resource limitations, the provider needs to carefully assess if the amount of additional information obtained by a test is sufficiently large to justify the expense. The model presented in this paper explictly links the quality of information to the cost of obtaining that information, in a setting where the service provider can choose the quality of information (but at a cost). This formulation allows us to characterise the optimal level of costly information gathering, in, for instance, a health care setting.
Our research topic is related to the literature on information gathering and signal extraction. Papers in this literature generally consider a situation where an underlying signal X is added to a white noise random variable ε to yield the observed signal  (see e.g. Burman [1]; Sargent [2]; Boone and Hall [3]). Our paper takes a different approach by modeling noise (or signal quality) via the correlation parameter
(see e.g. Burman [1]; Sargent [2]; Boone and Hall [3]). Our paper takes a different approach by modeling noise (or signal quality) via the correlation parameter 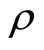 between the true signal X and the observed signal Y.1 In most of the previous literature signal quality is not modeled explicitly. An exception is Alles and Lundholm [4], who model signal quality in the context of public disclosure of information in the securities market. The authors introduce a signal precision variable and determine how much effort a trader should expend in order to obtain a more precise signal through costly reduction in the variance of the noise term. Our approach differs from Alles and Lundholm [4] in two regards. In Alles and Lundholm [4], the observed signal is the sum of a market signal (in this instance price) and an error term; that is, it follows the standard signal extraction model. In our paper, the provider observes a signal and noise is modeled via the correlation between the true need and the observed signal. Furthermore, in Alles and Lundholm [4] signal precision is increased by reducing the variance of the error term. In our setting, however, this approach does not yield an analytically tractable solution.
between the true signal X and the observed signal Y.1 In most of the previous literature signal quality is not modeled explicitly. An exception is Alles and Lundholm [4], who model signal quality in the context of public disclosure of information in the securities market. The authors introduce a signal precision variable and determine how much effort a trader should expend in order to obtain a more precise signal through costly reduction in the variance of the noise term. Our approach differs from Alles and Lundholm [4] in two regards. In Alles and Lundholm [4], the observed signal is the sum of a market signal (in this instance price) and an error term; that is, it follows the standard signal extraction model. In our paper, the provider observes a signal and noise is modeled via the correlation between the true need and the observed signal. Furthermore, in Alles and Lundholm [4] signal precision is increased by reducing the variance of the error term. In our setting, however, this approach does not yield an analytically tractable solution.
Thus a key contribution of our paper is the development of a signal extraction model that enables us to obtain tractable results in a setting where the standard signal extraction specification fails. The solution thus obtained provides insights into the link between the quality of information obtained and signal extraction costs. This is done by linking information cost to the correlation between the true distribution of client need and the observed distribution of client need. Furthermore, we endogenise the level of correlation by letting the provider optimally select the desired level of correlation given an arbitrary cost function defined over such correlation.
We find that for a provider with quadratic utility, optimal service is a linear transformation of the observed client need, parametrized by the correlation between true client need and observed client need as well as the variance of observed client need. We also derive the first and second order conditions which the optimal choice of correlation should satisfy, which, along with the optimal service relationship above, maximizes overall provider utility.
We illustrate our model by specifying a bounded domain exponential correlation cost function. We show that with such a correlation cost function, there exists a critical value of true client need variance below which it is optimal not to gather information and above which only correlations exceeding 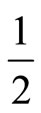 are optimal. Optimal correlation given a true client need standard deviation above the critical value is increasing at a decreasing rate, and in the limit as true client need standard deviation approaches infinity, optimal correlation tends towards one.
are optimal. Optimal correlation given a true client need standard deviation above the critical value is increasing at a decreasing rate, and in the limit as true client need standard deviation approaches infinity, optimal correlation tends towards one.
While our findings may apply in a variety of economic settings, there are clear applications in the public health and wellfare sector. Insights into the relationship between signal quality and information gathering costs could improve decision-making in the areas of waiting list prioritization, medication allocation and, more generally, needs-based wellfare schemes. Specifically, the identification of critical threshold client need variance levels may help service providers to identify situations in which it would be more efficient to withdraw from any information gathering.
This paper is structured as follows. In section two we describe our model and explain how our setting differs from existing approaches. Section three provides the solution to the model. To illustrate our findings we provide an example with a specific cost function in section four and outline applications in section five. Section six discusses empirical implications and section seven concludes.
2. Theoretical Model
Our model setting is as follows. A provider wishes to provide for the need of a recipient. Since we are considering the best course of action for the provider in expectation, the model should be interpreted as being applied to a large number of recipients with identically and independently distributed (IID) needs.2
The provider cannot directly observe the true need of the recipient, but instead can observe a related variable, the signal. We denote by X the numeric representation of the recipient’s true need and by Y the signal observed by the provider. X and Y are drawn from a bi-variate normal distribution3 with correlation 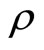 and their marginal distributions are given by
and their marginal distributions are given by  and
and 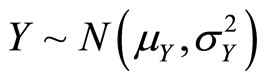 respectively. Note that although X and Y are both normally distributed they are not independent except for the special case where
respectively. Note that although X and Y are both normally distributed they are not independent except for the special case where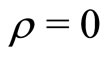 .
.
The provider would like to provide services, denoted by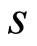 , to meet the recipient’s need. We assume that the provision of services above or below the recipient’s need are inefficient. The impact of inefficiency is modeled by subjecting the provider to quadratic utility
, to meet the recipient’s need. We assume that the provision of services above or below the recipient’s need are inefficient. The impact of inefficiency is modeled by subjecting the provider to quadratic utility 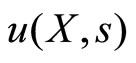 (or, equivalently, quadratic loss aversion) over inefficiencies (
(or, equivalently, quadratic loss aversion) over inefficiencies (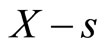 ).
).
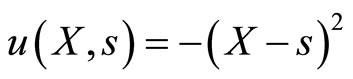 (1)
(1)
The degree to which the provider can avoid inefficiency is related to the correlation of its observed signal Y with the unobserved true recipient need X. We endogenise the correlation between signal and needs  by letting the provider choose
by letting the provider choose  4 subject to a cost function
4 subject to a cost function 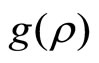 expressed in the same units as
expressed in the same units as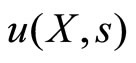 . The provider has overall utility
. The provider has overall utility 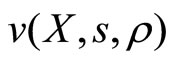 given by
given by
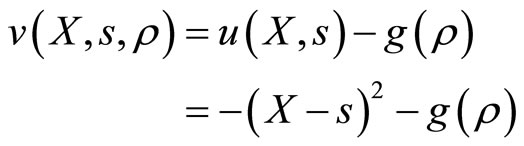 (2)
(2)
Hence the provider has utility defined over two choice variables, services s and correlation .
.
It is easy to show that the provider’s optimal choice of service s is simply X. However X—the true client need— is not directly observable by the provider and is also a random variable. Nonetheless, the provider knows the distribution of both X and Y and observes the realization of the observed client need Y = y, which is correlated with X. Therefore the provider can use Bayesian updating to obtain the posterior distribution of X given Y = y, which can then be used to compute the expected level of true recipient need X.
We show (in the Appendix as Theorem 1) that the optimal level of service delivery, conditional on the observed client need Y = y, is given by
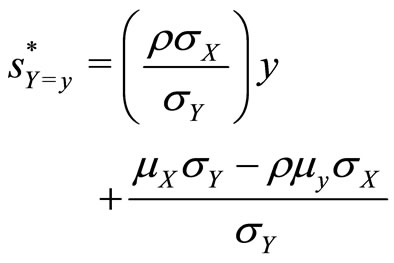 (3)
(3)
From the perspective of the provider observing Y = y the optimal quantum of services
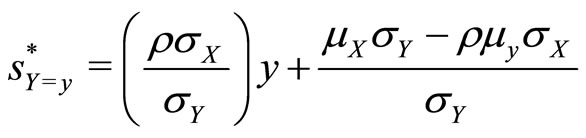 is therefore a point value that it can put forward as its best estimate of X under the circumstances. In general
is therefore a point value that it can put forward as its best estimate of X under the circumstances. In general 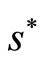 is a linear transformation of the random variable Y. Therefore
is a linear transformation of the random variable Y. Therefore 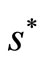 is itself normally distributed with mean
is itself normally distributed with mean 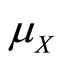 and variance
and variance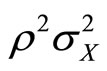 .5
.5
We now extend the model by endogenising the correlation parameter ; in simple terms, this allows the provider to choose how much to pay for better quality information. We show (in the Appendix as Theorem 2) that provider utility is maximized in expectation if the provider chooses optimal service
; in simple terms, this allows the provider to choose how much to pay for better quality information. We show (in the Appendix as Theorem 2) that provider utility is maximized in expectation if the provider chooses optimal service  as above and if it chooses a correlation
as above and if it chooses a correlation 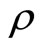 that satisfies one equation (the first order condition) and one inequality (the second order condition). Formally:
that satisfies one equation (the first order condition) and one inequality (the second order condition). Formally:
Provider utility 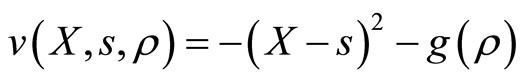 conditional on observed
conditional on observed 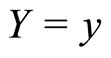 is maximized in expectation given joint normally distributed
is maximized in expectation given joint normally distributed 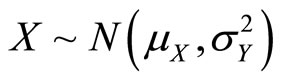 and
and  with endogenous correlation
with endogenous correlation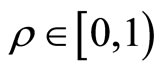 , if 1)
, if 1)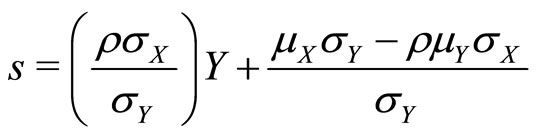 , and 2)
, and 2)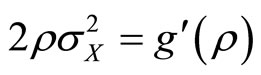 , and 3)
, and 3)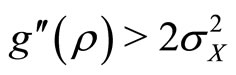 .
.
The first condition simply restates our finding regarding optimal service delivery, given some correlation . The second and third conditions characterizes the optimal correlation to be used in calculating the service delivery
. The second and third conditions characterizes the optimal correlation to be used in calculating the service delivery 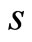 in condition one. The second condition states that the optimal choice of correlation for the provider should equate the marginal cost of information (
in condition one. The second condition states that the optimal choice of correlation for the provider should equate the marginal cost of information (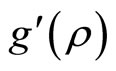 ) with the marginal benefit (
) with the marginal benefit (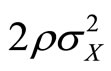 ). The third condition enforces second order conditions for maximum provider utility— this ensures that the correlation is chosen to maximize rather than minimize provider utility.
). The third condition enforces second order conditions for maximum provider utility— this ensures that the correlation is chosen to maximize rather than minimize provider utility.
3. Costly Information
To make the above more concrete, we consider a specific correlation cost function in the form
 (4)
(4)
as plotted in Figure 1, with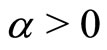 . Note that the parameter
. Note that the parameter 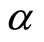 regulates the degree of curvature of
regulates the degree of curvature of 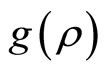 over the interval
over the interval .
.
This specific function has a number of properties that make it quite appealing as a correlation cost function. First, the correlation cost function 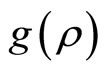 is strictly increasing in
is strictly increasing in , consistent with the intuition that additional information incurs additional cost. Second, it is increasing at an increasing rate in
, consistent with the intuition that additional information incurs additional cost. Second, it is increasing at an increasing rate in . This corresponds to the notion that obtaining additional information becomes increasingly expensive, or alternatively, that incremental dollars reveal less and less incremental information—the law of diminishing returns. Finally,
. This corresponds to the notion that obtaining additional information becomes increasingly expensive, or alternatively, that incremental dollars reveal less and less incremental information—the law of diminishing returns. Finally, 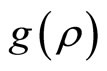 tends towards infinity as
tends towards infinity as  tends towards 1. In other words, perfect information (
tends towards 1. In other words, perfect information (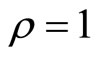 ) is prohibitively expensive, as is often the case in practice.
) is prohibitively expensive, as is often the case in practice.
We show (in the Appendix as Theorem 3) that, given a correlation cost function in this form, the optimal choice of correlation is given by
 (5)
(5)
if 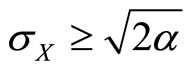 and by
and by 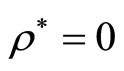 otherwise.
otherwise.
Graphically (Figure 2), this solution can be represented as the intersection of the plane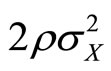 —representing provider marginal (inefficiency related) utility—and
—representing provider marginal (inefficiency related) utility—and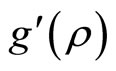 , representing provider marginal cost of correlation (this is the gray surface that does not vary along
, representing provider marginal cost of correlation (this is the gray surface that does not vary along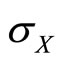 ).
).
To summarize, two major features emerge from the model. First, we show the existence of a critical value of true client need standard deviation 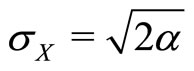 such that below that critical value there is never any benefit in increasing correlation
such that below that critical value there is never any benefit in increasing correlation 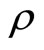 beyond zero. The provider’s optimal course of action for
beyond zero. The provider’s optimal course of action for  is to simply use
is to simply use 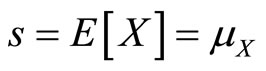 and let
and let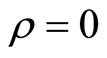 . Second, for
. Second, for 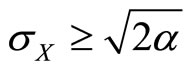
an optimal interior 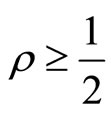 exists and the limit of this solution as
exists and the limit of this solution as 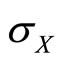 tends to infinity is
tends to infinity is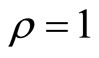 . Combined with the previous point, this means that it is never optimal to select a
. Combined with the previous point, this means that it is never optimal to select a 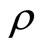 strictly between 0 and
strictly between 0 and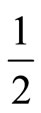 .
.
This is clearly illustrated in Figure 3 below, which plots the two optimal solutions to correlation 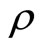 against recipient needs standard deviation
against recipient needs standard deviation 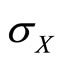 for
for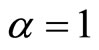 .
.
4. Empirical Predictions
While we have framed our model normatively—that is, what an optimal provider should do—it can also be interpreted descriptively, that is, as a theory of provider behavior that could be tested empirically.
Equation (14) can be rewritten as an ordinary least squares estimation in the form
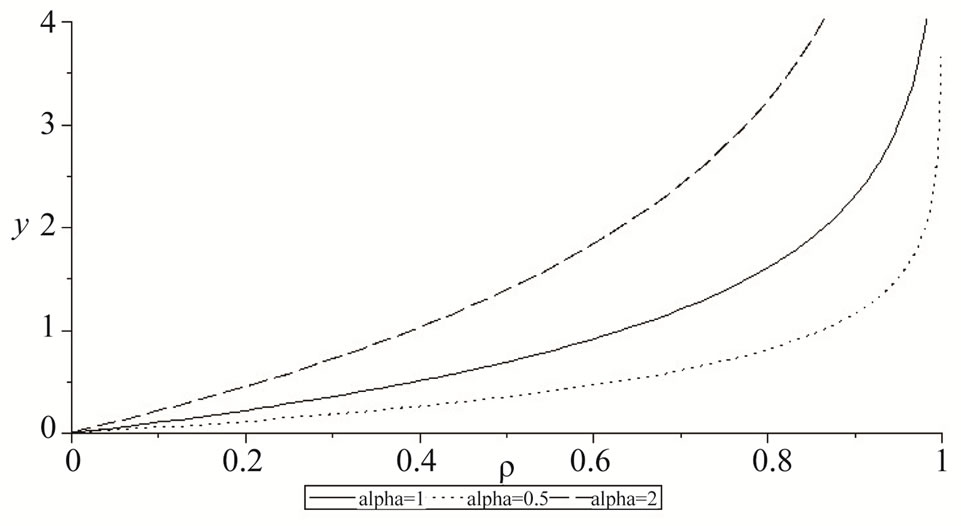
Figure 1. Correlation cost function 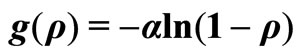 for
for 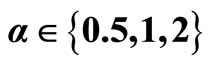 as a function of ρ.
as a function of ρ.

Figure 2. Marginal inefficiency related utility and marginal cost of correlation plotted against σX and ρ.
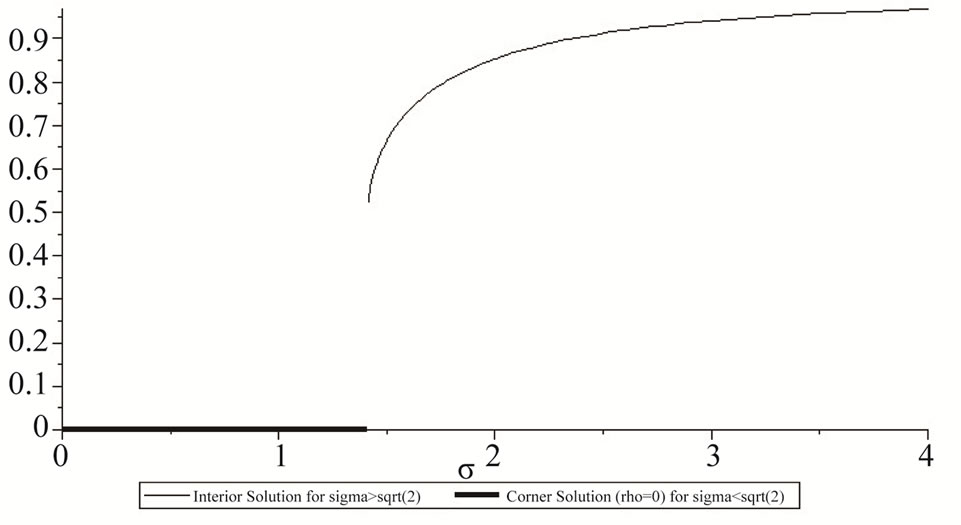
Figure 3. Optimal correlation ρ as a function of recipient needs standard deviation σX, with α = 1.
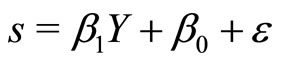 (6)
(6)
with theory predicting that 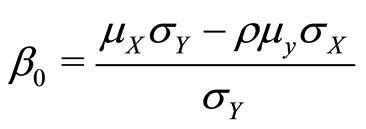 and
and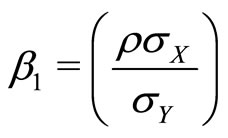 , which can be tested as formal hypotheses. (The coefficients in
, which can be tested as formal hypotheses. (The coefficients in 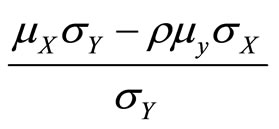 and
and 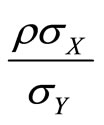 are all parameters of the joint distribution of X and Y, which could themselves be estimated.)
are all parameters of the joint distribution of X and Y, which could themselves be estimated.)
Furthermore, if the cost of obtaining additional information is described well by  for a suitable choice of
for a suitable choice of , then our theory predicts a critical value of client need variance
, then our theory predicts a critical value of client need variance 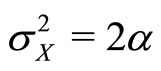 below which providers will cease to spend money on costly observation or monitoring. It also suggests that, if providers do spend money on observation or monitoring, this will only be the case if the resultant correlation between what they observe and the true state of affairs exceeds
below which providers will cease to spend money on costly observation or monitoring. It also suggests that, if providers do spend money on observation or monitoring, this will only be the case if the resultant correlation between what they observe and the true state of affairs exceeds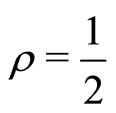 .
.
5. Conclusion
Operating in an environment that is characterized by resource constraints, public service providers have to be efficient in their service provision, that is, match the quantum of service delivery for each recipient with the need experienced by that recipient. However in practice, recipient need is often difficult and costly to observe accurately. Providers therefore face a trade-off between better information and increased cost of information gathering with regards to individual recipients. The framework we suggest formally models this tension and provides criteria for the optimal trade-off between better information and higher cost. This model is normative, in the sense that it yields the optimal course of action for a provider facing a prescribed problem. But it can also be interpreted as a descriptive model that yields empirically testable implications. Using a correlation parameter to model the signal-quality of observed patient need, our model provides a tractable solution to the problem of optimal information gathering and identifies thresholds.
REFERENCES
- J. P. Burman, “Seasonal Adjustment by Signal Extraction,” Journal of the Royal Statistical Society, Series A, Vol. 143, No. 3, 1980, pp. 321-337. doi:10.2307/2982132
- T. J. Sargent, “Equilibrium with Signal Extraction from Endogenous Variables,” Journal of Economic Dynamics and Control, Vol. 15, No. 2, 1991, pp. 245-273. doi:10.1016/0165-1889(91)90012-P
- M. Alles and R. Lundholm, “On the Optimality of Public Signals in the Presence of Private Information,” Accounting Review, Vol. 68, No. 1, 1993, pp. 93-112.
- L. Boone and S. G. Hall, “Signal Extraction and Estimation of a Trend: A Monte Carlo Study,” Journal of Forecasting, Vol. 18, No. 2, 1999, pp. 129-137. doi:10.1002/(SICI)1099-131X(199903)18:2<129::AID-FOR718>3.0.CO;2-9
Appendix: Formal Proofs
Theorem 1. For given correlation 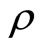 the optimal choice of service
the optimal choice of service  under Bayesian updating is given by
under Bayesian updating is given by

Proof. The joint density of X and Y, with correlation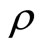 , is given by
, is given by
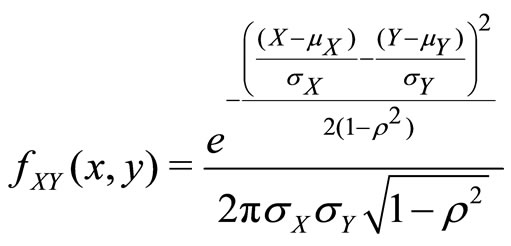 (7)
(7)
Hence the marginal densities of X and Y is given respectively by
 (8)
(8)
Recall that provider utility, for given service provision 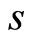 and correlation
and correlation , is given by
, is given by
 (9)
(9)
The provider’s first order conditions with regards to service  is thus
is thus
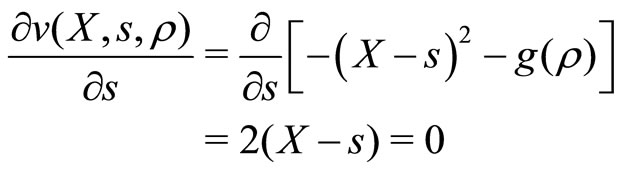 (10)
(10)
which is solved by
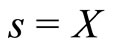 (11)
(11)
The second order requirement for optimality with regards to s is given by
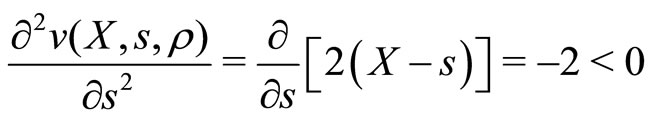 (12)
(12)
Therefore 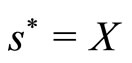 is the optimal choice of s. However, the stochastic variable X is by definition unobservable. Hence the provider uses Bayesian updating to form an expectation of true recipient need X given the observed signal
is the optimal choice of s. However, the stochastic variable X is by definition unobservable. Hence the provider uses Bayesian updating to form an expectation of true recipient need X given the observed signal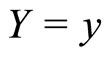 .
.
First, the provider uses Bayesian updating to obtain the posterior distribution of X given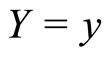 .
.
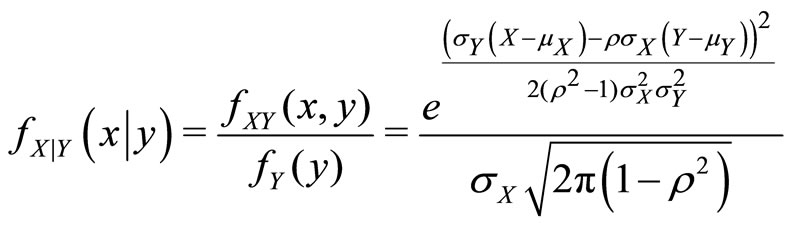 (13)
(13)
The provider can then takes expectations of X under the probability distribution  which optimally incorporates all the information contained in
which optimally incorporates all the information contained in 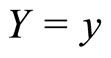 in a Bayesian sense. This yields the optimal choice of service s.
in a Bayesian sense. This yields the optimal choice of service s.
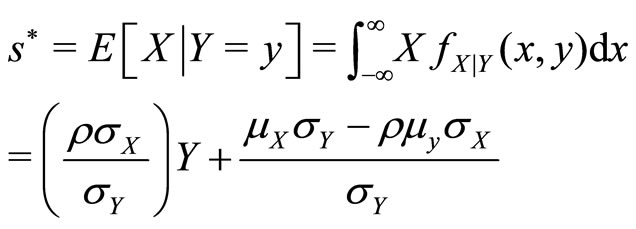 (14)
(14)
Theorem 2. Provider utility 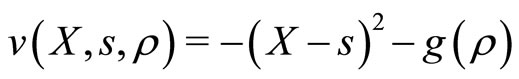 conditional on observed
conditional on observed  is maximized in expectation given joint normally distributed
is maximized in expectation given joint normally distributed  and
and  with endogenous correlation
with endogenous correlation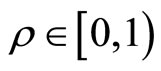 , if the following three conditions are met 1)
, if the following three conditions are met 1) , and 2)
, and 2)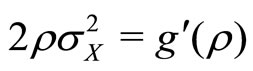 , and 3)
, and 3)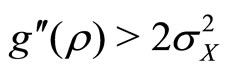 .
.
Proof. Condition (1) follows from Theorem 1. Optimal s is itself a function of 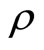 in Equation (14). Hence, by the Envelope Theorem, we can rewrite optimal utility as
in Equation (14). Hence, by the Envelope Theorem, we can rewrite optimal utility as
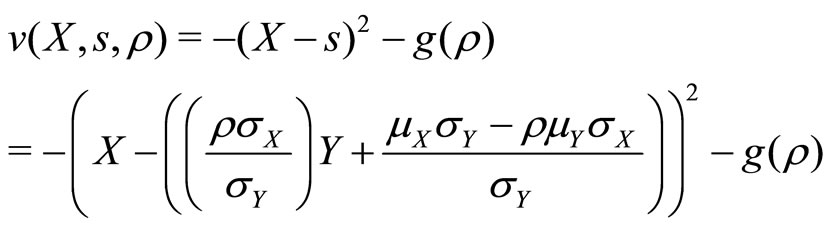 (15)
(15)
So optimal expected utility is now a function of  and the two random variables X and Y. By taking expectations over X and Y using joint density
and the two random variables X and Y. By taking expectations over X and Y using joint density , optimal expected utility is reduced to
, optimal expected utility is reduced to
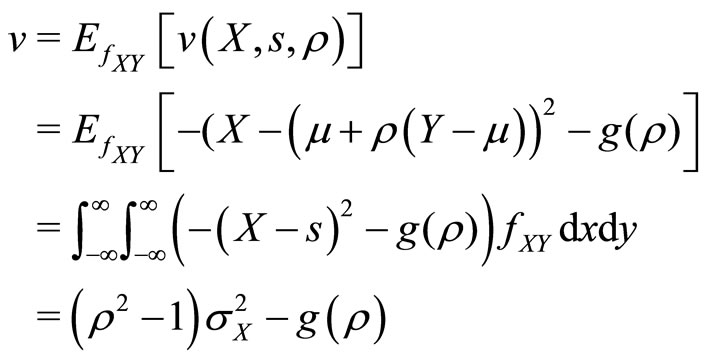 (16)
(16)
Therefore optimal expected provider utility can be expressed as a function of 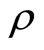 parametrized by the variance
parametrized by the variance 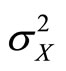 of true recipient need X.
of true recipient need X.
Optimal 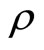 should satisfy first order conditions for utility maximization
should satisfy first order conditions for utility maximization
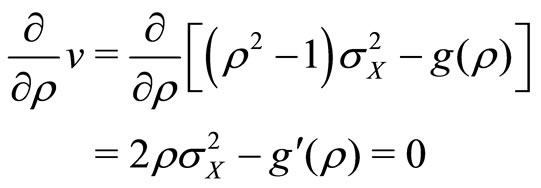 (17)
(17)
This yields Condition (2):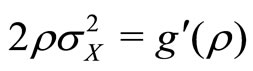 .
.
Second order conditions for utility maximization  requires
requires
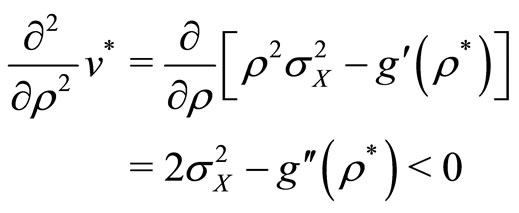 (18)
(18)
This yields Condition (3):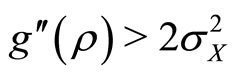 .
.
Theorem 3. Given a correlation cost function of the form  optimal correlation is given by
optimal correlation is given by

Proof. First and second derivatives of 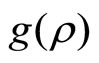 is given by
is given by
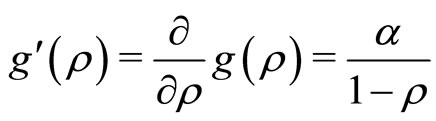 (19)
(19)
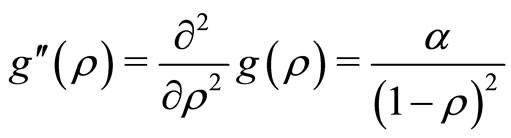 (20)
(20)
The provider’s expected utility is given by substituting Equation (4) into Equation (16).
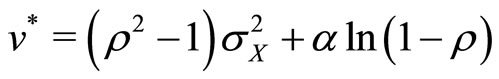 (21)
(21)
From Equation (10), optimal  should solve
should solve
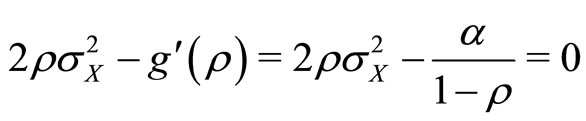 (22)
(22)
yielding two solutions of 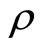
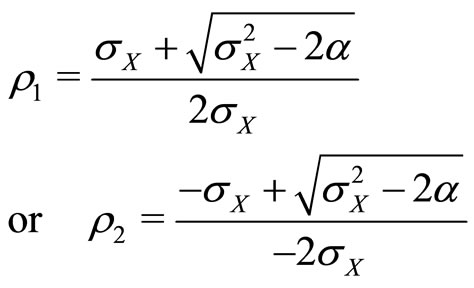 (23)
(23)
for 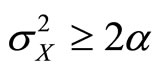 and no real interior solutions for
and no real interior solutions for  .
.
Second order conditions for maximum expected utility as per Equation (18) requires
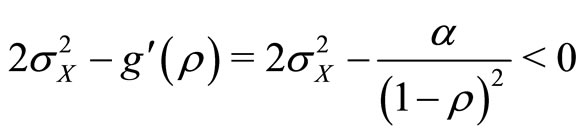 (24)
(24)
Substituting the solutions in Equation (23) into Equation (24), we obtain
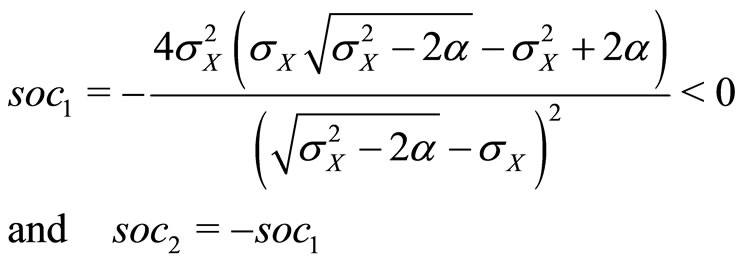
Closer analysis shows that  for
for 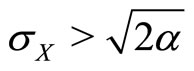 and
and 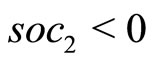 for
for , as is required for a maximum. But since we assume
, as is required for a maximum. But since we assume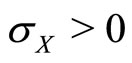 , only the first solution is admissible. Therefore optimal
, only the first solution is admissible. Therefore optimal  is given by
is given by
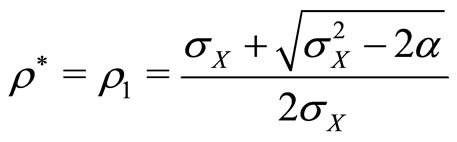 (25)
(25)
provided that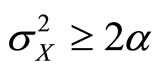 .
.
Now consider the case where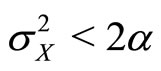 . Taking the first derivative of Equation (21) with regards to
. Taking the first derivative of Equation (21) with regards to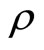 , we obtain
, we obtain
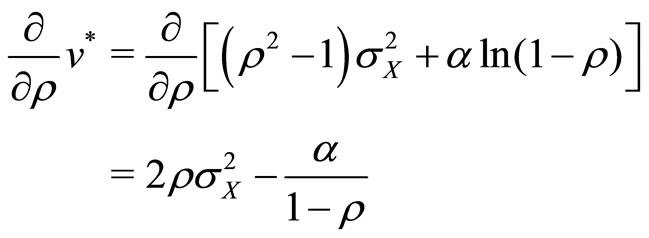
which is negative over the range  for
for
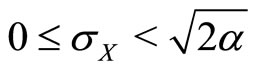 . (To show this note that the maximum of
. (To show this note that the maximum of
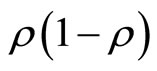 is given by
is given by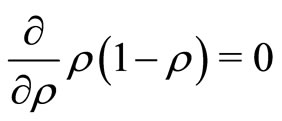 , which is solved by
, which is solved by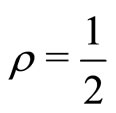 . Hence, the maximum that
. Hence, the maximum that  can be is
can be is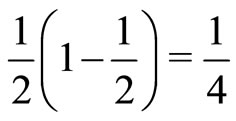 . Therefore
. Therefore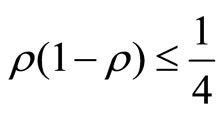 , and so
, and so
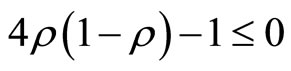 . Multiplying by
. Multiplying by 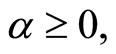 we have
we have
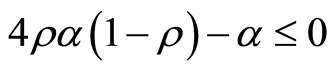 . Dividing by
. Dividing by 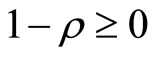 we obtain
we obtain
 . Noting that
. Noting that  in this case, we replace
in this case, we replace 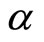 with
with 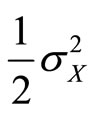 to obtain
to obtain 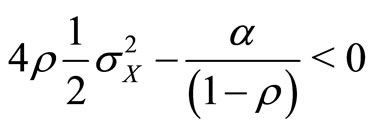 or
or 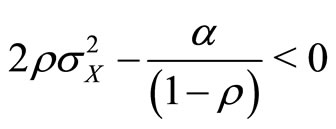 as required).
as required).
Hence, expected utility is strictly decreasing over this range and there will be no interior maximum—instead, the maximum will be found at  for all
for all 
NOTES
*Corresponding author.
1That is, 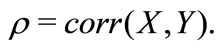
2As long as the recipient’s needs are IID, it does not matter whether they are arranged chronologically or cross-sectionally (or both).
3The true distribution of client need is the distribution of client need conditional on the person being a client presenting with a particular need and is not the same as the unconditional distribution of need in the general population.
4This excludes the choice of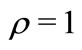 , in which case
, in which case 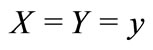 is perfectly observed and the model is trivially solved with
is perfectly observed and the model is trivially solved with . We exclude
. We exclude 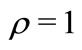 because the joint density function
because the joint density function 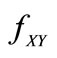 requires
requires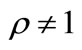 . The other corner solution
. The other corner solution 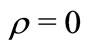 implies that X is independent of Y (since they are jointly normal) and therefore the provider should simply use
implies that X is independent of Y (since they are jointly normal) and therefore the provider should simply use .
.
5For expectation,
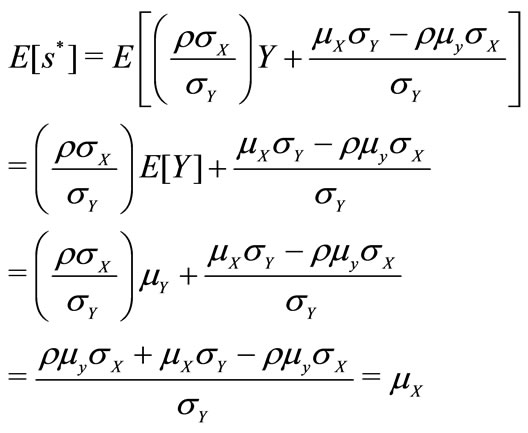
and for variance
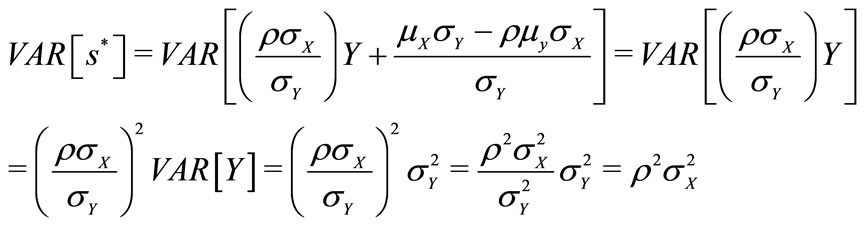 .
.

