Open Journal of Statistics
Vol.06 No.06(2016), Article ID:73204,15 pages
10.4236/ojs.2016.66096
A Markov Approach to Exchange Rate Sentiment Analysis of Major Global Currencies
Kuthyar Shesha Madhava Rao1*, Anjana Ramachandran2
1Department of Statistics, University of Botswana, Gaborone, Botswana
2Department of Mathematics, University of Botswana, Gaborone, Botswana

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 16, 2016; Accepted: December 27, 2016; Published: December 30, 2016
ABSTRACT
The paper deals with the analysis of exchange rates sentiments. In the approach suggested here a typical exchange rate sentiment is defined on the basis of certain function of mean and standard error of the logarithm of the ratio of successive daily exchange rates. Based on this surmise, the exchange rate sentiments are classified into various states, whereby states are named according to the perceptions of the market player. A Markov model is built to capture the uncertainties in exchange rates sentiments. The approach advocated here will be of interest to researchers, exchange rate traders and financial analysts. As an application of the proposed line of approach, we analyse weekly and monthly exchange rate sentiments that govern exchange rates of the major global currencies―EUR, GBP, SDR, YEN, ZAR, USD, using data from 2001-2012. Some interesting conclusions are revealed based on the data analysis approach advocated in this paper.
Keywords:
Ergodicity, Exchange Rates Sentiments, Markov Model, Transition Probability, Weekly and Monthly States

1. Introduction
The analysis of stochastic volatility models is vital due to its applications in the areas of high frequency finance. In a statistical perspective, methods for fitting stochastic volatility (SV) models have the potential for wider applications. But applications for the modeling and prediction of time-varying volatility on financial markets cannot be undermined. These models are fundamental tools in risk management, asset pricing and asset allocation. The appropriate fitting of models with stochastic volatility is one of the demanding problems in time series analysis.
Stochastic volatility models can be interpreted as non-linear state space models in which the unobserved state is the stochastically evolving log volatility of the process. Since data is characteristically observable only at discrete points in time, discrete-time formulations of SV models are important in empirical applications. In financial mathematics and financial economics, stochastic volatility is typically modeled in a continuous-time setting. This formulation proves beneficial for derivative pricing and portfolio optimization. Constant volatility models have been shown to provide an inferior fit of financial time series. A more practical approach to volatility modeling is provided by dynamic structures. Stochastic volatility models are propellers for the modeling and prediction of time-varying volatility on financial markets.
Derivative pricing and portfolio optimization have benefitted from continuous-time stochastic volatility models and thus have figured prominently in financial mathematics and financial economics. The data being only observable at discrete points in time, discrete-time formulations of SV models are essential. Estimation of volatility, the wide swings observed in daily, weekly or monthly exchange rates can be studied, by convention, using discrete-time process. The arbitrary shift of volatility of exchange rates from one state to another in a random fashion is the corner stone of the approach advocated in this paper.
Literature Review
One approach to modeling time-varying volatility comes from the stochastic volatility models. The mixture-of-distribution hypothesis (MDH) postulated by Clark [1] , efficiently supports SV models. According to this hypothesis, asset returns follow a mixture of normal distributions with a mixing process depending on the (unobservable) information arrival process. A characteristic feature of financial return series is revealed for a positively auto correlated mixing process, namely volatility clustering. The MDH proposed that asset return volatility follows its own stochastic process which is restructured by unobservable developments, in contrast to the other approach, an autoregressive conditional heteroscedasticity (ARCH) model introduced by Engle [2] , followed by its generalization (GARCH) by Bollerslev [3] and other dynamic versions. Here, given the available information set, the conditional variance is a function of past observations.
The two approaches differ in the structure of the volatility process. The former follows its own stochastic process, with potential dependence coming through the correlation structure between the series and the volatility processes while the latter assumes dependence on the previous realized shocks in the series.
The likelihood of SV models is not directly available making it more complex compared to the widely used (Generalized) ARCH model. This SV framework requires the use of simulation techniques, like simulated maximum likelihood, method of simulated moments or Markov Chain Monte Carlo (MCMC) techniques. Computational costs render SV models less popular in financial practice although increasing computer efficiency and progress of competent sampling techniques weaken this drawback to a great extent. The basic SV model has been found to be restrictive for many financial time series. In this context, the relationship between volatility and price/return has been studied extensively.
SV models provide an ideal framework to accommodate specific properties of financial return processes such as fat-tailedness, leverage effects and the occurrence of jumps.
Estimation of stochastic volatility models has been widely studied. Generalizations of these models include jumps in returns and in volatilities and/or fat tails in distributions. Extensions include Bayesian analysis of univariate stochastic volatility (SV) processes, as in Jacquier et al., [4] and multivariate stochastic volatility models proposed by Harvey et al., [5] .
Previous study by Rebonato [6] assumed that the instantaneous volatility of the forward rates was a deterministic function of time to maturity only. A model of the swaption market that consisted of a hidden Markov chain with a normal and excited state was the focus of this study. The original deterministic volatility model does not accurately describe a market that is in a temporary “excited” state. The study by White et al. [7] extended this model in which two volatility curves exist: an excited curve and a normal curve for the instantaneous forward volatility. The volatilities in the swaption matrix result from averaging over all possible paths along the Markov chain. At any given time, the market was in one of these states and the transitions between these states were governed by a hidden Markov chain. Previous studies have used Markov chain models to describe option prices, but this study in interest rates involved transitions between functions rather than level. This model was applied to a longer period of US dollars at-the-money swaption volatility market data.
The study by Hautsch et al. [8] reviewed the general framework of discrete-time stochastic volatility models (SV) and illustrated the major principles of corresponding Markov Chain Monte Carlo (MCMC) based statistical inference. A practical approach was provided and that was implemented in empirical applications and financial practice. The results were based on different SV specifications using returns on stock indices and foreign exchange rates. The model was unable to capture the distributional properties of the returns.
Park [9] investigated the relationship between volatility and herd behaviour, a mounting topic in financial economics. The study developed a herd-behaviour-sto- chastic-volatility model that explained herding in financial markets and considered a Markov Chain Monte Carlo method as a competent method for estimating the model. The study illustrated theoretically that herd behaviour lead to a high increase in volatility but not trading volume as opposed to information inputs that increased in both volatility and trading volume. Empirical application with high frequency data in the Korean equity market supported this theory. The study proposed a methodology for detecting trading days with herding. This was based on the theoretical results from the percolation model that was based on the hypothesis of information cascades due to flawed information and the concepts of realized volatility and realized bipolar variation.
Hahn et al. [10] estimated the parameters governing a continuous time Markov switching model with observations given at discrete times only. The states for drift, volatility and the generator matrix of the underlying Markov process based on discretely observed data were estimated.
The extent of liquidity risk due to co-movements was studied within each class of market capitalization by Beaupain et al. [11] . The analysis of liquidity co-movements was dependent on volatility regime states. On an average, the extent of liquidity co-movements was positively related to the market capitalization of the portfolio. Also liquidity co-movements were least intense among small caps and most intense among large caps. On a cross-sectional basis, the extent of class-wide liquidity co-movements was typically greater in quiet markets for both large and mid-caps.
Chun et al. [12] proposed a method for calibrating the local volatility surface that reduced the computational complexity associated with many models and price options with the volatility skew. A continuous time semi-closed form solution based on the Markov chain approximation of Kushner [13] was adopted which could explain diffusion or a jump-diffusion. The study showed that the out-of-sample options can be accurately priced for both cases without regularisation.
The superiority of MRS-GARCH models to GARCH type of models in terms of modelling and forecasting gold price volatility was investigated by Sopipan et al. [14] . The study forecast the volatility of gold prices using Markov Regime Switching GARCH (MRS-GARCH) models. The models allow volatility to follow different dynamics according to unobserved regime variables. The closing prices of gold to trade future contract were predicted.
In this paper we advocate a new approach based on the market sentiments to analyse financial data rather than the traditional approach based on volatility measures. The analysis of financial data based on the market sentiments rather than the volatility has been recently advocated by Rao and Moseki [15] . Rao and Moseki, defined a typical market sentiment on the basis of certain function of mean and standard error of the Domestic Company Indices of Botswana Stock Exchange. Based on this surmise, the market sentiments were classified into various states, whereby states were named according to the perceptions of the market player. A multinomial probability model was built to capture the uncertainties in market sentiments. Two asymptotically distribution-free tests, namely the chi-square and the likelihood ratio test of goodness of fit for the hypothesis of the symmetry in market sentiments were suggested. Later on, Rao and Moseki [16] advocated an alternative approach, namely, a Markov model approach to analyse stock market sentiments based on the constructs detailed in [15] . They examined stationarity of the transition probability matrix associated with the market sentiments in DCI of BSE. Following the works of [15] , Rao and Anjana [17] analysed market sentiments of exchange rates of major global currencies. The data considered in their analysis referred to the logarithm of the ratio of successive daily exchange rates as opposed to the daily DCI considered in [16] .
The objective of this paper is to apply Markov approach of [16] to analyse market sentiments associated with major global currencies. The approach advocated here will be of interest to researchers, exchange rate traders and financial analysts. Section 2, describes a Markov model for market sentiments. The section deals with a certain classification rule that generates market sentiment states for the exchange rate data. The method of construction of a transition probability matrix and derivation of steady state probabilities are also discussed. The application of the proposed model and the related weekly and monthly market sentiment analysis pertaining to exchange rate of major global currencies is carried out in Section 3. The exchange rates data were drawn from the Bank of Botswana’s Botswana Financial Statistics database. The six currencies considered in the analysis are Euro (EUR), British Pound (GBP), Special Drawing Rights (SDR), Japanese Yen (YEN), South African Rand (ZAR) and US Dollar (USD). All the exchange rates have been quoted in terms of Botswana Pula (BWP). The time series data refers to the working day exchange rates of the six stated currencies for 12 years starting from 2001 and ending with 2012. Section 4 concludes the paper.
2. A Markov Model for Exchange Rate Sentiments
In this section we develop the approach which lead to the construction of market sentiment states from the given time series data of exchange rate. From the so obtained sequence of exchange rate market sentiment states, we build a Markov Model which captures the movement of exchange rate phenomena in terms of the transition probabilities among the exchange rate states. Using the estimated transition probability matrix (TPM), we explore the behaviour of market sentiment states.
2.1. A Seven State Exchange Rate Sentiment Classification Rule
Suppose that the time series data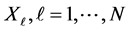 , related to exchange rates of major global currencies for period of N working days is available on a day to day basis. As in Rao and Anjana [17] , we use the following notations and the associated classification rule: “N”―total number of days in a study period, “
, related to exchange rates of major global currencies for period of N working days is available on a day to day basis. As in Rao and Anjana [17] , we use the following notations and the associated classification rule: “N”―total number of days in a study period, “ ”―refers to the day, “W”―total number of weeks in a study period, “w”―refers to the week, “
”―refers to the day, “W”―total number of weeks in a study period, “w”―refers to the week, “ ”―denotes the number of business days in a week. Here,
”―denotes the number of business days in a week. Here, 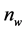 varies between 1 and 5 in a typical FOREX market. The data considered for the analysis here refer to the logarithm of the ratio of the day’s exchange rate
varies between 1 and 5 in a typical FOREX market. The data considered for the analysis here refer to the logarithm of the ratio of the day’s exchange rate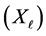 , with the previous day’s exchange rate
, with the previous day’s exchange rate , i.e., log return defined by
, i.e., log return defined by
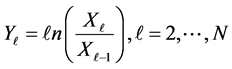 .
.
Let the average 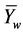 of
of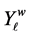 , for the week w be given by
, for the week w be given by
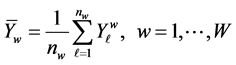 , (1)
, (1)
and the variance 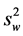 of
of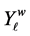 , for the week w be given by
, for the week w be given by
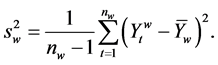 (2)
(2)
For the week , the weekly market sentiment of exchange rate is said to belong to
, the weekly market sentiment of exchange rate is said to belong to
1) State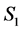 , if
, if 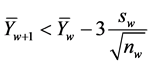
2) State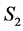 , if
, if 
3) State
4) State

5) State
6) State
7) State

Rao and Anjana [17] named these seven states respectively as: the dread sentiment










2.2. A k-State Sentiment Model for Exchange Rates
We assume that volatility in foreign exchange rates can be described by a Markov-like model so that the weekly and monthly market sentiments can be classified into seven states based on the classification rule (3) discussed in the previous section. The assumption is valid since the weekly market sentiments constructs are designed such that immediate future market sentiment construct depends only on the current state construct and not on the past states. Suppose that for a given log return data





For a given initial state i and a number of trials






Once we estimate the transition probability matrix P by 





Finally the expected value of the recurrence time for state “i” is given by

It may be pointed out that the theoretical discussion of the aforementioned concepts can be found in Isaacson & Madsen [19] and we shall give the necessary computations in the example to be discussed in section 3 below. Further, a second problem of interest would be to investigate whether the weekly or monthly exchange rate market sentiments are stationary over a certain study period say
Suppose that the weekly TPM corresponding to the year “t” be given by



Let 


Let 





Note that 




Using straight forward simplifications it can be shown that,

and under the null hypothesis 







3. Applications to Major Global Currency Exchange Rate Sentiments
The application of the proposed model and the analysis of related weekly and monthly exchange rate is considered in this section. The daily FOREX data were drawn from the Bank of Botswana’s Botswana Financial Statistics database. The six currencies considered for the purpose of analysis are Euro (EUR), Great Britain Pound (GBP), Special Drawing Rights (SDR), Japanese Yen (YEN), South African Rand (ZAR) and United States Dollar (USD). The data considered is for a 12 year period from January 2001 to December 2012. The computations leading to weekly and monthly log returns, classification of the log returns to the exchange rate sentiment states according to the rule (3), derivation of steady state distributions and likelihood ratio test are not reported in this paper; but readers interested in these elaborate computations may contact the first author. Given time series of exchange rates consisting of W weeks of the year


“i” to state “j” and 



3.1. Analysis of Weekly Exchange Rate Sentiments
The application of the proposed model and the related weekly and monthly analysis pertaining to FOREX rate is carried out in this section. The time series data refers to the working day exchange rates of the six stated currencies for 12 years starting from January of 2001 and ending with December of 2012. The data considered for the analysis here refer to the logarithm of the ratio of the day’s exchange rate
vious day’s exchange rate

into 626 weeks, where each week consists of 5 working days, Monday through Friday. The movements in the exchange rates are classified into the seven states


and so on.
Table 1. Weekly transition count matrix for EURO sentiments during 2001 to 2012.
Table 2. Weekly TPM for EURO sentiments during 2001 to 2012.
Following standard computations, (see for example, Isaacson & Madsen [19] ), it can be shown that the transition probability matrix given by 


The practical interpretation is that the EURO exchange rate bounced back to dread sentiment state 

Turning to the test of the hypothesis of stationarity of weekly EURO FOREX sentiments during the study period 2001 to 2012, the application of the likelihood ratio test statistic given by (11) for Euro exchange rate yields


bilities 

sidered. It is clearly seen from Table 3 that across the six exchange rates considered, the mean recurrence time for dread sentiment is around 14 - 21 weeks, for calm sentiment
Table 3. Summary of weekly FOREX sentiments for the period 2001 to 2012.
it is around 4 - 5 weeks, for greed sentiment it is around 8 - 10 weeks and so on. Further, it is interesting to note that for all the FOREX currencies considered, mean recurrence time for states towards the dread sentiment is uniformly more than that of greed sentiment. Table 4 provides the summary of the likelihood ratio tests for the stationarity of FOREX sentiments. It is seen that the hypothesis of stationarity of exchange rate sentiments during the period 2001 to 2012 is rejected in all the cases. It is not surprising though, because of the fact that the period 2001 to 2012 witnessed a whole lot of economic crises such as US housing bubble which peaked in 2004, 2007-08 global economic crises triggered by US stock markets, European sovereign-debt crisis, among others.
3.2. Analysis of Monthly Exchange Rate Sentiments
In this section we proceed to analyse monthly exchange rate sentiments. The data are clustered into 144 months, where each month consists of 20 - 22 working days. We modify the formula (1), (2) and (3) for the monthly data and accordingly generate the transition count matrix and estimated TPM as displayed in Table 5 and Table 6.
As in section 3.2, based on the monthly data, stationary probability distribution

Table 4. Summary of likelihood ratio test for stationarity of weekly FOREX sentiments.
Table 5. Monthly transition count matrix for EURO sentiments during 2001 to 2012.
Table 6. Monthly TPM for EURO sentiments during 2001 to 2012.
Table 7. Summary of monthly FOREX sentiments for the period 2001 to 2012.
Table 8. Summary of likelihood ratio test for stationarity of monthly FOREX sentiments.
We can make the following inference from the stationary probabilities.



The weekly expected recurrence time 


This implies that the EURO currency bounced back to dread sentiment state 


4. Discussion and Conclusion
In this paper, we have revisited the analysis of exchange rate sentiments in six major global currencies during the year 2001 to 2012. The global currencies considered are Euro (EUR), Great Britain Pound (GBP), Special Drawing Rights (SDR), Japanese Yen (YEN), South African Rand (ZAR) and United States Dollar (USD). The data considered is for a 12 year period from January 2001 to December 2012. The weekly and monthly fluctuations in exchange rates are the key to the proposed analysis. The interdependence in the weekly and monthly average exchange rates is captured in terms of a Markov model. The state space of the finite dimensional Markov Chain is arrived at using a data driven classification rule. The states of the Markov model are ordinal in nature and are appropriately named based on the common perceptions witnessed in a stock market. The analysis of the data is carried out in two directions. In the first place, we consider the aggregate data from 2001 to 2012 and estimate the transition probability matrix for each of the six FOREX currencies considered. We derive the stationary probabilities of the seven exchange rate sentiments and estimate the expected recurrence time for the process to each of the seven states. The conclusions drawn from the weekly expected recurrence for the seven states 









The second direction of the analysis is to examine the weekly and monthly exchange rate sentiments for each year of study from 2001 to 2012. This analysis is carried out by examining the stationarity of the estimated TPM for the weekly and monthly data. The analysis revealed that the pattern of transition from one sentiment state to another is altered from year to year.
Cite this paper
Rao, K.S.M. and Ramachandran, A. (2016) A Markov Approach to Exchange Rate Sentiment Analysis of Major Global Currencies. Open Journal of Statistics, 6, 1181-1195. http://dx.doi.org/10.4236/ojs.2016.66096
References
- 1. Clark, P.K. (1973) A Subordinated Stochastic Process Model with Finite Variance for Speculative Prices. Econometrica, 41, 135-156.
https://doi.org/10.2307/1913889 - 2. Engle, R.F. (1982) Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50, 987-1008.
https://doi.org/10.2307/1912773 - 3. Bollerslev, T.A. (1987) A Conditional Heteroscedastic Time Series Model for Speculative Prices and Rates of Return. Review of Economics and Statistics, 69, 542-547.
https://doi.org/10.2307/1925546 - 4. Jacquier, E., Polson, N.G. and Rossi, P.E. (2004) Bayesian Analysis of Stochastic Volatility Models with Fat-Tails and Correlated Errors. Journal of Econometrics, 122, 185-212.
https://doi.org/10.1016/j.jeconom.2003.09.001 - 5. Harvey, A.C. and Shephard, N. (1996) The Estimation of an Asymmetric Stochastic Volatility Model for Asset Returns. Journal of Business and Economic Statistics, 14, 429-434.
- 6. Rebonato, R. (2005) Forward-Rate Volatilities and the Swaption Matrix: Why Neither Time-Homogeneity Nor Time Dependence Will Do. International Journal of Theoretical and Applied Finance, 9, 705-746.
https://doi.org/10.1142/S0219024906003767 - 7. White, R. and Rebonato, R. (2008) A Swaption Volatility Model Using Markov Regime Switching. The Journal of Computational Finance, 12, 79-114.
https://doi.org/10.21314/JCF.2008.182 - 8. Hautsch, N. and Ou, Y. (2008) Discrete-Time Stochastic Volatility Models and MCMC-Based Statistical Inference. Humboldt-Universitatzu Berlin, Germany, SFB 649 “Economic Risk” Discussion Paper 2008-063.
- 9. Park, B.-Jo. (2008) Herd Behaviour and Volatility in Financial Markets. The 3rd International Conference on Asia-Pacific Financial Markets.
- 10. Hahn, M. and Sass. J. (2009) Parameter Estimation in Continuous Time Markov Switching Models: A Semi-Continuous Markov Chain Monte Carlo Approach. Journal of Bayesian Analysis, 4, 63-68.
https://doi.org/10.1214/09-BA402 - 11. Beaupain, R., Giot, P. and Mikael, P. (2010) Volatility Regimes and Liquidity Co-Movements in Cap-Based Portfolios. Revue de l’Association francaise de finance, 31, 55-79.
- 12. Chun, C.Lo. and Konstantinos, S. (2011) Local Volatility Calibration with the Markov Chain Approximation. London Metropolitan Business School, Working Paper Series, No. 29.
- 13. Kushner, H.J. (1990) Numerical Methods for Stochastic Control Problems in Continuous time. SIAM Journal of Control and Optimization, 28, 999-1048.
https://doi.org/10.1137/0328056 - 14. Sopipan, N., Pairote, S. and Bhusana, P. (2012) Forecasting Volatility of Gold Price Using Markov Regime Switching and Trading Strategy. Journal of Mathematical Finance, 2, 121-131.
https://doi.org/10.4236/jmf.2012.21014 - 15. Rao, K.S. and Moseki, K.K. (2009) A Probabilistic Approach to Categorise Equity Index Volatility. Management Dynamics, 18, 22-34.
- 16. Rao, K.S. and Moseki, K.K. (2011) Analyzing Volatility in Equity Indices—A Markov Approach for Botswana Domestic Company Indices. South African Journal of Industrial Engineering, 22, 83-98.
- 17. Rao, K.S.M. and Anjana, R. (2014) Exchange Rate Market Sentiment Analysis of Major Global Currencies. Open Journal of Statistics, 4, 49-69.
https://doi.org/10.4236/ojs.2014.41006 - 18. Bhat, N.U. (1972) Elements of Applied Stochastic Processes. John Wiley & Sons Inc., New York.
- 19. Isaacson, D.L. and Madsen, R.W. (1976) Markov Chains Theory and Applications. John Wiley & Sons Inc., London.








