Received 2 November 2015; accepted 27 December 2015; published 30 December 2015

ABSTRACT

In the presence of multicollinearity in logistic regression, the variance of the Maximum Likelihood Estimator (MLE) becomes inflated. Şiray et al. (2015) [1] proposed a restricted Liu estimator in logistic regression model with exact linear restrictions. However, there are some situations, where the linear restrictions are stochastic. In this paper, we propose a Stochastic Restricted Maximum Likelihood Estimator (SRMLE) for the logistic regression model with stochastic linear restrictions to overcome this issue. Moreover, a Monte Carlo simulation is conducted for comparing the performances of the MLE, Restricted Maximum Likelihood Estimator (RMLE), Ridge Type Logistic Estimator(LRE), Liu Type Logistic Estimator(LLE), and SRMLE for the logistic regression model by using Scalar Mean Squared Error (SMSE).

Keywords:

Logistic Regression, Multicollinearity, Stochastic Restricted Maximum Likelihood Estimator, Scalar Mean Squared Error

1. Introduction

In many fields of study such as medicine and epidemiology, it is very important to predict a binary response variable, or to compute the probability of occurrence of an event, in terms of the values of a set of explanatory variables related to it. For example, the probability of suffering a heart attack is computed in terms of the levels of a set of risk factors such as cholesterol and blood pressure. The logistic regression model serves admirably this purpose and is the most used for these cases.

The general form of logistic regression model is

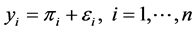(1)

which follows Bernoulli distribution with parameter as

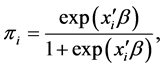(2)

where is the row of X, which is an data matrix with p explanatory variables and is a vector of coefficients, 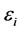is independent with mean zero and variance 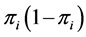of the response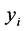. The maximum likelihood method is the most common estimation technique to estimate the parameter, and the Maximum Likelihood Estimator (MLE) of can be obtained as follows:

(3)

where; Z is the column vector with element equals and , which is an unbiased estimate of. The covariance matrix of is

(4)

As many authors have stated (Hosmer and Lemeshow (1989) [2] and Ryan (1997) [3] , among others), the logistic regression model becomes unstable when there exists strong dependence among explanatory variables (multi-collinearity). For example, we suppose that the probability of a person surviving 10 or more extra years is modelled using three predictors Sex, Diastolic blood pressure and Body mass index. Since the response “whether the person surviving 10 or more extra years” is binary, the logistic regression model is appropriate for this problem. However, it is understood that the predictors Sex, Diastolic blood pressure and Body mass index may have some inter-relationship within each person. In this case, the estimation of the model parameters becomes inaccurate because of the need to invert near-singular information matrices. Consequently, the interpretation of the relationship between the response and each explanatory variable in terms of odds ratio may be erroneous. As a result, the estimates have large variances and large confidence intervals, which produce inefficient estimates.

To overcome the problem of multi-collinearity in the logistic regression, many estimators are proposed alternatives to the MLE. The most popular way to deal with this problem is called the Ridge Logistic Regression (RLR), which is first proposed by Schaffer et al. (1984) [4] . Later Principal Component Logistic Estimator (PCLE) by Aguilera et al. (2006) [5] , the Modified Logistic Ridge Regression Estimator (MLRE) by Nja et al. (2013) [6] , Liu Estimator by Mansson et al. (2012) [7] , and Liu-type estimator by Inan and Erdogan (2013) [8] in logistic regression have been proposed.

An alternative technique to resolve the multi-collinearity problem is to consider parameter estimation with priori available linear restrictions on the unknown parameters, which may be exact or stochastic. That is, in some practical situations there exist different sets of prior information from different sources like past experience or long association of the experimenter with the experiment and similar kind of experiments conducted in the past. If the exact linear restrictions are available in addition to logistic regression model, many authors propose different estimators for the respective parameter. Duffy and Santer (1989) [9] introduce a Restricted Maximum Likelihood Estimator (RMLE) by incorporating the exact linear restriction on the unknown parameters. Recently Şiray et al. (2015) [1] proposes a new estimator called Restricted Liu Estimator (RLE) by replacing MLE by RMLE in the logistic Liu estimator.

In this paper we propose a new estimator which is called as the Stochastic Restricted Maximum Likelihood Estimator (SRMLE) when the linear stochastic restrictions are available in addition to the logistic regression model. The rest of the paper is organized as follows. The proposed estimator and its asymptotic properties are given in Section 2. In Section 3, the mean square error matrix and the scalar mean square error for this new estimator are obtained. Section 4 describes some important existing estimators for the logistic regression models. Performance of the proposed estimator with respect to Scalar Mean Squared Error (SMSE) is compared with some existing estimators by performing a Monte Carlo simulation study in Section 5. The conclusion of the study is presented in Section 6.

2. The Proposed Estimator and its Asymptotic Properties

First consider the multiple linear regression model

(5)

where y is an observable random vector, X is an known design matrix of rank p, is a vector of unknown parameters and is an vector of disturbances.

The Ordinary Least Square Estimator (OLSE) of is given by

(6)

where.

In addition to sample model (5), consider the following linear stochastic restriction on the parameter space;

(7)

where r is an stochastic known vector, R is a of full rank with known elements and is an random vector of disturbances with mean 0 and dispersion matrix, and is assumed to be known positive definite matrix. Further it is assumed that is stochastically independent of, i.e..

The Restricted Ordinary Least Square Estimator (ROLSE) due to exact prior restriction (i.e.) in (7) is given by

(8)

Theil and Goldberger (1961) [10] proposed the mixed regression estimator (ME) for the regression model (2.1) with the stochastic restricted prior information (7)

(9)

Suppose that the following linear prior information is given in addition to the general logistic regression model (1)

(10)

where h is an stochastic known vector, H is a of full rank known elements and is an random vector of disturbances with mean 0 and dispersion matrix, and is assumed

to be known positive definite matrix. Further, it is assumed that is stochastically independent of, i.e..

Duffy and Santner (1989) [9] proposed the Restricted Maximum Likelihood Estimator (RMLE) for the logistic regression model (1) with the exact prior restriction (i.e.) in (10)

(11)

Following RMLE in (11) and the Mixed Estimator (ME) in (9) in the Linear Regression Model, we propose a new estimator which is named as the Stochastic Restricted Maximum Likelihood Estimator (SRMLE) when the linear stochastic restriction (10) is available in addition to the logistic regression model (1).

(12)

Asymptotic Properties of SRMLE:

The is asymptotically unbiased.

(13)

The asymtotic covariance matrix of SRMLE equals

(14)

3. Mean Square Error Matrix Comparisons

To compare different estimators with respect to the same parameter vector in the regression model, one can use the well known Mean Square Error (MSE) Matrix (MSE) and/or Scalar Mean Square Error (SMSE) criteria.

(15)

where is the dispersion matrix, and denotes the bias vector.

The Scalar Mean Square Error (SMSE) of the estimator can be defined as

(16)

For two given estimators and, the estimator is said to be superior to under the MSE criterion if and only if

(17)

The MSE and SMSE of the proposed estimator SRMLE is

(18)

(19)

(20)

Note that the difference given in (20) is non-negative definite. Thus by the MSE criteria it follows that has smaller Mean square error than.

4. Some Existing Logistic Estimators

To examine the performance of the proposed estimator SRMLE over some existing estimators, the following estimators are considered.

1) Logistic Ridge Estimator

Schaefer et al. (1984) [4] proposed a ridge estimator for the logistic regression model (1).

(21)

where is the ridge parameter and.

The asymptotic MSE and SMSE of,

(22)

where.

(23)

2) Logistic Liu Estimator

Following Liu (1993) [11] , Urgan and Tez (2008) [12] , Mansson et al. (2012) [7] examined the Liu Estimator for logistic regression model, which is defined as

(24)

where is a parameter and.

The asymptotic MSE and SMSE of,

(25)

where.

(26)

3) Restricted MLE

As we mentioned in Section 2, Duffy and Santner (1989) [9] proposed the Restricted Maximum Likelihood Estimator (RMLE) for the logistic regression model (1) with the exact prior restriction (i.e.) in (10).

(27)

The asymptotic MSE and SMSE of,

(28)

(29)

where

and

Mean Squared Error Comparisons

・ SRMLE versus LRE

(30)

where and. One can obviously say that

and are positive definite and is non-negative definite matrices. Further by

Theorem 1 (see Appendix 1), it is clear that is positive definite matrix. By Lemma 1 (see Appendix 1), if, where is the largest eigen value of then is a positive definite matrix. Based on the above arguments, the following theorem can be stated.

Theorem 4.1. The estimator SRMLE is superior to LRE if and only if.

・ SRMLE Versus LLE

(31)

where and. One can obviously say that and are positive definite and is non-negative defi-

nite matrices. Further by Theorem 1 (see Appendix 1), it is clear that is positive definite matrix. By Lemma 1 (see Appendix 1), if, where is the the largest eigen value of then is a positive definite matrix. Based on the above arguments, the following theorem can be stated.

Theorem 4.2. The estimator is superior to if and only if.

・ SRMLE versus RMLE

(32)

where and. One can obviously say that and are positive definite and is non-negative definite matrices. Further by Theorem 1 (see Appendix 1), it is clear that is positive definite matrix. By Lemma 1 (see Appendix 1), if, where is the the largest eigen value of then is a positive definite matrix. Based on the above arguments, the following theorem can be stated.

Theorem 4.3. The estimator is superior to if and only if.

Based on the above results one can say that the new estimator SRMLE is superior to the other estimators with respect to the mean squared error matrix sense under certain conditions. To check the superiority of the estimators numerically, we then consider a simulation study in the next section.

5. A Simulation Study

A Monte Carlo simulation is done to illustrate the performance of the new estimator SRMLE over the MLE, RMLE, LRE, and LLE by means of Scalar Mean Square Error (SMSE). Following McDonald and Galarneau (1975) [13] the data are generated as follows:

(33)

where are pseudo- random numbers from standardized normal distribution and represents the correlation between any two explanatory variables. Four explanatory variables are generated using (33). We considered four different values of corresponding to 0.70, 0.80, 0.90 and 0.99. Further four different values of n corresponding to 20, 40, 50, and 100 are considered. The dependent variable in (1) is obtained from the Ber-

noulli () distribution where. The parameter values of are chosen so that and.

Moreover, for the restriction, we choose

(34)

Further for the ridge parameter k and the Liu parameter d, some selected values are chosen so that and.

The experiment is replicated 3000 times by generating new pseudo-random numbers and the estimated SMSE is obtained as

(35)

The simulation results are listed in Tables A1-A16 (Appendix 3) and also displayed in Figures A1-A4 (Appendix 2). From Figures A1-A4, it can be noticed that in general increase in degree of correlation between two explanatory variables inflates the estimated SMSE of all the estimators and increase in sample size n declines the estimated SMSE of all the estimators. Further, the new estimator SRMLE has smaller SMSE compared to MLE with respect to all the values of and n. However, when and, SRMLE performs better compared to the estimators LRE, and LLE. From Table A17 (Appendix 3), it is clear that when k and d are small LLE is better than other estimators in the MSE sense, and LRE is better when k and d are large. For moderate k and d values the proposed estimator is good, but this will change with the n and values. Therefore we then analyse the estimators LRE, LLE and SRMLE further by using different k and d values and the results are summarized in Table A18 and Table A19 (Appendix 3). According to these results it is clear that SRMLE is even superior to LRE and LLE for certain values of k and d.

6. Concluding Remarks

In this research, we introduced the Stochastic Restricted Maximum Likelihood Estimator (SRMLE) for logistic regression model when the linear stochastic restriction was available. The performances of the SRMLE over MLE, LRE, RMLE, and LLE in logistic regression model were investigated by performing a Monte Carlo simulation study. The research had been done by considering different degree of correlations, different numbers of observations and different values of parameters k, d. It was noted that the SMSE of the MLE was inflated when the multicollinearity was presented and it was severe particularly for small samples. The simulation results showed that the proposed estimator SRMLE had smaller SMSE than the estimator MLE with respect to all the values of n and. Further it was noted that the proposed estimator SRMLE was superior over the estimators LLE and LRE for some k and d values related to different and n.

Acknowledgements

We thank the editor and the referee for their comments and suggestions, and the Postgraduate Institute of Science, University of Peradeniya, Sri Lanka for providing necessary facilities to complete this research.

Cite this paper

VarathanNagarajah,PushpakanthieWijekoon,11, (2015) Stochastic Restricted Maximum Likelihood Estimator in Logistic Regression Model. Open Journal of Statistics,05,837-851. doi: 10.4236/ojs.2015.57082

References

Appendix 1

Theorem 1. Let A: and B: such that and. Then. (Rao and Toutenburg, 1995) [14] .

Lemma 1. Let the two matrices , , then if and only if. (Rao et al., 2008) [15] .

Appendix 2

Appendix 3