International Journal of Geosciences, 2012, 3, 211-221
http://dx.doi.org/10.4236/ijg.2012.31024 Published Online February 2012 (http://www.SciRP.org/journal/ijg)
Simulation Vacuum Preloading Method by
Tri-Axial Apparatus
Ngo Trung Duong1, Wanchai Teparaksa1, Hiroyuki Tanaka2
1Department of Civil Engineering, Faculty of Engineering, Chulalongkorn University, Bangkok, Thailand
2Faculty of Engineering, Hokkaido University, Sapporo, Japan
Received October 25, 2011; revised December 14, 2011; accepted January 13, 2012
ABSTRACT
It is very important to control any risk of instability of embankment during vacuum construction, the simulation vacuum
preloading method using tri-axial apparatus is proposed to predict the behavior of soft soil improvement in the labora-
tory, as well as to make this method become familiar and easier in the future. The tri-axial apparatus is used instead of
the large-scale one, which has been performed by Bergado (1998) and Indaratna (2008). The tri-axial test on small size
specimen can be carried out in one week compared to the large-scale apparatus takes one month for big specimen. In
addition, the lateral deformation as well as the shear strength increase with time can determine accurately.
Keywords: Soft Soil; Soil Improvement; Vacuum Preloading; Degree of Consolidation
1. Introduction
Nowadays the vacuum preloading consolidation method
becomes the popular method to improve soft soil. This
method is an effective method of improving soft soil
conditions as introduced by Kjellman (1952) [1] in early
1952. With the merging of new materials and technolo-
gies, this method has been further improved in recent
years.
The modeling vacuum method to improve soft soil in
the laboratory has been performed by Indaratna 2008 [2]
using the large-scale apparatus and follows one-dime-
nsional consolidation theory (Tezaghi). The results ob-
tained from this modeling partially evaluated the behav-
ior of soft soil reinforced by vacuum preloading method
in the laboratory. Using the large specimen 45 cm × 90
cm in diameter and height respectively in the large-scale
apparatus, the time used for this test was more than one
month.
The horizontal deformation εr during the tested time,
which is the typical deformation of soft soil improvement
by vacuum, and also the increasing of shear strength
could not be measured. So far, the controlling surcharge
processing during vacuum construction has not been
discussed sufficiently.
The new method is proposed using tri-axial apparatus
to simulate the comprehensive behavior of soil impro-
vement by vacuum preloading method in the laboratory
to support the engineering task quickly. In addition, it is
desired to make the method become familiar in the fu-
ture.
The finite element method (FEM) is used to analyze
two cases of drainage condition at the boundary and cen-
ter of the axisymmetric soil cell.
The study aspects to solve these matters are as follows:
1) Simulation the behavior of soft soil improved by
vacuum method by tri-axial apparatus under axisymetric
consolidation condition;
2) The lateral deformation and vertical settlement are
concerned during soil improvement by vacuum prel-
oading method;
3) Evaluating the degree of consolidation during soil
improvement;
4) Combination surcharge and vacuum preloading to
estimate the increasing shear strength).
2. Tri-Axial Apparatus
Tri-axial apparatus can clearly evaluate the failure mech-
anism as well as the capacity of increasing shear strength
of soil in the laboratory. From the tri-axial test, the result
parameters are used to predict the behavior of soil in the
field during construction.
Under vacuum pressure condition alone, the soil mass
at depth is subjected the isotropic stress status (K = 1).
With flexible functions of the tri-axial machine as shown
in Figure 1, the isotropic condition of the soil mass can
generate the same vacuum condition by controlling the
lateral earth pressure (K).
During vacuum condition, the surcharge loading can
C
opyright © 2012 SciRes. IJG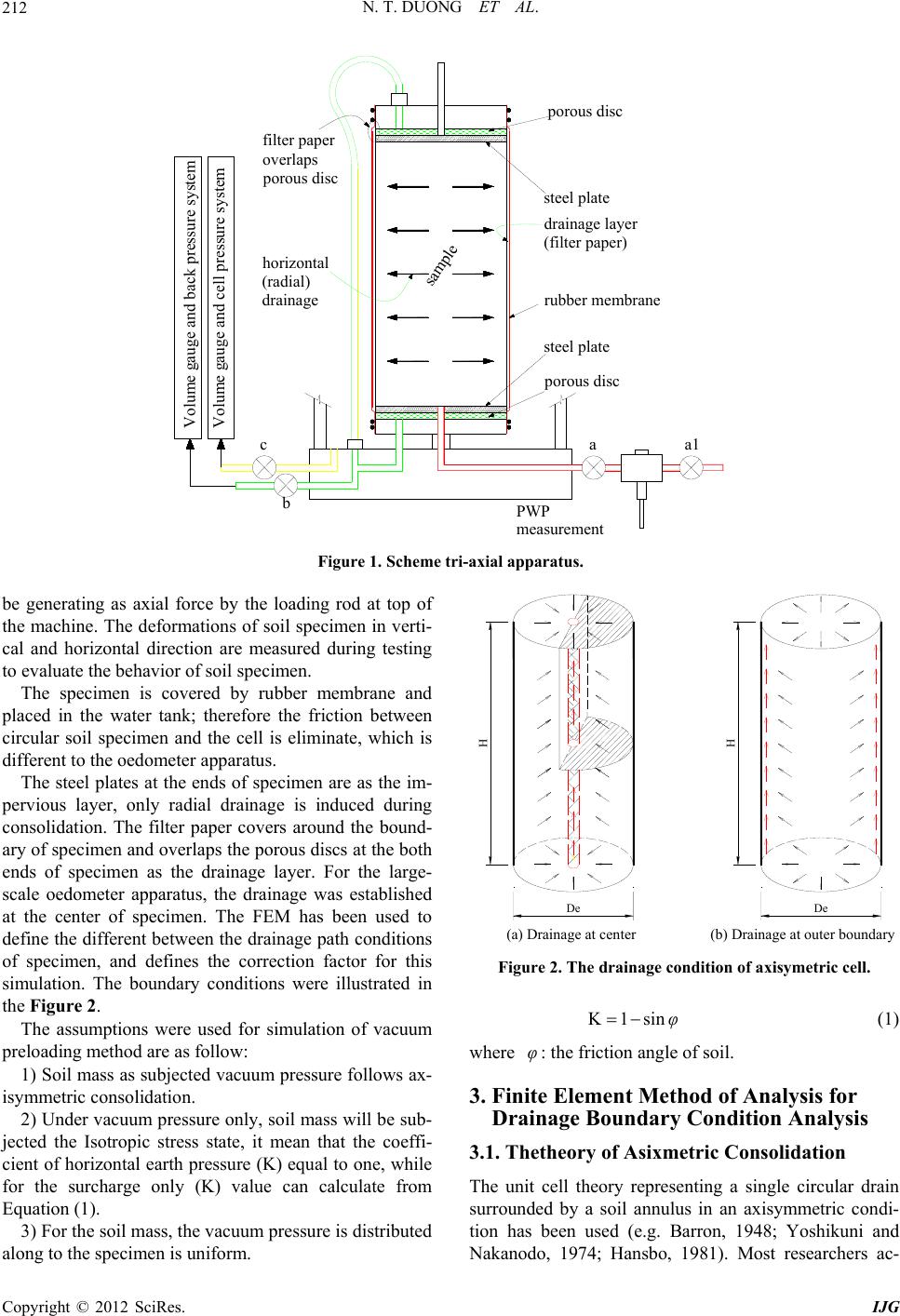

N. T. DUONG ET AL. 212
drainage layer
(filter paper)
rubber membrane
porous disc
Volume gauge and back pressure system
filter paper
overlaps
porous disc
horizontal
(radial)
drainage
Volume gauge and cell pressure system
PWP
measurement
ac
b
sample
steel plate
a1
porous disc
steel plate
Figure 1. Scheme tri-axial apparatus.
be generating as axial force by the loading rod at top of
the machine. The deformations of soil specimen in verti-
cal and horizontal direction are measured during testing
to evaluate the behavior of soil specimen.
The specimen is covered by rubber membrane and
placed in the water tank; therefore the friction between
circular soil specimen and the cell is eliminate, which is
different to the oedometer apparatus.
The steel plates at the ends of specimen are as the im-
pervious layer, only radial drainage is induced during
consolidation. The filter paper covers around the bound-
ary of specimen and overlaps the porous discs at the both
ends of specimen as the drainage layer. For the large-
scale oedometer apparatus, the drainage was established
at the center of specimen. The FEM has been used to
define the different between the drainage path conditions
of specimen, and defines the correction factor for this
simulation. The boundary conditions were illustrated in
the Figure 2.
The assumptions were used for simulation of vacuum
preloading method are as follow:
1) Soil mass as subjected vacuum pressure follows ax-
isymmetric consolidation.
2) Under vacuum pressure only, soil mass will be sub-
jected the Isotropic stress state, it mean that the coeffi-
cient of horizontal earth pressure (K) equal to one, while
for the surcharge only (K) value can calculate from
Equation (1).
3) For the soil mass, the vacuum pressure is distributed
along to the specimen is uniform.
H
De
H
De
(a) Drainage at center (b) Drainage at outer boundary
F
K1sinφ
igure 2. The drainage condition of axisymetric cell.

 (1)
where φ: the friction angle
3. Finite Element Method of Analysis for
3.1
drain
Nakanodo, 1974; Hansbo, 1981). Most researchers ac-
of soil.
Drainage Boundary Condition Analysis
. Thetheory of Asixmetric Consolidation
The unit cell theory representing a single circular
surrounded by a soil annulus in an axisymmetric condi-
tion has been used (e.g. Barron, 1948; Yoshikuni and

N. T. DUONG ET AL. 213
cepted that under embankment loading, the single drain
analysis could not provide an accurate prediction due to
lateral yield and heave compared to plane strain multi-
drain analysis (Indraratna, et al., 1997) although the de-
gree of consolidation (DOC) in this model is acceptable
accuracy.
In this topic, the method is proposed to model the be-
havior of soft soil improvement by vacuum combine with
su
variation of the
pe
d-
ar
re Hooke’s
la
ring application.
o
(1
rcharge preloading method while the lateral displace-
ment is concerned during consolidation.
The following assumptions are based on Hansbo solu-
tion (1981) about equal strains (ε), the
rmeability (k) when void ratio (e) decrease during
consolidation and the volume compressibility (mv).
1) Soil is homogeneous and fully saturated; the Darcy’s
law is adopted. Depend on the purposes the outer boun
y of unit cell the drainage path is occurred.
2) Soil strain is uniform at the boundary of the unit cell
and the small strain theory is valid, therefo
w should be applied for calculation.
3) For the mass soil, the vacuum pressure distribution
along to the drain boundary is uniform du
The accuracy of the FE analysis was checked against
the analytical solutions of Barron (1948) and Hansb
981) [3]. According to Barron (1948) [4], the degree of
consolidation U for “equal-strain” consolidation is given
in Equation (2).
8T
U1exp
μ

 


(2)
with
22
22
n3n1
ln n4n


(3)
n1
μ



e
w
D
nD  (4)
where De and Dw are diameters
lent of vertical drain respectively. Hansbo (1981) intro-
of unit cell and equiva-
duced a circular smear zone (of diameter Ds) in the solu-
tion which resulted in a modified expression for μ
ho
k n3
lnln m
mk 4
μ  


hs
(5)
s
w
D
mD  (6)
For two dimensional consolida
pressed in terms of integrals of the excess pore water
pr
tion U(%) can be ex-
essure over the unit cell domain as Madhav et al. 1993.
yx
u(x, y,T)dxdy

0
yx
U1 udxdy
  (7)
where u(x,y,T) = excess pore water pressure at any point
with x, y dimension at a time factor T, an
excess pore water pressure.
Terzaghi-Rendulic proposed differential equation for
d uo is the initial
two-dimensional consolidation as
22
2
e
uuu
d



22
Tx
y



(8)
h
Ct
T 
2
e
D (9)
where
Ch: horizontal coefficient of consolidation.
As the strains are small, if E'
effective stress, n' is Poisson’s ratio for effective stress
material is isotropic, Hooke’s law is
is Young’s modulus for
and the
rr
θr
r z
1'1 ' '
E' ''1 '
δενν δσ
νν δσ δε
' 1'' δε δσ νν




 
 

 

 


 
(10)

where:
{r, q, z} is the principal axes set.
{εr, εq, εz} are the strain in radial, circumferential and
vertical respectively.
oefficient of consolidation Ch in the horizontal
ditrain deformation is
sh
The c
rection for axisymmetric plane s
owed as:


 
hh
h
ww
'E'kk
C1'
12' m
v
ν
ννγγ

 (11)
where
1
kh: horizontal hydraulic conductivity

w: unit weight of water
Dummy research, for the axisymetric unit cell the co-
t of volume compressibility (mv) varies during
co ression:
efficien
nsolidation; mv value calculate by exp
v
a
Δ
mΔ
v
ε
σ
 (12)
where:

v: volume strain of specimen
σ'a: is the axial effective stress
of consolidation.
3.2nit Cell under
stem of clay unit cell is used to model
re-
T7.5 cm × 15.0 cm in diameter
κ = 0.06, the horizontal and vertical
at time reach to degree
. Solution for Axisymetric U
Vacuum Pressure
An axisymetric sy
the behavior of soil specimen improved by vacuum p
loading method.
he unit cell with size
(De) and height (H) respectively (H = 2D), the effective
Young’s modulus E' = 500 kN/m2, Poisson’s ration v' =
0.33, λ = 0.55,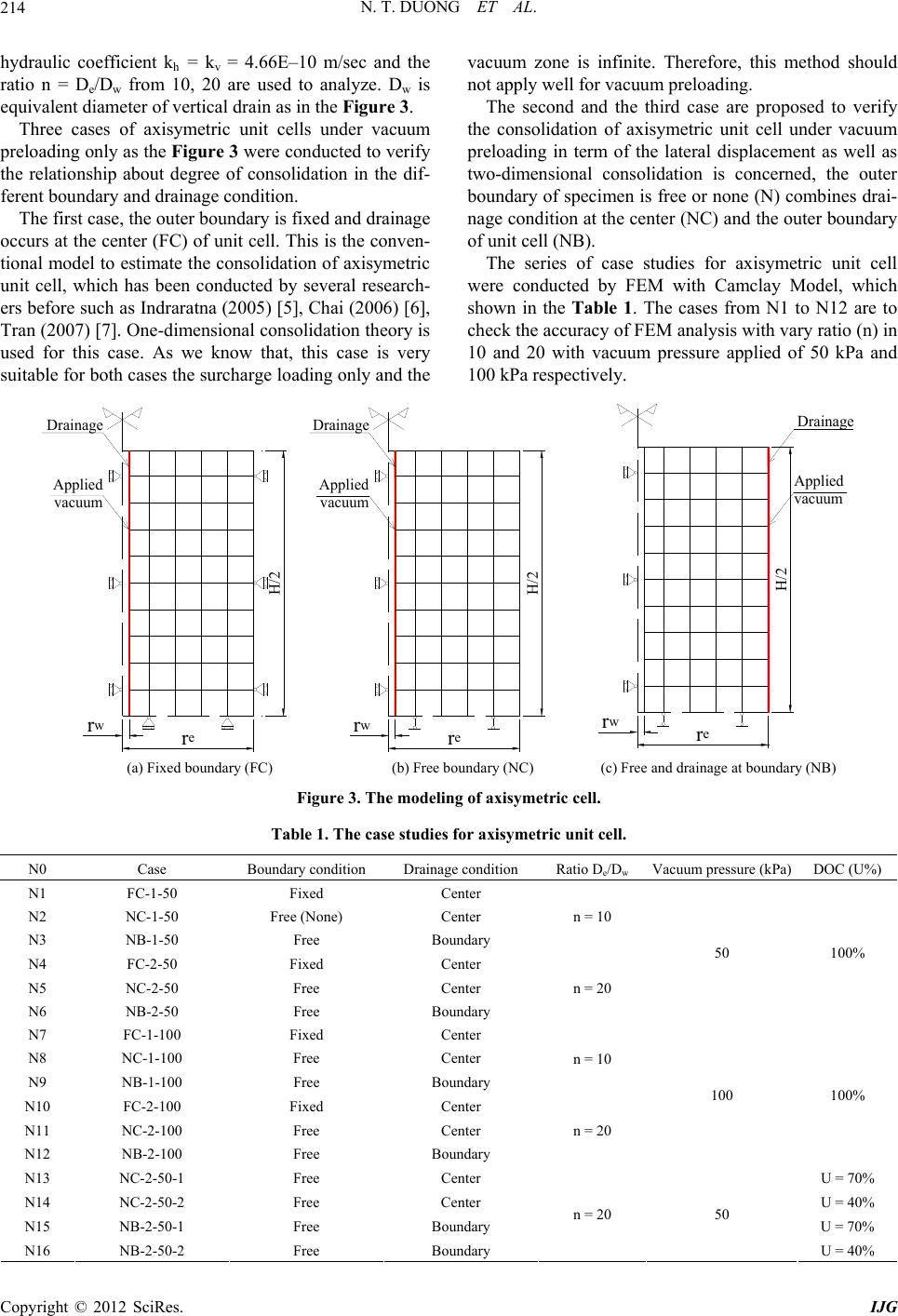

N. T. DUONG ET AL. 214
hy
veral research-
er
ell under vacuum
pr
y FEM with Camclay Model, which
sh
draulic coefficient kh = kv = 4.66E–10 m/sec and the
ratio n = De/Dw from 10, 20 are used to analyze. Dw is
equivalent diameter of vertical drain as in the Figure 3.
Three cases of axisymetric unit cells under vacuum
preloading only as the Figure 3 were conducted to verify
the relationship about degree of consolidation in the dif-
ferent boundary and drainage condition.
The first case, the outer boundary is fixed and drainage
occurs at the center (FC) of unit cell. This is the conven-
tional model to estimate the consolidation of axisymetric
unit cell, which has been conducted by se
s before such as Indraratna (2005) [5], Chai (2006) [6],
Tran (2007) [7]. One-dimensional consolidation theory is
used for this case. As we know that, this case is very
suitable for both cases the surcharge loading only and the
vacuum zone is infinite. Therefore, this method should
not apply well for vacuum preloading.
The second and the third case are proposed to verify
the consolidation of axisymetric unit c
eloading in term of the lateral displacement as well as
two-dimensional consolidation is concerned, the outer
boundary of specimen is free or none (N) combines drai-
nage condition at the center (NC) and the outer boundary
of unit cell (NB).
The series of case studies for axisymetric unit cell
were conducted b
own in the Table 1. The cases from N1 to N12 are to
check the accuracy of FEM analysis with vary ratio (n) in
10 and 20 with vacuum pressure applied of 50 kPa and
100 kPa respectively.
r
w
r
e
H/2
r
w
r
e
H/2
Drainage Drai nage
Applied
vacuum
Applied
vacuum
Drainage
Applied
vacuum
r
w
r
e
H/2
(a) Fixed boundary (FC) (b) Free boundary (NC) (c) Free and drainage at boundary (NB)
Figure 3. The modeling of axisymetric cell.
Tall.
N0 Case BouVacuum pressure (kPa) DOC (U%)
ble 1. The case studies for axisymetric unit ce
ndary condition Drainage condition Ratio De/Dw
N1 FC-1-50 Fixed Center
N2 N
B
B
n = 20
50 100%
B
n = 10
B
n = 20
100 100%
U = 70%
U = 40%
B
B
C-1-50Free (None) Center
N3 NB-1-50 Free oundary
n = 10
N4 FC-2-50 Fixed Center
N5 NC-2-50 Free Center
N6 NB-2-50 Free oundary
N7 FC-1-100 Fixed Center
N8 NC-1-100 Free Center
N9 NB-1-100 Free oundary
N10 FC-2-100 Fixed Center
N11 NC-2-100 Free Center
N12 NB-2-100 Free oundary
N13 NC-2-50-1 Free Center
N14 NC-2-50-2 Free Center
N15 NB-2-50-1 Free oundaryU = 70%
N16 NB-2-50-2 Free oundary
n = 20 50
U = 40%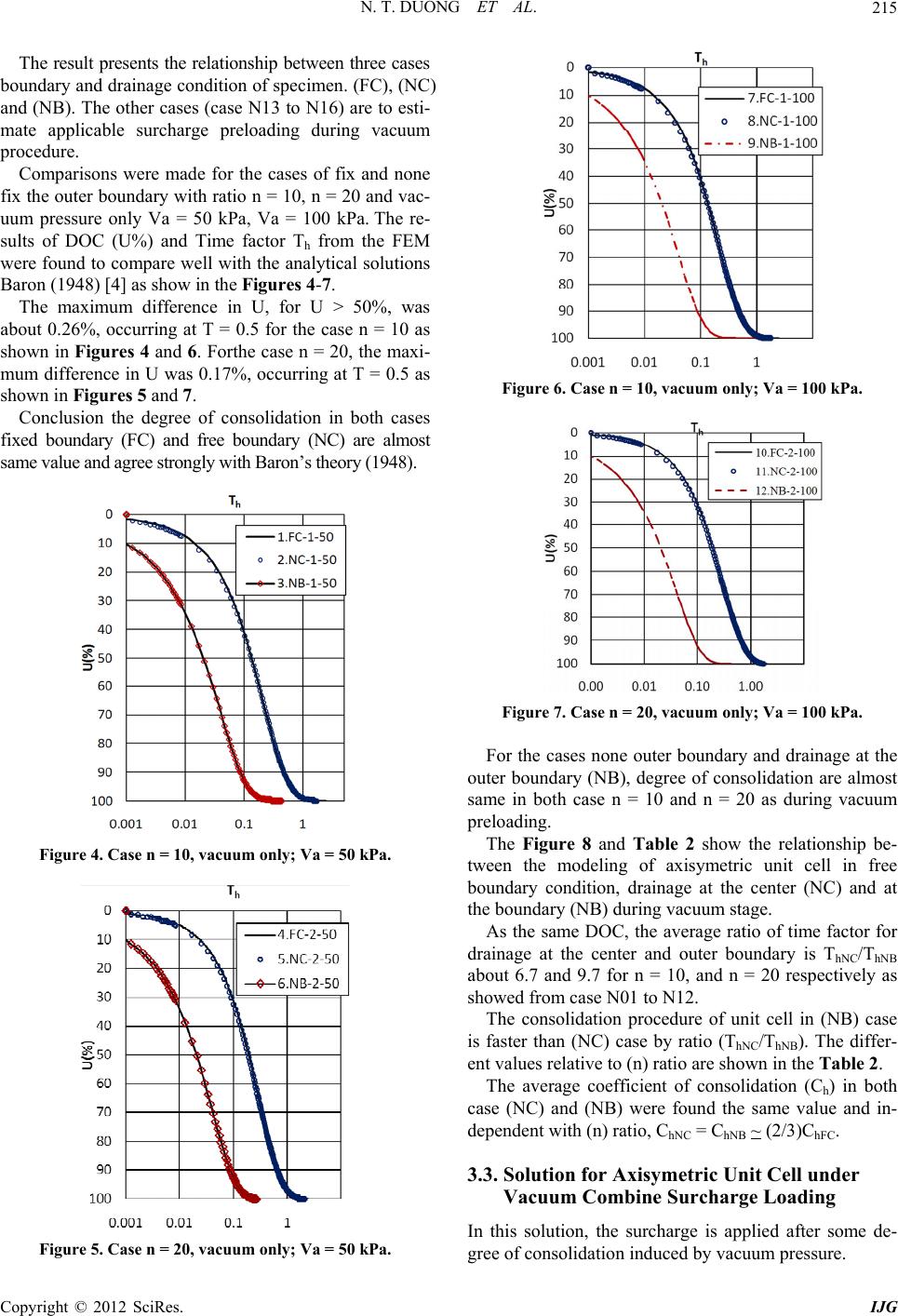

N. T. DUONG ET AL. 215
esult prrelationship between three cases
bo and dndition of spn. (FC), (NC
n
The resents the
undaryrainage coecime)
ad (NB). The other cases (case N13 to N16) are to esti-
mate applicable surcharge preloading during vacuum
procedure.
Comparisons were made for the cases of fix and none
fix the outer boundary with ratio n = 10, n = 20 and vac-
uum pressure only Va = 50 kPa, Va = 100 kPa. The re-
sults of DOC (U%) and Time factor Th from the FEM
were found to compare well with the analytical solutions
Baron (1948) [4] as show in the Figures 4-7.
The maximum difference in U, for U > 50%, was
about 0.26%, occurring at T = 0.5 for the case n = 10 as
sh 20own in Figures 4 and 6. Forthe case n = , the maxi-
mum difference in U was 0.17%, occurring at T = 0.5 as
shown in Figures 5 and 7.
Conclusion the degree of consolidation in both cases
fixed boundary (FC) and free boundary (NC) are almost
sam
Figure 6. Case n = 10, vacuum only; Va = 100 kPa.
e value and agree strongly with Baron’s theory (1948).
Figure 7. Case n = 20, vacuum only; Va = 100 kPa.
For the cases none outer boundary and drainage at the
outer boundary (NB), degree of consolidation e almost
same in both case n = 10 and n = 20 as during vacuum
The Figure 8 and Table 2 show the relationship be-
tween the modeling of axisymetric unit cell in free
boundary condition, drainage at the center (NC) and at
the boundary (NB) during vacuum stage.
As the same DOC, the average ratio of time factor for
drainage at the center and outer boundary is ThNC/ThNB
about 6.7 and 9.7 for n = 10, and n = 20 respectively as
showed from case N01 to N12.
The consolidation procedure of unit cell in (NB) case
is faster than (NC) case by ratio (ThNC/ThNB). The differ-
ent values relative to (n) ratio are shown in the Table 2.
The average coefficient of consolidation (Ch) in both
case (NC) and (NB) were found the same value and in-
depe
Figure 4. Case n = 10, vacuum only; Va = 50 kPa.
ar
preloading.
ndent with (n) ratio, ChNC = ChNB ~ (2/3)ChFC.
3.
idation induced by vacuum pressure.
3. Solution for Axisymetric Unit Cell under
Vacuum Combine Surcharge Loading
In this solution, the surcharge is applied after some de-
gree of consol
Figure 5. Case n = 20, vacuum only; Va = 50 kPa.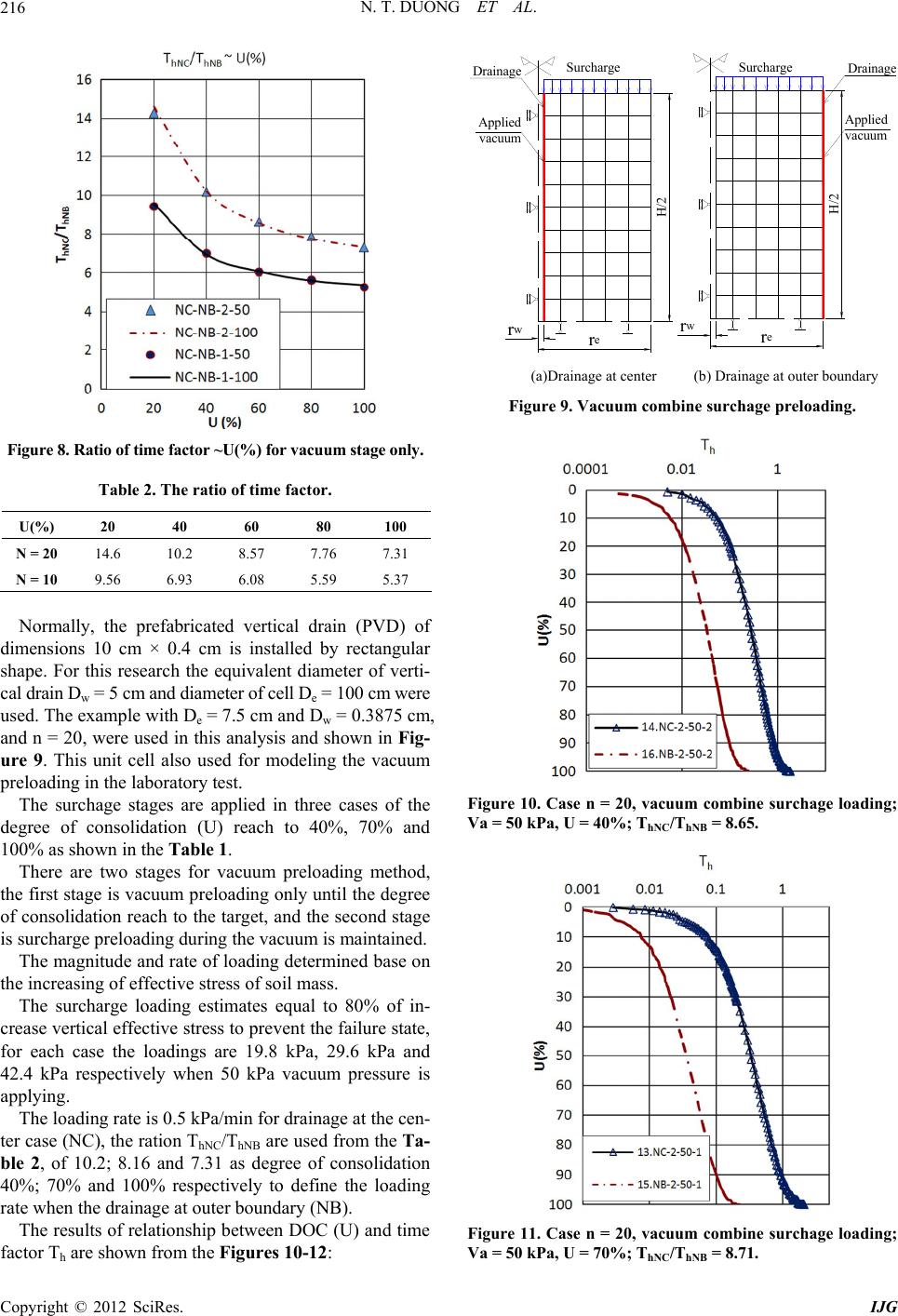

N. T. DUONG ET AL. 216
Figure 8. Ratio of time factor ~U(%) for vacuum stage only.
Table 2. The ratio of time factor.
U(%) 20 40 60 80 100
N = 20 14.6 10.2 8.57 7.76 7.31
N = 10 9.56 6.93 6.08 5.59 5.37
Normally, the prefabricated vertical drain (PVD) of
dimensions 10 cm × 0.4 cm is installed by rectangular
shape. For this research the equivalent diameter of verti-
cal drain Dw = 5 cm and diameter of cell De = 100 cm were
used. The example with De = 7.5 cm and Dw = 0.3875 cm,
and n = 20, were used in this analysis and shown in Fig-
ure 9. This unit cell also used for modeling the vacuum
preloading in the laboratory test.
The surchage stages are applied in three cases of the
degree of consolidation (U) reach to 40%, 70% and
100% as shown in the Table 1.
onsolidatnd stage
is surcharge preloading during the vacuum is maintained.
agnie and of log detened b
thasineffectresoil m
rch loadstimequa80% of in-
rease vertical effective stress to prevent the failure state,
o
factor T
There are two stages for vacuum preloading method,
e first stage is vacuum preloading only until the degree th
of cion reach to the target, and the seco
The mtudrateadinrmiase on
e increg of tive ss of sass.
The suargeing eates l to
c
fr each case the loadings are 19.8 kPa, 29.6 kPa and
42.4 kPa respectively when 50 kPa vacuum pressure is
applying.
The loading rate is 0.5 kPa/min for drainage at the cen-
ter case (NC), the ration ThNC/ThNB are used from the Ta-
ble 2, of 10.2; 8.16 and 7.31 as degree of consolidation
40%; 70% and 100% respectively to define the loading
rate when the drainage at outer boundary (NB).
The results of relationship between DOC (U) and time
are shown from the Figures 10-12:
h
rwre
H/2
Drainage
Applied
vacuum
rwre
H/2
Drainage
Applied
vacuum
Surcharge Surcharge
(a)Drainage at center (b) Drainage at outer boundary
Figure 9. Vacuum combine surchage preloading.
Figure 10. Case n = 20, vacuum combine surchage loading
V
;
a = 50 kPa, U = 40%; ThNC/ThNB = 8.65.
Figure 11. Case n = 20, vacuum combine surchage loading;
Va = 50 kPa, U = 70%; ThNC/ThNB = 8.71.

N. T. DUONG ET AL. 217
Figure 12. Case n = 20, vacuum combine surchage loading;
Va = 50 kPa, U = 100%.
average of ratio
of time factor are equal to 8.71 & 8.65 for vacuum pres-
sure are 100 kPa and 50 kPa respectively, when U =
100% the ratio of time factor is nearly same value 7.4.
In the Figure 14, degree of consolidation at 70%, the
maximum different in volume strain is 1.75% occuring at
420 min for case 40% is almost the same in the Figure 15.
From the analyzing above, the final volume strain in
case outer boundary is almost same value as that in
drainage at the center as surcharge applied at 40%; 70%
and 100%.
Under vacuum 50 kPa and surcharge was applied as
degree of consolidation is 100%, the Figure 16 showed
the deformation of unit cell (volume strain εv) during
time of vacuum and vacuum combine surcharge are same
in two cases (NC) and (NB) after adjustment with the
ratio of time factor ThNC/ThNB.
.98 during the surcharge was apply. These results are
go
c-
cu
ar
4.
From the Figure 13 and Table 3 the
The strain ration εr/εa are the same in both cases and
vary from 4 to 1.3 during vacuum stage and reduce to
0
od agreement with vacuum preloading theory, the lat-
eral deformation of embankment is internal during ap-
plying vacuum pressure.
The maximum different in volume strain is 2.13% o
rring at 350 min while the final volume strain is the
same in 13.24 (%).
These results also agree strongly with the solution in
ticle 2. To make this solution more effectively, the
laboratory test by Tri-axial apparatus should be carried
out to support this research.
Simulation in Laboratory Test
4.1. Soil Specimen
The serial tests were performed by tri-axial apparatus in
Figure 13. Ratio of time factor
surchage preloading. ~U(%) for vacuum combine
vacuum com-
g.
Table 3. The ratio of time factor for n = 20,
bine surchage preloadin
U(%) 20 40 60 80 100
100 kPa 9.33 9.31 9.16 8.41 7.32
50 kPa 9.10 8.70 8.63 8.17 7.41
8.71.
Figure 14. Case n = 20, vacuum combine surchage; Va = 50
kPa, U = 70%; ThNC/ThNB =
Figure 15. Case n = 20, vacuum combine surchage; Va = 50
kPa, U = 40%; ThNC/ThNB = 8.65.

N. T. DUONG ET AL. 218
Figure 16. Case n = 20, Vacuum combine surchage; Va = 50
Pa, U = 100%; ThNC/ThNB = 7.31.
the laboratory in Hokkaido University to simulate the
behavior of Akasaoka clay improved by vacuum prelo-
ading method. The specimens of clay in sizes 75 mm ×
150 mm in diameter and height respectively were used
for this research, the specimens is suitable to control
consolidation time under vacuum condition by tri-axial
apparatus, also the retrieved samples from the field. For
dummy research specimens were remodel in the labora-
tory from the commercial Akasaoka clay powder.
The reconstituted Akasaoka clay was pre-consolidated
under a pressure of 100 kPa and OCR = 1.25, e physi-
ard odometer test result.
The pre-consolidated condition, the effective vertical
stress and the effective horizontal stress are 80 kPa and
40 kPa respectively (the coefficient of horizontal earth
pressure at rest K0 = 0.5).
Series conventional tri-axial test were carried out to
verify the failure line (Kf) and relationship between the
coefficient K and the ratio su/σv' as show in Figure 18.
4.2. Test Procedure
Before application vacuum pressure, the specimen is
saturated with B value more than 0.98 and reach to the
initial pre-compression stress with effective vertical and
horizontal stress are 80 kPa and 40 kPa respectively after
ted by applying the ef-
ctive stress target with the lateral earth ratio equal to
k
th
cal properties of soil are listed in the Tab le 4 and Figure
17. The permeability coefficient (k) and compression
index (Cc) deduced from the stand
24 hours (Step loading and recompression step).
The vacuum pressure is simula
fe
one (K = 1), the soil specimen is subjected the same con-
dition under vacuum pressure as the period research, the
behavior of soil mass under surcharge and vacuum pres-
sure is shown in the Figure 19.
While the effective stress is applied, the drainage vale
is clocked, under the undrained condition the excess pore
water pressure has been increasing up to the vacuum
Table 4. Akasaoka clay’s properties.
Soil properties Values
Unit weight (kN/m3) 17.5
Water content, w (%) 46.5
Liquid limit, wL (%) 62
Plastic limit, wP (%) 27.5
Plasticity index, PI (%) 34.5
Specific gravity, Gs 2.67
Initial void ratio eo 1.17
Figure 17. Void ratio ~log(p') graph.
Fhear strength by effective strd ear-
tigure 18. Predict sess an h ratio.
Figure 19. Behavior of soil mass under vacuum and sur-
charge preloading.

N. T. DUONG ET AL. 219
pressure desired. In the dummy research vacuum pres-
sure, desired are 50 kPa and 100 kPa to concern the dep-
ths of specimen there for the total vertical effective stress
target of 130 kPa and 180 kPa were generating. (Vacuum
pressure supplying step). The parameters in vacuum pro-
ceed by tri-axial apparatus are shown in the Table 5.
The coefficient of horizontal earth pressure (K) is the
ratio of the effective horizontal earth pressure due to the
confinement from the surrounding soil mass to the verti-
cal effective stress. Then from the Figure 20, K value
can be calculated as follows:
3va
1va
''
K''
σσ
σσ

 (13)
During ation has
een occurred due to the excess pore water is dissipated,
the effective stress of soil as well as the shear strength
will be increase, this behavior is suitable with the vac-
uum mechanism, and the tri-axial apparatus’s gauges
record the behavior data and deformation of soil spe-
cimen automatically. The soil is consolidated completely
when the effective stress increase to the target and the
excess pore water dissipates completely. However, from
data from FEM and test the times of primary consolida-
tion reach to as the excess pore water pressure dissipates
about 95%.
Where:
CP: Cell pressure
Pore water pressure
σv': Vertical effective stress target
σh': Horizontal effective stress target
K: Coefficient of horizontal earth pressure
The shearing steps are carried out to define the undra-
ind shear strength of soil improved. Depend on the goals
these step could be performed at the time after vacuum
loading completely or with the increase of degree of
consolidation reach to 40%, 70%, 100% combine with
surcharge to estimate the capacity of soil embankment each
construction stage respectively. This step is performed
drained progress stage, the consolid
b
BP: Back pressure
PWP:
75mm
150mm
'1
'3 = '1
Pre-consolidated,
OCR=1.25, k0=0.5
'1+'va
'3 +'va
Vacuum condition,
'va (kPa), K
Figure 20. Soil specimen under vacuum c ondition.
Table 5. Parameter in vacuum proceed by tri-axial appar-
atus.
CP BP PWP v' h' (K)
Step
(kPa)
Step loading 220200 200 20 20 1
Recompression 240200 200 80 40 0.50
Vacuum supplying
(50kPa) (Undrained)290200 250 80 40 0.50
Vacuum applied 290200 200 130 90 0.692
Vacuum supplying
(100kPa) (Undrained)340200 300 80 40 0.50
Vacuum applied 340200 200 180 1400.778
to control the surcharge preloading at the site to avoid the
soas the surcharge is over the soil capacity as
we of embankment. The capacity of
somulation (as empirical me-
th
il failed
ell as instability stag
il can be predicted by for
od Tanaka):
uuS(s )*0.8*p
v
σ

 (14)
w
4.3. Test Results and Analysis
The Figures 21 and 22 are shown the relationship be-
tween case (NB) in FEM and lab test, the vacuum 50 kPa
was applied only and combination to surcharge respec-
tively. In the both cases the DOC in 100% were induced,
the largest different of U is 3.5% between FEM and lab
test occurring at Th = 0.3.
The final deformation of specimen nearly same value
at end of vacuum stage and vacuum combine surcharge
as shown in Figure 23. The largest different in volume
strain 0.3% occur at 350min as DOC at 95%.
The volume strain in 4.92% and 7.12% were found
both /e )
ted isotropic stress; this ratio is nearly one during
vacuum only and res archwas estabhe
Thelts agretrongwith behavi of-
provement by vacuum preg theory.
T24 is shown the increasing shearen
of soil specimn bepplica-
tio aeragre olida-
t a00%pely.
is shown in the Figure 25, there are
here
su/σv': determine with the lateral earth ratio K by the
conventional tri-axial test in Figure 1 8 .
p: the loading is applied (vacuum pressure or surch-
arge loading).
The undrain shear strength of soil specimen from lab
test result is analysis to check the capacity of soil im-
proved.
in
cases FEM and Lab Test. The strain ratio (er v
illustrated the inward lateral deformation of specimen
subjec
duce
e s
s su
ly
arge lis
soil
d.
imse resuor
loadin
he Figure r stgth
e
n vacuum preloa
fore im
ding
provem
t sev
ent and
l de
after a
e of cons
ion of 40%, 70%
The stress path
nd 1 resctive

N. T. DUONG ET AL. 220
Figure 21. Case n = 20, vacuum only; Va = 50 kPa, U = 10 0%.
Figure 22. Case n = 20, vacuum combine surchage; Va = 50
kPa, U = 100%.
Figure 24. Increasing undraine d shear strength.
Figure 25. Stress path.
some sections during simulate vacuum preloading me-
thod, pre-consolidation (AB), vacuum application (BC),
surcharge loading (CDEF). Under vacuum condition, the
stress path of soil moves from B to C far from the failure
line, while it changes from D to E close to the failure line
when surcharge was applied. The behavior of soil speci-
men under vacuum preloading method simulated by
Tri-axial apparatus is well matched the before studies.
5. Conclusions
The study has been developed based on the combination
of finite element analysis and the results of laboratory
experiments to simulate a new appropriate method. This
method can be widely applied for soft ground improve-
ment by vacuum preloading method. The results om the
etric unit cell used to model the behav-
Figure 23. Case n = 20, vacuum combine surchage; Va = 50
kPa, U = 100%.
fr
study can be summarized as follows:
1) The axisym

N. T. DUONG ET AL. 221
ior of soil treatment by vacuum preloading as none
boundary conditions are considered, the behavior of soil
is more close to real soil state in the field.
2) Two cases of drainages boundary showed that time
for consolidation in cases outside drainage of unit cell is
faster than at the center by ThNC/ThNB ratio. However, the
deformations of the specimens in all cases are in same
shape and value with the same applied condition.
3) Results of experiments by tri-axial apparatus en-
tirely agree with FEM model. It is suggesting that the
theories are given full compliance, highly compelling to
predict the behavior of soil improvement by vacuum
preloading method.
REFERENCES
[1] mos-
pheric Pressure,”
Stabilization, Massachusetts Institute of Technology, Bos-
ton, 1952, pp. 258-263.
[2] B. Indraratna and I. W. Redana, “Laboratory Determina-
tion of Smear Zone Due to Vertical Drain Installat
Journal of Geotechnical and Geoenvironmental Engi-
W. Kjellman, “Consolidation of Clayey Soils by At
Proceedings of a Conference on Soil
ion,”
neering, Vol. 124, No. 2, 1998, pp. 180-184.
doi:10.1061/(ASCE)1090-0241(1998)124:2(180)
[3] S. Hansbo, “Consolidation of Fine-Grained Soils by Pre-
. 1330-
fabricated Drains,” Proceedings of 10th International
Conference on Soil Mechanics and Foundation Engi-
neering, Stockholm, Vol. 3, 1981, pp. 677-682.
[4] R. A. Barron, “Consolidation of Fine-Grained Soils by
Drain Wells,” Transactions of ASCE, Vol. 113, 1948, pp.
718-742.
[5] B. Indraratna, C. Rujikiatkamjorn and I. Sathananthan,
“Radial Consolidation of Clay Using Compressibility In-
dices and Varying Horizontal Permeability,” Canadian
Geotechnical Journal, Vol. 42, No. 5, 2005, pp
1341. doi:10.1139/t05-052
[6] J. C. Chai, J. P. Carter and S. Hayashi, “Vacuum Con-
solidation and Its Combination with Embankment Load-
ing,” Canadian Geotechnical Journal, Vol. 43, No. 10,
2006, pp. 985-996. doi:10.1139/t06-056
[7] T. A. Tran and T. Mitachi, “Equivalent Plane Strain
Modeling of Vround under Em-
bankment CoPreloading,” Com-
ertical Drains in Soft G
mbined with Vacuum
puters and Geotechnics, Vol. 35, No. 5, 2008, pp. 655-
672. doi:10.1016/j.compgeo.2007.11.006