 International Journal of Geosciences, 2012, 3, 14-20 http://dx.doi.org/10.4236/ijg.2012.31002 Published Online February 2012 (http://www.SciRP.org/journal/ijg) A New Regularized Solution to Ill-Posed Problem in Coordinate Tr ansformation Xuming Ge1, Jicang Wu1,2 1Department of Surveying and Geo-Informatics, Tongji University, Shanghai, China 2Key Laboratory of Advanced Surveying Engineering of State Bureau of Surveying and Mapping, Shanghai, China Email: gexumingxmy@163.com, jcwu@tongji.edu.cn Received July 23, 2011; revised September 21, 2011; accepted November 15, 2011 ABSTRACT Coordinates transformation is generally required in GPS applications. If the transformation parameters are solved with the known coordinates in a small area using the Bursa model, the precision of transformed coordinates is generally very poor. Since the translation parameters and rotation parameters are highly correlated in this case, a very large condition number of the coefficient matrix A exists in the linear system of equations b A. Regularization is required to reduce the effects caused by the intrinsic ill-conditioning of the problem and noises in the data, and to stabilize the solution. Based on advanced regularized methods, we propose a new regularized solution to the ill-posed coordinate transforma- tion problem. Simulation numerical experiments of coordinate transformation are given to shed light on the relationship among different regularization approaches. The results indicate that the proposed new method can obtain a more rea- sonable resolution with higher precision and/or robustness. Keywords: Bursa; Coordinate Transformation; Ill-Posed; Methodology 1. Introduction Coordinate transformation plays a very importance role in the numerical treatment of global positioning system. For transforming GPS coordinates from WGS-84 coordi- nate system to a local coordinate system, the Bursa mo- del is generally used to solve transformation parameters, including three translation parameters, three rotation pa- rameters and one scale parameter. From a theoretical point of view, a great number of algorithms have been devel- oped to solve these problems. Early publications such as Grafarend et al. [1], Vanicek and Steeves [2], Vanicek et al. [3], Yang [4], and Grafarend and Awange [5] have given some detail algorithms of coordinate transformation. In general, their algorithms to solve transformation pa- rameters are all based on the classical least squares crite- rion. Recently, better methods are available in literature, e.g. hard or soft fixing of certain transformation parame- ters (e.g. rotation around some coordinate axes are strongly correlated with translations), reduction of coordinates to the centre of “gravity” etc., however, ill-posed problems were rarely considered in those methods. Actually, ill- posed problems often impact this kind of data processing. In the coordinate transformation, the Bursa model is more suitable for global data, so global distributed data is normally required to solve coordinate transformation pa- rameters. However, an engineering GPS control network covers only hundreds of square kilometers, or even smaller. In this case, the translation and rotation parame- ters are highly correlated and the mathematical model is thus ill-posed. Generally, parameters obtained by tradi- tional algorithms from the ill-posed model will have poor precision and robustness. As is well known, regularization is a powerful tool to solve ill-posed problems, which have been widely ap- plied to solve inverse ill-posed geodetic problems and sig- nal processing. Tikhonov proposed a well-known regu- larization method to ill-posed models [6,7]. Golub [8] pro- posed a singular value decomposition (SVD) method to least squares solutions and Hansen analyzed the truncated SVD as a method for regularization [9] in mathematics. Xu and Rummel [10] advanced a multiple parameters regularization method to solve ill-posed problems in ge- odesy [11]. These investigations are almost based on pure mathematics and not considered the characteristics of practical surveying applications. In this paper, we will propose a new approach to solve ill-posed problems in the coordinate transformation. The process starts with discussion of early methods for solv- ing ill-posed problems in mathematics, and analysis of the characteristics of ill-posed coordinate transformation problems. Taking account of the characteristics of coor- dinate transformation in GPS applications, a new algo- C opyright © 2012 SciRes. IJG  X. M. GE ET AL. 15 rithm is proposed. On other hand, based on the new algo- rithm we formulate a new approach to choose regulariza- tion parameters. In the new algorithm, information borne by small and large singular values has been kept by dif- ferent methods. 2. Main Equations and Notations We introduce main equations and notations used through- out this paper. Matrices are represented by the uppercase English alphabet and I denotes identity matrix. Scalars are represented by lowercase Greek letters or English alphabet with double subscripts. Superscript T denotes the transpose of a matrix. Let 2 denotes the 2-norm of matrix A. Let denotes the range of the matrix A. In this paper, we deal with the linear finite-dimension equations. ,, mn md ,, b b AA mnmd i (1) When the rotations are small, the mathematical model of the Bursa model can recast as 000 1 000 1 00 0 1 y T y z R z z yx xx yy zz T (2) where xyz and 000 , T Txyz R denote the translate parameters, rotation parameters and scale parameter, respectively. We also denote the SVD of A by 1 n TT iii i uv UVA (3) with 12 ,,Uuu, , ni uum T n UU I , 12 ,,Vvv, , ni vv n T n VV I ,nn n 0 n , , and 12 diag, , , 12 i . The numbers are called the singular values of A, while the vectors i and i are the left and right sin- gular vectors of A, respectively. u v exact noise ,,, mn md 3. Methodologies for Ill-Posed Problem The ill-posed problems are with a very large condition number of the coefficient matrix A in a linear system as Equation (1), and most of discussion about solutions of ill-condition-ed matrices require knowledge of the SVD of the matrix A [12]. In particular, the condition number of A is defined as the ratio between the largest and the smallest singular values of A. The numerical treatment of equations with an ill-condi- tioned coefficient matrix depends on the type of ill-con- dition of A. There are two classes of ill-posed problems. The first is rank-deficient problems in which the matrix A has a cluster of small singular values, and there is a well-determined gap between large and small singular values. The second is the discrete ill-posed problem that all of the singular values of A, on the average, decay gradually to zero, that means there is no gap in the sin- gular value spectrum. For some more details on ill-posed problems, the reader may refer to Hansen [13] and Tar- antola [14]. Considering an ill-posed linear system as Equation (1), with nonsingular matrix A and the right-hand side b pol- luted by white noise, thus Equation (1) can be rewritten in the form bb AbA bb (4) where exact noise 22 bb 1 exact exact (5) We wish to approximate Ab bb 1 TT LS (6) However, exact cannot be directly divided from a observation vector , we get the direct least squares solution AA Ab (7) It is well known that the direct solution is completely dominated by noise, when the coefficient matrix A is ill-posed. Based on the SVD of A, the direct solution can recast naive 1 T n i i ii uv b (8) exact noise 11 TT nn ii ii ii ii ub ub vv (9) Considering Equation (8), to get an applicable directly solution, it is necessary to make sure that the following assumption which is called the Discrete Picard Condition is satisfied: The exact SVD coefficient T ub i decay fas- ter than the i . More details and analysis can also be fund in Hansen [13,15]. When the coefficient matrix A is ill-posed, the solution naive is with poor robustness and not applicable. Next considering Equation (9), the first sum in Equa- tion (9) must converge to exact . It means the numerators in the first sum in Equation (9) decay faster than (or, at Copyright © 2012 SciRes. IJG  X. M. GE ET AL. 16 least, as fast as) the singular values in denominators, with growing i. On other hand, noise represents white noise in second sum in Equation (9). It means noise Fourier coefficients b noise cannot decay faster than (or, at least, after some point) the singular values, with growing i in ill-posed problems. That means noise will dominate the solution naive T i ub b after some point. Consequently, ill-posed problems with perturbations in observation vector may magnify the noise information by the corresponding sin- gular value which is very small. The magnified noise completely cover the useful information, 1 naive 1 exact , and noise AbAb thus does not ap- proximate to exact . For solving the first class ill-posed problems, for which there is a well-determined gap between the large and small singular value of coefficient matrix A, Hansen pro- posed a well-known approach [9,13,16,]—truncated SVD. The key idea in this approach is to obtain the truncated point k, then Equation (8) can recast as 1 T k i ki ii ub v k (10) The solution is referred to as the truncated SVD solution. For solving the second class ill-posed problems in which the singular values of matrix A decay gradually to zero, the above TSVD method cannot applied for solving this problem. Tikhonov regularization method is a well- known method for solving this kind of ill-posed problem. The key idea in Tikhonov’s method is to incorporate a priori assumptions about the size and smoothness of the desired solution. Tikhonov regularization in general form leads to the minimization problem 22 2 22 min xb Lx (11) where the regularization parameter λ controls the weight given to minimization of the regularization term, relative to the minimization of the residual norm, and L repre- sents regularization matrix. In this paper, we only con- cern L = I. Then the Tikhonov solution is given by 1 2TT AA I Ab (12) Tikhonov method can be rewritten in SVD form with filter factor defined as 2 22 i i i f (13) and the regularized solution is rank( ) 1 T A i ii ii ub reg In Equation (14), if the filter factor defined as fv 1 0 ii i ii f (14) x (15) Then the regularized solution is turn to the truncated SVD solution. Clearly, the key idea in Equation (14) is to modify the small singular values of matrix A, and Equa- tion (15) is use to decide from where the singular values should be modified. Here we propose a new method for modifying the singular values in a specific method, and its solution is noted as regk which is called as the modified singular value (MSV) solution. For solving ill-posed problems in GPS coordinate trans- formation by the Buras model, the characteristics of in- dividual real model should be considered. That is, after the ith, the true Fourier coefficients exacti cannot decay faster than singular values, however, there is still some useful information exist in T ub exacti, one of real example is presented in Figure 1. In Figure 1, singular values i T ub is connected with circle dash line, true Fou- rier coefficients exacti is connected with cross dash line, and total Fourier coefficients T ub T ub i is connected with red circle solid line. We can see from i = 5, error Fourier coefficients noise are greater than corresponding sin- gular values i T i ub , but the true Fourier coefficients exacti are still significant. If we use TSVD method, the true Fourier coefficients from i = 5 to i = 7 will be discarded. Our new MSV method will try to use these discarded items for improving the solution. T ub As above, Tikhonov regularization is to modify those small singular values, so as to absorb discarded items by TSVD. However, this method also modifies large singu- lar values, and thus influences the precision of coordinate transformation. Our proposed MSV method is similar with Tikhonov regularization method, but only items with small singular values in Equation (14) will be modified and items with large singular values will be kept unchanged, that means f = 1 in Equation (14). 4. Estimation of Regularization Parameter The key question in regularization method is how to choose the regularization parameter, either the Tikhonov method’s parameter or the TSVD method’s parame- ter k. Thus, estimation of regularization parameter plays a very importance role in solving ill-posed problems. Perhaps the most convenient graphical tool for deter- mining of regularization parameter is so-called L-curve which is a plot of regularization parameter solution (semi) norm e.g., the 2-(semi)norm 2, for all possible regu- larization parameters versus the corresponding residual norm e.g., Lx 2 xb. The L-curve clearly displays the compromise between minimization of these two quantities, Copyright © 2012 SciRes. IJG 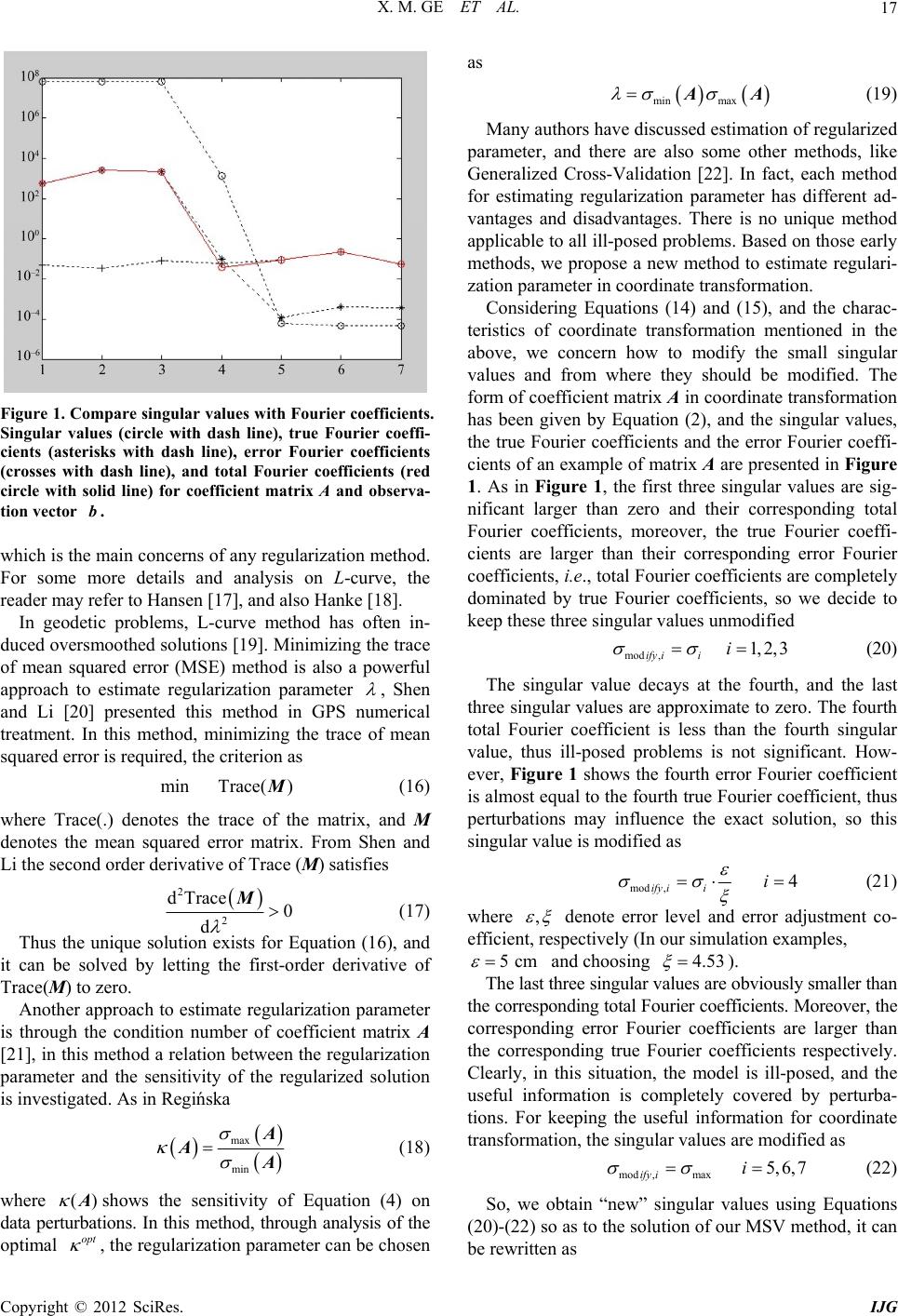 X. M. GE ET AL. 17 Figure 1. Compare singular values with Fourier coefficients. Singular values (circle with dash line), true Fourier coeffi- cients (asterisks with dash line), error Fourier coefficients (crosses with dash line), and total Fourier coefficients (red circle with solid line) for coefficient matrix A and observa- tion vector . b which is the main concerns of any regularization method. For some more details and analysis on L-curve, the reader may refer to Hansen [17], and also Hanke [18]. In geodetic problems, L-curve method has often in- duced oversmoothed solutions [19]. Minimizing the trace of mean squared error (MSE) method is also a powerful approach to estimate regularization parameter , Shen and Li [20] presented this method in GPS numerical treatment. In this method, minimizing the trace of mean squared error is required, the criterion as minTrace( )M (16) where Trace(.) denotes the trace of the matrix, and M denotes the mean squared error matrix. From Shen and Li the second order derivative of Trace (M) satisfies 2 d T 2 race 0 d M (17) Thus the unique solution exists for Equation (16), and it can be solved by letting the first-order derivative of Trace(M) to zero. Another approach to estimate regularization parameter is through the condition number of coefficient matrix A [21], in this method a relation between the regularization parameter and the sensitivity of the regularized solution is investigated. As in Regińska max min A (18) where () shows the sensitivity of Equation (4) on data perturbations. In this method, through analysis of the optimal , the regularization parameter can be chosen as min max A mod ,1, 2, 3 ify iii (19) Many authors have discussed estimation of regularized parameter, and there are also some other methods, like Generalized Cross-Validation [22]. In fact, each method for estimating regularization parameter has different ad- vantages and disadvantages. There is no unique method applicable to all ill-posed problems. Based on those early methods, we propose a new method to estimate regulari- zation parameter in coordinate transformation. Considering Equations (14) and (15), and the charac- teristics of coordinate transformation mentioned in the above, we concern how to modify the small singular values and from where they should be modified. The form of coefficient matrix A in coordinate transformation has been given by Equation (2), and the singular values, the true Fourier coefficients and the error Fourier coeffi- cients of an example of matrix A are presented in Figure 1. As in Figure 1, the first three singular values are sig- nificant larger than zero and their corresponding total Fourier coefficients, moreover, the true Fourier coeffi- cients are larger than their corresponding error Fourier coefficients, i.e., total Fourier coefficients are completely dominated by true Fourier coefficients, so we decide to keep these three singular values unmodified (20) The singular value decays at the fourth, and the last three singular values are approximate to zero. The fourth total Fourier coefficient is less than the fourth singular value, thus ill-posed problems is not significant. How- ever, Figure 1 shows the fourth error Fourier coefficient is almost equal to the fourth true Fourier coefficient, thus perturbations may influence the exact solution, so this singular value is modified as opt mod ,4 ify iii , (21) where 5cm denote error level and error adjustment co- efficient, respectively (In our simulation examples, and choosing 4.53 mod ,max5, 6, 7 ify ii ). The last three singular values are obviously smaller than the corresponding total Fourier coefficients. Moreover, the corresponding error Fourier coefficients are larger than the corresponding true Fourier coefficients respectively. Clearly, in this situation, the model is ill-posed, and the useful information is completely covered by perturba- tions. For keeping the useful information for coordinate transformation, the singular values are modified as (22) So, we obtain “new” singular values using Equations (20)-(22) so as to the solution of our MSV method, it can be rewritten as Copyright © 2012 SciRes. IJG  X. M. GE ET AL. 18 1mod , T i i ify i ub rank reg k i v A (23) 5. Numerical Experiments The data used in our experiments is the simulated coor- dinates of GPS stations distributed in 2000 square kilo- meters. We use five GPS points as control points, and apply “true” coordinate transformation parameters to get corresponding “true” coordinates in the local coordinate system. From initial investigations, we know that if points locate in the interior of a network composed by control points, we can get their corresponding coordi- nates with acceptable precision in a local coordinate sys- tem by coordinate transformation parameters even using the classical least squares method. Moreover, the results of coordinate transformation are also acceptable when coordinates of control points have smaller noise in both coordinate systems. So, the coordinates of points outside the region of the control network will be used to check the precision of coordinate transformation by different methods. In our experiments, we give five centimeters perturba- tions to coordinates of control points in both systems. Firstly, we use the “true” transformation parameters to get some “true” coordinates outside the control network in both coordinate systems. Secondly, we transform co- ordinates of those outside points to the local system with different coordinate transformation parameters which ob- tained by different regularization methods, and compare each of them with their “true” coordinates. Root mean square error (RMSE) of points by least squares method is presented in Figure 2. Here, we simu- lated coordinates of 100 points in exterior area with a white noise with zero means and standard deviations of 5 Figure 2. RMSE of transformed coordinates solving by least squares method. centimeters, and 500 coordinate transformation experi- ments have been repeated for obtaining mean of RMSE with statistical significance. Figure 2 shows that the mean of RMSE is clearly larger than the noise has been imposed in the coordinates, and the results have large oscillations. The results solving by TSVD, Tikhonov regularization with L-curve, and MSE methods are presented in Fig- ures 3(a)-(c) respectively. Clearly, the means of RMSE are smaller than the result in Figure 2, especially the mean value by MSE is approximate to the error which has been given before, and also has stronger robustness. Figure 4 presents the results solving by our MSV method with the modified “new” singular values. Obvi- ously, the results solving by MSV method have the smallest mean of RMSE and stronger robustness. Table 1 summarizes means of RMSE and their corresponding standard deviations of different methods. The performance about two of those points in 500 tests by MSV method are presented in Figure 5. Clearly, The No. 68 point (red) is more seriously corrupted by noise than the No. 28 point (black). In order to present some good properties of our new method, the results of the No. 68 point by MSV, TSVD, and Tikhovon regularization with L-curve are drawn in Figures 6(a)-(c), respectively. Table 2 summarizes mean of RMSE and their corre- sponding standard deviations of No. 68 points through using different methods. Clearly, when the point has poor precision, our MSV method can balance the point preci- sion and robustness well. 6. Conclusions It is well known that regularization has been successfully applied to solve ill-posed problems by significantly im- proving the condition number of ill-condition matrix. A very large condition number is usually caused by the small singular values of matrix, so we propose a new me- Table 1. Mean of RMSE and standard deviations. Mean of RMSE (m) Standard Deviations LS 0.1930 0.04989 TSVD 0.1408 0.04648 L-curve 0.1347 0.03743 MES 0.1351 0.02858 MSV 0.1116 0.03384 Table 2. Mean of RMSE and standard deviations of No. 68 point. Mean of RMSE (m) Standard Deviations MSV 0.1561 0.08363 TSVD 0.2076 0.1034 L-curve 0.1634 0.0910 Copyright © 2012 SciRes. IJG 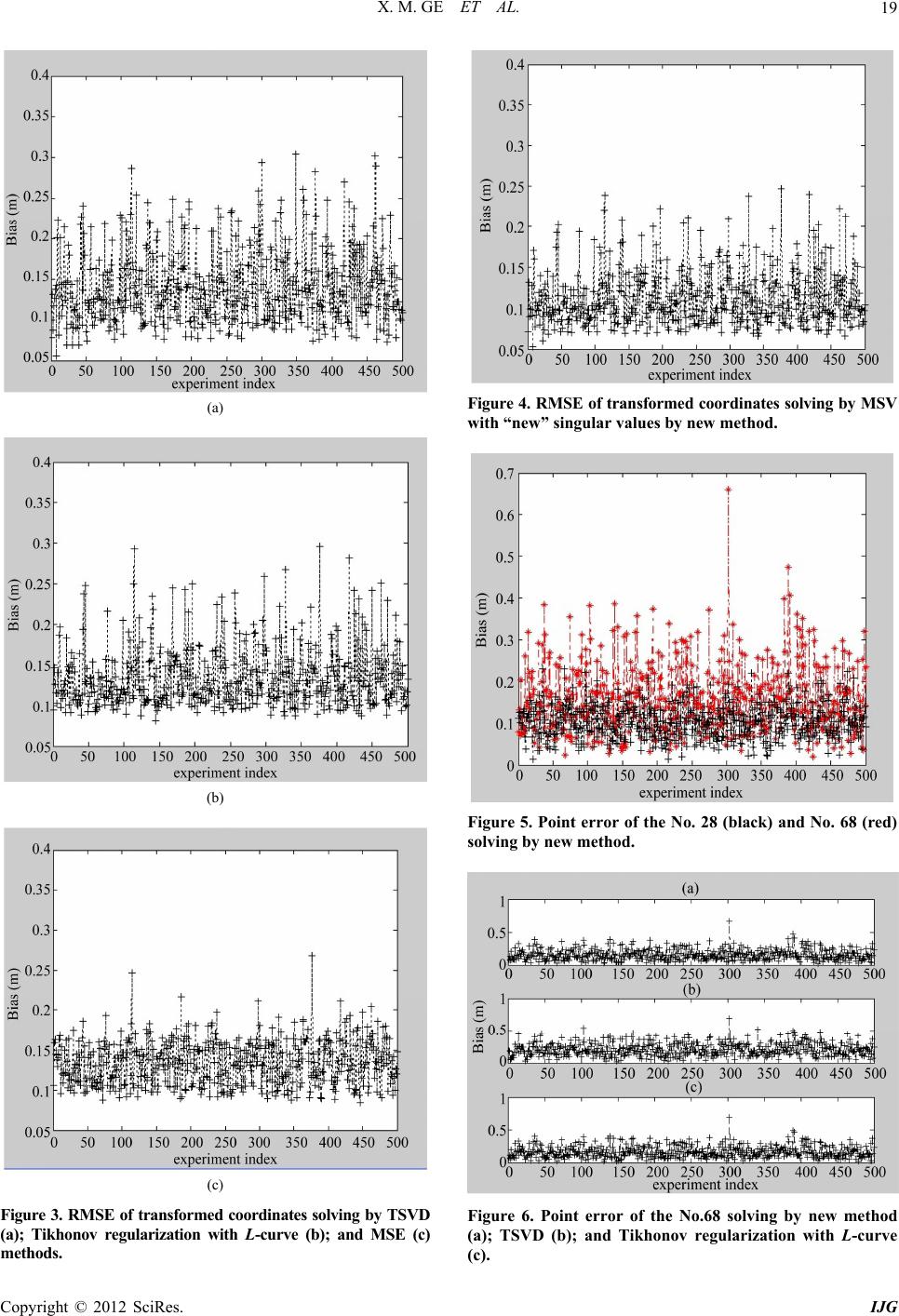 X. M. GE ET AL. 19 (a) (b) (c) Figure 3. RMSE of transformed coordinates solving by TSVD (a); Tikhonov regularization with L-curve (b); and MSE (c) methods. Figure 4. RMSE of transformed coor dinates solving by MSV with “new” singular values by new method. Figure 5. Point error of the No. 28 (black) and No. 68 (red) solving by new method. Figure 6. Point error of the No.68 solving by new method (a); TSVD (b); and Tikhonov regularization with L-curve (c). Copyright © 2012 SciRes. IJG  X. M. GE ET AL. Copyright © 2012 SciRes. IJG 20 thod for solving ill-posed problems in coordinate trans- formation through modifying small singular values. The numerical experiments have demons-trated that the new method can solve these kinds of ill-posed problems, and gain an applicable precision, moreover, perform stronger robustness. In practical coordinate transformation prob- lems, we do not know the true and error Fourier coeffi- cients, the total Fourier coefficients can be used to mod- ify the singular values so as to implement the MSV method. 7. Acknowledgements This paper is sponsored by the Natural Science Founda- tion of China (No. 41074019) and International coopera- tion project of Chinese ministry of Science (No. 2010- DFB20190). REFERENCES [1] E. W. Grafarend, F. Krumm and F. Okeke, “Curvilinear Geodetic Datum Transformations,” Z Vermessungswesen, Vol. 120, No. 4, 1995, pp. 334-350. [2] P. Vanicek and R. R. Steeves, “Transformation of Coor- dinates between Two Horizontal Geodetic Datum,” Jour- nal of Geodesy, Vol. 70, No. 11, 1996, pp. 740-745. [3] P. Vanicek, P. Novak and R. Craymerm, “On the Correct Determination of Transformation Parameters of Horizon- tal Geodetic Datum,” Geomatica, Vol. 56, No. 4, 2002, pp. 329-340. [4] Y. Yang, “Robust Estimation of Geodetic Datum Trans- formation,” Journal of Geodesy, Vol. 73, No. 9, 1999, pp. 268-274. doi:10.1007/s001900050243 [5] E. W. Grafarend and L. J. Awange, “Nonlinear Analysis of the Transformational Datum Transformation,” Journal of Geodesy, Vol. 77, 2003, pp. 66-76. doi:10.1007/s00190-002-0299-9 [6] A. N. Tikhonov, “Regularization of Ill-Posed Problems,” Doklady Akademi Nauk, Vol. 151, No. 1, 1963, pp. 49- 52. [7] A. N. Tikhonov, “Solution of Incurrectly Formulated Pro- blems and the Regularization Method,” Doklady Akade- mi Nauk, Vol. 151, No. 3, 1963, pp. 501-504. [8] G. H. Golub and C. Reinsch, “Singular Value Decompo- sition and Least Squares Solutions,” Numerical Mathe- matics, Vol. 14, 1970, pp. 403-420. doi:10.1007/BF02163027 [9] P. C. Hansen, “The Truncated SVD as a Method for Re- gularization,” BIT, Vol. 27, 1987, pp. 534-553. doi:10.1007/BF01937276 [10] P. L. Xu and R. Rummel, “Generalized Ridge Regression with Applications in Determination of Potential Fields,” Manuscripta Geodaetica, Vol. 20, No. 1, 1994, pp. 8-20. [11] P. L. Xu, Y. Fukuda and Y. Liu, “Multiple Parameter Regularization: Numerical Solution and Application to the Determination of Geopotential from Precise Satellite Orbits,” Journal of Geodesy, Vol. 80, No. 1, 2006, pp. 17-27. doi:10.1007/s00190-006-0025-0 [12] G. H. Golub and C. F. Van Loan, “Matrix Computation,” 3rd Edition, The Johns Hopkins University Press, Balti- more, 1996. [13] P. C. Hansen, “Rank-Deficient and Discrete Ill-Posed Pro- blems,” SIAM, Philadelphia, 1998. doi:10.1137/1.9780898719697 [14] P. Tarantola, “Inverse Problem Theory,” SIAM, Phila- delphia, 2005. [15] P. C. Hansen, “The Discrete Picard Condition for Dis- crete Ill-Posed Problems,” BIT, Vol. 30, No. 4, 1990, pp. 658-672. doi:10.1007/BF01933214 [16] P. C. Hansen, “Truncated SVD Solutions to Discrete Ill- Posed Problems with Ill-Determined Numerical Rank,” Journal on Scientific and Statistical Computing, Vol. 11, 1990, pp. 503-518. doi:10.1137/0911028 [17] P. C. Hansen, “Analysis of Discrete Ill-Posed Problems by Means of the L-Curve,” SIAM Review, Vol. 34, No. 4, 1992, pp. 561-580. doi:10.1137/1034115 [18] M. Hanke, “Limitations of the L-Curve Method in Ill- Posed Problems,” BIT, Vol. 36, No. 2, 1996, pp. 287-301. doi:10.1007/BF01731984 [19] P. L. Xu, “Truncated SVD Methods for Discrete Linear Ill-Posed Problems,” Geophysical Journal International, Vol. 135, No. 2, 1998, pp. 505-514. doi:10.1046/j.1365-246X.1998.00652.x [20] Y. Z. Shen and B. F. Li, “Regularized Solution to Fast GPS Ambiguity Resolution,” Journal of Surveying Engi- neering, Vol. 133, No. 4, 2007, pp. 168-172. doi:10.1061/(ASCE)0733-9453(2007)133:4(168) [21] T. Regińska, “Regularization of Discrete Ill-Posed Prob- lems,” BIT, Vol. 44, No. 3, 2004, pp. 119-133. [22] G. H. Golub, M. T. Heath and G. Wahba, “Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter,” Technometrics, Vol. 21, No. 2, 1979, pp. 215- 223. doi:10.2307/1268518
|