Paper Menu >>
Journal Menu >>
 J. Software Engineering & Applications, 2010, 3: 477-486 doi:10.4236/jsea.2010.35054 Published Online May 2010 (http://www.SciRP.org/journal/jsea) Copyright © 2010 SciRes. JSEA Test Cost Optimization Using Tabu Search Anu Sharma*, Arpita Jadhav, Praveen Ranjan Srivastava, Renu Goyal Computer Science and Information System Group, Birla Institute of Technology and Science, Pilani, India. Email: {*anu11sharma1123, arpitajadhav, praveenrsrivastava}@gmail.com Received January 5th, 2010; revised February 21st, 2010; accepted February 25th, 2010. ABSTRACT In order to deliver a complete reliable software product, testing is performed. As testing phase carries on, cost of testing process increases and it directly affects the overall project cost. Many a times it happens that the actual cost becomes more than the estimated cost. Cost is considered as the most important parameter with respect to software testing, in software industry. In recent year’s researchers have done a variety of work in the area of Cost optimization by using various concepts like Genetic Algorithm, simulated annealing and Automation in generation of test data etc. This paper proposes an efficient cost effective approach for optimizing the cost of testing using Tabu Search (TS), which will provide maximum code coverage along with the concepts of Dijkstra’s Algorithm which will be implemented in Aspiration criteria of Tabu Search in order to optimize the cost and generate a minimum cost path with maximum coverage. Keywords: Tabu Search, Test Cost Optimization, Dijikstra’s Algorithm 1. Introduction Software engineering is not just to develop new software but also that product should be more reliable and cost effective so that client can effectively use that. According to Bezier B [1], Software testing is an important factor in software development life cycle in which one-third to one-half of the total cost of the product is consumed only on the testing process. Software testing is a process to trace out the errors in software that intended to meet the desired result of the programmer by satisfying all the pre condition factors setup by the tester. Since, software testing is becoming more popular and demanding area in the software development industry in past few years [2]. Resulting product is very reliable if testing covers maximum errors. But on the contrary, during testing the cost can increase more than the expected value due to inappropriate test cases. These inappropriate test cases cause wastage of organizational resources as well as time. There is a need to minimize the cost for getting an ac- ceptable product. In order to deal with the above issue and also to provide good quality software within desired time and least cost Researchers have applied several techniques on minimi- zation of cost in testing of product, such as fuzzy logic, automatically generation of test data [3]. But here we are using Tabu Search [4]. Tabu Search will choose appro- priate test paths and concepts of Dijkstra algorithm will be implemented in Aspiration Criteria to optimize the cost. If any test case does not provide maximum coverage, pro- posed algorithm will backtrack and starts with a new path. This paper is organized as follow: Section 2 describes the general introduction to software testing, Section 3 shows historical detail of the tabu search in testing area, Section 4 describes about the tabu search, Section 5 shows dijkstra algorithm used in proposed ap- proach, Section 6 is the proposed technique which uses tabu search with dijkstra algorithm, Section 7 is showing experimental illustration of the proposed algorithm Sec- tion VIII is conclusion and further work. 2. Software Testing Although crucial to software quality and widely deployed by programmers and testers, software testing still remains an art, due to limited understanding of the principles of software [1,2]. The software testing strategy is an impor- tant process in case of software development lifecycle model [2]. Testing is a process which leads delivery of higher quality products, low cost, more accurate and re- liable results of developed computer software. The pur- pose of testing includes quality assurance, verification and validation, or reliability estimation. If all shortest paths which can be measured by plotting the control flow graph [2], with maximum coverage are known to the tester, estimated cost taken by testing process can be reduced. 3. Related Work Organizations facing the challenge of solving testing cost problems. Classical approaches often suggested solution  Test Cost Optimization Using Tabu Search Copyright © 2010 SciRes. JSEA 478 to the coverage problem but there is very less number of solutions that control the cost while providing the rea- sonable quality to the software. On tabu search research is going on rapidly but no method exists to control the cost of testing, Even if we do the automation there should be some criteria to select the appropriate test cases. Several attempts have been made over the years to develop such an algorithm for the Optimization of the cost to find out an efficient path automatically. Research has applied many approaches for the same purpose [5]. The basic algorithm of Tabu Search is ex- plained in [6]. The concept of Tabu Search has also been applied to optimize the Cost of the program with maxi- mum code coverage [6]. Previously the work has been done on the automation of test cases using Tabu search algorithm on complex programs under test and large number of input variables. Using these automation tools cost can be reduced and saves the time [3,7]. Another approach suggests the use of tabu search algorithm for generation of structural software tests [4]. It also com- bines the use of memory with a backtracking process to avoid getting stuck in local minima [8]. To explore the regions and to avoid the revisiting of candidate list a po- sition guided tabu search based on metric search space has been covered. To improve the intensification (search the local optimal solution) and diversification (exploring new regions)[9] ITS based approach has been used in a re- search Tabu search implemented to “genetic” methods and evolutionary method, to deal with the complex path tabu search have adaptive memory structure so it can also be applied to the neural networks. Tabu Search has been also applied to solve the Job Shop Scheduling problem using Genetic Algorithms [10]. Most of the scheduling problems require either exponential time or space to generate an optimal answer. Many researchers have been done for identifying the infeasible paths of a program [11]. Different algorithms and techniques have been proposed by the researchers to detect optimized paths [12,13].Generating test data automatically and identifying infeasible paths reduces the testing cost, time and effort [14]. Since cost and code coverage play an important role in testing. But not much of work has been suggested for cost optimization with maximum code coverage. This paper provides the solution for the above problem. Which em- ploy Tabu Search algorithm with the concept of greedy approach to provide a minimum cost path by covering most of the nodes and storing the best path solution into memory. 4. Tabu Search [6] Tabu search is a metaheuristic approach which is used to solve the optimization problems, [6,15]. It is designed to guide other methods to escape the trap of local optimality, also called local minima. Overview of Tabu Search: Three primary themes form the basis of Tabu search: 1) Flexible attribute-based memory structure: It is de- signed in such a way so that the evaluation criteria as well as historical search information can be exploited more thoroughly than by rigid memory structures (as in branch bound) or by memory less systems (as in case of simulated annealing). 2) An associated mechanism of control is embodied for employing the memory structures, which are based on the interplay between conditions that constrain the search process. 3) At different time spans, the incorporation of memory functions, from short term to long term, as well as to im- plement strategies for intensifying and diversifying the search process to give optimal results. a) Intensification strategies, helps in reinforcing and moving combinations and solution features historically that are found good. b) Diversification strategies, drives the search process into new regions as to explore every possible area and region. Distinguishable Features: Short-term Memory and Aggressive Search: Short-term memory constitutes a form for aggressive exploration and captures the best move possible under tabu restrictions. Tabu restrictions prevent the reversal and repetition of certain moves by rendering selected attributes covered in previous moves (forbidden). Primary goal of tabu restriction is to permit the method to go be- yond the points of local optimality during its iterations. Tabu restrictions help in preventing cycles and induce the search to follow a new trajectory, in case if cycling occurs. Tabu Restriction [15]: These are certain conditions which are imposed on moves that make some of the moves forbidden. These forbidden moves, in-turn are listed to a certain size called as tabu. And this list is considered as “tabu list”. The reason behind to denote a move as forbidden is to prevent cycling and avoiding returning to the local optimum that has been visited. In order to identify a good tabu list size, simply watch the occurrence of cycling (if it occurs) when the size of the list is too small and deteriorate the quality of solution when the size of the list is too large which is caused by forbidding too many moves. Remember, that the size of tabu list should grow with the size of the problem. Also it prevents the added edges from being dropped as well as it prevents the dropped edges from being added. A general approach for the tabu search [3,15] is as shown in Figure 1 and the basic elements of TS are as follows: 1) Current solution: it comprises a set of the optimized parameter values for a given iteration. It plays a crucial role in order to generate the neighbor trial solutions. 2) Moves: These are related to current solution and  Test Cost Optimization Using Tabu Search Copyright © 2010 SciRes. JSEA 479 characterize the process of generating the trial solutions. 3) Set of candidate moves: It comprises the set of all possible moves or may be trial solutions. 4) Aspiration Criterion: It is a rule for overriding the tabu restrictions, for example if certain move is forbidden by tabu restriction, aspiration criterion has to be satisfied, once it is satisfied, it can only make this move allowable. One we considered here is to override the tabu status of a move if this particular move yields a solution which has better objective function (let it be J), than the one that was obtained earlier within the same move. The phenomenon behind using aspiration criterion is to add flexibility in the tabu search by directing it towards better moves. 5) Long Term and Short Term Memory: Tabu incor- porate two type of memory long term memory and short term memory. Short term memory stores more recent moves and long term memory keeps all the related moves. 6) Stopping Criterion: When best solution already reached, maximum iterations have been performed and when certain conditions are not meet. 5. Dijkstra Algorithm Dijkstra’s algorithm [16] is a graph search algorithm, that traverses all the nodes and it helps in providing minimum cost path from source to destination node. It is also known as greedy approach and it finds the shortest path between single source to all other nodes. That’s why sometime it is also called as single source shortest path problem. It can also be used for finding costs of shortest paths from a single source node to a single destination node by stopping the algorithm once the shortest path to the destination has been determined. For example: in case of city problem, in which the vertices of the graph represent cities and edge represents the distance between the cities. 6. Proposed Solution (Tabu Search with Dijkstra Algorithm) Since cost and coverage are two important factors in case of testing. Here in our proposed algorithm we are using the Tabu Search concept to resolve both of the issues. The algorithm as shown in the Figure 3. Which we have developed uses tabu search [3,6,15] with the con- cepts of Dijkstra’s Algorithm [16] which will be imple- mented in Aspiration criteria of Tabu Search in order to optimize the cost and generate a minimum cost path with maximum coverage. For fulfilling the desired purpose we are require to inspect the program thoroughly to check the aspiration criteria. For this our software will generates the control flow graph of the statement automatically. Where node represents the statement and link represents the flow of control between the statements. Our algorithm states that in case of fulfilment of all the begin Initialise some current solution Calculate the cost of current solution and store it as best cost Store current solution as new solution Add new solution to tabu list do Calculate neighbourhood candidates Calculate the cost of candidates Store the best candidate as new solution Add new solution to tabu list if (the cost of new solution<best cost) then Store new solution as best solution Store the cost of new solution as best cost endif Store new solution as current solution while NOT Stop Criteria end Figure 1. Basic tabu search algorithm [3] three conditions given in aspiration criteria will move further to next iteration otherwise system goes in backtracking stage. The flow of all related activities is as depicted in Figure 2. 7. General Illustration of Proposed Algorithm In this section we have presented a simple program for the calculation of the ship charge that depends on amount, tax and rush charge. And then we have made its correspond- ing control flow graph. This control graph is taken as input for the software. In the graph, the nodes represent the statements and the edges represent the flow between the statements. The cost for several edges can be calculated by using Halsted’s Software Science [2] or with the prior experience of developer for the application. Case Study: To test the proposed approach we have applied that to the program given in Figure 4, and we will check the solution iteration by iteration. At the end tabu List store the best optimized path in its memory. 1) Figure 5. represents the intial control flow graph. Here node ‘a’, represents the starting node and n repre- sents ending node. Any graph can be provided as input. This algorithm will provide minimum cost and maximum code coverage. 2) Once the algorithm starts, here node ‘b’ is selected to be the next node as its cost is minimum.Same criteria will be used with respect to all other nodes. 3) Here the next node will be chosen as ‘c’ as c is the other node with minimum cost. 4) Here the next node will be chosen as ‘d’. 5) Here the next node will be chosen as ‘n’. 6) In this step the algorithm will backtrack since the path through ‘d’ did not give the least cost path. The next node will be chosen as ‘e’.  Test Cost Optimization Using Tabu Search Copyright © 2010 SciRes. JSEA 480 Start Initialize Tabu list Make candidate list Apply Aspiration Criteria Put recent moves (Short term memory), Put Rest all moves (long term memory) Does it give max coverage in min cost? Back track (stopping criteria) Does it satisfy any two conditions of AC? Enters into Tabu list Enters into Tabu list Figure 2. Flow graph 7) Here the next node will be chosen as ‘f’. 8) Here the next node will be chosen as ‘n’. In this step this algorithm will backtrack since the path through ‘f’ did not give the least cost path. The next node will be chosen as ‘g’. 9) Here the next node will be chosen as ‘h’. 1. Start algorithm For(N:=1; N<=candidate list C1; N++) If 2. Aspiration criteria(Ac)(max. coverage && min. cost && reach to subgoal) 3. Calculate cost 4. Enter in the tabu list Else 5. Backtracking beginning Stopping Criteria (SC)[(max coverage && min. cost)!! (Max. coverage && reach to subgoal) 6. Calculate cost 7. Enter in the tabu list End Figure 3. Proposed algorithm Public double calculate(int amount) { Double rushcharge=0; If(nextday.equals(“yes”)){ Rushcharge=14.50; } Double tax=amount*.0725; If(amount>=1000){ Shipcharge=amount*.06+rushcharge; } Elseif(amount>=200) { Shipcharge=amount*.08+rushcharge; } Elseif(amount>=100) { Shipcharge=13.25+rushcharge; } Elseif(amount>=50) { Shipcharge=9.95+rushcharge; } Elseif(amount>=25) { Shipcharge=7.25+rushcharge; } Else { Shipcharge=5.25+rushcharge; } Total=amount+tax+shipcharge; Return total; End calculate Figure 4. Sample program 10) Here the next node will be chosen as ‘n’. In this step the algorithm will backtrack since the path through ‘h’did not give the least cost path. The next node will be chosen as ‘i’. 11) Here the next node will be chosen as ‘j’. 12) Here the next node will be chosen as ‘n’.In this step the algorithm will backtrack since the path through ‘j’ did not give the least cost path. The next node will be chosen as ‘k’. 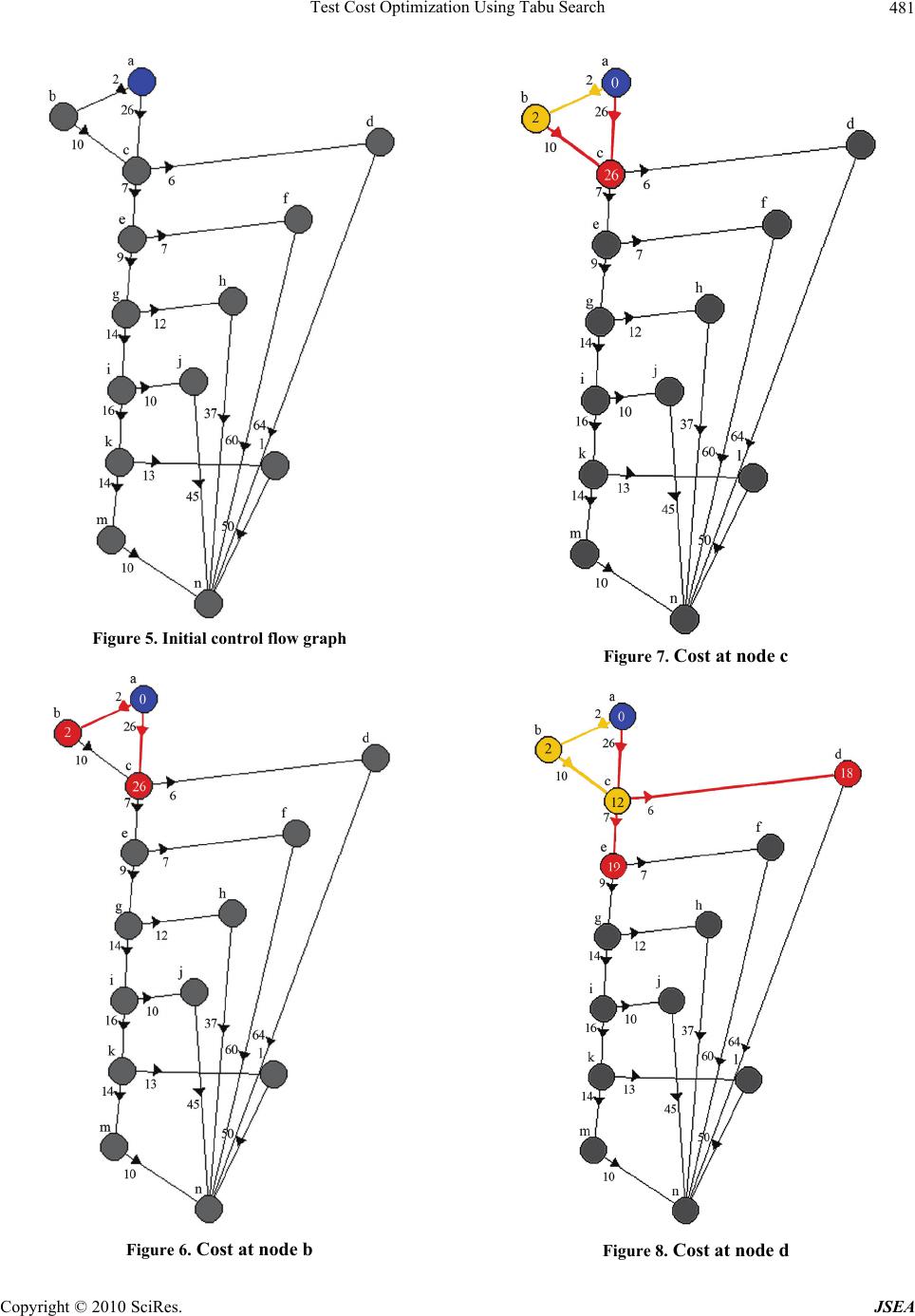 Test Cost Optimization Using Tabu Search Copyright © 2010 SciRes. JSEA 481 Figure 5. Initial control flow graph Figure 6. Cost at node b Figure 7. Cost at node c Figure 8. Cost at node d  Test Cost Optimization Using Tabu Search Copyright © 2010 SciRes. JSEA 482 Figure 9. Cost at node n Figure 10. Cost at node e Figure 11. Cost at node e Figure 12. Cost at node f  Test Cost Optimization Using Tabu Search Copyright © 2010 SciRes. JSEA 483 Figure13. Cost at node g Figure14. Cost at node h Figure15. Cost at node i Figure16. Cost at node j  Test Cost Optimization Using Tabu Search Copyright © 2010 SciRes. JSEA 484 Figure17. Cost at node k Figure18. Cost at node l Figure19. Cost at node m 13) Here the next node will be chosen as ‘l’. 14) Here the next node will be chosen as ‘n’. In this step the algorithm will backtrack since the path through ‘l’ did not give the least cost path. The next node will be chosen as ‘m’. 15) Here the next node will be chosen as ‘n’. Hence in accordance, with the above illustration we conclude that proposed algorithm gives maximum code coverage along with least cost. Hence from the table we can see that in the long term memory all paths have been tested. Tabu list will provide least cost path with maximum coverage in the future if the similar type of module comes for the development then only tabu path can be tested. 8. Conclusions and Further Work This paper presents a meta-heuristic search technique that depends upon the neighborhood solution. There are a lot of real world problems that have been solved by tabu search. Many authors have published their work on tabu search in area of software testing. But this is unique kind of work what we have proposed in this paper solves the problem of cost optimization in software testing. This paper presents use of tabu search with dijksra algorithm (a greedy approach) to provide an efficient path with maxi- mum code coverage and minimum cost. The structure of the paper shows that tabu search de- 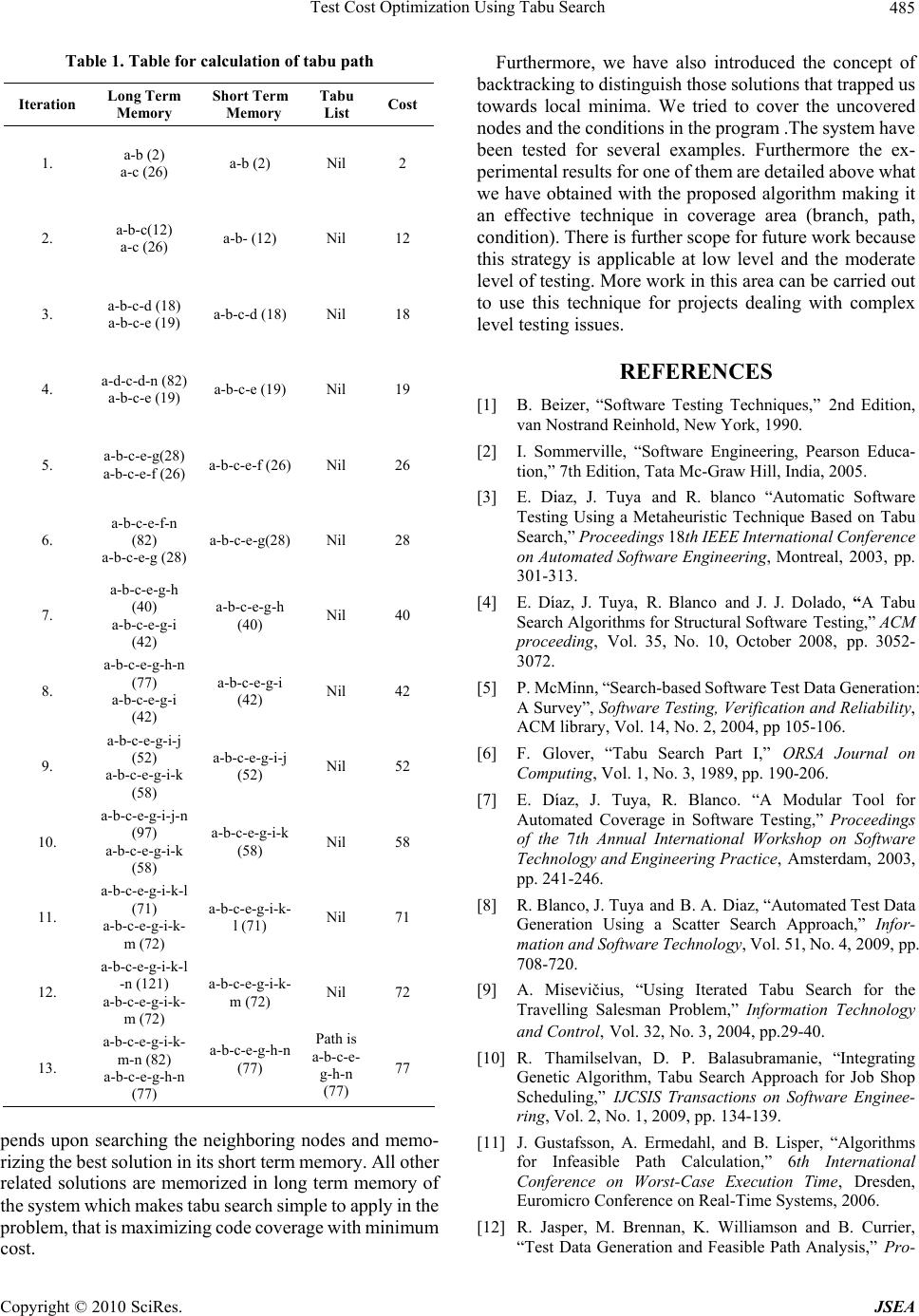 Test Cost Optimization Using Tabu Search Copyright © 2010 SciRes. JSEA 485 Table 1. Table for calculation of tabu path Iteration Long Term Memory Short Term Memory Tabu List Cost 1. a-b (2) a-c (26) a-b (2) Nil 2 2. a-b-c(12) a-c (26) a-b- (12) Nil 12 3. a-b-c-d (18) a-b-c-e (19) a-b-c-d (18) Nil 18 4. a-d-c-d-n (82) a-b-c-e (19) a-b-c-e (19) Nil 19 5. a-b-c-e-g(28) a-b-c-e-f (26) a-b-c-e-f (26) Nil 26 6. a-b-c-e-f-n (82) a-b-c-e-g (28) a-b-c-e-g(28) Nil 28 7. a-b-c-e-g-h (40) a-b-c-e-g-i (42) a-b-c-e-g-h (40) Nil 40 8. a-b-c-e-g-h-n (77) a-b-c-e-g-i (42) a-b-c-e-g-i (42) Nil 42 9. a-b-c-e-g-i-j (52) a-b-c-e-g-i-k (58) a-b-c-e-g-i-j (52) Nil 52 10. a-b-c-e-g-i-j-n (97) a-b-c-e-g-i-k (58) a-b-c-e-g-i-k (58) Nil 58 11. a-b-c-e-g-i-k-l (71) a-b-c-e-g-i-k- m (72) a-b-c-e-g-i-k- l (71) Nil 71 12. a-b-c-e-g-i-k-l -n (121) a-b-c-e-g-i-k- m (72) a-b-c-e-g-i-k- m (72) Nil 72 13. a-b-c-e-g-i-k- m-n (82) a-b-c-e-g-h-n (77) a-b-c-e-g-h-n (77) Path is a-b-c-e- g-h-n (77) 77 pends upon searching the neighboring nodes and memo- rizing the best solution in its short term memory. All other related solutions are memorized in long term memory of the system which makes tabu search simple to apply in the problem, that is maximizing code coverage with minimum cost. Furthermore, we have also introduced the concept of backtracking to distinguish those solutions that trapped us towards local minima. We tried to cover the uncovered nodes and the conditions in the program .The system have been tested for several examples. Furthermore the ex- perimental results for one of them are detailed above what we have obtained with the proposed algorithm making it an effective technique in coverage area (branch, path, condition). There is further scope for future work because this strategy is applicable at low level and the moderate level of testing. More work in this area can be carried out to use this technique for projects dealing with complex level testing issues. REFERENCES [1] B. Beizer, “Software Testing Techniques,” 2nd Edition, van Nostrand Reinhold, New York, 1990. [2] I. Sommerville, “Software Engineering, Pearson Educa- tion,” 7th Edition, Tata Mc-Graw Hill, India, 2005. [3] E. Diaz, J. Tuya and R. blanco “Automatic Software Testing Using a Metaheuristic Technique Based on Tabu Search,” Proceedings 18th IEEE International Conference on Automated Software Engineering, Montreal, 2003, pp. 301-313. [4] E. Díaz, J. Tuya, R. Blanco and J. J. Dolado, “A Tabu Search Algorithms for Structural Software Testing,” ACM proceeding, Vol. 35, No. 10, October 2008, pp. 3052- 3072. [5] P. McMinn, “Search-based Software Test Data Generation: A Survey”, Software Testing, Verification and Reliability, ACM library, Vol. 14, No. 2, 2004, pp 105-106. [6] F. Glover, “Tabu Search Part I,” ORSA Journal on Computing, Vol. 1, No. 3, 1989, pp. 190-206. [7] E. Díaz, J. Tuya, R. Blanco. “A Modular Tool for Automated Coverage in Software Testing,” Proceedings of the 7th Annual International Workshop on Software Technology and Engineering Practice, Amsterdam, 2003, pp. 241-246. [8] R. Blanco, J. Tuya and B. A. Diaz, “Automated Test Data Generation Using a Scatter Search Approach,” Infor- mation and Software Technology, Vol. 51, No. 4, 2009, pp. 708-720. [9] A. Misevičius, “Using Iterated Tabu Search for the Travelling Salesman Problem,” Information Technology and Control, Vol. 32, No. 3, 2004, pp.29-40. [10] R. Thamilselvan, D. P. Balasubramanie, “Integrating Genetic Algorithm, Tabu Search Approach for Job Shop Scheduling,” IJCSIS Transactions on Software Enginee- ring, Vol. 2, No. 1, 2009, pp. 134-139. [11] J. Gustafsson, A. Ermedahl, and B. Lisper, “Algorithms for Infeasible Path Calculation,” 6th International Conference on Worst-Case Execution Time, Dresden, Euromicro Conference on Real-Time Systems, 2006. [12] R. Jasper, M. Brennan, K. Williamson and B. Currier, “Test Data Generation and Feasible Path Analysis,” Pro-  Test Cost Optimization Using Tabu Search Copyright © 2010 SciRes. JSEA 486 ceeding of the International Symposium on Software Testing and Analysis, Seattle, ACM, 1994, pp.95-107. [13] J. Carlos, M. Alberto and Francisco, “A strategy for Evaluating Feasible and Unfeasible Test Cases for The Evolutionary Testing of Object-oriented Software,” 30th International Conference on Software Engineering, Leip- zig, 2008, pp. 85-92. [14] J. C. Lin and P. L. Yeh, “Automatic Test Data Generation for Path Testing Using GAs,” Information Sciences, Vol. 131, No. 1-4, 2006, pp. 2380-2401. [15] F. Glover and M. Laguna, “Tabu Search,” Kluwer Aca- demic Publishers, 1997. [16] “Dijkstra’s Algorithm,” Wikipedia. http://en.wikipedia. org/wiki/Dijkstra’s_algorithm |

