J. Software Engineering & Applications, 2010, 3: 426-435
doi: 10.4236/jsea.2010.35048 Published Online May 2010 (http://www.SciRP.org/journal/jsea)
Mapping UML 2.0 Activities to Zero-Safe Nets
Sabine Boufenara1, Faiza Belala1, Kamel Barkaoui2
1LIRE Laboratory, Mentouri University of Constantine, Algeria; 2CEDRIC-CNAM, Rue Saint-Martin, Paris, France.
Received February 18th, 2010; revised April 6th, 2010; accepted April 6th, 2010.
ABSTRACT
UML 2.0 activity diagrams (ADs) are largely used as a modeling language for flow-oriented behaviors in software and
business processes. Unfortunately, their place/transition operational semantics is unable to capture and preserve
semantics of the newly defined high-level activities constructs such as Interruptible Activity Region. Particularly, basic
Petri nets do not preserve the non-locality semantics and reactivity concept of ADs. This is mainly due to the absence of
global synchronization mechanisms in basic Petri nets. Zero-safe nets are a high-level variant of Petri nets that ensure
transitions global coordination thanks to a new kind of places, called zero places. Indeed, zero-safe nets naturally
address Interruptible Activity Region that needs a special semantics, forcing the control flow by external events and
defining a certain priority level of executions. Therefore, zero-safe nets are adopted in this work as semantic framework
for UML 2.0 activity diagrams.
Keywords: UML Activity Diagrams Formalization, Interruptible Activity Region, Zero-Safe Nets
1. Introduction
The Unified Modelling Language (UML) [1] has recently
undergone a significant upgrade of its basic concepts,
giving rise to a new major version, namely UML 2.0.
Being widely used for specification and documentation
purposes in the software development process, UML
offers a spectrum of notations for capturing different
aspects of software structure and behaviour. Activity
diagram (AD) notations are intended to model behav-
ioural aspects of software systems, particularly control
and data flows.
Activity Diagrams (ADs) are widely used to model
various types of applications fluctuating from basic
computations to high level business processes, embedded
systems and system-level behaviors. They facilitate the
modelling of control and object (or data) flows by intro-
ducing a multitude of new concepts and notations such as
collections, streams, loops and exceptions. Several se-
mantics models have been defined to support these con-
cepts. Nevertheless, many problems persist and reduce the
usability of ADs [2,3]. This is mainly due to the new
constructs and principles complexity and their formal
semantics lack, leading to inconsistent interpretations of
the model. For example, in a workflow process, described
in terms of tasks and execution orders between them,
Termination (or Cancelation) concept may be modeled via
ADs Interruptible Activity Region. This modelling may
have several interpretations since the used modelling
concepts are still informal. Thus, a large gap has to be
bridged prior to obtain an execution model and automated
reasoning.
The abstract semantics of ADs have also completely
changed in UML 2.0. They are no longer considered as a
kind of state-machine diagrams and their semantics is
being well explained in terms of Petri net concepts. But,
basic Petri nets do not preserve semantics of new con-
structs of UML 2.0 ADs. We believe that this is essen-
tially due to the locality character (local activations at
transitions enabling) of basic Petri nets, whilst in UML 2.0,
contrary to UML 1.x, the activation of computational
steps may be not local.
Many attempts are currently led to give UML 2.0 ADs
an operational semantics via some well known formal
models such as high-level Petri nets [4], Abstract State
Machine [5] and so on, for eventual analysis and simula-
tion purposes. The objective of this paper is to describe
how Zero Safe Nets (ZSNs for short) are very suitable to
handle semantics of UML 2.0 ADs Interruptible Activity
Region. ZSN is a new variant of Petri-net model intro-
duced by Bruni [6] to define synchronization mechanisms
among transitions without introducing any new interac-
tion mechanism. On the basis of this formalism, we sug-
gest a set of mapping rules to define a formal semantic of
UML 2.0 ADs complex constructs. ZSNs semantics is
then used to conduct control flow in the net guarantying
atomicity and isolation of a transaction that is all what we
need in the cancellation schema. This formal specification

Mapping UML2.0 Activities to Zero-Safe Nets 427
is precise enough to enable a unique model interpretation
at an utmost detail level. It can therefore serve as tools
implementation basis. Finally, it participates to ensure that
the specified behaviour meets the intended intuition of the
modeller.
The remainder of this paper is structured as follows. A
detailed discussion of related works is given in Section 2.
Section 3 presents syntax and informal semantics of both
Interruptible Activity Region in UML 2.0 ADs and ZSNs.
In Section 4, we describe our contribution by presenting
first the problematic, then the intuitive mapping to address
the Interruptible Activity Region formalization and finally
the formal definition of this mapping. Section 5 concludes
the paper with remarks and outlook on future work.
2. Related Works and Paper Contribution
The state of the art concerning UML 2.0 activity diagrams
semantics covers three different approaches: the first
based on Petri-nets, the second using graph transformation
rules and the third generating pseudo-code. Since the two
latter approaches are out of the scope of the present paper,
we therefore discuss UML 2.0 semantics related work
only in terms of Petri-nets.
Since UML specification envisions a “Petri-like se-
mantics” for activity diagrams, it is quite interesting to
propose a mapping between the two notations. Barros [7]
suggests translating a subset of ADs concepts to Petri nets
ones. Actions considered as activities in Petri nets are no
longer atomic, inducing to ADs semantics violation in the
UML specification standard ([1] p. 203). Moreover, only
locally behaved activities are considered in Petri nets,
whereas non-locality semantics is one major innovative
characteristic of UML 2.0 ADs.
In [8], an AD is transformed into FMC (Fundamental
Modeling Concepts) for their attractive feature, and then,
a Colored Petri net is constructed for execution and vali-
dation purposes. This approach focuses on abstract syntax
and thus, does not preserve semantics, especially for the
atomicity principle.
Störrle uses different variants of Petri nets (from col-
ored to procedural and exception Petri nets) to propose a
formal semantics to UML 2.0 ADs. The author tackles the
formalization of many concepts [9-12] such as control-
flow, procedure calling, data-flow, exceptions, loop-
nodes, conditional-nodes and expansion-regions using
various versions of Petri nets. However, different con-
cepts can generally coexist in the same AD. Therefore,
analysis of the whole system behavior is not possible due
to non-unified formalism.
The development culminates in [13-15] concluding that
Petri-nets might, after all, not be appropriate for formal-
izing activity diagrams. Especially, mapping advanced
concepts, such as interruptible activity regions, is found to
be not intuitive. Moreover, Petri-nets formalization of
ADs concepts is not unified and integrates different
variants of Petri-nets to map concepts belonging to the
same diagram. Additionally the traverse-to completion
semantics insurance is identified as being the major
problem in Petri-nets mapping. In [16], we have proposed
a generic mapping from UML 2.0 ADs to Zero-Safe Nets
(ZSNs) and have shown by several examples how this
Petri net variant can surmount this latter problem. Indeed,
non-locality semantics of ADs is preserved via a global
synchronization, offered by ZSNs, rather than a local one
as in basic Petri nets. In [17], we have been interested by
streaming parameters and exception outputs constructs in
UML 2.0 ADs, their formal semantics has been defined in
terms of these Petri nets variant without losing an impor-
tant characteristic of those concepts that is atomicity.
In this paper, we extend these recent works by im-
proving the proposed mapping to be more formal and
general. Indeed, we examine semantics of Interruptible
Activity Region construct in which actions need to be
promptly cancelled on the reception of an external event.
This can not be provided with basic Petri nets that are
local and not reactive.
3. Basic Concepts
We are interested in this section to remind fundamental
notions used in this study. For more details, the reader
can consult [1,18] (for Interruptible Activity Region in
ADs) and [6] (for ZSNs).
3.1 Interruptible Activity Region
The UML 2.0 specification made by the OMG [1] stan-
dard provides a meta-model to define the abstract syntax
for activity diagrams including Interruptible Activity
Region.
These ADs special regions are groups of nodes where
all execution might be terminated, if an edge traverses an
interruptible activity, before leaving the region. Inter-
rupting edges must have their source node in the region
and their target node outside it, but in the same AD con-
taining the region.
An Interruptible Activity Region is notated by a
dashed, round-cornered rectangle drawn around the
nodes contained in the region. An interrupting edge is
notated with a lightning-bolt activity edge.
During the process of an Interruptible Activity Region,
the reception of an event (exception-event) triggers the
block abort of that part of the Activity, and resumes exe-
cution with another action that may be the excep-
tion-handler. The standard specification [1] states, that
“When a token leaves an interruptible region via edges
designated by the region as interrupting edges, all tokens
and behaviours in the region are terminated”. Interruptible
regions are introduced to support more flexible non-local
termination of flow.

Mapping UML2.0 Activities to Zero-Safe Nets 428
Example 1. Figure 1 gives an example taken from [1]
illustrating these concepts. This example illustrates that if
an order cancellation request ‘Order Cancel Request’ is
made, while executing one of the actions (receive, fill, or
ship orders), the ‘Cancel Order’ behaviour is immedi-
ately invoked and the action being executed is aborted.
Cancellation is a very common behavior in the execu-
tion of workflows process. It is used to capture the inter-
ference of an event or an activity in other activities exe-
cution of a workflow preventing execution or termination.
A cancellation can involve a cancellation area, a sub
process or an entire workflow. In UML 2.0 ADs, Inter-
ruptible Activity Region has been defined to hold such
behavior.
3.2 Introducing ZSNs
Zero-safe nets have been introduced by Bruni in [6] to
define synchronization mechanism among transitions,
without introducing any new interaction mechanism be-
sides the ordinary token-pushing rules of nets. Their role
is to ensure the atomic execution of complex transitions
collections, which can be considered as synchronized.
Atomic execution of multiple coordinated transitions
is forth possible in ZSNs thanks to a new kind of places,
called zero places. From an abstract viewpoint, those
transitions will appear as synchronized. Zero places are
bound to zero tokens in a system observable state. A to-
ken in a zero place is equivalent to a system internal state
that is non-observable. ZSN synchronized evolution must
begin at an observable state, evolve in non-observable
markings and must end at an observable state. Therefore,
ZSNs define two sorts of places; stable places corre-
sponding to net places, and zero places. A ZSN evolution
is considered as a transaction. A stable token generated
in a transaction is frozen all over the evolution; it is re-
leased only once the transaction is finished. We notice
that a transaction in this case, is represented by a system
activity possibly composed of a set of concurrent but
atomic sub-activities.
Zero places coordinate the atomic execution of transi-
Figure 1. Interruptible Activity Region enclosed by a dashed
line. The Interrupting edge is expressed by a lightning-bolt
style
tions which, from an abstract viewpoint, will appear as
synchronized. At the abstract level, we are not interested in
observing the hidden state. Modeling of the well- known
example of ‘dining philosophers’ problem’ is sufficient to
show how ZSNs are powerful to synchronize transitions in
an atomic way (see [19] for more details).
Example 2. (taken from [19]). There are n philoso-
phers (here, we suppose n = 2) sitting on a round table;
each having a plate in front and between each couple of
plates there is a fork, with a total of n forks on the table.
Each philosopher cyclically thinks and eats, but to eat he
needs both the left hand side fork and the right hand one
of his plate. After eating a few mouthfuls, the philoso-
pher puts the forks back on the table and starts thinking
again.
It is not difficult to imagine conflict situations leading
to a deadlock when each philosopher takes one fork and
cannot continue. This is due to the fact that the coordina-
tion mechanism is hidden inside transitions (Take1 and
Take2) that are too abstract (see Figure 2(a) modeling a
centralized non-terminism). Places Fki denote forks. A
token in the place Fki means that the ith fork is on the
table.
The same model is redrawn using free choice nets.
Decisions are now local to each place i.e. decisions are
made independently (see Figure 2(b)) and deadlock
situation is clear. One decision concerns the assignment
of the first fork whether to the first or to the second phi-
losopher, the other decision concerns the assignment of
the second fork. Note that Chi,j stands for Choicei,j where
i denotes Forki and j denotes PHilosopherj. Then, it might
happen that the first fork is assigned to the first philoso-
pher (Ch1,1) and the second fork is assigned to the second
philosopher (Ch2,2), and in such case the free choice net
deadlocks and none of the Takei actions can occur. Thus,
the translated net admits non-allowed computations in
the abstract sub-system of Figure 2(a).
Zero-safe nets surmount this deadlock problem by
executing only some atomic transactions, where tokens
produced in low-level resources are also consumed. In
the example, the ow-level. This is possible, but at the
expense of preseinvisible resources consist of places Fki,j
for 1  i, j  2, that can be interpreted as zero places. In
this way the computation performing Ch1,1 and Ch2,2 is
forbidden, because it stops in an invisible state, i.e., a
state that contains zero tokens (see Figure 2(c)).
While basic Petri nets fail to conserve the system se-
mantics at a low-level, free choice nets make local deci-
sions possible at lrving execution semantics. Zero-safe
nets are able to preserve execution semantics even when
expressed in refined way.
Formal Definitions [6]
A ZSN is a 6-tuple B = (SB, TB, FB, WB, uB, ZB) where NB
= (SB, TB, FB, WB, uB) is the underlying place/ transition

Mapping UML2.0 Activities to Zero-Safe Nets 429
Figure 2. Example of dining philosophers: (a) Centralized
nondeterminisme, (b) Local nondeterminisme presenting
deadlock, (c) Atomic free choice
net. SB is a non-empty set of places. TB is a non-empty
set of transitions. FB  (SB × TB)  (TB × SB) is a set of
directed arcs. WB is the weight function that associates a
positive integer to each arc. uB is the places marking as-
sociating positive tokens number to each place. ZB  SB
is the set of zero places (also called synchronization
places). The places in SB \ ZB are stable places. A stable
marking is a multiset of stable places. The presence of
one or more zero places of a given marking makes it un-
observable, while stable markings describe observable
states of the system.
Let B be a zero safe net and let s = u0[t1>u1…un-1[tn>un
be a firing sequence of the underlying net NB of B,
 The sequence s is a stable step of B if:
 a  SB \ ZB, Σn
i =1 pre(ti)(a) ≤ u0(a)
(Concurrent enabling)
u0 and un are stable markings of B
(Stable fairness)
Pre(t)(a) defines the weight of the arc from place a
input of transition t to this one. Post(t)(a) defines the
weight of the arc from transition t to its output place a. The
concurrent enabling property insures the initial simulta-
neous enabling of all step transitions by stable places and
not only those transitions allowing the initial triggering of
the first execution. We notice that this property prohibits
the consummation of stable tokens produced in the step by
its transitions.
 Stable step s is a stable transaction of B if in addition:
Markings u1,…, un-1 are not stable
(Atomicity)
a  SB \ ZB, Σn
i =1 pre(ti)(a) = u0(a)
(Perfect enabling)
The perfect enabling ensures the consummation of all
initial stable tokens before the transaction ends.
In a stable transaction, each transition represents a mi-
cro-step carrying out the atomic evolution through in-
visible states. Stable tokens produced during the transac-
tion become active in the system, only at the end of the
transaction.
Example 3. Consider the zero-safe net example of
Figure 2(c). The firing sequence {Fk1,Fk 2}(Ch1,1>{Fk1,1,
Fk2} (Ch1,1>{Fk2,2,Fk1,1} is not a stable step since the
stable fairness is not satisfied. The marking {Fk2,2,Fk1,1}
enables no transition, defining hence a deadlock situation.
Since the sequence above is not a stable step and dead-
locks at a non-visible state, so it is forbidden.
The two following firing sequences are the unique sta-
ble transactions:
{Fk1,Fk2}(Ch1,1>{Fk1,1,Fk2}(Ch2,1>{Fk2,1,Fk1,1}(Take1
>{PhE1}.
{Fk1,Fk2}(Ch1,2>{Fk1,2,Fk2}(Ch2,2>{Fk1,2,Fk2,2}(Take2
>{PhE2}.
In what follows, we exploit features offered by
zero-safe nets to define a priority level in ADs actions
executions, leading to the reactivity definition.
4. Handling Interruptible Activity Region
via ZSNs
Formalizing ADs using Petri nets seems to be a good
approach. The specification states that “Activities are
redesigned to use a Petri-like semantics” [1]. Unfort-
unately, basic Petri nets present some limits.
In [16], we have shown that Petri nets, supposed to be
a semantic framework for ADs, are not well suitable to
handle new UML semantics such as traverse-to- comple-
tion principle. Indeed, the latter requires a global synchro-
nisation and not a local one as defined by Petri nets. We
defined a generic mapping from ADs to zero-safe nets that
preserves ADs operational semantics while focusing on
traverse-to-completion principle and synchronization of
fork and join nodes. Therefore, we covered control/data
flows and concurrency. Besides, in [17], we have focused
on semantics of streaming parameters and exception out-
puts, and showed also that ZSNs are able to express such
complex semantics. Atomic transactions have been de-
fined in ZSNs under a token game based on freezing to-
kens that have been created in the transaction until it ends.
This becomes possible thanks to the zero-places.
The contribution of this paper is to define a suitable
mapping of ADs to ZSNs, dealing with more complex
concepts of UML 2.0 ADs, namely the Interruptible Ac-
tivity Region. We show how basic Petri nets are not able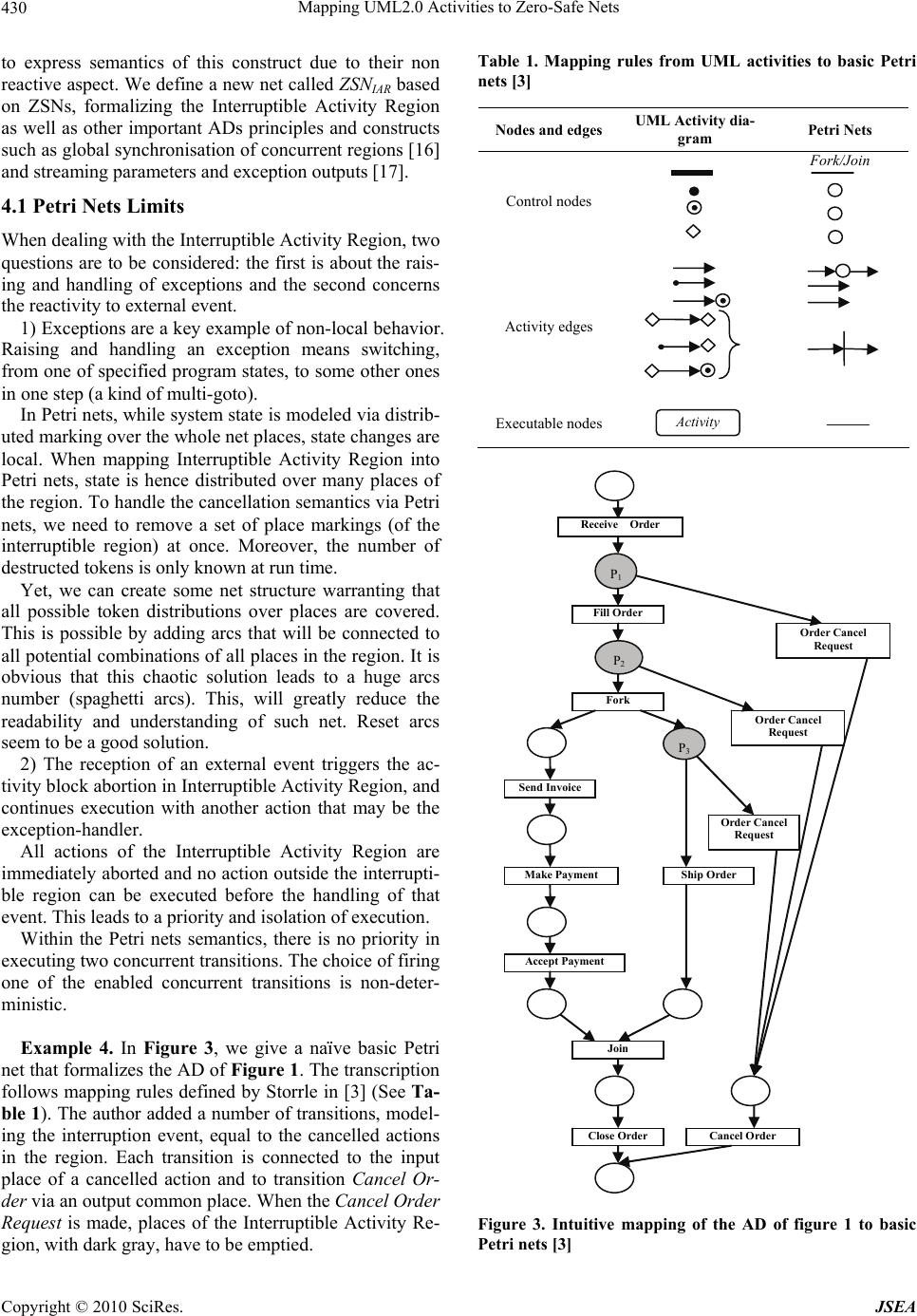

Mapping UML2.0 Activities to Zero-Safe Nets 430
to express semantics of this construct due to their non
reactive aspect. We define a new net called ZSNIAR based
on ZSNs, formalizing the Interruptible Activity Region
as well as other important ADs principles and constructs
such as global synchronisation of concurrent regions [16]
and streaming parameters and exception outputs [17].
4.1 Petri Nets Limits
When dealing with the Interruptible Activity Region, two
questions are to be considered: the first is about the rais-
ing and handling of exceptions and the second concerns
the reactivity to external event.
1) Exceptions are a key example of non-local behavior.
Raising and handling an exception means switching,
from one of specified program states, to some other ones
in one step (a kind of multi-goto).
In Petri nets, while system state is modeled via distrib-
uted marking over the whole net places, state changes are
local. When mapping Interruptible Activity Region into
Petri nets, state is hence distributed over many places of
the region. To handle the cancellation semantics via Petri
nets, we need to remove a set of place markings (of the
interruptible region) at once. Moreover, the number of
destructed tokens is only known at run time.
Yet, we can create some net structure warranting that
all possible token distributions over places are covered.
This is possible by adding arcs that will be connected to
all potential combinations of all places in the region. It is
obvious that this chaotic solution leads to a huge arcs
number (spaghetti arcs). This, will greatly reduce the
readability and understanding of such net. Reset arcs
seem to be a good solution.
2) The reception of an external event triggers the ac-
tivity block abortion in Interruptible Activity Region, and
continues execution with another action that may be the
exception-handler.
All actions of the Interruptible Activity Region are
immediately aborted and no action outside the interrupti-
ble region can be executed before the handling of that
event. This leads to a priority and isolation of execution.
Within the Petri nets semantics, there is no priority in
executing two concurrent transitions. The choice of firing
one of the enabled concurrent transitions is non-deter-
ministic.
Example 4. In Figure 3, we give a naïve basic Petri
net that formalizes the AD of Figure 1. The transcription
follows mapping rules defined by Storrle in [3] (See Ta-
ble 1). The author added a number of transitions, model-
ing the interruption event, equal to the cancelled actions
in the region. Each transition is connected to the input
place of a cancelled action and to transition Cancel Or-
der via an output common place. When the Cancel Order
Request is made, places of the Interruptible Activity Re-
gion, with dark gray, have to be emptied.
Table 1. Mapping rules from UML activities to basic Petri
nets [3]
Order Cancel
Request
Receive Order
Fork
Fill Order
Send Invoice
Ship Order
Accept Payment
Join
Close OrderCancel Order
Order Cancel
Request
Order Cancel
Request
Make Payment
P
3
P
2
P
1
Figure 3. Intuitive mapping of the AD of figure 1 to basic
Petri nets [3]
Nodes and edges UML Activity dia-
gram Petri Nets
Control nodes
Fork/Join
Activity edges
Executable nodes
Activity

Mapping UML2.0 Activities to Zero-Safe Nets 431
We notice that semantics of cancellation (first point)
does not appear in the net: First, the cancel event is not
visible (sketched by transitions Order Cancel Request
that are enabled by internal places) and second, the net is
supposed to be 1-safe.
Regarding the second point mentioned above: when
place p1 is marked, both transitions Fill Order and Order
Cancel Request are enabled and have the same probabil-
ity to fire (situation of effective conflict). Whereas in this
context, we would like to fire the aborting transition, that
is Order Cancel Request.
The ZSNs model offers transitions coordination thanks
to zero places. It guarantees atomicity and isolation of
transaction, and this is all what we need in the cancella-
tion schema. In what follows, we use ZSNs semantics to
conduct the control flow in the net.
4.2 Mapping Intuition
In what follows, we discuss two zero-safe nets based
approaches to formalize AD interruptible region with
regard to semantics via the running example 1.
The first solution introduces reset arcs and no new
mechanism is necessary beyond the zero-safe nets se-
mantics. In the net of Figure 4, we introduce a transition
called ‘cancel’, and then we connect all places in the
Interruptible Activity Region to that transition by a reset
arc for each. The firing of transition ‘cancel’ empties all
its input places at once, regardless of their marking. Thus,
the net is no longer forced to be 1-safe. To overcome the
second shortcoming pointed out, we add an input place
‘interface place’ to transition ‘cancel’. This place repre-
sents the external cancel event. It is connected to transi-
tion ‘cancel’ via an arc of weight 1. When the place ‘in-
terface place’ is marked, the transition ‘cancel’ is enabled.
Possibly, other transitions of the region are enabled at the
same time. We need to guide the control to fire transition
‘cancel’ first. This is known as isolation and atomicity. To
achieve this, we assume that ‘interface place’ is a zero
place and not a stable one, so when marked, transition
‘cancel’ is enabled and immediately fired. This is due to
the enabling property of ZSNs. Then another problem
arises: when combining both solutions i.e. reset arcs and
the interface zero place, enabling of transition cancel is
made via the zero place connected with a non-reset arc.
Thus, if another input place that has to be emptied by
cancel, has an other output transition, it could be possible
to fire that transition first and then ‘cancel’ transition
indeterminably without impeding ZSNs rules. This is
essentially caused by the presence of reset arcs. To
overcome this problem, we can easily create a stable token
in the transaction that is frozen until the transaction ends.
The corresponding place is also an input one to cancelled
transitions via reset arcs. (see Figure4).
In Figure 4, firing the external transition creates one
stable token in the stable place pfreeze and one zero token in
t
2
t
1
external
transition
interface
place
Interruptible Activity Region
Cancel
…
P
freeze
Figure 4. Formal semantics of the Interruptible Activity
Region via ZSNs augmented with reset arcs
interface place. The stable token cannot be consumed
until the transaction ends, hence prohibiting the firing of
the region enabled transitions such as t1 and t2. The unique
transition that satisfies firing conditions is cancel. The
created token in pfreeze can be consumed in the first next
firing not being a cancellation procedure.
It is clear that such construction greatly improves
modeling cancellation patterns and preserves semantics.
However, adopting such technique has its drawbacks; the
number of used reset arcs in this model depends always on
the number of places in the interruptible region. This
reduces considerably the net readability.
In Figure 5, we define a special cancellation transition
cancel (pictured by an underlined rectangle) with its new
enabling and firing semantics. Cancel may have many
stable inputs and one zero input place, that is interface
place. There are two different conditions to enable tran-
sition cancel:
1) Necessary condition but not sufficient to fire cancel:
the input zero place is marked.
2) Effective firing condition: the instantaneous marking
of cancel input places, i.e., input places markings when
the zero token is created. This marking is calculated at run
time, and this one is the enabling marking. Thus, once
firing cancel transition, all of its input places are emptied.
When the zero place is marked (via an external transition),
cancel is enabled, the current marking is then calculated
interface
place
P
2
P
1
Interruptible Activity
Region
Cancel
……
t
1 t
2
E
X
T
E
R
N
S
Y
S
T
E
M
Figure 5. Formal semantics of the Interruptible Activity
Region via ZSNs and a special transition cancel

Mapping UML2.0 Activities to Zero-Safe Nets 432
and is equal to the destroyed tokens. This latter is neces-
sary to the transition firing. Hence, it is forbidden to fire t1
or t2 first. In such case, the cancel firing condition would
not be satisfied leading to a deadlock situation in an in-
visible state (non-observable marking). Firing cancel will
switch, from one of specified program states ({p1}, {p2} or
{p1, p2}), to some other ones in one step.
In our proposed semantics, event triggering cancella-
tion is not formalized via a transition (this should be the
intuition), but via a zero place. Hence, coordinating the
execution of the termination action is made possible.
With basic Petri nets, this is not possible since it is
agreed that an enabled transition can be fired or not, i.e.
firing one of two concurrently enabled transitions is non-
determinitic. With ZSNs, interface place is modeled with
a zero place rather than a stable one. Whenever, an
out-transition (a transition not belonging to the system) is
fired, a zero token is created in the interface place indi-
cating that the system is actually executing a transaction.
Transactions have a higher execution priority compared to
transitions. Hence, firing cancel transition is prior to any
other transition.
Figure 6 presents the mapping of the Interruptible Ac-
tivity Region part of Figure 1. When Ship Order is enabled,
a cancellation event occurs. This is traduced by marking
the zero place interface place. The effective firing condi-
tion of cancel is calculated and it is equal to {interface
place, p3}. Two transitions are now enabled: Ship Order
and Cancel. Firing transition Cancel is prior than transition
Ship Order. Firing Ship Order first, leads to a deadlock
P
3
Interface place
Receive Order
Fill Order
Ship Order
Cancel
Fork
Figure 6. Intuitive mapping of the Interruptible Activity
Region of the AD of Figure 1 to ZSNs
situation (non finishing transaction) caused by the con-
sumption of cancel transition enabling tokens.
4.3 Formal Mapping
Table 2 defines preliminarily hints on formalizing UML
2.0 ADs via ZSNs. This generic mapping covers basic
constructs, concurrent-region, traverse-to-completion pri-
nciple, streaming parameters, exception outputs and the
Interruptible Activity Region.
Executable and fork/join nodes are mapped to transi-
tions. Control nodes become stable or zero places, de-
pending of the synchronization schema to be modeled.
Specific Petri nets models are given in particular cases such
as streaming parameters, exception outputs and the Inter-
ruptible Activity Region. Most of these notations have
already been examined in earlier work. The semantics of
the Interruptible Activity Region is discussed in this paper.
To formalize the mapping, we propose, for both basic
activity diagram AD of UML 1.x and a complete one of
UML 2.0, rigorous notations as given below. Extended
activity diagram AD2 encloses new constructs and se-
mantics, namely object nodes, traverse-to-completion
principle, streaming parameters, exception outputs and
Inturruptible Activity Region. Next, we define a formal
semantic definition of AD2 in terms of ZSNs.
Definition 1:
An activity diagram is defined by a tuple AD = (EN, BN,
CN, iN, fN, CF) where:
EN: denote Executable Nodes, i.e., elementary actions.
EN = {A1, A2, ..., An}.
BN: denote Branch Nodes i.e. decisions and merges.
BN = {d1, ..., dk; m1, ..., mk'}, such as : k  k'.
CN: denote Concurrency Nodes i.e. forks and joins.
CN = {f1, ..., fm; j1, ..., jm'}, such as: m  m'.
iN: denotes the initial Node.
fN: denotes the final Node.
CF: is a function denoting Control Flows. CF  ((EN,
BN, CN, iN)  (EN, BN, CN, fN)). A directed arc sketches
the control flow where the source may be an action, a
branch, a control or the initial node and the arc target
may be an action, a branch, a control or the final node.
Definition 2:
An UML2.0 AD is defined by a tuple AD2 = (AD, ON,
OF, CR, SA, EA, IAR) where:
AD: is the corresponding basic activity diagram as de-
fined above.
ON: denotes Object Nodes. In this work, we deal with
pins. ON = {o1, ..., or}. Objects may represent data or
streams {s1, …, sr' } or exceptions {e1, …, ew'}.
OF: is a function denoting Object (token) Flows. OF
 ((BN, CN, iN, ON)  (BN, CN, fN, ON)). OF =
{of1, …ofx}. As tokens move across an object flow edge,
they may undergo transformations. An object flow might
carry a transformation behavior denoted tb.

Mapping UML2.0 Activities to Zero-Safe Nets 433
Table 2. The intuition of ADs formal semantics via ZSNs:
Zero places are pictured with small circles
CR: denotes Concurrent Regions. A concurrent region
is a sub-AD2 delimited with a fork and a join. Concurrent
regions have a special semantics under the traverse-to-
completion principle. This one has been discussed in [16]
along with a generic mapping to ZSNs.
SA: is a set of Streaming Actions {S1, …, Sr}. A
streaming action is an elementary action Ai with in-
put/output streaming parameters si.
EA: is a set of Exception Actions {E1, …, Ew}. An ex-
ception action is an elementary action Ai having excep-
tion outputs ei.
IAR: denotes Interruptible Activity Regions. An inter-
ruptible region is a sub-AD2 bound to a special specifica-
tion Sp ec that can, informally, be Spec (IAR) = (evt, can-
cel) where evt is the interruption triggering event and
cancel is the cancellation action. We note that evt and
cancel do not belong to the IAR. In the perspective of
cancellation, only actions EN and control nodes CN may
be interrupted, thus the enclosed actions and control
nodes define an IAR. IARi= {Ag, …, Ag', fh, ..., fh'; jv, ...,
jv'}, such that, A, f and j stand respectively for actions,
forks and joins enclosed in the region.
For the sake of the presentation, we restrict our ZSN
definition purpose to control flow, data flow and Inter-
ruptible Activity Region. Let ADIAR be a sub-AD2, such
that, ADIAR = (EN, BN, CN, iN, fN, CF, ON, OF)) and let
Spec be a specification such that:
Spec (IAR) = (evt, cancel). We define ADIAR by identi-
fying, in addition to IAR nodes, the input and output ob-
ject and branch nodes connected to each IAR node via a
control or object edge, including edges. Recall that an
IARi= {Ag, …, Ag', fh, ..., fh'; jv, ..., jv'}.
Next, we define a formal mapping from a sub AD2
ADIAR to a zero-safe net ZSNIAR.
Example 5. Consider the AD of Figure 1: let IAR1 be
IAR1 = {ReceiveOrder, FillOrder, ShipOrder, f1}, where
f1 stands for the fork node and {ReceiveOrder, FillOrder,
ShipOrder}  EN.
We define ADIAR1 by identifying inputs and outputs of
IAR1 nodes. ADIAR1 = {ReceiveOrder, FillOrder, ShipOr-
der, f1, d1, ReceiveOrder, d1, d1, FillOrder, FillOrder,
f1), f1, ShipOrder} where d1 stands for the decision node
and pairs of the form x, y stand for edges such as x is
the edge source and y is its target. Spec (IAR1) = (Or-
derCancelRequest, CancelOrder) where OrderCancel-
Request stands for evt and CancelOrder for Cancel.
Definition 3:
ZSNIAR is a special ZSN defining the semantic of ADIAR,
an UML 2.0 sub activity diagram with the Spec specifi-
cation.
ZSNIAR = (ZSN, SIAR, Zcancel, Cancel, ip, sp) where:
- There is a single source place ip, such that, ip
 SB, ip =.
- There is a single sink place sp, where sp  SB,
ZSNs Nodes
Activities Nodes Basic
Activity
Nodes
Concurrent
Region
Executable Nodes
Object Nodes
Control Nodes
Object Flows
Control Flows
Unless
Except
Exception
Outputs
Streaming Parameters
Events
zero place
Interface
InterruptibleActivityRegion
Zero place
{stream}
{stream}
Activity
Activity
.
.
N
E
synch1
synch2
Cancel
…
interface place
Cancel
{stream}
{stream}
z

Mapping UML2.0 Activities to Zero-Safe Nets 434
sp =.
- Every node n in the instance net is on the path
from ip to sp.
1) Zcancel  ZB: is a set of zero places {zcanc1, …, zcancx},
such that,  zcanci  Zcancel, zcanc

= {canci}
2) SIAR  P. SIAR is a set of places. SIAR = {p  (p  SB)
 (p = n  n  {ADIAR  {BN  ON – {poi of  OF and
of = oi  oi' and tb on of}  {iN, fN}  {pc c 
CF}}}
3) Cancel  T: a set of special transitions {can c1, …,
cancx}, such that, the enabling condition to each transi-
tion canci is the marking of zcanci and the effective firing
condition is the instantaneous marking calculated, when
zcanci is marked. Given a transition canci, the firing se-
quence is given by:
{zcanci, MSIAR}(canci > M'/ zcanci, M'  M'SIAR =  and
canci = {SIAR, zcanci} where MSIAR and M'SIAR respec-
tively stand for SIAR markings before and after firing
canci.
4) ZSN: denotes a zero-safe net, i.e., ZSN = (SB, TB; FB,
WB, uB; ZB) as defined in Section 3.2 such that:
SB = BN  ON – {poi  of = (poi, poi+1) and   tb on
of}  {iN, fN}  {pc c  CF}
For each branch or object node, we create a place.
When two object nodes are connected via an edge not
carrying a transformation behavior, just one place is cre-
ated and takes the name of one of the two (since they
have the same name).
TB = EN  CN  {toi of  OF and of = oi  oi' and
tb on of}  {td id i' of  OF and of = di  di' or cf 
CF and cf = di  di' }  {tm im i' of  OF and of = mi  mi'
or cf  CF and cf = mi  mi' }  Cancel.
Executable and control nodes are mapped into transi-
tions. An object flow gives rise to a new transition iff this
edge carries a transformation behavior. For each control
flow, we define a transition.
FB = {x, y  x, y  CF  (x  TB)  (y  SB)} 
{x, y  x, y  CF  (x SB)  (y  TB)}  {x, y  (x
 TB)  (y  SB)   Ai  x = Ai  y = oi'}.
WB: FB  lN.
ip = iN.
sp = fN.
uB = {iN}
ZB = {evt}, zcanc = evt.
The above definition, mapping an ADIAR to a ZSN, is
faithful to the intuitive mapping given in Table 2. Con-
current regions, streams, and exceptions are not yet taken
into account. The semantics of cancellation is deeply
considered. So far, none of the previous works authors
has considered the problem of reactivity in ADs cancel-
lation behavior.
5. Conclusions
This paper is a continuation of our last two papers [16],
[17]. Their main goal was to propose a generic mapping
of ADs basic concepts to ZSNs ones. Especially, they
handle formalization of concurrent-region, while con-
sidering the traverse-to-completion semantics and excep-
tion outputs streaming parameters via ZSNs.
This paper highlights also the failure of Petri nets to
cover high semantics of ADs, namely the Interruptible
Activity Region. Here, we have proposed, with the same
spirit, the use of ZSNs as a formal semantic framework
to handle this region.
A generic mapping from ADs to ZSNs, covering basic
constructs, concurrent-region, traverse-to-completion
principle, streaming parameters, exception outputs and
the Interruptible Activity Region has been defined. Its
formal definition based on ZSNs covers until now con-
trol flow, data flow and Interruptible Activity Region.
Concurrent region, streaming parameters and exceptions
are not yet covered, but they can be integrated very sim-
ply in the defined ZSNIAR .
Some other constructs namely expansion-region and
exception handling are to be considered in future works.
Our aim is to define an EZS-Net (Extended Zero-Safe
Net) for all new constructs defined in AD2. The EZS-Net
will be dedicated to formalize UML ADs in a complete
and unified way.
ZSNs are tile logic based models which is an extension
of rewriting logic, taking into account the concept of side
effects and dynamic constraints on terms. Mapping
UML2 ADs to ZSNs can be followed by the projection
of these latter in rewriting logic and thus, exploiting its
practical system Maude for verification and validation
aims.
REFERENCES
[1] “OMG Unified Modelling Language: Superstructure,” Fi-
nal Adopted Specification Version 2.0,Technical Report,
Object Management Group, November 2003.
http://www .omg.org
[2] T. Schttkowsky and A. Föster, “On the Pitfalls of UML 2
Activity Modeling,” International Workshop on Modeling
in Software Engineering, Minneapolis, IEEE Computer
Society, 2007.
[3] H. Störrle and J. H. Hausmann, “Towards a Formal
Semantics of UML 2.0 Activities,” Software Engineering
Vol. 64, 2005, pp. 117-128.
[4] T. Murata, “Petri Nets: Properties, Analysis and Appli-
cations,” Proceedings of the IEEE, Vol. 77, No. 4, April
1989, pp. 541-580.
[5] E. Borger and R. Stark, “Abstract State Machines,” Sprin-
ger Verlag, 2003.
[6] R. Bruni and U. Montanari, “Zero-Safe Nets, or Transition
Synchronization Made Simple,” In C. Palamidessi and J.
Parrow, Eds., Proceedings of the 4th workshop on Expre-
ssiveness in Concurrency, Electronic Notes in
Theoretical Computer Science, Santa Margherita

Mapping UML2.0 Activities to Zero-Safe Nets 435
Ligure, Elsevier Science, Vol. 7, 1997.
[7] J. P. Barros and L. Gomes, “Actions as Activities and
Activities as Petri Nets,” In Jan J¨urjens, Bernhard Rumpe,
Robert France, and Eduardo B. Fernandey, Eds., UML
2003 Workshop on Critical Systems Development with
UML, San Francisco, 2003, pp. 129-135.
[8] T. S. Staines, “Intuitive Mapping of UML 2 Activity
Diagrams into Fundamental Modeling,” “Concept Petri
Net Diagrams and Colored Petri Nets,” 15th Annual IEEE
International Conference and Workshop on the Engi-
neering of Computer Based Systems, Belfast, 2008.
[9] H. Störrle, “Semantics of Exceptions in UML 2.0 Acti-
vities,” Journal of Software and Systems Modeling, 9 May
2004. www.pst.informatik.uni-muenchen.de/stoerrle
[10] H. Störrle, “Semantics of Control-Flow in UML 2.0
Activities,” In N.N. Ed., Proceedings IEEE Symposium on
Visual Languages and Human-Centric Computing, Rome,
Springer Verlag, 2004.
[11] H. Störrle, “Semantics and Verification of Data Flow in
UML 2.0 Activities,” Electronic Notes in Theoretical
Computer Science, Vol. 127, No. 4, 2005, pp. 35-52.
www. pst.informatik.uni-muenchen.de/-stoerrle
[12] H. Störrle, “Semantics and Verification of Data-Flow in
UML 2.0 Activities,” Proceedings International Work-
shop on Visual Languages and Formal Methods, IEEE
Press, 2004, pp. 38-52. www.pst.informatik.uni-muench
en.de/_stoerrle
[13] R. Eshuis and R. Wieringa. “Comparing Petri Net and
Activity Diagram Variants for Workflow Modelling–A
Quest for Reactive Petri Nets,” In Weber et al. Petri Net
Technology for Communication Based Systems, Lecture
Notes in Computer Science, Vol. 2472, 2002, pp. 321-351.
[14] R. Eshuis and R. Wieringa. “A Real-Time Execution
Semantics for UML Activity Diagrams,” In H. Hussmann,
Ed., Fundamental Approaches to Software Engineering,
Lecture Notes in Computer Science, Genova, Springer
Verlag, Vol. 2029, 2001, pp. 76-90.
[15] R. Eshuis and R. Wieringa. “An Execution Algorithm for
UML Activity Graphs,” Proceedings of the 4th Interna-
tional Conference on The Unified Modeling Language,
Modeling Languages, Concepts, and Tools, Lecture
Notes in Computer Science, Toronto, Springer Verlag,
Vol. 2185, 2001, pp. 47-61.
[16] S. Boufenara, F. Belala and C. Bouanaka, “Les Zero-Safe
Nets Pour la Préservation de la TTC Dans les Diagrammes
d’activité d’UML, ” “Revue des Nouvelles Technologies
de l’Information RNTI-L-3,” Cépaduès éditions, 15ème
Conférence Internationnale sur les Langages et Modèles à
Objets : LMO, 2009, pp. 91-106.
[17] S. Boufenara, F. Belala and N. Debnath, “On Formalizing
UML 2.0 Activities: Stream and Exception Parameters,”
22nd International Conference on Computers and Their
Applications in Industry and Engineering CAINE-2009,
San Francisco, 4-6 November 2009.
[18] C. Bock, “UML 2 Activity and Action Models,” Part 6:
Structured Activities, 2005. http://www.jot.fm/issues/issue
_2005_05/column4
[19] R. Bruni and U. Montanari, “Transactions and Zero-Safe
Nets,” In: H. Ehrig, G. Juhás, J. Padberg and G. Rozenberg,
Eds., Proceedings of Advances in Petri Nets: Unifying
Petri Nets, Lecture Notes in Com- puter Science,
Springer Verlag, Vol. 2128, 2001, pp. 380-426.