Vol.2, No.1, 388-397 (2010) Natural Science
http://dx.doi.org/10.4236/ns.2010.24047
The multiplicity of particle production from hadron-
hadron and nucleus-nucleus interaction
Ahmed Abdo Ahmed Al-Haydari1, Mohmmed Tarek Hussein2
1Physics Department, Faculty of Applied Science Taiz University, Taiz, Yemen;
2Physics Department, Faculty of Science, Cairo University, Giza, Egypt;
Received 21 October 2009; revised 26 November 2009; accepted 23 February 2010.
ABSTRACT
The particle production in hadron-nucleon (h-N),
hadron-nucleus (h-A) and nucleus-nucleus (A-A)
collisions at high energies are studied in view of
the multi-peripheral model. A multi-peripheral
T-matrix element is assumed with multi surface
parameter that is functionally dependent on the
number of particles in the final state and control
the kinematical path of the reaction. A Monte
Carlo code is designed to simulate events ac-
cording to a hypothetical model, the quark
structure of the interacting nucleons is consid-
ered. The number of possible nucleon collisions
inside the target nucleus plays an important role
in folding the (h-N) to generate the (h-A) and
(A-A) collisions. The predictions of the model
give reasonable agreement with the recently
examined experimental data.
Keywords: Monte-Carlo Generators; Multiplicity
Distribution; Integral Phase Space
1. INTRODUCTION
In the last few years, research work has been concen-
trated on the possible existence of the quark-gluon
plasma phase, considering of unconfined quarks and
gluons at high temperature or high density. In the labo-
ratory, nucleus-nucleus collisions at very high energies
provide a promising way to produce high temperature or
high-density matter. As estimated by Bajorken [1] the
energy density can be so high that these reactions might
be utilized to explore the existence of the quark-gluon
plasma. One of the many factors that lead to an optimis-
tic assessment that matter at high density and high tem-
perature may be produced with nucleus-nucleus colli-
sions is the occurrence of multiple collisions. By this we
mean, a nucleon of one nucleus may collide with many
nucleons in the other and deposit a large amount of en-
ergy in the collision region. In the nucleon-nucleon cen-
ter of mass system, the longitudinal inter-nucleon spac-
ing between target nucleons is Lorentz contracted and
can be smaller than 1 fm in high-energy collisions. On
the other hand, particle production occurs only when a
minimum distance of about 1 fm separates the leading
quark and antiquark in the nucleon-nucleon center of
mass system [2,3]. Therefore when the projectile nu-
cleon collides with many target nucleons, particle pro-
duction arising from the first N-N collision is not fin-
ished before the collision of the projectile with another
target nucleon begins. There are models [4-11] that de-
scribe how the second collision is affected by the first
one. Nevertheless, the fundamental theory of doing that
remains one of the unsolved problems. Experimental
data suggest that after the projectile nucleon makes a
collision, the projectile-like object that emerges from the
first collision appears to continue to collide with other
nucleons in the target nucleus on its way through the
target nucleus. In each collision the object that emerges
along the projectile nucleon direction has a net baryon
number of unity because of the conservation of the
baryon number. One can speak loosely of this object as
the projectile or baryon-like object and can describe the
multiple collision process in terms of the projectile nu-
cleon making many collisions with the target nucleons.
Then, losing energy and momentum in the process, and
emerging from the other side of the target with a much
diminished energy. The number of collisions depends on
the thickness of the target nucleus. Experimental evi-
dence of occurrence of multiple collision process can be
best illustrated with the data of p-A reactions in the pro-
jectile fragmentation region [3,12]. In the present work,
we shall investigate the particle production mechanism
in heavy ion collision by introducing the multi- periph-
eral model [13-16,18] which is based on the phase space
integral to describe the multi-particle production in the
Hadron-Hadron, Hadron-Nucleus and Nucleus-Nucleus
interaction at different energies. In this technique the
many body system is expanded into subsystems, each
one concerns a two body collision where we have used
the matrix element of the multi-peripheral nature whose

A. A. A. Al-Haydari et al. / Natural Science 2 (2010) 388-397
389
parameters are strongly correlated to the final state mul-
tiplicity. The simplified quark-quark interaction picture
is considered to improve the results; we suppose that all
the quarks which constitute the hadrons contribute in the
reaction. It is assumed that each Hadron in the final state
is produced at the specific peripheral surface that is
characterized by a peripheral parameter.
2. THE MULTI-PERIPHERAL MODEL
We start with the initial single state of center of mass
energy s, let us denote by i
t the square of the
4-vectore momentum transferred from the particle a
p
of mass ma to the system of 4-momenta 1n
k with mass
1n
M. This will reduce the many body problem into
1n iterative diagram, each of them has only two par-
ticles in the final state. For example, the ith diagram has
two in the final state, the first one is the particle number
1n, and the other has an effective mass i M, equiva-
lent to the rest of the i particles of the system. The gen-
eral expression for i
t in the center of mass frame of
Ki+1 is Kinematically calculated as,
222 (1)0
(1)
() 2
2cos
i
iaii ai
i
aii
tpk maM Ek
PK 


 
 (1)
where i
K and P(i) are the magnitude of the 3-vector
momentum of a system of i particles and the ith splitted
one, i

and 0
i
k are the scattering angle and the energy
of the system i M. The recursion relations of P(i) and
i
K are given by,
1
1
22
1
2
2
),,(



i
i
i
i
i
iM
mMM
K

(2)
i
a
i
i
i
aM
mtM
P2
),,( 22
)(

 (3)
Figure 1. The basic process diagram of nnba pKpp  1
expressed as a sequence of two particles decay.
and the corresponding energies 0
i
k and )(i
a
E
of the sys-
tem i M are given by,
2
1
220 )( iii KMk  ,sMk nn  0 (4)
2/1
22)()( )( a
i
a
i
amPE  (5)
For the case where ni

, we get
s
mms
Pab
n
a2
),,( 22
)(

 (6)
where a
m and b m are the masses of the initially in-
teracting particles. The function denotes the Lorentz
invariant function which is defined by,
yzzyxzyx 4)(),,( 2  (7)
The phase space integral )(SIn which expresses the
probability of obtaining a final state of n-particles with
total center of mass (C. M)
s
in which energy and
momentum are conserved is given by,
34 2
()........./2() |() |
niiabii
I
sdpEpppTP  


(8)
where )( i pT is the transition matrix element that
represents the transition probability from an initial state
ba pp

to the final state 11  nn PK with the definite
momentum i p. Once the phase space integral is defined,
one can easily find the reaction cross-section as
)()/1( sIF nn


(9)
where F is the flux function defined by,
4222 )2(),,(2 
n
abmmsF
 (10)
If )( i
pxx

is any physical quantity depending on
the pi, the differential cross-section dx
dn

is obtained by
transforming the integral in Eq.8 so that
x
appears as
a variable and then omitting the integration over x. This
can be most simply carried out by inserting the con-
straint )( i pxx

in the integrand as a δ function so
that
3
44
2
(1/) .......()
2
(())|()|
ni
ab i
i
ii
ddp
Fppp
dx E
xxp Tp




 



(11)
The multiperipheral matrix element [17] is introduced
in the form,



1
1
)(
n
iii tgT (12)

A. A. A. Al-Haydari et al. / Natural Science 2 (2010) 388-397
390
The function )( ii tg cuts of large values of i t for in-
stance one may choose
() exp()
ii ii
g
tat (13)
where i a is a peripheral parameter that play an impor-
tant role in converging the particles in phase space and
consequently, control the energy of the particles in final
state. So that the values of i a are adjusted to conserve
the total energy. The energy E
(i) of the particle number i
is related to its rapidity i
y through the relation,
() cosh( ) i
ti
Em y
where t
m is defined by,
22
itt mPm  (14)
so that the total energy of the particles in the final state is
1cosh( )(/)
n
it
n
myddydy 

 (15)
n
i
 , is the function of the parameters i a which should
be compared with the total center of mass energy
s
of
the initial state. We first start with n=1 to get 1
a, which
is inserted again in the case n = 3 to get a2 and so on.
These are repeated sequentially to get the values of the
rest parameters. The integral phase space Eq.8 is then
calculated as,
1
1
33 21
21
2
1111
() 10
1
22
22222 1111
(3) (2)
20 0
11
( ).exp()..............
24
11
..........exp()exp( )
44
nn n
n
Mm t
nnnnn
nnt n
na
Mm tt
tt
aa
IsdMat dtd
MP
dMatdtda tdtd
Pp















 

(16)
The multiple integration in Eq.16 may be solved by
using the Monte-Carlo technique [21-23]. At extremely
high energy, Eq.16 has an asymptotic limit in the form,






)!2(
)(
}
2
{
2
1
)(
2
)1(n
s
ea
ee
P
s
sI
n
n
ta
i
tata
i
a
nii
iiii

(17)
where }{ ii
iiii
ta
i
tata
ea
ee   is the normalization density and
n

is defined by,
ijm
jji ,......1, 



(18)
Let )(i
r
be a group of i-random numbers, 10 )( i
r,
then the invariant mass i
M for a system of i-particles
can be generated according to
)(1
)(
ii
i
ii MrM
   (19)
It means that, the invariant masses vary between the
limits 11   iiii mMM

, i=2,…, n-1 for the special
case where T is constant (no dynamical effect), the mo-
mentum transfer i
t should vary homogeneously be-
tween the two limiting values 
i
t,
i
i
ai
i
aiai KPkEMmt )1(0)1(22 22   (20)
and the Monte-Carlo will generate the t values according
to
()
()
i
iii i
tt rt t

 (21)
The limiting values 
t define the physical region
boundaries of 22 reaction on the Chow-Low plot
shown in Figure 2.
On the other hand, using a multiperipheral form in T
as in Eq.13, we can generate events with anisotropic
behavior so as to satisfy the simulation identity [16].
()
exp( )/exp( )
ii
ii
tt
i
ii iii i
tt
at dtatdtr




then
)}exp())exp()(exp(ln{)/1( )( iiiiii
i
ii tatatarat (22)
The condition Eq.22 will spread the points in a con-
fined Zone in the Chow-Low Plot by cutting of the high
t values. The parameters i
a are directly reproduced
from the comparison with experimental distributions.
2.1. Effect of the Quark Structure
Let use assume that the interaction takes place not with
the interacting particles as a whole but rather among
Figure 2. The basic process at stage i of iteration.

A. A. A. Al-Haydari et al. / Natural Science 2 (2010) 388-397
391
their minute constituent quarks. Neglecting the spin ef-
fect of the quark and considering, for example, πp, sys-
tem as two bags containing, respectively, two and three
quarks each of effective mass q m, we assume that the
reaction goes through one of the following channels:
1) One of the projectile quarks interacts with one of
the target quarks. We use the symbols () and
() to describe the two states of the first channel.
The number of possible permutation of these states is 3.
2) In the second channel, the two projectile quarks
may interact with the three target quarks in a collective
manner. This state is symbolized by () with
only one possible permutations. The square of the cen-
ter-of-mass energy of each state is calculated according
to;
qqaqqba eNNmmNNs 2)(222  (23)
where a N and b N are the number of quarks partici-
pating in the reaction from the target and projectile, re-
spectively; q m is the effective quark mass and q e is
the laboratory energy per quark. The multiplicity distri-
bution )(nF of an n-particle system is calculated in
terms of the distribution functions of the different states
of the reaction. For our example case (π p-system), let us
assume that )(
11 nf and )( 12 nf represent the phase
space integrals of the state () and () for
the first channel, so that the distribution of the first
channel is obtained by a restricted superposition of the
two functions;
11112
()()[(()())(())]
ij
f
nZnfifjnij  

(24)
where the normalization factor, )(nZ is given by
1
() [(())]
ij
Znni j 


 (25)
The second channel has only one state ()
represented by a phase space integral )(
2nf , then the
overall distribution function )( nF is
2211
)( fkfknF  (26)
where 1
k and 2 k are the number of possible permuta-
tions in each channel. The distribution function for any
other physical quantity
x
is simply given by
11 22
()() ()
i
H
xk hxkhx
 (27)
2.1.1. Hadron-Nucleus Collision
On extending the model to the hadron-nucleus or nu-
cleus-nucleus collision, we follow the NN-base super
position as expected from the features of the experimen-
tal data. We should consider the possible interactions
with the nucleons forming the target nucleus t
A. The
incident hadron makes successive collisions inside the
target. The energy of the incident hadron (leading parti-
cle) slows down after each collision, producing a num-
ber of created hadrons each time which depends on the
available energy. The phase space integral In
NA in this
case has the form;
()()(,) ()
tt
AA
NA
nnvvti
vi
I
sIsPvAnn  

 (28)
where ),( t AP

is the probability that ν nucleons out of
t
A will interact with the leading particle and )(


sIn
is the phase space integral of NN collision that produces
hadrons at energy s. The delta function in Eq.28 is to
conserve the number of particles in the final state. All
the nucleons are treated identically, and the NN
X is the
N-N phase shift function [20,24-26]. Then, according to
the eikonal approximation,
(,)( 1){1exp(2Re())}
j
l
t
ttNN
j
Al
pl Ai Alj X
j
l
 
 
 
 

(29)
This approach was then worked out by putting the
multi-dimension integration of Eq.16 and the generated
kinematical variables into a Monte-Carlo program which
was created by the author. This in turn is restored ν
times, where ν is the number of collisions inside the tar-
get nucleus that is generated by a Monte-Carlo Genera-
tor according to the probability distribution Eq.29. In the
first one, the incident hadron has its own incident energy
and moves parallel to the collision axis (0)( 0



axisZ .
The output of the program determines the number of
created hadrons 1
n as well as the energy )( 01 EE

and the direction 1
q of the leading particle. The leading
particle leads the reaction in its second round with 1
E
and 1

as input parameters and creates new number of
2

n and so on. The number
j
n is determined ac-
cording to a multiplicity generator which depends on the
square of the center of mass energy
j
s
in the round
number j:
jNNjEmms 22 2 (30)
3. NUCLEUS-NUCLEUS COLLISIONS
The extension of the multi peripheral model to the nu-
cleus-nucleus case is more complicated. The number of
available collisions is multi-folded due to the contribu-
tion of the projectile nucleons. By analogy of the AN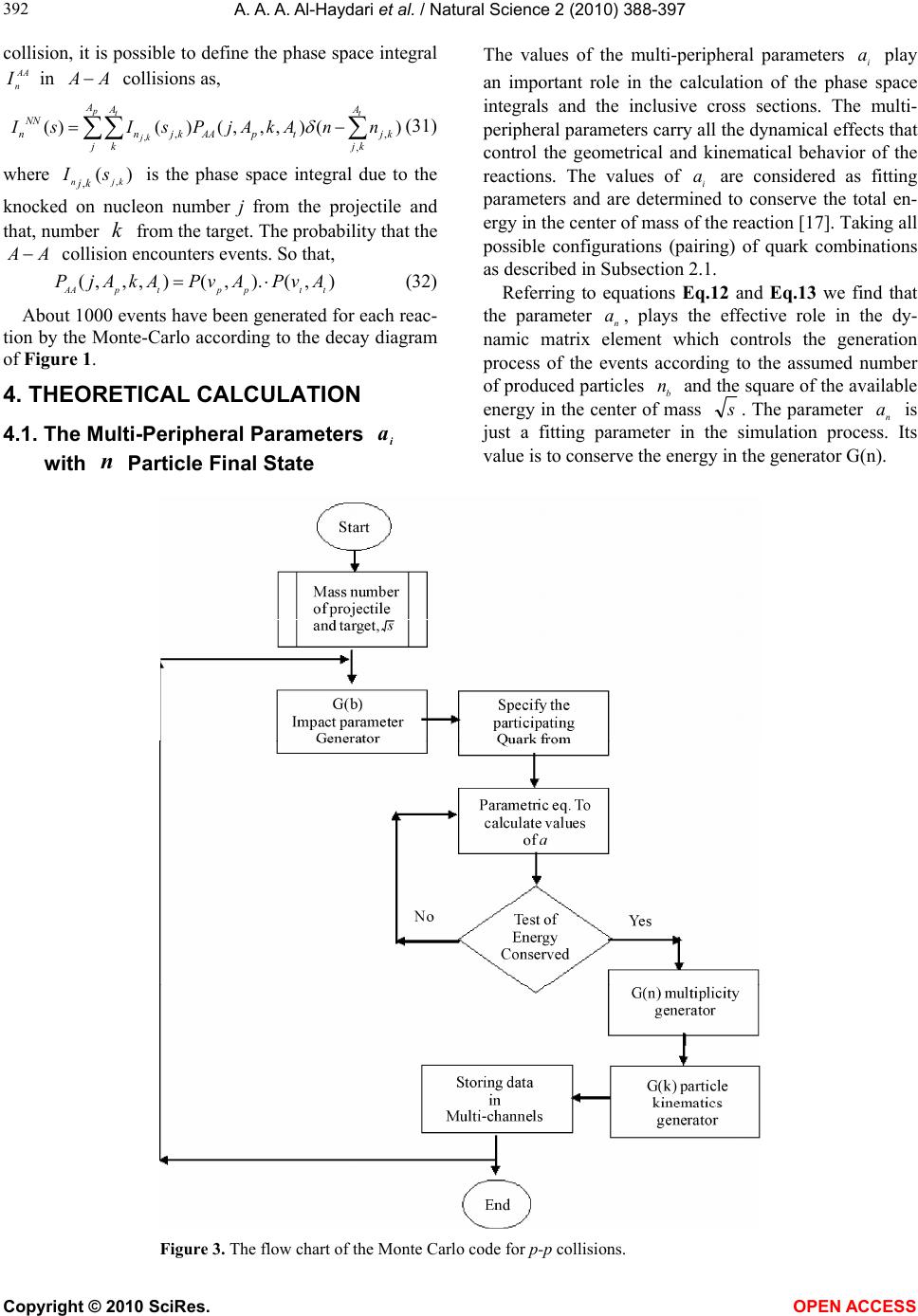


A. A. A. Al-Haydari et al. / Natural Science 2 (2010) 388-397
392
collision, it is possible to define the phase space integral
AA
n
I in
A
A
 collisions as,
,,,
,
()()(,, ,) ()
ptt
jk
AAA
NN
nnjkAAptjk
jk jk
IsIsPjAkAn n  
 (31)
where )( ,
,kjn sI kj is the phase space integral due to the
knocked on nucleon number j from the projectile and
that, number k from the target. The probability that the
A
A
 collision encounters events. So that,
),().,(),,,( ttpptpAA AvPAvPAkAjP  (32)
About 1000 events have been generated for each reac-
tion by the Monte-Carlo according to the decay diagram
of Figure 1.
4. THEORETICAL CALCULATION
4.1. The Multi-Peripheral Parameters i
a
with n Particle Final State
The values of the multi-peripheral parameters i a play
an important role in the calculation of the phase space
integrals and the inclusive cross sections. The multi-
peripheral parameters carry all the dynamical effects that
control the geometrical and kinematical behavior of the
reactions. The values of i
a are considered as fitting
parameters and are determined to conserve the total en-
ergy in the center of mass of the reaction [17]. Taking all
possible configurations (pairing) of quark combinations
as described in Subsection 2.1.
Referring to equations Eq.12 and Eq.13 we find that
the parameter n a, plays the effective role in the dy-
namic matrix element which controls the generation
process of the events according to the assumed number
of produced particles b n and the square of the available
energy in the center of mass s. The parameter n a is
just a fitting parameter in the simulation process. Its
value is to conserve the energy in the generator G(n).
Figure 3. The flow chart of the Monte Carlo code for p-p collisions.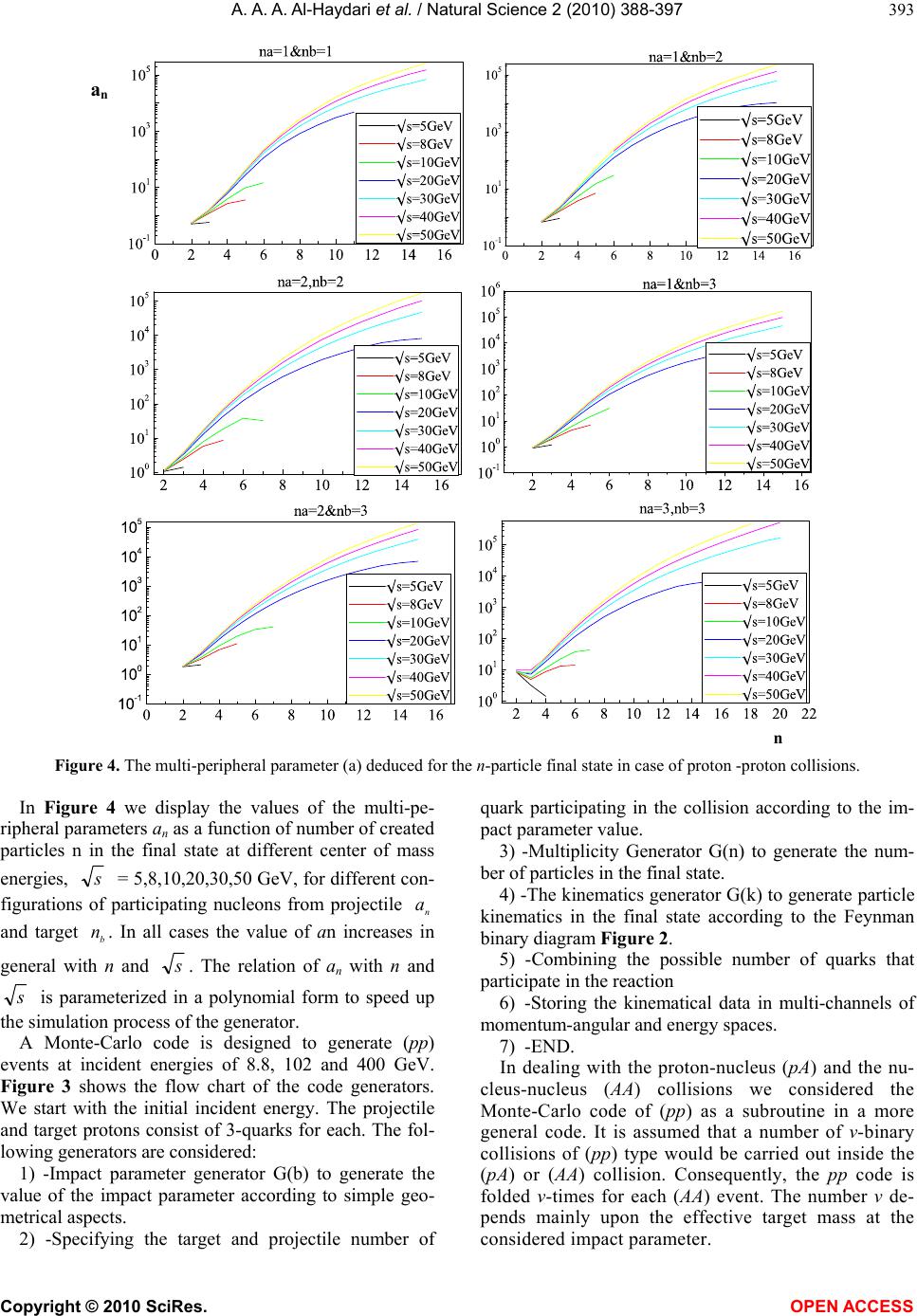

A. A. A. Al-Haydari et al. / Natural Science 2 (2010) 388-397
393
a
n
n
Figure 4. The multi-peripheral parameter (a) deduced for the n-particle final state in case of proton -proton collisions.
In Figure 4 we display the values of the multi-pe-
ripheral parameters an as a function of number of created
particles n in the final state at different center of mass
energies, s = 5,8,10,20,30,50 GeV, for different con-
figurations of participating nucleons from projectile n a
and target b
n. In all cases the value of an increases in
general with n and s. The relation of an with n and
s is parameterized in a polynomial form to speed up
the simulation process of the generator.
A Monte-Carlo code is designed to generate (pp)
events at incident energies of 8.8, 102 and 400 GeV.
Figure 3 shows the flow chart of the code generators.
We start with the initial incident energy. The projectile
and target protons consist of 3-quarks for each. The fol-
lowing generators are considered:
1) -Impact parameter generator G(b) to generate the
value of the impact parameter according to simple geo-
metrical aspects.
2) -Specifying the target and projectile number of
quark participating in the collision according to the im-
pact parameter value.
3) -Multiplicity Generator G(n) to generate the num-
ber of particles in the final state.
4) -The kinematics generator G(k) to generate particle
kinematics in the final state according to the Feynman
binary diagram Figure 2.
5) -Combining the possible number of quarks that
participate in the reaction
6) -Storing the kinematical data in multi-channels of
momentum-angular and energy spaces.
7) -END.
In dealing with the proton-nucleus (pA) and the nu-
cleus-nucleus (AA) collisions we considered the
Monte-Carlo code of (pp) as a subroutine in a more
general code. It is assumed that a number of ν-binary
collisions of (pp) type would be carried out inside the
(pA) or (AA) collision. Consequently, the pp code is
folded ν-times for each (AA) event. The number ν de-
pends mainly upon the effective target mass at the
considered impact parameter.

A. A. A. Al-Haydari et al. / Natural Science 2 (2010) 388-397
394
The Monte-Carlo code is run to the case of p-C col-
lision at 200 GeV. All possible values of a projectile
nucleon participant in the reaction are considered. The
case of 1
p
n and 1
t
n refers to the single nu-
cleon-nucleon collision. It rather happened for the con-
ditions of peripheral interactions. As collision orients
towards the central collision, more target nucleons
contribute to the reaction. Figure 5(a) Shows that the
shower particle production (created particles) increases
with increasing the number of target participant nu-
cleons; where the available center of mass energy in-
creases. The multiplicity distribution of the shower
created particles may fit a Gaussian distribution, the
peak and the dispersion of which shifts forward as t n
increases. The contribution of each t
n value has a
certain weight factor that is related to the impact pa-
rameter weight. Averaging over all possible values of
the impact parameters results in the overall multiplic-
ity distribution that is displayed in Figure 5(b). It was
found that the average value of the charged particle
multiplicity is 4.35 and the dispersion is 1.37557 for
the p-C interaction at 200 GeV. The same procedure is
carried out for the He-Be interaction as an example of
(AA) collision at the same incident energy for the sake
of comparison. In this case both the number of projec-
tile and target participant nucleons p n and t n have
appreciable effect in shaping the charged particle multi-
plicity distributions. The number p n plays the role of
multiplication factor in the production process.
In Figure 6 we demonstrate the family of curves rep-
resenting the results of multiplicity distributions for the
case where all projectile nucleons participate the reac-
tion 4

p
n while parts of the target contribute as t n =
4, 5, 6, 7 and 8.
5. RESULTS AND DISCUSSION
The numerical computation of the charged and negative
charged multiplicity distribution of the outgoing parti-
cles in (p-p) interactions at 8.8 GeV Figure 7, 102 GeV
Figure 8, 400 GeV Figure 9, (p-d) interaction at 28 GeV
Figure 10 and (He-He) interaction at 120 Gev Figure 11
are calculated. A Monte-Carlo program designed by the
authors is used to simulate about 1000 events for each
final state of specific n-values. The multi-peripheral ma-
trix element is used according to Eq.12 to calculate the
phase space integral and the production cross section.
The cut-off boundaries 
i
t of the physical region is
used according to Eq.22.
The proposed model is a statistical model in its nature.
It assumes a large phase space and consequently large
number of quantum states to work in a relevant envi-
ronment.
Figures 7-11 show that the prediction of the model
comes closer to the experimental data as simple as in-
creasing both the available energy and the number of
interacting particles (the size of the target and the pro-
jectile nuclei) that meets with the increase of the volume
of phase space.
Table 1 shows the Chi-square values for the reaction
under consideration to test the validity or the behavior of
the model against the projectile-target size and the en-
ergy of the reaction.
(a) (b)
Figure 5. (a) Multiplicity distributions of the produced particles for 200 GeV proton-Carbon p-C in-
teractions for different number of target participants; (b) Total multiplicity distribution of the produced
particles for 200 GeV p-C interactions.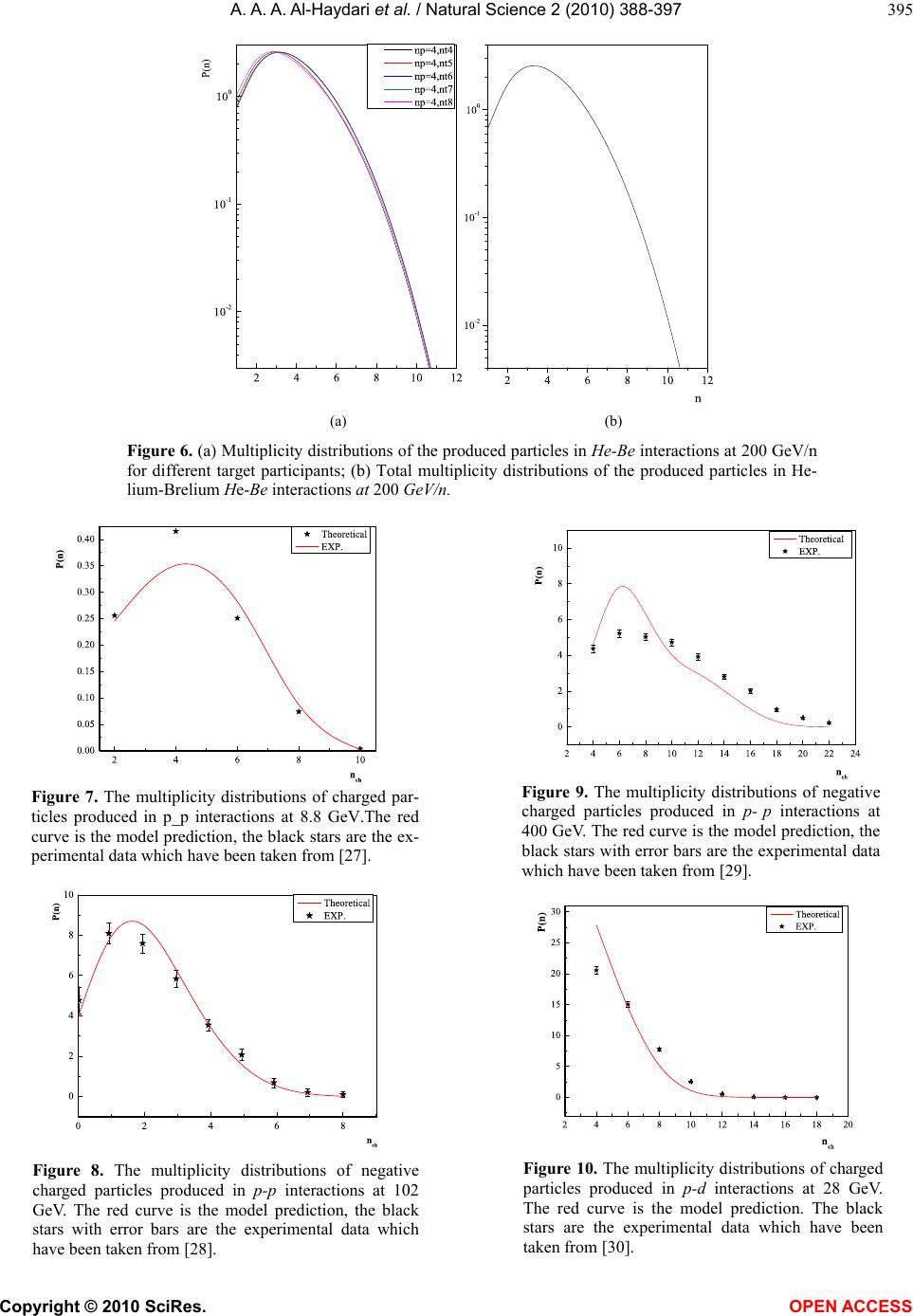

A. A. A. Al-Haydari et al. / Natural Science 2 (2010) 388-397
395
(a) (b)
Figure 6. (a) Multiplicity distributions of the produced particles in He-Be interactions at 200 GeV/n
for different target participants; (b) Total multiplicity distributions of the produced particles in He-
lium-Brelium He-Be interactions at 200 GeV/n.
Figure 7. The multiplicity distributions of charged par-
ticles produced in p_p interactions at 8.8 GeV.The red
curve is the model prediction, the black stars are the ex-
perimental data which have been taken from [27].
Figure 8. The multiplicity distributions of negative
charged particles produced in p-p interactions at 102
GeV. The red curve is the model prediction, the black
stars with error bars are the experimental data which
have been taken from [28].
Figure 9. The multiplicity distributions of negative
charged particles produced in p- p interactions at
400 GeV. The red curve is the model prediction, the
black stars with error bars are the experimental data
which have been taken from [29].
Figure 10. The multiplicity distributions of charged
particles produced in p-d interactions at 28 GeV.
The red curve is the model prediction. The black
stars are the experimental data which have been
taken from [30].

A. A. A. Al-Haydari et al. / Natural Science 2 (2010) 388-397
396
Figure 11. The multiplicity distribution of the particles pro-
duced in He-He interactions at 120 GeV. The red curve is the
model prediction. The black stars are the experimental data
which have been taken from [31].
Table 1. The Chi-square of the reactions.
Reaction Energy Chi-Square
p − p 8.8 GeV 0.005066
p − p 102 GeV 0.004561
p − p 400 GeV 0.822473
p − d 28 Gev 0.034502
He-He 120 GeV 0.000382
5. CONCLUSIONS
The multi-peripheral model is extended to the nu-
cleon-nucleus and the nucleus-nucleus interaction on the
basis of nucleon-nucleon collisions, where the phase
space integral of the nucleon-nucleon and nucleus-nu-
cleus interaction is folded several times according to the
number of encountered nucleons from the target. The
number of created particles in each collision is summed
over to get the production in the nucleon-nucleon case,
where the conservation of number of particles in the
final state is taken into consideration. The inclusive
cross section is calculated and showed a fair agreement
with experimental data.
REFERENCES
[1] Bjorken, J.D. (1983) Principles of opticsoo. Physical
Review D, 27, 140.
[2] Busza, W. and Goldhaber, A. (1984) Nuclear stopping
power. Physics Letters B, 139(4), 235-238.
[3] Barton, D.S., et al. (1983) Experimental-study of the
A-dependence of inclusive hadron fragmentation. Physi-
cal Review D, 27(11), 2580-2599.
[4] Andersson, B., Gustafson, G. and Nilsson-Almqvist, B.
(1987) A model for low-pT hadronic reactions with gen-
eralizations to hadron-nucleus and nucleus-nucleus colli-
sions. Nuclear Physics B, 281(1-2), 289-309.
[5] Nilsson-Almqvist, B. and Stenlund, E. (1987) Interac-
tions between hadrons and nuclei: The Lund Monte
Carlo - FRITIOF version 1.6. Computer Physics Com-
munications, 43(3), 387-397.
[6] Sorge, H., Von Keitz, A., Mattiello, R., Stocker, H. and
Greiner, W. (1990) Energy density, stopping and flow in
10-20 A GeV heavy ion collisions. Physics Letters B,
243, 7-12.
[7] Mattiello, R., et al. (1991) Multistrangeness production in
heavy ion collisions. Nuclear Physics B, 24(2), 221-233.
[8] Wang, X.N. and Gyulassy, M. (1991) HIJING: A Monte
Carlo model for multiple jet production in pp, pA, and
AA collisions. Physical Review D, 44, 3501-3516.
[9] Geiger, K. and Muller, B. (1992) Dynamics of parton
cascades in highly relativistic nuclear collisions. Nuclear
Physics A, 544(2), 467-470.
[10] Geiger, K. (1992) Thermalization in ultrarelativistic nu-
clear collisions I. Parton kinetics and quark-gluon plasma
formation. Physical Review D, 46(11), 4965.
[11] Geiger, K. (1993) Particle production in high energy
nuclear collisions: Parton cascade—cluster hadronization
model. Physical Review D, 47, 133.
[12] Brenner, A.E., et al. (1982) Experimental study of sin-
gle-particle inclusive hadron scattering and associated
multiplicities. Physical Review D, 26, 1497-1553.
[13] Amati, D., Stanghellini, A. and Fubini, S. (1962) Theory
of high-energy scattering and multiple production. Nuovo
Cimento, 26, 896-954.
[14] Hassan, N.M. (2007), Charged particle multiplicity pro-
duced in neutrino-nucleon interactions at high energies.
Scientific Research and Essays, 2(6), 171-176.
[15] Hussein, M.T., Hassan, N. M. and Rabea, A. (1994)
ICTP, Trieste, internal report IC/93/111. Nuovo Cimento
A, 107, 749.
[16] Hussein, M.T. (1993) ICTP, Trieste, internal report
IC/92/166. Nuovo Cimento A, 106, 481.
[17] Byckling, E. and Kajantie, K. (1973) Particle kinematics.
John Wiley and Sons, New York, 190.
[18] Hussein, M.T., Hassan, N.M. and Rabea, A. (1994)
Hadron fragmentation at high energies. Particle World,
4(1), 4.
[19] Hussein, M.T., Hassan, N.M. and Allam, M.A. (1997) A
Multi-cluster model in hadron nucleus interactions at
high energies. Turkish Journal of Physics, 21, 241.
[20] Hegab, M.K., Hussein, M.T. and Hassan, N.M. (1990)
Nucleus-nucleus collisions at high energies. Zeitschrift
für Physik A, 336, 345.
[21] Hussein, M.T. (1996) Monte Carlo simulation for hadron
fragmentation at high energies. Invited Talk, First Inter-
national Conference on Basic Science and Advanced
Technology, Assiut, 9-12 November 1996.
[22] Hussein, M.T., Rabea, A., El-Naghy, A. and Hassan, N.M.
(1995) A string model for hadron interactions at high en-
ergies. Progress of Theoretical Physics Japan, 93(3),
585.
[23] Hassan, N.M., El-Harby, N. and Hussein, M.T. (2000) A
Monte Carlo generator for high energy nucleus-nucleus
collision. Acta Physiologica Academiae Scientiarum Hun-
garicae, 12, 33-46.
[24] Meggiolaro, E. (1998) High-energy quark-quark scatter-
ing and the eikonal approximation. Nuclear Physics B-
Proceedings Supplements, 64, 191.
[25] Pereira, F. and Ferreira, E. (1999) Eikonal profile func-

A. A. A. Al-Haydari et al. / Natural Science 2 (2010) 388-397
397
tions and amplitudes for pp and p¯p scattering. Physical
Review D, 59(1).
[26] Ducati, M.B.G., Goncalves, V.P. (1999) The AGL equa-
tion from the dipole picture. Nuclear Physics B, 557(1),
296-306.
[27] Booth, C.N., Ansorge, R.E. and Carter, J. (1983) Differ-
ences between p¯p and pp interactions at 8.8 GeV/c and
their relationship to p¯p annihilations. Physical Review D,
27, 2018-2040.
[28] Aznauryan, I.G. and Ter-Isaakyan, N.L. (1980) Anoma-
lous magnetic-moments of quarks in magnetic dipole
transitions of hadrons. Soviet Journal of Nuclear Physics,
31(6), 871-875.
[29] Kass, R.D., Ko, W., Lander, R.L., et al. (1979) Charged-
and neutral-particle production from 400-GeV/c pp colli-
sions. Physical Review D, 20(3), 605-614.
[30] Hanlon, J., Panvini, R.S., Walters, J.W., Webster, M.S.
and Morris, T.W. (1979) Multiplicity distributions in
28-GeV/c pd interactions and double scattering in deute-
rium. Physical Review D, 19(1), 49-54.
[31] Akesson, T., Albrow, M.G., Almehed, S., et al. (1982)
Multiplicity distributions in p-α and α-α collisions in the
CERN ISR. Physics Letters B, 119, 464.