Vol.3, No.1, 1-15 (2012) Journal of Bio physical Chemistry
http://dx.doi.org/10.4236/jbpc.2012.31001
Thermodynamic contributions of 5’- and 3’-single
strand dangling-ends to the stability of short duplex
DNAs
Rebekah Dickman1,2, Fidelis Manyanga1, Greg P. Brewood1, Daniel J. Fish1*,
Cameron A. Fish1,3, Charlie Summers1,4, M. Todd Horne1, Albert S. Benight1,2
1Portland Bioscience, Inc., Portland, USA; *Corresponding Author:
2Portland State University, Portland, USA
3Cleveland High School, Portland, USA
4LaSalle Catholic College Preparatory, Milwaukee, USA
Received 27 August 2011; revised 20 October 2011; accepted 11 November 2011
ABSTRACT
Differential scanning calorimetry (DSC) melting
analysis was performed on 27 short double
stranded DNA duplexes containing 1 5 to 2 5 base
pairs. Experimental duplexes were divided into
two categories cont ainin g either t wo 5’ dangling-
ends or one 5’ and one 3’ dangling-end. Duplex
regions were incrementally reduced from 25 to
15 base pairs with a concurrent increase in
length of dangling-ends from 1 to 10 bases.
Blunt-ended duplexes from 15 to 25 base pairs
served as controls. An additional set of mole-
cules containing 21 base pair duplexes and a
single four base dangling-end were also exa-
mined. DSC melting curves were measured in
varying concentrations of sodium ion (Na+). From
these measurements, thermodynamic parame-
ters for 5’ and 3’ dangling-ends were evaluated
as a function of dangling end length. 5’ ends
were found to be slightly stabilizing but essen-
tially constant while the 3’ ends were desta-
bilizing with increasing length of the dangling-
end. 3’ ends also display a stronger depen-
dence on Na+ concentration. In lower Na+ en-
vironment, the 3’ ends were more destabilizing
than in higher salt environment suggesting a
more significant electrostatic component of the
destabilizing interactions. Analysis of thermo-
dynamic parameters of dangling ended dup-
lexes as a function of Na+ concentration indicated
the 3’ dangling ends behave differently than 5'
dangling ended and blu nt-ended duplexes. Mole-
cules with one 5’ and one 3’ dangling end showed
variation in excess specific heat capacity (Cp)
when compared to the blunt-ended molecule,
while the molecules with two 5’ ends had Cp
values that were essentially the same as blunt-
ended duplexes. These observations suggested
differences exist in duplexes with 3’ and 5’
dangling ends, which are interpreted in terms of
composite differences in interactions with Na+,
solvent, and terminal base pairs of the duplex.
Keywords: DNA Thermodynamics; Dangling-Ends;
DNA Stability
1. INTRODUCTION
The generic scheme for the design of optimum probes
for use in multiplex hybridization reactions involves two
independent alignment and comparison steps [1-3]. In
the first step, all possible probes of a given length cover-
ing the targeted region of interest are generated and com-
pared with one another in a pairwise fashion. All possible
pairs of strands are aligned in an antiparallel manner and
the thermodynamic stability is determined for each align-
ment. In this process, the first alignment of two strands
of the same length is the maximally overlapped one, with
no single strand dangling ends. In subsequent alignments,
one strand slides incrementally across the other, one base
at a time, in the 5’ direction. Stability of the duplex at
each alignment is determined from the number of com-
plementary base pairs and mismatches in the overlap
(duplex) region, and the contribution of the two 5’ dan-
gling ends (both of the same length) on the ends of the
duplex [4]. For each alignment, the length of the dan-
gling ends increases with concomitant shortening of the
overlap duplex region. Once all possible strands have
been aligned and compared, and thermodynamic results
processed, the optimum probe set can be determined.
During the second stage of probe design, the optimum
probe set must be scanned against the entire genome in

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15
2
which the target sequence resides [5-7]. In this step, the
shorter (probe) strand is iteratively scanned against the
much longer (target genome) strand, which offers a 5’
dangling end and 3’ dangling end at each alignment step.
The primary aim of this work was evaluation of the
thermodynamic contributions of the dangling single strand
ends to duplex stability. If this is achieved, a more realis-
tic thermodynamic stability can be determined at each
alignment through inclusion of better thermodynamic
parameters for the 5’ and 3’ dangling ends.
In this study, the relative contributions of 5’ and 3’
dangling ends to overall duplex stability as a function of
end length were quantitatively evaluated. Results ob-
tained in three Na+ environments indicate 5’ ends were
stabilizing while 3’ ends were neutral or destabilizing.
Use of how evaluated parameters augment duplex stabil-
ity calculations is demonstrated.
2. MATERIALS AND METHODS
2.1. DNA Molecules
DNA strands for duplex molecules were purchased
from Integrated DNA Technologies (IDT, Coralville, IA)
and subjected to the standard desalting protocol per-
formed by the supplier. As part of the design process, all
sequences were inspected for potential intramolecular
hairpin formation using the IDT oligoanalyzer [8]. Se-
quence composition for the duplex was maintained around
50% G-C base pairs and thermodynamic screening was
used to remove any molecules with potential intramole-
cular structures above 20˚C. DNA strands were received
from the supplier as a dried powder.
2.2. Quantification of Samples
DNA solutions for DSC melting curves were solvated
with NaCl (85, 300 or 1000 mM) and buffered in 10 mM
Na2PO4 and 0.1 mM EDTA. Solution pH was adjusted to
7.3 ± 0.1 using an Orion 4-Star pH/Conductivity Meter
(Thermo Electron Corporation, Beverly, MA). Further
details of buffer preparation have been described else-
where [9,10]. Samples were initially hydrated with 2.0
mL of 85 mM buffered sodium solution and allowed to
stand for at least one hour at room temperature. Concen-
trations of diluted single strand DNAs were determined
by absorbance at 260 nm (A260) using the molar extinc-
tion coefficient provided by the supplier [11,12]. DNA
samples were diluted with buffer so that A260 values
ranged from 0.2 - 0.9 optical density (OD) units. Ab-
sorbance measurements were made using a Hewlett-
Packard 8452A Diode Array Spectrophotometer (Hew-
lett-Packard Corporation, Palo Alto, CA). Quartz cu-
vettes having 1.0 cm path lengths were used. After con-
centration determination, single strands were mixed in a
1:1 ratio and the final duplex concentration adjusted with
buffer to around 1.0 mg/ml. Duplexes were annealed at
room temperature for at least one hour prior to duplex
characterization and melting experiments. After initial
mixing, the A260 was noted and compared to the A260
value measured at higher temperatures well above the
melting transition. This value was then used to estimate a
suitable molar extinction coefficient for the duplex. Sub-
sequently, duplex concentrations were determined from
the low and high temperature A260 values.
2.3. Buffer Exchange
To change the ionic strength of the buffer, sample
solutions were transferred to a DNA Centricon YM-3
centrifugal filter (Millipore, Bedford, MA) having a
molecular weight cut-off of 3000 Daltons. Samples were
washed with 2 ml of nanopure water and spun for
approximately 90 minutes at 4000 - 4500 rpm. An addi-
tional 1 ml of nanopure water was added and the sample
spun to dryness. Recovered samples were reconstituted
in the desired buffer solution and stored at 4˚C.
Following buffer exchange, sample concentrations were
determined using optical absorbance measurements at
260 nm. Generally sample recovery was greater than
95%. A comparison of pre- and post-transition duplex
absorbance values was used to assess possible degrada-
tion. Sample quality was also determined by polyacryla-
mide gel electrophoresis. Electrophoresis was performed
on 12% polyacrylamide gels using a Hoeffer MiniVE,
vertical electrophoresis mini gel system. Other details of
DNA quantification protocols have been described else-
where [6,13,14].
2.4. Differential Scanning Calorimetry
Thermodynamic parameters, ΔHcal and ΔScal, of the
heat induced melting transitions of duplex DNAs were
evaluated from measurements of the excess heat capacity,
ΔCp, versus temperature values obtained by DSC
measurements over the range of 10˚C to 120˚C. ΔCp
values were made using a Nano-Differential Scanning
Calorimeter (Calorimetry Sciences Corporation, Provo,
UT). The instrument utilizes a two-cell design and
electronic comparison scheme to measure excess heat
capacity of a sample as it is heat denatured. Prior to
loading, samples were degassed by bubbling with helium
gas for 10 minutes. Experiments were performed under
positive pressure (3 atm) with a heating rate of 2.0˚C/min.
Concentrations of melted DNA samples were between
0.5 and 1.2 mg/ml. Multiple heating and cooling curves
were collected for each sample and analyzed individually.
Three different DSC instruments were used to collect the
data. Variations in the thermodynamic parameters re-
sulting from small differences in different DSC cell

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15 3
volumes were within experimental error (<10%). Re-
gardless of the direction of transition (heating or cooling)
or DSC employed, all melting curves were highly
reproducible. Prior to measuring samples, a standard
curve (i.e. buffer versus buffer curve) was taken at the
same heating rate, over the same temperature range and
at the same buffer concentration as sample melting
curves. These curves were used to standardize subsequent
DSC sample curves.
2.5. Data Analysis
Analysis of DSC data was performed using the CpCalc
2.1 (Applied Thermodynamics, Middlesex, NY) software
package supplied by the manufacturer. After being stan-
dardized for machine noise by the buffer-buffer curve,
ΔCp versus temperature curves were normalized for total
DNA strand concentration, molecular mass, cell volume
and partial specific volume. A progressive polynomial
baseline was fit to connect linear regions in the lowest
and highest temperature portions of the curve to allow
for curve integration. The integrated area under the curve
provided a measurement of the calorimetric transition
enthalpy, ΔHcal, given by

2
1
d
T
cal p
T
H
CT T
. (1)
For all DSC melting experiments performed,
values were measured from T1 = 10˚C to T2 =
120˚C. The corresponding calorimetric entropy, ΔScal,
was determined by dividing by the tempera-
ture and integrating over the same temperature range.

p
CT

p
CT

2
1
d
Tp
cal T
CT
ST
T


. (2)
Reported values of the calorimetric free-energy,
, were then determined at T = 298.15 K using
the Gibb’s relation,

cal
GT
cal calcal
GHTS. (3)
In the analyses performed, it was assumed that the
overall difference in excess heat capacity from the be-
ginning to the end of the melting transition was negligi-
bly small, (i.e. 1pp
~ 0). Consequences
of this assumption are that evaluated thermodynamic
parameters are most accurate in the transition region and
that the parameters are temperature independent.
 
2
CT CT
2.6. Sequence Design
Short DNA molecules were used to evaluate the ther-
modynamic contributions of single strand dangling ends
on overall duplex stability. Duplexes were grouped into
three sets according to the orientation of their dangling
ends with respect to the core region. By design it is im-
plicitly assumed the molecules studied can be partitioned
into two separate regions: 1) a duplex region (of length
nD) and 2) single strand dangling ends (of length nL).
Explicit sequences are shown in Table 1. Blunt-ended
control sequences, designated as set I, are shown in the
column on the left. These core sequences range in length
from 25 to 15 base pairs. Two types of single strand dan-
gling ended molecules are also shown in Table 1. The set
II molecules (center column) contain two 5’ dangling
ends (5’/5’) and the set III molecules (right column) con-
tain one 5’ and one 3’ dangling end (5’/3’). For all mole-
cules of the same nD, the duplex sequence was main-
tained to allow for relative thermodynamic calculations.
In order to eliminate variations due to end stacking, the
final (terminal) base pair at each end of the duplex was
kept constant along with the initial base of the dangling
end. Although core sequences were not identical, efforts
were made to keep the composition of the duplex con-
stant at 50% GC as the length of the central region was
decreased.
Duplex molecules shown in Ta b l e 1 are composed of
two annealed single strands. For set II molecules the
length of each strand was maintained at 25 base pairs.
Here, the duplex region was decreased incrementally
while the length of 5’ single strands on both ends was
increased. Ten different dangling-ended sequences were
studied with nD ranging from 24 to 15 base pairs and nL
ranging from 1 to 10 bases. Likewise, for set III mole-
cules, as duplex length decreased, the length of 5’ and 3’
dangling ends increased. To accomplish this, one strand
was lengthened while the other shortened. Six different
dangling ended sequences were studied with nD ranging
from 24 to 17 base pairs and nL ranging from 1 to 8 bases.
An additional set of molecules was employed to assess
the additive properties of thermodynamic parameters
found for dangling ended sequences. They are referred to
as set IV molecules and are shown in Table 2. Briefly,
they are the half molecules of set II and set III DNAs
with a duplex core of 21 base pairs and a four base dan-
gling end from one of the strands. For completeness, all
four possible orientations of placement of the dangling
end were included.
3. RESULTS
3.1. Dangling Ends
Thermodynamic parameters measured as a function of
sodium ion concentration ([Na+]) are listed in Table 3 for
the 27 duplexes studied. Plots of ΔH versus TΔS were
linear with a mean correlation coefficient of R2 = 0.96 for
all molecules in the three Na+ environments (see Sup-
plementary Figure 1). Such a high linearity is typically
observed for short duplex melting and indicates entropy-
nthalpy compensation. Although not fully understood, e

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15
4
Table 1. DNA sequences and controls. Set I duplexes are blunt-ended control molecules. Set II molecules show the duplexes in the
first column (i.e. set I) having 5’ dangling ends on both strands of the duplex. For clarity, only sequences of the dangling ends are
shown explicitly. The core duplex regions, matching the molecules of set I, are indicated by dashed lines. Sequences of set III mole-
cules are given in the third column. For all molecules having a 5’ overhang, the terminal 5’ stack identity is retained (5’AC/3’G). For
those having a 3’ overhang, the terminal 3’ stack is retained as (5’C/3’AG).
I II III
Control Sequences nD 5’/5’ Sequences nL5’/3’ Sequences
5’ CATCATCGAACTCAGGTCTCACTTG
3’ GTAGTAGCTTGAGTCCAGAGTGAAC 25
5’ CATCATCGAACCAGGTCTCACTTG
3’ GTAGTAGCTTGGTCCAGAGTGAAC 24 5’ A------------- -------------A 15’ A-------------A -------------
5’ CATCATCGACCAGGCTTCACTTG
3’ GTAGTAGCTGGTCCGAAGTGAAC 23 5’ GA------------ ------------AG 25’ GA------------AG ------------
5’ CAAGTGATCGCTGAGAGAGTTG
3’ GTTCACTAGCGACTCTCTCAAC 22 5’ AGA----------- -----------AGA 35’ AGA-----------AGA -----------
5’ CATGTGATCGCTAGTGAGATG
3’ GTACACTAGCGATCACTCATC 21 5’ TAGA---------- ----------AGAT 45’ TAGA----------AGAT ----------
5’ CATCTCACAGCGATCACTTG
3’ GTAGAGTGTCGCTAGTGAAC 20 5’ CTAGA--------- ---------AGATC 5
5’ CATCTCACAGCGTAACTTG
3’ GTAGAGTGTCGCATTGAAC 19 5’ CCTAGA-------- --------AGATCC 65’ CCTAGA--------AGATCC --------
5’ CATCACAGGCGTTACATG
3’ GTAGTGTCCGCAATGTAC 18 5’ TCCTAGA------- -------AGATCCT 7
5’ CATCCGACTCTGCAATG
3’ GTAGGCTGAGACGTTAC 17 5’ ATCCTAGA------ ------AGATCCTA 85’ATCCTAGA------AGATCCTA ------
5’ CATTCGAAGTCCAGTG
3’ GTAAGCTTCAGGTCAC 16 5’ GATCCTAGA-----
-----AGATCCTAG 9
5’ CATAGCTGCACGTTG
3’ GTATCGACGTGCAAC 15 5’ TGATCCTAGA----
----AGATCCTAGT 10
Table 2. Sequences for set IV molecules. Duplex sequences
with either one 3’ or 5’ dangling end and one blunt end. The
dashed duplex region is given by the duplex sequence shown in
Table 1 for nD = 21 and nL = 4.
IV Sequences nD n
L
a 5’ TAGA----------
---------- 21 4
b 5’ ----------
----------AGAT 21 4
c 5’ ----------TAGA
---------- 21 4
d 5’ ----------
TAGA---------- 21 4
such behavior is reportedly typical for melting of short
duplex DNAs [1-3]. Apparently there is only a slight
dependence of the slopes and intercepts on the concen-
tration of sodium ions.
3.2. Thermodynamic Contributions to
Duplex Stability
From the data of Table 3, quantitative estimates can be
made on thermodynamic contributions of both 5’ and 3’
dangling ends to duplex stability. The melting thermo-
dynamics of short blunt-ended duplexes can be predicted
with reasonable accuracy using the nearest-neighbor (n-n)
model and corresponding sets of sequence dependent
stability parameters [4,5]. The n-n model assumes the
duplex region for a dangling ended molecule has the
same calculated thermodynamic stability as the matching
blunt ended duplex. Thus, the thermodynamic parameters
of short duplex DNAs can be reliably parsed into two
distinct contributions, those from the duplex region, and
those from dangling ends. Following this principle, by
preserving the duplex region and varying only the se-
quences of the dangling ends, it should be possible to
determine individual contributions from dangling ends.
Of course, reliability of this estimate assumes that inter-
actions between the duplex and single strand regions are
separable as described, and that the duplex region and
inherent structure and stability remain unaffected (in a
thermodynamic sense) by the presence of dangling ends.
3.3. Thermodynamic Characterization
Given the set of DNA molecules and thermodynamic
arameters evaluated, and under the umbrella of the afo- p

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15 5
Table 3. Measured Thermodynamic Parameters for sets I, II and III molecules in 85 mM, 300 mM, and 1.0 M Na+ salt environments.
Average errors for duplexes in all [Na+] were: ΔH = 4.2 kcal/mol, ΔS = 9 e.u., ΔG = 0.7 kcal/mol.
85 mM 300 mM 1.0 M
nL n
D ΔH kcal/molΔS e.u. ΔG25 kcal/molΔH kcal/molΔS e.u.ΔG25 kcal/molΔH kcal/mol ΔS e.u. ΔG25 kcal/mol
0 25 –186.9 –530.8 –28.6 –192.3 –544.3–30.0 –205.2 –578.9 –32.6
0 24 –171.3 –500.0 –22.2 –169.6 –481.8–25.9 –181.6 –508.3 –30.0
0 23 –159.2 –462.5 –21.3 –146.5 –414.8–22.8 –157.5 –440.3 –26.2
0 22 –151.9 –444.5 –19.4 –149.4 –426.8–22.1 –153.9 –433.3 –24.8
0 21 –142.3 –410.9 –19.8 –152.5 –440.0–21.3 –156.3 –444.0 –23.9
0 20 –138.7 –406.0 –17.7 –137.3 –394.3–19.8 –137.2 –389.3 –21.1
0 19 –130.2 –381.9 –16.4 –129.2 –372.2–18.2 –129.5 –368.9 –19.5
0 18 –121.8 –357.9 –15.1 –121.1 –350.2–16.7 –121.8 –348.4 –18.0
0 17 –109.7 –322.3 –13.6 –122.2 –353.3–16.8 –121.0 –346.8 –17.6
0 16 –103.3 –305.8 –12.1 –91.9 –269.5–11.6 –98.8 –286.8 –13.3
I Controls
0 15 –96.3 –285.7 –11.1 –96.8 –284.0–12.2 –98.8 –287.0 –13.2
0 25 –186.9 –530.8 –28.6 –192.3 –544.3–30.0 –205.2 –578.9 –32.6
1 24 –185.0 –525.8 –28.2 –191.1 –542.5–29.3 –190.2 –535.0 –30.7
2 23 –179.3 –510.8 –27.0 –183.0 –519.3–28.2 –184.6 –517.0 –30.4
3 22 –171.9 –491.5 –25.4 –180.5 –515.5–26.8 –182.8 –513.8 –29.6
4 21 –161.5 –459.1 –24.6 –163.2 –457.9–26.7 –169.6 –469.8 –29.5
5 20 –161.5 –464.8 –22.9 –148.7 –429.5–20.7 –162.8 –460.0 –25.7
6 19 –151.3 –444.8 –18.7 –141.0 –407.3–19.5 –153.0 –440.0 –21.8
7 18 –141.1 –414.3 –17.6 –137.4 –396.5–19.2 –144.7 –412.5 –21.7
8 17 –135.2 –397.3 –16.7 –135.8 –392.8–18.7 –137.0 –390.0 –20.7
9 16 –120.3 –356.5 –14.0 –113.5 –331.3–14.8 –129.2 –371.3 –18.5
II 5’/5’ Ends
10 15 –117.6 –347.3 –14.1 –113.3 –329.3–15.2 –121.5 –348.3 –17.7
0 25 –186.9 –530.8 –28.6 –192.3 –544.3–30.0 –205.2 –578.9 –32.6
1 24 –180.0 –520.0 –24.9 –182.3 –516.7–28.2 –181.8 –510.0 –29.7
2 23 –157.2 –457.0 –21.0 –160.2 –454.3–24.7 –175.8 –490.5 –29.6
3 22 –155.6 –454.8 –20.0 –161.9 –460.0–24.7 –174.8 –490.3 –28.6
4 21 –140.8 –416.7 –16.5 –152.7 –434.1–23.2 –156.8 –447.2 –23.5
6 19 –117.0 –345.3 –14.1 –117.6 –339.5–16.3 –131.5 –380.0 –18.2
III 5’/3’ Ends
8 17 –102.9 –304.0 –12.2 –117.1 –340.0–15.8 –125.2 –360.0 –17.8
rementioned assumptions, the following descriptions
apply to all experimental DNA molecules studied. Dan-
gling ended molecules contained nD double strand pairs
with nL single strand dangling ends. In general, experi-
mentally determined values of thermodynamic parame-
ters from the DSC melting transition (i.e. enthalpy, en-
tropy and free energy at 25˚C) can be represented as
cal cal
X
H

II ,
calD L
, cal or cal , respectively. For in-
stance, if the measured parameters for set II molecules,
S

G
X
nn, arise from individual energies of the du-
plex region and two dangling end regions, the generic
molecule with two 5’-dangling ends can be characterized
as



III 5
,2
cal DLcal Dss L

X
nnXnX n   (4)
where

I
cal D
X
n is the measured thermodynamic pa-
rameter for the blunt-ended duplex molecule having the
same core sequence, and

5
s
sL
X
n  is the thermody-
namic contribution of a 5’ single strand dangling end
comprised of L bases. This term is added twice because
two 5’ dangling ends are present in each set II molecule.
Although explicit sequence dependence of the ends is not
considered, utilization of the n-n approximation requires
that the terminal stack, that is, the duplex terminal base
pair and adjoining single strand base, be the same in all
molecules.
Set III molecules differ from those in set II in that they
have one 5’ and one 3’ dangling end. Modifying Eq.4
above, the measured parameters for set III,


III ,
calD L
X
nn, can be expressed as






I 3
,
calDLcalDssL
III 5
ss L
X
nnXXn   n Xn   (5)
where


I
cal D
X
n is again the measured thermody-
namic energy for the blunt-ended duplex,


5
s
sL
X
n  is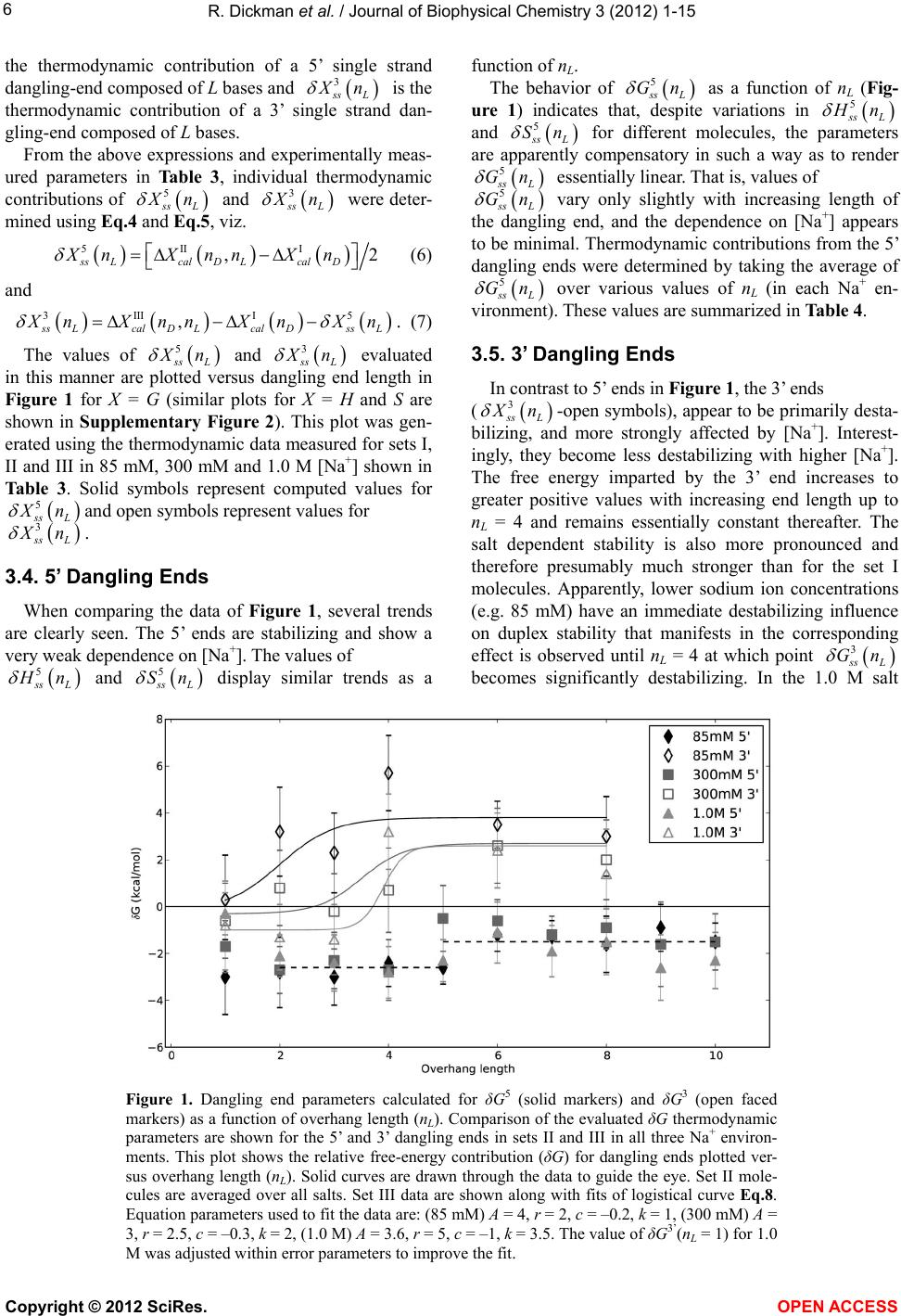

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15
6
the thermodynamic contribution of a 5’ single strand
dangling-end composed of L bases and

3
s
sL
X
n  is the
thermodynamic contribution of a 3’ single strand dan-
gling-end composed of L bases.
From the above expressions and experimentally meas-
ured parameters in Table 3, individual thermodynamic
contributions of

5
s
sL
X
n  and

3
s
sL
X
n

 were deter-
mined using Eq.4 and Eq.5 , viz.
 
5II I
,
ssLcal DLcalD
XnX nnX n 

 
2


(6)
and
 


3IIII 5
,
s
sLcalDL calDssL
X
nXnnXnXn     . (7)
The values of

5
s
sL
X
n  and

3
s
sL
X
n  evaluated
in this manner are plotted versus dangling end length in
Figure 1 for X = G (similar plots for X = H and S are
shown in Supplementary Figure 2). This plot was gen-
erated using the thermodynamic data measured for sets I,
II and III in 85 mM, 300 mM and 1.0 M [Na+] shown in
Table 3. Solid symbols represent computed values for

5
s
sL
X
n 

3
and open symbols represent values for
s
sL
X
n  .
3.4. 5’ Dangling Ends
When comparing the data of Figure 1, several trends
are clearly seen. The 5’ ends are stabilizing and show a
very weak dependence on [Na+]. The values of

5
s
sL
H
n  and

5
s
sL
Sn  display similar trends as a
function of nL.
The behavior of


5
s
sL
Gn  as a function of nL (Fig-
ure 1) indicates that, despite variations in


5
s
sL
H
n 
and


5
s
s
Sn 
L
for different molecules, the parameters
are apparently compensatory in such a way as to render


5
s
sL
Gn  essentially linear. That is, values of


5
s
sL
vary only slightly with increasing length of
the dangling end, and the dependence on [Na+] appears
to be minimal. Thermodynamic contributions from the 5’
dangling ends were determined by taking the average of
Gn 


5
s
sL
over various values of nL (in each Na+ en-
vironment). These values are summarized in Table 4.
Gn 
3.5. 3’ Dangling Ends
In contrast to 5’ ends in Figure 1, the 3’ ends
(


3
s
sL
X
n  -open symbols), appear to be primarily desta-
bilizing, and more strongly affected by [Na+]. Interest-
ingly, they become less destabilizing with higher [Na+].
The free energy imparted by the 3’ end increases to
greater positive values with increasing end length up to
nL = 4 and remains essentially constant thereafter. The
salt dependent stability is also more pronounced and
therefore presumably much stronger than for the set I
molecules. Apparently, lower sodium ion concentrations
(e.g. 85 mM) have an immediate destabilizing influence
on duplex stability that manifests in the corresponding
effect is observed until nL = 4 at which point


3
s
sL
Gn 
becomes significantly destabilizing. In the 1.0 M salt
Figure 1. Dangling end parameters calculated for δG5 (solid markers) and δG3 (open faced
markers) as a function of overhang length (nL). Comparison of the evaluated δG thermodynamic
parameters are shown for the 5’ and 3’ dangling ends in sets II and III in all three Na+ environ-
ments. This plot shows the relative free-energy contribution (δG) for dangling ends plotted ver-
sus overhang length (nL). Solid curves are drawn through the data to guide the eye. Set II mole-
cules are averaged over all salts. Set III data are shown along with fits of logistical curve Eq.8.
Equation parameters used to fit the data are: (85 mM) A = 4, r = 2, c = –0.2, k = 1, (300 mM) A =
3, r = 2.5, c = –0.3, k = 2, (1.0 M) A = 3.6, r = 5, c = –1, k = 3.5. The value of δG3’(nL = 1) for 1.0
M was adjusted within error parameters to improve the fit.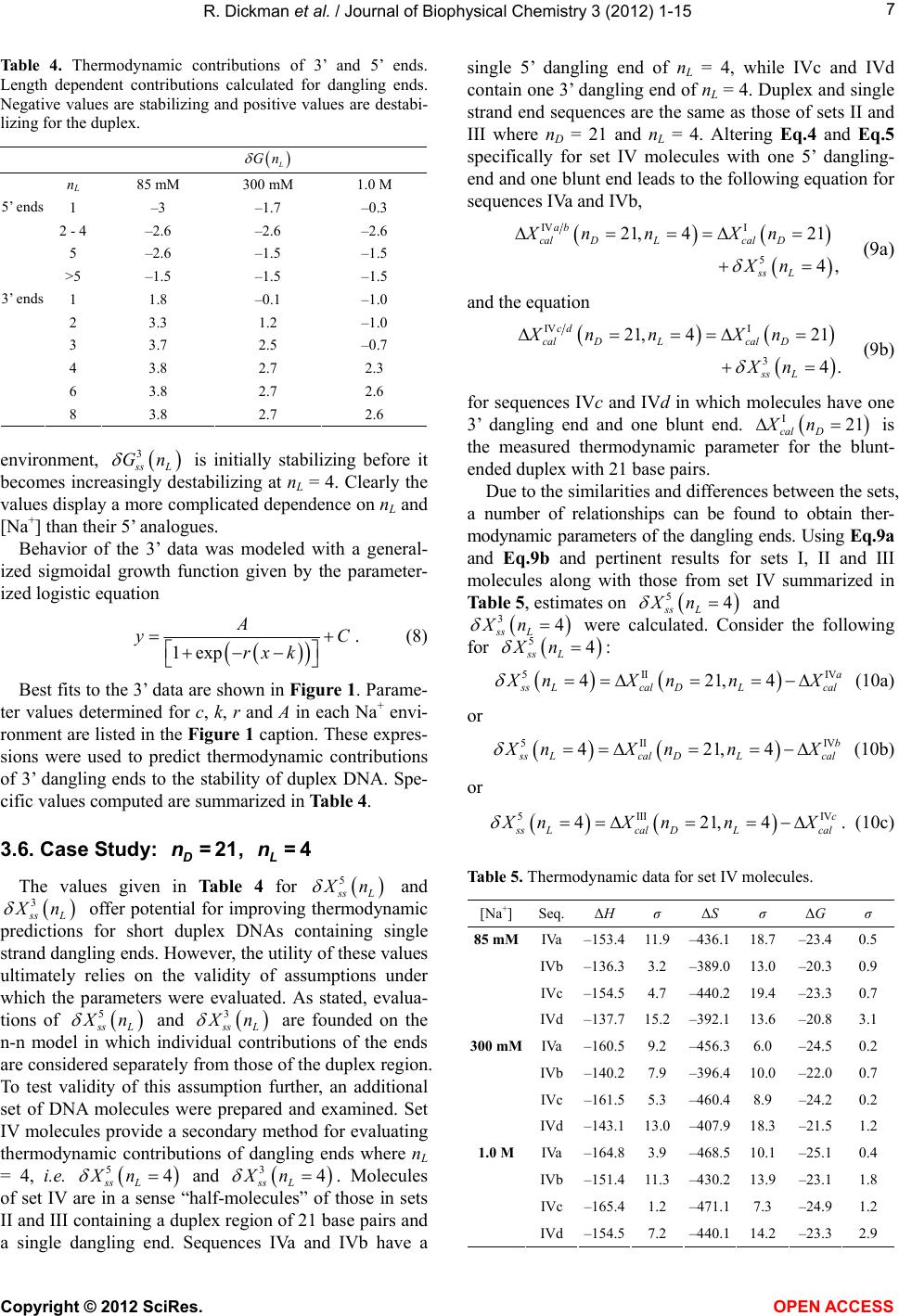

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15 7
Table 4. Thermodynamic contributions of 3’ and 5’ ends.
Length dependent contributions calculated for dangling ends.
Negative values are stabilizing and positive values are destabi-
lizing for the duplex.

L
Gn 
nL 85 mM 300 mM 1.0 M
1 –3 –1.7 –0.3
2 - 4 –2.6 –2.6 –2.6
5 –2.6 –1.5 –1.5
5’ ends
>5 –1.5 –1.5 –1.5
1 1.8 –0.1 –1.0
2 3.3 1.2 –1.0
3 3.7 2.5 –0.7
4 3.8 2.7 2.3
6 3.8 2.7 2.6
3’ ends
8 3.8 2.7 2.6
environment,

3
s
sL
Gn  is initially stabilizing before it
becomes increasingly destabilizing at nL = 4. Clearly the
values display a more complicated dependence on nL and
[Na+] than their 5’ analogues.
Behavior of the 3’ data was modeled with a general-
ized sigmoidal growth function given by the parameter-
ized logistic equation


1exp
A
yC
rx k




. (8)
Best fits to the 3’ data are shown in Figure 1. Parame-
ter values determined for c, k, r and A in each Na+ envi-
ronment are listed in the Figure 1 caption. These expres-
sions were used to predict thermodynamic contributions
of 3’ dangling ends to the stability of duplex DNA. Spe-
cific values computed are summarized in Table 4.
3.6. Case Study: ,
D
n=21L n=4
The values given in Table 4 for


5
s
sL
X
n  and

3
s
sL
X
n  offer potential for improving thermodynamic
predictions for short duplex DNAs containing single
strand dangling ends. However, the utility of these values
ultimately relies on the validity of assumptions under
which the parameters were evaluated. As stated, evalua-
tions of

5
s
sL
X
n  and


3
s
sL
X
n 

3
Xn 
are founded on the
n-n model in which individual contributions of the ends
are considered separately from those of the duplex region.
To test validity of this assumption further, an additional
set of DNA molecules were prepared and examined. Set
IV molecules provide a secondary method for evaluating
thermodynamic contributions of dangling ends where nL
= 4, i.e. and ssL. Molecules
of set IV are in a sense “half-molecules” of those in sets
II and III containing a duplex region of 21 base pairs and
a single dangling end. Sequences IVa and IVb have a
single 5’ dangling end of nL = 4, while IVc and IVd
contain one 3’ dangling end of nL = 4. Duplex and single
strand end sequences are the same as those of sets II and
III where n
D = 21 and nL = 4. Altering Eq.4 and Eq.5
specifically for set IV molecules with one 5’ dangling-
end and one blunt end leads to the following equation for
sequences IVa and IVb,

5
ss L
Xn4 

4



IV I
5
21, 421
4,
ab
calDLcal D
ss L
Xn nXn
Xn 



(9a)
and the equation



IV I
3
21, 421
4.
cd
calDLcal D
ss L
Xn nXn
Xn 




(9b)
for sequences IVc and IVd in which molecules have one
3’ dangling end and one blunt end. is
the measured thermodynamic parameter for the blunt-
ended duplex with 21 base pairs.

I21
cal D
Xn
Due to the similarities and differences between the sets,
a number of relationships can be found to obtain ther-
modynamic parameters of the dangling ends. Using Eq.9a
and Eq.9b and pertinent results for sets I, II and III
molecules along with those from set IV summarized in
Table 5, estimates on and

54
ss L
Xn  


34
ss L
Xn 

were calculated. Consider the following
for


4
5
ss L
Xn 

:




421,4
a5II IV
s
sLcalDLcal
X
nXnn   X (10a)
or




5II
421,4
bIV
s
sLcalDLcal
X
nXnn   X (10b)
or




5 IIIIV
421,4
c
s
sLcalDLcal
X
nXnn   X. (10c)
Table 5. Thermodynamic data for set IV molecules.
[Na+]Seq. ΔH σ ΔS σ ΔG σ
IVa –153.411.9–436.1 18.7 –23.40.5
IVb–136.3 3.2 –389.0 13.0 –20.30.9
IVc–154.5 4.7 –440.2 19.4 –23.30.7
85 mM
IVd–137.7 15.2–392.1 13.6 –20.83.1
IVa –160.59.2 –456.3 6.0 –24.50.2
IVb–140.2 7.9 –396.4 10.0 –22.00.7
IVc–161.5 5.3 –460.4 8.9 –24.20.2
300 mM
IVd–143.1 13.0–407.9 18.3 –21.51.2
IVa –164.83.9 –468.5 10.1 –25.10.4
IVb–151.4 11.3 –430.2 13.9 –23.11.8
IVc–165.4 1.2 –471.1 7.3 –24.91.2
1.0 M
IVd–154.5 7.2 –440.1 14.2 –23.32.9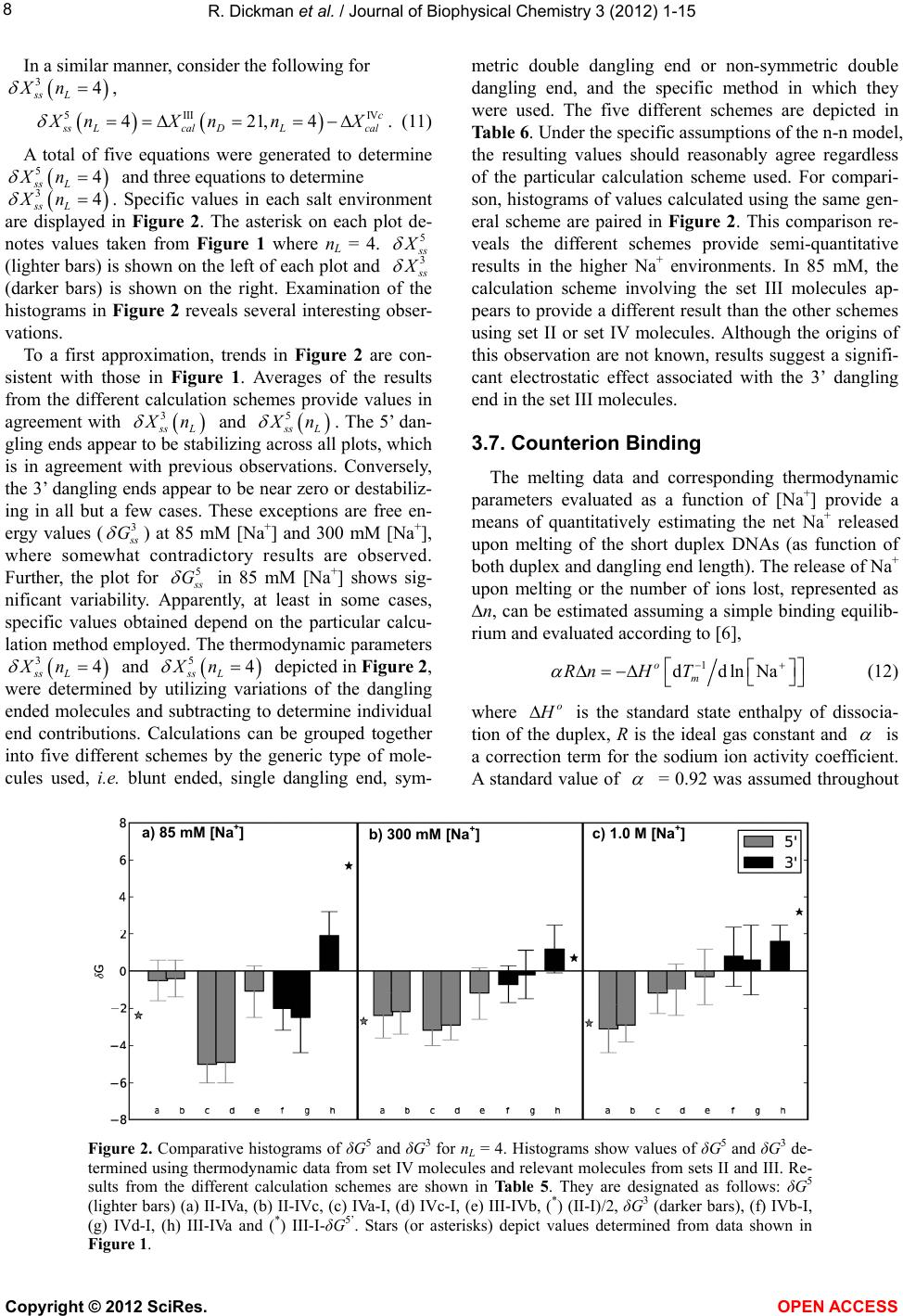

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15
8
In a similar manner, consider the following for
,

34
ss L
Xn  
 
5III
421,4
cIV
s
sLcalDLcal
X
nXnn   X


. (11)
A total of five equations were generated to determine
and three equations to determine
. Specific values in each salt environment
are displayed in Figure 2. The asterisk on each plot de-
notes values taken from Figure 1 where nL = 4.

54
ss L
Xn  

34
ss L
Xn  
5
s
s
X

3
(lighter bars) is shown on the left of each plot and
s
s
X

(darker bars) is shown on the right. Examination of the
histograms in Figure 2 reveals several interesting obser-
vations.
To a first approximation, trends in Figure 2 are con-
sistent with those in Figure 1. Averages of the results
from the different calculation schemes provide values in
agreement with

3
s
sL
X
n  and

5
s
sL
X
n  . The 5’ dan-
gling ends appear to be stabilizing across all plots, which
is in agreement with previous observations. Conversely,
the 3’ dangling ends appear to be near zero or destabiliz-
ing in all but a few cases. These exceptions are free en-
ergy values (3
s
s
5
G  ) at 85 mM [Na+] and 300 mM [Na+],
where somewhat contradictory results are observed.
Further, the plot for
s
s
G 

5
Xn 
in 85 mM [Na+] shows sig-
nificant variability. Apparently, at least in some cases,
specific values obtained depend on the particular calcu-
lation method employed. The thermodynamic parameters
and ssL

34
ss L
Xn  

4

depicted in Figure 2,
were determined by utilizing variations of the dangling
ended molecules and subtracting to determine individual
end contributions. Calculations can be grouped together
into five different schemes by the generic type of mole-
cules used, i.e. blunt ended, single dangling end, sym-
metric double dangling end or non-symmetric double
dangling end, and the specific method in which they
were used. The five different schemes are depicted in
Table 6. Under the specific assumptions of the n-n model,
the resulting values should reasonably agree regardless
of the particular calculation scheme used. For compari-
son, histograms of values calculated using the same gen-
eral scheme are paired in Figure 2. This comparison re-
veals the different schemes provide semi-quantitative
results in the higher Na+ environments. In 85 mM, the
calculation scheme involving the set III molecules ap-
pears to provide a different result than the other schemes
using set II or set IV molecules. Although the origins of
this observation are not known, results suggest a signifi-
cant electrostatic effect associated with the 3’ dangling
end in the set III molecules.
3.7. Counterion Binding
The melting data and corresponding thermodynamic
parameters evaluated as a function of [Na+] provide a
means of quantitatively estimating the net Na+ released
upon melting of the short duplex DNAs (as function of
both duplex and dangling end length). The release of Na+
upon melting or the number of ions lost, represented as
∆n, can be estimated assuming a simple binding equilib-
rium and evaluated according to [6],
1
ddlnNa
o
m
RnH T 




 

 (12)
where o
H

is the standard state enthalpy of dissocia-
tion of the duplex, R is the ideal gas constant and

is
a correction term for the sodium ion activity coefficient.
A standard value of

= 0.92 was assumed throughout
a) 85 mM [Na
+
] b) 300 mM [Na
+
]c) 1.0 M [Na
+
]
Figure 2. Comparative histograms of δG5 and δG3 for nL = 4. Histograms show values of δG5 and δG3 de-
termined using thermodynamic data from set IV molecules and relevant molecules from sets II and III. Re-
sults from the different calculation schemes are shown in Table 5. They are designated as follows: δG5
(lighter bars) (a) II-IVa, (b) II-IVc, (c) IVa-I, (d) IVc-I, (e) III-IVb, (*) (II-I)/2, δG3 (darker bars), (f) IVb-I,
(g) IVd-I, (h) III-IVa and (*) III-I-δG5’. Stars (or asterisks) depict values determined from data shown in
Figure 1.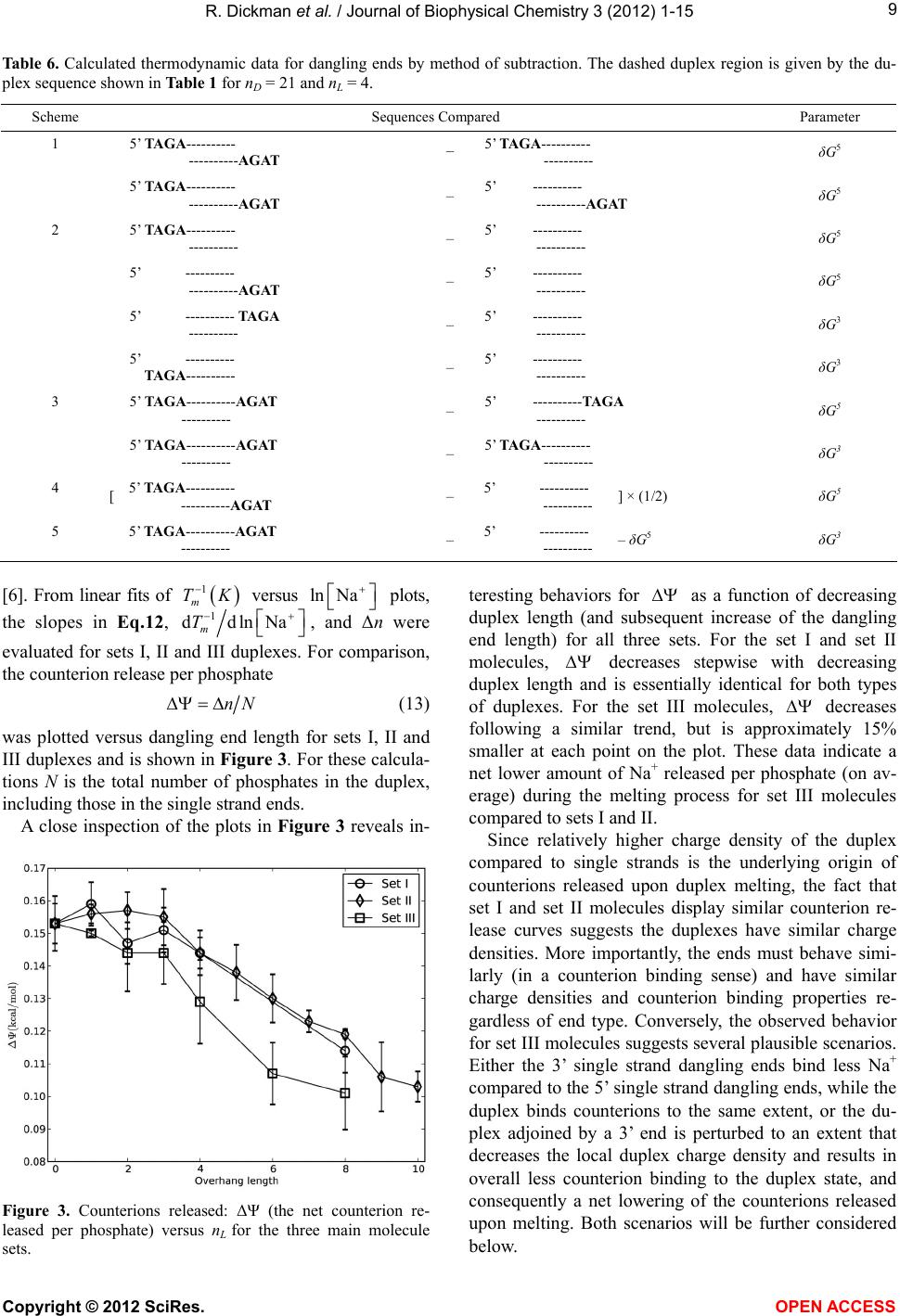

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15 9
Table 6. Calculated thermodynamic data for dangling ends by method of subtraction. The dashed duplex region is given by the du-
plex sequence shown in Table 1 for nD = 21 and nL = 4.
Scheme Sequences Compared Parameter
5’ TAGA----------
----------AGAT − 5’ TAGA---------- ---------- δG5
1
5’ TAGA----------
----------AGAT – 5’ ---------- ----------AGAT δG5
5’ TAGA----------
---------- – 5’ ---------- ---------- δG5
5’ ----------
----------AGAT – 5’ ---------- ---------- δG5
5’ ---------- TAGA
---------- – 5’ ---------- ---------- δG3
2
5’ ----------
TAGA---------- – 5’ ---------- ---------- δG3
5’ TAGA----------AGAT
---------- – 5’ ----------TAGA ---------- δG5
3
5’ TAGA----------AGAT
---------- – 5’ TAGA---------- ---------- δG3
4 [ 5’ TAGA----------
----------AGAT – 5’ ---------- ---------- ] × (1/2) δG5
5 5’ TAGA----------AGAT
---------- – 5’ ---------- ---------- – δG5 δG3
[6]. From linear fits of versus

1
m
TK
ln Na


 
plots,
the slopes in Eq.12, 1 ddT lnNa
m



, and Δn were
evaluated for sets I, II and III duplexes. For comparison,
the counterion release per phosphate
nN  (13)
was plotted versus dangling end length for sets I, II and
III duplexes and is shown in Figure 3. For these calcula-
tions N is the total number of phosphates in the duplex,
including those in the single strand ends.
A close inspection of the plots in Figure 3 reveals in-
Figure 3. Counterions released: ΔΨ (the net counterion re-
leased per phosphate) versus nL for the three main molecule
sets.
teresting behaviors for

 as a function of decreasing
duplex length (and subsequent increase of the dangling
end length) for all three sets. For the set I and set II
molecules,

 decreases stepwise with decreasing
duplex length and is essentially identical for both types
of duplexes. For the set III molecules, decreases
following a similar trend, but is approximately 15%
smaller at each point on the plot. These data indicate a
net lower amount of Na+ released per phosphate (on av-
erage) during the melting process for set III molecules
compared to sets I and II.

Since relatively higher charge density of the duplex
compared to single strands is the underlying origin of
counterions released upon duplex melting, the fact that
set I and set II molecules display similar counterion re-
lease curves suggests the duplexes have similar charge
densities. More importantly, the ends must behave simi-
larly (in a counterion binding sense) and have similar
charge densities and counterion binding properties re-
gardless of end type. Conversely, the observed behavior
for set III molecules suggests several plausible scenarios.
Either the 3’ single strand dangling ends bind less Na+
compared to the 5’ single strand dangling ends, while the
duplex binds counterions to the same extent, or the du-
plex adjoined by a 3’ end is perturbed to an extent that
decreases the local duplex charge density and results in
overall less counterion binding to the duplex state, and
consequently a net lowering of the counterions released
upon melting. Both scenarios will be further considered
below.

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15
10
3.8. Heat Capacities of Dangling Ends
In DSC experiments, the thermodynamic parameters
of the melting transition, cal
H
 and cal are evalu-
ated from the area under the melting curve,
S


p
CT
versus Temperature. The experimental transition en-
thalpy is given by,


ΔΔ
oo
cal p

H
THHCTT   (14)
where is an arbitrary reference temperature and
o
T
H

is a correction term for small variations in different
salt environments. Generally for short duplex DNA the
assumption is made that differences between and
are small in the transition region where the thermo-
dynamic parameters are evaluated, thus
o
T
0
T
p
C

[1].
As a matter of practice, calculated values of ca l
H
 and
cal are routinely used to predict thermodynamic sta-
bilities of duplexes at temperatures far below (37˚C) the
actual transition region (55˚C - 75˚C), where there is
more biological relevance and where practical applica-
tions occur. The accuracy of such predictions relies on
the validity of the assumption that evaluated parameters
are temperature independent and the overall change in
excess heat capacity (
S
p
C). If then the ther-
modynamic parameters evaluated from analysis of the
melting transition region may not be accurate for predic-
tions at lower temperatures.
0
p
C
As the technology to measure these transitions has
grown in sophistication and precision over the past 15
years, some studies have reported the existence of a rela-
tive standard transition heat capacity for all DNA du-
plexes. Estimates for this value are as high as 100
cal·deg–1·(mol·base·pair)–1 and vary slightly with se-
quence and salt [2,3,7]. Recently, the average value of
cal·deg–1·(mol·base·p air)–1 has been
reported as a good approximation [8]. Inclusion of the
64.6 21.4
p
C 
p
C parameter allows for more accurate predictions of
the transition enthalpy and entropy at temperatures below
the transition region [6,7].
For dangling ended molecules, a question arises re-
garding their effect on, and contributions to
p
C

. To
address this question, plots of cal
H
 versus m T in all
Na+ environments for sets I, II and III were constructed
and are shown in Figure 4. Using all of the data, each set
of molecules displays a different linear slope. Values of
p
C determined from slopes are 31.2 cal·deg–1·base
pair–1 for set I, 25.1 cal·deg–1·base·pair–1 for set II, and
68.9 cal·deg–1·base·pair–1 for set III. These values for
sets I and II differ somewhat from the average reported
p
C value of 64.6 ± 21.4 cal·deg–1·(mol·base·pair)–1.
However, if values from the lowest [Na+] are omitted,
p
C val- ues of 54.1, 54.6, 85.2 cal·deg–1·b ase·pa ir–1
are found for sets I, II and III respectively, which is in
reasonable agreement with the reported best value.
Figure 4.


m vs Tm for each type of molecule in all salts.
Set II molecules display a ΔCp value of 25.1 cal·deg–1·base·pair–1,
set III molecules have 68.9 cal·deg–1·base·pair–1 and ΔCp for
set I molecules is 31.2 cal·deg–1·base·pair–1.
HT
Differences in
p
C

values for each type of duplex
were estimated using Eq.14. For each dangling-ended
duplex, the difference between transition enthalpies of
the dangling ended molecule of set II and corresponding
blunt-ended molecule of set I, evaluated at the transition
temperature of the corresponding dangling-ended duplex,
, is
II
m
T


IIII IIIIo
mp

mm
H
TTHHCT T 

 (15)
where II IIII
p
p
CC

p
C

 is the difference in the
heat capacities of the dangling-ended duplexes of set II
and the corresponding blunt-ended duplexes of set I.
Clearly a plot of


II
m
H
TT 
II I
p
C
versus should
have a slope of
II
m
T

 , viz.


IIIIII I
dd
mm p
H
TT TC

 . (16)
An analogous expression for can also be
found with . If there were no difference in
III I
p
C 
III
m
TT
p
C

for set II and set I molecules, a plot of II I
p
C


III I
p
C 
versus
would produce a line having zero slope. Such a line
is seen in Figure 5 for the dangling ended molecules of
set II. Conversely, if a plot of versus
produces a line having some non-zero slope, as observed
in Figure 5 for the set III dangling ended molecules,
additional factors related to the dangling ends must con-
tribute to their
II
m
T
III
m
T
p
C

. The slope for set III molecules
from the plot in Figure 5 provides an estimated value of
cal·deg–1·base·pair–1, which is in excess
to
IIII
p
C52.5
p
C

of the blunt ended molecule. Thus, if the re-
ported average value of p cal·deg–1·base
pair–1 for the blunt-ended molecules is used, an estimated
64.6C

117 cal·deg–1·base·pair–1 is found for the set III
molecules. Inclusion of this difference with the noted

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15 11
Figure 5.


m vs Tm for each type of molecule in all
salts. As compared to the set I molecules, set II molecules dis-
play a ΔΔCp = –5.8 cal·deg–1·base·pair–1 and set III molecules
have ΔΔCp = 52.5 cal·deg–1·base·pair–1.
HT
difference in sodium release per phosphate further sug-
gests changes in the set III duplexes. These will be dis-
cussed in more detail below.
4. DISCUSSION
4.1. 5’ Dangling Ends
A number of factors are involved in determining the
relative influence a dangling single strand end will have
on the adjoining duplex. These include: the type of
molecule (i.e. whether it is DNA or RNA), identities of
the terminal duplex base pair and initial dangling-end
base, and relative orientation of the first dangling base
with respect to the terminal duplex base pair. Here, the
duplex terminal base pair and adjoining single strand
base were held constant in order to focus on relative ef-
fects of the end position (5’ versus 3’) as a function of
increasing length. Previous studies have examined ther-
modynamic contributions of various permutations and
combinations of dangling end length, end sequence and
sequence of terminating duplex base pair of DNA dan-
gling ends to duplex stability [9,10,13-16]. None, how-
ever, have examined effects of end length in an incre-
mental fashion for ends ranging in length from nL = 1 to
10 bases, nor have they compared 5’ and 3’ ends in dif-
ferent Na+ environments. However, there remain several
places where these results can be compared with pub-
lished work.
Thermodynamic effects of all possible single base
dangling ends were studied by Santa Lucia and cowork-
ers through UV melting analysis [13,17]. In their sys-
tematic study, molecules were designed to have a duplex
fixed at eight base pairs and single dangling bases at-
tached to the 5’ or 3’ ends. Relevant sequence dependent
interactions (e.g. those of the terminal 5’AC/3’G stack)
determined in their study should be comparable with our
results in 1.0 M [Na+]. After conversion to 25˚C, they re-
port an observed stabilization of kcal/
mol. It appears that our value of at 25˚C
for the 5’AC/3’G stack of −0.3 kcal/mol is not nearly as
stabilizing as reported. However, for longer ends where
nL is greater than 1, an average value of 25
25 1.21G

25 1 L
Gn
G

2.6



kcal/mol was obtained, which is in better agreement with
published results.
Over 20 years ago, Doktycz et al. published results
from melting studies of four-base dangling-ended DNA
hairpin molecules [14]. The general sequence, 5’(XY)2-
(GGATAC)2(T)4, naturally folds to form a hairpin with a
six base duplex stem, a T4 single strand loop connecting
one end of the duplex and a four base 5’ dangling end on
the other. Considering only the molecules with the same
specific end sequences (i.e. those with a terminal stack of
5’AC/3’G), the reported 25
G

had an average value of
−1.17 kcal/mol in 115 mM [Na+]. In this salt environ-
ment, for nL = 4 our data has coalesced to an average
value of −1.5 kcal/mol, in reasonable agreement with
published results.
Ohmichi published results of melting studies using an
eight base pair duplex molecule with 5’ dangling ends
varying from one to four bases [9]. The terminating se-
quence in their molecules was slightly different, 5’AG/3’C
instead of 5’AC/3’G, which prohibits a direct comparison.
Nonetheless, trends reported as a function of increasing
length can be considered. For a single base 5’ dangling
end in 1.0 M [Na+], a stabilization of 25 0.3G

 kcal/
mol was reported. Addition of a second dangling end
base increased stabilization to −0.4 kcal/mol. This trend
seemed to reach a constant value at three bases with
25 0.6G


 kcal/mol. This increase in stability coupled
to the lengthening of the single strand dangling end is
qualitatively consistent with our observations.
4.2. 3’ Dangling Ends
Compared to 5’ dangling ends, fewer studies of 3’ dan-
gling ends have been performed. Overall, reports have
found that 3’ dangling ends make favorable contributions
to duplex stability, and are thus stabilizing, but less so
than their 5’ counterparts [4,9]. In contrast we found 3’
ends to be generally destabilizing. Although unexpected,
observations of destabilizing dangling ends are not un-
precedented. The terminal stacks, 5’GT/3’A, 5’T/3’AC and
5’T/3’TA were found by SantaLucia to be mildly destabi-
lizing [13]. Additionally comparison of the published
temperature corrected value for the 5’C/3’AG stack,
25 1.0G


 kcal/mol [13], is in good agreement with
our results in 1.0 M [Na+], where 25 0.8G

 kcal/mol.
Perhaps by focusing only on single dangling bases in

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15
12
high salt, the case found here to have the greatest stabi-
lizing effect, the appearance of 3’ dangling end destabi-
lization was overlooked.
4.3. Origins of Stabilization
Our results indicate that 5’ dangling ends are equally
or more stabilizing than their 3’ counterparts. This be-
havior has been previously documented and can possibly
be explained by examining DNA single strand structure.
In the duplex state, DNA adopts the preferable B-form,
which persists to some degree in the single strand state.
NMR studies of single strand DNA hexamers with mul-
tiple A-A base stacks showed that in DNA, the imidazole
stacks above the pyrimidine in the 5’ to 3’ direction [18].
A systematic review of crystal structures from the pro-
tein database demonstrated for DNA that addition of a
single strand base on the 5’ end is positioned in such a
way that it can freely interact with the hydrogen bonds of
the terminal base pair. In contrast, a 3’ base end is posi-
tioned away from the same hydrogen bonds, and there-
fore is less likely to experience such stabilization [19].
Thus, placement of the dangling base is optimal for ter-
minal base pair interactions in DNA on the 5’ end but
when an additional base is added to the 3’ end of DNA
minimal overlap occurs which apparently translates to
fewer stabilizing interactions.
4.4. Structural Perturbations
Our results indicate a 3’ dangling end is generally de-
stabilizing to a DNA duplex. Previous studies of counte-
rion binding to duplex DNA suggests fewer Na+ ions
bind near the ends compared to in the middle [6,20]. This
suggests differences between the dangling ended and
blunt molecules should result in negligible changes in
counterion binding if the duplex region of the dangling-
ended duplex is not affected by the ends. Comparison of
the blunt ended duplexes and set II molecules support
this assumption. The net counterion release per phos-
phate is the same for the two sets (I and II) of molecules
and the plots of vs. nL (in Figure 3) are the same.
Conversely, for the set III molecules having 3’/5’ dan-
gling ends, the plot of vs. nL is approximately 15%
lower than for the set I and set II molecules and indicates
a net lower Na+ release during melting suggesting the
duplex region for set III is perturbed in some way that
results in slight differences of the associated counterion
binding properties.


When DNA molecules anneal from their single strand
state to form a duplex state, a net change in solvent ex-
posed surface occurs. This change is accompanied by the
burying of hydrophobic residues, which contributes to
p
C. Differences in the estimated
p
C values for set
II, when compared to set III (Figures 4 and 5), further
support the idea of subtle differences between the duplex
regions. Comparison of
p
C

values for the blunt-ended
set I molecules and the set II molecules revealed an es-
sentially constant
p
C

 with a cal
H
 difference of
about 1 cal·deg–1·base·pair–1. There was also no marked
length dependence, indicating that most of the stability
came from interactions of the first base with the terminal
base pair, presumably due to the favorable stacking in-
teractions. Conversely, comparison of
p
C values for
set III and set I molecules revealed a significant differ-
ence, p52C.5

 cal·deg–1·base·pair–1. Here cal
H


is initially around 0.5 and decreases to −0.5 as the length
of the dangling end increases to nL = 10. This suggests an
initial smaller buried surface area as compared to the 5’
dangling end, which is lost as the dangling end increases
in length. The continued loss of enthalpy suggest that
with longer dangling ends, the duplex region itself may
be perturbed in this particular molecular environment.
4.5. Predictive Ability and Applications to
Probe Design
Ascertaining specific thermodynamics involved in
probe/target alignment and being able to further predict
energies of all possible alignments is key to optimal
probe design. The ability to design probes with exquisite
accuracy is imperative to successfully locate target se-
quences differing by as little as a single nucleotide. In
fact, molecules used in this study were designed to
mimic those that might occur in a multiplex hybridiza-
tion reaction (such as on a DNA microarray) where dan-
gling ends presumably occur with a moderate to high
frequency. The more specific the predictive ability of
thermodynamic binding properties, the more effective
probe design can be achieved.
In the n-n model the free energy of melting a duplex
molecule is given by
initiation
oo
s onal 
tack a
o
G
dditi
o
GGG 

. (17)
For calculations involving the duplex region, this
model uses combinations of the 10 possible n-n values
(stack ) experimentally determined by a number of in-
dependent labs that are generally in good agreement with
one another [17]. The first term, initiation, is the cost
required to begin the annealing process and therefore has
a positive free energy contribution. This value has re-
cently been determined by our group, as well as other
investigators [21,22]. The last term, additional , encom-
passes any extra terms such as those arising from sym-
metry considerations, a terminating A·T base pair or sin-
gle strand dangling ends. The sum of terms estimates the
total free energy.
o
G
o
G
o
G
Current prediction programs relying on the n-n model
o calculate thermodynamic properties are limited by the t

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15
13
Table 7. ΔG values predicted using length dependent overhang parameters. Sequences used to predict ∆G25 kcal/mol are shown in
column one. The dashed duplex region is given by the duplex sequence shown in Table 1 for nD = 21 and nL = 4. Unified N-N values
were used in calculations [13]. All predicted values were corrected with an averaged difference for set I (i.e. ∆Gexp – ∆Gmfold, 85 mM
= +6.2, 300 mM = +6.7), and (1000 mM = +7.8).
85 mM [Na+] 300 mM [Na+] 1.0 M [Na+]
Sequence Exp Mfold NN Exp Mfold NN Exp Mfold NN
5’ ----------
3’ ---------- –19.8 –18.6 –19.2 –21.3 –20.9 –21.5 –23.9 –22.4 –23.0
5’ TAGA----------
3’ ----------AGAT –24.6 –20.7 –24.4 –26.7 –23.1 –26.7 –29.5 –25.8 –28.2
5' TAGGA----------
3’ ----------AAGTCGAT
* –20.7 –23.5 * –23.1 –24.9 * –25.8 –26.4
5’ TAGA----------AGAT
3’ ---------- –16.5 –20.5 –18.1 –23.2 –22.9 –21.4 –23.5 –24.6 –23.3
5' ATCGA----------AGAATCT
3’ ----------
* –20.5 –18.0 * –22.9 –20.5 * –24.6 –22.1
quality of parameters used in the calculation. Mfold is
one such program readily available via the Internet [23].
In this program, a computational algorithm searches for
the most stable structure formed from the sequence of
two DNA strands, through a calculation of the thermo-
dynamic stabilities using tabulated n-n parameter values.
To include effects of dangling ends, the specific value of
–1.18 kcal/mol for the 5’ dangling end (5’AC/3’G) and
–1.05 kcal/mol for the 3’ dangling end (5’C/3’AG) are
added to n-n calculations [13]. Potential stability differ-
ences due to dangling ends longer than one base are not
considered.
OPEN A CCESS
To test the applicability and utility of dangling end
parameters evaluated here, five sequences having a 21
base pair duplex region were designed with variable end
lengths. Calculated thermodynamic parameters were
generated using two methods, Mfold and the n-n model.
Sequences differed in the placement and length of dan-
gling ends. The sequences were: 1) a 21 base blunt ended
control, 2) a 21 base duplex with two four-base 5’ dan-
gling ends, 3) a 21 base duplex with two 5’ dangling ends
having five and eight bases respectively, 4) a 21 base
duplex with one four-base 3’ and one four-base 5’ dan-
gling end, and 5) a 21 base duplex with one five-base 3’
dangling end and one seven-base 5’ dangling end. Where
available, experimental data has been included as a com-
parison. Results of computations are shown in Table 7.
Upon closer examination, the n-n model and Mfold
stability predictions are quite comparable for 5’ ended
molecules. However, Mfold predicts a greater stability
for the 3’ ended molecules than that predicted using the
end parameters described here. Since no reported meas-
urements have been made of these specific 3’ ends desta-
bilizing the duplex, it is not surprising the standard pro-
gram (Mfold) overestimates the stability of those mole-
cules. These comparisons suggest the dangling ended
parameters in Ta b l e 4 may provide more accurate quan-
titative predictions of the stability of dangling ended
molecules. Confirmation of the ultimate practical utility
of the evaluated dangling end parameters must be dem-
onstrated through more accurate probe design and im-
proved quantitative performance of multiplex hybridiza-
tion reactions.
5. ACKNOWLEDGEMENTS
Portions of this work appeared in a thesis by Rebekah Dickman sub-
mitted in partial fulfillment for requirements of the Master of Science
in Chemistry at Portland State University, December 2010. This work
was supported by grants GM080904 and GM084603 from the National
Institutes of Health.
REFERENCES
[1] Petersheim, M. and Turner, D.H. (1983) Base-stacking
and base-pairing contributions to helix stability—Ther-
modynamics of double-helix formation with CCGG,
CCGGP, CCGGAP, ACCGGP, CCGGUP, and ACCGGUP.
Biochemistry, 22, 256-263. doi:10.1021/bi00271a004
[2] Rouzina, I. and Bloomfield, V.A. (1999) Heat capacity
effects on the melting of DNA. 1. General aspects. Bio-
physical Journal, 77, 3242-3251.
doi:10.1016/S0006-3495(99)77155-9
[3] Wu, P., Nakano, S. and Sugimoto, N. (2002) Temperature
dependence of thermodynamic properties for DNA/DNA
and RNA/DNA duplex formation. European Journal of
Biochemistry, 269, 2821-2830.
doi:10.1046/j.1432-1033.2002.02970.x
[4] Freier, S.M., Sugimoto, N., Sinclair, A., Alkema, D.,
Neilson, T., Kierzek, R., Caruthers, M.H. and Turner, D.H.
(1986) Stability of XGCGCP, GCGCYP, and XGCGCYP
helixes—An empirical estimate of the energetics of hy-
drogen-bonds in nucleic-acids. Biochemistry, 25, 3214-
3219. doi:10.1021/bi00359a020
[5] SantaLucia, J. (1998) A unified view of polymer, dumbbell,
and oligonucleotide DNA nearest-neighbor thermodyna-

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15
14
mics. Proceedings of the National Academy of Sciences of
the United States of America, 95, 1460-1465.
doi:10.1073/pnas.95.4.1460
[6] Owczarzy, R., You, Y., Moreira, B.G., Manthey, J.A.,
Huang, L.Y., Behlke, M.A. and Walder, J.A. (2004)
Effects of sodium ions on DNA duplex oligomers: Im-
proved predictions of melting temperatures. Biochemistry,
43, 3537-3554. doi:10.1021/bi034621r
[7] Holbrook, J.A., Capp, M.W., Saecker, R.M. and Record,
M.T. (1999) Enthalpy and heat capacity changes for
formation of an oligomeric DNA duplex: Interpretation in
terms of coupled processes of formation and association
of single-stranded helices. Biochemistry, 38, 8409-8422.
doi:10.1021/bi990043w
[8] Chalikian, T.V., Volker, J., Plum, G.E. and Breslauer, K.J.
(1999) A more unified picture for the thermodynamics of
nucleic acid duplex melting: A characterization by calori-
metric and volumetric techniques. Proceedings of the
National Academy of Sciences of the United States of
America, 96, 7853-7858. doi:10.1073/pnas.96.14.7853
[9] Ohmichi, T., Nakano, S., Miyoshi, D. and Sugimoto, N.
(2002) Long RNA dangling end has large energetic con-
tribution to duplex stability. Journal of the American
Chemical Society, 124, 10367-10372.
doi:10.1021/ja0255406
[10] Senior, M., Jones, R.A. and Breslauer, K.J. (1988)
Influence of dangling thymidine residues on the stability
and structure of 2 dna duplexes. Biochemistry, 27, 3879-
3885. doi:10.1021/bi00410a053
[11] Cantor, C.R., Warshaw, M.M. and Shapiro, H. (1970) Oli-
gonucleotide Interactions III. Circular Dichroism Studies of
the Conformation of Deoxyoligonucleotides. Biopolymers,
9, 1059-1077. doi:10.1002/bip.1970.360090909
[12] Cavaluzzi, M.J. and Borer, P.N. (2004) Revised UV
extinction coefficients for nucleoside‐5’‐monophosphates
and unpaired DNA and RNA. Nucleic Acids Research, 32,
e13. doi:10.1093/nar/gnh015
[13] Bommarito, S., Peyret, N. and SantaLucia, J. (2000)
Thermodynamic parameters for DNA sequences with
dangling ends. Nucleic Acids Research, 28, 1929-1934.
doi:10.1093/nar/28.9.1929
[14] Doktycz, M.J., Paner, T.M., Amaratunga, M. and Benight,
A.S. (1990) Thermodynamic stability of the 5’dangling-
ended dna hairpins formed from sequences 5’-(xy)
2ggatac(t)4gtatcc-3’, where x, y = A, T, G, C. Bio-
polymers, 30, 829-845. doi:10.1002/bip.360300718
[15] Quartin, R.S. and Wetmur, J.G. (1989) Effect of
ionic-strength on the hybridization of oligodeoxynu-
cleotides with reduced charge due to methylphosphonate
linkages to unmodified oligodeoxynucleotides containing
the complementary sequence. Biochemi st ry , 28, 1040-
1047. doi:10.1021/bi00429a018
[16] Riccelli, P.V., Mandell, K.E. and Benight, A.S. (2002)
Melting studies of dangling-ended DNA hairpins: Effects
of end length, loop sequence and biotinylation of loop
bases. Nucleic Acids Research, 30, 4088-4093.
doi:10.1093/nar/gkf514
[17] SantaLucia, J. and Hicks, D. (2004) The thermodynamics
of DNA structural motifs. Annual Review of Biophysics
and Biomolecular Structure, 33, 415-440.
doi:10.1146/annurev.biophys.32.110601.141800
[18] Isaksson, J., Acharya, S., Barman, J., Cheruku, P. and
Chattopadhyaya, J. (2004) Single-stranded adenine-rich
DNA and RNA retain structural characteristics of their
respective double-stranded conformations and show dir-
ectional differences in stacking pattern. Biochemistry, 43,
15996-16010. doi:10.1021/bi048221v
[19] Isaksson, J. and Chattopadhyaya, J. (2005) A uniform
mechanism correlating dangling-end stabilization and sta-
cking geometry. Biochemistry, 44, 5390-5401.
doi:10.1021/bi047414f
[20] Manning, G.S. and Mohanty, U. (1997) Counterion
condensation on ionic oligomers. Physica A, 247, 196-
204. doi:10.1016/S0378-4371(97)00413-5
[21] Sugimoto, N., Nakano, S., Yoneyama, M. and Honda, K.
(1996) Improved thermodynamic parameters and helix
initiation factor to predict stability of DNA duplexes.
Nucleic Acids Research, 24, 4501-4505.
doi:10.1093/nar/24.22.4501
[22] Manyanga, F., Horne, M.T., Brewood, G.P., Fish, D.J.,
Dickman, R. and Benight, A.S. (2009) Origins of the
“nucleation” free energy in the hybridization thermo-
dynamics of short duplex DNA. Journal of Physical
Chemistry B, 113, 2556-2563. doi:10.1021/jp809541m
[23] Zuker, M. (2003) Mfold web server for nucleic acid
folding and hybridization prediction. Nucleic Acids Re-
search, 31, 3406-3415. doi:10.1093/nar/gkg595

R. Dickman et al. / Journal of Biophysical Chemistry 3 (2012) 1-15 15
Supplementary Figures
85 mM [Na
+
]
300 mM [Na
+
]
1000 mM [Na
+
]
Supplementary Figure 1. cal versus cal TS (T = 298.15 K) for
the 27 duplex DNAs in 85 mM, 300 mM and 1.0 M [Na+].
H
Supplementary Figure 2. Comparison of the evaluated thermodynamic parameters for
the 5’ and 3’ dangling ends in sets II and III ((a) δH and (b) δS), in the three Na+ envi-
ronments plotted versus overhang length, nL.