Paper Menu >>
Journal Menu >>
 Journal of Transportation Technologies, 2012, 2, 50-62 http://dx.doi.org/10.4236/jtts.2012.21006 Published Online January 2012 (http://www.SciRP.org/journal/jtts) Multi Model Criteria for the Estimation of Road Traffic Congestion from Traffic Flow Information Based on Fuzzy Logic Hari Shankar, P. L. N. Raju, K. Ram Mohan Rao Geoinformatics Division, Indian Institute of Remote Sensing, Dehradun, India Email: rammohan@iirs.gov.in Received September 26, 2011; revised October 28, 2011; accepted November 20, 2011 ABSTRACT In this study, the road traffic congestion of Dehradun city is evaluated from traffic flow information using fuzzy tech- niques. Three different approaches namely Sugeno, Mamdani models which are manually tuned techniques, and an Adaptive Neuo-Fuzzy Inference System (ANFIS) which an automated model decides the ranges and parameters of the membership functions using grid partition technique, based on fuzzy logic. The systems are designed to human’s feel- ings on inputs and output levels. There are three levels of each input namely high, medium and low for input density, fast, medium and slow for input speed, and five levels of output namely free flow, slow moving, mild congestion, heavy congestion and serious jam for the road traffic congestion estimation. The results, obtained by fuzzy based techniques show that the manually tuned Sugeno type technique achieves 72.05% accuracy, Mamdani type technique achieves 83.82% accuracy, and Adaptive Neuro-Fuzzy Inference System technique achieves 88.23% accuracy. ANFIS technique appears better than the manually tuned fuzzy technique, and also the manually tuned fuzzy technique gives good accu- racy which leads that the fuzzy inference system can capture the human perception better through manual adjustment of input/output membership functions. Keywords: Fuzzy Inference Systems; Fuzzy Rules; Congestion; Human Perception 1. Introduction In general, the road traffic congestion of urban transport is defined as the ratio of volume to the capacity of the road [1,2]. However, the volume and capacity (demand) of the road are not directly measurable quantities and thus the value of congestion becomes subjective in nature. Hence, in this paper the directly and precisely measur- able quantities such as density and speed of the vehicles, are used for the estimation of road traffic congestion [3]. These two traffic parameters are considered in this paper by keeping in mind that general perception about the congestion on the roads increases when the number of traffic (traffic density) increases and also increases when the speed of the traffic decreases. By the same terminol- ogy the road traffic congestion can be defined as the ratio of density to the speed of the vehicles. These two pa- rameters are the inputs to the fuzzy model, and the output of the model is level of congestion. In fact, the actual traffic conditions are not perfectly matches with the con- ventional way of determining the congestion level using volume and capacity, because there are a number of other factors which affect the congestion and also depends upon the human feelings [4]. But using these directly measurable quantities, the subjectivity of the conven- tional method of determining congestion level using volume to capacity ratio is removed. The road traffic congestion is one of the most confus- ing tasks, because there is no standard way of measuring congestion level on the roads and intersections. It results in serious environmental, time wastage, health hazards, and economic problems. Thus, it is very important to detect where the congestion occurs, as well as to measure and estimate how the congestion is. There may be a number of solutions of road traffic congestion like road pricing, fuel levies, expansion and improvisation of rail- way lines, and elimination of roundabouts. The main objective of this study is to estimate the road traffic con- gestion using fuzzy techniques. Therefore, the fuzzy techniques are used to tackle this problem by using the traffic flow information such as speed and density of the vehicles. The fuzzy logic is well known to be suitable for handling problems that are nonlinear in nature such as human feelings [5,6]. Road congestion is a subjective quantity, because it comes from the feelings of vehicle driver and decision makers which may be different for different drivers or decision makers. In the same road C opyright © 2012 SciRes. JTTs  H. SHANKAR ET AL. 51 conditions, some may feel that the road is heavily con- gested, while some others may feel that the road is only slightly congested. This is the problem of mismatching data interpretation due to different user’s perception. In traveler navigation system, publication of congestion degree will provide drivers useful information, thus, re- duce traffic jam, increase efficiency of trips, and avoid wastage of fuel consumption. It is well known that the process from free flow to serious jam is continuous. It can be represented by a continuous number, say level of congestion (LOC). The LOC is related to the basic traffic parameters such as speed and density. There are other traffic parameters also which affects the congestion level but in this study we use only two traffic parameters i.e. speed and density, which affect mostly to congestion. The objective of this study is to estimate the level of congestion of a road segment using different fuzzy mod- els namely Sugeno-type Fuzzy Inference System, Mam- dani-type Fuzzy Inference System and Adaptive Neuro- Fuzzy Inference System [7], to evaluate the performance of fuzzy inference systems by measuring accuracy of system outputs against human opinion. 2. Study Area Dehradun city is chosen as the study area for assessing the traffic congestion. A road segment with two lanes from Inter State Bus Terminal Dehradun to Saharanpur is taken as a test case to quantify the road traffic congestion. Figure 1 shows the study area depicting the road net- work of Dehradun city. This road segment has two lanes, going from ISBT Dehradun to Saharanpur, near ISBT Dehradun Uttarakhand. In this research framework, five levels of congestion are defined for traffic congestion, namely free flow, slow moving, mild congestion, heavy congestion and serious jam, and estimating them by us- ing only traffic video. 3. Literature Review Porikli and Li, 2004 determine five level of congestion from traffic flow information and video images using a Hidden Markov Model [8]. Atikom and Pongpaibool, 2006 estimates the road traffic congestion by using vehi- cle velocity [9]. Krause and Altrock, 1996 uses fuzzy logic to determine six discrete levels of congestion [10]. The system use velocity and vehicle density as inputs its. fuzzy inference system. Sule, 1988; Jia and Li, 2003 uses different factors which affect the road traffic congestion [11,12]. This study also uses fuzzy inference systems, but quite different from the previous studies that it examine both manually tuned fuzzy inference systems and adap- tive neuro-fuzzy inference system. The motivation be- hind this study is adaptive neuro-fuzzy and the effecti- veness of the manually tuned fuzzy system which de- pends highly on the fuzzy rules and membership function ranges created by human. There is no systematic way to create these rules and deciding the ranges, and types of membership functions. Therefore, it has to adjust these rules by keeping in mind that congestion is directly proportional to density and inversely proportional to the speed, and adjust ranges and type of the membership function by trial and error me- thod according to the situation until the results are satis- fied. The adaptive neuro-fuzzy inference system can solve this problem by automatically creating fuzzy rules according to given inputs and outputs [13-15]. In addi- tion, we limit the traffic congestion status to only five levels-free flow, slow moving, mild congestion, heavy congestion and serious jam, to facilitate a quick and easy to understand report. 4. Methodology To estimate the road traffic congestion of a road segment of Dehradun city, we obtain the traffic flow information at the desired location. The input parameters average speed and density of the vehicle per fixed interval of time are extracted from a video file using manual technique. Subjective congestion evaluation is conducted by watch- ing a traffic video, and the average traffic congestion of Figure 1. Location of the study area. Copyright © 2012 SciRes. JTTs 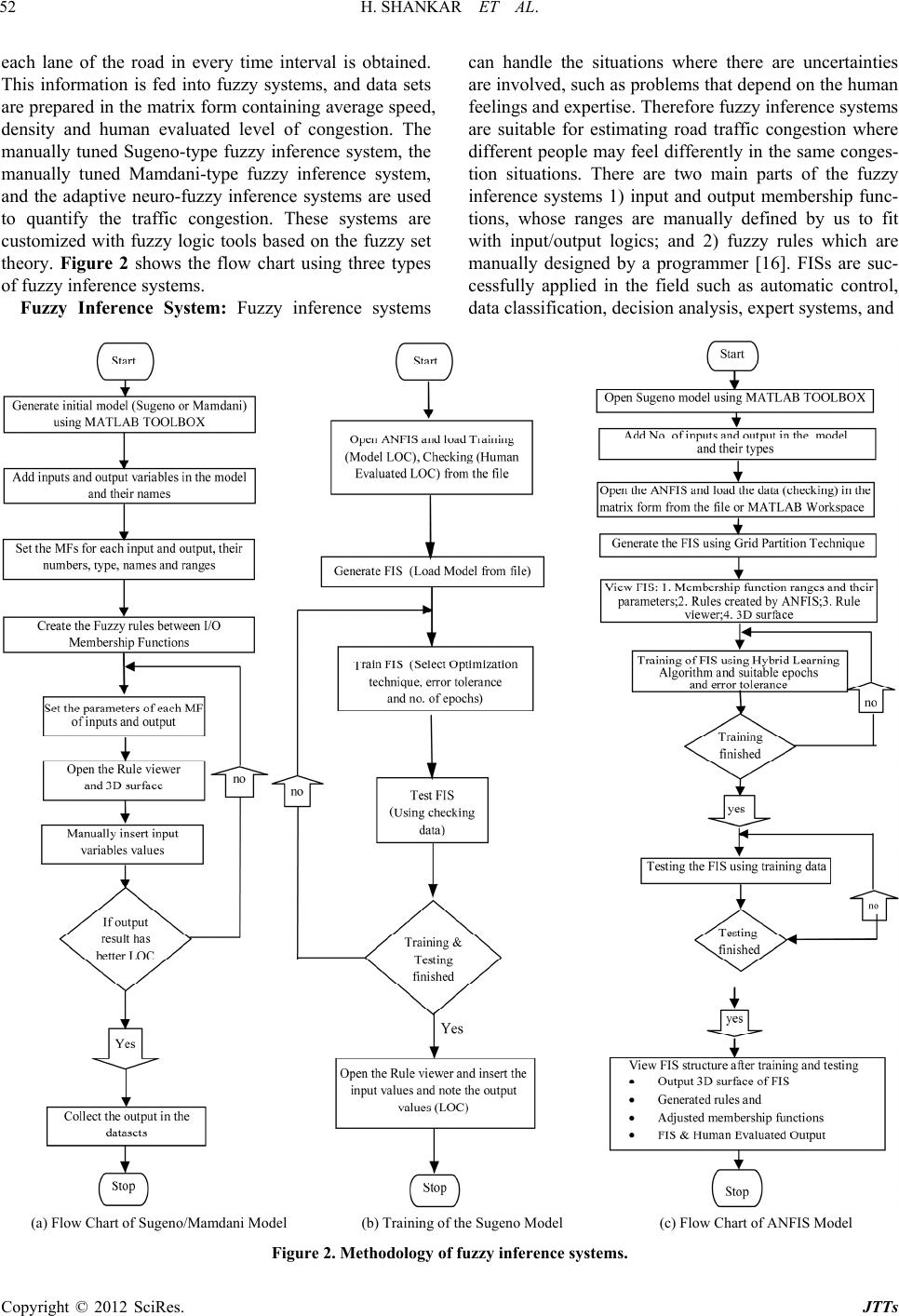 H. SHANKAR ET AL. Copyright © 2012 SciRes. JTTs 52 each lane of the road in every time interval is obtained. This information is fed into fuzzy systems, and data sets are prepared in the matrix form containing average speed, density and human evaluated level of congestion. The manually tuned Sugeno-type fuzzy inference system, the manually tuned Mamdani-type fuzzy inference system, and the adaptive neuro-fuzzy inference systems are used to quantify the traffic congestion. These systems are customized with fuzzy logic tools based on the fuzzy set theory. Figure 2 shows the flow chart using three types of fuzzy inference systems. Fuzzy Inference System: Fuzzy inference systems can handle the situations where there are uncertainties are involved, such as problems that depend on the human feelings and expertise. Therefore fuzzy inference systems are suitable for estimating road traffic congestion where different people may feel differently in the same conges- tion situations. There are two main parts of the fuzzy inference systems 1) input and output membership func- tions, whose ranges are manually defined by us to fit with input/output logics; and 2) fuzzy rules which are manually designed by a programmer [16]. FISs are suc- cessfully applied in the field such as automatic control, data classification, decision analysis, expert systems, and (a) Flow Chart of Sugeno/Mamdani Model (b) Training of the Sugeno Model (c) Flow Chart of ANFIS Model Figure 2. Methodology of fuzzy inference systems.  H. SHANKAR ET AL. 53 computer vision. Because of its multidisciplinary nature, FISs are also associated with a number of names, such as fuzzy rule-base systems, fuzzy expert systems, fuzzy modeling, fuzzy associated memory, fuzzy logic control- lers, and simply fuzzy systems. There are mainly six conventional blocks namely input, fuzzification, knowledge base, decision-making unit, de- fuzzification and output for evaluating the crisp value of output variable in the fuzzy inference system (Figure 3). Mamdani Model: Mamdani FIS is the most used in the developing fuzzy models. Mamdani architecture used in this paper for estimation of road traffic congestion is illustrated in Figure 4 with two inputs, one output vari- ables and nine fuzzy rules, which consists of five layers of nodes. Out of five layers, first and fourth layers con- sist of adaptive nodes there are Fuzzification and De- fuzzification, and are called Fuzzy layer and De-fuzzy layer, while the second, third and fifth layers consists of fixed nodes there are Rules (or product), Normalization and Summation, and are called product layer, normaliza- tion layer and summation layer respectively. The rule base for Mamdani model can be written as 1, 2, Premise Part , Consequent Part Fuzzy Rule : If (is)AND is Then iii i ioj xA MyBM fM where x, y, Ai and Bi represent the input1, input2, linguis- tic label of input1 (slow, medium etc.), and linguistic label of input2 respectively, and M1i, M2i, fj and Moj rep- resent the ith MF of input1 (x), the ith MF of input2 (y), the output of the jth rule, and the jth output MF respec- tively. Both input and output MF have their own para- meters depending upon the shape of the MF and are cal- led premise, and consequent parameters respectively. The computational mechanism of Mamdani FIS at each layer is explained as follows: Layer 1 (Fuzzification Layer): In this layer the, crisp input values are converted to the fuzzy values sby the input MFs, and the output of every node is the fuzzy membership grade of the inputs, which are given by 1, 1, 1, 2, for 1,2,3 for 1,2,3 ii ii OMx i OMyi (1) where O1,i are the membership grade of a fuzzy set {A1, A2, A3, B1, B2, B3}. In this paper, the following trape- zoidal MFs for the inputs are used 1) Trapezoidal MFs: (see Equation (2)) The another membership functions are also used in this study as input MF. 2) Generalized bell MFs: , ,,,, 2 , , 1 :,, 1 ki kiki ki kib ki ki MxGbellxabc xc a (3) where (aki, bki, cki, dki) are the parameters of membership Every node in this layer is a ci functions, known as premise parameters that characterize the shape of the input MFs. Where k = 1, 2 for first and second input respectively. Layer 2 (Rule Layer): rcle node (fixed node) labeled π, whose output is the product of all incoming inputs and the output represents the firing strength or weighting factor of a fuzzy control rule. The node generates the output by cross multiplying all the incoming inputs and is given by 2,1, 2, j ji OWMxM j (4) where 1, 2, 3for1 4,5,6for 2 7,8,9for 3 i ji i Figure 3. Block diagram of fuzzy inference system. , , ,, ,, ,, ,,,,, , ,, ,, , 0, , 1, :,,, , 0, ki ki ki ki ki ki ki ki kiki ki kiki ki ki ki ki ki ki xa xa axb ba bxc MxTrapxabcd dx cxd dc dx (2) Copyright © 2012 SciRes. JTTs  H. SHANKAR ET AL. 54 Figure 4. Fuzzy inference system architecture with two inputs, one output and three rules. Layer 3 (Normalization Layer): Every node of this layer calculates the weight, which is normalized. For convenience, the outputs of this layer are called normal- ized firing strengths. 3, 9 1 1, 2,, 9 j jj j j W OW j W (5) re Wj is the o ery node is where O3,j is the output of the layer 3 and fj is the output of the jth fuzzy rule and Moj is the MFs of jth output. In of trapezoidal shape as de tions are also used in this study as output MF 1) Linear MFs: whe utput of layer 2. Layer 4 (Defuzzification Layer): The parameters in this layer are referred to as consequent parameters. The output of every node of this layer is simply the product of the normalized firing strength and a first order polyno- mial.The output of ev 4, 3,3,,1, 2,, 9 jjjjoj OOfOMj (6) this paper, MFs for the output are fined in Equation (2). The another membership func- ,,Linear,:,, ojjjjjjj M xyxy pqrpxqyr (7) 2) Constant MF: ,Constan ojj j M tr r (8) where pj, qj, rj are the parameters of the output MFs cor- consequent pa- Fs. responding to jth fuzzy rule, known as rameters, characterized by shape of the M Layer 5 (Summation Layer): The single node in this layer is a circle node (fixed node) labeled ∑ which com- putes the overall output as the summation of all incoming outputs from layer 4 i.e. 9 99 1 54, 3,9 11 1 112 29 9 j j Wf j jjj jj j j OO Of W WfWf Wf (9) Copyright © 2012 SciRes. JTTs  H. SHANKAR ET AL. 55 In this study, all the premise and consequent parame- teecided in MATLAB tools. Sugeno Model: The architecture and the fuzzy soodel is same as that of the Mamdani mly linear or constan the output variable. In this study we u ided in the M bines the adaptive learning capability of Artificial Neural Network (ANN) along with the intuitive Fuzzy logic (FL) into a single capsule. For a given input/output dataset, the ANFIS gener fuzzy inference system (FIS) using grid partiti nique and membership functions parameters are adjusted (tuned) automatically until reach the optimal solution us rning me- th pes of fuzzy reasoning and “if- th e optimal solution. econd interval of time. Here we judging D/S (Density over Speed ratio), and estion, namely free flow, slow taken as the validation data and depends up of the model is ev match with the co ion (10) rs are manually d rea- ning of Sugeno m odel, but it has ont type of MFs for se the trapezoidal MFs for both the inputs (Speed and Density) and con- stant MFs for the output (LOC). Here also all the premise and consequent parameters are manually dec ATLAB tools. ANFIS Model: Adaptive Neuro-Fuzzy Inference Sys- tem (ANFIS) is one of the most successful hybrid mod- eling technique which com ates the on tech- ing either a backpropagation algorithm or in combina- tion with least squares type method (hybrid lea od). We use the adaptive neuro-fuzzy inference system (ANFIS) [17], which use the hybrid learning algorithm [13] to create rules and adjust membership function pa- rameters to fit the training data. The membership func- tions used in ANFIS are gbell’s functions for inputs and linear functions for output. We train our ANFIS under 100 epochs. Depending on the ty en” rules, Sugeno’s fuzzy model, the output of each rule is a linear combination of input variables plus a con- stant term or purely constant, because membership func- tion of output variable are only linear or constant type and the final output is the weighted average of each rule’s output. Mamdani Model also has same units as in Sugeno model, but only difference is that the member- ship function of output variable may have different type like trapezoidal, triangulat, Gaussian, exponential etc. [18]. In our case we chose the trapezoidal membership function for the output variable (LOC). The ANFIS is like a fuzzy inference systems, except that here by using a learning algorithm (either a back propagation alone or in combination with a least squares estimation) the pa- rameters of input and output membership function of a fuzzy inference system constructed by ANFIS, have been tuned (adjusted) automatically based on the training data until reach th 4.1. Data Preparation The road traffic video is recorded by a video camera. The road traffic video is 90 minutes long taken in the after- noon (15:07 to 16:37 hours) of February 2, 2011. The speed of the vehicle is calculated by noting the distance between two consecutive poles (in the middle of two lanes i.e. on the divider) that is 24 meters, and also the travel time of a vehicle between these two poles (Figure 5). And thus the average speed and number of vehicles (road density) per 20-second and also per 40-second in- terval of time is collected in the form of matrix. The av- erage speed and density every 20-second and 40-second become the input of our fuzzy inference systems (Sugeno & Mamdani). Another type of input besides vehicle den- sity and speed, is the human evaluated of congestion level. By watching the traffic video several times, and we form a common sense to decide the level of congestion (LOC) every 20-second and 40-s evaluate five level of cong moving, mild congestion, heavy congestion and serious jam, ranging from “0” to “3”, in which “0” means free flow and “3” means serious jam. By this way six datasets are prepared in the form of matrices, in which column 1 is average speed, column 2 is density and column 3 is LOC (level of congestion), and each dataset contains 68 data pairs (no. of rows), thus we have six 68 × 3 matrix datasets as: Dataset I: Average speed, density and LOC every 20-second interval of Lane I (left lane); Dataset II: Average speed, density and LOC every 40-second interval of Lane I (left lane); Dataset III: Average speed, density and LOC every 20-second interval of Lane II (right lane); Dataset IV: Average speed, density and LOC every 40-second interval of Lane II (right lane) Dataset V: Average speed, total density and LOC eve- ry 20-second interval of Lane I & Lane II; Dataset VI: Average speed, total density and LOC eve- ry 40-seconds interval of Lane I & II. 4.2 Accuracy Assessment For each input pair (Speed and Density) there is an out- put value of LOC which is called a data point, the human evaluated LOC is taken as the standard data of LOC and depends on the human perceptions, and the model evalu- ated LOC is on the adjustment of input/output membership func- tions of the model. The performance aluated by a metric, called accuracy which shows how many output data points of the model rresponding human evaluated output data points. The accuracy of the system is defined by Equat Total DataPointsIncorrectDataPoints Accuracy TotalData Points (10) In addition, to measure how far the incorrect data points are from the human opinion, another metric is lled average deviation and is given by ca Copyright © 2012 SciRes. JTTs  H. SHANKAR ET AL. Copyright © 2012 SciRes. JTTs 56 Figure 5. Images taken from traffic video. AverageDeviation FuzzyScoreHumanOpinion Score TotalData Points (11) Human Opinion Score is the LOC rated by human pioneers, corresponding to each pair of inputs, and Fuzzy Score is the LOC rated by the fuzzy system, correspond- ing to the same input pair. The lower value of average deviation means higher the accuracy of the system and vice-versa. Results and Discussions There are eighteen experiments on LOC evaluat on the derived parameters described previously, six ex- periments for each technique. In each experiment, we va ut LOC are different for different inference of congestion (0 - 3) is ach model, the MFs of Rule 7: If (Speed is fast) AND (Density is high) then (LOC is slow moving1); Rule 8: If (Speed is fast) AND (Density is medium) then (LOC is free flow2); Rule 9: If (speed is fast) AND (Density is low) then (LOC is free flow1). Experiment I: Average Speed, Density Evaluation of Lane I, 20-Second by Sugeno Model Inputs into the Sugeno model are the average speed e left lane. Here the input MFs are nd the output MFs are constant type. Th and density in th trapezoidal type a e range of the speed is between 0 - 60 km/hr and den- sity range between 0 - 40 vehicles per 20 seconds. The M 5. ion based F ranges for average speed are less than 18 km/hr for slow, 15 - 35 km/hr for medium and more than 30 km/hr for fast. The MF ranges for density are 0-10 vehicles for low, 7 - 22 vehicles for medium and more than 18 vehi- cles for high. The output LO ry types of input parameters and the evaluation interval. In all the experiments the membership function ranges are changed. There are three membership functions of Speed namely slow, medium and fast, three membership function of Density namely low, medium and high. The MFs of outp C has nine MFs, namely 2 free flow, 2 slow moving, 1 mild congestion, 2 heavy congestion and 2 serious jam corresponding to the ranges 0, 0.67, 1, 1.33, 1.67, 2, 2.33, 2.67, and 3. First we get the LOC by manually putting the values of speed and density in the model and then train this model using AN- FIS tool using model output as systems, but the range of the level same for all the experiments. For e training data and under 80 epochs. ANFIS automatically adjusted MF parameters and gives better result. Th output (LOC) are nine in numbers namely—2 free flow, 2 slow moving, 1 mild congestion, 2 heavy congestion and 2 serious jam. The “if-then” fuzzy rules are applied on the experiments (Sugeno, 1983), as follows: Rule 1: If (Speed is slow) AND (Density is high) then (LOC is serious jam1); Rule 2: If (Speed is slow) AND (Density is medium) then (LOC is serious jam2); Rule 3: If (Speed is slow) AND (Density is low) then (LOC is heavy congestion1); Rule 4: If (speed is medium) AND (Density is high) then (LOC is heavy congestion2); Rule 5: If (Speed is medium) AND (Density is me- dium) then (LOC is mild congestion) Rule 6: If (speed is medium) AND (Density is low) then (LOC is slow moving2); e MFs and Fuzzy rules, and 3D surface are shown in Figure 6. The list of output LOC for every data pair is shown in the Table 1. The human evaluated values and model ba- sed LOC values are closely matching with respected to the given input variables. The difference of 0.20 in val- ues of LOC is considered as acceptable error for conven- ience (0.20 is about 7% of LOC range). The MFs above yield the accuracy of 55.88%, and average deviation of 0.0426323 levels. Experiment II: Average Speed and Density Evalua- tion of Lane II, 20-Second by Sugeno Model In a 20 second evaluation interval and Sugeno-type inference system, inputs fed into the system i.e. average speed and density of the right lane. The model is trained 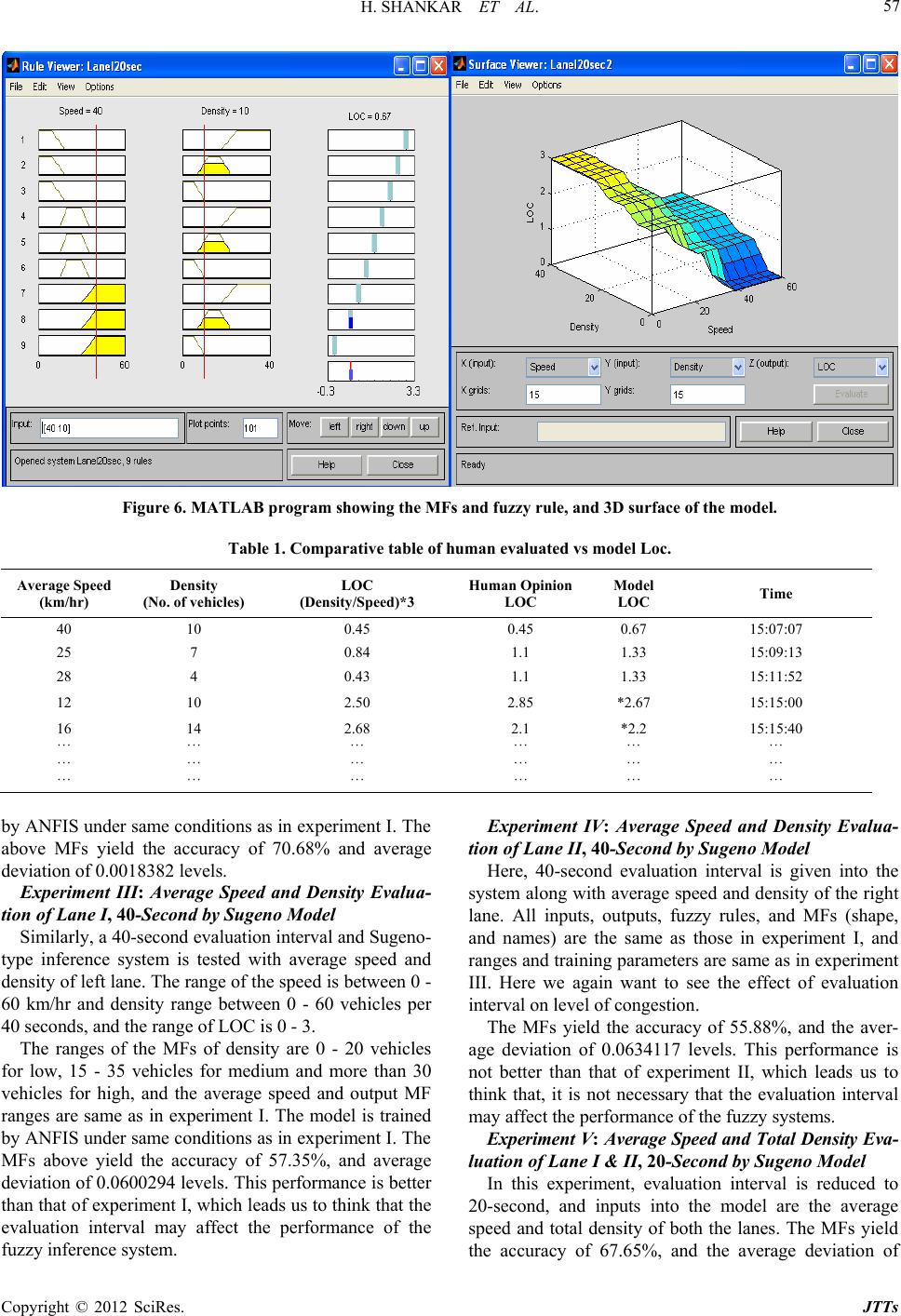 H. SHANKAR ET AL. 57 Figure 6. MATLAB program showing the MFs and fuzzy rule, and 3D surface of the model. Table 1. Comparative table of human evaluated vs model Loc. Average Speed (km/hr) Density (No. of vehicles) LOC (Density/Speed)*3 Human Opinion LOC Model LOC Time 40 10 0.45 0.45 0.67 15:07:07 25 7 0.84 1.1 1.33 15:09:13 28 4 0.43 1.1 1.33 15:11:52 12 10 2.50 2.85 *2.67 15:15:00 16 ··· ··· ··· 14 ··· ··· 2.68 ··· ··· 2.1 ··· ··· *2.2 ··· ··· 15:15:40 ··· ··· ··· ··· ··· ··· ··· by ANFIS under same conditi above MFs yield the accuracy of 70.68% de 01838 Ex Id and- tion of I, 40-Second by Sugeno Model Similarly, a 40-secondaluation interval augeno- type inference system issted with averagd and density lane. The ge of the speed iseen 0 - 60 km/hr and density ra between 0 - 60 ve 40 seco and the rang LOC is 0 - 3. The ges of the MFf density are 0 - hicles for low - 35 vehicler medium and mthan 30 ehicles for high, and the average speed and output MF of 57.35%, and average de ink that the ev Speed and Density Evalua- by Sugeno Model ondtion intervaliven into the systeng with e speed and dey of the right lane. All inputs, ou, fuzzy ruleFs (shape, and ns) are thee as those ient I, and ranged training eters are sa experiment III. Here we again want to see the effect of evaluation interval The MFs yield thcuracy of 55.88%, and the aver- age dtion of 0.0117 levels. Therformance is not better than that of experiment II, h leads us to think that, it is not necessary that the evaluation interval no Model ons as in experiment I. The and average Experiment IV: Average tion of Lane II, 40-Second viation of 0.0 periment II2 levels. : Average Spee Density Evalua Lane evnd S tee spee of leftran betw ngehicles per nds,e of rans o20 ve , 15s foore v ranges are same as in experiment I. The model is trained by ANFIS under same conditions as in experiment I. The MFs above yield the accuracy viation of 0.0600294 levels. This performance is better than that of experiment I, which leads us to th aluation interval may affect the performance of the fuzzy inference system. may affect the performance of the fuzzy systems. Experiment V: Average Speed and Total Density Eva- luation of Lane I & II, 20-Second by Suge Here, 40-sec m alo evalua averag is g nsit tputss, and M ame samn experim s anparamme as in on level of congestion. e ac evia634is p whic In this experiment, evaluation interval is reduced to 20-second, and inputs into the model are the average speed and total density of both the lanes. The MFs yield the accuracy of 67.65%, and the average deviation of Copyright © 2012 SciRes. JTTs  H. SHANKAR ET AL. 58 0.1573970 levels. Experiment VI: Average Speed and Total De nsi ty Eva- luation of Lane I & II, 40-Second by Sugeno Model In this experiment, we assume 40 second evaluation interval with inputs average speed and total density of both the lanes into the system. All inputs, outputs, fuzzy ru xperiment is s evaluation interval in- cr stem is us ne. H 18 km/hr for slow, 15 - 35 km/hr for m for m les and MFS (shape, and names) are the same as those in experiment I. Average speed range in the e same as experiment I, and we have changed the range of total density to 0 - 80. The MF ranges of total density are low (below 22 vehicles), medium (18 - 40 vehicles) and high (above 35 vehicles). The MFs yield the accu- racy of 72.05%, and the average deviation of 0.1564117 levels. Here, the evaluation interval improves the accu- racy of the model, it means a eases, accuracy of the model also increases and vice- versa. Experiment VII: Average Speed and Density Evalua- tion of Lane I, 20-Second by Mamdani Model In this experiment, Mamdani-type inference sy ed with 20-second evaluation interval. Inputs into the system are the average speed and density of left la ere the input MFs are trapezoidal type and the output MFs are also trapezoidal. The range of the speed is be- tween 0 - 60 km/hr and density range is between 0 - 40 vehicles per 20-seconds. The MF ranges for average speed are less than edium and more than 30 km/hr for fast. The MF ranges for density are 0 - 10 vehicles for low, 8 - 22 vehicles edium and more than 19 vehicles for high. The output level of congestion has nine members, namely 2 free flow, 2 slow moving, 1 mild congestion, 2 heavy conges- tion and 2 serious jam corresponding to the ranges below 0.65, between 0.55 - 1.25, 1.15 - 1.85, 1.75 - 2.45 and above 2.35. The LOC is obtained by manually putting the values of speed and density in the model (in rule viewer) and then compare with the human evaluated LOC. In Figure 7, shows the MFs of input/output variable and Fuzzy Rule viewer, and 3D surface of the model. The MFs above yield the accuracy of 82.35%, and the aver- age deviation of 0.1115213 levels. Experiment VIII: Average Speed and Density Eva- luation of Lane II, 20-Second by Mamdani Model In this experiment, Mamdani-type inference system is used with 20-second evaluation interval, and inputs into the system are the average speed and density in the right lane. All inputs, output, fuzzy rules, and MFs (shape, ranges and names) are the same as those in experiment VII. The MFs above yield the accuracy of 83.82%, and the average deviation of 0.0917643 levels. Experiment IX: Average Speed and Density Evalua- tion of Lane I, 40-Second by Mamdani Model In this experiment, a 40-second evaluation interval, and inputs into the system are the average speed and den- sity in the left lane. All inputs, output, fuzzy rules, and MFs (shape, and names) are the same as those in experi- ment VII. The ranges of input speed and output LOC and their MFs are same as those of experiment VII. The range of density between 0 - 60 vehicles per 40 seconds and the ranges of MFs of density are, below 20 for Low, between 15 - 35 for Medium and above 31 for High. The MFs above yield the accuracy of 77.94%, and the aver- age deviation of 0.1112561 levels. This performance is not better than that of experiment VII, which infers that it is not necessary that the evaluation interval could im- prove the accuracy of the Mamdani-type fuzzy inference system. Figure 7. MATLAB program showing MFs and fuzzy rules, and 3D surface of the model. Copyright © 2012 SciRes. JTTs  H. SHANKAR ET AL. 59 Experiment X: Average Speed and Density Evalua- tion of Lane II, 40-Second by Mamdani Model In this experiment, under similar conditions of ex- periment IX, the MFs yield the accuracy of 73.52%, and the average deviation of 0.1441361 levels. This per- formance is not better than that of experiment VIII, wh- ich again leads to think that it is not necessary that the evaluation interval could improve the accuracy of the Mamdani-type fuzzy inference system. Experiment XI: Average Speed and Density Evalua- tion of Lane I & II, 20-Second by Mamdani Model In this experiment, Mamdani-type inference system is used with 20-second evaluation interval, and inputs into the system are the average speed and density of both the lanes. All inputs, output, fuzzy rules, and MFs (shape, and names) are the same as those in experiment VII. The ranges of inputs and output LOC and their MFs of are same as those of experiment IX. The MFs above yield of . Experiment XIII: Average Speed and Density Eva- luation of Lane I, 20-Second by ANFIS Model ANFIS model is deployed with the three gbell’s MF for each input, and nine linear MF for the output. The ranges of each variable are automatically decided by us- ing grid Partition technique using Matlab ANFIS tools. Inputs into the system are the inputs average speed, den- sity and output human opinion LOC of left lane in the form of a matrix (dat.file). The input-output dataset are then passed through the ANFIS tool for learning and automatically adjusting the output. After 100 epochs, and using hybrid learning algorithm, the automatically gener- ated FIS is trained, and thus the ANFIS is ready to evaluate the congestion status. The ANFIS outputs after training,model and structure are shown in Figure 8(a) and (b). The MFs above yields the accuracy of 72.05%, and the average deviation of 0.0005667 levels. Experiment XIV: Average Speed and Density E odel the accuracy 0 64.70%, and the average deviation of luation of Lane II, 20-Second by ANFIS M 1756654 levels Experiment XII: Average Speed and Density Evalua- tion of Lane I & II, 40-Second by Mamdani Model This experiment is deployed with Mamdani-type in- ference system with 40-second evaluation interval, and inputs into the system are the average speed and density of both the lanes. All inputs, output, fuzzy rules, and MFS (shape, and names) are the same as those in ex- periment VII. The ranges of input speed and output LOC and their MFs are same as those in experiment VII. The range of density between 0 - 60 vehicles per 40 seconds and the ranges of membership functions of density are, below 22 for Low, between 18 - 40 for Medium and above 35 for High. The MFs above yield the accuracy of 63.23%, and the average deviation of 0.1867251 levels. This performance is not much better after increasing the evaluation interval for both the lanes. Again it is not clear that evaluation interval could improve the performance of the model. va- In this experiment, we repeat the same procedure as in experiment XIII, but the input-output dataset of left lane is loaded into the ANFIS tool. The MFs above yield the accuracy of 80.88%, and the average deviation of 0.0870766 levels. Experiment XV: Average Speed and Density Evalua- tion of Lane I, 40-Second by ANFIS Model In this experiment, we repeat the same procedure as in experiment XIII, but the evaluation interval increases from 20 seconds to 40 seconds, and input-output dataset of left lane is loaded into the ANFIS tool. The MFs above yields the accuracy of 88.23%, and the average deviation of 0.0109558 levels. This performance is better than that of experiment VII, which leads to think that the evaluation interval may affect the performance of the ANFIS. Experiment XVI: Average Speed and Density Eval- uation of Lane II, 40-Second by ANFIS Model In this experiment, we repeat the same procedure as in (b) (a) Figure 8. (a) Training and FIS output; (b) ANFIS model str ucture . Copyright © 2012 SciRes. JTTs  H. SHANKAR ET AL. 60 experiment XV, but input-output dataset of right lane is loaded into the ANFIS tool. The MFs yield the accuracy of 77.94%, and the average deviation of 0.0018514 levels. This performance is impressive than that of experiment could im XIV, which leads to think that it is not necessary that the evaluation interval could improve the accuracy of the ANFIS. Experiment XVII: Average Speed and Total Density Evaluation of Lane I & II, 20-Second by ANFIS Model In this experiment, we repeat the same procedure as in experiment XIII, but the input-output dataset of both the lanes is loaded into the ANFIS tool. The MFs yield the accuracy of 73.52%, and the average deviation of 0.0018 661 levels. Experiment XVIII: Average Speed and Total Density Evaluation of Lane I & II, 40-Second by ANFIS Model In this experiment, the same process is repeated as in experiment XIII and XVII, but the evaluation interval increases from 20-second to 40-second. The uracy of 72.05 prove the performance of ANFIS. Table 2 sum- m model is higher than the manually tuned Mamdani and Sugeno model. However, the accuracy achieved by manually tuned Mamdani and Sugeno model is very near to that of ANFIS model, which shows that fuzzy infer- ence systems can capture the human perceptions as well. Overall the maximum accuracy achieved by Sugeno model is 72.05%, Mamdani model is 83.82% and ANFIS model is 88.23%. These models are also applied after changing the evaluation interval of each lane individually and combination of both and evaluate the accuracy of the models. For left lane, as the evaluation interval increases from 20 seconds to 40 seconds then the accuracy of Sugeno model increases from 55.88% to 57.35%, but the ame time accuracy of Mamdani model reduces nd the accuracy of ANFIS model 3%, which shows that it is f m rs MFs above 82.35% to 77.94% a yield the acc%, and the average deviation increases from 72.05% to 88.2 reach to 0.0003088 levels. This performance is not again very impressive after increasing the evaluation interval. Therefore, it is not conclusive that evaluation interval Table 2. Summary o Experiment No. Fuzzy System Input par amete arizes the accuracy and average deviation of all the above experiments. In most of the cases the accuracy achieved by ANFIS s from not necessary that evaluation interval could improve the accuracy of the model. Also for right lane as the evalua- tion interval increases from 20 seconds to 40 seconds, the odel performance. Evaluation Interval Accuracy Average deviation I Sugeno-type Avg.Speed, Density of left lane 20 seconds 55.88% 0.0426323 II Sugeno-type Avg.Speed, Density of right lane e th l th l e e th l h l XIII ANFIS Avg.Sp 20 seconds 70.58% 0.0018382 40 seconds 57.35% 0.0600294 40 seconds 55.88% 0.0634117 anes 20 seconds 67.65% 0.1573970 anes 40 seconds 72.05% 0.1564117 20 seconds 82.35% 0.1115213 20 seconds 83.82% 0.0917643 40 seconds 77.94% 0.1112561 40 seconds 73.52% 0.1441361 anes 20 seconds 64.70% 0.1756654 anes 40 seconds 63.23% 0.1867251 III Sugeno-type Avg.Speed, Density of left lane IV Sugeno-type Avg.Speed, Density of right lan V Sugeno-type Avg.Speed, Total Density of bo VI Sugeno-type Avg.Speed, Total Density of bo VII Mamdani-type Avg.Speed, Density of left lan VIII Mamdani-type Avg.Speed, Density of right lane IX Mamdani-type Avg.Speed, Density of left lane X Mamdani-type Avg.Speed, Density of right lan XI Mamdani-type Avg.Speed, Total Density of bo XII Mamdani-type Avg.Speed, Total Density of bot eed, Density and Human opinion LOC o f left laneconds 72.05% 0.0005667 Avg.Speed, Dinion LOC o e 20 s f XIV ANFIS ensity and Human op right lane X opinion LOC o 20 seconds 80.88% 0.0870766 V ANFIS Avg.Speed, Density and Human f left lane X pinion LOC o 40 seconds 88.23% 0.0109558 VI ANFIS Avg.Speed, Density and Human o f right lane Avg.Speed, Total Density and 40 seconds 77.94% 0.0018514 XVII ANFIS Human opinion20 seconds 73.52% 0.0018661 XVIII ANFIS an opinion LOC of both lanes 40 seconds 72.05% 0.0003088 LOC of both lanes Avg.Speed, Total Density and Hum Copyright © 2012 SciRes. JTTs  H. SHANKAR ET AL. 61 accuracy of Sugeed 55.88%, accuracy of Mamdani model decreases from 83.82% 73.52%f from 8% to 77rl both the lanes, the accuracy Suge from 5% to 7r decrearom 643 FIS mel decrea.5 again shows that it is val coproven 6. Conclusions In this study, we prophe a of fuzzy infer- ence system (Sugeno-type, Mam neuro-fuzzy inference system) the lestion. Basically the level of congestion (LOC) offi able to express the situation frolow to serious traffi The perfo of evaluated by measuring accurac an n. Througent e interval cy, but this effect depends on nature articular road segment and particular Practical applications of Research,” US Department of Commercen DC, D. Branston, Fun portation Rl. 10, 76, p doi:10.1016 (76)90 no model ruced from 70.58% to to, and that oANFIS model decreases [2] 0.88.94%. Similay for the combination of of 2.05%, accu no model increases acy of Mamdani model 67.6 ses f.70% to 63.2%, and that of the AN- odses from 73 not necessary t 2% to 72.05%, which hat evaluation inter- uld im the performace of the model. osed tdvantage dani-type and adaptive technology, to evaluate vel of road traffic conge road trafcs is a continuous vari- m free f c jam.rmanceour proposed systems is y of outputs against hu- xperiments, we find that mopinioh differ the manually tuned fuzzy inference system achieve the accuracy which is very near to the accuracy achieved by adaptive neuro-fuzzy inference system. It means the fuzzy inference system can capture the human expertise better than manual adjustment of input/output member- ship functions. Two types of fuzzy logic inputs- average speed and density within an interval. We investigate the effect of using single lane traffic information as opposed to two lane information. It is also observed that how the evaluation interval affects the accuracy of the system. The results are not conclusive whether longer can improve accura of traffic flow at p time. The systems used in this study have advantage of minimum requirement of input data, and better accuracy and reduced error margin. Therefore, it is possible to use fuzzy system to evaluate the road traffic congestion with greater accuracy and low error margins. However, accu- racy of fuzzy systems depends highly on the types of rules, and how the rules are defined along with member- ship function ranges. Future Scope: In general, the congestion is the re- striction in the movement of the vehicles on the roads, therefore it can be compared with the impedance of the roads which can be used in the network analysis in GIS. In addition to that, congestion can be evaluated for dif- ferent times and thus temporal impedance can be calcu- lated which can be used in temporal network analysis. REFERENCES [1] Bureau of Public Roads, “Highway Capacity Manual: , Washingto 1950. “Link Capacity esearch, Vo ctions: A Re No. 4, 19 view” Trans- p. 223-236. /0041-1647 055-1 [3] P. Posawang,ard, W. Atikom, “Pased Rfic Colas- sification Ual NetProcethe World Congress on Engineering [4] A. P. Addepalli, “Study of Mraffic ac- teristics: Ac Simulation Approachm,” M.Tech Thesis, IIT, Mad. C.-C. Lee, ic in Cstemgic ller ransac Syste Cyberneticso. 2, 1 404-4 110 S. Phosa erception-B Polnigongit and W oad Traf . Pattara- ngestion C sing Neurworks,” , London, 1-3 edings of July 2009. ixed TFlow Char Microscopi ras, 2000 [5] “Fuzzy Logontrol Sys: Fuzzy Lo ControI,” IEEE T , Vol. 20, N tions on 990, pp. ms, Man and 18. doi:10. 9/21.52551 [6] C.-C. L Contro ee, “Fuzzy Logic in Control Systems: Fuzzy Logic ller ransa Syst etics, Vol. 20, No. 2, 1990, pp. 419-435. II,” IEEE Tctions onems, Man and Cybern doi:10.1109/21.52552 [7] A. Kablan,Neuroferen Financial Tng Intason odel ademy ce, En Technology o. , 2079-48 “Adaptive rading Usi -Fuzzy In raday Se ce System for ality Observa- tion M,” World Ac , Vol. 58, N of Scien 09, pp. 4 gineering and 8. [8] F. Porikli and X. Li, “Traffic Congestion Estimation Us- ing HMM Models without Vehicle Tracking,” IEEE In- telligent Vehicles Symposium, Parma, 14-17 June 2004, pp. 188-193. doi:10.1109/IVS.2004.1336379 [9] W. Pattara-Atikom and P. Pongpaibool, “Estimating Road Traffic Congestion Using Vehicle Velocity,” Proceeding of 6th International Conference on Telecommunications, Chengdu, June 2006, pp. 1001-1004. [10] B. Krause and C. von Altrock, “Intelligent Highway by Fuzzy Logic: Congestion Detection and Traffic Control on Multi-Lane Roads with Variable Road Signs,” 5th In- ternational Conference on Fuzzy Systems, New Orleans, 8-11 September 1996, pp. 1832-1837. doi:10.1109/FUZZY.1996.552649 [11] A. S. Alfa, “Understanding Urban Traffic Congestion dur- ing Peak Periods,” Proceedings of International Confer- ence on Road and Road Transport Problems (ICORT-88), Roorkee, 12-15 December 1988, pp. 518-527. [12] L. Jia and C. Li, “Congestion Evaluation from Traffic Flow Information Based on Fuzzy Logic,” IEEE Intelli- gent Transportation Systems, Vol. 1, 2003, pp. 50-53. [13] P. Mitra, “ANVoltage Regulator with Hybrid Learning Algorithal Journal daptive Neuro-Fuz- ment, Vol. 4, No. 1, FIS Based Automatic m,” Internation of Advances in Soft Computing and Applications, Vol. 2, 2010. [14] S. M. Seyedhoseini, “Application of A zy Inference System in Measurement of Supply Chain Agility: Real Case Study of a Manufacturing Company,” African Journal of Business Manage 2010, pp. 83-96. [15] T. O. S. Hanafy, “A Modified Algorithm to Model Highly Nonlinear System,” Journal of American Science, Vol. 6, No. 12, 2010, pp. 747-759. [16] T. Takagi and M. Sugeno, “Derivation of Fuzzy Control Rules from Human Operator’s Control Actions,” Pro- Copyright © 2012 SciRes. JTTs  H. SHANKAR ET AL. 62 ceedings of IFAC Symposium on Fuzzy Inform 2005. d ation, Transactions on Systems, Man and Cybernetics, Vol. 3, No. 1, 1973, pp. 28-44. [19] N. Patchanee, P. Tangamchit and P. Pongpaibool, “Roa Knowledge Representation and Decision Analysis, Mar- seilles, 19-21 July 1983, pp. 55-60. [17] A. P. Paplinski, “Adaptive Neuro-Fuzzy Inference S tem (ANFIS),” 20 May ys- T [18] L. A. Zadeh, “Outline of a New Approach to the Analysis of Complex Systems and Decision Processes,” IEEE raffic Estimation from a GPS-Equipped Car Using Fuz- zy Logic,” Proceeding of 29th Electrical Engineering Con- ference, Chonburi, 9-10 November 2006, pp. 1081-1084. Copyright © 2012 SciRes. JTTs |

