Journal of Transportation Technologies, 2012, 2, 41-49
http://dx.doi.org/10.4236/jtts.2012.21005 Published Online January 2012 (http://www.SciRP.org/journal/jtts)
The Dynamic Location Model to Consider
Backgr ound Traffic
Nahry Yusuf, Sutanto Soehodho
Department of Civil Engineering, Faculty of Engineering, Universitas Indonesia, Depok, Indonesia
Received October 15, 2011; revised November 17, 2011; accepted December 9, 2011
ABSTRACT
This study concerns to the determination of location of freight distribution warehouses. It is part of a series of research
projects on a distribution system we developed to deal with cases in a public service obligation state-owned company
(PSO-SOC). This current research is characterized by the consideration of background traffic of the entire time period
of planning rather than one certain time target on location model. It is aimed that the location decision to be more
applicable and accommodative to the dynamic of the traffic condition. Once the decision is implemented, it will give
the best outcome for the entire time period, not only for the initial time, end time or certain time of time period. A
heuristic approach is proposed to simplify complexity of the model and network representation technique is applied to
solve the model. A hyphotetical example is discussed to illustrate the mechanism of finding the optimal solution in term
of both its objective function and applicability.
Keywords: Background Traffic; Location Model; Freight Distribution
1. Introduction
Research on determination location of facilities of freight
distribution system has been done for many years. Those
research works are differentiated in many aspects, such
as number of types of commodities, number of channels,
variables involved, mathematical complexity, objective
of the system, and other features [1-4]. Nevertheless, this
research area is still challenging to be explored in order
to enhance the previous works and solve particular pro-
blems.
This current research is part of series of research on
location model which concerns to Public Service Obli-
gation State-Owned Company’s (PSO-SOC) distribution
system [5-7]. It is a continuation of our most recent re-
search concerning the dynamic of background traffic [8].
Background traffic is the terminology used for the move-
ment of vehicles which occupy the highway system to-
gether with freight vehicles. In our previous model, we
considered the effect of background traffic on the loca-
tion decision of warehouses. Such model, as well as other
previous location models takes into account the back-
ground traffic of certain time target (time reference).
Most of them do not mention explicitly which part of
time period of planning to represent the traffic condition
[9]. As the location decision is designed for a long time
period, such as 15 - 20 years, and it is commonly known
that the traffic is very dynamic in nature, then to consider
only one certain time to be the reference of the number of
background traffic may cause the decision obsolete prior
to its final year.
In order to accommodate the dynamic of background
traffic, we propose a dynamic location model which con-
siders the fluctuation of background traffic using time
increment during time period of planning. The location
decision of such model is amenable for people to con-
struct or operate warehouses in stages throughout time
period of planning. This current research is focused to
develop the mechanism of choosing the best combination
of warehouses to be opened to accommodate the real
traffic condition at the most and at the same time it could
be applicable in practice.
The structure of this paper is as follows. Section 2 in-
troduces the model formulation and Section 3 presents
the model solution. An illustrative example is discussed
in Section 4 to show the mechanism proposed in Section
3. Finally, Section 5 provides conclusion and future re-
search directions.
2. Model Formulation
In order to show the effect of the dynamic of background
traffic on the location decision, Figure 1 shows the rela-
tions among the determinants of location decision.
From Figure 1 it is shown that the existence of certain
warehouse may generate traffic flow, both in direct and
indirect way. It is clear that the activities of warehouse
must produce and attract some traffic flows in direct way,
C
opyright © 2012 SciRes. JTTs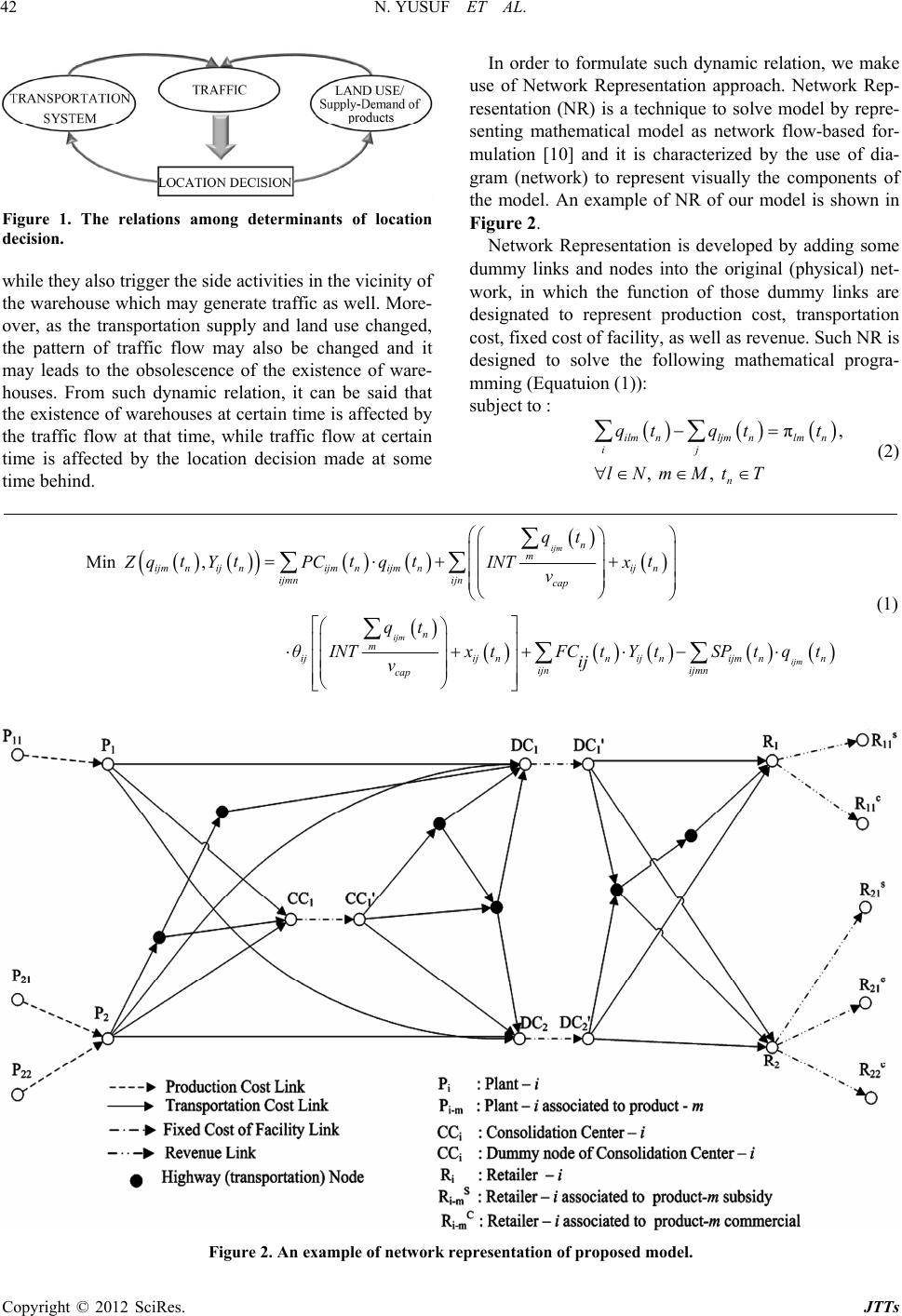

N. YUSUF ET AL.
42
Figure 1. The relations among determinants of location
decision.
while they also trigger the side activities in the vicinity of
the warehouse which may generate traffic as well. More-
over, as the transportation supply and land use changed,
the pattern of traffic flow may also be changed and it
may leads to the obsolescence of the existence of ware-
houses. From such dynamic relation, it can be said that
the existence of warehouses at certain time is affected by
the traffic flow at that time, while traffic flow at certain
time is affected by the location decision made at some
time behind.
In order to formulate such dynamic relation, we make
use of Network Representation approach. Network Rep-
resentation (NR) is a technique to solve model by repre-
senting mathematical model as network flow-based for-
mulation [10] and it is characterized by the use of dia-
gram (network) to represent visually the components of
the model. An example of NR of our model is shown in
Figure 2.
Network Representation is developed by adding some
dummy links and nodes into the original (physical) net-
work, in which the function of those dummy links are
designated to represent production cost, transportation
cost, fixed cost of facility, as well as revenue. Such NR is
designed to solve the following mathematical progra-
mming (Equatuion (1)):
subject to :


π,
, ,
ilmljm lnnm
ij
n
qq
lNmM
tt
T
t
t

 

n

 (2)
     
  
Min ,
ijm
ijm
ijm
nn nn
nn
n
m
ijmijijm nijmij
ijmnijn cap
n
m
ijijij ijm
ijn ijm
n
cap
nn
n
q
Zq YPCqINTx
v
q
θINTxFC YSP
t
ttt tt
t
tt q
ij
vtt




 








 










t
(1)
Figure 2. An example of network representation of proposed model.

N. YUSUF ET AL. 43
 

π,
,Fixed CostofFacility Link,,
m
nnijm ijs
sS
n
n
qt ttY
ijmM tT


 

(3)
 
0, ,,,
nijm n
qijAmMt   tT (4)
 


0,1 ,,,
nij n
YitjA tT (5)
Sets:
et of nodes of network representation.
ted to product-m.
M:
D
of product-m that flow from i to j at
th
house associated to (i,j) is opened at
th
it cost of production in plant-j at
th
N: S
A: Set of links of network representation.
T: Set of time of observation.
m
S: Set of plant nodes associa
Set of products.
ecision Variables:

ijm n
qt : quantity
e n-th time.

1
ij n
Yt , if ware
e n-th time, otherwise ij Y= 0.
Input Parameters:

ijm n
PCt is the un
e n-th time, where j is plant node.
cap
v is capacity of freight vehicle.

ij n
x
t is background traffic flow at the n-th time.

ij n
F
Ct is fixed cost of facility of warehouse-i at the
n-
roduct-m at retailer
associated to
pr
th time, where i is CC or DC node.

ijm n
SPt is the selling price of the p
– i at the n-th time, where i is retailer node.

πlm n t is flow requirement of node-l
oduct-m
de-l
at the n-th time, where: if l is sink node,
πlm  demand of product-m in retailer associated to
at the n-th time, if l is source node,

πlm t no n

cap-
acity of plant associated to node-l to prodct-m
at the n-th time,otherwise,
uce produ


π0
lm n
t.
Input Function:


Φ.
ij : is per unit transportation cost from i to j (a
co
of our
pr
s the production
co
e trans-
po
hown in the third term
of
Equation (1) shows the component of
re
nk has zero
va
the
flo
sed model is closely related to the minimum
co
nvex function of total quantity of traffic flow).
Equation (1) denotes the objective function
oposed model. It is actually intended to maximize the
profit, in which profit is represented by revenue minus
cost. Surely, this objective function can be replaced by a
minimization of minus profit, which is represented by
cost minus revenue. All the variables of the model are
represented in dynamic form and it is epitomized by the
use of notation

n
t. In order to state the variables in
their dynamic forme divide the time of planning T into
n-increment time. The time difference between two con-
secutive times

t does not need to be similar. For the
example, for 2ars of period of planning, we may
divide 20 years into 4 time increments with similar time
increment t and we may find 5 sets of time of ob-
servation, se are 0 t, 1 t, 2 t, 3 t and 4 t The time
0
t is representation ofhe initial ti of plaing, 1 t is
r the fifth year of time of planning, 2 t is for the h
year of time of planning and so on. Since the model
includes all the sets of time of observation, it is shown
that the model is intended to optimize the costs of the
entire time of planning simultaneously.
The first term of Equation (1) represent
, w
0 ye
tho
tmenn
fo tent
sts and it is a function of per unit of production cost
and total number of flow of the associated link. In our
NR, links associated to production cost ( production cost
links) have the unit cost which is related to the type of
product and the plant that produce such product.
The second term of Equation (1) denotes th
rtation cost. Here, both flows of freight vehicles and
the ones of background traffic contribute to the cost of
transportation. It is assumed that the unit cost of trans-
portation will increase as the volume of traffic increased
and the cost to transport any type of product is similar.
BPR’s convex function may be applied to count such
cost and it generally assumes that the transportation cost
is proportional to the travel time.
The fixed charge problem is s
Equation (1), where the variable of fixed cost of fa-
cility is not affected by the number of flows. The cost of
facility will be charged only if the warehouse is opened.
The decision to open certain warehouse is depend on
the binary number ij Y. Equation (5) shows that ij Y
will be valued by eithr 0 or 1 and it will come to t
decision to close or open warehouse related to link (i,j),
respectively.
The last term of
e he
venue of the model and negative signed is introduced
to represent the opposite character between revenue and
cost. Revenue link is characterized by the per unit selling
price of the product associated to the link.
It is clear that each of production cost li
lue for its per unit transportation cost and other com-
ponents of cost, and transportation cost link has zero
value for its production cost and other costs, so on.
Minimization problem of the model is limited by
w requirements which are related to the capacity of
plants to produce each type of products and the demand
of each retailer on such products. This constraint is
shown in Equation (2). Equation (3) is applied to gua-
rantee that there will be no flow through certain ware-
house if such warehouse is not opened. Furthermore,
Equation (4) is set as non negative flow constraint. It is
also assumed that the warehouse is unlimited in its
capacity.
The propo
st flow problem. It is one of the network flow problem
which is aimed to determine a least cost shipment of a
commodity through a network in order to satisfy de-
mands at certain nodes from available supplies at other
nodes [11].

N. YUSUF ET AL.
44
3. Model Solution
In order to minimize th
del discussed in the p
e complexity of the proposed mo-
revious section, we make use of
ctivities,
an
r time of ∆t would
be
the time period
of
heuristic approach to solve the problem. Figure 3 shows
the mechanism which is used to synthesize the dynamic
concept of the proposed location model. Based on the
capacity of plant, demand of retailers, as well as the con-
dition of the traffic and all related costs at time t0, we can
determine the decision to open a set of warehouses. Such
decision may be derived from any location model which
is aimed to minimize the cost of the system [6].
Furthermore, as the traffic changed after time t0 due to
land use development, included the warehouse a
d the demand and supply side of the products may also
be changed, we can determine the best set of warehouses
for time t1. The similar phenomenon is treated to make
location decision of time t2, t3 and t4.
In certain situation where the traffic change is pre-
dicted to be very dynamic, the shorte
required to find the best location decision which fit to
the real traffic condition at the most.
The decisions made for time t1 - t4 are actually the best
decision to locate the warehouses during
planning. This mechanism is essentially represented in
the proposed mathematical programming of Equation (1),
in which the total cost of the system during the time
period of planning is the summation of total cost of the
system of all time observations during time period of
planning. It is clear that the minimum cost of each time
of observation must make contribution to the minimum
cost of the entire time period of planning.
From the mathematical point of view, such location
decision is guaranteed to be the best decision to locate
some warehouses among one set of potential warehouses.
However, in some condition the decision could not be
applied in practice. It can be explained through Figure 3.
From the example on Figure 3, it can be seen that
warehouse 1, 2, 4 and 5 are opened at t0 but warehouse 2
is not feasible to be opened at time t1 and t2 and it is
replaced by warehouse 3 at time t2. Practically it is
actually not common to open and close warehouse con-
secutively and then open them at the following time, as
experienced by warehouse 2 and 3 of the example (Fi-
gure 3). If this is the rule, justification should be made to
decide the combination of warehouses which shall be the
second best suited to the background traffic condition
during the time period of planning while at the same it
could be feasible from the practical side.
The mechanism of making location decision which
taking into account the dynamic of traffic is presented in
Figure 4 and it could be explained as follows:
Figure 3. Dynamic of location decision.

N. YUSUF ET AL. 45
Figure 4. Step wise of choosing the second best combination of warehouses.
Step 0 : Define the time increment ∆t and time period
of planning T.
Make projection of freight supply and demand and
cost of transportation for each time of observation tn
during T, where the number of observation = T/∆t + 1.
Set n = 0.
Step 1: Do User Equilibrium traffic assignment to find
background traffic of the n-th year. The assignment must
be based on the forecasted generated trips due to land use
development (included warehouse activities) during the
period of (n – 1)-th year to n-th year.
Step 2: Make location decision of the n-th year. If the
n-th year is the final year T, go to Step 4.
Step 3: Set n := n + 1, go to Step 1.
Step 4: Set the rule for choosing the second best com-
bination of warehouses.
Step 5: Determine alternatives of combination of war-
ehouses to be opened during T.
Step 6: Do production assigment and distribution of all
time observations for all alternative combinations of ware-
houses.
Step 7: Choose the best alternative to be the second
best choice of location.
Some considerations could be used for the rule of dete-
rmining alternatives of warehouse combination (Step 4).
The rule is applied to the initial (best) combination of
warehouses and it could be explained as follows:
1) The most frequently appeared warehouses must be-
come member of the second best combination.
2) When certain warehouse is opened at certain time, it
must be opened until the final year T.
3) When there is more than ∆t years time lapse be-
tween two consecutive times of opening certain ware-
house (see the example of warehouse 2 or 3 in Figure 3),
coefficient α could be used for final decision.
4) Coefficient α represents the tolerable percentage of
lapse time between two consecutive times of opening
certain warehouse if it is compared to time T.
5) The most frequently appeared combination of ware-
houses (at the initial condition) could be the alternative
combination.
By applying such rules, we can find one or more alter-
natives of combination and we can compare the objective
function of all the alternatives and finally choose the best
one.
4. Illustrative Example
In order to show the mechanism proposed in Section 3,
the ensuing contrived example is discussed. The 2-stage

N. YUSUF ET AL.
46
distribution network consists of 2 plants, 2 potential sites
of distribution center level 1, 3 potential sites of distri-
bution centers level 2 and 3 retailers (Figure 5). It deals
with 1 type of product and 2 types of demand, those are
commercial and subsidized demand. Table 1 shows cap-
acity of each plant, as well as its production cost. Table 2
shows the demand of each retailer on each product, as
well as its selling price.
We design the time period of planning T as 20 years,
with the increment time is 5 years, so that we have 5
times of observation. As the scenario of the system, the
capacity of some links of the network is set to be 1.5
times of its initial capacity at year 10 (time t2 ) and some
other links’s are increased at year 15 (time t3). Regarding
the tolerable percentage of lapse time between two
consecutive times of opening certain warehouse, we
assume to apply coefficient α as 20%. It implies that we
may consider the existence of certain warehouse only if
maximum time lapse between two consecutive times of
opening such warehouse is 10 years (equal to 1 time of
observation).
The solution is initialized by carrying out the traffic
assignment for the initial time t0. Using any kind of traf-
fic assignment tool, link traffic flow for the entire net-
work could be determined. Based on these flows and
other parameters of supply and demands of products, lo-
cation decision of time t0 could be determined using any
kind of location model
ouse 2, 3, 4 and 5 is t0
u
make projection of the generated trips for time t1 due to
the land use development during time t0 to t
1, included
the activities of warehouses, and it is then followed by
the prediction of background traffic of the entire network
for time t1. Again, based on these flows and the projec-
tion of demand and supply of the products at time t1, lo-
cation decision of time t1 is determined. Furthermore, the
location decisions of the remaining time of observation
may be determined with the similar way. The more the
number of time increment (time of observation), the
more fit the decision to the real condition of traffic. From
this notion, we may also find that if the location model
only considers one certain time for representing the back-
ground traffic (such as initial time, mid year or final
year), we may lose the opportunity to reduce the cost (or
increase the profit) from the system.
Figure 6 shows the best combination of warehouses of
the illustrative example for the entire period of planning.
From Figure 6, it can be seen that at the initial time (t0)
the best composition of warehouses is 2, 3, 4, and 5. At
time t1, the location decision is not changed even though
the composition of background traffic is changed. As
some link capacities are changed at time t2, the com-
position of warehouses is changed to warehouse 1 and 4.
Finally, at time t3 and t4 warehouse 1, 3, 4 and 5 become
the best composition. Since such compositions are der-
ived from the location model which is applied at the
is clear that the com-
6 could be considered
[6]. Figure 6 shows that ware-
he best combination for time t.
entire time period of planning, it
bination of warehouses on Figureh
F rthermore, having the best location of time t0, we can
as the best composition of warehouses.
work of the example. Figure 5. Distribution net

N. YUSUF ET AL. 47
Table 1. Plant capacity.
Plant Capacity (unit cost of production)
Plant
Product-1
1 1000 (4)
2 2000 (5)
Total 3000
Table 2. Demand.
Demand on product(selling price)
Retailer
1S 1
C
1 400 (20) 600 (50)
2 200 (20) 700 (75)
3 200 (20) 900 (50)
Total 3000
S: Subsidy, C: Commercial.
Furthermore, when we investigate the best combina-
tion on Figure 6, we can see that warehouse 2 is actually
not feasible to be opened since it is just opened at time t0
and t1, and it is not required at the remaining time. For
warehouse 3 and 4, even though they are not required at
time t2, we may still consider them due to the existence
of the coefficient of α.
By applying some rules as described in Section 3, we
can propose 3 alternatives of combination of warehouses
to be applied. For each of alternatives we can determine
its objective function throughout the time period (Table
3). It is carried out in the slightly similar way with Step 1
and 2 of step wise on Figure 4. The only difference is the
location decision of step 2 is replaced by allocation deci-
sion. In allocation problem, the existence (location) of
warehouses is predetermined.
Figure 6. The (initial) best combination of warehouses (Ob-
jective function = 246659).
among the three
alternatives in term of its objective function and it in-
dicates that warehouse 1, 3, 4 and 5 are feasible to be
opened during the time period of planning to replace the
initial best combination as shown in Figure 6. From the
context of objective function, it is understood that the
alternative 1 is supposed to give more profit than the
others and it is the closest alternative to the best one.
Table 3. The objective functions of the alternatives of warehouse combination.
Objective Function (DC opened)
Figures 7(a)-(c) and Table 3 show the three alterna-
tives, together with the associated objective function for
the entire time of planning. Since our mathematical mo-
del is a minimization problem, in which the value of the
objective function represents minus profit which will be
gained by the company by opening the associated ware-
houses, the bigger the number, the worse the value of the
decision. Since the initial best combination is found
through the optimization of location model, then the ob-
jective functions of all the alternatives must be worse
than the initial best one but it may be more practical to be
applied.
From Figures 7(a)-(c) and Tab le 3, it can be seen that
alternative 1 (Figure 7(a)) is the best
Alternatives of warehouse
combination
t0 t1 t2 t3 t4 Total
The initial (best) combination –52,769
(2, 3, 4, 5)
9198
(2, 3, 4, 5)
50,244
(1, 4)
76,872
(1, 3, 4, 5)
163,014
(1, 3, 4, 5) 246,659
Alternative 1 –35,507
(1, 3, 4, 5)
29,769
(1, 3, 4, 5)
122,439
(1, 3, 4, 5)
76,872
(1, 3, 4, 5)
163,014
(1, 3, 4, 5) 356,587
Alternative 2 –52,769
(2, 3, 4, 5)
9198
(2, 3, 4, 5)
83,135
(2, 3, 4, 5)
126,153
(2, 3, 4, 5)
219,116
(2, 3, 4, 5) 384,833
Alternative 3 –52,769
(2, 3,
9,198 84,865 126,689
4, 5)
217,528
(1, 2, 3, 4, 5) 385,511 4, 5) (2, 3, 4, 5) (1, 2, 3, 4, 5) (1, 2, 3,

N. YUSUF ET AL.
48
(a)
(b)
(c)
Figure 7. ative 1 of waombin
jective function = 356587); (b) Thtive 2
house combination (Objective function = 384833);e
Alternativouse combijectiv
= 385511).
5.
(a) The Alternrehouse catb-
of ware-
ion (O
e Alterna (c) Th
e 3 of warehnation (Obe function
Conclusions
We propose a new approach of finding the best location
of distribution warehouses which is aimed not only to
minimize the cost (or maximize the profit) but also to
accomodate the practical side of development a set of ware-
houses. The main characteristic of the model is the in-
clusion of the background traffic of the entire time period
of planning which is divided into some increment times.
The location decision could be utilized to build or open
the warehouse(s) in stages during time period of planning.
Mechanism proposed to select the best composition of
warehouses is dominated by the heuristic approach. Fur-
ther research is recommended to scrutinize the rules of
warehouse selection in order to find the second best
decision which is as close as possible to the best one.
REFERENCES
[1] R. K. Ahuja, T. L. Magnanti and J. B. Orlin, “Network
Flows,” Prentice Hall, Hoboken, 1993.
[2] K. S. Bhutta, F. Huq, G. Frazier and Z. Mohamed, “An
Integrated Location, Production, Distribution and Invest-
ment Model for a Multinational Corporation,” Interna-
tional Journal Production Economics, Vol. 86, No. 3, 2003,
pp. 201-216. doi:10.1016/S0925-5273(03)00046-X
[3] L. Dupont, “Branch and Bound Algorithm for a Facility
Location Problem with Concave Site Dependent Costs,”
International Journal Production Economics, Vol. 112,
No. 1, 2008, pp 245-254. doi:10.1016/j.ijpe.2007.04.001
[4] F. Glover, D. Klingman and N. V. Phillips, “Network
Models in Optimization and Their Applications in Prac-
tice,” John Wiley & Sons, Inc., Hoboken, 1992.
doi:10.1002/9781118033173
[5] Nahry and S. Soehodho, “Consideration of the Dy- namic
of Traffic Congestion on Location Model,” Proceedings
the 16th HKSTS International Conference, Hong Kong,
2011, (Unpublished).
[6] G. T. Ross and R. M. Soland, “A Multicriteria Approach
to the Location of Public Facilitis,” European Journal of
. 5, 1980, pp. 307-321.
doi:10.1016/0377-2217(80)90142-3
e
Operational Research, Vol. 4, No
y, “Strategic Design of Dis- tri-
bution System of State-Owned Companies: Preliminary
tage of Logistics Research Ses and Eva on
Model Parameters,” International Journal on Logistics
TranspoVol. 3, N9.
[8] Soehodhry, “T Consideration in
Design of Freight Distribution System,” IATSS Research,
34, Nopp. 55-
[9] S. Soehodho and Nahry, “Optimization of Location Mo-
of Capaetwork Transpol.
o. 1, 2-68.
[10] ty Location Pro-
ing ch,s andons
ch,9, 23-2589.
[7] S. Soehodho and Nahr
Seri luation
and rtation, o. 1, 200
S. o and Nahraffic Flow
Vol. ., 1, 201061.
del citated N,” Jurnal ortasi, V
11, N011, pp. 59
M. Sun, “Solvin
blem
g the Uncapac
Tabu S
itated Facili
Compute Us
Resear
ear
Vol. 33, No.
” r
006, pp. 256
Operati

N. YUSUF ET AL. 49
doi:10.1016/j.cor.2005.07.014
[11] Y. Bai, T. Hwang, S. Kang and Y. Ouyang, “Biofuel Re-
finery Location and Supply Chain Planning under Traffic
ransportation Research, Part B, Vol. 45,
162-175. doi:10.1016/j.trb.2010.04.006
Congestion,” T
No. 1, 2011, pp.