Journal of Transportation Technologies, 2012, 2, 32-40
http://dx.doi.org/10.4236/jtts.2012.21004 Published Online January 2012 (http://www.SciRP.org/journal/jtts)
Developing a Novel Method for Road Hazardous Segment
Identification Based on Fuzzy Reasoning and GIS
Meysam Effati1, Mohammad Ali Rajabi1, Farhad Samadzadegan1, J. A. Rod Blais2
1Department of Geomatics Engin eer ing, University of Tehran, Tehran, Iran
2Department of Geomatics Engineering, University of Calgary, Calgary, Canada
Received October 29, 2011; revised December 1, 2011; accepted December 15, 2011
ABSTRACT
Roads are one of the most important infrastructures in an y countr y. One prob lem on road based transportation networks
is accident. Current methods to identify of high potential segments of roads for accidents are based on statistical ap-
proaches that need statistical data of accident occurrences over an extended period of time so this cannot be applied to
newly-built roads. In this research a new approach for road hazardous segment iden tification (RHSI) is introdu ced using
Geospatial Information System (GIS) and fuzzy reasoning. In this research among all factors that usually play critical
roles in the occurrence of traffic accidents, environmental factors and roadway design are considered. Using incomplete
data the consideration of uncertainty is herein investigated using fuzzy reasoning. This method is performed in part of
Iran's transit roads (Kohin-Loshan) for less expensive means of analyzing the risks and road safety in Iran. Comparing
the results of this approach with existing statistical metho ds shows advantages when data are uncertain and incomplete,
specially for recently built transportation roadways where statistical data are limited. Results show in some instances
accident locations are somewhat displaced from the segments of highest risk and in few sites hazardous segments are
not determined using traditional statistical methods.
Keywords: Fuzzy Inference Systems (FIS); Geospatial Information System (GIS); Road Hazardous Segment
Identification (RHSI)
1. Introduction
The road based transportation networks have become the
most important part of the infrastructure in all countries.
Roads are not only important as the physical structure of
the society, but also as the foundation for social and eco-
nomic developments. An increased demand for suburban
mobility also increases the problems caused by transpor-
tation networks. One of these problems is accident oc-
currence. Several factors such as human factors, vehicle
factors, environmental factors and roadway design usu-
ally play a role in traffic accident occurrence [1]. At pre-
sent in Iran, accident data obtained from the “Analysis
Form for Traffic Accidents” are used to identify the road
segments with high potential for accident. This form is
filled out by a police officer for each traffic accident with
casualties on a public road in Iran. Based on the informa-
tion in these forms this method picks some segments
with high potential for accident and then the danger re-
lated to these segments is estimated using statistical ap-
proaches. Since there is no statistical information for the
newly-built route available, this method cannot be used
for transportation networks that have been recently built.
This research introduces a new and general method for
identification of road segments with high potential for
accident in transportation networks. Although driver mis-
takes often contribute greatly to the occurrence of any
particular accident event, spatial analysis of road haz-
ardous segments help to explain why accidents are more
frequent in some segments than in others. The study area
is Kohin-Loshan transit road that connects Tehran to the
North of Iran and is located in a mountainous region that
has most factors for accident occurrences. Since the
study area is an old one and adequate spatial data were
not available, among several factors that usually play a
role in traffic accident occurrence, in this research only
environmental factors and roadway design are considered.
Moreover, integrated use of GIS and fuzzy reasoning is
used for identification of roads hazardous segments. Geo-
spatial Information System (GIS) is a technology which
when incorporated in the analysis of road hazards, can
facilitate a quick way of data retrieval, in addition to fa-
cilitating a means of making precise remedial engineer-
ing designs to improve road sections which are prone to
road traffic accidents [2]. The most straightforward use
of GIS for accidents analysis is the examination of spatial
characteristics of accident locations [3]. Road hazardous
C
opyright © 2012 SciRes. JTTs

M. EFFATI ET AL. 33
segment identification can benefit from the data man-
agement, representation and spatial analytical functions
offered by a GIS. This research shows how integrated
use of GIS and fuzzy reasoning can be properly applied
in modeling uncertainty of road hazardous segment iden-
tification. The terminology of fuzzy logic for spatial in-
formation management and modeling localities is intro-
duced in Section 2.1. In the following related researches
and proposed method is introduced. Section 3 presents
implementation process and the first successful applica-
tion of this new approach. Evalu ating of result points out
in Section 4.
Background
In [4], Jha and McCall explored the applications of GIS
based computer visualization techniques in highway pro-
jects. In this project they found that GIS serves as a re-
pository of geographic information and enables spatial
manipulations and database management. Implementa-
tion of this project in a real highway project from Mary-
land indicated that integration of GIS and computer visu-
alization greatly enhances the highway development
process. Another research project conducted by Carreker
and Bachman demonstrated that by applying GIS, the
accuracy and efficiency of locating crashes could be im-
proved [5]. In [6], Fu ller et al. used GIS and remote sen-
sing data and analyzed several geometric road risk fac-
tors in the U.S. Southwest. This research used four road
geometry factors and geology-based criteria and did not
consider weather condition and road proximity land use
effect on road hazardous location identification. They
also did not use expert knowledge for determination of
fuzzy membership functions. In 2003, a so-called novel
adaptive neuro-fuzzy logic model was developed by
Adeli and Jiang to estimate freeway work zone capacity.
The model combined fuzzy logic with neuro-computing
concepts and was used for the nonlinear mapping of 17
different factors impacting the freeway work zone capac-
ity. This method provides two advantages over the exist-
ing methods. First, it incorporates a large number of fac-
tors impacting the work zone capacity. Second, unlike
the empirical equations, this model does not requ ire sele-
ction of various adjustment factors or values by the work
zone engineers based on prior experience [7]. In [3],
Steenberghen et al. found the usefulness of GIS and
point pattern techniques for defining road-accident black
zones within urban agglomerations. This research showed
the usefulness of GIS and point pattern techniques for
defining road-accident black zones within urban agglo-
merations. In their research one-dimensional (line) and
two dimensional (area) clustering techniques for road
accidents were compared. Their method needs previous
accident data in the study area for spatial clustering, so
cannot be used in newly-built roads. In [8], Cheng and
Washington by using experimentally derived simulated
data evaluated three hotspot identification methods ob-
served in practice: simple ranking, confidence interval,
and Empirical Bayes. The results showed that the Em-
pirical Bayes technique significantly outperforms ranking
and confidence interval techniques. Erdogan et al. used
GIS as a management system for accident analysis and
determined the hotspots in the highways with two dif-
ferent methods of kernel density analysis and repeatabil-
ity analysis in 2008. They realized that the hotspots de-
termined with two methods reflect really problematic
places such as cross roads, junction points etc. [9]. The
performance of various methods in hotspot identification
was compared in [10] by Montella. In this research, se ven
commonly applied hotspot identification methods (crash
frequency, equivalent property, damage only crash fre-
quency, crash rate, proportion method, empi rical Bayes es-
timate of total-crash frequency, empirical Bayes estimate
of severe-crash frequency, and potential for improvement)
were compared against for robust and informative quan-
titative evaluation criteria. In [11] Polat and Durduran
used four classifier algorithms comprising ANN, ANFIS,
SVM, and C4.5 decision tree to classify the traffic acci-
dent cases with the help of GIS after a data preprocessing
method called SCAW applied to traffic accidents data-
base. Since there is no statistical information for the
newly-built route available, these methods cannot be used
for transportation networks that are recently built. These
methods have used GIS only as a visualization tool to
show their results. The proposed method of this research
uses GIS functions to analysis and extracts useful infor-
mation from raw data and integrates GIS and fuzzy rea-
soning through expertise knowledge to assist road de-
partments in suburban jurisdictions improve the safety of
the roads under their management.
2. The Proposed Method
Research methodology is based on integration of GIS
and fuzzy reasoning which helps decision makers to de-
termine which risks are the most important ones, and
ultimately decide where hazard mitigation strategies should
be employed. Figure 1 shows different steps of research
methodology for creating composite risk map for identi-
fication of road hazardous se gments.
2.1. Fuzzy Logic in Spatial Information
Fuzzy set theory, introdu ced by Zadeh in the 1960 s, rese-
mbles human reasoning in its use of approximate infor-
mation and uncertainty to generate decisions [12]. Fuzzy
logic allows objects to take partial membership in vague
concepts. The main idea of fuzzy logic is that items in
the real world are better described by having partial

M. EFFATI ET AL.
34
Figure 1. Research methodology for identification of road hazardous segments.
membership in complementary sets than by having com-
plete membership in exclusive sets [12]. In classic logic
the membership of an element to a set is represented by 0
if it does not belong and 1 if it does, hav ing the set {0, 1}.
On the other hand, in fuzzy logic this set extends to the
interval [0, 1]. Therefore, it could be said that fuzzy logic
is an extension of the classic systems [13]. A fuzzy set A
over a universe of discourse X (a finite or infinite inter-
val within which the fuzzy set can take a value) is a set of
pairs (Equati on (1)):
  



/: ,0,1
AA
AxxxXx   (1)
In Equation (1),

A
x
 is called the membership de-
gree of the element x to the fuzzy set A. This degree
ranges between the extremes 0 and 1 of the dominion of
the real numbers. Depending on the type of membership
function, different types of fuzzy sets will be obtained.
Zadeh proposed a series of membership functions that
could be classified into two groups: those made up of
straight lines being “linear” ones, and to the contrary the
Gaussian forms, or “curved” ones. A linguistic label is
the word, in natural language, that expresses or identifies
a fuzzy set that may or may not be formally defined.
Thus, the membership function

A
x
 of a fuzzy set A
expresses the degree in which x verifies the category
specified by A. Membership functions are at the core of
fuzzy logic, so proper use of fuzzy reasoning depends on
proper construction of membership functions. A number
of methods are available to construct membership func-
tions using expert kno wledge. As such as in this research
expert knowledge is used to construct membership func-
tions and fuzzy rules, proper selection of experts must
ensure the use of appropriate expert knowledge. Selected
experts should be familiar with an analysis of the public
concern in terms of multiple issues and be able to judge
measurements of corresponding indicators in linguistic
terms. As such as in this research road geometry and en-
vironmental factors for road hazardous segment identifi-
cation have been considered, a heterogeneous group of
experts (both scientific and practical) from Ministry of
Road and Urban Development Transportation Research
Institute and Meteorological Organization was selected.
Another issue that should be considered is the method of
expert knowledge elicitation. Different methods (point
estimation, interval estimation, direct rating, and transi-
tion interval estimation) are available to elicit expert
knowledge for the construction of membership functions.
Since research variables are in different type and point
estimation method can be applied to nominal, discrete
and continuous variables, a point estimation based me-
thod has been used in this research. The main advantage
of this method is the simple processing of elicited expert

M. EFFATI ET AL. 35
knowledge. In point estimation, an expert j (j = 1,, J)
determines unambiguously whether each x does or does
not have propertyi
A
. An overall assessment is computed
as Equation (2):
 
1
ii
J
AA
jj
x
xJ 



(2)
In this method to obtain a proper membership function
more than one expert is needed [14].
Fuzzy logic based methodology in spatial information
can provide a conservative representation tool for indi-
vidual differences in the perception. A basic difference
between perceptions and measurements is that, in general,
measurements are crisp whereas perceptions are fuzzy. In
a fundamental way, this is the reason why to deal with
perceptions it is necessary to employ a logical system
that is fuzzy rather than crisp [15]. From this simple con-
cept, a complete mathematical and computing theory has
been developed that facilitates the solution of certain
problems in spatial information. The types of uncertainty
that appear in geospatial information systems are not just
simple randomness of observation (as in weather data
that is used as a environmental factor in this research) but
are manifested in many other forms including impreci-
sion, incompleteness and granularization. The multiplic-
ity of uncertainty appearing in GIS data and analysis re-
quires a variety of formalisms to model these uncertain-
ties. In light of this it is natural that fuzzy set theory has
become a topic of intensive interest in many areas of
geospatial research and applications [16].
2.2. Road Hazardous Segment Identification
Based on Fuzzy Inference System
This research shows how fuzzy reasoning can be prop-
erly applied in modeling localities. Identification of road
hazardous locations by fuzzy reasoning has a definite
advantage over a crisp set. A fuzzy logic based method-
ology is used in this research for the following reasons:
 It makes best possible use of sparse information to
reconstitute details.
 Fuzzy logic is well suited for modeling continuous,
real world systems.
 Fuzzy logic based methodology for modeling locali-
ties provides a conservative representation tool for
individual differences in the perception and consti-
tutes a closer depiction of reality.
 Research variables are continuous, imprecise, or am-
biguous.
 Fuzzy set modeling over the reference data can mini-
mize the problems caused by the imperfection of
source data
 Fuzzy sets are an extension of crisp (two valued) sets
to handle the concept of partial truth, which enables
the modeling of uncertainties of natural language [17]
in this research.
Traffic crashes are caused due to interaction of vehicle,
driver, roadway and environmental factors. All these
factors interact with each other and influence the occur-
rence and severity of crashes simultaneously. Although
driver error often contributes greatly to the occurrence of
any particular crash event, analysis of roadway and en-
vironmental factors help to explain why crashes are more
frequent in some locations than in others. In this research
considering accessibility to data several roads hazard
criteria have been taken into consideration. Table 1 il-
lustrates these criteria and their descriptions. This re-
search is an attempt to implement the road and environ-
mental related factors for road hazardous segment identi-
fication and thus help in identifying the required reme-
dial measures.
According to Table 2 these factors can be divided into
two classes:
 Road geometry design factors;
 Environmental factors.
Each of these variables is treated as a risk factor in
analysis of risks associated with the roads. Fuzzy proc-
essing of the hazard descriptors requires a specification
of the linguistic labels which represent fuzzy sets. The
linguistic variables and linguistic labels used for investi-
gations of each geometry and environmental factors are
listed in Table 2.
The type of fuzzy membership functions for each risk
factor is very important so in this research various func-
tions are tested and appropriate function for each risk
factor is determined. Widely applied membership func-
tions are bell-shaped and trapezoidal functions with
Table 1. Description of roads hazard criteria.
Factor Description
Radius The shorter the radius the higher the
hazard potential
Slope Sections with higher slope have higher
potential for hazard
Visibility Sections with less visibility have higher
potential for hazard
Distance from
Intersection Sections closer to intersections have
higher hazard potential
Road Width Whatever the narrower the road width is,
the higher the hazard potential is
Distance from the
Starting Point of
Roads (cities)
Sections closer to cities have higher
hazard potential
Distance from
Population Centers Sections closer to the population
centers have higher hazard potential
Rain Value The higher the rain value is, the higher
the hazard potential is

M. EFFATI ET AL.
36
Table 2. Linguistic variables and labels for the fuzzy-based
road hazardous segment identification process.
Type Linguistic Variable Linguistic Labels
Radius Very Small, Small,
Appropriate, High
Slope Low, Appropriate,
High
Visibility Appropriate,
Inappropriate
Dist. from Intersection Very Near,
Near, Far
Road Geometry
Factors
Road Width Very Narrow, Narrow,
Appropriate, Wide
Distance From the
Starting Point of Roads Very Near, Near, Far
Distance from
Population Centers Near, Moderate, Far
Input
Environmental
Factors
Rain Value Very Low, Low,
High, Very High
Output - Danger
Absolutely Safe,
Safe, Danger
Prone , Dangerous,
Very Dangerous
maximum equal to 1 and minimum equal to 0. According
to Equation (3) trapezoidal functions are modeled with
four parameters

,, ,



. Figure 2 shows the trape-
zoidal function.



1if
1if
1if
0otherwise
A
x
x
xxx
x

 



 
 


 



(3)
In special cases like symmetrical trapezoids and trian-
gles the number of parameters reduces to three. As the
values of these parameters change, the membership func-
tions vary accordingly, thus exhibiting various forms of
membership functions [18]. This research uses the trape-
zoidal membership functions because of their simplicity,
their learning capability, and the short amount of time
required for designing the system. The main steps of this
fuzzy inference system are: input, fuzzification, implica-
tion, aggregation and defuzzification. After implement-
ing the criteria, in order to create a useful statement,
complete sentences have to be formulated. Conditional
statements, IF-THEN rules, are statements that make
fuzzy logic useful. A single fuzzy IF-THEN rule can be
formulated according to Equation (4):
If is ; Then is
x
AyB
on the range of all possible values of x and y, respect-
(4)
where A and B are linguistic labels defined by fuzzy sets
Figure 2. Trapezoidal membership function.
tively. cedent
r premise, the THEN part of the rule “y is B” is called
ent identi-
fic
The IF part of the rule “x is A” is called ante
o
consequent. The antecedent is an interpretation that re-
turns a single number between 0 and 1, whereas the con-
sequent is an assignment that assigns the entire fuzzy set
B to the output variable y. The antecedent may integrate
several inputs using logical AND and OR. Fuzzy rea-
soning with fuzzy IF-THEN rules enables linguistic
statements to be treated mathematically. In a fuzzy sys-
tem with the increase of the number of rules the level of
qualitative complexity also increases. In this research for
complexity reduction we tried to reduce the number of
fuzzy rules by reducing the number of linguistic values
that fuzzy inference system input variables can takes.
The formulation of the fuzzy rules demands a careful
assessment of the importance of the descriptors for a
mostly unique characterization of hazard classes. Accor-
ding to Table 2 this study restricts output of fuzzy proc-
ess to five classes, namely absolutely safe, safe, danger
prone, dangerous and very dangerous. Some samples of
the IF-THEN fuzzy rules for determination of road haz-
ardous segments have been given in Table 3.
This research uses the fuzzy Takagi and Sugeno (TSK)
concept for fuzzy based road hazardous segm
ation, because it offers some advantages with regard to
computational efficiency and adaptive optimization [19].
In TSK approach membership values in the premise part
are combined by product inference to get the firing
strength of each rule and the consequent part of each rule
is modeled by a linear combination of the input variables
plus a constant term (Equation (5)). The TSK rules can
be expressed as follows (Takagi and Sugeno, 1983):
112 1
:If is and is and and is ,
01 1
Then
j
jj j
nn
RxA xAxA
jj j
jnn
faaxKax (5)
where
j
R is the jth rule, 1, 2,,
J
m, i
x
is ith in
variab put le, 1, 2,,in

,
j
i
A
are linguistic ter
Small, Appms of the premise part (e.g. Very Small,roiate, High), pr
j
f
is the i.e. fuzzy indicator for the
amount of dangerous), and
output variable (
j
i
aare coefficients of linear
ations. The process of shaping the consequent (im-
plication) is carried out anden aggregates the output
fuzzy sets over all rules. The final output
equ th
y
(centroid
defuzzifier) of hazardous segment identification fuzzy
inference system is calculated using Equation 6): (

M. EFFATI ET AL. 37
Table 3. Some fuzzy rules.
Sample Fuzzy Rules
1—IF radius is Very igh AND visibility is
Inappropriate AND d is Very Near AND
Small AND slope is H
istance from intersection
road width is Very Narrow AND rain value is Very High AND
distance from cities is Very Near THEN point is Very Dangerous.
3—IF distance from population centers is Near AND radius is Very
Small AND slope is Appropriate AND visibility is Inappropriate
idth is Very Narrow AND
ities is Far
ow AND visibility is Appropriate AND
opriate AND visibility is Appropri-
slope is Appropriate AND visibility is Appropriate AND
AND distance from intersection is Very Near AND road width is
Very Narrow AND rain value is Low AND distance from cities is
Near THEN point is Very Dangerous.
4—IF slope is High AND visibility is Inappropriate AND distance
from intersection is Far AND road w
distance from cities is Near THEN point is Dangerous.
5—IF radius is Very Small AND visibility is Inappropriate AND
distance from intersection is Far AND distance from c
THEN point is Dangerous.
6—IF distance from population centers is Near AND radius is
Appropriate AND slope is L
distance from intersection is Far AND road width is Appropriate
AND rain value is Low AND distance from cities is Far THEN
point is Danger Prone.
7—IF distance from population centers is Moderate AND radius is
Appropriate AND slope is Appr
ate AND distance from intersection is Near AND road width is
Appropriate AND rain value is Low THEN point is Danger Prone.
8—IF distance from population centers is Far AND radius is High
AND slope is Appropriate AND visibility is Appropriate AND
distance from intersection is Far AND road width is Width AND
rain value is High AND distance from cities is Far THEN point is
Safe.
9—IF distance from population centers is Far AND radius is High
AND
distance from intersection is Far AND road width is Width AND
rain value is Very Low AND distance from cities is Far THEN
point is Absolutely Safe.
11
mm
j
jj
jj
yf




(6)
where,


 
12
12
jj j
n
j
n
A
AA
x
xx
 
The final output is the weighted average othe conse-
quent equations rules. Figure 3 shows the overall process.
mentation steps of
ition and prepara-
. The study area is Kohin-
cts Tehran to the North of
f
3. Implementation and Result
This section briefly explains the imple
proposed method including data acquis
tion, modeling road hazardous segments based on fuzzy
reasoning, and finally the evaluation of results.
3.1. Data and Study Area
Figure 4 shows the study area
Loshan transit road that conne
Iran (Gilan). Research area is located in a mountainous
Figure 3. Takagi and Sugeno fuzzy reasoning structure.
Figure 4. Study area.
region where elevation ranges from approxiately 300 to
2394 m. The lengtoximately 73 km.
his route has most of factors for accidents occurrence
atabase. Road crash data and
ex
the first step after selec-
he required layers
a to a unique GIS
m
h of study area is appr
T
and road segments have high potential for hazard.
This study uses several primary and digital data. The
databases are obtained from numerous sources and in
various formats (Table 4).
Geometric specification data of study area was paper
based text attributes that should be converted to digital
format for inputting to the d
cising black segments of this transit road are used for
validation of proposed method.
3.2. Experimental Investigations
For testing the proposed method
tion of the study area is extraction of t
from data source. After converting dat
format and reference coordinate system, geometric and
topological corrections are performed on data. In the next
step the route is divided into smaller segments where
each segment contains at least one of hazard potentials.
A special code is assigned to each of these segments. In
the next step one point symbol is considered as a candidate
for each line segment. Meanwhile, by considering experts’
opinion and existing information of the study area, other
segments that were prone to accident and hazard are se-
lected. After preparing data and selecting criteria and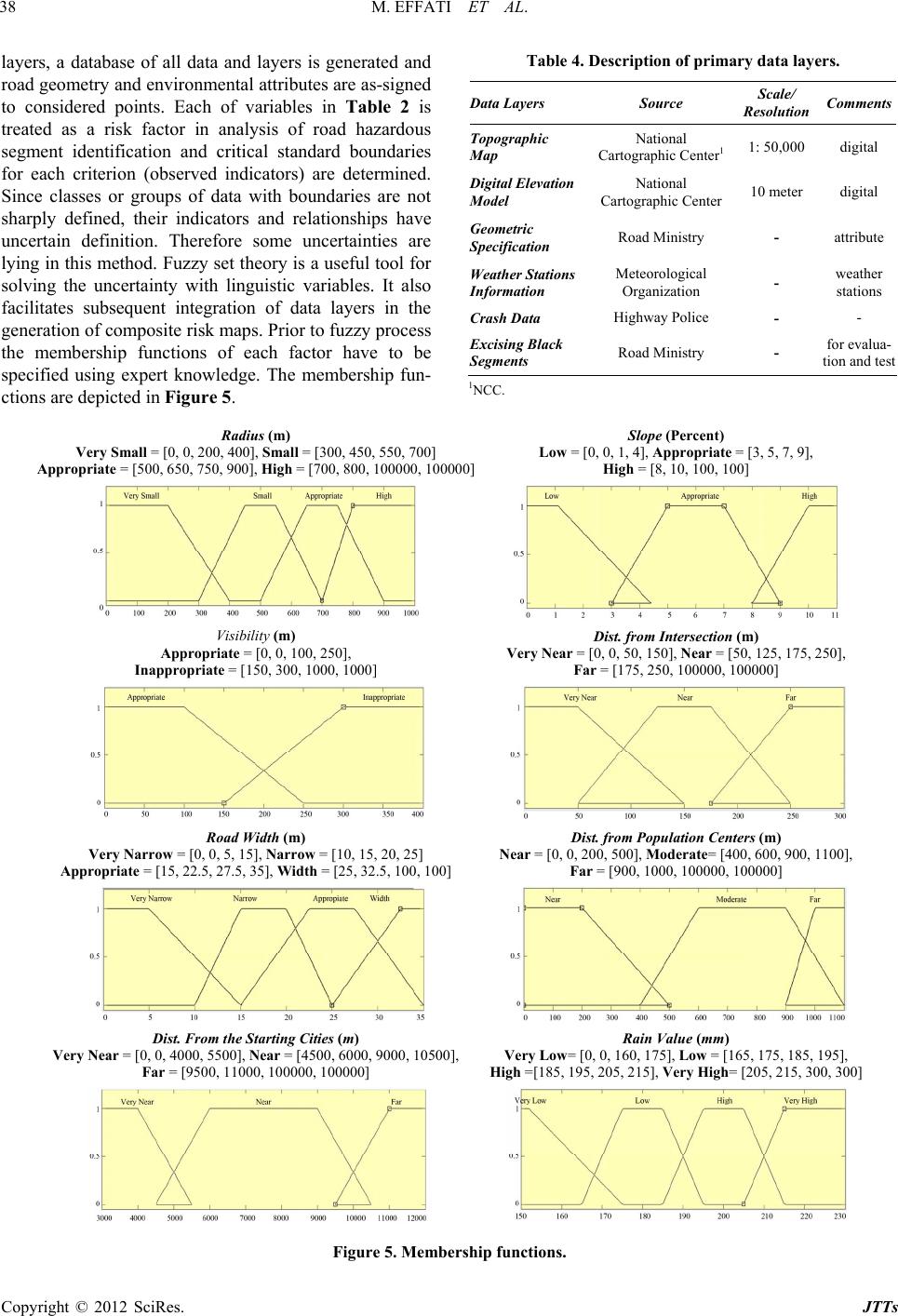

M. EFFATI ET AL.
38
Table 4. Description of primary data layers.
Data Layers Source Resolution Comments
layers, a database of all data and layers is generated and
road geometry and environmental attributes are as-signed
to considered points. Each of variables in Table 2 is
treated as a risk factor in analysis of road hazardous
segment identification and critical standard boundaries
for each criterion (observed indicators) are determined.
Since classes or groups of data with boundaries are not
sharply defined, their indicators and relationships have
uncertain definition. Therefore some uncertainties are
lying in this method. Fuzzy set theory is a useful tool for
solving the uncertainty with linguistic variables. It also
facilitates subsequent integration of data layers in the
generation of composite risk maps. Prior to fuzzy process
the membership functions of each factor have to be
specified using expert knowledge. The membership fun-
ctions are depicted in Figure 5.
Scale/
Topographic National
Carto nter1 1: 50,000 digital Map graphic Ce
Digital Elevation Carto ter 10 meter digital
ric Road Ministry - attribute
ns Meteorological - weather
Highway Police -
ck Road Ministry - for evalua-
Model
Geomet
National
graphic Cen
Specification
Weather Statio
Information
Crash Data
Organization stations
-
Excising Bla
Segments tion and test
1NCC.
Slope (Percent)
Low = [0, 0, 1, 4], Appropriate = [3, 5, 7, 9],
High = [8, 10, 100, 100]
Radius (m)
Very Small = [0, 0, 200, 400], Small = [300, 450, 550, 700]
Appropriate = [500, 650, 750, 900 ], = [700,High 800, 100000, 100000]
Visibility (m)
Appropriate = [0, 0, 100, 250],
Inappropriate 1000, 10 00] = [150, 300,
Dist. from Intersection (m)
Very Near = [0, 0, 50, 150], Near = [50, 125, 175, 250
Far ], = [175, 250, 100000, 100000]
Dist. from Population Centers (m)
Near = [0, 0, 200, 500], Moderate= [400, 600, 900, 1100
Far ], = [900, 1000, 100000, 100000]
Road Width (m)
Very Narrow = [0, 0, 5, 15], Narrow = [10, 15, 20, 25]
Appropriate = [15, 22.5,Width = [25, 32.5, 100, 100] 27.5, 35],
Rain Value (mm)
Very Low= [0, 0, 160, 175], Low = [165, 175, 185, 195
High =[185, 195, 205, 215], Very High= [205, 215, 300, 300]
],
Dist. From the Starting Cities (m)
Very Near = [0, 0, 4000, 5500], Near = [4500, 6000, 9000, 10500 ],
Far = [9500, 11000, 100000, 100000]
Figure 5. Membership functions.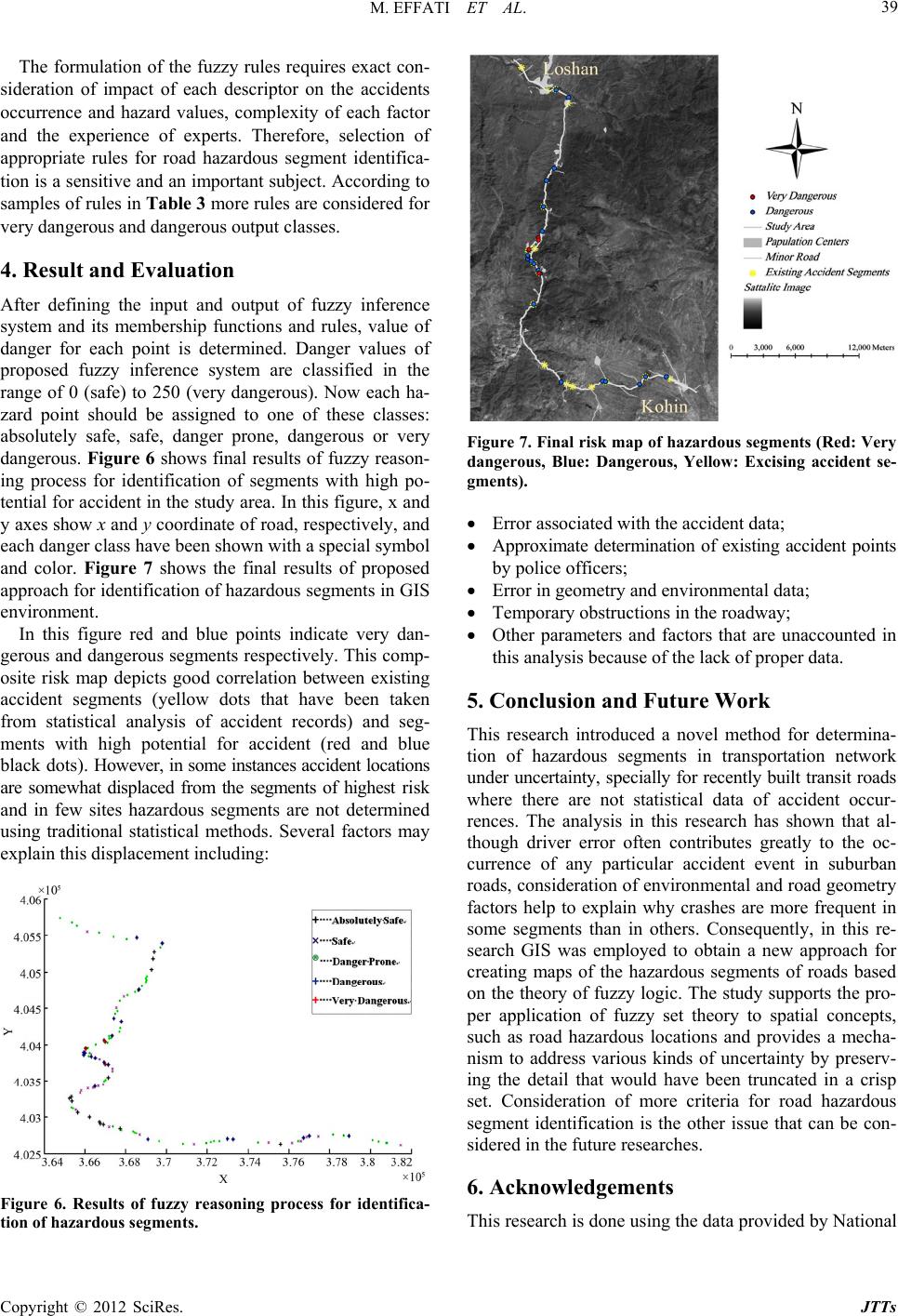

M. EFFATI ET AL. 39
The form
sideration
occurrence and hazard values, complexity of each factor
and the experience of experts. Therefore, selection of
appropriate rules for road hazardous segment identifica-
tion is a sensitive and an important subject. According to
samples of rules in Table 3 more ru les are con sider ed for
very dangerous and dangerous output classes.
A
gh po-
rea. In this figure, x and
ad, respectively, and
placement including:
ulation act con-
of impacidents
of the fuzzy rules requires ex
ct of each descriptor on the ac
4. Result and Evaluation
fter defining the input and output of fuzzy inference
system and its membership functions and rules, value of
danger for each point is determined. Danger values of
proposed fuzzy inference system are classified in the
range of 0 (safe) to 250 (very dangerous). Now each ha-
zard point should be assigned to one of these classes:
absolutely safe, safe, danger prone, dangerous or very
dangerous. Figure 6 shows final results of fuzzy reason-
ing process for identification of segments with hi
tential for accident in the study a
y axes show x and y coordinate of ro
each danger class have been shown with a special symbol
and color. Figure 7 shows the final results of proposed
approach for identification of hazardous segments in GIS
environment.
In this figure red and blue points indicate very dan-
gerous and dangerous segments respectively. This comp-
osite risk map depicts good correlation between existing
accident segments (yellow dots that have been taken
from statistical analysis of accident records) and seg-
ments with high potential for accident (red and blue
b la ck do t s) . However, in some instan ces accident location s
are somewhat displaced from the segments of highest risk
and in few sites hazardous segments are not determined
using traditional statistical methods. Several factors may
explain this dis
Figure 6. Results of fuzzy reasoning process for iden
tion of hazardous segments. tifica-
Figure 7. Final risk map of hazardous segments (Red: Very
dangerous, Blue: Dangerous, Yellow: Excising accident se-
gments).
 Error associated with the accident data;
 Approximate determination of existing accident points
by police officers;
 Error in geometry and environmental data;
ctors that are unaccounted in
this analysis because of the lack of proper data.
5. Conclusion and Future Work
This research introduced a novel method for determina-
tion of hazardous segments in transportation network
under uncertainty, specially f or recently built transit roads
where there are not statistical data of accident occur-
rences. The analysis in this research has shown that al-
though driver error often contributes greatly to the oc-
currence of any particular accident event in suburban
roads, consideration of environmental and road geometry
factors help to explain why crashes are more frequent in
some segments than in others. Consequently, in this re-
search GIS was employed to obtain a new approach for
creating maps of the hazardous segments of roads based
on the theory of fuzzy logic. The study supports the pro
ould have been truncated in a crisp
ad hazardous
 Temporary obstructions in the roadway;
 Other parameters and fa
-
per application of fuzzy set theory to spatial concepts,
such as road hazardous locations and provides a mecha-
nism to address various kinds of uncertainty by preserv-
g the detail that win
set. Consideration of more criteria for ro
segment identification is the other issue that can be con-
sidered in the future researches.
6. Acknowledgements
This research is done using the data provided by National

M. EFFATI ET AL.
40
Cartographic Center (NCC), National Geographic Or-
ganization and Iran Ministry of Road and Urban Devel-
opment Transportation Research Institute.
REFERENCES
[1] M. Effati, F. Samadzadegan and M. A. Rajabi, “Risk
Analysis of Transportation Networks Using a Fuzzy
Based Multi-Criteria Decision Making System,” 1st An-
nual International Conference on Transportation and Lo-
gistics, Chiangmai, 17-19 December 2009.
[2] J. K. Z. Mwatelha, “Application of Geographical Infor-
mation Systems (GIS) to Analyze Causes of Road Traffic
Accidents (RTAs) Case Study of Kenya,” International
Conference on Spatial Information for Sustainable De-
velopment, Nairobi, 2-5 October 2001.
[3] T. Steenberghen, T. Dufays and I. B. Flahaut, “Intra-Urban
Location and Clustering of Road Accidents Using GIS: A
Belgian Example,” International Journal of Geographi-
cal Information Science, Vol. 18, No. 2, 2004, pp. 169-
181. doi:10.1080/13658810310001629619
[4] M. Jha, C. McCall and P. Schonfeld, “Using GIS, Genetic
Algorithms and Visualization in Highway Development,”
Journal of Computer—Aided Civil and Infrastructure En-
gineering, Vol. 16, No. 6, 2001, pp. 399-414.
chman, “Geographic Informa-
Improve Speed and Accuracy
D. James, “
and Risk Analysis alongRoads,”
grating Remot, Regional and Lo-
[5] L. E. Carreker and W. Ba
tion System Procedures to
in Locating Crashes,” Transportation Research Record
1719, TRB, National Research Council, Washington DC,
2000, pp. 215-218.
[6] D. Fuller, M. Jeffe, R. A. Williamson and
ellite Remote Sensing and Transportation Lifelines: Safety
Sat-
Rural Southwest
e Sensing at the Global Inte-
cal Scale. Pecora 15/Land Satellite Information IV Con-
ference, Denver, 11-15 November 2002, p. 8.
[7] H. Adeli and X. Jiang, “Ne uro-Fuzzy Logic Model for Free-
way Work Zone Capacity Estimation,” Journal of Trans-
portation Engineering, Vol. 129, No. 5, 2003, pp. 484- 493.
doi:10.1061/(ASCE)0733-947X(2003)129:5(484)
[8] W. Cheng and S. P. Washington, “Experimental Evalua-
tion of Hotspot Identification Methods,” Elsevier Journal
of Accident Analysis and Prevention, Vol. 37, No. 5, 2005,
pp. 870-881. doi:10.1016/j.aap.2005.04.015
[9] S. Erdogan, I. Yilmaz, T. Baybura and M. Gullu “Geo-
graphical Information Systems Aided Traffic Accident
Analysis System Case Study: City of Afyonkarahisar,”
Elsevier Journal of Accident Analysis and Prevention, Vol.
40, No. 1, 2008, pp. 174-181.
doi:10.1016/j.aap.2007.05.004
[10] A. Montella, “A Comparative Analysis of Hotspot Identi-
fication Methods,” Elsevier Journal of Accident Analysis
and Prevention, Vol. 42, No. 2, 2009, pp. 571-581.
doi:10.1016/j.aap.2009.09.025
[11] K. Polat and S. S. Durduran, “Subtractive Clustering At-
tribute Weighting (SCAW) to Discriminate the Traffic
Accidents on Konya-Afyonkarahisar Highway in Turkey
with the Help of GIS: A Case Study,” Elsevier Advances
in Engineering Software Jou rnal, Vol. 42, No. 7, 2011, pp .
491-500. doi:10.1016/j.advengsoft.2011.04.001
rnational Series in Engi-
Vol. 165, 1992, pp. 1-25.
[12] L. A. Zadeh, “Fuzzy Sets,” Information and Control, Vol.
8, No. 3, 1965, pp. 338-353.
[13] L. A. Zadeh, “Knowledge Representation In Fuzzy Logic.
In an Introduction to Fuzzy Logic Applications in Intelli-
gent Systems,” The Kluwer Inte
neering and Computer Science,
doi:10.1007/978-1-4615-3640-6_1
[14] G. J. Klir and B. Yuan. “Fuzzy Sets and Fuzzy Logic:
Theory and Applications,” Prentice Hall, Upper Sa
River, 1995. ddle
[15] L. A. Zadeh, “From Computing with Words to Comput-
ing with Perceptions, Fundamental Theory and Applica-
tions, Perceptions,” IEEE Journal of Transactions on Cir-
cuits and Systems, Vol. 45, No. 1, 1999, pp. 105-119.
doi.org/10.1109/81.739259
[16] F. E. Petry, V. B. Robinson and M. Cobb, “Fuzzy Mod-
eling with Spatial Information for Geographic Problems,”
Springer, New York, 2005. doi:10.1007/b138243
16/j.isprsjprs.2005.02.010
[17] A. P. Engelbrecht, “Computational Intelligence: An In-
troduction,” 2nd Edition, John Wiley & Sons, Ltd., Ho-
boken, 2007
[18] F. Samadzadegan, A. Azizi, M. Hahn and C. Lucas, “Au-
tomatic 3D Object Recognition and Reconstruction Based
on Neuro-Fuzzy Modeli ng,” ISPRS Journal of Pho to gr am -
metry & Remote Sensing, Vol. 59, No. 5, 2005, pp. 255-
277. doi:10.10
r-
5-60.
[19] T. Takagi and M. Sugeno, “Derivation of Fuzzy Control
Rules from Human Operator’S Control Actions,” Pro-
ceeding of the IFAC Symposium on Fuzzy Information,
Knowledge Representation and Decision Analysis, Ma
seille, 19-21 July 1983, pp. 5