 Open Journal of Forestry 2012. Vol.2, No.1, 17-22 Published Online January 2012 in SciRes (http://www.SciRP.org/journal/ojf) http://dx.doi.org/10.4236/ojf.2012.21003 Copyright © 2012 SciRes. 17 Mathematical Modeling of Crown Forest Fire Spread Valeriy Perminov Department of Mathematics and Natural Sciences, Belovo Branch of Kemerovo State University, Belovo, Russia Email: p_valer@mail.ru Received August 20th, 2011; revised November 9th, 2011; accepted November 17th, 2011 Mathematical model of forest fire was based on an analysis of known experimental data and using con- cept and methods from reactive media mechanics. In this paper the assignment and theoretical investiga- tions of the problems of crown forest fire spread in windy condition were carried out. In this context, a study—mathematical modeling—of the conditions of forest fire spreading that would make it possible to obtain a detailed picture of the change in the temperature and component concentration fields with time, and determine as well as the limiting condition of fire propagation in forest with fire break. Keywords: Forest Fire; Mathematical Model; Turbulence; Ignition; Fire Spread; Control Volume; Discrete Analogue Introduction A great deal of work has been done on the theoretical prob- lem of crown forest fire initiation. Crown fires are initiated by convective and radiative heat transfer from surface fires. How- ever, convection is the main heat transfer mechanism (Van Wag- ner, 1977). The theory proposed by Van Wagner (1977) de- pends on three simple crown properties: crown base height, bulk density of forest combustible materials and moisture con- tent of forest fuel. Also, crown fire initiation and hazard have be e n st udied and mo deled in deta ils later (Alexan der, 1998 ); Va n Wagner (1989); Xanthopoulos (1990); Rothermel (1991); Cruz and others (2002); Albini and others (1195); Scott and Reinhardt (2001). The more complete discussion of the prob- lem of crown forest fires is provided by coworkers at Tomsk University (Grishin, 1997); Grishin et al. (1998); Perminov (1995, 1998). In p art ic ul ar, a ma th ema ti ca l mo del of for est fi re s was obtained by Grishin (1997) based on an analysis of known and original experimental data; Konev (1977), and using con- cepts and methods from reactive media mechanics. The physi- cal two-phase models used by Morvan & Dupuy (2001, 2004) may be considered as a continuation and extension of the for- mulation proposed in (Grishin 1997). This study gives a two dimensional averaged mathematical setting and method of nu- merical solution of a problem of a forest fire spread. The bound- ary-value problem is solved numerically using the method of splitting according to physical processes. It was based on nu- merical solution of two dimensional Reynolds equations for the description of turbulent flow taking into account for diffusion equations chemical components and equations of energy con- servation for gaseous and condensed phases, volume of fraction of condensed phase (dry organic substance, moisture, con- densed pyrolysis products, mineral part of forest fuel). Mathematical Model It is assumed that the forest during a forest fire can be mod- eled as 1) a multi-phase, multi storied, spatially heterogeneous me- dium; 2) in the fire zone the forest is a porous-dispersed, two-tem- perature, single-velocity, reactive medium; 3) the forest canopy is supposed to be non- deformed medium (trunk s, large branches, small twigs and needles), which affects only the magnitude of the force of resistance in the equation of conservation of mo- mentum in the gas phase, i.e., the medium is assumed to be quasi-solid (almost non-deformable during wind gusts); 4) let there be a so-called “ventilated” forest massif, in which the vo- lume of fractions of condensed forest fuel phases, consisting of dry organic matter, water in liquid state, solid pyrolysis prod- ucts, and ash, can be neglected compared to the volume fraction of gas pha se (component s of air and gaseou s pyroly sis pr oducts ) ; 5) the flow has a developed turbulent nature and molecular trans- fer is neglected; 6) gaseous phase density doesn’t depend on the pressure because of the low velocities of the flow in compare- son with the velocity of the sound. Let the point x1, x2, x3 = 0 is situated at the centre of the surface forest fire source at the height of the roughness level, axis 0x1 directed parallel to the Earth’s surface to the right in the direction of the unperturbed wind speed, axis 0x2 directed perpendicular to 0x1 and axis 0x3 directed upward (Figure 1). Because of the horizontal sizes of forest massif more than height of forest—h, system of equations of general mathematic- cal model of forest fire (Grishin, 1997) was integrated between the limits from height of the roughness level—0 to h. Besides, suppose that Figure 1. Basic scheme of forest fire initiat i o n and propagation.  V. PERMINOV 3 0 d h h —average value of . The problem formulated above is reduced to a solution of the following system of equation: ,1,2,3; j j vQmmhj tx (1) d d ,1,2,3; i ijd ii jj iii vp vvsc vg txx Qvh i v (2) 55 d; d ppjvsT j T ccvTqRTTq tx T qh (3) 5 d()/,1, dj j cvcRQcJ Jh tx 5; (4) 4 4 3R RSRR jj cUkcUTq qh xk x 0; (5) 44 33 22 1 4 S ipii RSVS i T cqRqRkcUTT t ; T(6) 12 1122 34 3134 1 ,, ,0 C C RR tt M aR R tMt (7) 55 123 11 1,,,,,0,0, a ae aa a c cpRTvvvg M vg The system of Equations (1)-(7) must be solved taking into account the in itial and bound a ry conditions: 123 1 1: 0,0,0,,,,; ea aeseie tv vv TTccTT 3 1112 1 1 :,0,0,,, 20; 3 ee eaa R R v e xvVvTTc c x cU cU kx (8) 123 11 11111 1 :0,0,0, 0, 0; 32 e R R vvv cT xx xxxxx cUc U kx 0, (9) 123 220 22222 2 :0,0,0,0, 0; 32 R R vvvcT xx xxxxx cUc U kx 0, (10) 123 22 22 2 2 2 2 :0,0,0,0,0 0; 32 e R R vv vcT xx xxxxx cUc U kx , (11) 312 33 3301 2 312 0:0,0,0,0, 32 ,, , 0, ,, ; R R g e ccUc xvv U xkx vvTTx x vTTxx (12) 123 33 33 3 33 3 :0,0, 0,0, 0. 32 e R R vv vc T xx xxxxx cUc U kx 0, (13) Here and above d dt is the symbol of the total (substantial) derivative; v is the coefficient of phase exchange; —density of gas-dispersed phase, t is time; vi—the velocity components; T, TS—temperatures of gas and solid phases, UR—density of radiation energy, k—coefficient of radiation attenuation, P—pressure; cp—constant pressure specific heat of the gas phase, cpi, i, i—specific heat, density and volume of fraction of condensed phase (1—dry organic substance, 2—moisture, 3— condensed pyrolysis products, 4—mineral part of forest fuel), Ri—the mass rates of chemical reactions, qi—hermal effects of chemical reactions; kg, kS—radiation absorption coefficients for gas and condensed phases; Te—the ambient temperature; c — mass concentrations of -component of gas-dispersed medium, index = 1, 2, 3, where 1 corresponds to the density of oxygen, 2—to carbon monoxide CO, 3—to carbon dioxide and inert components of air, 4, 5—soot and ash; R—universal gas con- stant; M , MC, and M molecular mass of -components of the gas phase, carbon and air mixture; g is the gravity acceleration; cd is an empirical coefficient of the resistance of the vegetation, s is the specific surface of the forest fuel in the given forest stratum. In system of Equations (1)-(7) are introduced the next designations: 333 ,, , ii T mvvvJvcJ vT 3 Upper indexes “+” and “–” designate values of functions at x3 = h and x3 = 0 correspondingly. It is assumed that heat and mass exchange of fire front and boundary layer of atmosphere are governed by Newton law and written using the formulas: , . TT e ep qqh TTh Jh cchc To define source terms which characterize inflow (outflow of mass) in a volume unit of the gas-dispersed phase, the follow- ing formulae were used for the rate of formulation of the gas- dispersed mixture, outflow of oxygen m 51 , changing carbon monoxide 52 . 1 12351 35 12 5215 53 1, 2 1,0. c c gc MM QRRRRR MM RRRR , R Here g—mass fraction of gas combustible products of py- rolysis, 4 and 5—empirical constants. Reaction rates of these various contributions (pyrolysis, evaporation, combustion of coke and volatile combustible products of pyrolysis) are approxi- mated by Arrhenius laws whose parameters (pre-exponential constant ki and activation energy Ei) are evaluated using data for mathematical models (Grishin, 1997; Perminov, 1995). 0.5 12 11112 222 3 3331 0.25 2.25 125 552 12 exp ,exp , exp , exp . s ss s EE RkRk T RT RT E Rk scRT cM cME RkM T MM RT 1 8 Copyright © 2012 SciRes. 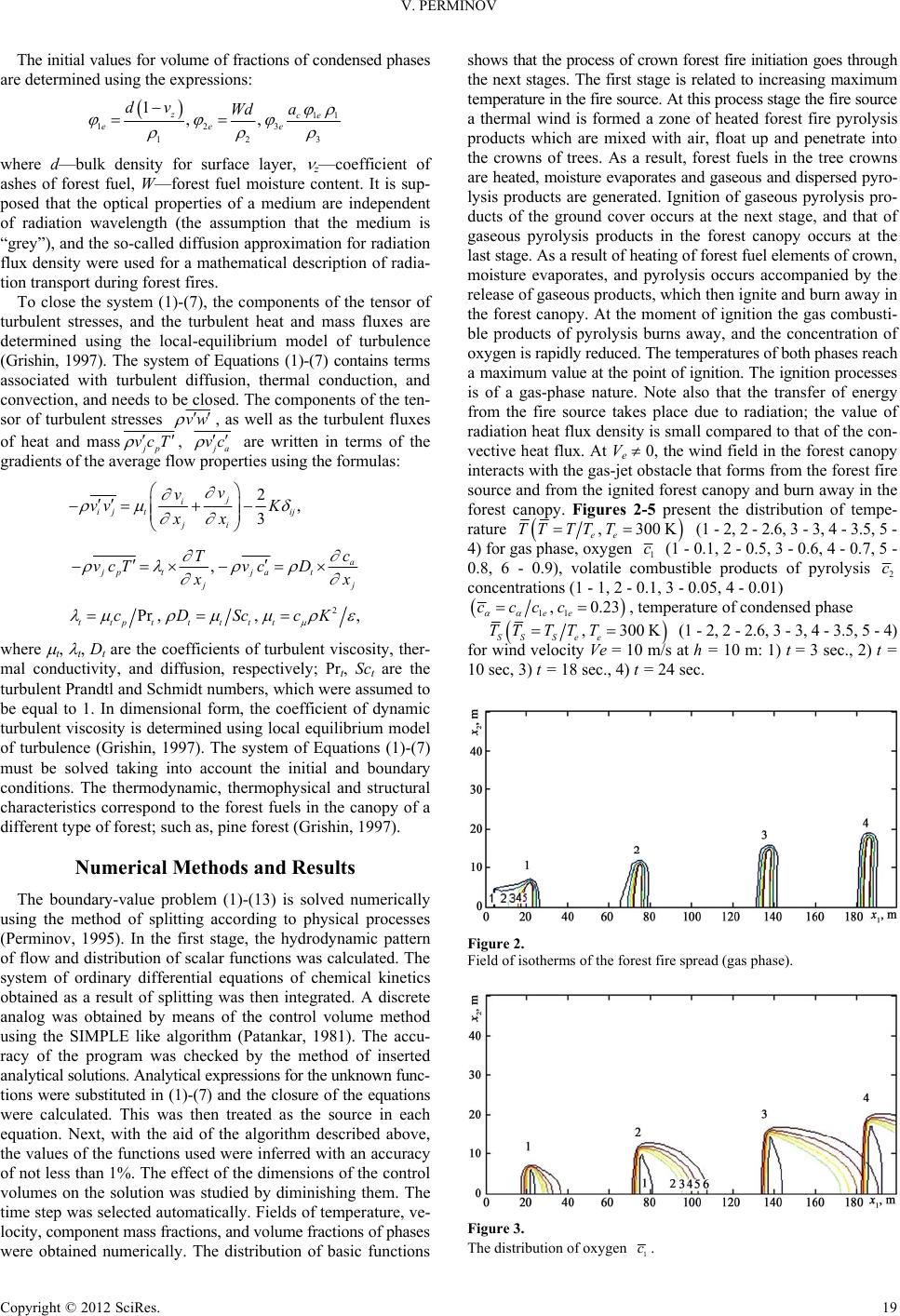 V. PERMINOV The initial values for volume of fractions of condensed phases are determined using the expressions: 11 123 12 1,, zce eee dv Wd a 3 where d—bulk density for surface layer, z—coefficient of ashes of forest fuel, W—forest fuel moisture content. It is sup- po proximation for radiation flux density were used for a mathematical description of radia- tion transport during forest fires. sed that the optical properties of a medium are independent of radiation wavelength (the assumption that the medium is “grey”), and the so-called diffusion ap To close the system (1)-(7), the components of the tensor of turbulent stresses, and the turbulent heat and mass fluxes are determined using the local-equilibrium model of turbulence (Grishin, 1997). The system of Equations (1)-(7) contains terms associated with turbulent diffusion, thermal conduction, and convection, and needs to be closed. The components of the ten- sor of turbulent stresses vw , as well as the turbulent fluxes of heat and mass jp vcT , a are written in terms of the gradients of the average flow properties using the formulas: vc 2, 3 j i ij tij ji v v vv K xx ,a jp tjat Tc vcTvc D jj x 2 Pr ,,, ttpttttt cDSccK where t, t, Dt are the coefficients of turbut viscosity, ther- mal conductivity, and diffusion, respective; Prt, Sct are the turbulent Prandtl and Schmidt numbers, which were assumed to be equal to 1. In dimensional form, the coefficient of dynamic turbulent viscosity is determined using local equilibrium model of turbulence (Grishin, 1997). The system of Equations (1)-(7) must be solved taking into account the initial and boundary . tics obtained as a result of splitting was then integrated. A discrete analog wae method using the SIMPLE likThe accu- ra len ly conditionsThe thermodynamic, thermophysical and structural characteristics correspond to the forest fuels in the canopy of a different type of forest; such as, pine forest (Grishin, 1997). Numerical Methods and Results The boundary-value problem (1)-(13) is solved numerically using the method of splitting according to physical processes (Perminov, 1995). In the first stage, the hydrodynamic pattern of flow and distribution of scalar functions was calculated. The system of ordinary differential equations of chemical kine s obtained by means of the control volum e algorithm (Patankar, 1981). cy of the program was checked by the method of inserted analy tical solutions. Analytical expressio ns for the unkno wn func - tions were substituted in (1)-(7) and the closure of the equations were calculated. This was then treated as the source in each equation. Next, with the aid of the algorithm described above, the values of the functions used were inferred with an accuracy of not less than 1%. The effect of the dimensions of the control volumes on the solution was studied by diminishing them. The time step was selected automatically. Fields of temperature, ve- lo city , component ma ss fraction s, and vol u me fractions of p hase s were obtained numerically. The distribution of basic functions shows that the process of crown forest fire initiation goes through the next stages. The first stage is related to increasing maximum temperature in the fire source. At this process stage the fire source a thermal wind is formed a zone of heated forest fire pyrolysis products which are mixed with air, float up and penetrate into the crowns of trees. As a result, forest fuels in the tree crowns ar e heated, moisture evaporates and gaseous and dispe rsed pyro- lysis products are generated. Ignition of gaseous pyrolysis pro- ducts of the ground cover occurs at the next stage, and that of gaseous pyrolysis products in the forest canopy occurs at the la st stage. As a result of heating of forest fuel elements of crown, moisture evaporates, and pyrolysis occurs accompanied by the release of gaseous products, which then ignite and burn away in the forest canopy. At the moment of ignition the gas combusti- ble products of pyrolysis burns away, and the concentration of oxygen is rapidly reduced. The temperatures of both phases reach a maximu m value at the point of ignition. The ign ition processes is of a gas-phase nature. Note also that the transfer of energy from the fire source takes place due to radiation; the value of radiation heat flux density is small compared to that of the con- vective heat flux. At Ve 0, the wind field in the forest canopy interacts with the gas-jet obstacle that forms from the forest fire source and from the ignited forest canopy and burn away in the forest canopy. Figures 2-5 present the distribution of tempe- rature ,300 K ee TTTT T (1 - 2, 2 - 2.6, 3 - 3, 4 - 3.5, 5 - 4) for gas phase, oxygen 1 c (1 - 0.1, 2 - 0. 5 , 3 - 0. 6, 4 - 0. 7 , 5 - 0.8, 6 - 0.9), volatile combustible products of pyrolysis 2 c concentrations (1 - 1, 2 - 0.1, 3 - 0.05, 4 - 0.01) 11 ,0.23 ee cсcс , temperature of condensed phase ,300 K SS See TT TTT (1 - 2, 2 - 2.6, 3 - 3, 4 - 3.5, 5 - 4) for wind velocity Ve = 10 m/s at h = 10 m: 1) t = 3 sec., 2) t = 10 sec, 3) t = 18 sec., 4) t = 24 sec. Figure 2. Field of isotherms of the forest fire spre ad (gas phase). Figure 3. The distribution of oxy g en 1 c. Copyright © 2012 SciRes. 19 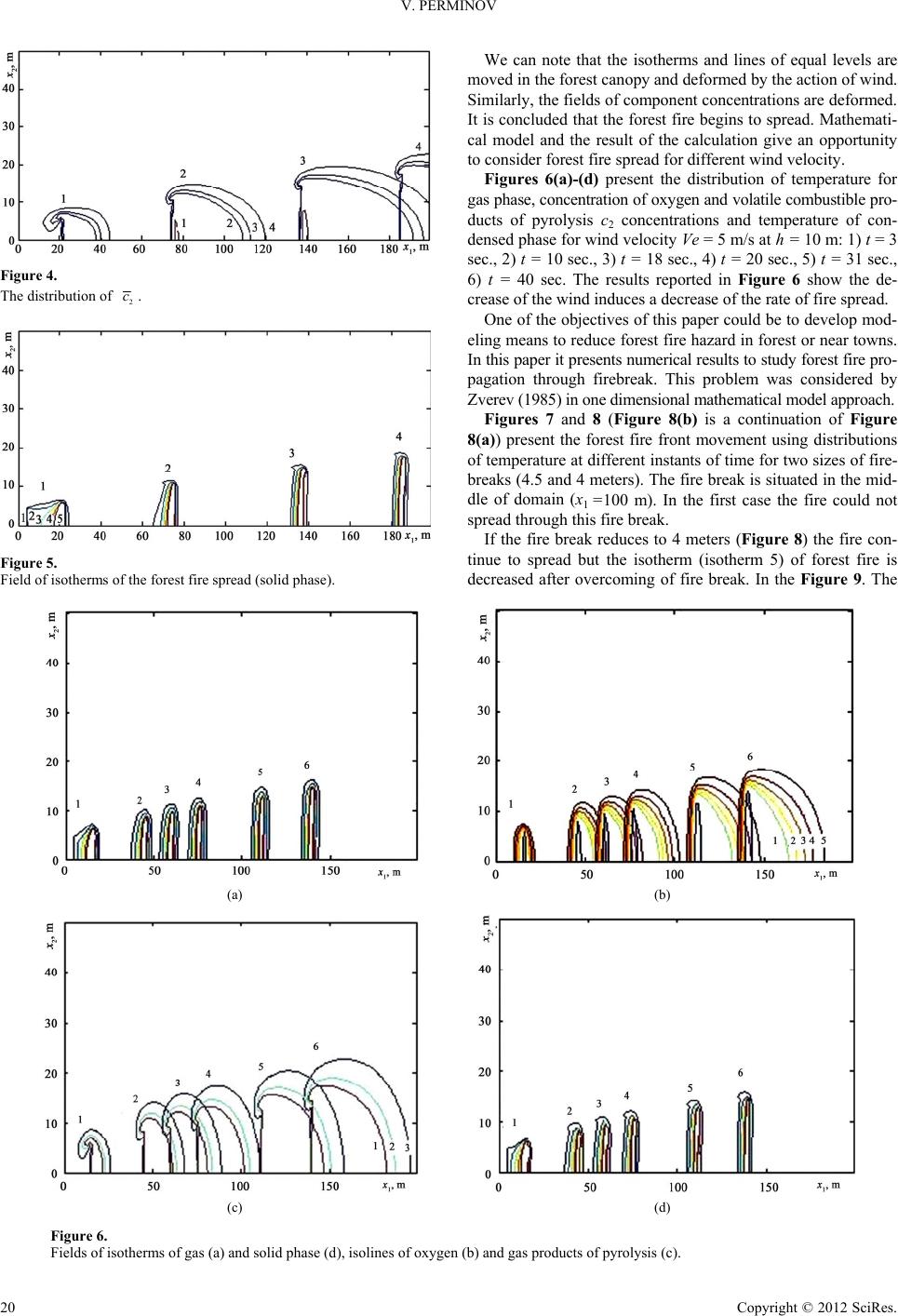 V. PERMINOV 20 Copyright © 2012 SciRes. Figure 4. The distribution of 2 c. Figure 5. ield of isotherms of the forest fire spread ( solid phase). al levels are m re for ga el 8( meters (Figure 8) the fire con- tin We can note that the isotherms and lines of equ oved in the forest canopy and deformed by the action of wind. Similarly, the fields of component concentrations are deformed. It is concluded that the forest fire begins to spread. Mathemati- cal model and the result of the calculation give an opportunity to consider forest fire spread for different wind velocity. Figures 6(a)-(d) present the distribution of temperatu s phase, concentration of oxygen and volatile combustible pro- ducts of pyrolysis c2 concentrations and temperature of con- densed phase for wind velocity Ve = 5 m/s at h = 10 m: 1) t = 3 sec., 2) t = 10 sec., 3) t = 18 sec., 4) t = 20 sec., 5) t = 31 sec., 6) t = 40 sec. The results reported in Figure 6 show the de- crease of the wind induces a decrease of the rate of fire spread. One of the objectives of this paper could be to develop mod- ing means to reduce forest fire hazard in forest or near towns. In this paper it present s numerical results to study forest fire pro- pagation through firebreak. This problem was considered by Zverev (1985) in one dimensional mathematical model approach. Figures 7 and 8 (Figure 8(b) is a continuation of Figure a)) present the forest fire front movement using distributions of temperature at different instants of time for two sizes of fire- breaks (4.5 and 4 meters). The fire break is situated in the mid- dle of domain (x1 =100 m). In the first case the fire could not spread through this fire break. If the fire break reduces to 4 ue to spread but the isotherm (isotherm 5) of forest fire is decreased after overcoming of fire break. In the Figure 9. The F (a) (b) (c) (d) Figure 6. Fields of isotherm s of gas (a) and solid phase (d), isolines of oxygen (b) and gas products of pyrolysis (c).  V. PERMINOV Figure 7. Field of isotherms. Fire break equals 4.5 m. (a) (b) Figure 8. Field of isotherms. Fire break equals 4 m. Figure 9. The influence of wind velocity at the size of fire break. dependence of critical fire break value for different wind velo- cities is presented. Of course the size of safe distance depends not only of wind velocity, but type and quality of forest com- bustible materials, its moisture, height of trees and others con- ditions. This model allows to study an influence all these main factors. Conclusion The results of calculation give an opportunity to evaluate critical condition of the forest fire spread, which allows apply- ing the given model for preventing fires. It overestimates the velocity of crown forest fire spread that depends on crown pro- , moisture content of forest fuel and etc. a detailed picture of the change t concentration fields with time, and determine as well as the influence of different conditions n. The results obtained agree with the laws of physics and experimental data (Konev, 1977; Grishin, 1997). From an analysis of calculations and experi- mental data it was found that for the cases in question the minimum total incendiary heat pulse is 2600 kJ/m2 (Grishin, 1997). Calculations demonstrated that the value of the radiant heat flux for both problems is considerably less than the con- vective one, therefore radiation has a weak effect on local and integral characteristics of the problem discoursed above. REFERENCES Albini, F. A., et al. (1995). Modeling ignition and burning rate of large woody natural fuels. International Journal of Wildland Fire, 5, 81-91. doi:10.1071/WF9950081 perties: bulk density The model proposed there gives in the temperature and componen on the crown forest fire initiatio Alexander, V. E. (1998). Crown fire thresholds in exotic pine planta- tions of Australasia. Ph.D. Thesis, Acton: Australian National Uni- versity. Cruz, M. G., Alexander, M. E., & Wakimoto, R. H. (2002). Predicting ire behaviour to support forest fire management deci- th international ition of tree crowns. Combustion, Explosion, and Shock 34, 378-386. doi:10.1007/BF02675602 crown f sion-making. In D. X. Viegas (Ed.), Proceedings of 4 conference on Forest fire research/2002 wildland fire safety summit. Rotterdam: Millpress Scie nce Publishers. Grishin, A. M. (1997). Mathematical modeling forest fire and new methods fighting them. Tomsk: Publishing House of Tomsk Univer- sity. Grishin, A. M., & Perminov, V. A. (1998). Mathematical modeling of the ign Waves, Konev, E. V. (1977). Then of vegetative materials combustion. Novosibirsk M physical foundatio : Nauka. orvan, D., & Dupuy, J. L. (2001). Modeling of fire spread through a forest fuel bed using a multiphase formulation. Combustion and Flame, 127, 1981-1994. doi:10.1016/S0010-2180(01)00302-9 Morvan, D., & Dupuy, J. L. (2004). Modeling the propagation of wild- fire through a Mediterranean shrub using a multiphase formulation. Combustion and Flame, 138, 199-210. doi:10.1016/j.combustflame.2004.05.001 Patankar, S. V. (1981). Numerical heat transfer and fluid flow. New York: Hemisphere Publishing Corporation. Perminov, V. A. (1995). Mathematical modeling of crown and mass forest fires initiation with the allowance for the radiative—Conve- ctive heat and mass transfer and two temperatures of medium. Ph.D Thesis, Tomsk: Tomsk State University. Perminov, V. A. (1998). Mathematical modeling of crown forest fire initiation. Proceedings of III International conference on forest fire research and 14th conference on fire and forest meteorology. Luso. Rothermel, R. C. (1991). Crown fire analysis and interpretation. Pro- ceedings of 11th international conference on Fire and forest meteor- Copyright © 2012 SciRes. 21  V. PERMINOV ology. Bethesda, MA: Society of American Foresters. Scott, J. H., et al. (2001). Assessing crown fire potential by linking Vwn fire behavior in conifer Z fire spread. Ph.D. Thesis, models of surface and crown fire behaviororest Service, Rocky Mountain Forent Station. Colorado: Fort Collins. . USDA F est and Range Experim Van Wagner, C. E. (1977). Conditions for the start and spread of crown fire. Canadian Journal of Forest Research, 7, 23-34. doi:10.1139/x77-004 an Wagner, C. E. (1989). Prediction of cro stands. Proceedings of 10th conference on fire and forest meteorology. Ottawa, Ontario: Forestry Canada. Xanthopoulos, G. (1990). Development of a wildland crown fire initia- tion model. Ph.D. Thesis, Missoula: University of Montana. verev, V. G. (1985). Mathematical modeling of aerodynamics and heat and mass transfer at crown forest Tomsk: Tomsk State University. 2 2 Copyright © 2012 SciRes.
|