J. Mod. Phys., 2010, 1, 77-82
doi:10.4236/jmp.2010.110010 Published Online April 2010 (http://www.scirp.org/journal/jmp)
Instability of Thermally Conducting
Self-Gravitating Systems
Shaista Shaikh, Aiyub Khan
Department of Mathematics and Statistics, Jai Narain Vyas University, Jodhpur, India
Received February 23, 2010; r evis ed M arch 25, 2010; accepted March 25, 2010
Abstract
The gravitational instability of a thermally conducting self-gravitating system permeated by a uniform and
oblique magnetic field has been analyzed in the framework of Tsallis’ nonextensive theory for possible mod-
ifications in the Jeans’ instability criterion. It is concluded that the instability criterion is indeed modified
into one that depends explicitly on the nonextensive parameter. The influence of thermal conductivity on the
system stability is also examined.
Keywords: Jeans’ Criterion, Nonextensivity, Thermally Conducting, Self-Gravitating
1. Introduction
In any subject of astrophysics and cosmology, many-
body gravitating systems play an essential role. Globular
clusters and elliptical galaxies, which are recognized as
self-gravitating stellar systems, are typical examples.
Hence, the study of stability of self-gravitating systems
becomes very essential.
The condition of gravitational instability of self- gra-
vitating systems is determined by the Jean s’ criterion put
forward by James Jeans [1] in 1902. In terms of wave-
number, the criterion reads: “An infinite homogenous
self-gravitating atmosphere is unstable for all wavenum-
bers k less than the Jeans’ wavenumber
J
k

0
4S Gv

, where 0

is the density, G is the gravita-
tional constant, B
S
vkTm is the speed of sound, B
k
is the Boltzmann’s constant, T is the physical tempera-
ture and m is the mass of the particle.”
The Jeans’ problem has been extensively studied
under varying assumptions. A comprehensive account
of these studies has been given by Chandrasekhar [2]
in his monograph on hydrodynamic and hydromagnetic
stability. The Hall Effect on plasma stability has been
analyzed by several researchers (Ariel [3], Bhowmik [4]
and Ali & Bhatia [5]) leading to the conclusion that
Hall Currents are destabilizing in nature. Vyas &
Chhajlani [6], Sharma & Chand [7], Khan & Bhatia [8 ]
have investigated the influence of permeability of po-
rous medium on plasma instability due of the impor-
tance of such studies in geology and heavy oil recovery.
In view of the role played by thermally conducting
fluids in various astrophysical and geophysical phe-
nomena as well as industrial and engineering processes,
the stability of such fluids has been the center of nu-
merous analyses (Kumar [9],Chhajlani and Vaghela
[10], Mehta and Bhatia [11]).
In all these investigations, the Bo ltzmann-Gibbs statis-
tical mechanics have been employed to study the ther-
modynamics of the system. However, the physical re-
strictions of this formalism have been recently pointed
out in different literatures based on various studies in-
volving long-range interacting systems (Padmanabhan
[12], Taruya & Sakagami [13]). As an alternative, the
nonextensive theory proposed by Tsallis [14] is gaining
considerable attention.
The new framework for thermodynamics based on
Tsallis’ nonextensive theory has been applied exten-
sively to deal with a variety of interesting problems to
which the standard B-G statistical mechanics cannot be
applied. Examples include the study of waves and insta-
bility phenomena, such as th e plasma oscillations [15,16],
the relativistic Langmuir waves [17], the linear or nonli-
near Landau damping in plasmas [18] and dark matter
and gas density profiles observed in galaxies and clusters
[19]. The study of self-gravitating stellar systems has
been one of the most interesting applications of Tsallis’
nonextensive thermodynamics [20-24].
In this paper, we analyze the stability of a thermally
conducting self-gravitating system embedded by a uni-
form and oblique magnetic field for possible modification

S. SHAIKH ET AL. 78
in the Jeans’ instability criterion due to the presence of
nonextensive effects. The influence of thermal conductiv-
ity on the growth rate of the system is also examined.
2. Nonextensive Theory
The physical restrictions of the Boltzmann-Gibbs statis-
tical mechanics have stressed the need for a possible ge-
neralization of this formalism. Such a generalization was
proposed by Tsallis in 1988 (known as “Tsallis’ Statis-
tics”) by constructing a new form of entropy written as

1/1
q
qi
Bi
Sk pq




 (1)
where i
p is the probability of the i th microstate and q
is a parameter quantifying the degree of nonextensivity
of the system. In the limit 1q, the celebrated B-G
extensive formula, namely
ln
ii Bi
Skpp  (2)
is recovered.
Various literatures involving the thermo-statistical
analysis of many astrophysical systems and processes
(Plastino & Plastino [25], Abe [26]) make it clear that
Tsallis’ statistics may be the appropriate theory for de-
scription of astrophysical systems with long-range inter-
action of gra vitati on .
The nonextensivity in the Jeans’ problem is introduced
through the equation of state of an ideal gas. In the frame-
work of nonextensive theory, the q-nonextensive velocity
distribution function for free particles is given by


1
21
11 2
q
qB
mv
fvBq kT
 



 (3)
where q
B
is a normalization constant and the other va-
riables have their usual meanings.
If N denotes the particle number density, pressure is
defined by 2
1
3
PNmv
with 2
v
the mean square
velocity of the particle defined in Tsallis’ statistics by


23
23
q
q
vfvdv
v
f
vdv






 (4)
In 2003, Silva & Alcaniz [27] calculated the q expec-
tation value for the square velocity of the particle as

26,0 5/3
53 B
qkT
vq
qm

 (5)
Clearly, the standard mean square velocity
23/
B
vkTm is perfectly recovered when 1q.
Thus, the equation of state of an ideal gas in the nonex-
tensive kinetic theory is obtained as
2
12
353
B
qq
kT
PNmv qm


 (6)
where we have written /Nm


. Note that the standard
equation of state is correctly recovered in the limit
1q. The above equation can also be written in the
form qq
B
PNkT

, with the physical temperature q T, a
variable that depends on the nonextensive parameter q as
2
53
qT
Tq 

. Consequently, the speed of sound can be
written as
2
53
q
B
qkT
SS
mq

 (7)
significantly different from the one in B-G statistics (q
=1, TT
q

). We shall use this modified form while
writing the perturbation equations of the self-gravitating
system considered in this paper.
3. Perturbation Equations
Following standard lines, we write the linearized pertur-
bation equations characterizing the flow of a thermally
conducting self-gravitating fluid embedded by a uniform
and oblique magnetic field denoted by

,0,
x
z
HH H
 .
1.0u
t







 (8)

11 1
1u
p
hH
t








(9)

1
huH
t


 




 (10)
211
G

  (11)




222
11 11qq
pS pS
t

 



(12)
where




111
,,,,,, ,uuvwh hhhp
xyz


 and 1

are respec-
tively the perturbations in velocity u
 , magnetic field H

 ,
density

, pressure

and gravitational potential

,
G is the gravitational constant,

denotes an adiabatic
exponent and x is the coefficient of thermal conductivity.
We seek the solutions of the Equations (8)-(12) whose
dependence on the space coordinates (x,y,z) and time t is
of the form


expsin.cos ..ikx ikzit



 (13)
where


sin ,0, coskk k

 

 is the wavenumber of per-
turbation making angle

with the x-axis and

is
the frequency of perturbation. Eliminating 11 1
,&p


from the above equations, we get six equations govern-

S. SHAIKH ET AL. 79
ing the perturbation of velocity and magnetic field which
can be written in the matrix form
0AB
 
   (14)
where [A] is a sixth order square matrix and [B] is a sin-
gle column matrix in which the elements are


,, ,,,T
xyz
uvwh hh. The elements of [A] are
2
11 sin ,AiiD

 

12 13
0,sincos,AAiD

 
1415 16
cos ,0,sin ,
z z
HH
AikAAik



 
21 2223
0,, 0,AAiA

 
24 2526
0,(sincos ),0,
xz
ik
AAHH A 

 


2
3132 33
sincos ,0,cos,AiD AAiiD

 
3435 36
4142 43
cos ,0,sin ,
cos,0,cos,
xx
zx
HH
AikAA ik
AHikA AHik






 
4445 46
,0,0,AiA A


51 5253
0,(sincos ),0,
xz
AAikHH A

  
54 5556
0,, 0,AAiA

 
6162 63
sin, 0,sin,
zx
AHikAA Hik

 
64 0,A65 66
0,
A
Ai


(15)
where we have written
 

22 22
2
q
SkikGik
Dik
 
 
 
 (16)
4. Dispersion Relation
The vanishing of
A
gives the dispersion relation as the
product of three factors:


 


22
22
222 22
.. xz
HH
iik ViiiDikiDk V
 



 



(17)
By writing in

 and using the value of D in the
third factor of Equation (17), we obtain the resulting
dispersion relation, which is an equation of degree five in
n of the form
5432
43210
0ncncncncnc


(18)
with the coefficients 4
c to 0
c given by
2
4
ck





22
22 2
3
xz
q
HH
cSkGk  




22
222 2
2
xz
q
HH
ckSkG k  








22 22
1q
ckVSk G




42 22
0q
ckVSkG
 

(19)
where we have taken

2
2sin cos
xz
HH
V





5. Analysis of Dispersion Relation
In the study of Jeans’ instability, the boundary between
stable and unstable solutions is achieved by setting
0n

in the dispersion relation (Equation (17)). The
result is a family of q-parameterized critical wave-
numbers q
k given by
53
2
qJ
q
Gq
kk
S
 

(20)
Note that the standard values as obtained fro m fluid the-
ory are recovered only if 1q

. We have, thus, obtained a
modified form of Jeans’ Criterion which shall now be ana-
lyzed for different values of q. As we know, the value of
nonextensive parameter q lies between 0 and 5/3. Hence,
we will analyze the Jeans’ criterion for different values of q
in this range. Let us calculate the cr itic al wav e nu mbers for
q = 1, q = 0.3, i.e. 0 < q < 1 and q = 1.6, i.e. 1 < q < 5/3. For
these calculations, we take nu merical values for conditions
prevailing in magnetic collapsing clouds:
21 3
1.7 10,kgm 



1
113 2
2 822
2 822
6.65810,
2.5 10,
510.
Gkgms
Sms
Vms








 (21)
The following critical wave numbers are obtained
through numerical calculations
20 1
1.0 2.1210 q
km

 (22)
20 1
0.3 3.0410 q
km

 (23)
20 1
1.6 0.6710
q
km

 (24)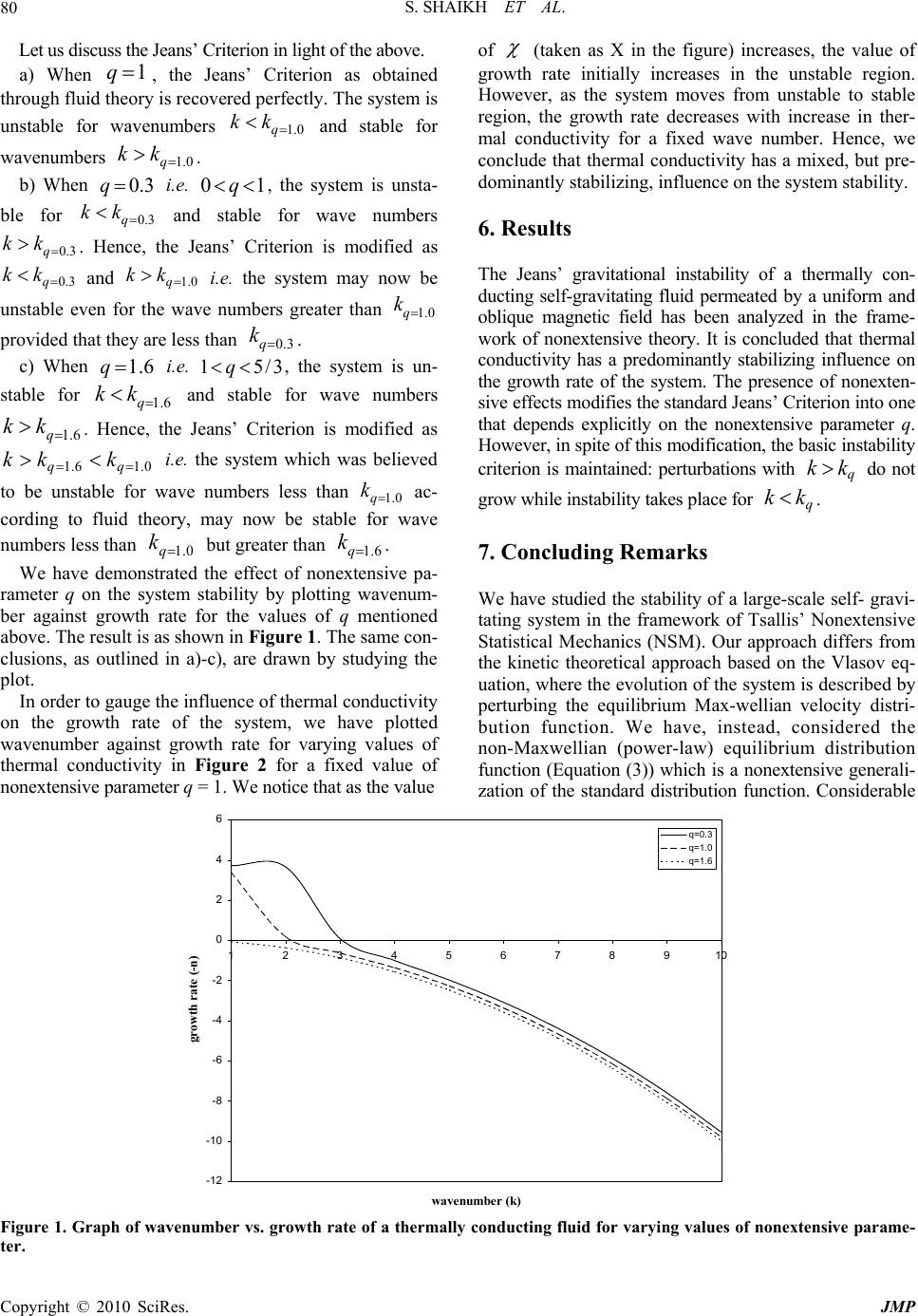

S. SHAIKH ET AL. 80
Let us discuss the Jeans’ Criterion in light of the above.
a) When 1q, the Jeans’ Criterion as obtained
through fluid theory is recovered perfectly. The system is
unstable for wavenumbers 1.0q
kk

 and stable for
wavenumbers 1.0q
kk

.
b) When 0.3q i.e. 01q , the system is unsta-
ble for 0.3q
kk

 and stable for wave numbers
0.3q
kk

. Hence, the Jeans’ Criterion is modified as
0.3q
kk

 and 1.0q kk

 i.e. the system may now be
unstable even for the wave numbers greater than 1.0q
k

provided that they are less than 0.3q
k.
c) When 1.6q i.e. 15/3q , the system is un-
stable for 1.6q
kk

 and stable for wave numbers
1.6q
kk

. Hence, the Jeans’ Criterion is modified as
1.6 1.0qq
kk k


i.e. the system which was believed
to be unstable for wave numbers less than 1.0q
k

ac-
cording to fluid theory, may now be stable for wave
numbers less than 1.0q
k but greater than 1.6q k.
We have demonstrated the effect of nonextensive pa-
rameter q on the system stability by plotting wavenum-
ber against growth rate for the values of q mentioned
above. The result is as shown in Figure 1. The same con-
clusions, as outlined in a)-c), are drawn by studying the
plot.
In order to gauge the influence of thermal conductivity
on the growth rate of the system, we have plotted
wavenumber against growth rate for varying values of
thermal conductivity in Figure 2 for a fixed value of
nonextensive parame ter q = 1. We notice that as the value
of

(taken as X in the figure) increases, the value of
growth rate initially increases in the unstable region.
However, as the system moves from unstable to stable
region, the growth rate decreases with increase in ther-
mal conductivity for a fixed wave number. Hence, we
conclude that thermal conductivity has a mixed, but pre-
dominantly stabilizing, influence on the system stability.
6. Results
The Jeans’ gravitational instability of a thermally con-
ducting self-gravitating fluid permeated by a uniform and
oblique magnetic field has been analyzed in the frame-
work of nonextensive theory. It is concluded that thermal
conductivity has a predominantly stabilizing influence on
the growth rate of the system. The presence of nonexten-
sive effects modifies the standard Jeans’ Criterion into one
that depends explicitly on the nonextensive parameter q.
However, in spite of this modification, the basic inst abi lity
criterion is maintained: perturbations with q
kk do not
grow while instability takes place for q
kk.
7. Concluding Remarks
We have studied the stability of a large-scale self- gravi-
tating system in the framework of Tsallis’ Nonextensi ve
Statistical Mechanics (NSM). Our approach differs from
the kinetic theoretical approach based on the Vlasov eq-
uation, where the evolution of the system is described by
perturbing the equilibrium Max-wellian velocity distri-
bution function. We have, instead, considered the
non-Maxwellian (power-law) equilibrium distribution
function (Equation (3)) which is a nonextensive generali-
zation of the standard distribution function. Considerable
-12
-10
-8
-6
-4
-2
0
2
4
6
12345678910
wavenumber (k)
growth rate (-n)
q=0.3
q=1.0
q=1.6
Figure 1. Graph of wavenumber vs. growth rate of a thermally conducting fluid for varying values of nonextensive parame-
ter.

S. SHAIKH ET AL. 81
-60
-50
-40
-30
-20
-10
0
10
20
12345678910
wavenumber (k)
growth rate (-n)
X= 0 .1
X= 1 .0
X= 2 .0
X= 5 .0
Figure 2. Graph of wavenumber vs. growth rate of a thermally conducting fluid for varying values of coefficient of thermal
conductivity.
amount of experimental evidence supports the employ-
ment of such a distribution (e.g. Liu et al. [28]), clearly
indicating that the standarsd Maxwellian velocity distri-
bution might provide only a very crude description of the
velocity distribution for a self-gravitating gas, or gener-
ally for any system endowed with long range interactions.
Infact, a well determined criterion for gravitational insta-
bility is not a privilege of the exponential velocity dis-
tribution function, but is shared by an entire family of
power-law functions (named q-exponentials) which in-
cludes the standard Jeans’ result for the Maxwellian dis-
tribution as a limiting case (q = 1). This being said, it
must also be stressed that all nonextensive systems need
not require the Tsallis’ statistics to understand their be-
haviors (Cohen [29]). In the light of present understand-
ing, it is still unclear which class of nonextensive sys-
tems requires Tsallis’ statistics for its statistical descrip-
tion, mainly due to the fact that the physical meaning of
the nonextensive parameter q is yet to be settled. Al-
though some progress in this regard is being made (Du
[22,23]), the Nonextensive Statistical Mechanics remains
open to further verification and deeper understanding.
Further Reading: Interested readers may refer to simi-
lar works by the authors [30,31,32] on the instability of
thermally conducting self-gravitating systems in the
framewor k o f n o nextensive s t at ist ics.
Acknowledgements: This work was carried out as part
of a major research project (F. No. 36-103/2008 (SR))
awarded by University Grants Commission (UGC), India
to the one of the authors, Aiyub Khan. The financial as-
sistance from UGC is gratefully acknowledged. The au-
thors are also grateful to the reviewer for useful sugges-
tions, which have helped in improving the overall pres-
entation and quality of the paper.
8. References
[1] J. H. Jeans, “The Stability of Spherical Nebulae,” Phi-
losophical Transactions of the Royal Society of London,
A 199, 1902, pp. 1-53.
[2] S. Chandrasekhar, “Hydrodynamics & Hydromagnetic
Stability,” Clarendron Press, Oxford, 1961.
[3] P. D. Ariel, “The Character of Equilibrium of an Inviscid
Infinitely Conducting Fluid of Variable Density in the
Presence of a Horizontal Magnetic Field with Hall-Ur-
rent,” Journal of Plasma Physics, Vol. 4, 1970, pp.
523-530.
[4] G. Bhowmik, “Rayleigh Taylor Instability of a Viscous
Hall Plasma with Magnetic Field,” Journal of Plasma
Physics, Vol. 7, 1972, pp. 117-132.
[5] A. Ali and P. K. Bhatia, “Magnetic Resistivity and Hall
Currents Effects on the Stability of a Self-Gravitating
Plasma of Varying Density in Variable Magnetic Field,”
Astrophysics and Space Science, Vol. 201, 1993, pp.
15-27.
[6] M. K. Vyas and R. K. Chhajlani, “Gravitational Instabil-
ity of a thermally-conducting Plasma Flowing through a
Porous Medium in the Presence of Suspended Particles,”
Astrophysics and Space Science, Vol. 149, 1988, pp.
323-342.
[7] R. C. Sharma and T. Chand, “Gravitational Instability for
Some Astrophysical Systems,” Astrophysics and Space
Science, Vol. 183, 1991, pp. 215-224.
[8] A. Khan and P. K. Bhatia, “Stability of Two Superposed
Viscoelastic Fluid in a Horizontal Magnetic Field,” In-
dian Journal of Pure and Applied Mathematics, Vol. 32,
2001, pp. 98-108.
[9] S. S. Kumar, “On Gravitational Instability, III,” Publica-
tions of the Astronomical Society of Japan, Vol. 13, 1961,

S. SHAIKH ET AL. 82
pp. 121-124.
[10] R. H. Chhajla ni and D. S. Vaghela, “Magnetogravitational
Stability of Self-Gravitating Plasma with Thermal Conduc-
tion and Finite Larmor Radius through Porous Medium,”
Astrophysics and Space Science, Vol. 134, 1987, pp. 301-
315.
[11] V. Mehta and P. K. Bhatia, “Gravitational Instability of a
Rotating Viscous Thermally Conducting plasma,” Con-
tributions to Plasma Physics, Vol. 29, 1989, pp. 617-626.
[12] T. Padmanabhan, “Statistical Mechanics of Gravitating
Systems,” Physics Reports, Vol. 188, 1990, pp. 285-362.
[13] A. Taruya and M. Sak aga mi, “Thermodynamic Properties
of Stellar Polytrope,” Physica A, Vol. 318, 2003, pp.
387-413.
[14] C. Tsallis, “Possible Generalization of Boltzmann-Gibbs
Statistics,” Journal of Statistical Physics, Vol. 52, 1988,
pp. 479-487.
[15] R. Silva, J. A. Alcaniz and J. A. S. Lima, “Constraining
Nonextensive Statistics with Plasma Oscillation Data,”
Physica A, Vol. 356, 2005, pp. 509-516.
[16] S. Shaikh, A. Khan and P. K. Bhatia, “Jeans’ Gravita-
tional Instability of a Thermally Conducting, Unbounded,
Partially Ionized Plasma,” Zeitschrift für Naturforschung,
Vol. 61, 2006, pp. 275-280.
[17] V. Munoz, “A Nonextensive Statistics Approach for
Langmuir Waves in Relativistic Plasmas,” Nonlinear
Processes in Geophysics, Vol. 13, 2006, pp. 237-241.
[18] F. Valentini, “Nonlinear Landau Damping in Nonex-
ten-sive Statistics,” Physics of Plasmas, Vol. 12, 2005, pp.
1-7.
[19] M. P. Leubner, “Nonextensive Theory of Dark Matter
and Gas Density Profiles,” The Astrophysical Journal,
Vol. 632, 2005, pp. L1-L4.
[20] J. A. S. Lima, R. Silva and J. Santos, “Jeans’ Gravita-
tional Instability and Nonextensive Kinetic Theory,” As-
tronomy and Astrophysics, Vol. 396, 2002, pp. 309-313.
[21] J. L. Du, “Jeans’ Criterion and Nonextensive Velocity
Distribution Function in Kinetic Theory,” Physics Letters
A, Vol. 320, 2004, pp. 347-351.
[22] J. L. Du, “Nonextensivity in Nonequilibrium Plasma
Systems with Coulombian Long-Range Interactions,”
Physics Letters A, Vol. 329, 2004, pp. 262-267.
[23] J. L. Du, “What Does the Nonextensive Parameter Stand
for in Self-Gravitating Systems?” Astrophysics and Space
Science, Vol. 305, 2006, pp. 247-251.
[24] J. L. Du, “Nonextensivity and the Power-Law Distribu-
tions for the Systems with Self-Gravitating Long-Range
Interactions,” Astrophysics and Space Science, Vol. 312,
2007, pp. 47-55.
[25] A. Plastino and A. R. Plastino, “Stellar Polytropes and
Tsallis’ Entropy,” Physics Letters A, Vol. 174, 1993, pp.
384-386.
[26] S. Abe, “Thermodynamic Limit of a Classical gas in
Nonextensive Statistical Mechanics: Negative Specific
Heat and Polytropism,” Physics Letters A, Vol. 263, 1999,
pp. 424-429.
[27] R. Silva and J. S. Alcaniz, “Negative Heat Capacity and
Non-Extensive Kinetic Theory,” Physics Letters A, Vol.
313, 2003, pp. 393-396.
[28] J. M. Liu, J. S. D. Groot, J. P. Matte, T. W. Johnston and
R. P. Drake, “Measurements of Inverse Bremsstrahlung
Absorption and Non-Maxwellian Electron Velocity Dis-
tributions,” Physical Review Letters, Vol. 72, 1994, pp.
2717-2720.
[29] E. G. D. Cohen, “Statistics and Dynamics,” Physica A,
Vol. 305, 2002, pp. 19-26.
[30] S. Shaikh, A. Khan and P. K. Bhatia, “Stability of Ther-
mally Conducting Plasma in a Variable Magnetic Field,”
Astrophysics and Space Science, Vol. 312, 2007, pp.
35-40.
[31] S. Shaikh, A. Khan and P. K. Bhatia, “Thermally Con-
ducting Partially Ionized Plasma in a Variable Magnetic
Field,” Contributions to Plasma Physics, Vol. 47, No. 3,
2007, pp. 147-156.
[32] S. Shaikh, A. Khan and P. K. Bhatia, “Jeans’ Gravita-
tional Instability of a Thermally Conducting Plasma,”
Physics Letters A, Vol. 372, 2008, pp. 1451-1457.