Paper Menu >>
Journal Menu >>
 J. Mod. Phys., 2010, 1, 44-47 doi:10.4236/jmp.2010.11005 Published Online April 2010 (http://www.scirp.org/journal/jmp) Copyright © 2010 SciRes. JMP Computation of the Schrödinger Equation via the D isc rete Derivatives Representation Method: Improvement of Solutions Using Particle Swarm Optimization Abdelwahab Zerarka, H. Saidi, A. Attaf, N. Khelil Laboratory of Theoretical Physics, University Med Khider, Biskra, Algeria E-mail: azerarka@hotmail.fr Received January 16, 2010; revised February 3, 2010; accepted March 18, 2010 Abstract We develop the discrete derivatives representation method (DDR) to find the physical structures of the Schrödinger equation in which the interpolation polynomial of Bernstein has been used. In this paper the particle swarm optimization (PSO for short) has been suggested as a means to improve qualitatively the solu- tions. This approach is carefully handled and tested with a numerical example. Keywords: Discrete Derivatives, Spectra, Wave Function, Particle Swarm 1. Introduction Several different methods, analytical and numerical have also been formulated and modeled during the past dec- ades for the study of the solutions of the wave equation with different structures. It is known also that for very limited potentials, Schrödinger equation is exactly solv- able [1-6]. The latest numerical approach to date is the differential quadrature method [1] introduced for energy spectra es- timate. It was first applied to Schrödinger equation in the linear case, where the solution is not correctly reproduced in the domain in which strong oscillations can arise, or simply for instance in the case of highly excited states. Further calculations are pursued for the construction of the solution by a suitable choice of the interpolating points using the particle swarm optimization (PSO) [7] together with the discrete derivatives representation method. The aim of the present work is to develop a gen- eral numerical procedure for the wave equations that is universally applicable. 2. Formulation of the Discrete Derivatives Representation Method (DDR) In this section, the description of the discrete derivatives representation method can be summarized as follows: the radial Schrödinger equation in the framework of the spherically symmetric potential ( ) Vr r = is written as () () nl nl dwrS reS r dr 2 ,, 2 -() é ù êú += êú ë û (1) where mE 2 2 e=. We treat the case where the potential is central, and the Equation (1) is identified as the reduced Schrödinger equation, 22 2m K wrV r h r () ()=+ is the ef- fective potential where K is expressed in terms of the angular momentum quantum number l by ll(1)+, and the radial function nl Rr ,() is related to () nl Sr , by the relation ( ) nl nl Sr rRr ,, ()=. The radial variable rruns from a to b with a0> and b can be infinite. In general, in some problem, the Schrödinger operator re- quires a change of variables. At this point, we need to make a universal transformation on the variable r. Let zr()j= be the new variable, where r()j is a smooth invertible function (rz()j- =), and it is also easy to see that this definition preserves always the ei- genvalue equation. We can express the solution nl Sz ,() by making the substitution Ψ as Sz Szzz(())() () r j-= (2) where we have now dropped the nl, subscript for sim- plicity. z()Y is a polynomial function in which will be defined in the following, as Sz() is a asymptotic solution to be determined, and r is arbitrary quantity, and can be  A. ZERARKA ET AL. Copyright © 2010 SciRes. JMP 45 expressed in terms of the parameters of the potential. After substitution in (1) it can be verified that the func- tion z()Y must be solution of the equation Ψhz() 0= (3) where the differential operator h is defined by dd hFzAz Dz dz dz 2 2 ()2 ()()=--+ (4) for simplicity, we abbreviate as follows () () () where as as as asas Fz S Az Sz Dz wzCzzz CzS SS z 2 2 2 2 2 2 1 2 () () 2 (1) 2 ()(())() 2 () j rj j j rr rj jej j rj j ¢ æö ÷ ç÷ ç÷ ç÷ ÷ ç èø - æö ÷ ç÷ ç÷ ç÷ ÷ ç èø -¢ ¢¢ æö ÷ ç÷ ç÷ ç÷ ÷ ç èø ¢ = éù êú ¢¢ êú ¢ =++ êú ê¢ú êú ëû é ù ê ú ¢¢ - ê ú ¢ =-- ++ ê ú ¢ ê ú ë û éæö ÷ ç÷ 碢 ÷ ç÷ =++ ç÷ ç÷ ç÷ ¢÷ ç÷ ç èø ë ì ï ï ï ï ï ï ï ï ï ï ï ï ï ï ï ï ï í ï ï ï ï ï ï ïù ï ïêú ï ïêú ïêú ï ïêú ï ïêú û ï î (5) Now, we introduce the discrete derivatives representa- tion method in which any derivative discretized at any grid point can be expressed by a linear combination of functional values at all discrete points over the interval a[()j, b()]j of the variable z. The term Ψh éù êú ëû involves the different derivatives and can be expressed as a constant coefficient eigenfunction combination at all discrete points over the interval a[()j, b()]j as ΨΨ N ij j i j hβzi N 0 () for 0,..., = éù == êú ëû å (6) i z()F represents the eigenfunction value at grid point i z. The weighting coefficients ij β are established with the choice of the test function and specifically taken as the Bernstein interpolated polynomial of N th degree as () 10,1 Nj j Nj N Bxx xjNx j ,( ),0,...,, and - æö ÷ ç é ù÷ ç =- =Î ÷ ç ê ú ÷ ë û ç÷ ç èø (7) and the associated sequences j z{}, 1jN££ of the z -variable linked to Bernstein points j j N x= by the relation () jj zbaxa() ()()jj j=- + . The term N j æö ÷ ç÷ ç÷ ç÷ ç÷ ç èø in (7) denotes the binomial coefficient. A given function g x() can then be approached using (7) by N NjNj j g xgxgxBx , 0 ()()( )() = »= å (8) It follows that from (6,7,8), we can establish the un- known weighting coefficients ij b for the total Hamilto- nian h as iji iji iji ij DzAz Fz (0)(1) (2) ()2()() ,ba aa=- - (9) the superscripts 0, 1 and 2 in parentheses do not indicate powers, but merely identify the derivatives of the Bern- stein’s polynomial with which the quantities ij a are associated. () k Nj i k ij kk dB x k dx ba , () () 1, 0,1,2 () () a jj == - (10) Having found the weighting coefficients ij b in terms of the energy, one can accurately solve the following ma- trix equation and therefore the original problem (1) Ψ0 b é ù= ê ú ë û (11) In the above expression, b éù êú ëû is a ( ) ( ) 11NN+´ + matrix with elements i j b, and F is a column vector with components 0 (Ψ(),z 1 Ψ(),z... ,ΨN z()). more complete description will be given later on with two spe- cific examples. 3. Strategy of Particle Swarm Optimization A new stochastic algorithm has recently appeared, namely “particle swarm optimization” PSO. The term ‘particle’ means any natural agent that describes the swarms behavior. The PSO model is an appropriate parti- cle simulation concept, and was first proposed by Eber- hart and Kennedy [11-13]. In what follows, we present the main steps of the strat- egy of the PSO algorithm. We assume that each agent (particle) i can be represented in a multidimensional search space N by its current position ii X x1 (,= i x 2,..., iN x ) and its corresponding specific velocity , ii Vv 1 (= 2, i v..., iN v). Also a memory of its personal (previous) best position is represented by ii P p1 (,= 2i p , ..., iN p ), called (pbest), the subscript i range from 1 to s , where s indicates the size of the swarm. Commonly, each particle localizes its best value so far (pbest) and its position, and consequently identifies its best value in the group (swarm), called also (sbest) among the set of values (pbest). Now each particle i moves according to the following system as 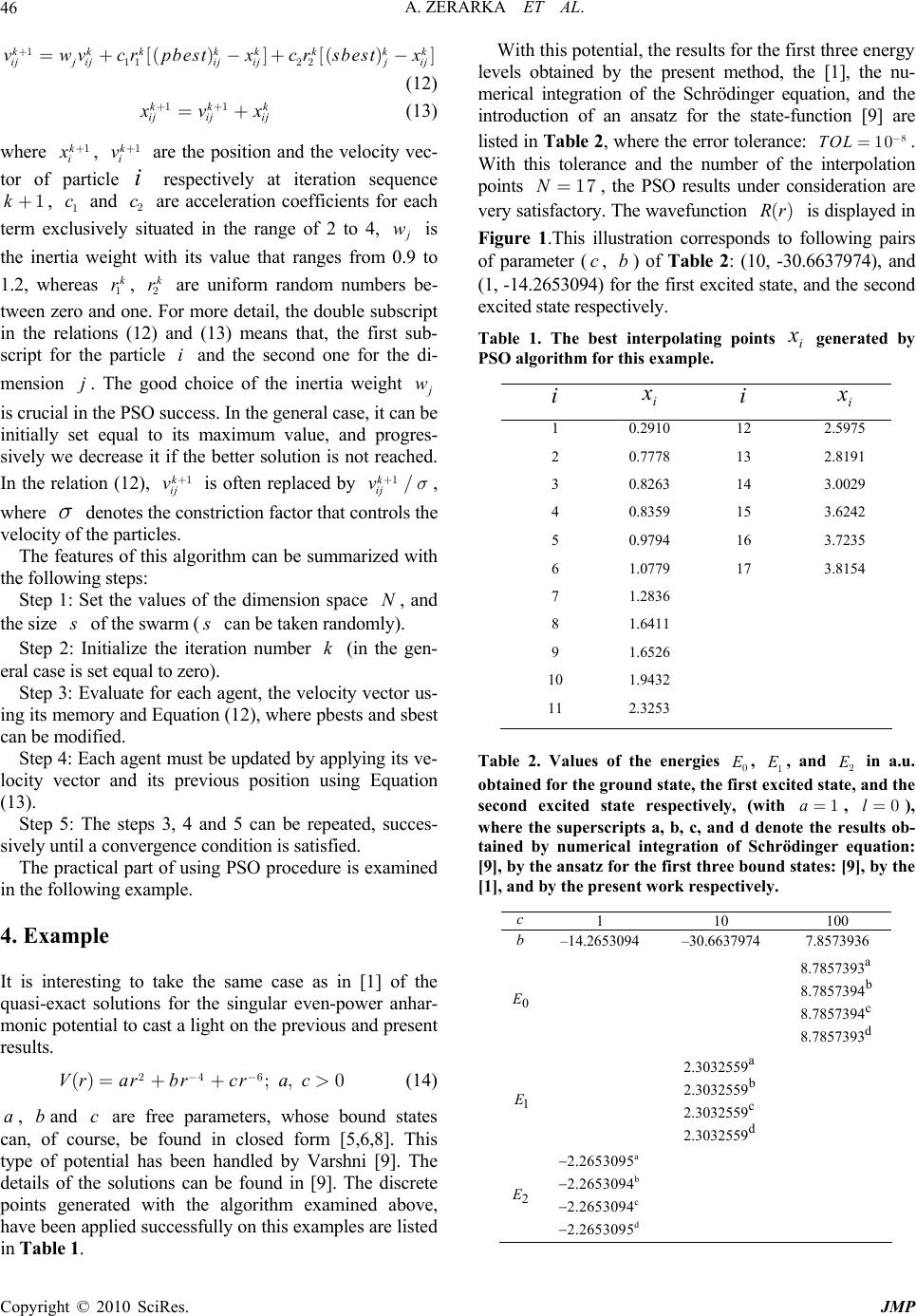 A. ZERARKA ET AL. Copyright © 2010 SciRes. JMP 46 kkkkkkkk ijjijijijjij vw vcrpbestxcrsbestx 111 22 [()][( )] +=+-+ - (12) kkk ijij ij x vx 11++ =+ (13) where k i x 1+, k i v1+ are the position and the velocity vec- tor of particle i respectively at iteration sequence k1+, c1 and c2 are acceleration coefficients for each term exclusively situated in the range of 2 to 4, j w is the inertia weight with its value that ranges from 0.9 to 1.2, whereas k r 1, k r 2 are uniform random numbers be- tween zero and one. For more detail, the double subscript in the relations (12) and (13) means that, the first sub- script for the particle i and the second one for the di- mension j. The good choice of the inertia weight j w is crucial in the PSO success. In the general case, it can be initially set equal to its maximum value, and progres- sively we decrease it if the better solution is not reached. In the relation (12), k ij v1+ is often replaced by k ij v1/s +, where s denotes the constriction factor that controls the velocity of the particles. The features of this algorithm can be summarized with the following steps: Step 1: Set the values of the dimension space N, and the size s of the swarm ( s can be taken randomly). Step 2: Initialize the iteration number k (in the gen- eral case is set equal to zero). Step 3: Evaluate for each agent, the velocity vector us- ing its memory and Equation (12), where pbests and sbest can be modified. Step 4: Each agent must be updated by applying its ve- locity vector and its previous position using Equation (13). Step 5: The steps 3, 4 and 5 can be repeated, succes- sively until a convergence condition is satisfied. The practical part of using PSO procedure is examined in the following example. 4. Example It is interesting to take the same case as in [1] of the quasi-exact solutions for the singular even-power anhar- monic potential to cast a light on the previous and present results. Vrarbrcra c 246 (); , 0 -- =+ +> (14) a, band c are free parameters, whose bound states can, of course, be found in closed form [5,6,8]. This type of potential has been handled by Varshni [9]. The details of the solutions can be found in [9]. The discrete points generated with the algorithm examined above, have been applied successfully on this examples are listed in Table 1. With this potential, the results for the first three energy levels obtained by the present method, the [1], the nu- merical integration of the Schrödinger equation, and the introduction of an ansatz for the state-function [9] are listed in Table 2, where the error tolerance: TOL8 10- =. With this tolerance and the number of the interpolation points N17=, the PSO results under consideration are very satisfactory. The wavefunction Rr() is displayed in Figure 1.This illustration corresponds to following pairs of parameter (c, b) of Table 2: (10, -30.6637974), and (1, -14.2653094) for the first excited state, and the second excited state respectively. Table 1. The best interpolating points i x generated by PSO algorithm for this example. i i x i i x 1 0.2910 12 2.5975 2 0.7778 13 2.8191 3 0.8263 14 3.0029 4 0.8359 15 3.6242 5 0.9794 16 3.7235 6 1.0779 17 3.8154 7 1.2836 8 1.6411 9 1.6526 10 1.9432 11 2.3253 Table 2. Values of the energies E0, E1, and E 2 in a.u. obtained for the ground state, the first e xcited state, and the second excited state respectively, (with a1=, l0=), where the superscripts a, b, c, and d denote the results ob- tained by numerical integration of Schrödinger equation: [9], by the ansatz for the first three bound states: [9], by the [1], and by the present work respectively. c1 10 100 b–14.2653094 –30.6637974 7.8573936 0 E d c b a 8.7857393 8.7857394 8.7857394 8.7857393 1 E d c b a 2.3032559 2.3032559 2.3032559 2.3032559 2 E a b c d 2.2653095 2.2653094 2.2653094 2.2653095  A. ZERARKA ET AL. Copyright © 2010 SciRes. JMP 47 [ \ [ \ # 7 7 DX Figure 1. wavefunction R r() obtained with the present method, where r is in a.u. for the singular even-power anharmonic potential. Full curve (10 c=, 30.6b=- 637974 ), first excited state; dash curve (1c=,b= 14.26-53094), second excited state. 5. Comments and Concluding Remarks In this work we have presented a new formulation that uses the PSO algorithm together with the DDR method for the computation of the bound-state eigenvalues and the associated eigenfunctions of linear differential op- erators such as the Schrödinger-like equation resulting from a quantum system, with which one can receive re- sults that are not available with the interpolating points of Tchebychev type, especially when the wavefunction is not smooth. Although the previous DDR method with the PSO procedure provides substantially better accuracy than the conventional Tchebychev’s interpolating points used in [1] which are always known to be the only best points which permits a good approach of the interpolating func- tion. The preliminary results, obtained through the use of the PSO method, show a good improvement of solutions for the example which has been selected here as a testbed. For instance, Figure 1 shows graphically the wavefunc- tion obtained by PSO procedure. Furthermore, the shape of the wave functions is preserved for all configurations and the error tolerance is 10-8. 6. Acknowledgments The authors are grateful to Prof. Hans for interesting discussions and for a support of this work. One of the authors (A. Z) wishes to express its sincere thanks to Dr. Dyn Keit for bringing his attention to the PSO method. This work was sponsored in part by the M.E.R.S (Min- istère de l’Enseignement et de la Recherche Scientifique): Under contract No. D0701/01/08. 7. References [1] A. Zerarka, S. Hassouni, H. Saidi and Y. Boumedjane, “Energy Spectra of the Schrödinger Equation and the Dif- ferential Quadrature Method,” Communication in Nonlin- ear Science and Numerical Simulation, Vol. 10, 2005, pp. 737-745. [2] A. Zerarka and A. Soukeur, “A Generalized Integral Quadratic Method: I. An Efficient Solution for One-Di- mensional Volterra Integral Equation,” Communication in Nonlinear Science and Numerical Simulation, Vol. 10, 2005, pp. 653-663. [3] F. Iachello, “Algebraic Methods in Quantum Mechanics with Applications to Nuclear and Molecular Structure,” Nuclear Physics A, Vol. 560, 1993, pp. 23-34. [4] M. Selg, “Numerically Complemented Analytic Method for Solving the Time-Independent One-Dimensional Sch rödinger Equation,” Physical Review E, Vol. 64, No. 5, 2001, 056701. [5] S. H. Dong, “Exact Solutions of the Two-Dimensional Schrödinger Equation with Certain Central Potentials,” International Journal of Theoretical Physics, Vol. 39, 2000, p. 1119. [6] S. K. Bose and N. Gupta, “Exact Solution of Nonrelativis- tic Schrödinger Equation for Certain Central Physical Po- tentials,” Il Nuovo Cimento B, Vol. 113, 1998, p. 299. [7] J. Kennedy and R. C. Eberhart, “Particle Swarm Optimi- zation,” Proceedings IEEE International Conferences Neural Networks, Piscataway, 1995, pp. 1942-1948. [8] Maitland, et al., “Intermolecular Forces,” University Press, Oxford, 1987. [9] Y. P. Varshni, “The First Three Bound States for the Po- tential V rarbrcr 4 26 () -- =+ +,” Physics Letters A, Vol. 183, 1993, pp. 9-13. [10] S. H. Dong, “Quantum Monodromy of Schrödinger Equa- tion with the Decatic Potential,” International Journal of Theoretical Physics, Vol. 41, No. 1, January 2002, pp. 89-99. [11] R. C. Eberhart and J. Kennedy, “A New Optimizer Using Particles Swarm Theory,” Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 1995, pp. 39-43. [12] R. C. Eberhart and Y. Shi, “Parameter Selection in Particle Swarm Optimization,” Lecture Notes in Computer Sci- ence-Evolutionary Programming VII, Porto, V. W., Sara- vanan, N. Waagen, D., Eiben, A. E., Springer, Vol. 1447, 1998, pp. 591-600. [13] T. I. Cristian “The Particle Swarm Optimization Algo- rithm: Convergence Analysis and Parameter Selection,” Information Processing Letters, Vol. 85, No. 6, 2003, pp. 317-325. |

