J. Mod. Phys., 2010, 1, 17-32
doi:10.4236/jmp.2010.11003 Published Online April 2010 (http://www.scirp.org/journal/jmp)
On the Nature of Dark Matter and Dark Energy
Baurov Yury Alexeevich1, Malov Igor Fedorovich2
1Central Research Institute of Machine Building, Korolyov, Russia
2P. N. Lebedev Physical Institute, Russian Academy of Sciences, Moscow, Russia
Received February 19, 2010; revised March 17, 2010; accepted March 20, 2010
Abstract
It is known that all candidates in dark matter (DM) particles (neutrinos, axions, supersymmetric particles etc.)
can not explain the basic properties of DM. The same can be said on the proposed candidates in dark energy
(DE) (for example, quintessence). In the paper it is shown that some problems connected with DM and DE
can be solved in the framework of the byuon theory. Basic axioms and some conclusions of this theory are
discussed. The existence of fundamental unobserved elements in nature, byuons is declared. Physical space
in our Universe is the quantum medium of special objects 4b, formed in four-contact interactions of byuons
(m4b c
2 ≈ 33eV). These objects determine the average density of substance (DM) in the Universe ~10-29 g
cm-3. The byuon theory predicts a new interaction of natural objects with physical vacuum. This new force
can cause the observed acceleration of our Universe. The estimations show that it is higher than the gravita-
tional force at distances of order to 1026-1028 cm. Some other consequences of the byuon theory are consid-
ered.
Keywords: Dark Matter, Dark Energy, Byuon, New Force
1. Introduction
Some hard problems have appeared in astrophysics dur-
ing the last dozens of years. Observations show that ap-
proximately 4% of the cosmological energy density is
accounted for by baryons, 23% by “the dark matter” and
the reminder by “the dark energy” (see, for example,
[1,2]).
There are some evidences for the existence of dark
matter (DM) and dark energy (DE). Here we enumerate
basic ones only.
1) In 1937 F.Zwicky measured velocities of galaxies
in the Coma cluster and concluded that the total mass of
this cluster must be much more than observable one to
prevent the escaping of investigated galaxies from the
cluster.
2) The summarized mass of the observed gas and gal-
axies in the number of clusters is not enough to keep
them inside of the cluster.
3) The gravitational lensing by clusters of galaxies
gives the mass of such lens much more than calculated
masses of clusters.
4) The rotation curves of galaxies [3] show that the
total mass of the individual galaxy is approximately one
order higher than the mass of gas and all stars observed
in this galaxy.
5) The observations of supernovae in distant galaxies
(see, for example, [4]) show that our Universe expanses
with an acceleration, and there is a source causing such
type of expansion.
The nature of dark matter and dark energy is unknown
up to now.
2. Dark Matter
DM is not observed as a shining matter and must be
characterized by extremely weak electromagnetic inter-
actions. It must be approximately collisionless and non-
relativistic.
DM is not primarily baryonic. The calculated amount
of deuterium should be much smaller than observed one
if the average baryon density was an order of magnitude
higher than the modern value (~0.3 baryons per cubic
meter).
The mass interval for the possible candidates in DM is
huge (from 10 -22 eV to 106 M⊙ ≈ 1072 eV).
Let us discuss the most probable candidates in DM.
1) Axions, light pseudo-scalar bosons [5,6] with mass
μeV ≲ m ≲ meV. They could be detected by resonant
axion-photon conversion in a magnetic field [7,8].
2) Neutrinos. Some laboratory experiments and cos-

Y. A. BAUROV ET AL. 18
mological restrictions give the mass interval for all kinds
of neutrinos:
50 meV ≲ Σ mν ≲ 0.7 eV, or 0.0005 < Ων h2 < 0.0076,
where Ων = ρν/ρc , h = H0/100 km/sec/Mpc, ρc = 3 H0
2/
(8 π G) is the critical density of the Universe, H0 is the
Hubble constant.
Super-symmetric theories put bosons and fermions in
common multipletes. They give some possible candi-
dates in DM.
1) The super-partner of the graviton, gravitino with the
spin 3/2 [9].
2) Neutralinos. These are the four spin ½ Majorana
fermion super-partners of the neutral gauge and Higgs
bosons (χ0
1-4) [10]. There are also two charged Dirac
fermion super-partners of charge gauge and Higgs bos-
ons, charginos (χ±
1-2).
3) Axinos, a spin ½ partner of the axion [11].
4) Non-topological solitons, Q-balls [12].
5) If our four-dimensional space-time is embedded in
a higher dimensional space, the Kaluza – Klein excita-
tions of Standard Model states along the orthogonal di-
mensions may be as DM candidates [13].
6) Objects of many dimensions (branes) are described
in string theories. Their fluctuations have been consid-
ered as particles (branons) which could be DM candi-
dates [14].
7) DM could be an ordinary matter in the mirror world
where the only communication is gravitational. In this
case our Universe and a mirror universe are two branes
in a higher dimensional space [15].
8) At the last stages of inflation gravitational interac-
tions can produce a lot of weakly interacting massive
particles which for mass scales of 1013 GeV could ac-
count for DM [16].
9) Primordial black holes have been considered as
candidates in DM as well [17].
So, as observations give, baryons provide approxi-
mately 4% of DM, neutrinos ~0.3-3% of it. The rest
(20-25%) is a non-baryonic DM. The nature of this part
of DM is unclear. There are many problems with theo-
retical foundations and experimental evidences of the
existence of particles mentioned above and described in
cited papers.
3. Dark Energy
The nature of DE is much more unclear than that of DM.
It is necessary for it to have the equation of state of the
following form (see, for example, [18]):
p = w ρ (1)
where p is pressure and ρ is the energy density. The most
probable value of the parameter w is approximately –1,
as follows from the known observations. This implies
that the energy density of such substance is constant and
corresponds to the flat universe, i.e. the curvature K of
the spatial sections (slices at constant cosmic time) is
equal to zero. DE causes the acceleration of the expan-
sion of our Universe. Figure 1 shows the sum (solid line)
of two potentials: The usual (negative) gravitational po-
tential φ1 (broken line) causing the attraction of two
bodies and a positive constant potential φ2 giving the
repulsion at large distances (r > r*).
One of the possible sources of DE is “quintessence”
[19], a scalar field Φ rolling slowly in a potential. Most
quintessence models give for such scalar fields
mΦ c2 ~ 10-33 eV (2)
In quantum field theory light scalar fields are hard to
understand. In any case these fields should give rise to
long-range forces which must be observable. It is sur-
prisingly why such quintessence field has not been de-
tected up to now.
There are many problems with other models of DE
(see, for example, [18]).
In this paper we shall try to explain DM and DE in the
framework of the byuon theory. First of all we will de-
scribe briefly the foundations of this theory.
4. Basic Axioms and Hypotheses: Space,
Time, and Physical Vacuum in the Light
of the Byuon Theory
Any theory begins with axioms, that is, with basic pos-
tulates accepted without proofs.
Thus, let us assume that there are no space, no time,
no world of elementary particles of which all physical
bodies consist, but there is an unobservable object, a
byuon (i) [20-25], being unobservable in itself and
characterized by discrete states (i.e. numbered by the
series of natural numbers) having inherent “vectorial”
property. The expression for (i) is
Ф(i) = [Ag X(i)]  (–1 [Ag X(i)] ) (3)
where X(i) is “length” of the byuon, a real (positive or
negative) value depending on the index i = 0,1,2,…k,…
Figure 1. Scheme of two body interactions in our Universe.

Y. A. BAUROV ET AL. 19
Index i is a quantum number for (i)1. The explanation
of square brackets has been given further. The dimension
of byuons is equal to the dimension of electric charge (in
the CGSE-system) or of magnetic flux or of the Dirac’s
monopole. The quantity Ag is some internal potential
being equal in magnitude to the cosmological vectorial
potential Ag, a new fundamental vectorial constant in-
troduced in [26,27] (Ag  1.951011Gscm).
Thus, Ф()i

can take both real and pure imaginary
values.
The whole set (i) forms a one-dimensional space R1
in index i.
According to this conception, by the discrete time is
meant, for the byuon, a discrete change in the index i (its
increase or decrease) is possible. In connection with the
discrete time, a quantum of time 
0 and quantum of space
0
~
x are introduced in the one-dimensional discrete space
R1 formed by byuons (

0
 0.9  10–43 s, 0
~
x 2.8  10–33
сm). The distance between byuons is defined therewith
as a difference in their lengths x(i). The space R1 is dis-
crete by definition.
Since the space R1 is discrete, one of methods of pa-
rametrization of X(i) is X(i) =o
x
~
 i, or X(i) = -o x
~
i.
Statics. In the set {(i)}, there are meant no static
states with time t > 
0.
Kinematics. Depending on whether the length X(i)
positive or negative, decreases or increases in magnitude,
free byuons (i.e. not interacting one with another) can be
only in one of the four so called vacuum states (VS) II+,
I+, I–, II–. Further we will omit sometimes VS in the ex-
pressions like VS II+.
Introduce the following definitions.
1) A free byuon is in the state II+ if its positive length
discretely, in a quantum of time 
0, increases by a quan-
tum of distance 0
~
x with the speed of propagation (in-
crease in length) 0
0
00
~
c
x
c



(c0 is the light speed).
Hence the speed of byuons is the ratio of their lengths to
the postulated quantum of time.
2) A free byuon is in the state I+ if its positive length
discretely, in a quantum of time 
0, decreases by 0
~
x. In
this case 0
0
0
~
0c
x
c



.
3) A free byuon is in II– if the modulus of its negative
length increases by 0
~
x in time 
0 with 0
0
0
x
c




0
c .
4) A free byuon is in I– if the modulus of its negative
length discretely, in time 
0, decreases by 0
~
x. In this
case 0
0
0)
~
(0 c
x
c




.
From the definition of byuons it is seen that they are in
perpetual dynamics of generation and annihilation, ex-
tension and contraction. The collection of free (not in-
teracting) byuons in VSs II+, I+, I–, II– forms physical
vacuum of the one-dimensional space R1 of index i
(about properties of R1 will be said below). Recall how-
ever that in this model of physical vacuum, time is a se-
quence of events of byuon generation (extension) and
“collapse” (contraction). These correspond to each byuon
its own count of time measured by the natural number
series. One of the two directions of the one-dimensional
space R1, coincident with that of a byuon with the maxi-
mum x(i) in VS II+, is taken for the positive direction of
the vector
А

G and )(iФ

.
The average magnitudes for byuons being in the above
described VSs at maximum i=k, are determined from the
following expressions (see 1, and [20-22]):
11
1
1
11
21
[] 0,
2
21
[] 10,
2
2() 1
[] 10,
2
2() 1
[] 0,
2
i
G
II
G
i
G
I
G
ki
G
II
G
ki
G
I
G
const i
AX AX
kA
const i
AX AX
kA
const ki
AX AX
kA
const ki
AX AX
kA










 






 






 






 








(4)
where .
34 2
0
0
0
1e
hc
hc
const  is some constant. As we will
see later h is equal to the Plank constant and e0 is the
electron charge. (See Appendix 1). The square brackets
mean the average value for byuons between previous and
subsequent magnitudes because any observations are
possible during time intervals much more than a time
quantum only.
Assume that for the byuons with the length greater
than 0
~
x, only contact interactions are realized, by which
we will mean existence of at least two byuon VSs at a
quantum of space R1.
Hypothesis 1. Assume the observable three-Dimen-
sional space R3 to appear as a result of minimization of
the potential energy (PE) of VSs byuon interactions in
the one-dimensional space R1 formed by them. We con-
struct PE from the taking into consideration of dimen-
sions. More precisely, the space R3 is fixed by us as the
result of this byuon dynamics. In the space R3 therewith
the dynamical processes for objects with the residual
positive potential energy of byuon interactions originate,
and in consequence, the wave properties of elementary
1It should be explained that the vector (i) is not an ordinary vector in
some space but an object with “inner” vectorial properties that are
manifesting themselves when the value x(i) changes in the process o
f
p
hysical space formation.

Y. A. BAUROV ET AL. 20
particles arise.
PE means the extreme value of the expression with the
dimension of energy. This expression is formed using all
possible vacuum states of byuons and the distance in the
R1 space. This distance is taken positive values only.
The proposed hypothesis requires to develop a
mathematical model based on a new algebra of probabil-
istic events since the elementary events (a discrete de-
crease (
Ä
) or increase (D) in the length of byuon) are
assumed to be probabilistic in character. Hence for the
byuons of the minimum length we may say about the
existence, with certain probability, of the events
Ä
D
0. Note that in [9] an algebra of events is given, being a
development of the Boolean algebra with the proviso that
Ä
D = 1. For the deterministic approach used in [28],
the event
Ä
D  0 is illogical by von Neumann, but in
the probabilistic space of events the existence of
Ä
D 
0 is possible.
In this paper only the physical statement of the prob-
lem will be considered, and results of evaluations made
in support of the hypothesis advanced, will be given.
The space R1 is formed from the set of byuons in such
a manner that at its i-th point there exist all the byuons
with the lengths smaller than X(i) or equal to X(i) for X(i)
> 0, and those with the absolute values smaller than X(k-i)
for X(k-i)<0, where k is some period in i.
The assumption that two neighboring byuons (the i-th
and (i + 1)-th; (i + 1)-th and (i + 2)-th etc.) being in vac-
uum states II+
will interact, is unreasonable since in this
case the definition of byuons for this VS would be violated
at the point of interaction. Such interaction is possible only
between the i-th and (i-k)-th byuons in the state II+ if they
form a “loop” in the space R1 (by the “loop”, the periodic-
ity of the process in i is implied), i.e. the two byuons 
i
II
and 
ki
II will be observed simultaneously at one point
of the space R1. The least possible value of k is k = 3. In
Figure 2 shown is the interaction of byuons in the vacuum
states 
1
II and 
4
II (the smallest loop). The byuons in
the state II– interact likely.
0
12
II
+
4
II
+
1
II
+
3
II
+
2
Figure 2. Interaction of byuons in vacuum states II1+ and
II4+ (the smallest loop).
The byuon states I+ and I– can occur only if the byuons
have already been in VS II+ and II–, respectively. At
maximum positive potential energy of byuon interaction
there exists a single variant of “occupancy” (Figure 3).
The probability of the minimum four-contact interac-
tion of the neighboring in i byuons I+II+  I–II– (“”
symbolizes interaction) with randomly appearing states
I+ and I–, is equal to 1/16 [20-22]. That is quite under-
standable when analyzing possible four-contact interac-
tions (see Figure 4)). All other possible variants of the
four-contact interaction are unobservable either because
one cannot introduce them without violating the defini-
tion of byuons or in view of imaginary energy of such
interaction.
Note once more that there exist only two directions in
the one-dimensional world, the first of which corre-
sponds to increasing index i for byuons with X > 0 (vac-
uum II+), and the second corresponds to decrease in i for
I
0
II
NkP – i – 4
II
NkP – i – 2
II
2
+
II
k
–
II
NkP – i
–
–
–
I
i
I
i–2
I
i–4
+
+
+
II
i+2
II
i–2
II
i
+
+
+
+
I
k2 –
–
I
NkP – i – 6
I
NkP – i – 4
I
NkP – i – 2
–
–
–
A
DX > 0
DX < 0
Figure 3. Completion of vacuum states II+ and II– by vac-
uum states I+ and I–, respectively, at the maximum potential
energy of interaction.

Y. A. BAUROV ET AL. 21
II
+
II
+
II
+
II
+
II
+
II
+
II
+
II
+
I
+
I
+
I
+
I
+
I
+
I
+
I
+
I
+
I
+
II
–
II
–
II
–
II
–
II
–
II
–
II
–
II
–
II
–
I
–
I
–
I
–
I
–
I
–
I
–
I
–
I
–
I
–
I
–
I
–
I
–
II
–
II
–
II
–
II
–
II
–
II
–
I
–
I
–
I
–
I
–
II
–
II
+
II
+
I
+
I
+
I
+
I
+
II
+
II
+
II
+
II
+
II
+
I
+
I
+
I
+
II
+
i (x<0)
i (x>0)
Figure 4. The possible variants of four-contact interaction
of byuons. Square means that this interaction can realize in
nature.
such byuons (vacuum I+). These directions are coinci-
dent with those for byuons with X < 0: II– with I+, and
I– with II+. It is clear from above definitions that the
byuon with the maximum length X(i) in VS II+ deter-
mines the positive direction, and directions of other
byuons are correspondent with it.
The four-contact interaction of byuons is realized
within a time  =0
~

only at points D of the R1-space
(Figure 3), i.е. at the points where introducing an inter-
action with PE > 0 is possible. In Figure 3 the arrows
corresponding to byuons show directions of a decrease or
an increase in their lengths relative to the origin of the
coordinates introduced, for example, where i  0 (in its
direction the absolute value of the byuon length de-
creases (states I+ and I–), and it increases in the opposite
directions (states II+ and II–)). At the points A in Figure
3, the coordinate denoting place (time) of byuon interac-
tion cannot be fixed because of violating, in such a case,
the definitions of the byuon states (in one quantum of the
R1-space within a time 
0, the byuons with II+I+ I
–II–
should not be present). It is assumed that before the ori-
gin of VS II+ with the minimum length (i = 1), the byuon
vacuum states II– and I– with any possible lengths are
already in existence.
The propagation of byuons in VSs II+I+ and I–II–, the
interaction between which occurs with imaginary energy
(see below ), presents two wave-like processes (see be-
low) directed towards each other at X(i) > 0 and X(i) < 0,
respectively. These processes are unobservable. A really
observable signal can be transmitted by means of such
processes only in the four-contact byuon interaction II+I+ 
I–II–.
Let us obtain an equation characterizing the propaga-
tion of the four-contact interaction of byuons in R1. In-
troduce functions of index i, characterizing the origin of
such or another VS by byuons: 2,
iki
I
III



, determining
the processes of byuon length magnitude origin and in-
crease at positive and negative X(i), respectively;
2
,
iki
I
I



 , determining the processes of byuon length
magnitude cancellation and decrease at positive and
negative X(i), respectively.
The physical sense of the introduced functions consists
in that their product determines the probability of
two-contact interaction of byuons (for example, 2i
I
I



2ik
I
I



determines the probability of interaction of
byuons
k
i
I
I
i
I
I
X
A
X
A





2
2
][][ и), the product of four
functions determines the probability of four-contact in-
teraction, the product of eight functions gives the prob-
ability of eight-contact interaction. These products
should be positive, and in this case only they can de-
scribe an observed event.
The probability of a single event is no greater than 1.
Depending on which range is i in (0  i < k, k < i <
Nk, Nk < i < NkP where k, N, P are the assumed periods
in i) various types of contact interactions between
byuons may be introduced. Hence the normalization of
the introduced functions should be dependent on i.
Let us normalize the introduced functions for the case
0  i < k in the following manner
()/2
22222
00 2
NkP kj i
jjNkPjNkPj
III III
j
NP


 





(5)
12
10
ji
NP NkP jNkP jk
II II
j
P







 
 , (6)
()/2
222
00 2
NkP kj i
jNkPj
II I
j
NP






 
 , (7)
()/2
22
00 2
NkP kji
jNkPj
III
j
NP



 

 
 . (8)
When normalizing, it is taken into account that within
a period in i = k, one four-contact interaction occurs with
probability 1.
Let us obtain an equation in terms of -functions, de-
scribing the propagation of a four-contact interaction of
byuons. For that we may write the following relation-
ships as to the origin of VSs II+(
II
f), I+(
I
f), II- (
II
f),
I - (
I
f) depending on certain VSs of the byuons
neighbouring in the index i:
212 2
12
112
2122
[, ,,],
[, ,,],
[, ,,],
[, ,,].
iiiNkPiNkPi
IIII IIIIII
iiiNkPiNkPi
III IIIII
NkP iNkP iNkP iii
IIII IIIIII
NkP iNkP iNkP iii
IIIIIIII
f
f
f
f
 

 




 
  
 

 
(9)

Y. A. BAUROV ET AL. 22
Assuming only linear dependences in Expressions (9)
as well as equiprobability of VSs of byuons neighbour-
ing in i, we obtain the following equations for -func-
tions of four-contact interactions of byuons:
212 2
12
112
2122
,
,
,
.
iiiNkP iNkP i
IIII IIII
iiiNkP iNkP i
IIIIIII
NkPi NkPiNkPiii
IIIIIII I
N
kP iNkP iNkP iii
IIIIII I
 
 
 

 


 
 
 


(10)
From the first and second pairs of Equations (10) we
obtain, respectively, the following equations:
11 11
[] 0
ii ii
II III I
 
 
 , (11)
0][ 1111 

iNkP
I
iNkP
II
iNkP
I
iNkP
II (12)
where  denote the second finite differences in index i.
It is seen from Equations (11) and (12) that the process
in i is of oscillatory character for the functions




1
(i
I
I
)
1



i
I
and )( 11 
  iNkP
I
iNkP
I
I. These functions de-
termine the A-type points in the space of index i shown
in Figure 3, i.e. the points at which we cannot introduce
interaction of byuons. The A-type points in the space R1
determine as if “ruptures” in i, between which there exist
objects with energy E > 0.
For the case i  k, write an equation for an increment in
potential energy of a byuon interaction
 E(i), correspond-
ing to the occurrence of VSs 2

i
II and .I
i
 Minimiza-
tion of E(i) is assumed to be going at each step in i.
,22,
33, 222,2
() coscos
cos ...c
NkP i kNkP iNkP i k NkP iNkP ikNkP iNkP ik NkP i
IIIIII IIIIIIII II II IIII II
NkP ikNkP iNkP ik NkP iiNkP iiNkP i
IIIIIIIIIII II IIII I
Ei EE
EE
  
   
   
 
 
 
2222,22 22222,222
22232,223 ,
os
cos cos
cos ...cos
II I
iNkPi iNkPiiNkPiiNkPi
IIIII IIIIII I II III I
iNkP iiNkP iNkP iiNkP ii
IIIII IIIIII II II III I
EE
EE

    
   
 
 

 
  22,
22 22,23 23,
cos
coscos ...
NkP iiNkP ii
II III II I
NkPiiNkPiiNkPii NkPii
IIIIII IIIIII II III I
E
EE
  
   
 
  

 
22 ,22,
2222,2 22,2
2222
cos cos
cos cos
iiNkP iNkP iiiNkP iNkP i
IIIIIII III II III III
iiNkP iNkP iiiNkP iNkP i
IIIIIII IIIII III III
iiNkP iNkP i
IIII II
EE
EE
   
   
 
 
 

 
 
 22, 2222,22
222323,2223,23
cos cos
coscos ...
iiNkPi NkPi
III III III III
iiNkP iNkP iiiNkP iNkP i
IIII IIIIIIII III III
EE
EE
   
   
   
 

 
(13)
where 2,, ,..., 

ii
III
iNkPkiNkP
IIII EE , etc. are maximum values
of potential energy of interactions of byuons with the
lengths X(NkP-i-k) < 0 and X(NkP-i) < 0 in VS II–, as well
as byuons with the lengths X(i) and X(i + 2) in VSs I+
and II+, respectively; сosI+II+, сosI–II– etc. are functions
minimizing the potential energy of interactions of byuons
entering into the expressions for ,,...,,22,iNkPiNkP
I
I
I
ii
I
I
I
EE 

etc.; these functions are “responsible” for the appearance
of a minimum plane object and the introduction of the
concept of spin (see below). Functions сosI+II+ are not the
usual Cos-functions, because we work up to now in
one-dimensional space of i –indices. These Cos\s can
have values from 0 to 1. Upper and lower indices in (13)
correspond to interactions of byuon VSs,
The difference in the average values of byuon lengths
calculated basing upon the definition of byuons with the
use of the rule of circular arrow (see Figure 5), is taken
as a distance between the interacting byuons to find
 E(i)
> 0. The meaning of this rule is that the said distance is
calculated as the difference in the length values of the
subsequent and preceding byuons in the direction pointed
by an arrow.
II
+
I
–
I
+
II
–
Figure 5. The rule of circular arrow for determining the
distance between byuons.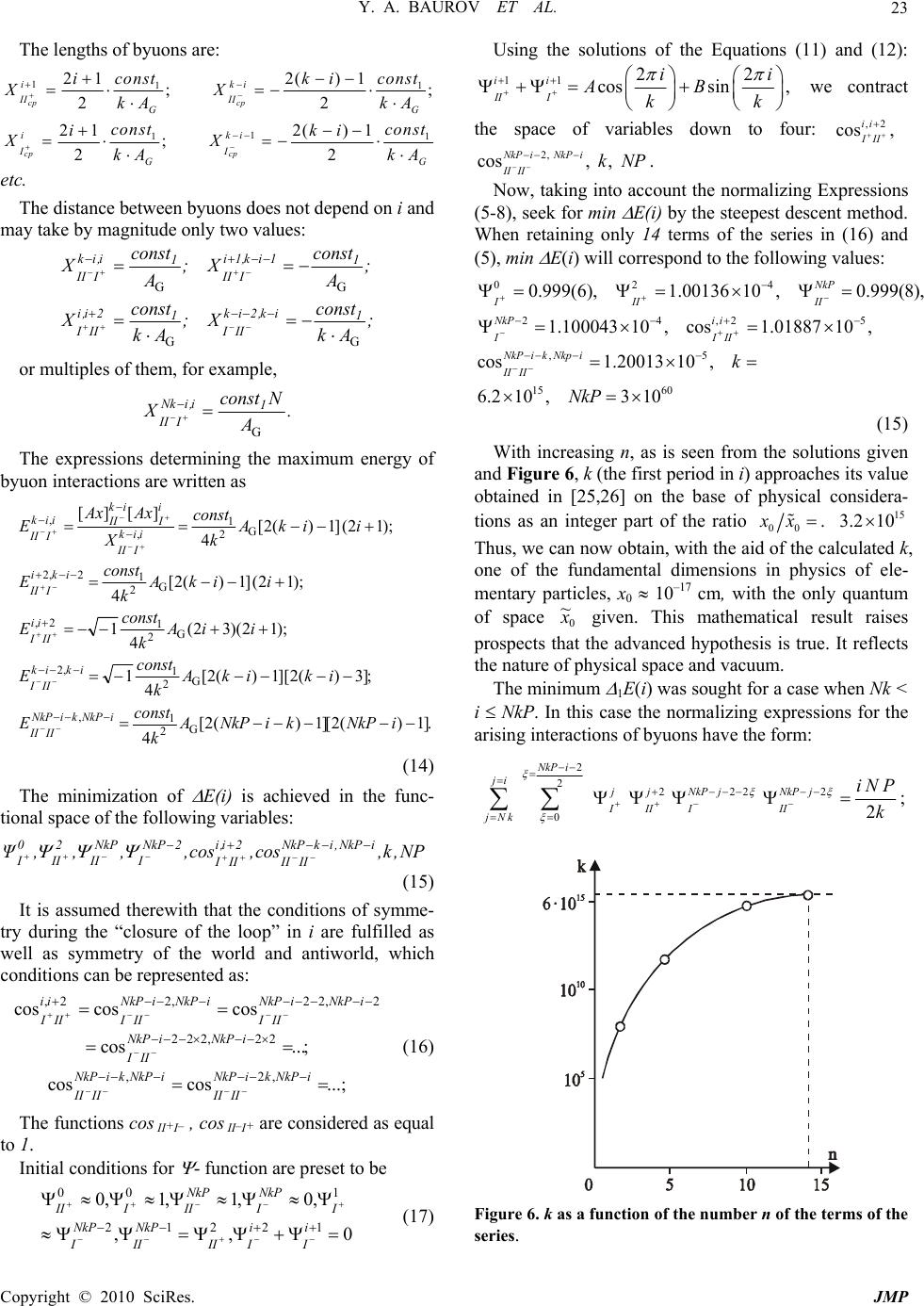

Y. A. BAUROV ET AL. 23
The lengths of byuons are:
111
1 11
212()1
;;
22
212()1
;
22
cp cp
cp cp
iki
II II
GG
iki
II
GG
const const iki
XX
kA kA
const const iki
XX
kA kA





 


 

etc.
The distance between byuons does not depend on i and
may take by magnitude only two values:
;
Ak
const
X;
Ak
const
X
;
A
cons
t
X;
A
cons
t
X
1
ik,2ik
III
1
2i,i
III
1
1ik,1i
III
1
i,ik
III
GG
GG









or multiples of them, for example,
.
A
Nconst
X1
i,iNk
IIIG



The expressions determining the maximum energy of
byuon interactions are written as
.]1)(2[]1)(2[
4
;]3)(2][1)(2[
4
1
);12)(32(
4
1
);12(]1)(2[
4
);12(]1)(2[
4
][][
2
1
,
2
1
,2
2
1
2,
2
1
2,2
2
1
,
,



















iNkPkiNkPA
k
const
E
ikikA
k
const
E
iiA
k
const
E
iikA
k
const
E
iikA
k
const
X
AxAx
E
iNkPkiNkP
IIII
ikik
III
ii
III
iki
III
iik
III
i
I
ik
II
iik
III
G
G
G
G
G
(14)
The minimization of
 E(i) is achieved in the func-
tional space of the following variables:
NP,k,cos,cos,,,,ΨiNkP,ikNkP
IIII
2i,i
III
2NkP
I
NkP
II
2
II
0
I
 



(15)
It is assumed therewith that the conditions of symme-
try during the “closure of the loop” in i are fulfilled as
well as symmetry of the world and antiworld, which
conditions can be represented as:
...;coscos
;...cos
coscoscos
,2,
22,222
2,22,22,









iNkPkiNkP
IIII
iNkPkiNkP
IIII
iNkPiNkP
III
iNkPiNkP
III
iNkPiNkP
III
ii
III
(16)
The functions сos II+I– , сos II–I+ are considered as equal
to 1.
Initial conditions for
 - function are preset to be
0,,
,0,1,1,0
12212
100


 

i
I
i
III
NkP
II
NkP
I
I
NkP
I
NkP
IIIII (17)
Using the solutions of the Equations (11) and (12):
11 22
cossin ,
ii
II I
ii
AB
kk


  

 
 
we contract
the space of variables down to four: ,2 cos ,
ii
III


2,
cos, ,
NkPiNkPi
II IIkNP

 .
Now, taking into account the normalizing Expressions
(5-8), seek for min  E(i) by the steepest descent method.
When retaining only 14 terms of the series in (16) and
(5), min  E(i) will correspond to the following values:
024
24,25
,5
15 60
0.999(6),1.00136 10,0.999(8),
1.100043 10,cos1.0188710,
cos1.20013 10,
6.210 ,3 10
NkP
IIIII
NkPi i
IIII
NkPikNkpi
II IIk
NkP
 




 
 
 
 

(15)
With increasing n, as is seen from the solutions given
and Figure 6, k (the first period in i) approaches its value
obtained in [25,26] on the base of physical considera-
tions as an integer part of the ratio 00.xx
 15
3.210
Thus, we can now obtain, with the aid of the calculated k,
one of the fundamental dimensions in physics of ele-
mentary particles, х0  10–17 cm, with the only quantum
of space 0
~
x given. This mathematical result raises
prospects that the advanced hypothesis is true. It reflects
the nature of physical space and vacuum.
The minimum

1E(i) was sought for a case when Nk <
i  NkP. In this case the normalizing expressions for the
arising interactions of byuons have the form:
2
2222 2
02
NkPi
ji
jj NkPjNkPj
III III
jNk
iN P
k



 


 

 
 ;
Figure 6. k as a function of the number n of the terms of the
series.

Y. A. BAUROV ET AL. 24
2
2
1
NkPi
NkPiNkPi k
II II
NkP i
Nk









 

/22
1
ik iik
II II
i
Nk






;
2
2222
02
NkPi
ji
jNkPj
II I
jNk
iN P
k







 
 ;
2
22
02
NkPi
ji
NkP jj
II I
jNk
iN P
k








 . (19)
The expression for

1E(i) becomes more complicated:
222, 22222, 22
1
222,2 2222,22
( )coscos...
cos cos
iikiik iikiik
IIIIII IIIIIIII II II IIII II
iNkPiiNkPiiNki iNkPi
IIIII IIIII I II IIII I
Ei EE
EE
   
   
 
  
 
  
22222,222222,2
2222,22
2222
cos ...cos
cos
iNkP iiNkPiikNkP ikikNkP ik
IIIII IIIIII I II III I
ikNkPikikNkPi k
IIIII I II I
ik NkPik
II III
EE
E
E
  
 

 
     

 
 
 
 2,222
222222,22
cos ...
cos...()
ikNkPi k
II I I
ik NkPikikNkPik
IIIII I II I
EEi
 
  
 
 

 
(  E(i) is taken from Equation (10), taking into account for
multiplication over index i as was shown above (i + 2, I +
2-k, i + 2-2k etc.).
The search for min  E(i) with the use of the chain of
Equations (7) in the space of similar variables with simi-
lar initial conditions (where i = 0 corresponds now to i =
Nk), leads to practically the same results:
24
24,22,2
5
,5 15
60
0.9998,1.006 10,
0.9999,
1.101 10,coscos
1.1019 10,
cos1.203 10,4.475 10 ,
3.169 10
Nk NkNkP
III II
NkPi iiik
IIIIIIII
NkPik Nkpi
II IIkNk
P
 
 




 


 

 

It is interesting that at i < k and even at i  Nk (Table
1), a significant part in the magnitude of
 E(i) is poten-
tial energy of the byuon interaction in VS II

II

, and at i
 NkP the four-contact interaction of byuons in VS
II+I+I

II

becomes determining.
Let us consider a simplified case when only the period
in i, equal to k, is present in the antiworld. Then we have
from the necessary condition of minimum
 E(i) with
respect to the function 2
Ψi
I
I


(i.e. from the equa-
tion 0
)(
2




i
I
I
i
E


):
Table 1. The values of potential energy E in vacuum states
(II+ II+), (II+I+ I

II

), (II

II

) depending on the i index.
i
E [erg] Nk NkP
EII+II+ 1013 1095
EII+I+I –II – 1070 10111
EII – II – 1095 1013
.
]3)2([)32(
)12(]1)([
11
cos 



 

 iki
iik
k
ik
II
i
I
III (20)
If i << k, N = P = 1, and hence, according to Equation
(5)
0
1
j
i
jkj
III
j





 
, we obtain from Equation (20)
сosII+I+  1/k.
Thus, as show our numerical calculations and analyti-
cal estimations, the minimization of  E(i) leads to values
of functions сos II+I+ etc. if not zero but extremely small.
Note that the functions сos II+I+ for the case of NP
“loops” in VS II

(see (18)) and for the case when N = P
= 1, differ by ten orders of magnitude. The physical
meaning of these functions will be shown further.
Put a question, where disappears and into what kind of
energy the potential energy of byuon interaction trans-
forms? An answer seems to be simple, of course, - into
the kinetic energy of rotation (since сosII+I+ << 1, see (18,
20)). But the rotation of what and around what? And why
do we assume the law of conservation of energy to be
fulfilled here? After all, it makes no sense to say about
uniformity in time for this statement in which the time is
discrete! Let us answer these questions.
As it was shown above, the optimum values of the
functions ,cos,cos 2,,2 

iNkPiNkP
III
ii
III etc., are much less
than 1 but non-zero. The smallest values of сosII+I+  1/k
correspond to residual (finite) potential energies Ek, from
which, as we will further assume, the smallest part (asso-
ciated with the formation of the own space of elementary
particles) of the potential self-energy of elementary par-
ticles corresponding to the known Einstein’s relationship
Ek = mc2, is added together. Determine the minimum
value of Ek. It is seen from Equation (13) that for the

Y. A. BAUROV ET AL. 25
simplest objects with N and P approximately equal to 1,
the minimum Ek is equal to the potential energy of the
four-contact interaction of byuons with the minimum
values of сosII+I+, сos II–I–.
In view of the normalization (5) we have for this case


III
kk
IIIIIIIII
kEEEcoscos,22,0)0(
min . (21)
From that, with the condition (16), and using Equation
(14) and the equality сosII+I+  1/k, we obtain 
)0(
min
k
E
33 eV.
Consider the process of energy transformation for the
four-contact byuon interaction occurring within a time
quantum 
0 (Hence, the transformation must be discrete).
Any value of i can be redenoted with an another index,
for example, with j,  ,  , etc., which may be set equal to
zero. At each point then, where j =  =  =...= 0, there
will be always present an own system of account of the
indices j,  ,  , etc., as well as the minimum energy of
four-contact byuon interaction 
)0(
min
k
E33eV. Note that
this minimum energy is limited in index i by values i = 0
and i = 2 (point A Figure 3).
Thus, we have in R1 two sets of points A({A}) and
D({D}), between which the dynamic process of renumera-
tion goes in connection with the properties of vacuum
states of the discrete objects, the byuons II+, I+, I–, II–:
the time

i+1 




...,,2}{
...,1,1}{
iiA
iiD
the time

i+1+

0




...,1,3}{
...,,2}{
iiA
iiD
The set R1 may be represented, at some i-th point of time
as the join of {A} and {D}, i.e. R1 = {A} U {D} (Figure 7).
Hence the space R1 segregates into the subspaces RD
of D-points and RA of A-points. Thus, we may say about
the motion of D-points relative to A-points. A new, sec-
ond coordinate appears, symbolize it by YAD (Figure 7).
D
i+1
Y
i, i+1
{R }
1
D
i–1
A
i
AD
{A} {D}
Figure 7. Representation of the set {R1} as a union of sets of
the points {A} and {D}.
The minimum value of YAD:)1(|
00
min iCY AAD 

.
~
|0 XiD The minimum object appears. Assume that
its appearance (new coordinate) corresponds to the
minimum action h ( see [1-3], h = (([Агxo]II
+[Aгxo]I -)/co)
xo/ct* and elementary electric charge eo
2 = (1/(4√3))
Аg
2xo 2(xo/ct*)3/2 ). We may then introduce the concept of
momentum for objects with the residual PE of a byuon
interaction by writing the relationship hYPii
AD
i
D



1,1
where 1

i
D
P is the momentum of the point D numbered
i+1 relative to the point A with the number i. Similar
relationship can be written in any point from {A}. The
direction of the momentum vector 1i
D
P

corresponds to
that towards the point Di+3 of the subspace RD. The direc-
tion of the coordinate 1, ii
AD
Y corresponds to the vector
directed from the point Ai to the point Di+1.
The appearance of the minimum plane object and re-
alization of the minimum action are connected with the
origin of the quantum spin number ,][ 1,1   ii
AD
i
DYPS
expressed numerically in minimum actions h.
The function сosII+I+ etc. minimizing
 E(i), will be
further considered by us as cosines of the angles between
the vector 1

i
D
P and 1,

ii
AD
Y i.e. before the byuon inter-
action, the space R1 represents, at some time point  , a
certain discrete straight line of points {D} and {A}, and
at the time point  + 
0 forms a line, broken at points {D}.
That is the minimum interaction of byuons has occurred.
If an “observer” was able to perceive objects with E>0
only every
 = k 
0, he would simultaneously (within a
time quantum 
0) fix all the planes arrived to the point of
“observation”, and “see” already the three-dimensional
world formed from the plane world in the result of its
dynamics within the time  = 
0. Why the three-dimen-
sional and not N-dimensional one? Because the set of
two-contact interactions of byuons is divided, depending
on reference point (Figure 2, i = 0, 1, 2), into three sub-
sets M0, M1, M2 (the lower index denotes reference point),
corresponded by three one-dimensional subspaces R1,0,
R1,1, R1,2 while introducing metric properties. Explain the
above said.
As was indicated above, any value of index i can be
always redenoted by j and then j = 0, 1, 2 corresponds to
reference points. Redenoting i + 1 by  , i + 2 by  etc.
leads, depending on reference points, to formation of
three families of subspaces embedded in each other:
reference point “0”

0,10,10,10,1 RRRR ji  etc.;
reference point “1”

1,11,11,11,1 RRRR ji  etc. ;
reference point “2”

2,12,12,12,1RRRR ji  etc., if
i > j >  >  etc.
Thus, in connection with the existence of three inde-
pendent reference points for the new pair interactions,

Y. A. BAUROV ET AL. 26
the three independent coordinates should be given to fix
a pair interaction with respect of the three reference
points, i.e. R3 can be represented as R3 = R1,0  R1,1  R1,2.
Note that R1,0, R1,1, R1,2 consist of the sets of points {A}
and {D}, i.e. at each subsequent point in time, renumera-
tion of points A and D and “spinning” of objects with E
> 0 in the subspaces R1,0, R1,1, R1,2, occur. In this manner
the concept of spin is introduced for objects with E > 0
in R3. For objects of a big size (as a result of described
minimization of PE), the rotation will be always take
place since the byuons are not closed in a volume of R3
due to cosII+II+  0. That is why, planets, stars and so on
rotate, with the main part of potential energy of byuons
being transformed into energy of rotation.
Advance (without proving) the following theorem:
If a system is closed, the amount of information in it is
constant.
That is, transformation of one information image into
another is possible in the system, but the total amount of
information does remain invariable.
Note that by information we mean here not informa-
tivity as in theory of information developed by Hartly
and Shannon [29] on the basis of entropic approach, but
the numbers of information bits (the values “0” and “1”)
in one or another information subsystems of the system
of considered objects (the combinatoric approach [30]).
By “1” we imply here accomplishing the minimal act
(minimum action h/2) in the system with formation of an
object with E > 0 from byuons, and by “0” disappearing
of the object with E > 0 is meant.
On the base of the theorem, write the following equal-
ity for informational units (bits) in the subspaces R1 and
R3:
NS
h
kSE
3
110
22
2

 
(22)
where N is the number of information images in R3
(N=сt*/х0 - the second period in i); S3 the complex of the
information image in R3 (number of “loops” of length N;
S3 = 1, 2, ...); E1 potential energy of minimum four-con-
tact interaction of byuons in R1 if сosII+I+ = сos II–I– = 1;
h
SE2
110 

is a transformation factor of recounting the
number of information images (k) in R1 into that in R3 for
i  kN; S1 is complex of the information image in R1
(number of “loops” of length k, S1 = 1, 2, ...).
By an information image in R3, one means one or an-
other quantum number of an elementary particle.
With Equation (22), the expressions for lepton masses
obtained in [20-22] (see Appendix 1) become more un-
derstandable (for example, min
20 *
0
33
ek
m cENeVctx
2*
0
2e mcct x

 ).
Taking k from the solution of the problem of searching
the minimum
 E and substituting S3 = 1, S1 = 1 into
Equation (22), we find N = 1.544  104 = сt*/х0 , and
knowing N and NP from this solution, determine P 
1042. The value of 0
~
xkN  10-13 сm.
Thus, we find all the periods of byuon motion in i,
corresponding to the following scales of our World: 10-17
cm is a characteristic scale of weak interactions ( for
larger lengths our World is three-dimensional and almost
orthogonal, for an empty space with the 10-15 precision);
10-13 cm is a characteristic size of proton and atomic nu-
clei, 1028 cm is the radius of our Metagalaxy or the ob-
servable part of our Universe.
(See: Appendix 1 – The expressions for masses of ul-
timate particles; Appendix 2 – A qualitative distinction
between the theory of byuons and previous physical
theories. See in [21] “Force-free physics. A qualitative
pattern of a common approach to unifying all interac-
tions. A novel principle of relativity.”)
It should be also noted that to calculate the fundamen-
tal constants h, e0, c; constants of known interactions,
masses of main baryons, leptons, and mesons , only three
numbers o
x
~

0, |Ag| should be given since the charac-
teristic dimensions o x
~
 10-17 cm, ct*  10-13 cm and
1028 cm are found from the minimum PE of byuons and
from the information theorem.
5. Dark Matter and Dark Energy in the
Byuon Theory
Determine the average density of substance in the Uni-
verse while taking i = NkP and, hence, its characteristic
dimension cmNkPx 28
010
~ (it coincides with the as-
sumed radius of the Universe). The total energy in the
Universe can be represented as NkP
h
0

. Its value is 5.4 
1077 erg, and the corresponding equivalent mass  6 
1056 g. The uniformity of distribution of substance over
the sphere with the radius NkPx0
~
gives the density of
substance in the Universe  10-29 g cm-3, which is meas-
ured in the known observations.
Through the set {A}, information exchange occurs
between points of the set {D}, which is the main mecha-
nism determining physical essence of the Heisenberg
uncertainty interval in the conception of physical space
and physical vacuum. Without introducing the points {A},
the connection between D-points is realized in one direc-
tion only, in that of increasing index i with the speed no
greater than c0.
According to the developed conception of physical
vacuum structure, we can determine a momentum and a
coordinate of such a complex object as an elementary
particle only with an accuracy of the momentum and the
coordinate entering into the relationship PD
i+1
YAD
i,i+1
= h
governing the momentum of D-points mapped into R3

Y. A. BAUROV ET AL. 27
according to (22). Here YAD
i,i+1 is any distance in
one-dimensional space between the points A and D (cf.
Figure 7). That is, writing the uncertainty relation in R3
for some elementary object
 as  P  X  h/2, we mean
 P and  X to be caused by the process of R3 formation
from byuons, i.e. determined by quantities of PD and YAD
type.
Its momentum corresponding to the minimum mo-
mentum for elementary particles, can be given in general
form as [20-22]
cEФPk
0
min
 ,
where  is probability of observing the object 4b formed
in the process of the four-contact interaction in some
region of space R3.
If the objects 4b are free (that is, they create not an
elementary particle but space free of them), then
0
2
0
3
0~
4
~
16
1
xx
x
Ф

 , where 0
~
x 10-33 cm, and x0  10-17 cm.
In this case, if the scatter in values of the momentum is P
for an elementary object Δp, then the uncertainty in the
coordinate in R3 for the object 4b will be equal to 1028 cm.
This value
 X has given us earlier the possibility to ob-
tain the density of matter in the Universe, observed
in experiment, by way of averaging it over the sphere
1028 cm in radius. From the modern point of view [cf.
Arxiv: 0710.3018v1 [physics.gen-ph] 16 Oct.2007 ] the
4b-objects with m4bc2 = 33 eV and  X= 1028 cm, form
the so-called the cold dark matter – the quantum medium
corresponding to the observed physical R3 – space.
If the object 4b is not free (that is, it forms the internal
geometry of an electron, for instance), then
3
0
2
00
1
Ф164()
x
Nx x 
 , (23)
and we can write the following expression for an assem-
blage of objects 4b forming an electron (for which mec2 =
NEkmin):
Nc
E
c
NE
xNx
x
pkk
00
0
2
0
3
0minmin
64
1
)(416
1

(24)
Using Equation (24) we obtain the uncertainty in co-
ordinate Δx in R3 of the order to 10 cm for the assem-
blage of N objects 4b, that is, the electron, due to wave
properties of N objects 4b, carries information on its
properties not over distances of 10-8 cm (characteristical
dimension of the de Broglie wave for electron at the
temperature of 300 K) as would be in the case of a point-
wise particle but over distances of the order to 10 cm.
When considering not N objects but one object 4b in
the electron (that is, when Formula (23) is valid) then Δx
 105 cm. Hence the less is an information on conditions
of internal spatial characteristics of electron, the more is
the scatter in coordinate.
In the modern terminology [cf. Arxiv: 0710.3018v1
[physics.gen-ph] 16 Oct.2007 ] 4b-objects forming ele-
mentary particles (their charges, masses and so on) and
having
 X from 10 to 105 cm create the hot or warm dark
matter.
In [21] a qualitative pattern of a common approach to
unifying all interactions is shown
The byuon theory predicts a new anisotropic interac-
tion of natural objects with physical vacuum.
Peculiar “taps” to gain new energy are elementary par-
ticles because their masses are proportional to the
modulus of some summary potential A
 that contains
potentials of all known fields (Appendix 1). The value of
A cannot be larger than the modulus of Ag [20-22]. In
accordance with the experimental results shown in
[22,31], this force ejects any substance from the area of
the weakened A potential along conal surfaces at angles
of 100о ± 10о around the vector A direction. This vector
has the following coordinates in the second equatorial
system of coordinates: right ascension   293  10
(19h 20m ), declination   36  10 [22,31]. The vector
A is parallel to the vector Ag practically.
The new force is of nonlinear and non-local character
as to variation of some summary potential A and may be
represented by some series in A [20-22,32].
The expression for the new force takes the form :
1
2
0
)(
)(||2|| X
A
A
A
AcANmF









 G


(25)
Here N is the number of stable elementary particles in
the body (electrons, protons and neutrons).
Note that expression for the new force (25) is local
(we cannot deal with the nonlocal ones as yet), therefore,
to account for the nonlocality of the phenomenon, we
will take  А equal to the difference in changes of the
summary potential |
А

| at the location points of a test
body and a sensor element [20-22].
These changes being equal, the force will be absent.
Depending on the relative position of the sensor and the
test body,  A can take as a positive, so a negative value.
To estimate a role of gravitational field in a change of
|
А

| we put forward the maximal gravitational potential
φmax, determined for proton by the following relation-
ship:
mp φmax= e| Ag |, (26)
where mp is the proton mass. Then the contribution of
φmax in the change of |
А

| is described by the following
equality:
φmax cos mp=eAv/c, (27)
where v is in this case the velocity of our Galaxy relative
to the neighbouring galaxies, cos =iNkPiNkP
IIII


,2
cos (15).
It characterizes nonorthogonality of our World at the
moment of the formation of the space of elementary par-

Y. A. BAUROV ET AL. 28
ticles.. It is worth noting that potentials of physical fields
have the physical meaning only for interacting byuons
when elementary particles are generated with their
masses and charge numbers. As for the vector potential
of magnetic field it is gauged so that its value on the axis
for example of the solenoid equals zero; x1 is the coordi-
nate, directed from the point of the most decreased
А


on a winding to the vector
А

G.
The analysis of the specific experimental results with
high field magnets (see [20-22,32-35]) has led to the
following expression for  (  A):
k
k
k
kA
x
ct
y
r
A
A
A






























 
1
2/3
0
*
exp)(
G

(28)
Here r is the radius of the circle where the test body is
located on;  y is the difference in coordinates y of the
sensor and the body [20-22]; 23*
0)( ctx is the part of
energy 2
00
2
0||22 cAmcm eG



, which can be acted upon
by the electromagnetic field potentials.
Using the linear term only in the expansion of (25) by
 А, we obtain the following formula for the modulus of
the new force:
F =2Nmνc2 
1
2.ΔA (ΔA/ΔX).
(29)
It is worth noting that the experiments for the scanning
the celestial sphere by the pulsed plasma generator [22,31]
to detect some directions in space, where energy is more
than the average value, are the final stage in the determi-
nation of the direction of the new force. This direction
was determined before by the using the high field mag-
nets [20-22,32-35], by the investigations of the rate of β -
decay for a number of radioactive elements [20-22,24,
25,36], by the investigations with high precision gra-
vimeters [20-22,37], and by plasma generators of other
types [20-22,38].
Experiments with high field magnets [1,2] showed that
the new interaction had the most probably an isotropic
component as well.
Let us discuss the nature of the dark energy in the
framework of the byuon theory on the base of potentials
of physical fields.
It is known that the gravitational potential φ is nega-
tive, and therefore for any summation of potentials it
decreases the modulus of A. Masses of elementary par-
ticles are proportional to this modulus. Hence the new
force will push out any material body from the region of
the decreased modulus of A, because a defect of energy
ΔE = Δmc2 will appear and the corresponding force will
act to the region with undisturbed value of A. Any ma-
terial body decreases in its own region the modulus A.
due to potentials of physical fields of all its elementary
components, i.e. creates the gradient ΔA/ΔX.. Gravita-
tionally acting mass, for example, our Galaxy, creates
around itself the gravitational potential φ. To estimate the
action of one galaxy to another we put in the Formula
(29) the potential φmax from (26) and ΔA from (27)
(ΔA = A). Let us estimate the distance RGG where the
new force F from (29) will be higher than the gravita-
tional force Fg (Figure 1):
RGG ≥ GMg
2/(2Nmνc2

1
2 cos2 φmax 2 (mpc/ve)2) (30)
where G is the gravitational constant.
Here Mg is the mass of the one of interacting galaxies.
We consider an interaction of two galaxies with 1010
stars, assume that the mass of each star is of order to the
solar mass (~ 1033 g) and a relative velocity of each gal-
axy v = 100 km/sec and 1000 km/sec. From our experi-
ments 
1 = 10-12 [20-22,51]. As the result we obtain from
(30) RGG ≥ 1026 cm for v = 100 km/sec and RGG ≥ 1028
cm for v = 1000 km/sec.
Thus we have estimated the magnitude of the distance
between galaxies above which they scatter under the
action of the new force. The estimate obtained seems as
reasonable and indicates that the physics of byuons is
perspective to explicate the nature of dark energy and
dark matter.
6. References
[1] M. J. Rees, “Dark Matter: Introduction,” Astro-Physics,
Vol. 361, 2003, pp. 2427-2434.
[2] E. A. Baltz, “Dark Matter Candidates,” Astro-Physics,
Vol. 1, 8 December 2004.
[3] V. Rubin, W. K. Ford and N. Thonnard, Astrophysical
Journal, Vol. 238, 1980, p. 471.
[4] J. Garcia-Boldino, “Cosmology and Astrophysics,” As-
tro-Physics, Vol. 2, 2005, p. 139.
[5] R. D. Peccei and H. R. Quinn, “CP Conservation in the
Presence of Pseudoparticles,” Physical Review Letters,
Vol. 38, 1977, p. 1440.
[6] M. S. Turner, “Windows on the Axion,” Physics Reports,
Vol. 197, 1990, pp. 67.
[7] P. Sikivie, “Experimental Tests of the ‘Invisible’ Axion,”
Physical Review Letters, Vol. 51, 1983, p. 1415.
[8] S. J. Asztalos, et al. “Experimental Constraints on the
Axion Dark Matter Halo Density,” Astrophysical Journal,
Vol. 571, 2002, p. L27.
[9] H. Pagels and J. R. Primack, “Supersymmetry, Cosmol-
ogy, and New Physics at Teraelectronvolt Energies,”
Physical Review Letters, Vol. 48, 1982, p. 223.
[10] G. Jungman, M. Kamionkowski and K. Griest, “Super-
symmetric Dark Matter,” Physics Reports, Vol. 267, 1996,
p. 195.
[11] L. Covi, J. E. Kim and L. Roszkowski, “Axinos as Cold
Dark Matter,” Physical Review Letters, Vol. 82, 1999, p.
4180.
[12] A. Kusenko and P. J. Steinhardt, “Q-Ball Candidates for
Self-Interacting Dark Matter,” Physical Review Letters,

Y. A. BAUROV ET AL. 29
Vol. 87, 2001, p. 141301.
[13] K. R. Dienes, E. Dudas and T. Gheghetta, “Grand Unifi-
cation at Intermediate Mass Scales through Extra Dimen-
sions,” Nuclear Physics B, Vol. 537, 1999, p. 47.
[14] J. A. R. Cembranos, A. Dobado and A. L. Maroto, “Bra-
non Dark Matter,” High Energy Physics-Phenomenology,
p. 0406076.
[15] Z. Berezhiani, D. Comelli and F. L. Villante, “The Early
Mirror Universe: Inflation, Baryogenesis, Nucleosynthe-
sis and Dark Matter,” Physics Letters B, Vol. 503, 2001,
p. 362.
[16] D. J. H. Chang, E. W. Kolb and A. Riotto, “Superheavy
Dark Matter,” Physical Review D, Vol. 59, 1999, p.
b3501.
[17] K. Jedamzik, “Primordial Black Hole Formation during
the QCD Epoch,” Physical Review D, Vol. 55, 1997, p.
5871.
[18] M. Trodden and S. M. Carrol, “TASI Lectures: Intro-
duction to Cosmology,” Astro-Physics/0401547.
[19] P. J. E. Peebles and B. Ratra, “The Cosmological Con-
stant and Dark Energy,” Reviews of Modern Physics, Vol.
75, 2003, p. 559.
[20] Y. A. Baurov, “Structure of Physical Space and New
Method of Obtaining Energy (Theory, Experiment, App-
lications),” Moscow, Krechet, in Russian, 1998.
[21] Y. A. Baurov, “On the Structure of Physical Vacuum and
a New Interaction in Nature (Theory, Experiment and
Applications),” Nova Science, NY, 2000.
[22] Y. A. Baurov, “Global Anisotropy of Physical Space
(Experimental and Theoretical Basis),” Nova Science,
2004.
[23] Y. A. Baurov, “Structure of Physical Space and Nature of
Electromagnetic Field,” in Coll. Work. PHOTON: Old
Problems in Light of New Ideas, Nova Science, New
York, 2000, pp. 259-269.
[24] Y. A. Baurov, “Structure of Physical Space and New
Interaction in Nature (Theory and Experiment),” Pro-
ceedings of conference Lorentz group, CPT and Neutri-
nos, World Scientific, 2000, pp. 342-352.
[25] Y. A. Baurov, “Structure of Physical Space and Nature of
de Broglie Waves (Theory and Experiment),” Journal
Annales de Fondation de Broglie, Contemporary Electro-
dynamics, Vol. 27, No. 3, 2002, pp. 443-461.
[26] Y. A. Baurov, Y. N. Babaev and V. K. Ablekov, Doklady
Akademii Nauk, Vol. 259, 1981, p. 1080.
[27] Y. N. Babaev and Y. A. Baurov, “Preprint P-0362 of
Institute for Nuclear Research of Russian Academy of
Sciences (INR RAS),” Moscow, 1984 (in Russian).
[28] V. V. Kolpachev and C. A. Nikolaev, “Preprint N 1695 of
Institute for Space Researches of Russian Academy of
Sciences (ISR RAS),” Moscow, in Russian, 1990.
[29] C. E. Shannon, Bell Labs Technical Journal, Vol. 27,
1948, pp. 379,623.
[30] A. I. Kholmogorov, “Information Theory and Theory of
Algorithms,” Moscow, Nauka, in Russian, 1987.
[31] Y. A. Baurov, I. B. Timofeev, V. A. Chernikov, S. F.
Chalkin and A. A. Konradov, “Experimental Investiga-
tion of the Distribution of Pulsed-Plasma-Generator at its
Various Spatial Orientation and Global Anisotropy of
Space,” Physics Letters A, Vol. 311, 2003, p. 512.
[32] Y. A. Baurov, “Space Magnetic Anisotropy and a New
Interaction in Nature,” Physics Letters A, Vol. 181, 1993,
p. 283.
[33] Y. A. Baurov, E. Y. Klimenko and S. I. Novikov, “Ex-
perimental Observation of Space Magnetic Anisotropy”,
Doklady Akademy Nauk SSSR (DAN), Vol. 315, 1990, p.
1116.
[34] Y. A. Baurov, E. Y. Klimenko and S. I. Novikov, “Ex-
perimental Observation of Space Magnetic Anisotropy,”
Physics Letters A, Vol. 162, 1992, p. 32.
[35] Y. A. Baurov and P. M. Ryabov, “Experimental Investi-
gations of Magnetic Anisotropy Using Quartz Piezore-
sonance Balances,” Doklady Akademy Nauk SSSR (DAN),
Vol. 326, 1992, p. 73.
[36] Y. A. Baurov, A. A. Konradov, E. A. Kuznetsov, V. F.
Kushniruk, Y. B. Ryabov, A. P. Senkevich, Y. G.
Sobolev and S. Zadorozsny, “Experimental Investigations
of Changes in -Decay Rate of 60Co and 137Cs,” Modern
Physics Letters A, Vol. 16, No. 32, 2001, p. 2089.
[37] Y. A. Baurov and A. V. Kopaev, “Experimental Investi-
gation of Signals of a New Nature with the Aid of Two
High Precision Stationary Quartz Gravimeters,” Had-
ronic Journal, Vol. 25, 2002, p. 697.
[38] Y. A. Baurov, G. A. Beda, I. P. Danilenko and V. P. Ig-
natko, “Experimental Investigation of New Method of
Energy Generation in Plasma Devices Caused by Exis-
tence of Physical Space Global Anisotropy,” Hadronic
Journal Supplement, Vo. 15, 2000, pp. 195-210.
[39] R. A. Alpher, M. Bethe and G. Gamov, Physical Review,
Vol. 70, 1946, p. 572; Vol. 73, 1948, p. 803.
[40] A. D. Linde, Uspehi Fizicheskih Nauk, Vol. 144, 1984, p.
177.
[41] G. Y. Bogoslovsky, “Theory of Locally Anisotropic Spa-
ce-Time,” edited by Moscow State University, in Russian,
1992.
[42] K. Rund, “Differential Geometry of Finsler’s Spaces,”
Moscow, Nauka, 1981.
[43] “Time Structures in Natural Sciences: On the Road to
Right Understanding of Time Phenomenon,” Part 1, In-
terdisciplinary Research, edited By Moscow State Uni-
versity, in Russian, 1996.
[44] N. N. Bogolyubov and D. V. Shirkov, “Introduction to
the Theory of Quantized Fields,” Moscow, Nauka, in
Russian, 1976.
[45] L. B. Okun’, “Leptons and Quarks,” Nauka, Moscow, in
Russian, 1990.
[46] J. H. Shwartz, “Superstrings,” World Scientific, Singa-
pore, 1985.
[47] L. D. Landau and E. M. Lifshitz, “Theory of the Field,”
Nauka, Moscow, in Russian, 1967.
[48] H. Weyl, “Raum, Zeit Material Vierte Erweiterte Auf-
lage,” Springer, Berlin, 1921.

Y. A. BAUROV ET AL. 30
[49] H. Weyl, “Raum, Zeit, Materie, FüNfte, Umgearbeitete
Auflaqe,” Springer, Berlin 1923.
[50] P. A. M. Dirac, Proceedings of the Royal Society, London,
1973, Vol. A333, p. 419.
[51] Y. A. Baurov, A. A. Shpitalnaya and I. F. Malov, “Global
Anisotropy of Physical Space and Velocities of Pulsars,”
International Journal of Pure & applied Physics, Vol. 1,
No. 1, 2005, pp. 71-82.

Y. A. BAUROV ET AL. 31
Appendix 1:
The Planck constant and electric charge is determined by
the following Expressions [20-22]:
h = (([Аг*xo]II
+
*[Aг*xo]I
-)/co)*xo/ct*
eo
2 = (1/(4√3))*Аг2xo 2(xo/ct*)3/2
The masses of ultimate particles can be described by
the following Expressions [20-22]:
3
2
200
*
2
0
*
43 3 1
1
22
1
11||
3
1
61 2
p
ex hc
mc hc ct
A
x
ct
 

 
 
 





 




 


= 924 meV,
(A1)
0
3
2
200
*
2
0
*
433
12
2
1
11||
3
612
ex
hc
mc hc ct
A
x
ct











 








= 132 meV.
Masses of all leptons:
2||
34
22
0
2
0A
e
hc
k
hc
cm












,
||
34
2
3
2
0
2A
e
hc
k
hc
cme










 ,
2||
34
32
5.5
2
0
412 A
hc
e
hccm













||
34
3
5.3
2
0
412 A
hc
e
hccm












(A2),
2||
34
2963
5.5
2
0
412A
hc
e
hccm













,
||
34
2123
5.3
2
0
412 A
hc
e
hccm












.
Appendix 2:
It is known that any novel physical model of the Uni-
verse must meet the following criteria. First, all the dis-
covered laws of nature as well as sufficiently well estab-
lished models of one or another physical phenomena
must follow from the new model as asymptotical ap-
proximations. Second, the new theory should have the
capability for predictions. That is, it should guide an ex-
perimental way to the gain of new knowledge, as the
theory itself gives nothing but only points such a way.
Criterion of truth is an accurately performed experiment
independently confirmed by various authors. The theory
of byuons [20-22] seems to meet the above criteria. That
is a theory of “life’ of special discrete objects from
which the surrounding space and the world of elementary
particles form. The intrinsic dynamics of byuons deter-
mines such fundamental phenomena as the course of
time, rotation of planets and stars, spins of elementary
particles, asf.
What is a qualitative distinction between the theory of
byuons and previous physical theories?
First, the physical space was always given, in one way
or another, and motion equations for a system of objects
under study were written in that space. Space could be
uniform continuum (Newton, Minkovsky) or discrete,
one-dimensional or multidimensional, asf. In present-day
cosmological models of the Universe origin (the Ga-
mov’s Big Bang [39], the Linde’s model of bulging
Universe [40], and so on), space is always given, too.
But in the theory of byuons, the physical space (neces-
sarily three-dimensional one, not ten-or-more-
dimensional as in some modern physical models) is a
special quantized medium arising as the result of interac-
tion of byuon’s vacuum states (VSs). That is, space is not
given but arises. Therewith the appearing
three-dimensional space must have an insignificant
global anisotropy, as distinct from all basic isotropic
models with the same properties in various directions.
The said anisotropy denotes the existence of some cho-
sen direction caused by the existence, in nature, of a new
fundamental vectorial constant, the cosmological vec-
tor-potential Ag entering into the definition of the byuon.
That new constant is associated with the prediction of a
novel anisotropic interaction of natural objects between
themselves and with the physical vacuum, a lowest en-
ergy state of physical fields.
It should be noted that in the literature spaces with lo-
cal rather than global anisotropy are considered [41], for
example, the Finsler’s space-time [42], but the local ani-
sotropy is given therein “by hand”. That is, an author
himself directively introduces it into his model instead of
obtaining from some general principle. For example,
there are domain models of the Universe.
Secondly, the physical sense of time notion is not yet
revealed in science in the present state of the art [43].
The general philosophic concept of time as a form of
matter existence, which expresses the order of change of
objects and phenomena as a sequence of events, does not
indicate a common nature of those events. As a rule,

Y. A. BAUROV ET AL. 32
people tie their time to a particular periodic process: ro-
tation of the Earth around its axis, Earth’s orbiting
around the Sun, oscillations of a quartz system, asf,
without becoming aware of inner, profound sense of time.
Standard physical time references, for example, quantum
or, what is the same, atomic clock with instrument error
on the level of 10-11 per year and moderate resolution of
the order to 10-13 seconds, give us no possibility of ap-
proaching the knowledge of time essence. The byuon
theory reveals physical essence of time as a discrete se-
quence of changes in the byuon’s “length”, its quantum
number. A possibility therewith arises, to synchronize
clocks at great distances comparable with dimensions of
our Metagalaxy, due to the quantum process of physical
space formation from the byuon’s vacuum states (VSs).
That possibility distinguishes substantially the theory of
byuon’s from A. Einstein’s special theory of relativity
(STR), in which clocks can be synchronized only when a
signal has passed between them with speed of light co. It
should be noted at once that in the byuon theory, material
objects cannot move with a speed faster than the light
speed (that is similar to the STR’s postulate on finite
propagation velocity of interactions), but synchronization
of clocks occurs by a quantum way without introducing
the concept of speed. That is, some object originated in
the course of interaction between byuon vacuum states
and forming the physical space, is at a time in two spatial
regions being very distant from each other in the
three-dimensional space arising.
Third, an essential distinction of the byuon theory
from modern models in the classical and quantum field
theories [44] is that the potentials of physical fields
(gravitational, electromagnetic, asf.) become, in the the-
ory of byuons, exactly fixable, measurable values. Recall
to the reader that ordinary methods of measurement are
capable to measure solely a difference of potentials.
Therefore, in the existing field theory, potentials are de-
fined only with a precision of an arbitrary constant or the
rate of change of the potentials in space or time (gauge
models). But in the theory of byuons, field potentials
become single-valued since there are formed, on the set
of byuon VSs, field charge numbers which generate the
fields themselves, as, for example, the electric charge of
an electron generates an electric field. The physical sense
of field as a special form of matter, loses its basic mean-
ing because all the observable events can be described on
the basis of the byuon theory without introducing the
concept of force, and hence of field.
An important methodic distinction between the byuon
model and all those existent in the theoretical physics of
today, is that the latter use images with properties of real
objects, - for example, strings in the physics of elemen-
tary particles [45], superstrings, membranes when creat-
ing a unified field theory [46], asf. But the byuons are
unobservable objects having no analogues in the nature
though all the natural objects appear in the result of in-
teraction of byuon VSs.
The proposed pattern of formation of the observed
space R3 on the basis of dynamics of the finite set of
byuons animates, fills with a sense, and supplements the
physical results on properties of elementary particles,
described in [34,35]. For example, if some elementary
object appearing in a byuon interaction has, with the
probability near 1, the vacuum state I+ of a byuon com-
pleting formation of its quantum numbers (the greatest
period of byuon interaction of the order of kN), such an
elementary object will be stable as well as its properties
will, since quite a definite amount of information will be
locked up by VS I+. This relates, for example, to the
electron.
Thus, as opposed to gauge models in which the level
of symmetry constantly grows for more complete, all-
embracing, and unified description of the surrounding
world [23-28], and to obtain massive particles it is nec-
essary to use “by hands” the Higgs mechanism (spontan
violation of symmetry), in the present model there exists
first a one-dimensional world (its direction, i.e. that of Ag,
is determined by the byuon with the maximum x(i)), then
its symmetrization takes place, and the space R3, with the
world of elementary particles originates. At that some
insignificant (~1/k (~10-15)) asymmetry of “empty” R3
remain as well as that of the 10-5 order inside the ele-
mentary particles.
It should be also noted that to calculate the funda-
mental constants h, e0, c; constants of known interactions,
masses of main baryons, leptons, and mesons according
to formulae (11e), only three numberso
x


0, |Ag| should
be given since the characteristic dimensions o
x
  10-17
cm, ct*  10-13 cm and 1028 cm are found from the mini-
mum PE of byuons and from the information theorem.
Notice that in [20-22,24,25,31-38], results of some
fundamental experiments in support of the basic theo-
retical statements have been described