J. Mod. Phys., 2010, 1, 1-8
doi:10.4236/jmp.2010.11001 Published Online April 2010 (http://www.scirp.org/journal/jmp)
Plastic Flow Macrolocalization: Autowave and
Quasi-Particle
Lev B. Zuev, Svetlana A. Barannikova
Institute of Strength Physics and Materials Science, Tomsk, Russia
Received March 2, 2010; revised March 26, 2010; accepted April 7, 2010
Abstract
A new approach is proposed to describe the autowave processes responsible for plastic deformation localiza-
tion in metals and alloys. The existence of a quasi-particle, which corresponds to a localized plastic flow
autowave, is postulated and its characteristics are determined. The above postulate leads to a number of cor-
ollaries and quantitative assessments that are considered herein. The deformation processes occurring on the
macro- and micro-scale levels are found to be directly related.
Keywords: Localization, Plastic Deformation, Autowave, Quasi-Particle
1. Introduction
The experimental studies of plastic flow in solids carried
out during last decades [1,2] allow one to throw light
upon the plasticity phenomenon and to detect the most
important experimental fact that the plastic flow would
exhibit a localization behavior from yield point to failure.
Recently strong experimental evidences for the above
viewpoint were presented independently by several
workers [3-5]. In order to visualize the localization pat-
terns observed by mechanical testing, a technique of dou-
ble-exposure speckle-photography was developed [6].
Some of the observed localization patterns are demon-
strated in Figure 1(a). As is seen from Figure 1(b),
these have very complex structure characterized by a
typical macroscopic scale of about 10-2 m. This suggests
that the deforming medium becomes spontaneously
stratified into macroscopic layers, with deforming (active)
layers alternating with non-deforming (passive) ones. In
a general case, the boundaries between such layers are
mobile; therefore, the process of plastic flow is conven-
tionally considered as evolution of localized plastic flow
patterns.
The phenomenology and quantitative characteristics of
the localization effect have been fully elucidated by now.
Thus a detailed investigation of space-time periodic lo-
calization patterns [1,2] allows one to refer the localiza-
tion phenomenon to self-organization processes. The
above assumption is only valid provided the term ‘self-
organization’ is taken to imply, according to Haken [7],
that the system acquires spatial, temporal or functional
structure in the absence of any specific periodic external
action. Of major importance is the finding that the local-
ized plastic flow patterns have all the particular features
of autowave (self-excited) process. This comes into par-
ticular prominence at the linear stage of deformation
hardening as the plastic flow localization takes on the
form of phase autowave, which has length


10-2 m
and propagation rate 541
1010m s
aw
V




. The auto-
waves in question are distinct from the well-known plastic
deformation waves that are generated in solids under
shock loading which are described by Kolsky in [8].
However, the nature of localized plastic flow phe-
nomena is poorly understood so that the challenge of
interpreting rich experimental evidences on plastic flow
macrolocalization can be daunting. To accomplish this
demanding task, a new model of plastic flow localization
is proposed herein.
2. On the Observation of Localization
Phenomena
As noted above, the experimental observation of local-
ized plastic flow autowaves was carried on with help of a
specially developed speckle photography technique re-
lated to focused-image holography [6]. The method de-
veloped makes feasible the experimental determination
of displacement vector fields and the calculation of plas-
tic distortion tensor components for the deforming
specimen. A vast array of wavelength and propagation
rate data has been acquired and stored digitally in a
computer.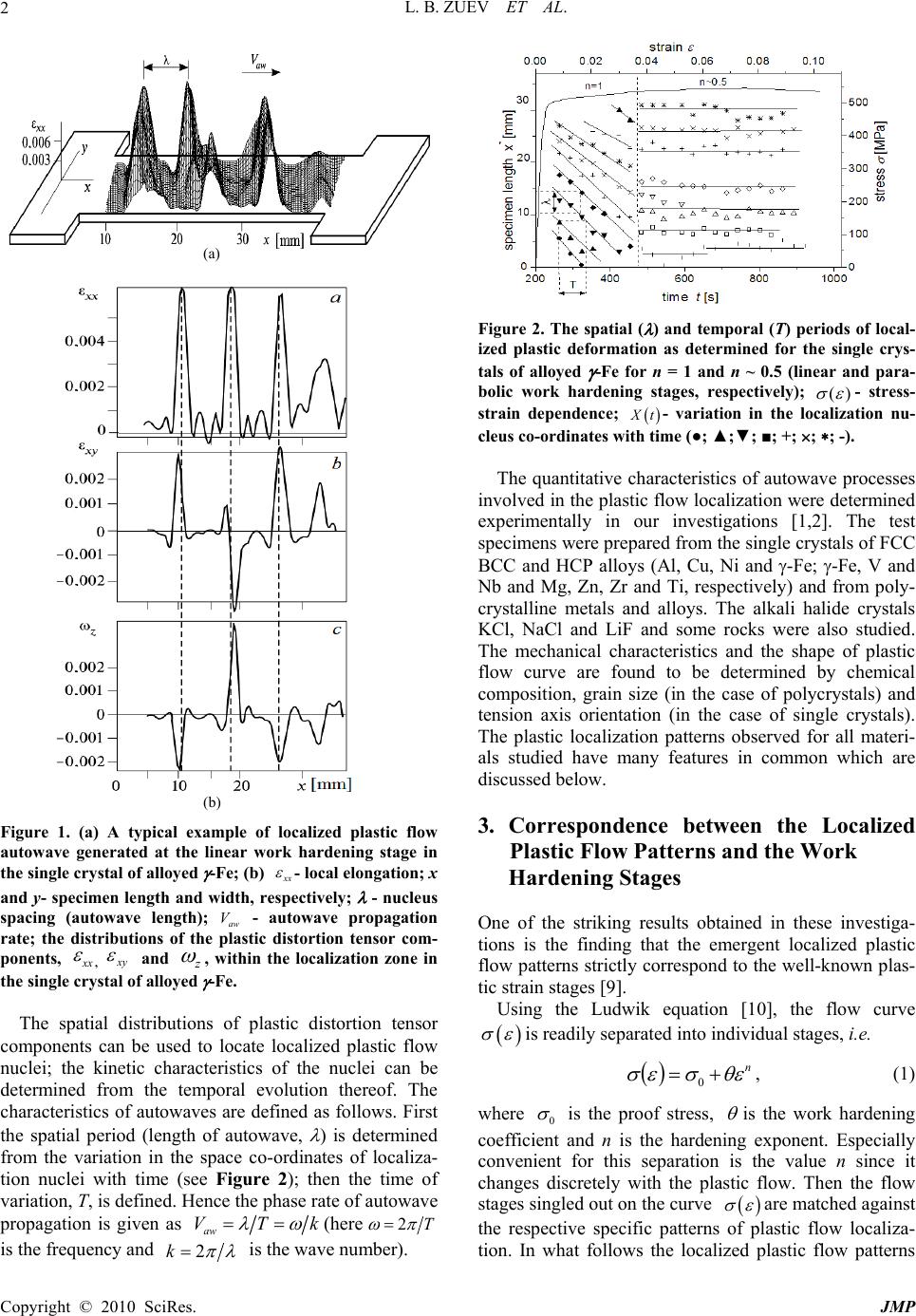

L. B. ZUEV ET AL. 2
Figure 1. (a) A typical example of localized plastic flow
autowave generated at the linear work hardening stage in
the single crystal of alloyed  -Fe; (b) xx

- local elongation; x
and y- specimen length and width, respectively;  - nucleus
spacing (autowave length); aw V - autowave propagation
rate; the distributions of the plastic distortion tensor com-
ponents,
x
x

, xy

and
z

, within the localization zone in
the single crystal of alloyed  -Fe.
The spatial distributions of plastic distortion tensor
components can be used to locate localized plastic flow
nuclei; the kinetic characteristics of the nuclei can be
determined from the temporal evolution thereof. The
characteristics of autowaves are defined as follows. First
the spatial period (length of autowave,
 ) is determined
from the variation in the space co-ordinates of localiza-
tion nuclei with time (see Figure 2); then the time of
variation, Т, is defined. Hence the phase rate of autowave
propagation is given as aw VTk

 (here T


2

is the frequency and


2
k
is the wave number).
Figure 2. The spatial (  ) and temporal (T) periods of local-
ized plastic deformation as determined for the single crys-
tals of alloyed  -Fe for n = 1 and n ~ 0.5 (linear and para-
bolic work hardening stages, respectively); )(


- stress-
strain dependence;


Xt- variation in the localization nu-
cleus co-ordinates with time (●; ▲;▼; ■; +; ; ; -).
The quantitative characteristics of autowave processes
involved in the plastic flow localization were determined
experimentally in our investigations [1,2]. The test
specimens were prepared from the single crystals of FCC
BCC and HCP alloys (Al, Cu, Ni and -Fe; -Fe, V and
Nb and Mg, Zn, Zr and Ti, respectively) and from poly-
crystalline metals and alloys. The alkali halide crystals
KCl, NaCl and LiF and some rocks were also studied.
The mechanical characteristics and the shape of plastic
flow curve are found to be determined by chemical
composition, grain size (in the case of polycrystals) and
tension axis orientation (in the case of single crystals).
The plastic localization patterns observed for all materi-
als studied have many features in common which are
discussed below.
3. Correspondence between the Localized
Plastic Flow Patterns and the Work
Hardening Stages
One of the striking results obtained in these investiga-
tions is the finding that the emergent localized plastic
flow patterns strictly correspond to the well-known plas-
tic strain stages [9].
Using the Ludwik equation [10], the flow curve




is readily separated into individual stages, i.e.


n
  0, (1)
where 0

is the proof stress,  is the work hardening
coefficient and n is the hardening exponent. Especially
convenient for this separation is the value n since it
changes discretely with the plastic flow. Then the flow
stages singled out on the curve


 are matched against
the respective specific patterns of plastic flow localiza-
tion. In what follows the localized plastic flow patterns
(a)
(b)

L. B. ZUEV ET AL. 3
are discussed in the order of their emergence.
The first to appear is a solitary front of localized plas-
tic flow, which travels along the specimen elongation
axis at the yield plateau in the polycrystals (n = 0) or at
the easy glide in the single crystals (n  0). In this case,
an elastic-plastic transition takes place. The motion of
such a front can be regarded as switching autowave [11].
The next pattern is a mobile set of parallel fronts sepa-
rated by distance
 , which is observed at the linear work
hardening stage in the single-crystal and polycrystalline
specimens (n = 1;


~
). In accordance with [8], the
latter pattern corresponds to a typical phase autowave
having length
 and propagation rate aw
V. The third in
the order of appearance is a group of immobile equidis-
tant localized plasticity nuclei, which occurs at the para-
bolic work hardening (Tailor’s) stage (n = ½; 21
~ 
) in
most materials [9]. This pattern might be considered a
stationary dissipative structure [11]. The autowave pat-
tern emergent at the pre-failure stage (0 n½) is spe-
cifically associated with ‘collapse’ of the autowave [12]
which takes place concurrently with the onset of
macro-necking. The final stage of the plastic flow proc-
ess (n0) is ductile failure of material. The above phe-
nomena would emerge spontaneously in the specimen
under constant-rate tensile loading. Following Seeger
and Frank [13], we regard these phenomena as processes
of structure formation.
On the base of conclusive evidence obtained for a
wide range of materials the following Rule of Corre-
spondence is introduced: in accordance with the acting
work hardening law,



, each plastic flow stage in-
volves a special kind of autowave process. The rule for-
mulated above applies to all the plastic flow phenomena
having a characteristic macro-scale of about 10-2 m.
However, the work hardening law governs the mecha-
nisms involved in the interaction of lattice defects [6].
Therefore, the said rule apparently applies to the defect
subsystem of the deforming crystal [9]. For this reason,
the plastic flow is expected to manifest certain micro-
scopic features that are indications of microscopic effects.
In our opinion, three such manifestations merit special
note. These are considered below.
4. On the Manifestations of Microscopic
Effects
4.1. Elastic and Plastic Deformation Invariant
On the base of experimental data a significant regularity
is established for the autowave process of plastic flow
localization in a range of metals. Thus a close correla-
tion is found to exist between the product of the macro-
scopic parameters of the autowave process, aw
V


, and
the product of the microscopic (lattice) parameters of
material, 

Vd. Here d is the spacing between the
close-packed planes of the lattice and 
Vis the trans-
verse elastic wave rate. The numerical data obtained for
studied metals is listed in Table 1. Matching of this data
suggests that the following equality is good within an
acceptable range of accuracy
12 32
aw i
VdVrV




 (2)
Indeed, a numerical analysis shows that 3i
dr

(here
i
r is the Pauling ion radius [14]). Equation (2) is vali-
dated by the fact that the average ratio 2aw
VdV




1.04  0.52 obtained for studied metals is about close
to unity and the dependence


aw
dV V 
 is a linear one
(see Figure 3).
Equation (2) is physically significant since it estab-
lishes a quantitative relationship between the micro-scale
(lattice) characteristics (d and  V) of elastic waves
which govern elastic deformation processes on the one
hand and the macro-scale characteristics (

and aw
V)
of localized plastic flow autowaves which are generated
Table 1. Matching of aw V


and dV

values calculated
from Equation (2).
aw
V 
·107d·1010 V·10-3 
Vd ·107
Metal
(m2s1) (m) (ms1) (m2s1) 


Vd
Vaw

2
Cu 3.60 2.08 2.30 4.78 1.50
Al 7.92 2.33 3.23 7.52 2.10
Zr 1.92 2.46 2.25 5.53 0.70
Ti 3.50 2.24 2.96 6.63 1.06
V 2.80 2.14 2.83 6.06 0.92
-Fe 2.55 2.07 3.32 6.87 0.74
-Fe 2.24 2.03 3.32 6.74 0.66
Ni 2.10 2.03 3.22 6.54 0.64
Figure 3. Verification of the validity of Equation (2) with help
of a linear dependence between the ratiosd

and aw
VV

;
■ – easy glide stage; ● – linear work hardening stage.

L. B. ZUEV ET AL. 4
in deforming media on the other hand. In this case, it
might be reasonable to regard the products

Vd and
aw
V 
as invariants of elastic and plastic deformation
processes, respectively. The above regularity suggests
that the elastic and the plastic processes simultaneously
involved in the deformation (
1

 and 1

, respec-
tively) are closely related. The quantity V is the rate of
elastic stress redistribution in the deforming solid and the
quantity aw
Vis the rate of localized plasticity front rear-
rangement in the same solid. Thus, the macro-scale local-
ization of plastic deformation can no longer be regarded as
a mere disturbance of plastic flow homogeneity by neck-
ing. What is more, the localization phenomena are taken to
be an attribute of the plastic deformation, with their char-
acteristics being closely associated with and largely de-
termined by the properties of crystal lattice.
4.2. Autowave Characteristics and the Planck
Constant
A numerical analysis suggests that for all metals and
alloys studied the following equality holds good:
hrV iaw 3 
, (3)
where
 is material density. In other words, the quantum
(Planck’s) constant h can be calculated by multiplying
the values aw
Vand which are localized plastic flow
characteristics measured experimentally by the values
and i
r
which are hand-book material constants. Indeed,
the calculated values h listed in Table 2 are close to the
Planck constant h = 6.626  10-34 Js, with the average
value h being (6.44  0.88)  10-34 Js and the ratio
hh 0.96  0.07 being close to unity. Thus the Planck
constant can be estimated directly from the macro-scale
characteristics aw V and  , which appears striking in
itself.
4.3. Form of Dispersion Relation
Let us consider the following quadratic dispersion law
[15]


2
00 kk 

, (4)
where
 , 0

and
0
k are empirical constants. The val-
ues of these constants were derived for localized plastic
flow autowaves from the experimental data in Figure 4.
Note that the value  can be both negative and positive,
i.e. for the easy glide stage,  and for the linear work
hardening stage,  . Equation (4) is readily reduced to
the canonic form 2 1k



 by substituting 0




and
0
0sign
~
 
 k kk (here

~
and k
~
are the di-
mensionless frequency and the wave number, respec-
tively, and the signum function of
 is 1
sign 1 







for 0
for 0




). Wave processes that have quadratic dis-
persion law of the latter form would generally satisfy a
number of nonlinear equations, e.g. the Schrödinger
nonlinear equation, the sine-Gordon equation, etc., which
are frequently employed to address self-organization
processes occurring in nonlinear media [16]. Therefore,
the dispersion relation (4) is taken to be an additional
proof for plastic flow localization being involved in the
self-organization of the deforming medium. Moreover,
Equation (4) turned out to be formally equivalent to the
de Broglie wave dispersion law for electrons in sharp-
cornered potential well [17], which is significant in itself.
5. A Postulate of Plastic Flow Localization
and the Ensuing Corollaries: Introduction
of a New Quasi-particle
Taken as a whole the above localization patterns demon-
strate that the phenomenon in question has not only
macroscopic characteristics of autowave process (  and
aw
V
) but also microscopic ones (h and d or i
r
). In view
of the ratio i
r

being about equal to 108, the key
problem in this case is how the macro- and micro-scales
could be reconciled. To overcome this problem, we pro-
pose to use an approach based on the wave-particle dual-
ism, which received wide application in the physics of
solids [18]. We are led to postulate the existence of aq-
uasi-particle having effective mass,ef m, quasimomentum,
p, and energy, E, which corresponds to the autowave of
localized plastic deformation having wavelength,  and
Figure 4. The dispersion law

k

established for local-
ized plastic flow autowaves generated at the stages of easy
glide (1) and linear work hardening (2); ● – single crystals
of Cu, Sn and alloyed  -Fe; ■ – single crystals of alloyed
 -Fe; ▲- polycrystalline Al.

L. B. ZUEV ET AL. 5
Table 2. Microscopic characteristics and the Planck constant values calculated from the data on localized plastic flow
autowaves.
 ·103
5
10
aw
V
ef
m 27
10

9
10

d
9
10
ion
r
h1034
Metal
(m) (ms1) (a.m.u)
2
10 
n
(m3) (m) (m)
ion
rd
(J·s)
Cu 4.5 8.0 1.1 1.74 1 0.21 0.059 0.072 0.82 8.14
Al 7.2 11 0.50 1.87 3 0.31 0.068 0.051 1.33 5.0
Zr 5.5 3.5 2.05 2.24 4 0.53 0.081 0.079 1.03 6.13
Ti 7.0 5.0 1.1 2.3 4 4.2 0.075 0.076 0.99 6.91
V 4.0 7.0 1.42 2.81 5 0.33 0.069 0.059 1.17 6.52
-Fe 5.0 5.1 1.76 2.81 8 0.33 0.069 0.064 1.08 6.32
-Fe 4.3 5.2 1.77 3.0 8 3.75 0.072 0.064 1.13 6.32
Ni 3.5 6.0 0.89 3.24 100.32 0.068 0.069 0.99 6.17
propagation velocity, aw V. Then it can be written that
awefVhm

. (5)
Equality (5) is a mathematical expression of the above
postulate to which we conventionally add the equa-
tions ef aw
p
mV k andE


 (here

2h) for
momentum and energy, respectively [19,20]. It is com-
mon knowledge that to validate a postulate, one has to
match the corollaries ensuing from the same against ex-
perimental evidence. It turns out that a set of corollaries
ensues from the above postulate which give an insight
into the nature of localized plastic flow processes. These
corollaries are considered below.
Corollary 1. First we will demonstrate that the effec-
tive mass, mef, calculated from Equation (5) has a physi-
cal meaning; this quantity depends on the characteristics
of the deforming crystal. Indeed, the calculated values
listed in Table 2 for a number of metals are in the range
0.5 ef m 2 a.m.u. (here 1 a.m.u. = 1.6610-27 kg is
atomic mass unit). Evidently, the volume is readily cal-
culated as

ef
m ; then the length is found
as 3

d. The latter value is close to the valuei
r, i.e.
i
r
d

, with the average ratio being i
r
d= 1.07 
0.091. Thus, the effective mass, mef, turns out to be re-
lated to the lattice characteristics, ρ and i r.
Apparently, the values mef calculated from Equation (5)
differ slightly for each particular metal. The normaliza-
tion of effective masses, mef, to the atomic masses, m A,
of respective metals yields normalized (dimensionless)
mass 1 mef
A
m

, which increases linearly with the
number of electrons per unit cell, n (see Figure 5) [21],
i.e.
n



0. (6)
The correlation coefficient for  and n values is ~0.95;
it has a high statistical significance.
Now we propose a physical interpretation of Equation
(6) which is based on the consideration of jump-like dis-
location motion. Thus a dislocation would become ar-
Figure 5. The dimensionless parameter, as a function of the
number of electrons per unit cell, n.
rested at a local barrier until the thermal fluctuation
causes its breakaway, which suggests that the plastic
deformation results from the dislocation motion in a vis-
cous medium [22]. For di sl Vconst, the motion of dis-
locations is controlled by viscous drag force per unit
length, dis
l
v
B
V
F

(here B is the viscous drag factor for
dislocations) [22]. For disl
V const, an inertial term
proportional to the dislocation acceleration, disl V
, is
added to the viscous drag force [23]. Then the total drag
force, 
F, is given by

vin disladisl
F
FF BVBV 


 
, (7)
where a

is the frequency of an elementary deforma-
tion act and B

apparently has the meaning of added
mass per unit length of dislocation.
In the case of metals, the factor B is determined by the
interaction of dislocations with phonon and electron
gases [22]; moreover, the contributions of phonon and
electron gases, i.e.
p
h
B ande B, respectively, are addi-
tive so that eph
B
B
B


. In this case, the first and the
second term in the right-hand side of Equation (6) are
evidently connected with the contributions to the added
mass, B

, of the viscous drag of both gases.

L. B. ZUEV ET AL. 6
The term 0

from (6) is apparently independent of
the kind of metal, which is reasonable since the proper-
ties of metal are only weakly dependent on the charac-
teristics of its phonon spectrum at temperatures exceed-
ing the Debye temperature [21]. However, the contribu-
tion of electron gas to the added mass should be propor-
tional to n, i.e. ~
e
Bn [22]. Hence it can be written





dis
l
dislephdislephin VnVmmVBBF  

0
~~~ (8)
Thus Equation (8) relates the normalized mass,
 , to
the contributions of phonon and electron gases.
Corollary 2. Equation (5) can be rewritten as


 

 3
ief
aw r
h
m
h
V. (9)
The quantity

from (9) is calculated as 3
i
hr

 .
Then the calculated values,

, are matched with the
experimental aw
V 
data. The average values obtained for
the single  -Fe crystals and polycrystalline Al are, re-
spectively, aw V  = (2.86  0.44) 107 m
2·s-1 (

= 3.2 
107 m
2·s-1) and aw
V 
= (7.75  1.36)107 m
2·s-1 (

=
18.4107 m2·s-1).
Corollary 3. Equation (5) can be also rewritten as
k
r
h
m
h
V
ief
aw 






 2
1 . (10)
It is shown above that dkdVV graw

 and
 dkkd 



2. Hence we can write



0
00
2
kk
dkkd





. (11)
It follows from (11) that dispersion relation of quad-
ratic form can be written for localized plastic flow
autowaves, i.e.




2
00
2
00 4kkkk




.
Apparently, the latter relation corresponds to (4). The
coefficient  from the dispersion relation of quadratic
form can be found by matching the experimental

 k

data against the calculated values



4 obtained
for Fe and Al. Thus the experimental values  obtained
for Fe and Al are 5.4108 m
2·s-1 and 7.9107 m 2·s-1, re-
spectively, and the calculated data are 2.5108 m2·s-1 and
1.46107 m
2·s-1, respectively. Both sets of data have
practically the same order of magnitude.
Corollary 4. It follows from Equation (5) that
3
iaw rhV 

. (12)
The terms in both sides of (12) evidently have the
units of dynamic viscosity, i.e. kgm1s1  Pas. The
calculated value


 aw V is about equal to 5104 Pas
for all studied metals. Hence the latter quantity can be
identified with the viscosity of phonon gas, B, which
controls dislocation mobility by quasi-viscous motion
[22]. This is good indirect evidence for the validity of the
same quantity, in particular, by interpreting the physical
meaning of dependence (6).
Corollary 5. The dispersion relation obtained for lo-
calized plastic deformation autowaves can be rewritten in
the form appropriate for quasi-particles, i.e.


EEp




2
00
Epp 


(here
0
E, 0
p and

 are constants).
Then the effective mass of the hypothetical quasi-particle
is estimated [17] as


1
22
1
22 

 kpEmef  . (13)
The experimental and calculated effective masses ob-
tained for iron and aluminum are 0.6 and 0.1 a.m.u., re-
spectively. This lends credence to the existence of the
hypothetical quasi-particle having ef
m1 a.m.u.
Corollary 6. As is seen from Figure 4, the oscillation
spectrum


2
00
kk    has a narrow gap in the
range 0
0



10-2 Hz. Hence for any temperature,
0B
kT


 (here B k is the Boltzmann constant). Lo-
calization phenomena are liable to occur spontaneously
at any temperature provided geometric constraints place
no restrictions, in particular, in the case of small-sized
specimens [1].
Corollary 7. Finally, the jump-like plastic deformation
in solids [24] can be explained with help of the above
postulate. Let us rewrite Equation (5) as

1
iaw
Lh rV 

. (14)
Now suppose that the specimen length L accommo-
dates an integer m = 1, 2, 3… of autowaves having
length  , i.e. Lm


, which precludes the occurrence
of deformation within the clamps of the testing machine.
With growing total deformation,  , the elongation of the
specimen occurs as

00
1LLLL

  (here 0 L
is the original specimen length). Hence from (14) follows
that

1
iaw
Lh rVm 


. (15)
For the linear work hardening stage, aw
Vconst

.
From (15) apparently follows that the specimen length
would vary discretely (~Lm

) in accord with the
jump-wise deformation behavior, i.e. the specimen
length would be accommodated to the emergent auto-
wave pattern. Deformation jumps may occur by different
mechanisms depending on the kind of material so that
Equation (15) only states that this kind of deformation
behavior is a must.
From (15) follows that 1
~aw LV

. The available ex-
perimental evidence [1] suggests that the autowave

L. B. ZUEV ET AL. 7
propagation rate is proportional to the cross-head motion
velocity, i.e. ~
aw mach
VV
. With increasing velocity of the
movable clamp of the test machine, the amplitude of
jumps is expected to grow less. The latter inference is
supported by the experimental data obtained for Al at 1.4
K [24].
Corollary 8. Now it transpires that Equation (3) of the
form 3
aw i
Vrh


is readily derived from the same
postulate provided 3
ef i
mr

.
6. Conclusions
It is pertinent to mention here the early efforts to apply
quantum ideas to problems of strength and plasticity
physics. Thus Steverding was the first to introduce the
notion of elastic waves quantization by fracture [25]. By
addressing the kinetics of brittle fracture, the existence of
a quasi-particle in the deforming medium was postulated.
The quasi-particle was identified with the tip of a grow-
ing crack; therefore, it got the name ‘crackon’ [26].
Quantum models were applied to explain the tunnel ef-
fect observed by dislocation motion [27,28]. On the other
hand, recent theoretical and experimental studies indicate
that the plastic flow involves wave processes [1-5,7,29,
30].
The above findings justify the use of quantum con-
cepts to address plastic flow development in solids. In
this approach one has to reconcile micro- and macro-
scale manifestations of the localization phenomenon;
therefore, physicists dealing with plasticity problems
might consider it invalid. When the micro-scale (disloca-
tion) level is addressed, the quantization idea appears
quite appropriate. In view of crystal lattice discreteness,
the minimal possible shear is by the Burgers vector, b,
which has microscopic scale d of about 10-10 m and
hence might be regarded as a ‘quantum of shear defor-
mation’. Hence the use of (2) allows the quantization
concept to be extended to the macro-scale level, i.e.
aw
V

12dV

.
The fact that the Planck constant value calculated from
the data derived in rather ‘rough’ macro-experiments is
close to a handbook value might be due to the manifesta-
tion of so-called ‘universality concept’ [31], which pos-
tulates that the system’s measurables are virtually unaf-
fected by the distribution of its major microscopic prop-
erties. In other words, both the qualitative and the quan-
titative characteristics of material substructure are only
partly responsible for, e.g. plastic flow evolution, flow
stress level, work hardening coefficient, etc.
The corollaries ensuing from the postulate proposed
herein have proven to be very fruitful to study deforma-
tion localization processes, which validates the concept
of wave-particle duality. By way of summary it should
be emphasized that the macro-scale effects (characteris-
tic scale macro


L) emerging in a plastically deforming
multi-scale system are found to be directly related to the
micro-scale effects (characteristic scale micro i
r

L), with
the scale ratio being
8
10
macro microi
r

LL .
The above gives justification to the use of a common
approach, i.e. postulation of a quasi-particle correspond-
ing to a localized plastic flow autowave. This turns out to
be a fruitful effort by explaining a number of relation-
ships in plasticity physics, which have remained poorly
understood in the frame of traditional models of crystal
plasticity. The postulated quasi-particle would be named
“auto-localizon”.
As far back as the 1960-ies Dzyaloshinski [32] was the
first to discuss the possibility of measuring the Planck
constant in mechanical experiments. In his paper this
worker emphasizes the importance of studying the mac-
roscopic manifestations of typical quantum effects, e.g.
superfluidity, superconductivity and the quantum Hall
effect discovered later on. In the light of the foregoing it
is maintained that the plastic flow in solids is analogous
to all these phenomena; therefore, this might also be re-
garded as a macroscopic quantum effect.
7. Acknowledgements
This work was partly supported by the grant of RFBR
(09-08-00213 -а).
8. References
[1] L. B. Zuev, “Wave Phenomena in Low-Rate Plastic Flow
of Solids,” Annals of Physics, Vol. 10, 2001, pp. 965-984.
[2] L. B. Zuev, “On the Waves of Plastic Flow Localization
in Pure Metals and Alloys,” Annals of Physics, Vol. 16,
2007, pp. 286-310.
[3] R. J. McDonald, C. Efstathiou and P. Curath, “The
Wave-Like Plastic Deformation of Single Crystals Cop-
per,” Journal of Engineering Materials and Technology,
Vol. 131, 2009, pp. 692-703.
[4] A. Asharia, A. Beaudoin and R. Miller, “New Perspec-
tives in Plasticity Theory: Dislocation Nucleation, Waves
and Partial Continuity of Plastic Strain Rate,” Mathemat-
ics and Mechanics of Solids, Vol. 13, 2008, pp. 292-315.
[5] C. Fressengeas, A. Beaudoin and D. Entemeyer, “Dislo-
cation Transport and Intermittency in the Plasticity of
Crystalline Solids,” Physical Review B, Vol. 79, 2009, pp.
014108-1-014108-9.
[6] L. B. Zuev, V. V. Gorbatenko and S. N. Polyakov, “In-
strumentation for Speckle Interferometry and Techniques
for Investigating Deformation and Fracture,” Proceedings
of SPIE, Vol. 4900, Part 2, 2002, pp. 1197-1208.
[7] H. Haken, “Information and Self-Organization,” A Mac-
roscopic Approach to Complex Systems, Springer Verlag,
Berlin, 1989.
[8] H. Kolsky, “Stress Waves in Solid,” Phoenix Education,

L. B. ZUEV ET AL. 8
Dover, 2003.
[9] F. R. N. Nabarro, Z. S. Basinski and D. B. Holt, “The
Plasticity of Single Crystals,” Tailor and Francis Ltd,
London, 1964.
[10] R. Hill, “The Mathematical Theory of Plasticity,” Uni-
versity Press, Oxford, 1998.
[11] V. A. Davydov, V. S. Zykov and A. S. Michailov,
“Kinematics of Autowave Structures in the Excited Me-
dia,” Physics-Uspekhi, Vol. 161, 1999, pp. 45-85.
[12] B. B. Kadomtsev, “Dynamics and Information,” Physics-
Uspekhi, Vol. 164, 1994, pp. 449-530.
[13] A. Seeger and W. Frank, “Structure Formation by Dissi-
pative Processes in Crystals with High Defect Densities,”
In L. P. Kubin and G. Martin Eds., “Non-Linear Phe-
nomena in Material Science,” Trans Tech Publications,
New York, 1987, pp. 125-137.
[14] L. Pauling, “The Nature of the Chemical Bond,” Cornell
University Press, Ithaca, 1960.
[15] S. A. Barannikova, “Dispersion of the Plastic Strain Lo-
calization Waves,” Technical Physics Letters, Vol. 30,
2004, pp. 338-340.
[16] A. Scott, “Nonlinear Science,” Emergence and Dynamics
of Coherent Structures, University Press, Oxford, 2003.
[17] L. D. Landau and E. M. Lifschitz, “Quantum Mechanics:
Non-Relativistic Theory,” Course of Theoretical Physics,
Pergamon, London, 1977.
[18] J. M. Ziman, “Electrons and Phonons,” University Press,
Oxford, 2001.
[19] J. P. Billingsley, “The Possible Influence of the De
Broglie Momentum-Wavelength Relation on Plastic
Strain ‘Autowave’ Phenomena in ‘Active Materials’,”
International Journal of Solids and Structures, Vol. 38,
2001, pp. 4221-4234.
[20] L. B. Zuev, “The Linear Work Hardening Stage and De
Broglie Equation for Autowaves of Localized Plasticity,”
International Journal of Solids and Structures, Vol. 42,
2005, pp. 943-949.
[21] A. P. Cracknell and K. C. Wong, “The Fermi Surface. Its
Concept, Determination and Use in the Physics of Met-
als,” Clarendon Press, Oxford, 1973.
[22] V. I. Al’shits and V. L. Indenbom, “Mechanisms of Dis-
locations Drag,” In F. R. N. Nabarro Ed., Dislocations in
Solids, Amsterdam, 1986, pp. 43-111.
[23] L. D. Landau and E. M. Lifshits, “Hydrodynamics,”
Nauka Publications, Moscow, 1988.
[24] V. V. Pustovalov, “Serrated Deformation of Metals and
Alloys at Low Temperatures,” Low Temperature Physics,
Vol. 34, 2008, pp. 683-723.
[25] B. Steverding, “Quantization of stress waves and Frac-
ture,” Materials Science and Engineering, Vol. 9, 1972,
pp. 185-189.
[26] E. M. Morozov, L. S. Polack and Ya. B. Fridman, “On
Variation Principles of Crack Development in Solids,”
Soviet Physics-Doklady, Vol. 156, 1964, pp. 537-540.
[27] T. Oku and J. M. Galligan, “Quantum Mechanical Tun-
neling of Dislocations,” Physical Review Letters, Vol. 22,
1969, pp. 596-597.
[28] B. V. Petukhov and V. L. Pokrovsky, “Quantum and
Classic Motion of Dislocations in the Potential Peierls
Relief,” Journal of Experimental and Theoretical Physics,
Vol. 63, 1972, pp. 634-647.
[29] E.C. Aifantis, “Nonlinearity, Periodicity and Patterning in
Plasticity and Fracture,” International Journal of Non-
Linear Mechanics, Vol. 31, 1996, pp. 797-809.
[30] E.C. Aifantis, “Gradient Plasticity,” In J. Lemaître, Ed.,
Handbook of Materials Behavior Models, Academic
Press, New York, 2001, pp. 291-307.
[31] Y. Imry, “Introduction to Mesoscopic Physics,” Univer-
sity Press, Oxford, 2002.
[32] L. P. Dzyaloshinski, “Macroscopic Quantum Phenom-
ena,” Soviet Physics-Uspekhi, Vol. 90, 1966, pp. 623-
629.